Visualizando dados - Gráficos básicos do R
Introdução
Nos capítulos passado aprendemos a usar as funções estatísticas para descrever um conjunto de dados, através de tabelas de frequência, a calcular os pontos centrais, as medidas de dispersão dos dados e a manipular um conjunto de dados através das funções filter() e select() do pacote dplyr. Essas medidas estatísticas servem para resumir um grande conjunto de dados com poucos números. Entretanto, essas medidas numéricas são bastante limitadas e tornam a apreciação dos conjunto de dados muito maçante e bastante técnica. Por outro lado, a análise visual dos dados, além de mais atrativa, é muitas vezes mais compreensiva. Na palavras de John Tukey:
“A grande virtude da representação gráfica é que ela serve para mostrar de forma clara e efetiva a mensagem por trás de quantidades cjuos cálculos ou observações estão longe de serem simples”
“One great virtue of good graphical representation is that it can serve to display clearly and effectively a message carried by quantities whose calculation is far from simple”
Nossa habilidade de pensar é grandemente aprimorada quando representamos quantidades numéricas de forma visual. Mas, apesar da criação de gráficos ser uma arte bem antiga, seu uso científico para representação de dados numéricos tem uma história relativamente recente. O uso de gráficos para apresentação de dados só se tornau uma prática comum depois dos trabalhos de William Playfair no final do século 19 e início do século 19 (Friendly & Denis, 2005; Fienberg, 1979).
Construir um gráfico nos séculos 18 e 19 era um árduo trabalho artístico e intelectual. Nos quase 200 anos desde que gráficos passaram a ser usados, sua construção deixou de ser uma tarefa de manual e se tornou um trabalho computacional. Com o advento das capacidades gráficas dos computadores, a partir do século 20, é que a criação dos mais variados tipos de gráficos estatísticos se tornou algo simples de ser realizado.
A linguagem R, desde seu início, foi criada com essa pretensão de ser uma linguagem estatística voltara para a construção de gráficos (Ihaka & Gentleman, 1996). Mas somente por volta de 2005 é que se tornou clara a noção do que é de fato um gráfico, como descrever um gráfico e como criar um gráfico. Foi com o trabalho entitulado “The grammar of graphics”, de Leland Wilkinson em 2005, que se tornou possível construir uma verdadeira linguagem computacional para os gráficos. E essa linguagem atingiu seu pleno potencial quando a gramática dos gráficos foi implementada no R com o pacote ggplot2, desenvolvido por Hadley Wickham em 2005 (Wickham, 2009).
Entretanto, essa aparente simplicidade pode ser enganosa. Numa pesquisa de 2012, foram detectados erros em 30% dos gráficos da revista Science, uma das mais prestigiadas revistas científicas do mundo (Cleveland, 2012). Atualmente, mais importante do que gerar um gráfico, é saber qual gráfico mais adequado usar e como interpretar corretamente as informações de um gráfico científico.
Objetivos de aprendizagem
Capacitar os alunos a criarem gráficos com as funções básicas do R. A criação de gráficos com o pacote ggplot será tema de outro capítulo.
Carregamento dos dados
Para facilitar essa aula, vamos usar o dataset mpg que já vem com o ggplot2.
A primeira etapa é instalar o pacote tidyverse, que contém o ggplot2. Se você já instalou esse pacote, passe para a próxima etapa. Lembre-se, que um pacote só precisa ser instalado uma única vez, se você já fez isso, não precisa fazer novamente.
A segunda etapa é carregar o pacote tidyverse na sessão. Isso é feito com o comando library(). O carregamento dos pacotes necesssários deve ser feito sempre no início de seu script.
1 > library(tidyverse)
A terceira etapa é carregar o dataset mpg. Para isso basta usar o comando abaixo:
1 > data(mpg)
Esse dataset já foi analisado numericamente nos capítulos passados, e possui 243 linhas (observações) com 11 variáveis. O significado de cada variável está descrito na documentação de ajuda do dataset mpg e pode ser visualizado com o comando ?mpg no console. A tabela abaixo mostra o significado de cada variável:
| variável | significado |
|---|---|
| manufacturer | marca |
| model | modelo |
| displ | cilindradas (Engine Displacement) |
| year | ano de fabricação |
| cyl | número de cilindros |
| trans | tipo de marcha: automática / manual |
| drv | tração: f=frontal, r=traseira, 4=4x4 |
| cty | milhas por galão na cidade |
| hwy | milhas por galão na estrada |
| fl | tipo de combustível: r=regular, p=premium, d=diesel, e=ethanol, c=CNG (gás) |
| class | tipo de carro: compact, midsize, suv, 2seater, minivan, pickup ou subcompact |
Parte 1 - Visualizando dados categóricos.
Variáveis categóricas podem ser representadas por gráficos de barras, gráficos de pizza.
Gráficos de Pizza - picharts
Gráfico de Pizza, também chamado de gráfico de torta ou de setor, é um diagrama circular fatiado como uma pizza, cujos valores de cada categoria são proporcionais à área de cada fatia. Ou seja, um gráfico de pizza é uma representação gráfica de uma tabela de frequências. Portanto, a criação da tabela de frequências deve sempre preceder a criação de um gráfico de pizza.
Mas é preciso ressaltar que gráficos de pizza tem um uso bastante restrito:
- São usados apenas para variáveis categóricas nominais, não são adequados para variáveis ordinais.
- São usados para explicitar a dominância de uma categoria sobre as outras
- Não servem para distinguir pequenas diferenças entre as categorias.
- Não são adequados para representar variáveis com mais de 5 níveis, pois o gráfico fica confuso.
Algumas dicas ajudam a criar gráficos de pizza adequados: jamais use efeitos de 3D em seus gráficos, nem mesmo nos gráficos de pizza; evita usar muitas cores, mas pode-se sar uma cor diferente para destacar o segmento de interesse.
O R tem uma função extremamente simples para criar gráficos de pizza: pie().
Vejamos como podemos usar um gráfico de pizza para representar o quanto é mais comum o uso de combustível regular pelos carros de nossa amostra:
1 # Criamos a tabela de frequencias com a função table
2 > tab.1 <- table(mpg$fl)
3
4 # geramos o gráfico com a tabela como argumento da função pie()
5 > pie(tab.1)
Ou simplesmente:
1 > pie(table(mpg$fl))
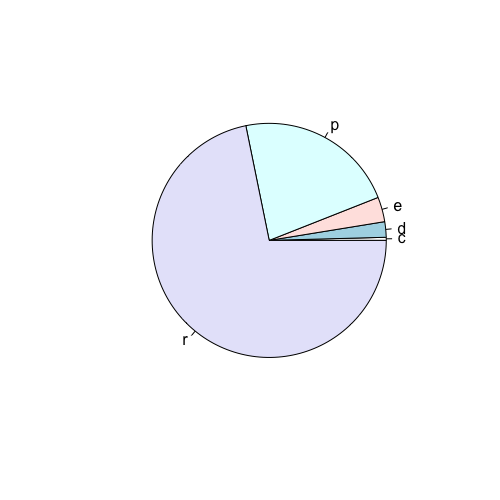
Um gráfico deve ter a função de simplificar a compreensão dos dados, portanto, é sempre adequado colocar títulos e legendas. Isso pode ser feito com os argumentos da função das funções gráficas no R.
main = "título"labels = c("nome do segmentos 1", "nome do segmento 2", ...)
1 > pie(table(mpg$fl),
2 main = "Combustíveis usados",
3 labels = c(c="Gás Veícular - CNG", d="diesel", e="etanol", p="premium", r="\
4 regular"))
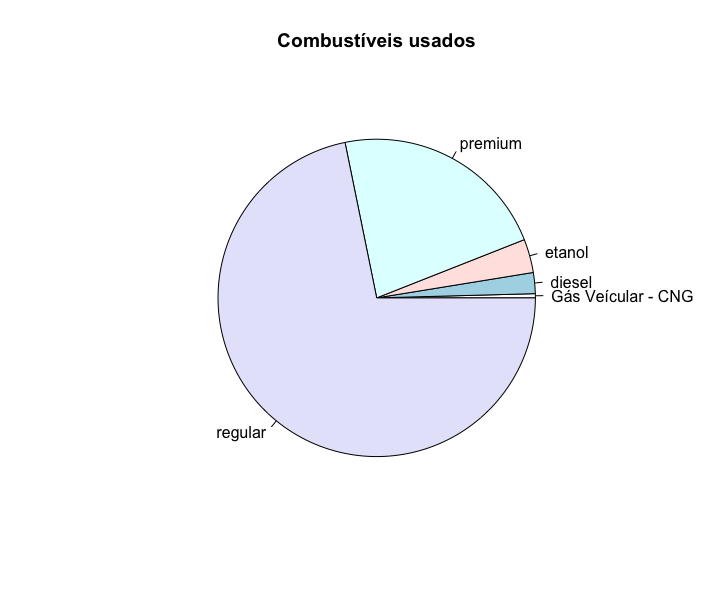
Se é do interesse do gráfico mostrar que a gasolina regular é mais frequentes que as outras, então podemos colorir de forma diferente o setor de interesse com o argumento col= c("cor do segmentos 1", "cor do segmento 2", ...).
1 > pie(table(mpg$fl),
2 main = "Combustíveis usados",
3 labels = c(c="gás Veícular - CNG", d="diesel", e="etanol", p="premium", r="\
4 regular"),
5 col = c(c="gray", d="gray", e="gray", p="gray", r="\
6 dodgerblue"))
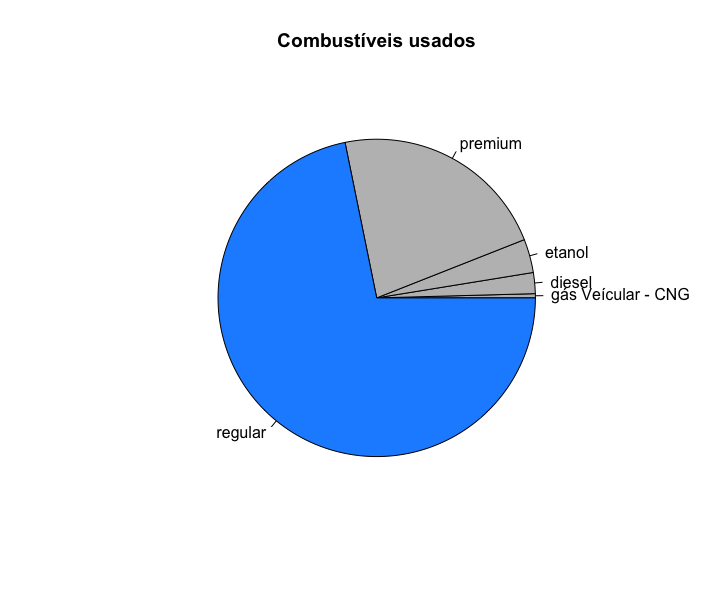
Finalmente, veja que num gráfico de pizza com muitos setores é difícil comparar as diferentes áreas, e portanto, o gráfico perde sua função de esclarecer os dados. Existem cerca de 7 diferentes tipos de carros nesse dataset, usar um gráfico de pizza para mostrar as frequencias de cada tipo não é uma boa idéia. Como você poderá ver, é muito difícil avaliar as diferentes áreas das fatias da pizza e portanto, não sabemos ao certo quais as frequencias dos carros: Existem mais pickups ou subcompactos ou midsizes?
1 > pie(table(mpg$class))
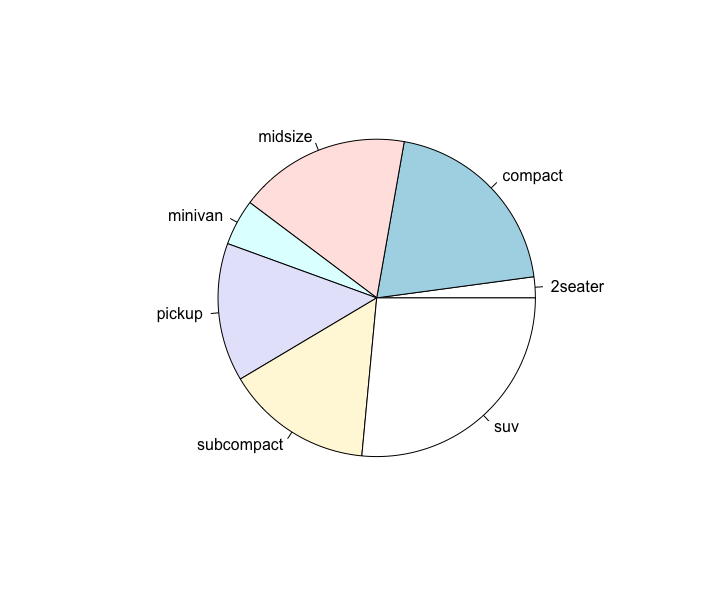
A forma mais adequada de representar as frequências de mais de 4 ou 5 categorias é através de um gráfico de barras, como veremos a seguir.
Gráficos de Barra - barplot
Um gráfico de barras é também uma representação gráfica de uma tabela de frequências. Portanto, a criação da tabela de frequências também deve sempre preceder a criação de um gráfico de barras. Num gráfico de barras o comprimento (ou área) das barras é proporcional aos valores que representam e podem ser desenhadas verticalmente ou horizontalmente.
Gráficos de barras tem uma utilização mais ampla, pois são fáceis de serem lidos, servem para representar frequências de variáveis categóricas nominais ou ordinais, são mais fáceis quando temos de comparar diferenças entre categorias, ainda que pequenas.
Algumas dicas ajudam a criar gráficos de barra adequados: jamais use efeitos de 3D em seus gráficos, evita usar muitas cores, mas pode-se usar uma cor diferente para destacar o segmento de interesse. Isso é mais útil do que colocar cada segmento com uma cor.
O R tem uma função extremamente simples para criar gráficos de barra: barplot().
Vejamos como podemos usar um gráfico de pizza para representar as frequências das categorias dos carros de nossa amostra:
1 > barplot(table(mpg$class))
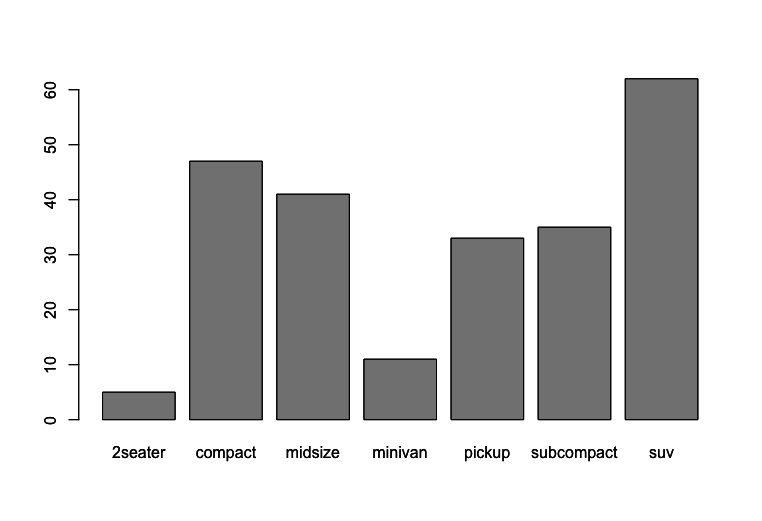
Assim como fizemos no gráfico de pizza, devemos também colocar o título, com o mesmo argumento que usamos anteriormente:main = "título".
Nos gráficos de barplot() podemos usar os argumentos xlab() e ylab() para nomear os eixos x e y do gráfico, como fizemos no gráfico a seguir. Podemos também reduzir o tamanho da fonte usada no eixo x com o argumento cex.names=, para que os nomes das categorias caibam embaixo das barras.
1 > barplot(table(mpg$class),
2 main = "Frequencia das categorias dos carros da amostra",
3 xlab = "Tipos de carros",
4 ylab = "Frequencia",
5 cex.names = 0.8)
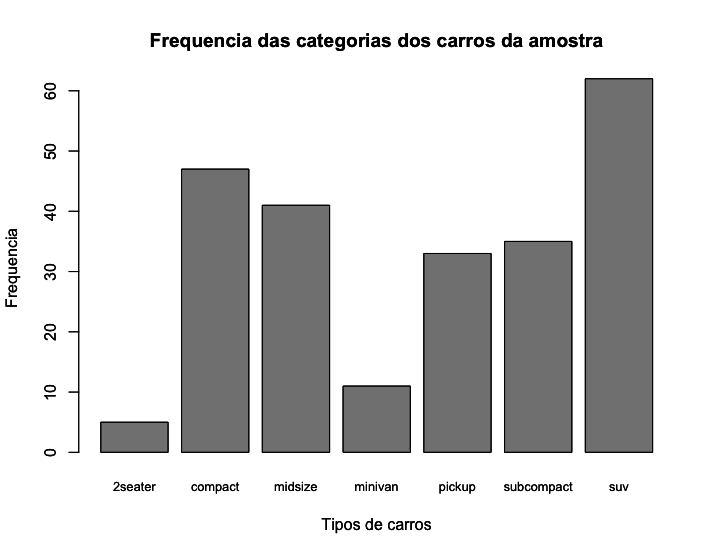
Podemos também colocar os nomes das categorias do eixo x na vertical, pois às vezes isso facilita a leitura dos nomes. Para fazer isso, basta inserir o argumento las=2 como fizemos abaixo. No caso abaixo, o texto do eixo x iria se sobrepor aos nomes dos tipos de carros, por isso deletei o argumento xlabs e coloquei o argumento sub = "subtítulo", pois o subtítulo fica um pouco mais abaixo na tabela e não se sobrepoe aos nomes das categorias.
1 > barplot(table(mpg$class),
2 main = "Frequencia das categorias dos carros da amostra",
3 sub = "Tipos de carros",
4 ylab = "Frequencia",
5 cex.names = 0.8,
6 las=2)
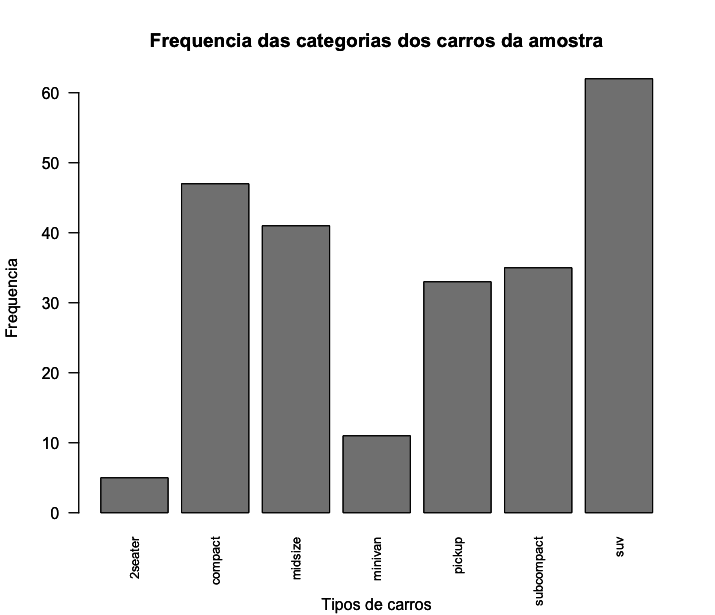
Muitas vezes é interessante, num gráfico de barras ordenar as barras de acordo com a frequência. Mas é preciso atentar para um ponto importante, isso só deve ser feito se a variável é nominal. No caso de variáveis ordinais, não devemos alterar a sequencia. Essa ordenação pode ser feita com a função sort() aplicada na tabela de frequencias criada antes de gerar o gráfico.
1 # criamos a tabela de frequências
2 > tabela_1 <- table(mpg$class)
3
4 # ordenamos a tabela criada acima
5 > tabela_ordenada <- sort(tabela_1)
6
7 # agora sim, plotamos a tabela ordenada
8 > barplot(tabela_ordenada, las=2)
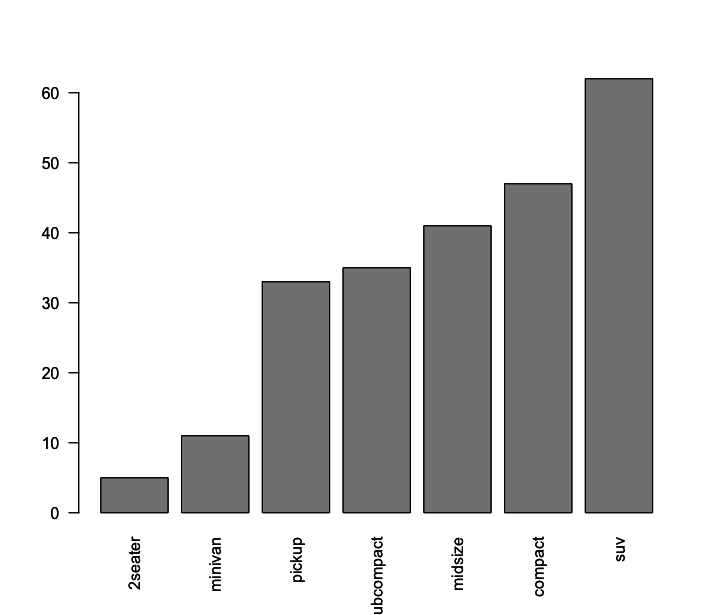
Podemos também ordenar de forma decrescente, para isso precisamos inserir o argumento decreasing=TRUE na função sort():
1 # criamos a tabela de frquencias
2 > tabela_1 <- table(mpg$class)
3
4 # ordenamos a tabela criada acima
5 > tabela_ordenada <- sort(tabela_1, decreasing = TRUE)
6
7 # agora sim, plotamos a tabela ordenada
8 > barplot(tabela_ordenada, las=2)
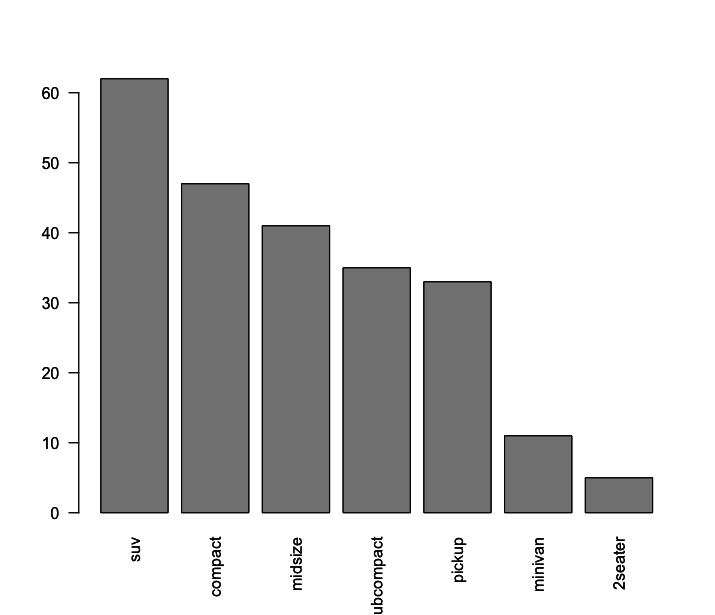
Podemos da mesma forma destacar a categoria de interesse modificando a cor conforme desejamos, com o argumento col=. Nesse exemplo aproveitei para mostrar como podemos colorir apenas a barra de nosso interesse e também mostrar como toda operação de criar a tabela de frequências e ordenar essa tabela pode ser colocado dentro da própria função barplot(), sem a necessidade de criar variáveis intermediárias.
1 > barplot(sort(table(mpg$class), decreasing = TRUE),
2 col = c("firebrick", "gray", "gray", "gray", "gray", "gray", "gray"),
3 las=2)
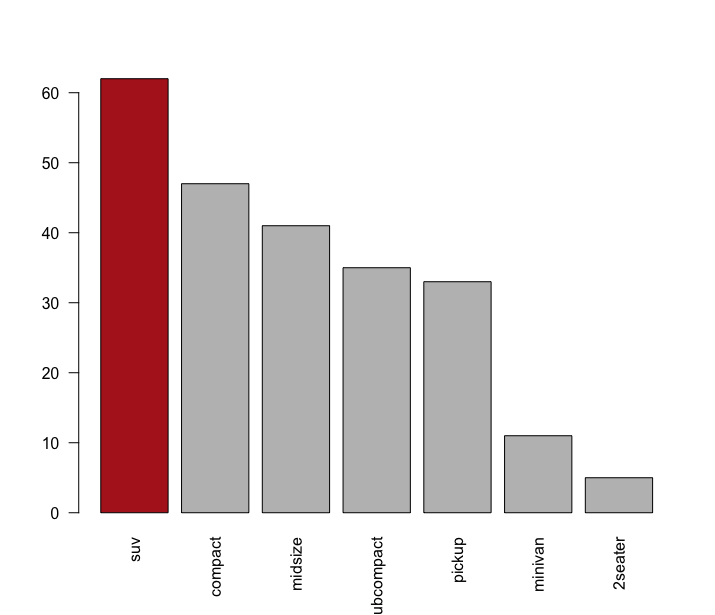
Podemos colocar as barras na horizontal com o argumento horiz=TRUE. No exemplo a seguir foi usado também o argumento las = 1 para colocar o nome de cada categoria de carros na horizontal.
1 > barplot(sort(table(mpg$class), decreasing = TRUE),
2 main = "Frequencia dos tipos de carros da amostra",
3 las = 1,
4 horiz=TRUE)
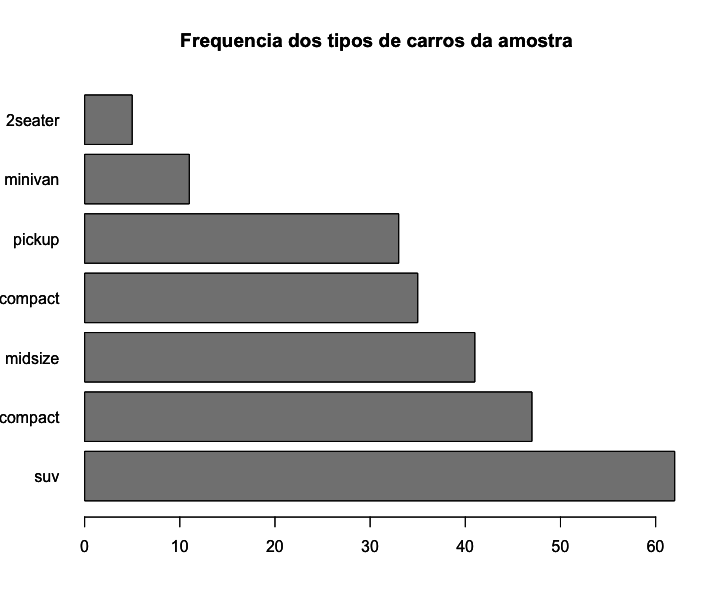
Finalmente, ao contrário de gráficos de pizza, num gráfico de barras podemos colocar muitas categorias. Veja como um gráfico de barras é bem mais adequado para representar variáveis com muitas categorias, tal como as montadoras dessa amostra (15 categorias).
1 # o comando par(mfrow=c(1,2)) indica que os dois gráficos devem ser plotados jun\
2 tos, numa mesma linha com duas colunas
3 > par(mfrow=c(1,2))
4
5 # cria o grafico de barras com as montadoras
6 > barplot(sort(table(mpg$manufacturer), decreasing = TRUE),
7 cex.names = 0.7,
8 horiz = TRUE,
9 las=1)
10
11 # cria o gráfico de pizza com as montadoras
12 > pie(table(mpg$manufacturer), cex=0.7)
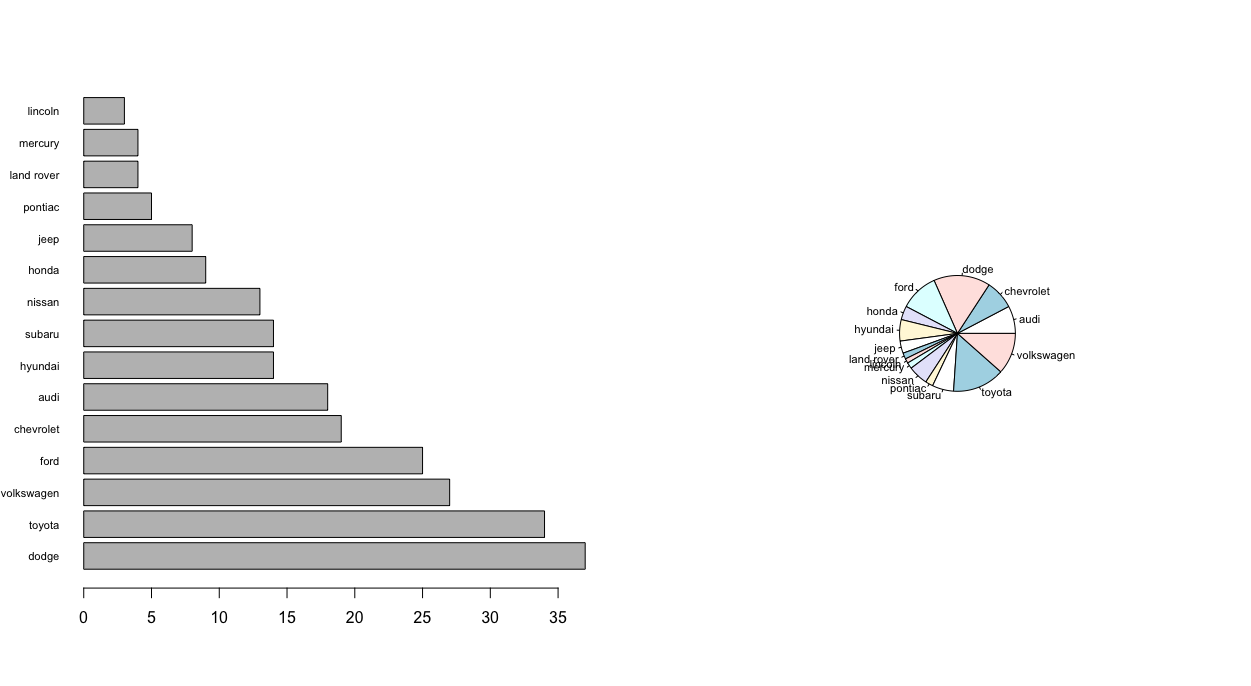
Parte 2 - Visualizando dados numéricos
Variáveis numéricas podem ter sua distribuição representada graficamente através de histogramas, gráficos de densidade de probabilidade e boxplots. Vamos ver cada um desses tipos de gráficos.
Histogramas
Um histograma é um gráfico de distribuição de frequências de dados numéricos (quantitativos). O objetivo de um histograma é resumir graficamente a distribuição de um conjunto de dados de uma única variável, permitindo visualizar o centro dessa distribuição, a moda, a dispersão dos dados, a presença de outliers e a forma da distribuição. A etapa mais importante na criação de um histograma é a divisão dos dados em classes, o que determina quantas colunas (bins) terá o histograma. Existem diversos modos de fazer esse cálculo, mas isso é totalmente dispensável com o R, pois o R faz isso automaticamente.
Apesar de se parecer um um gráfico de barras, um histograma é um gráfico totalmente diferente. Em primeiro lugar um gráfico de barras representa valores de variáveis categóricas enquanto um histograma representa a distribuição de valores de variáveis numéricas. Em segundo lugar, enquanto podemos reposicionar as barras num gráfico de barras, isso jamais pode ser feito num histograma, pois esse reposicionamento não faz sentido algum num conjunto numérico de dados. Para evitar que se confundam, um gráfico de barras deve sempre ter espaços entre as barras o que nunca deve acontecer num histograma. Assim, apenas pela a inspeção visual superficial, já podemos saber se o gráfico é um histograma ou um gráfico de barras.
Criar um histograma no R é extremamente fácil. Ao contrários dos gráficos de pizza e de barra, para criar um histograma no R não é necessário fazer nenhuma tabela de frequências, basta inserir o próprio vetor com os dados como argumento da função. A função para criar um histograma é hist().
No exemplo a seguir faremos um histograma dos dados numéricos do consumo dos carros na cidade (variável é cty).
1 > hist(mpg$cty)
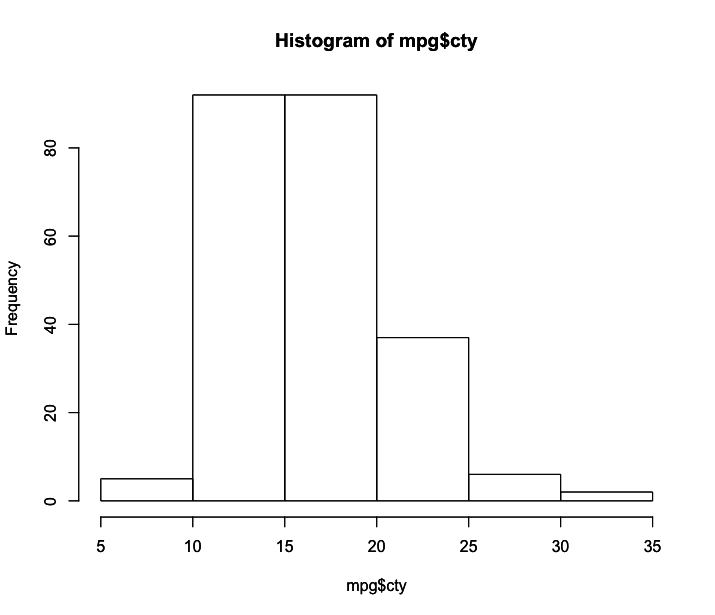
Veja que para construir o histograma tudo que fizemos foi inserir a variável cty como argumento da função hist(). O R calculou automaticamente a quantidade de colunas do histograma. Entretanto, podemos escolher manualmente quantas colunas desejamos, para que o gráfico se adeque melhor aos nossos interesses. Para isso basta alterar o argumento breaks, que define a quantidade de break points no gráfico. Você irá perceber que o número de colunas não corresponde exatamente ao número de break points, devido à maneira como R executa seu algoritmo para dividir os dados, mas o resultado é geralmente o que se pretende. Vamos testar refazer o histograma anterior indicando que desejamos 10 break points, e também colorindo as barras para melhorar o aspecto visual com o argumento col=.
1 > hist(mpg$cty, breaks = 10, col = "cornflowerblue")
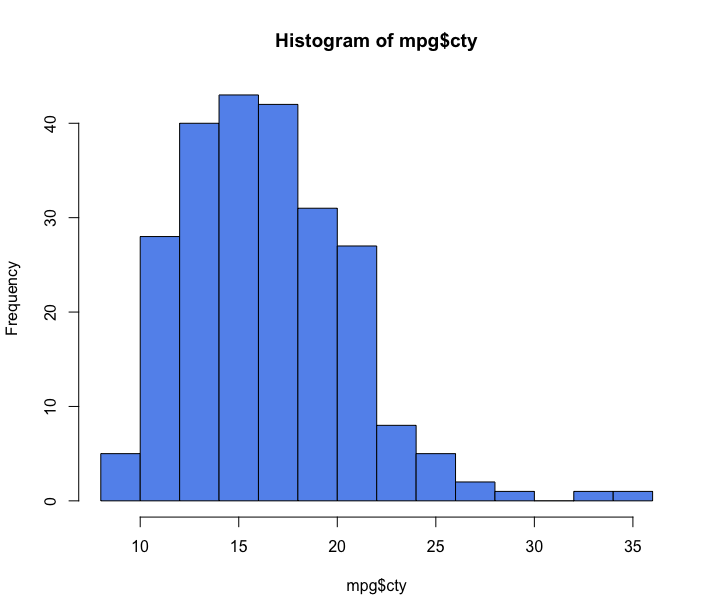
Podemos também melhorar esse histograma inserindo o título, e os nomes dos eixos com os mesmos argumentos usados anteriormente: main=, xlab=, ylab=.
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequência")
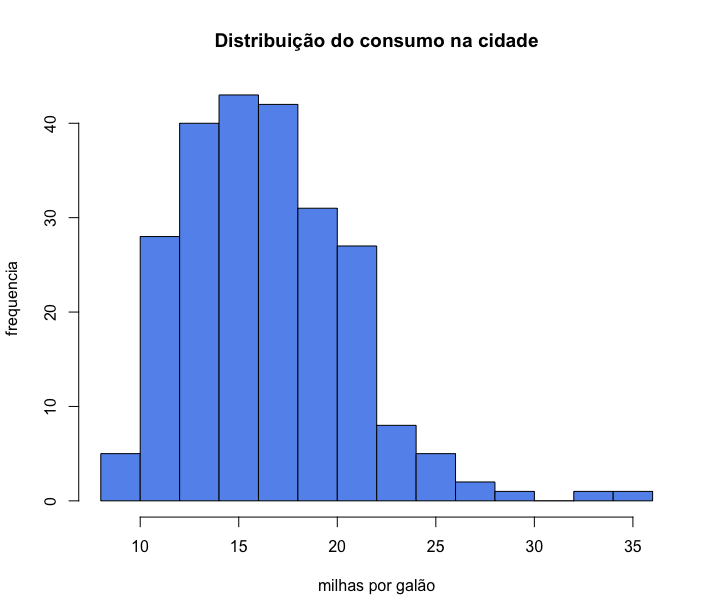
Veja que no gráfico acima os eixos x e y não comtemplam todo a amplitude de dados. Podemos ajustar os limites dos eixos x e y com os argumentos xlim e ylim:
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequencia",
7 xlim = c(0,40),
8 ylim = c(0,50))
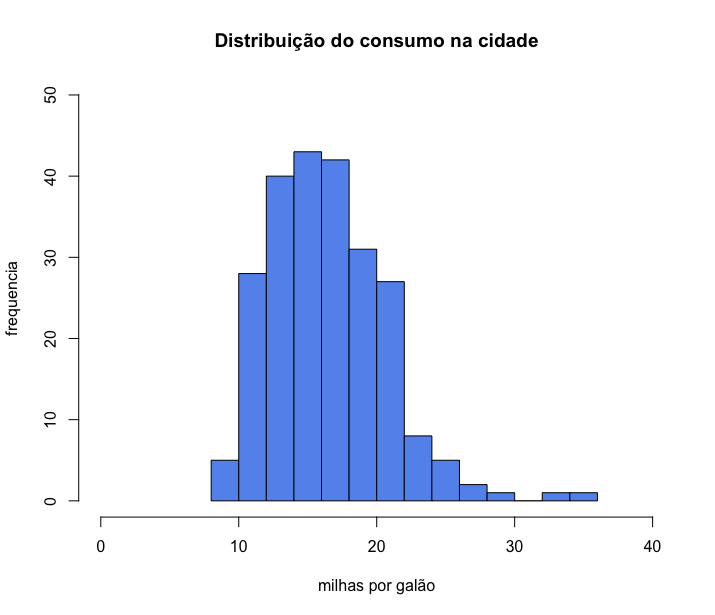
Uma das grandes vantagens do R é ser uma linguagem orientada a objetos. Tudo no R é um objeto, até um histograma. Assim, um objeto no R pode até mesmo armazenar o histograma. E ao fazer isso, podemos verificar vários detalhes do histograma.
1 > myhistogram <- hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequência",
7 xlim = c(0,40),
8 ylim = c(0,50))
Depois de armazenar o histograma num objeto, basta digitar o nome desse objeto para ter acesso aos detalhes do histograma.
1 > myhistogram
2
3 $breaks
4 [1] 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36
5
6 $counts
7 [1] 5 28 40 43 42 31 27 8 5 2 1 0 1 1
8
9 $density
10 [1] 0.010683761 0.059829060 0.085470085 0.091880342 0.089743590
11 [6] 0.066239316 0.057692308 0.017094017 0.010683761 0.004273504
12 [11] 0.002136752 0.000000000 0.002136752 0.002136752
13
14 $mids
15 [1] 9 11 13 15 17 19 21 23 25 27 29 31 33 35
16
17 $xname
18 [1] "mpg$cty"
19
20 $equidist
21 [1] TRUE
22
23 attr(,"class")
24 [1] "histogram"
Caso seja necessário acessar alguns desses dados isoladamente, basta usar o operador $, como fazedemos um data frame. Por exemplo, para acessar o valor de cada coluna, basta acessar counts.
1 > myhistogram$counts
2 [1] 5 28 40 43 42 31 27 8 5 2 1 0 1 1
Podemos ver que a primeira barra tem 5 carros, a segunda 28 carros, a terceira 40 carros etc.
Podemos também fazer um histograma com a densidade de probabilidade ao invés da contagem absoluta, para isso basta alterar o argumento freq para FALSE: freq = FALSE. Nesse caso, temos de ter cuidado de não usar o argumento ylim e sim deixar o R usar os limites adequados no eixo y.
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequencia",
7 xlim = c(0,40),
8 freq = FALSE)
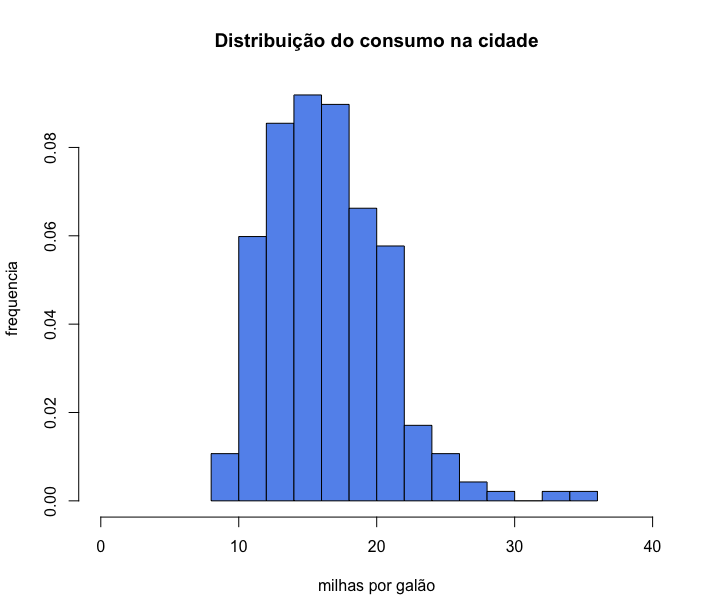
Até então nosso eixo y representava os valores absolutos, a contagem absoluta dos carros. No exemplo acima fizemos uma mudança no argumento freq e eixo y passou a representar as probabilidades. Nesse caso, se nosso histograma estiver usando probabilidades, podemos, então, inserir também uma linha de densidade com a função lines(). Observe que só podemos inserir essa linha de densidade se o histograma tiver sido criado com probabilidades, ou seja, se o indicarmos nos argumentos do histograma freq = FALSE.
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequencia",
7 xlim = c(0,40),
8 freq = FALSE)
9 > lines(density(mpg$cty))
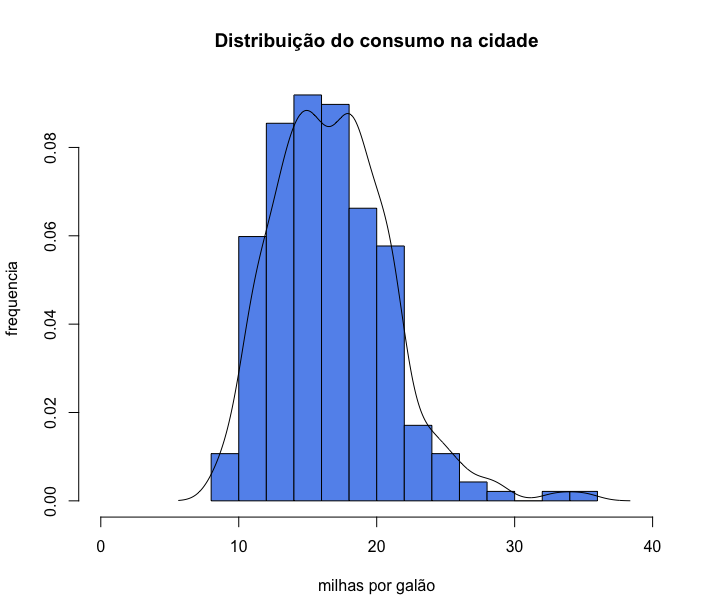
Gráficos de densidade
Um gráfico de densidade é uma variação de um histograma. Enquanto os histogramas vizualizam os dados em intervalos, um gráfico de densidade de probabilidade visualiza a distribuição dos dados num continuum. Uma vantagem dos gráficos de densidade sobre histogramas é que são melhores na determinação da forma da distribuição, pois não são afetados pelo número de barras usadas. Os picos de um gráfico de densidade ajudam a exibir onde os valores estão concentrados ao longo do intervalo. Veja que no último histograma plotado não era visivel que a curva seria bimodal, o que só ficou claro quando fizemos a sobreposição com a curva de densidade de probabilidade.
Quando geramos gráficos de barras ou de pizza foi necessário primeiro criar tabelas de frequencias dos dados. Do mesmo modo, para criar gráficos de densidade precisamos primeiro gerar os pontos do gráfico, o que é feito com a função density(). Depois, basta inserir esses dados como argumentos da função plot().
1 > densitypoints <- density(mpg$cty)
2 > plot(densitypoints,
3 main = "Densidade do consumo dos carros na cidade ")
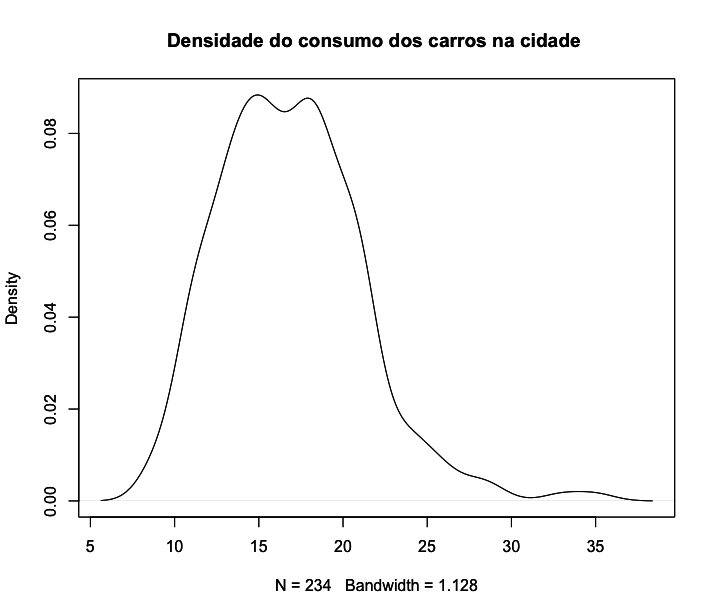
Boxplots
Um boxplot, também chamado de diagrama de caixa, é um gráfico para representar a variação (dispersão) de dados numéricos e seus quartis, sendo uma maneira padronizada de exibir a distribuição de dados com base em cinco números: mínimo, primeiro quartil, mediana, terceiro quartil e máximo.
O retângulo central de um box plot abrange o primeiro quartil para o terceiro quartil (intervalo interquartil ou IQR), correspondendo a 50% das medidas e a linha dentro do retângulo representa a mediana.
Num boxplot simples os “bigodes” (whiskers) nas extremidades da caixa mostram as localizações do mínimo e máximo. Entretanto, é mais comum que esses bigodes sirvam para separar valores extremos e outliers dos valores mais comuns do conjunto de dados.
REVER ESSE PARÁGRAFO:
Outliers são 3 × IQR acima do terceiro quartil ou 3 × IQR abaixo do primeiro quartil. Valores extremos são versões ligeiramente mais centrais de outliers: 1,5 × IQR acima do terceiro quartil ou 1,5 × IQR abaixo do primeiro quartil. Se houver valores como esses, o lado do lado apropriado é levado para 1,5 × IQR do quartil (a “cerca interna”) em vez do máximo ou mínimo, e os pontos de dados independentes individuais são exibidos como círculos preenchidos (por suspeitos de valores atípicos ) ou círculos cheios (para outliers). (A “cerca externa” é 3 × IQR do quartil).
Criar um boxplot no R é muito simples com a função boxplot(). Vamos criar um boxplot dos mesmos dados do consumo na cidade, para podermos comparar com os gráficos de histograma e de densidade feitos acima. Assim como no caso de um histograma, não é necessário criar tabelas antes de criar o gráfico, basta inserir o vetor com os dados na função boxplot().
1 > boxplot(mpg$cty)
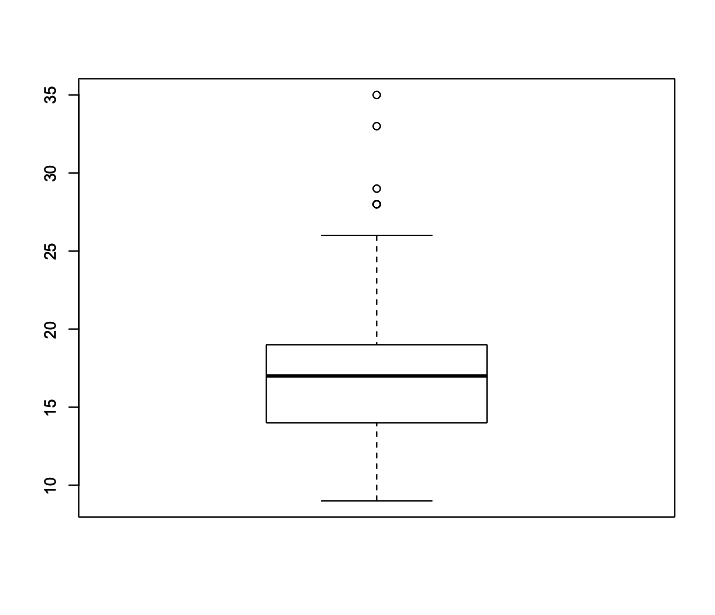
Da mesma forma que fizemos com os gráficos de histograma, podemos inserir o título, subtítulos e nomes dos eixos.
1 > boxplot(mpg$cty,
2 col = "cornflowerblue",
3 main = "Consumo de combustível",
4 ylab = "milhas por galão",
5 xlab = "cidade")
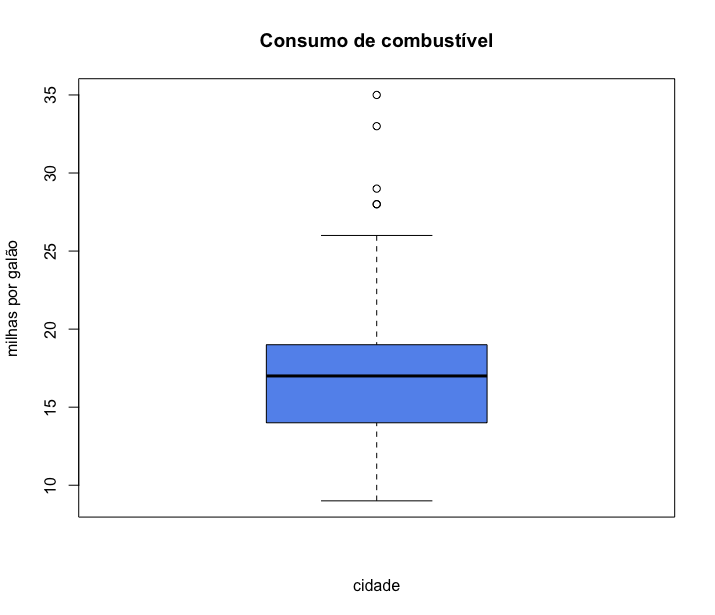
Uma das grandes vantagens do boxplot é que serve para podermos facilmente compararmos diferentes conjuntos de dados. Podemos por exemplo visualizar lado a lado a distribuição do consumo na cidade e do consumo na estrada. Nesse caso, quando temos mais de um boxplot, usamos o argumento names para nomearmos cada boxplot separadamente, como feito abaixo. Nesse caso é desnecessário nomear o eixo x e por isso não usei o argumento xlab.
1 > boxplot(mpg$cty, mpg$hwy,
2 col = "cornflowerblue",
3 main = "Distribuição do consumo de combustível",
4 ylab = "milhas por galão",
5 names=c("cidade","estrada"))
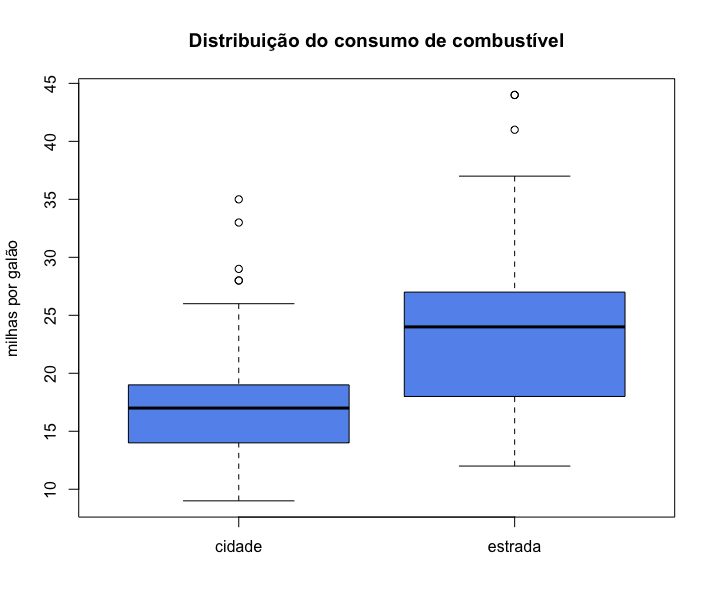
Parte 3 - Visualizando relações entre variáveis
Correlação entre uma variável numérica e uma variável categórica
A análise visual da relação entre uma variável categórica e uma variável numérica é geralmente feita através da plotagem de um gráfico de boxplot múltipo, como feito no último exemplo, no qual comparamos a distribuição do desempenho (variável numérica - milhas percorridas com um galão) com o local de trânsito (variável categórica: cidade ou estrada). Um outro gráfico comum é o de dotplot com margem de erro de cada média. Entretanto, esse tipo de gráfico é muito complexo para ser plotado com as funções básicas do R e não será analisado nessa aula. O pacote ideal para plotar gráficos mais complexos é o ggplot2.
Correlação entre duas variáveis numéricas
Gráficos de dispersão, ou scatter plots são gráficos nos quais duas variáveis numéricas são plotadas, uma em cada eixo, para que se possa analisar a relação entre elas. Através de um scatter plot podemos visualizar se existe uma correlação matemática entre essas variáveis. Podemos nos perguntar por exemplo, se existe alguma correlação entre as cililndradas e o consumo do carro? Um gráfico de dispersão (scatter plot) proporciona uma representaçõa visual bastante adequada para essa pergunta.
A função básica no R para gerar um scatter plot é simplemente plot(). Esse comando é bastante versátil e pode ser usado para plotar vários tipos de gráficos, inclusive de barras ou histograma, pois o comando plot() interpreta automaticamente o tipo de dado e escolhe o gráfico adequado. Entretanto, nunca é indicado deixar o que o R faça essa escolha, é sempre mais indicado usar os comando apropriados para cada tipo de gráfico.
Para usar o comando plot() para plotar um grafico de dispersão precisamos informar os dois conjuntos de dados a serem plotados. Para isso precisamos usar o operador $ para acessarmos cada variável a ser usada.
1 > plot(mpg$cty, mpg$displ)
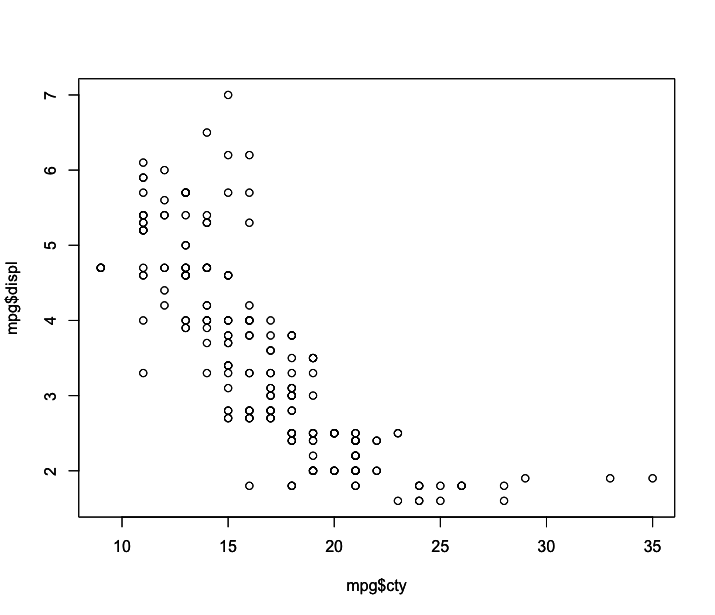
Como você pode observar, a primeira variável fica no eixo x e a segunda no eixo y. Podemos deixar indicado de forma explícita qual variável desejamos colocar em cada eixo.
1 > plot(x=mpg$cty, y=mpg$displ)
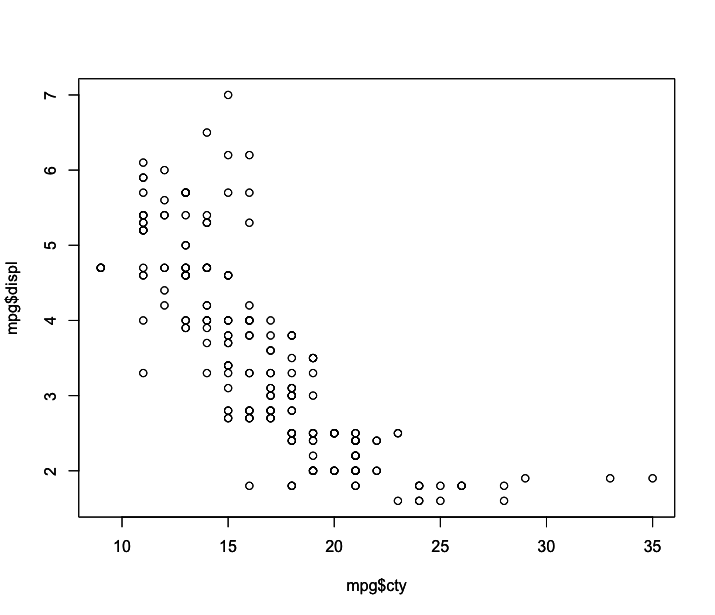
Podemos acrescentar o título e nomes dos eixos com os argumentos main, xlab e ylab, da mesma forma como fizemos com os gráficos anteriores.
1 > plot(x=mpg$displ, y=mpg$cty, # variáveis a serem plo\
2 tadas
3 main = "Corelação entre cilindradas e consumo", # título
4 xlab = "milhas por galão", # nome do eixo x
5 ylab = "cilindradas") # nome do eixo y
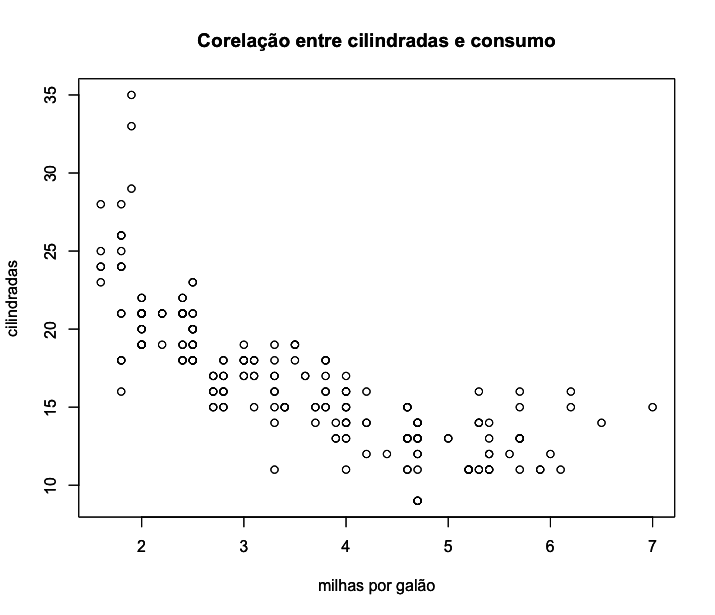
Podemos mudar o tipo de ponto no desenho com a o argumento pch, variando de 1 a 25. Experimente mudar o valor de pch para ver as alterações no gráfico.
1 > plot(x=mpg$displ, y=mpg$cty, # variáveis a serem plo\
2 tadas
3 main = "Corelação entre cilindradas e consumo", # título
4 xlab = "milhas por galão", # nome do eixo x
5 ylab = "cilindradas", # nome do eixo y
6 pch = 20)
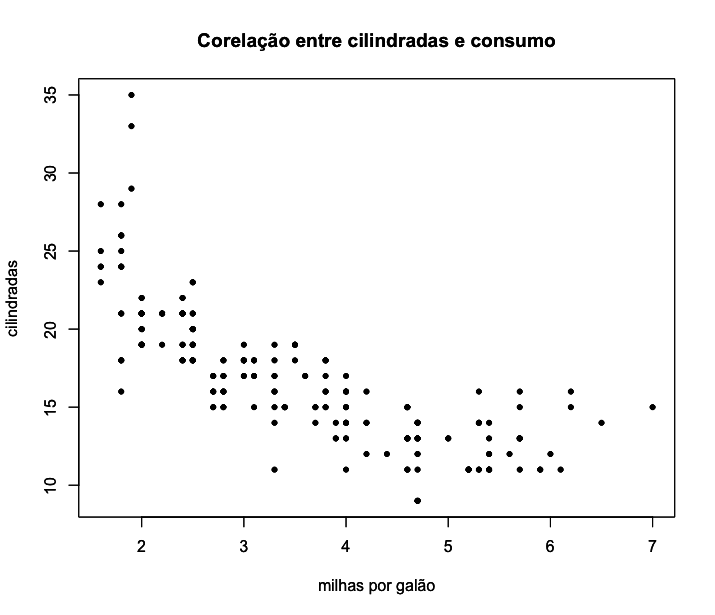
Um scatter plot server para visualizarmos a relação entre duas variáveis numéricas. Entretanto, a melhor e mais usual forma de visualizar essa correlação linear é através da inserção no gráfico de uma linha que represente a melhor relação linear possível entre essas duas variáveis (chamada de reta de regressão).
Podemos facilmente acrescentar uma reta de regressão linear no gráfico. Para isso teremos de usar uma função matemática lm(y~x) (linear model) para calcular a reta de regressão linear e depois pedir para plotar essa linha no gráfico usando a função abline(). Atenção para o fato de que a primeira variável na função lm() é a variável dependente e a segunda é a independente. Logo, a fórmula abaixo cty~displ indica que a variável cty (milhas percorridas) é a variável dependente de disp (cilindradas).
1 > plot(x=mpg$displ, y=mpg$cty, # variáveis a serem\
2 plotadas
3 main = "Corelação entre cilindradas e consumo", # título
4 xlab = "milhas por galão", # nome do eixo x
5 ylab = "cilindradas", # nome do eixo y
6 pch = 20)
7 > retaRegressao <- lm(cty~displ, data = mpg ) # cálculo da reta de re\
8 gressão linear
9 > abline(retaRegressao, col = "red") # insere a reta no gráf\
10 ico de cor "red"
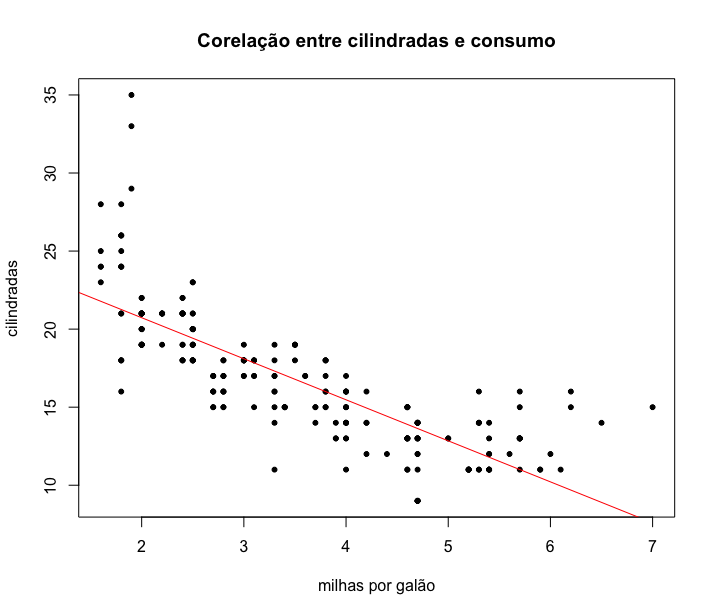
Através desse gráfico podemos verificar que parece haver uma relação negativa entre as cilindradas e as milhas percorridas, ou seja, quanto menor as cilindradas, maior a quantidade de milhas percorridas com um galão de combustível.
Mas além da inspeção visual, podemos também calcular a força dessa correlação. A medida estatística mais comum para mensurar a força da correlação entre duas variáveis numéricas é o Coeficiente de Correlação de Pearson - denotado por r.
O coeficiente de correlação é uma medida da força e direção da correlação linear entre duas variáveis. Ou seja, só serve para analisar correlações lineares.
A linguagem R tem uma função específica para calcular o coeficiente de correlação linear de Pearson (r) entre duas variáveis numéricas. A função cor() - de correlação - calcula o valor desse coeficiente com o sinal correto (positivo ou negativo). Para usar essa função basta inserir como argumentos as duas variáveis numéricas para as quais se deseja calcular o coeficiente.
1 > cor(mpg$displ, mpg$cty)
2 [1] -0.798524
A função lm() usada na criação da linha de regressão também faz o cálculo desse coeficiente de correlação, além de inúmeros cálculos matemáticos. Esse valor pode ser obtido na própria variável que criamos retaRegressao. Vejamos
1 > summary(retaRegressao)
2
3 Call:
4 lm(formula = cty ~ displ, data = mpg)
5
6 Residuals:
7 Min 1Q Median 3Q Max
8 -6.3109 -1.4695 -0.2566 1.1087 14.0064
9
10 Coefficients:
11 Estimate Std. Error t value Pr(>|t|)
12 (Intercept) 25.9915 0.4821 53.91 <2e-16 ***
13 displ -2.6305 0.1302 -20.20 <2e-16 ***
14 ---
15 Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
16
17 Residual standard error: 2.567 on 232 degrees of freedom
18 Multiple R-squared: 0.6376, Adjusted R-squared: 0.6361
19 F-statistic: 408.2 on 1 and 232 DF, p-value: < 2.2e-16
Veja que um dos valores calculados é o R-squared (ou seja, o r ao quadrado). Se desejarmos obter especificamente o valor de R-squared basta usar o operador $ como abaixo:
1 > summary(retaRegressao)$r.squared
2 [1] 0.6376405
E, finalmente, para obter o valor do coeficiente de correlação, basta extrair a raiz quadrada desse valor acima:
1 > r_squared <- summary(retaRegressao)$r.squared
2 > r <- sqrt(r_squared)
3 > r
4 [1] 0.798524
Podemos também fazer todo esse cálculo acima em apenas uma linha.
1 > sqrt(summary(retaRegressao)$r.squared)
2 [1] 0.798524
Veja que o coeficiente de correlação calculado acima foi positivo. Entretanto, lembre-se que esse resultado acima veio de uma extração de raiz quadrada e o resultado de uma operação de extração de raiz quadrada poderia tanto ser positivo ou negativo. No exemplo acima, sabemos que esse valor é na verdade negativo, pois já verificamos que a relação entre as variáveis cilindradas e milhas percorridas é negativa. Por outro lado, o valor absoluto encontrado indica que essa é uma correlação forte (correlação negativa forte).
A mensagem é clara: se deseja economizar combustível, prefira carros 1.0.
Referências
1. Hadley Wickham. ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag, New York, 2009.
2. Michael Friendly and Daniel Denis. The early origins and development of the scatterplot. Journal of the History of the Behavioral Sciences, Vol. 41(2), 103–130 Spring 2005.
3. Stephen E. Fienberg. Graphical Methods in Statistics. The American Statistician, Vol. 33(4): 165-178, 1979.
4. William S. Cleveland.Graphs in Scientific Publications. The American Statistician,
Vol. 38(4): 261-269, 1984
5. Ross Ihaka; Robert Gentleman. R: a language for data analysis and graphics. Journal of computational and graphical statistics, Vol. 5(3): 299-314, 1996.
6. Hadley Wickham. A layered grammar of graphics. Journal of Computational and Graphical Statistics, Vol. 19(1):3–28, 2010.