Correlação
Introdução.
No capítulo anterior aprendemos como gerar gráficos de dispersão - scatter plots - para analisar a relação entre duas variáveis numéricas. Vimos, resumidamente, que podemos calcular o coeficiente de correlação entre duas variáveis numérica. Precisamos, agora, aprofundar esse importante tópico.
O conceito de correlação se originou por volta de 1888, nos trabalhos do estatístico inglês Francis Galton (Stigler, 1989). Os estatísticos da era Vitorina estavam fascinados com a noção da hereditariedade e desejavam conseguir quantificar as influências genéticas no ser humano. Uma das pesquisas mais importantes dessa busca foi o estudo para quantificar as relações entre as alturas de pais e filhos. Galton e seu discípulo Karl Pearson coletaram uma grande quantidade de dados de alturas de pais e filhos para suas análises e, foi analisando esses dados que Galton concebeu a idéia de correlação (Galton, 1888 - 1889). E foi também Galton deu os primeiros passos na direção da construção do que hoje entendemos por um gráfico de dispersão ou scatter plot (Friendly & Denis, 2005).
O scatter plot, também chamado de gráfico de dispersão, ou diagrama de dispersão, é um dos gráficos mais usados na ciência. Estima-se que os scatter plots correspondam a cerca de 70-80% dos gráficos usados em publicações científicas (Tuft, 1983 APUD Friendly & Denis, 2005). Isso se deve à importância dessa análise de correlação e do gráfico de dispersão na busca da causa de eventos, na compreensão da causalidade dos fenômenos. Através da análise da correlação, buscamos compreender como uma variável afeta outra, se um determinada coisa afeta outra (Few, 2009). Esse tipo de conhecimento é fundamental na medicina, pois se sabemos que o uso de cigarro se correlaciona com o aumento do risco de câncer de pulmão podemos tentar evitar esse desfecho com campanhas anti-tabagismo; se sabemos que o uso de ácido fólico na gravidez se relaciona com a redução do risco de espinha bífida podemos então indicar o uso dessa substância para grávidas. Com isso já podemos perceber a importância de descobrirmos relações de causalidade e de como a interpretação da correlação é um tema de fundamental importância na medicina.
Entretanto, correlação não implica necessariamente em causalidade. Quando encontramos uma correlação entre duas variáveis, isso pode se dever a vários fatores:
- há uma relação de causalidade, uma das variáveis afeta a outra
- nenhuma das variáveis afeta a outra, as duas são afetadas por um outro ou mais fatores em comum
- nenhuma das variáveis afeta a outra, mas ambas podem estar conectadas por uma outra variável.
- a aparente correlação na verdade é resultado de um erro devido a uma amostra insuficiente ou enviesada.
É sempre válido reforçar que correlação não implica causalidade. A simples verificação de uma forte correlação entre duas variáveis não é suficiente para determinar a relação de causalidade entre elas. Tanto a correlação percebida visualmente como através da medida do coeficiente de correlação podem ocorrer entre variáveis que não tem nenhuma relação entre si. Esse tipo de correlação é chamdo de correlação espúria. Para maiores exemplos de correlações espurias veja o site http://www.tylervigen.com/spurious-correlations, de onde foi obtida a imagem abaixo, que mostra um exemplo de correlação meramente espúria.
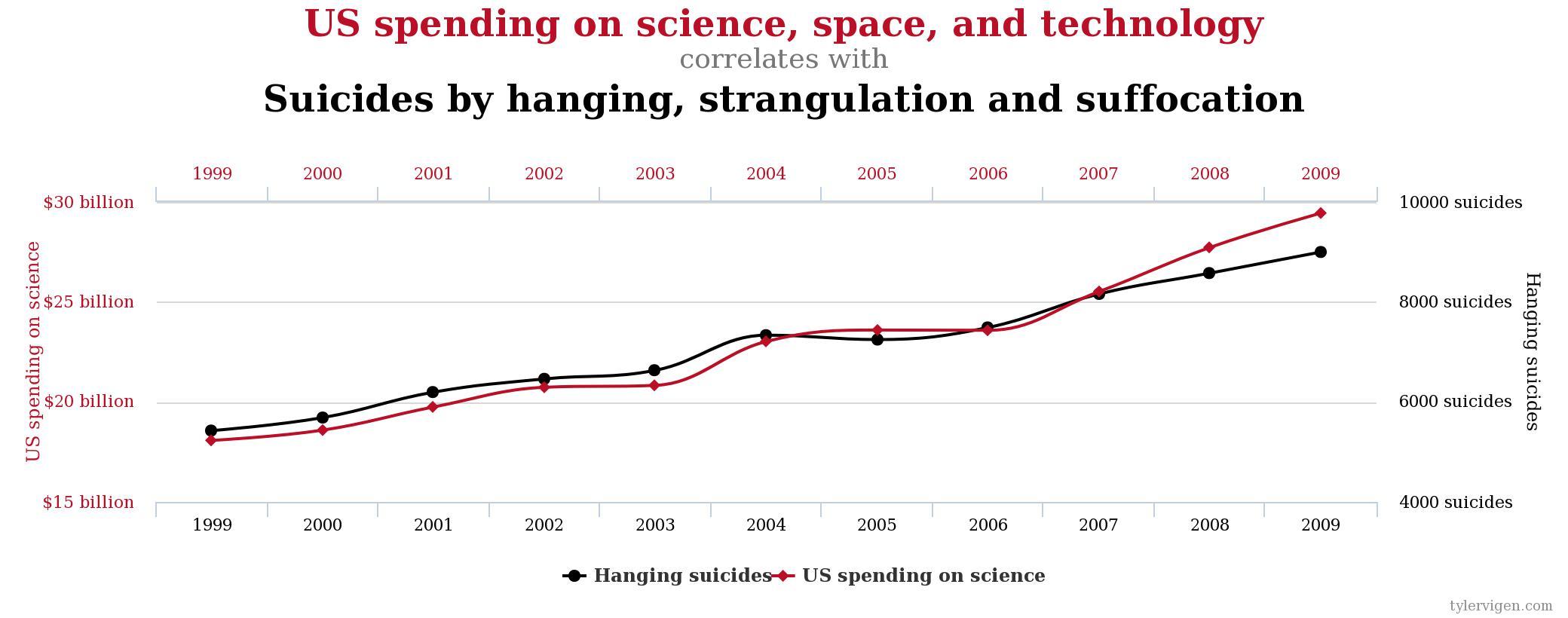
Esteja especialmente atento a correlações entre variáveis que evoluem no tempo. Muito frequentemente duas variáveis se modificam ao longo do tempo por motivos totalmente diversos e não por uma relação de causalidade entre uma e outra.
Carregamento dos pacotes necessários
Para esse capítulos serão necessários alguns pacotes do R. Se, ao usar a função library() para carregar esses pacotes, você receber a mensagem que algum pacote não existe, faça a instalação desse pacote e, depois, tente novamente usar a função library().
Será necessário já ter instalado os seguintes pacotes:
- tidyverse
- dplyr
- gridExtra
- HistData
Após a instalação é necessário carregar os pacotes com o comando library().
1 library(tidyverse)
2 library(dplyr)
3 library(gridExtra)
4 library(HistData)
Análise Univariada e Bivariada
Antes de iniciar o tema da correlação, é importante resumir dois termos comuns na estatística: análise univariada e análise bivariada.
A análise univariada é a forma mais simples de análise estatística. O que caracateriza a análise univariada é que apenas uma variável está envolvida. Dependendo do tipo dessa variável, poderemos fazer diversas análises descritivas ou inferenciais. No caso da análise descritiva de uma variável não numérica (nominal ou oridinal) podemos descrever a frequência de cada nível da variável e podemos construir gráficos de barra ou de pizza com essas frequências. Para variáveis numéricas, podemos descrever o aspecto visual da distribuição (a forma da distribuição), calcular a moda, a média, a mediana, a amplitude, o IQR, os quartis, a variância e desvio padrão. A análise inferencial de uma única variável (análise inferencial univariada) é o conjunto de análises, de inferências, sobre uma população a partir de uma amostra.
A análise bivariada é o nome dado às técnicas de análise da relação entre duas variáveis. Frequentemente essa análise serve para determinar a relação entre duas variáveis numéricas, sendo uma delas a variável explanatória (variável preditora ou independente) e a outra a variável de resposta (de desfecho ou variável dependente). Por convenção, quando representamos graficamente essas variáveis, plotamos a variável explanatória (preditora/independente) no eixo x e a variável de reposta (de desfecho ou dependente) no eixo y. A representação gráfica usual de uma relação entre duas variáveis numéricas é o scatter plot, também chamado de gráfico de dispersão.
Um scatter plot mostra as características da relação entre duas variáveis, os padrões dessa relação. Em uma avaliação da relação de duas variáveis através de um scatter plot geralmente devemos avaliar 4 características:
- forma do gráfico (linear ou não linear)
- direção da tendência (positiva ou negativa)
- força da relação (grau de disperção)
- presença de outliers. (pontos fora do padrão)
Forma
Forma diz respeito à forma que os pontos formam no gráfico, podendo ser, em resumo, linear ou não linear. Essa é uma análise visual.
Direção
Essa análise pode ser apenas visual ou calculada pelo que se chama de covariância: ou seja, o quanto as variáveis variam de forma conjunta. Quando ambas as variáveis variam na mesma direção, ou seja, uma aumenta quando a outra aumenta, ou uma diminui quando a outra diminui, a direção da variação é positiva, ou seja, a covariância é positiva.
A direção é negativa quando uma aumenta quando a outra diminui. Nesse caso a covariância é dita negativa.
Analisaremos a covariância logo a seguir.
Força
A força da relação diz respeito quão forte é a correlação, o que é mensurado pelo grau de dispersão dos pontos do gráfico. A força de uma correlação linear é mensurada pelo coeficiente de correlação.
Analisaremos o coeficiente de correlação logo a seguir.
Outliers
A presença de outliers pode influenciar enormemente a medida da força da correlação (o coeficiente de correlação), logo, é sempre importante verificar visualmente se existem outliers no gráfico de scatter plot.
Um scatter plot histórico
A título de exemplo, vamos recriar um scatter plot com dados da pesquisa de Francis Galton e Karl Pearson de 1888. Esses dados estão disponíveis no pacote HistData. Para ter acesso a esses dados é necessário já ter instalado esse pacote e já ter feito uso do comando library(HistData) para carregar esse pacote na sessão atual do R.
Para carregar os dados de Galton e Pearson use o comando abaixo:
1 data("Galton")
para ter uma idéia do dataset, use o comando str(Galton):
1 str(Galton)
2 'data.frame': 928 obs. of 2 variables:
3 $ parent: num 1.79 1.74 1.66 1.64 1.63 ...
4 $ child : num 1.57 1.57 1.57 1.57 1.57 ...
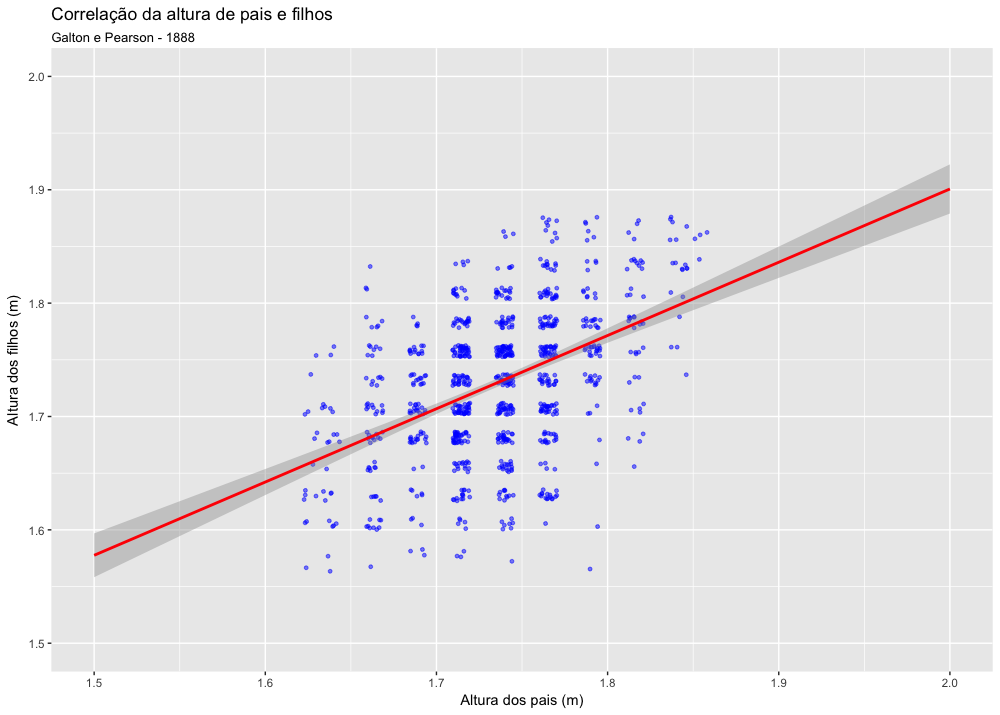
Podemos ver que esse é um data frame com 928 observações, com as alturas de pais e filhos. Entretanto, as medidas de altura desse dataset estão em polegadas (inches). É interessante converter essas as medidas para metros, unidade com a qual estamos mais acostumados a usar.
1 Galton$parent <- Galton$parent* 0.0254
2 Galton$child <- Galton$child * 0.0254
Vamos então gerar um scatter plot com o ggplot2:
1 ggplot(data=Galton, aes(x=parent, y=child)) +
2 geom_jitter(color="blue", size=1, alpha=0.5) +
3 geom_smooth(method = "lm", color = "red", fullrange = TRUE) +
4 ggtitle(label="Correlação da altura de pais e filhos",
5 subtitle ="Galton e Pearson - 1888") +
6 xlab("Altura dos pais (m)") +
7 ylab("Altura dos filhos (m)") +
8 xlim(c(1.5,2)) +
9 ylim(c(1.5,2))
Covariância
A covariância de duas variáveis x e y em um conjunto de dados mede como esses dois estão relacionados linearmente. A covariância da amostra é definida em termos da amostra como:
cov_{x,y}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n}{format: latex}
Observando a fórmula acima com atenção você poderá verificar que a covariância é o somatório da multiplicação de todos os desvios de cada variável. Ou seja, é calcula-se o desvio de cada dado em relação à sua média em cada eixo, multiplicam-se esses dois desvios e, finalment, faz-se o somatório de todos essas multiplicações.
Mas não se assuste com essa fórmula. Todos esses cálculos serão feitos automaticamente pelo R. O importante aqui é entender que quando os desvios são no mesmo sentido o sinal será positivo, quando os desvios são em sentidos diferentes o resultado será negativo. Ou seja, uma covariância positiva indica uma relação linear positiva entre as variáveis, e uma covariância negativa indica o oposto. Os gráficos abaixo ajudarão a compreender o que significa uma covariância positiva e negativa.
Vamos criar alguns conjuntos de dados de exemplo para plotarmos alguns gráficos de dispersão (scatter plots) e vamos calcular as covariâncias entres pares desses conjuntos de dados.
1 set.seed(0)
2 x = c(1:60)
3 A = 2*x
4 B = c(seq(from = 120,to = 2, by= -2))
5 C = x
6 D = (x^3)/1000
7 E = runif(60, 1, 120)
8
9 dat <- data.frame(x, A,B, C, D, E)
10
11 covA <- round(cov(dat$x,dat$A),2)
12 covB <- round(cov(dat$x,dat$B),2)
13 covC <- round(cov(dat$x,dat$C),2)
14 covD <- round(cov(dat$x,dat$D),2)
15 covE <- round(cov(dat$x,dat$E),2)
Agora vamos plotar alguns gráficos com esses dados para melhor compreensão do que é a covariância e interpretar o que é uma covariância positiva ou negativa.
1 plot1 <- ggplot(data = dat) +
2 geom_point(aes(x=x,y=A)) +
3 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
4 ggtitle("A \nCorrelação positiva perfeita") +
5 annotate("text", x=0, y=100, label= paste("cov=", covA), color="black", fontfa\
6 ce=1, size=4, hjust = 0)
7
8 plot2 <- ggplot(data = dat) +
9 geom_point(aes(x=x,y=B)) +
10 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
11 ggtitle("B \nCorrelação negativa perfeita") +
12 annotate("text", x=45, y=100, label= paste("cov=", covB), color="black", fontf\
13 ace=1, size=4, hjust = 0)
14
15 grid.arrange(plot1, plot2, ncol = 2, nrow=1)
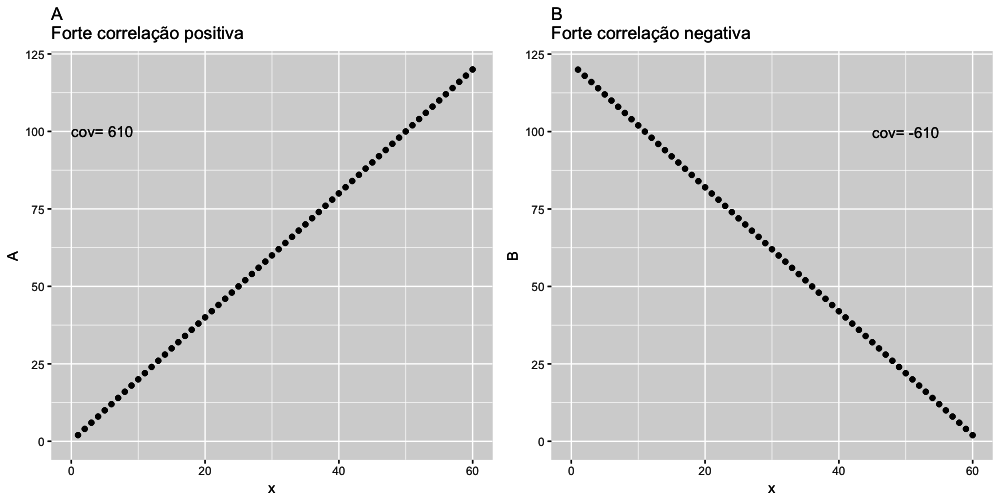
Analisando os gráficos A e B acima pode-se perceber que em ambos há uma correlação perfeita entre as variáveis dos eixos x e y e, além disso, podemos ver que a covariância serve para indicar a direção da correlação. No gráfico A as variáveis estão correlacionados de forma positiva: quando uma aumenta a outra aumenta, portanto a correlação é positiva (+610). No gráfico B as variáveis estão correlacionadas de forma negativa, quando a variável no eixo aumenta, a variável no eixo y diminui, portanto a medida da correlação é negativa (-610). Entretanto, o valor absoluto da covariância não tem muito valor para compararmos diferentes gráficos de dispersão. Veja no exemplo abaixo que duas correlações perfeitas podem ter covariâncias bastante diferentes.
1 # apesar de ser desnecessário, repeti aqui o código do plot1 para melhor compree\
2 nsão desse code chunk
3 plot1 <- ggplot(data = dat) +
4 geom_point(aes(x=x,y=A)) +
5 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
6 ggtitle("A \nCorrelação positiva perfeita") +
7 annotate("text", x=0, y=100, label= paste("cov=", covA), color="black", fontfa\
8 ce=1, size=4, hjust = 0)
9
10 plot3 <- ggplot(data = dat) +
11 geom_point(aes(x=x,y=C)) +
12 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
13 ggtitle("C \nCorrelação positiva perfeita") +
14 annotate("text", x=0, y=100, label= paste("cov=", covC), color="black", fontfa\
15 ce=1, size=4, hjust = 0)
16
17 grid.arrange(plot1, plot3, ncol = 2, nrow=1)
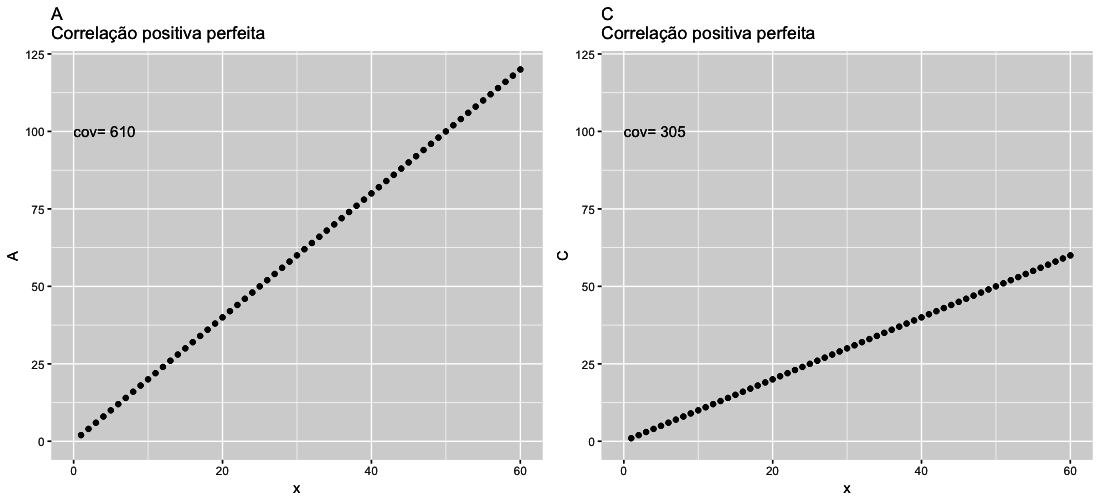
Analisando os gráficos A e C acima pode-se perceber que apesar da covariância servir para indicar a direção da correlação, ela não uma boa medida para comparar a força da correlação entre conjuntos diferentes de dados. Veja que os gráficos A e C tem uma correlação perfeita entre suas variáveis, entretanto, o valor da covariância entre os dois gráficos é muito diferente, sendo duas vezes maior no gráfico A. Essa diferença enorme entre os valores torna difícil usar a covariância como uma medida para comparar a força da correlação entre diferentes conjuntos de dados. Isso nos mostra que a medida da covariância não é adequada para comparar a força da correlação entre conjuntos diferentes de dados. Para isso, vamos precisar de outro tipo de medida.
Para podermos comparar a força da correlação entre diferentes gráficos ou diferentes conjuntos de dados, precisamos de uma medida normalizada. Para essa finalidade usamos o coeficiente de correlação.
Coeficiente de Correlação
O coeficiente de correlação é uma medida da força da correlação linear entre duas variáveis. Essa medida, que se originou dos trabalhos de Galton, teve seu desenvolvimento matemático feito por Karl Pearson. Devido a isso o coeficiente de correlação linear é também conhecido como coeficiente de correlação de Pearson e é denotado pela letra r.
O coeficiente de correlação é a versão normalizada da covariância, ou seja, o coeficiente de correlação de duas variáveis é simplesmente a covariância dessas variáveis dividida pelo produto dos desvios padrões de cada uma dessas variáveis. Essa divisão faz a normalização do coeficiente de correlação e possibilita sua comparação entre diferentes conjuntos de dados. Com isso, o coeficiente de correlação passa a ter uma varição de -1 até +1, sendo o sinal a indicação da direção da correlação e o valor absoluto desse coeficiente e indica a magnitude da relação linear entre essas duas variáveis. Como varia sempre de -1 a 1, possibilita a comparação de diferentes conjuntos de dados. Mas lembre-se, o coeficiente de correlação é uma medida da força e direção da correlação linear entre duas variáveis. Ou seja, só serve para analisar correlações lineares.
Direção da correlação linear
- correlação linear positiva -> coeficiente é positivo
- correlação linear negativa -> coeficiente é negativo
Força da correlação linear
- próxima de -1 ou +1 : correlação linear total
- próxima de -0.75 ou +0.75: correlação linear forte
- próximo de -0.50 ou +0.50: correlação linear moderada
- próximo de -0.20 ou +0.20: correlação linearfraca
- próxima de 0: não há correlação linear
Cuidados com a interpretacão do coeficiente de correlação
Cuidado com a interpretação de um coeficiente de correlação com valor absoluto pequeno. Isso não quer dizer que não há correlação entre as variáveis, mas sim que não há uma correlação linear. É importante salientar que duas variáveis podem ter uma forte correlação não linear e, logicamente, nenhuma correlação linear. Nesse caso o coeficiente de correlação não é uma medida útil, pois só mede a força da correlação não linear. Portanto, lembre-se, o coeficiente de correlação (linear) só é útil para analisar correlações lineares entre duas variáveis.
Além disso, cuidado com a interpretação de um coeficiente de correlação forte. Isso pode ser enganoso também. Um conjunto de dados pode ter um forte coeficiente de correlação apesar de não apresentarem nenhuma correlação real.
Calculando o coeficiente de correlação no R
A fórmula do coeficiente de correlação é:
r_{x,y}=\frac{cov_{x,y}}{\sigma_{x}\sigma{y}}{format: latex}
Mas não se assuste com essa fórmula, o R tem uma função para realizar esses cálculos: cor(x,y). A função cor(x, y) calcula o coeficiente de correlação de Pearson entre as variáveis x e y. Uma vez que esta quantidade é simétrica em relação a x e y, não importa em que ordem você colocar as variáveis.
Ao mesmo tempo, a função cor() é muito conservadora quando encontra dados faltantes (por exemplo NA). Quando essa função encontra algum dado NA o resultado será sempre NA. Usamos o argumento "use=pairwise.complete.obs" para alterar esse comportamento padrão de retornar NA sempre que qualquer um dos valores encontrados. Esse argumento, definido dessa forma, permite que a função cor() calcule o coeficiente de correlação para aquelas observações onde os valores de x e y não estão faltando, ou seja, levando em conta apenas os pares completos de observações.
O metodo default da função cor() é calcular o coeficiente de correlação de Pearson. Mas a função cor() pode calcular também outros coeficientes de correlação, tal como o de “kendall” ou de “spearman”. Para isso basta informar nos argumentos da função o método desejado:
1 cor(dat$x, dat$A, method = "pearson") # default: deve ser usado quando os dados \
2 estão normalmente distribuídos
3 cor(dat$x, dat$A, method = "kendal")
4 cor(dat$x, dat$A, method = "spearman") # usado quando os dados não estão normalm\
5 ente distribuídos
6 [1] 1
7 [1] 1
8 [1] 1
Ao analisar o coeficiente de correlação de duas variáveis, é sempre importante fazer também uma inspeção visual dos gráficos. Vamos ver nos gráficos abaixo a importância dessa inspeção visual.
1 corA <- round(cor(dat$x,dat$A),2)
2 corB <- round(cor(dat$x,dat$B),2)
3 corC <- round(cor(dat$x,dat$C),2)
4 corD <- round(cor(dat$x,dat$D),2)
5 corE <- round(cor(dat$x,dat$E),2)
6
7 plot1a <- ggplot(data = dat) +
8 geom_point(aes(x=x,y=A)) +
9 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
10 ggtitle("A \nCorrelação positiva perfeita") +
11 annotate("text", x=0, y=115, label= paste("r=", corA), color="black", fontface\
12 =1, size=4, hjust = 0)
13
14 plot2a <- ggplot(data = dat) +
15 geom_point(aes(x=x,y=B)) +
16 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
17 ggtitle("B \nCorrelação negativa perfeita") +
18 annotate("text", x=45, y=115, label= paste("r=", corB), color="black", fontfac\
19 e=1, size=4, hjust = 0)
20
21 plot4 <- ggplot(data = dat) +
22 geom_point(aes(x=x,y=D)) +
23 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
24 ggtitle("D \nAusência de correlação linear\nCorrelação não linear perfeita") +
25 annotate("text", x=5, y=115, label= paste("r=", corD), color="black", fontface\
26 =1, size=4, hjust = 0)
27
28
29 plot5 <- ggplot(data = dat) +
30 geom_point(aes(x=x,y=E)) +
31 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
32 ggtitle("E \nAusência de correlação\nNão há nenhum tipo de correlação") +
33 annotate("text", x=40, y=115, label= paste("r=", corE), color="black", fontfac\
34 e=1, size=4, hjust = 0)
35
36
37 grid.arrange(plot1a, plot2a, plot4, plot5, ncol = 2, nrow=2)
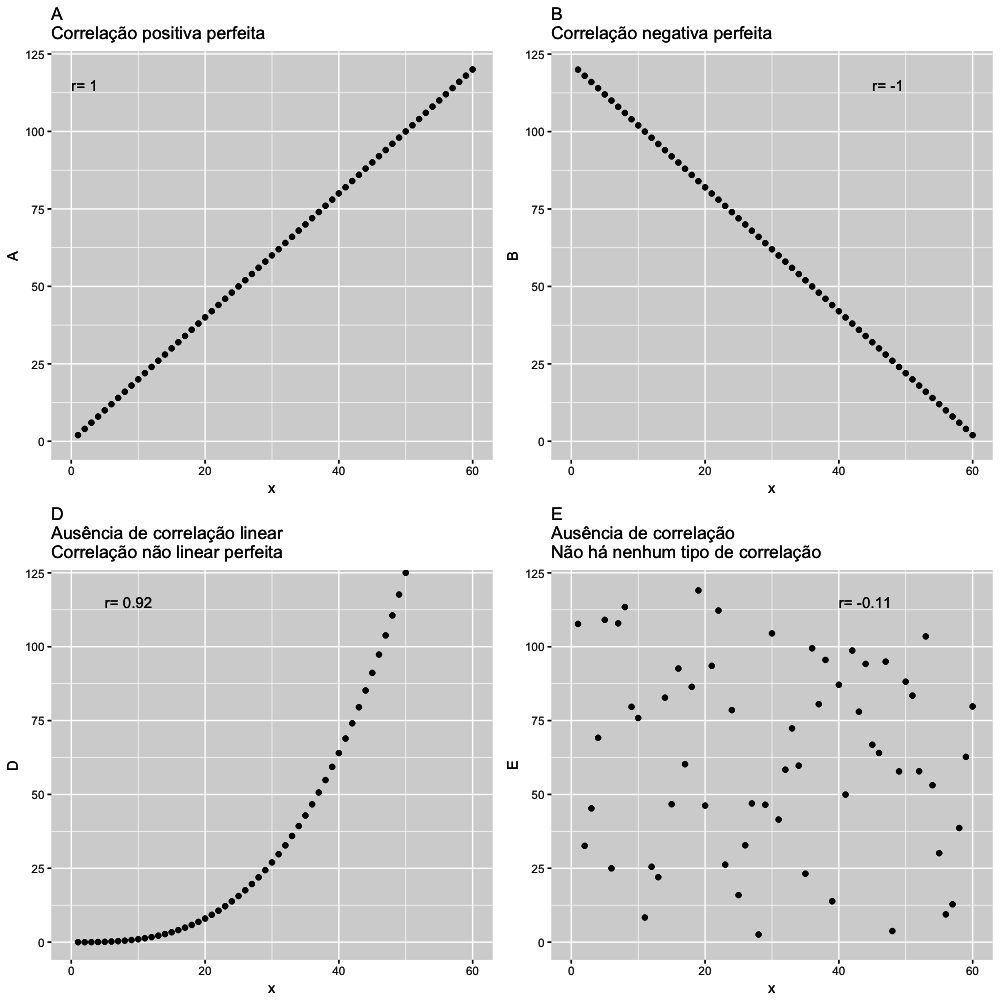
Analisando os gráficos acima podemos ver que os dados dos gráficos A e B tem uma correlação perfeita, respectivamente positiva e negativa. Em ambos esses gráficos o coeficiente de correlação tem o valor absoluto de 1, indicando uma correlação perfeita.
No gráfico D, apesar de um alto valor do coeficiente de correlação, na verdade a correlação entre as variáveis desse gráfico é perfeitamente não linear. A análise apenas do coeficiente de correlação linear poderia ser enganosa. A inspeção visual foi importante para podermos perceber não haver sentido em tentar calcular um coeficiente de correlação linear para esses dados.
No Gráfico E a ausência completa de correlação linear foi corretamente indentificada pelo valor de r= -0.11. O valor absoluto desse coeficiente, sendo tão próximo de zero é compatível a inspeção visual do gráfico.
Vamos analisar alguns exemplos de scatter plots interessantes de um conjunto de dados publicado por F. J. Anscombe em 1973 na revista The American Statistician (Vol. 27, No. 1, pp. 17-21). O objetivo desses gráficos é justamente mostrar que, juntamente com os cálculos numéricos dos dados, a inspeção visual dos dados é etapa fundamental na análise de dados. O conjunto de dados de F. J. Anscombe já faz parte do R e pode ser facilmente acessado no dataset anscombe.
1 anscombe
2 x1 x2 x3 x4 y1 y2 y3 y4
3 1 10 10 10 8 8.04 9.14 7.46 6.58
4 2 8 8 8 8 6.95 8.14 6.77 5.76
5 3 13 13 13 8 7.58 8.74 12.74 7.71
6 4 9 9 9 8 8.81 8.77 7.11 8.84
7 5 11 11 11 8 8.33 9.26 7.81 8.47
8 6 14 14 14 8 9.96 8.10 8.84 7.04
9 7 6 6 6 8 7.24 6.13 6.08 5.25
10 8 4 4 4 19 4.26 3.10 5.39 12.50
11 9 12 12 12 8 10.84 9.13 8.15 5.56
12 10 7 7 7 8 4.82 7.26 6.42 7.91
13 11 5 5 5 8 5.68 4.74 5.73 6.89
Vamos inicialmente calcular as medidas estatísticas do conjunto de dados de Anscombe. Calculando a média, desvio padrão e o coeficiente de correlação em cada um desses conjuntos de dados com o código abaixo.
1 # preparando os dados para melhor utilização
2 Anscombe <- with(anscombe, data.frame(x = c(x1, x2, x3, x4),
3 y = c(y1, y2, y3, y4),
4 group = gl(4, nrow(anscombe))))
5
6 Anscombe %>%
7 group_by(group) %>%
8 summarise(mean = mean(y),
9 std_dev = sd(y),
10 correlation = cor(x, y))
11
12 # A tibble: 4 x 4
13 group mean std_dev correlation
14 <fctr> <dbl> <dbl> <dbl>
15 1 1 7.500909 2.031568 0.8164205
16 2 2 7.500909 2.031657 0.8162365
17 3 3 7.500000 2.030424 0.8162867
18 4 4 7.500909 2.030579 0.8165214
Veja que as medidas estatísticas desse 4 pares de dados são extremamente parecidas. A simples análise desses números poderia indicar que se tratam de conjuntos muitos similares, com as mesmas médias, os mesmos desvios padrões e, inclusive, o mesmo coeficiente de correlação entre cada par de variáveis. Entretanto, como veremos, a análise visual desses dados mostra uma história basante diferente.
1 # plotando os 4 gráficos de Anscombe
2 ggplot(Anscombe, aes(x, y)) +
3 geom_point() +
4 geom_smooth(method='lm', se=FALSE) +
5 facet_wrap(~ group) +
6 annotate("text",
7 x=16,
8 y=5.2,
9 label= "mean = 7.5\nsd = 2.0\nr = 0.82",
10 color="black",
11 fontface=2,
12 size=3,
13 hjust = 0)
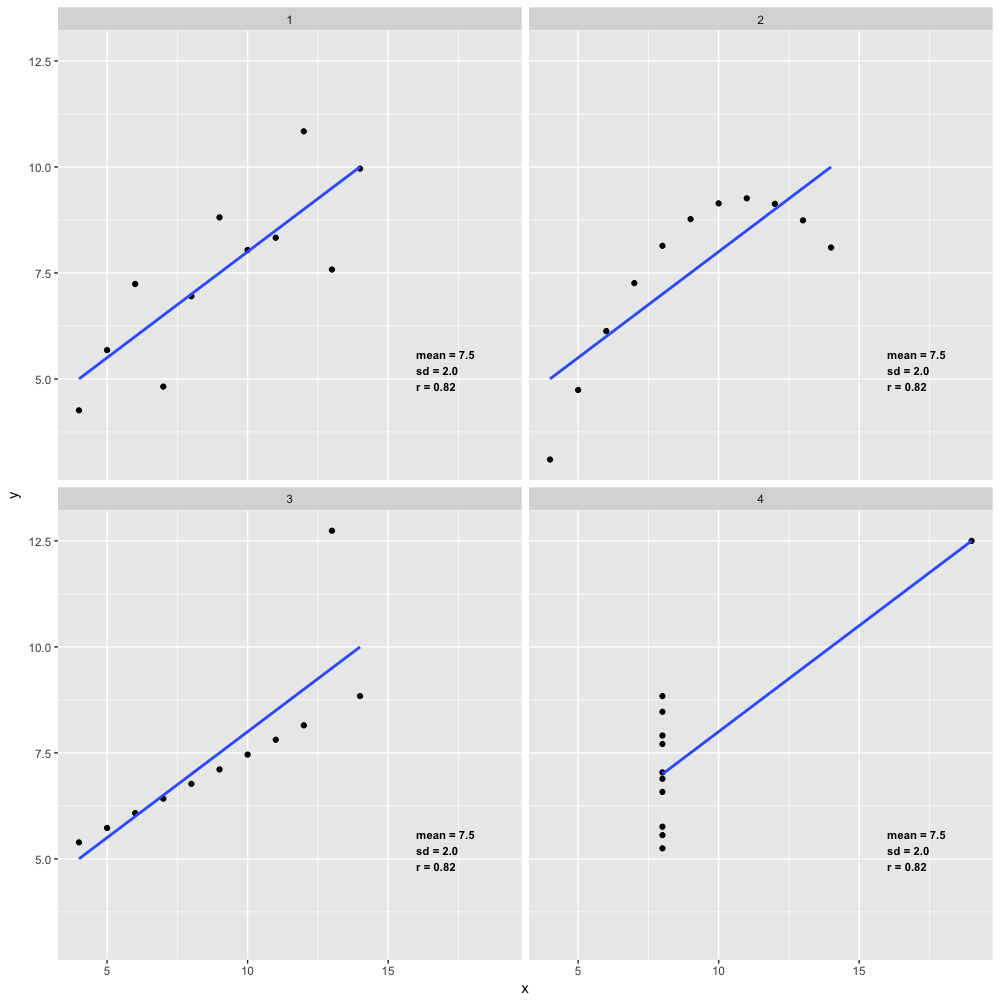
Veja que nesses 4 gráficos a linha de regressão é muito parecida. Na verdade é idêntica.
Veja também que a média dos dados, o desvio padrão e o coeficiente de correlação também são idênticos. Entretanto, apesar dessas estatísticas idênticas, é fácil verificar visualmente que os dados são bastante diferentes.
Os dados do grupo 1 tem uma forte correlação linear
Os dados do grupo 2, apesar de terem um coeficiente de correlação alto, na verdade tem uma correlação não linear.
Os dados do grupo 3 apresentam uma correlação linear quase absoluta, a não ser por um outlier.
Os dados do grupo 4 não apresentam correlação alguma, nem linear nem de qualquer outra forma.
Com esses exemplos de Anscombe podemos ver que as medidas estatísticas tradicionais não descrevem completamente os dados e que a visualização gráfica dos dados é extremamente importante.
\newpage
## Linha de Regressão - the best fit line
Em muitos gráficos do tipo scatter plot é comum haver uma linha reta que representa a correlação linear desses dados, a reta de regressão. Essa é reta que melhor representa os pontos (best fit line) e é calculada através do método de least squares.
Essa linha, denominada de least square regression line ou simplesmente linha de regressão, pode ser facilmente calculada no R através da função geom_smooth(). Para isso devemos especificar o argumento method="lm". lm significa linear model. Por padrão a linha será desenhada em azul com uma sombra de cinza ao redor, indicado o intrevalo de confiança de 95%. Se desejarmos NÃO plotar esse intervalo de confiança basta incluir o argumento se=FALSE. se significa standard error.
Vamos usar novamente alguns dados do dataset mpg que já vem junto com o ggplot2 R para criar essa linha de regressão, calcular a covariância e o coeficiente de correlação.
Vamos inicialmente verificar esses dados:
1 str(mpg)
2
3 Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 234 obs. of 11 variables:
4 $ manufacturer: chr "audi" "audi" "audi" "audi" ...
5 $ model : chr "a4" "a4" "a4" "a4" ...
6 $ displ : num 1.8 1.8 2 2 2.8 2.8 3.1 1.8 1.8 2 ...
7 $ year : int 1999 1999 2008 2008 1999 1999 2008 1999 1999 2008 ...
8 $ cyl : int 4 4 4 4 6 6 6 4 4 4 ...
9 $ trans : chr "auto(l5)" "manual(m5)" "manual(m6)" "auto(av)" ...
10 $ drv : chr "f" "f" "f" "f" ...
11 $ cty : int 18 21 20 21 16 18 18 18 16 20 ...
12 $ hwy : int 29 29 31 30 26 26 27 26 25 28 ...
13 $ fl : chr "p" "p" "p" "p" ...
14 $ class : chr "compact" "compact" "compact" "compact" ...
Esse dataset já foi analisado numericamente e graficamente nos capítulos passados, e possui 243 linhas (observações) com 11 variáveis. O significado de cada variável está descrito na documentação de ajuda do dataset mpg e pode ser visualizado com o comando ?mpg no console. A tabela abaixo mostra o significado de cada variável:
| variável | significado |
|---|---|
| manufacturer | marca |
| model | modelo |
| displ | cilindradas (Engine Displacement) |
| year | ano de fabricação |
| cyl | número de cilindros |
| trans | tipo de marcha: automática / manual |
| drv | tração: f=frontal, r=traseira, 4=4x4 |
| cty | milhas por galão na cidade |
| hwy | milhas por galão na estrada |
| fl | tipo de combustível: r=regular, p=premium, d=diesel, e=ethanol, c=CNG (gás) |
| class | tipo de carro: compact, midsize, suv, 2seater, minivan, pickup ou subcompact |
Vamos plotar novamente os dados de cilindradas e desempenho (milhas por galão) para uma inspeção visual inicial, mas dessa vez vamos usar o pacote ggplot2 para criar gráficos mais profissionais.
1 ggplot(data=mpg, aes(cty, displ)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 xlab("milhas por galão") +
5 ylab("cilindradas")
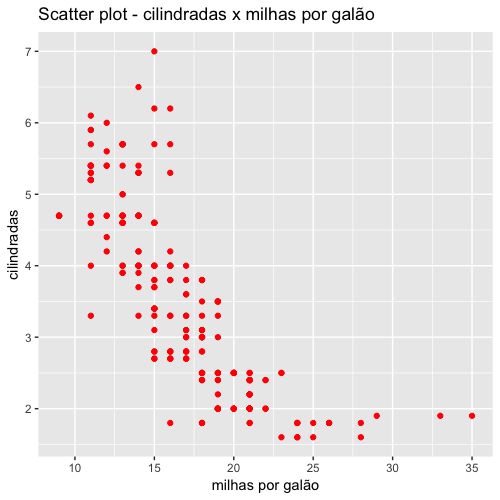
No capítulo passado adicionamos uma reta de regressão a esse gráfico com as funções gráficas básicas do R. Para efeitos didáticos, vamos novamente adicionar uma reta de regressão nesse gráfico, mas agora usando o ggplot2.
Com o ggplot2 é muito simples adicionar uma reta de regressão aos pontos do gráfico. Para isso, basta usar a função geom_smooth(method="lm"). O argumento method="lm" indica que a linha a ser incluida no gráfico será calculada pelo método de modelo linear (linear model = lm). Veja que essa função adiciona por padrão o intervalo de confiança de 95% do redor da reta.
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 geom_smooth(method=lm) # Add linear regression line
7 # (by default includes 95% confidence region)
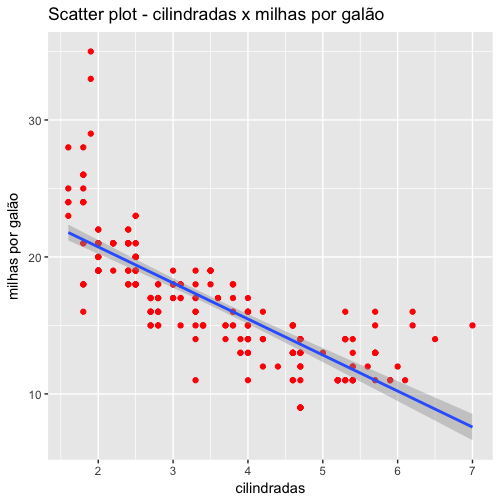
Já sabemos também calcular o coeficiente de correlação linear entre esses dados com a função cor().
1 cor(mpg$displ, mpg$cty)
2 [1] -0.798524
Veja que o coeficiente de correlação foi negativo e, em valores absolutos, teve um valor alto. Isso indica que há uma forte correlação negativa entre essas variáveis (cilindradas e milhas percorridas por galão), corroborando nossa hipótese anterior de que carros 1.0 são mais econômicos.
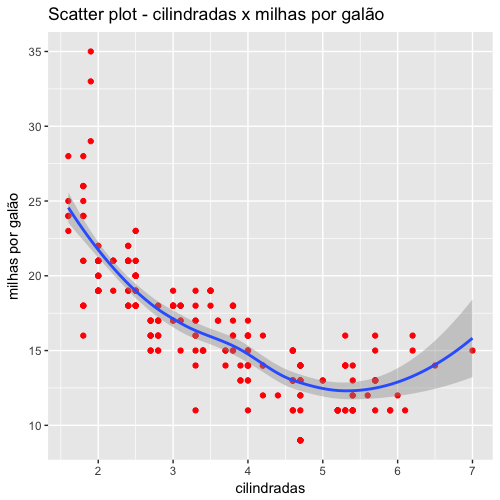
O pacote gráfico ggplot2 possui também funções que permitem facilmente inserir linhas curvas - não lineares - que melhor se ajustam aos pontos do gráfico. Na verdade esse é o comportamento padrão da função geom_smooth. Se usarmos essa função com seus valores default será inserida uma linha curva e não uma linha de regressão linear.
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 geom_smooth() # (by default includes 95% confidence region)
\newpage
Vamos analisar outro conjunto de dados que já vem no R: O dataset Indometh já faz parte do R e contém dados da farmacocinética do antibiótico indometacina. A primeira coluna do data frame é o nº do paciente (6 no total), a segunda coluna é o tempo da coleta do sangue e a terceira coluna é a concentração sérica do antibiótico no sangue.
Vamos inicialmente verificar esses dados:
1 str(Indometh)
2
3 Classes ‘nfnGroupedData’, ‘nfGroupedData’, ‘groupedData’ and 'data.frame': 66 ob\
4 s. of 3 variables:
5 $ Subject: Ord.factor w/ 6 levels "1"<"4"<"2"<"5"<..: 1 1 1 1 1 1 1 1 1 1 ...
6 $ time : num 0.25 0.5 0.75 1 1.25 2 3 4 5 6 ...
7 $ conc : num 1.5 0.94 0.78 0.48 0.37 0.19 0.12 0.11 0.08 0.07 ...
8 - attr(*, "formula")=Class 'formula' language conc ~ time | Subject
9 .. ..- attr(*, ".Environment")=<environment: R_EmptyEnv>
10 - attr(*, "labels")=List of 2
11 ..$ x: chr "Time since drug administration"
12 ..$ y: chr "Indomethacin concentration"
13 - attr(*, "units")=List of 2
14 ..$ x: chr "(hr)"
15 ..$ y: chr "(mcg/ml)"
Plotando os dados
1 ggplot(data=Indometh, aes(x=time, y=conc)) +
2 geom_point()
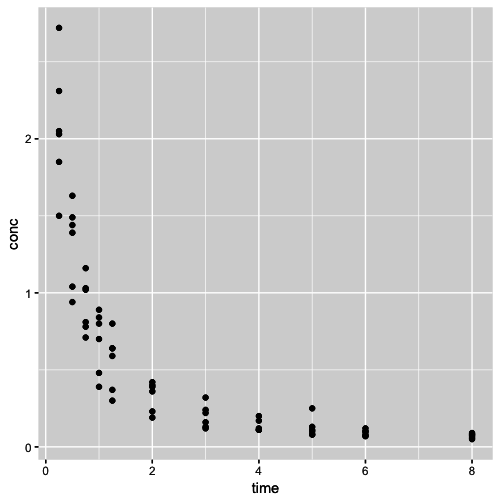
Podemos verificar visualmente que a relação entre o tempo e a concentração sérica não é linear. Vamos plotar a reta de regressão para mostrar como essa reta não se ajusta bem aos dados e, em seguida, calcular o coeficiente de correlação linear de Pearson.
1 ggplot(data=Indometh, aes(x=time, y=conc)) +
2 geom_point() +
3 geom_smooth(method = "lm")
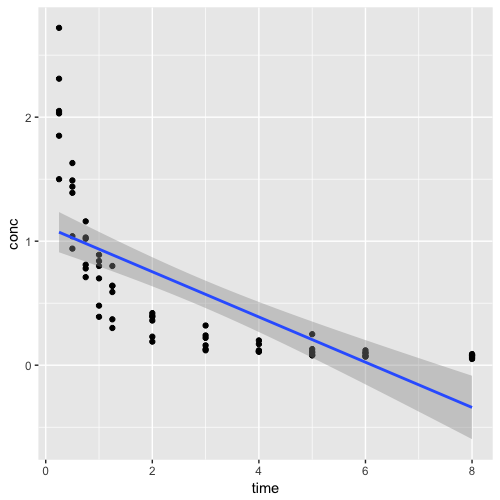
Calculando o coeficiente de correlação:
1 cor(Indometh$time, Indometh$conc)
2 [1] -0.7104719
Veja que o coeficiente foi negativo indicando haver uma relação negativa entre o tempo e a medida da concentração sérica, o que é bastante plausíve, pois a concentração sérica se reduz com o passar do tempo. Entretanto, o valor absoluto do coeficiente de correlação foi muito alto. Isso demonstra mais uma vez a inadequação de calcular o coeficiente de correlação num conjunto de dados que tem uma relação claramente não linear.
Como já vimos, o R nos permite facilmente plotar também linhas curvas para representar relações não lineares com a função geom_smooth() do pacote ggplot2. Se deixarmos a funçãp geom_smooth usar seu comportamento default, iremos gerar uma gráfico com uma curva que se ajusta aos dados da melhor forma possível.
1 ggplot(data=Indometh, aes(x=time, y=conc)) +
2 geom_point() +
3 geom_smooth()
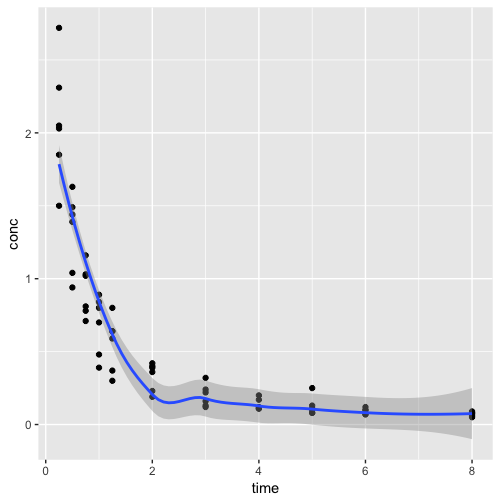
Apêndice Extra - Transformações logarítmicas
Existem diversas técnicas para conseguirmos para modelarmos de forma mais adequada a relação entre duas variáveis. Uma forma simples é através da transformação logaritmica dos dados. Isso pode ser feito facilmente no R com a função log que calcula o logarítmo natural dos dados. Vamos experimentar fazer uma transformação logarítmica em ambas as variáveis e verificar o resultado.
1 # criando um novo data frame chamado log.Indometh
2 log.Indometh <- Indometh
3
4 # Fazendo a transformação logarítmica das variáveis desse data frame
5 log.Indometh$conc <- log(Indometh$conc)
6 log.Indometh$time <- log(Indometh$time)
7
8 #plotando o gráfico com a linha de regressão (linear model)
9 ggplot(data=log.Indometh, aes(x=time, y=conc)) +
10 geom_point() +
11 geom_smooth(method = "lm")
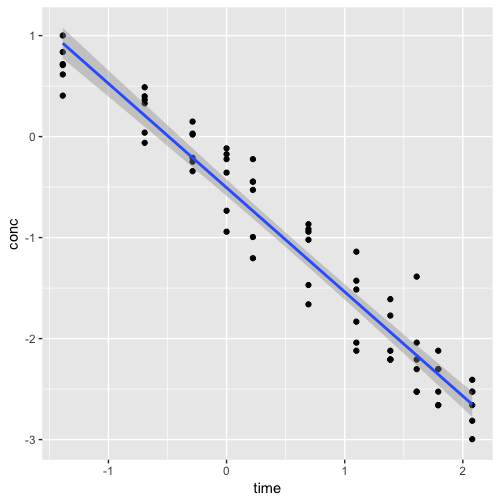
Vamos agora calcular o coeficiente de correlação dessas variáveis após a transformação logaritmica.
1 cor(log.Indometh$time, log.Indometh$conc)
2 [1] -0.9671346
Veja que o novo valor do coeficiente de correlação foi muitíssimo forte, indicando que a relação entre essas variáveis é melhor explicada por uma relação logarítmica e não por uma relação linear.
Referências
1. Stigler, Stephen M. Francis Galton’s Account of the Invention of Correlation.
Statist. Sci. 4 (1989), no. 2, 73–79. doi:10.1214/ss/1177012580. https://projecteuclid.org/euclid.ss/1177012580
2. Francis Galton. Co-Relations and Their Measurement, Chiefly from Anthropometric Data. Proceedings of the Royal Society of London. Vol. 45 (1888 - 1889), pp. 135-145. Disponível em: https://www.york.ac.uk/depts/maths/histstat/galton_corr.pdf.
3. Friendly, M. and Denis, D. (2005). The early origins and development of the scatterplot. J. Hist. Behav. Sci., 41: 103–130. doi:10.1002/jhbs.20078
4. Stephen Few. Now You See It. Simple Visualization Techniques for Quantitative Analysis. Analytic Press: Oakland, 2009.
5. F. J. Anscombe. Graphs in Statistical Analysis. The American Statistician. 1973, Vol. 27, No. 1, pp. 17-21.