Modelos Científicos
1 > library(tidyverse)
Introdução
O que é um modelo científico?
Um modelo é qualquer forma de representação simplificada a realidade que seja útil para analisamos e compreendermos os fenômenos em sua essência.
Um modelo pode ser um objeto físico, tal como um protótipo em miniatura de um avião ou uma peça de resina como um fêmur humano; pode ser uma teoria, tal como o modelo atômico de Bohr; pode ser um ser vivo, como nas situações em que um ratinho de laboratório é usado para testar os efeitos de um medicamento. Pode ser uma equação matemática, como a equação de uma reta de regressão linear. Um modelo pode ser também uma combinação de objetos físicos e softwares, tal como o manequim do SymMan, que simula as respostas biológicas humanas. Modelos nos ajudam a compreender os fenômenos pois ajudam a focar nossa atenção nos aspectos considerados mais importantes. O uso de simulações através de modelos tecnológicos é atualmente prática cada vez mais comum no ensino da medicina.
Modelos de relação linear no R
No capítulo anterior estudamos como o conceito de correlação é importante para a determinação da interação entre uma variável explanatória (independente) e uma variável de reposta (dependente). Vimos também que uma das etapas do estudo de correlação é a criação de uma reta de regressão, que é a reta que melhor se ajusta aos dados.
Precisamos agora relembrar que toda reta é definida por uma equação matemática muito simples:
[
y = mx + n
]
Na equação acima, m é chamado de coeficiente angular e representa a inclinação da reta e n é chamado de coeficiente linear da reta (ou intercept), sendo definido como o ponto em que a reta intercepta o eixo y.Com essa equação, dada uma coordenada no eixo x, podemos determinar qual será a coordenada no eixo y, bastando saber o valor dos coeficientes m e n. Toda reta é definida por essa simples equação, inclusive a reta de regressão linear. Ou seja, a geração da reta de regressão num gráfico depende apenas de conhecermos esses coeficientes. O processo de descobrir esses coeficientes depende de um processo conhecido na estatística como método dos quadrados mínimos. Entretanto, não precisamos nos preocupar com esse método num curso introdutório de estatística. O importante é saber que o R faz todos esses cálculos automaticamente e gera a reta de regressão como já vimos. Vamos repetir esse gráfico agora, mas extendendo os eixos um pouco mais para podermos ver os pontos de interceptação da reta nos eixos.
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 xlim(c(-1,11)) +
7 ylim(c(-1,40)) +
8 geom_vline(xintercept=0) +
9 geom_hline(yintercept=0) +
10 geom_smooth(method=lm, fullrange = TRUE) # Add linear regression line
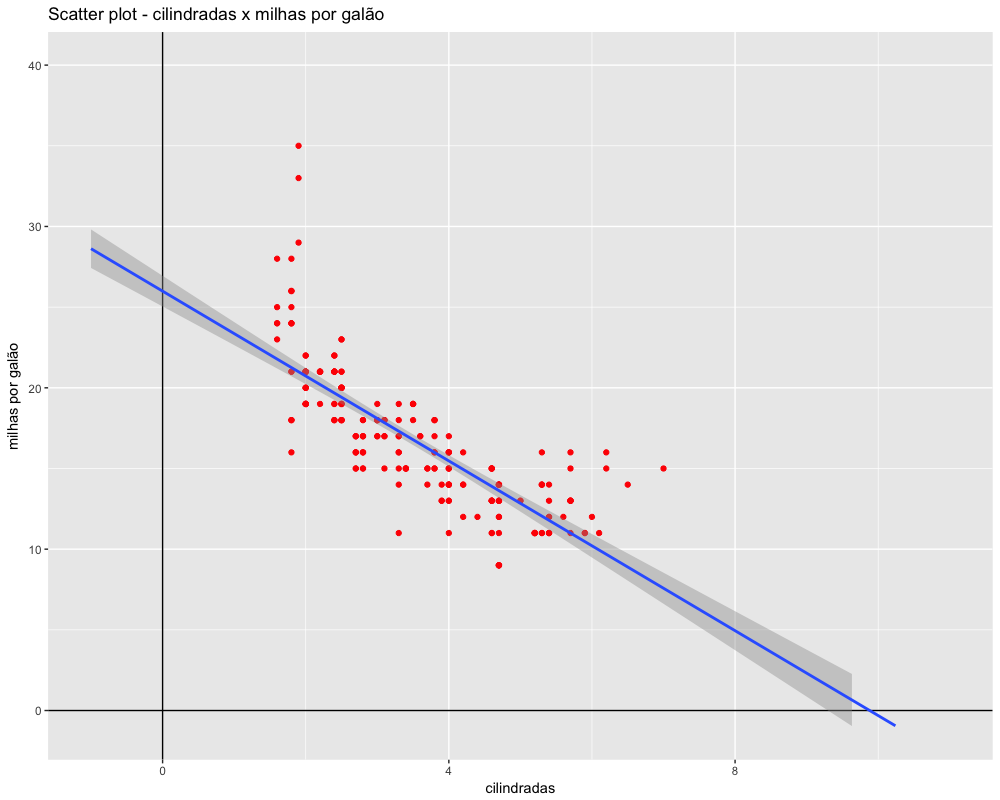
Observe no gráfico acima que a reta cruza o eixo y um pouco acima de 25 milhas e que a reta tem uma inclinação negativa. Ao calcularmos os valores exatos desses coeficientes você verá que eles coincidem com o gráfico. Calcular os coeficientes dessa reta é o próprio processo de criação de um modelo linear. Para obter os valores exatos dos coeficientes precisamos apenas pedir ao r para criar um modelo de relação liner com os dados que desejarmos. A função para criação de um modelo linear no R e lm()de linear model. Essa função tem a forma lm(y~x, data) que é interpretada pelo R como y depende de x. Observe que a fórmula inserida na função lm() deve ser na sequência:
variável_de_desfecho ~ variável_preditora
Vamos testar essa função usando os mesmos dados do gráfico acima: cilindradas como variável independente (explanatória ou independente) e milhas por galão como variável dependente (de desfecho ou dependente).
1 > lm(cty~displ, mpg)
2
3 Call:
4 lm(formula = cty ~ displ, data = mpg)
5
6 Coefficients:
7 (Intercept) displ
8 25.99 -2.63
Podemos ver no resultado acima a fórmula que foi usada no cálculo dos coeficientes e, logo abaixo, os coeficientes.
O valor mostrado logo abaixo de (intercept) é o coeficiente linear n = 25.99, o ponto do eixo y no qual a reta cruza o eixo vertical, ou seja, o ponto de interceptação da reta no eixo y. Veja que esse valor corresponde ao que havíamos notado no gráfico.
O outro valor é o coeficiente angular da reta m = -2.63.
Com isso temos tudo que precisamos para construir a reta de regressão. Ou seja, temos agora um modelo matemático para podermos prever qual será a distância percorrida por um carro, bastando saber suas cilindradas.
Vamos analisar os valores das cilindradas de nossa amostras:
1 > sort(unique(mpg$displ))
2
3 [1] 1.6 1.8 1.9 2.0 2.2 2.4 2.5 2.7 2.8 3.0 3.1 3.3 3.4 3.5 3.6 3.7 3.8 3.9
4 [19] 4.0 4.2 4.4 4.6 4.7 5.0 5.2 5.3 5.4 5.6 5.7 5.9 6.0 6.1 6.2 6.5 7.0
Veja que nessa amostra não temos carros de 3.2 cilindradas. Mas podemos usar nosso modelo (m = -2.63, n = 25.99) para prever quantas milhas esse carro irá percorrer com um galão de gasolina. Nossa fórmula será a seguinte:
1 > milhas_percorridas = -2.63 * 3.2 + 25.99
2 > milhas_percorridas
3 [1] 17.574
Vamos verificar que esse resultado no gráfico abaixo:
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 scale_x_continuous(breaks = seq(min(-1), max(15), by=0.5)) +
7 scale_y_continuous(breaks = seq(min(-1), max(40), by=1)) +
8 geom_vline(xintercept=0) +
9 geom_hline(yintercept=0) +
10 geom_vline(xintercept=3.2, color="blue", linetype="dotted") +
11 geom_hline(yintercept=17.574, color="blue", linetype="dotted") +
12 geom_smooth(method=lm, fullrange = TRUE) # Add linear regression line
13 # (by default includes 95% confidence region)
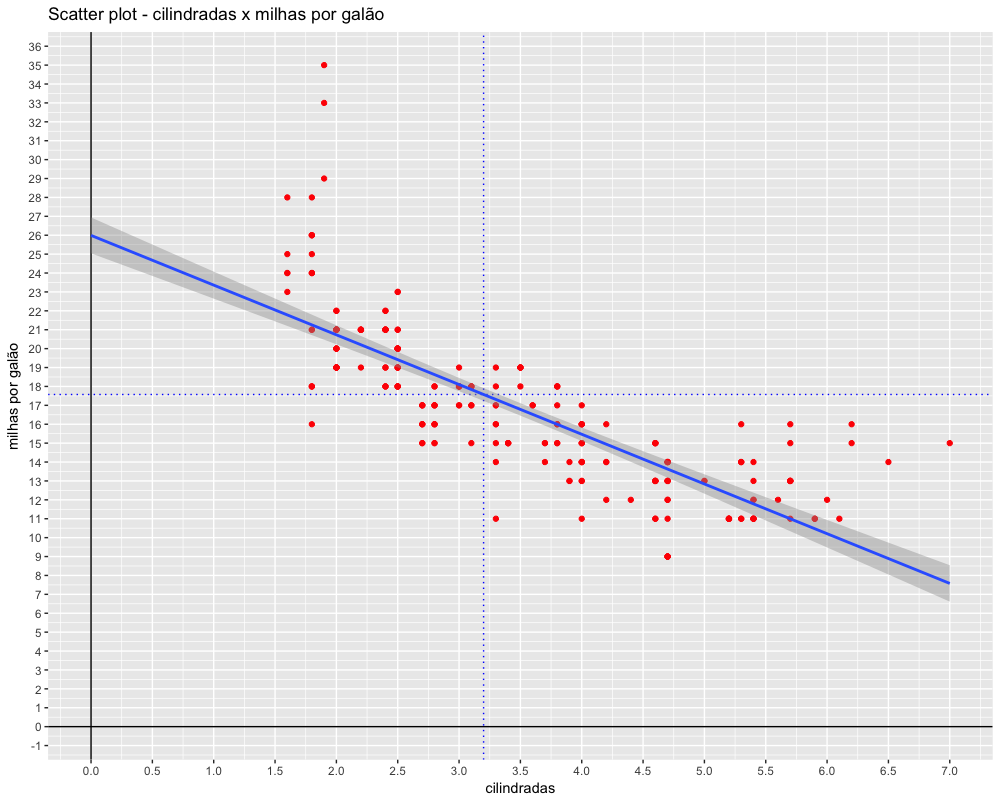
O Coeficiente de Determinação - magnitude do efeito
A função lm() tem muito mais dados do que apenas os coeficiente da reta. Para acessarmos esses dados completos basta usar a função summary() como abaixo:
1 > summary(lm(cty~displ, mpg))
2
3 Call:
4 lm(formula = cty ~ displ, data = mpg)
5
6 Residuals:
7 Min 1Q Median 3Q Max
8 -6.3109 -1.4695 -0.2566 1.1087 14.0064
9
10 Coefficients:
11 Estimate Std. Error t value Pr(>|t|)
12 (Intercept) 25.9915 0.4821 53.91 <2e-16 ***
13 displ -2.6305 0.1302 -20.20 <2e-16 ***
14 ---
15 Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
16
17 Residual standard error: 2.567 on 232 degrees of freedom
18 Multiple R-squared: 0.6376, Adjusted R-squared: 0.6361
19 F-statistic: 408.2 on 1 and 232 DF, p-value: < 2.2e-16
Veja que um dos resultados apresentados é o que se chama de R-Squared (R2). Essa medida é o coeficiente de determinação calculado pelo R para esse modelo linear. Esse coeficiente indica a proporção da variação da variável dependente pode ser explicada pela variável dependente. Nesse nosso exempplo o valor de R2 de 0.64 indica que 64% da variação do nº de milhas percorridas depende das cilindradas e o restante depende de outros fatores não analisados. Esse coeficiente indica a magnitude do efeito da variável independente (cilindradas) sobre a variável dependente (milhas percorridas).
A raiz quadrada desse coeficiente é justamente o coeficiente de correlação de Pearson que vimos no capítulo passado.
As limitações e utilidades dos modelos
Na seção anterior vimos que uma equação de uma reta servia como um modelo matemático da relação entre as cilindradas e a quantidade de milhas percorridas. Com esse modelo foi possivel inferir a quantidade de milhas percorridas com um galão por um carro de 3.2 cilindradas. É obvio que esse modelo é apenas uma simplificação da realidade. O resultado certamente irá depender de uma série de outras variáveis, tais como, por exemplo, o combustível usado, a idade do carro, os pneus usados, o tipo de asfalto e até mesmo o modo de condução do motorista. Modelos científicos serão sempre reducionistas, mas isso não é um defeito. Na verdade o papel do modelos não é representar a realidade em todos seus detalhes, o que seria impossível, mas simplificar a realidade de forma útil.
Modelos podem ser representações de um fenômeno natural mas também podem ser representações de um conjunto de dados. Existem diversos modelos matemáticos para representar distribuições de dados. Esses modelos teóricos de distribuição de dados são chamados de “Distribuições de Probabilidade”. Existe um número enorme de distribuições de probabilidade, cada uma apropriada para representar um tipo diferente de distribuição de dados. Esse é o tema do próximo capítulo.