p-values

1 library(ggplot2)

Introdução

Q: Why do so many colleges and grad schools teach p = 0.05?
A: Because that’s still what the scientific community and journal editors use.
Q: Why do so many people still use p = 0.05?
A: Because that’s what they were taught in college or grad school.
George Cobb, 2014

Como vimos no capítulo anterior, uma pesquisa científica visa produzir evidências a favor de uma de suas duas hipóteses: a hipótese nula ou a hipótese alternativa. Vimos também que o resultado de uma pesquisa pode ser falso de duas formas, falso positivo (erro tipo I) ou falso negativo (erro tipo II) e que, portando, nunca representa uma verdade absoluta, devendo sempre ser interpretado de forma probabilística. A medida de probabilidade usada para essa avaliação é o que se chama de valor de $p$, ou $p-value$.

Essa medida, o $p-value$, é calculada a partir dos resultados da pesquisa, ou seja, só pode ser calculada depois de coletados os dados. O mais adequado e intuitivo nesse momento seria nos perguntarmos tendo em vista esses dados, qual a chance da minha hipótese alternativa ser verdadeira?. Entretanto, a forma como a estatística lida com essa questão está bem longe de ser simples assim.

O $p-value$ não representa a probabilidade da hipótese alternativa ser verdadeira ou falsa e também não representa a probabilidade da hipótese nula ser verdadeira ou falsa. Muito pelo contrário, para o cálculo do p-value, a hipótese nula é dada como verdadeira. Ou seja, é a partir dessa premissa, que a hipótese nula seja verdadeira, é que o $p-value$ pode ser calculado.

O $p-value$ é a probabilidade de encontrarmos, apenas por acaso, o resultado que foi encontrado na pesquisa, ou resultados mais extremos. Ou seja, a probabilidade expressa pelo valor de $p$ não se refere às hipoteses, mas aos dados. O valor de $p$ representa a probabilidade de encontrarmos esses dados, ou dados mais extremos, apenas por acaso. É importante lembrar que afirmar que os resultados da pesquisa estão sendo influenciados apenas pelo acaso é o mesmo que dizer que a hipótese nula é verdadeira. A definição formal do valor de $p$ é usualmente descrita nesses termos:

A probabilidade do resultado encontrado, ou resultados mais extremos, terem sido observados, se a hipótese nula for verdadeira.

Origens e confusões

O $p-value$ foi proposto por Ronald Fisher por volta da década de 1920 para ser usado como uma medida da discrepância entre os dados observados e a hipótese nula, sendo apenas uma parte de um processo de análises dos resultados (GOODMAN, 1999). Para Fisher, um valor de $p<0.05$ significava apenas que a experiência merecia ser repetida novamente e que, se numa série desses experimentos subsequentes o valor de $p$ se mantivesse sempre abaixo de 0.05, isso sim seria um indício de que os resultados não se deviam apenas ao acaso. Ou seja, a função original do valor de $p$ era apenas indicar que o resultado era digno de atenção e não prova de nenhum resultado (GOODMAN, 2008).

Entretanto, o $p-value$ passou a ser uma das mais frequentes e mais mal interpretadas dentre as medidas estatísticas nas pesquisas científicas da área da saúde. Goodman (2008) lista frequentes erros de interpretação do valor de $p$ que merecem ser repetidos aqui:

Se $p=0.05$, a hipótese nula tem 5% de chance de ser verdadeira
Uma $p > 0.05$ significa que náo há diferença entre os grupos
Um resultado estatisticamente significativo é também clinicamente significativo
Estudos com valores de $p$ idênticos tem a mesma força de evidência sobre a hipótese nula
Um valor de $p = 0.05$ significa que a chance de encontrar por acaso exatamente os dados da pesquisa é de 5%.
$p = 0.05$ e $p \le 0.05$ tem o mesmo significado
$p-values$ devem ser escritos com sinal de $<$ ou $>$
$p=0.05$ significa que se você rejeitar a hipótese nula, a probabilidade de erro tipo I é de apenas 5%.
Uma conclusão científica ou decisão de tratamento deve ser fundamentada num valor de $p$ significativo

Interpretação gráfica do valor de p

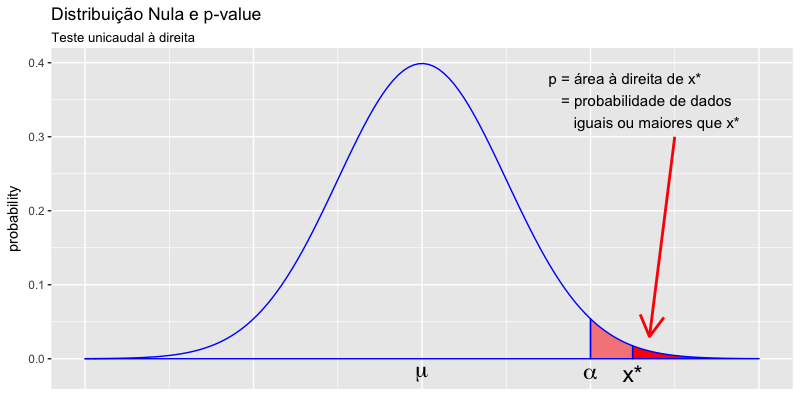
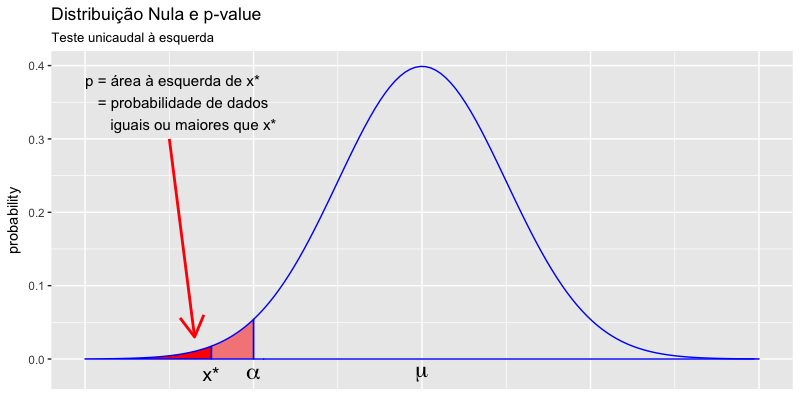
Um probabilidade é calculada a partir de uma curva de distribuição, como a área abaixo a curva, à esquerda ou à direita de um determinado ponto. O $p-value$ não é exceção. É calculado como a área abaixo de uma curva de distribuição, mais extrema que o ponto médio dos dados observados na pesquisa.

Precisamos então responder a seguinte pergunta: Qual a distribuição deve ser usada para calcular o valor de $p$.

A definição do valor de $p$ é a probabilidade de encontrarmos os dados da pesquisa, ou dados mais extremos, supondo que a hipótese nula seja verdadeira. Ou seja, o valor de $p$ é calculado levando em conta como os dados estariam distribuídos caso a hipótese nula fosse verdadeira. Isso significa que o valor de $p$ é calculado a partir da distribuição nula.

Referências

Ronald L. Wasserstein & Nicole A. Lazar (2016) The ASA’s Statement on p-Values: Context, Process, and Purpose, The American Statistician, 70:2, 129-133, DOI: 10.1080/00031305.2016.1154108

Goodman S. A dirty dozen: twelve p-value misconceptions. Semin Hematol. 2008
Jul;45(3):135-40. doi: 10.1053/j.seminhematol.2008.04.003. Review. Erratum in:
Semin Hematol. 2011 Oct;48(4):302.

Goodman SN. Toward evidence-based medical statistics. 1: The P value fallacy.
Ann Intern Med. 1999 Jun 15;130(12):995-1004.