Estatística Descritiva no R
Introdução
Veremos nesse capítulo as medidas mais importantes para descrever uma conjunto de dados: as medidas de localização central (média e mediana) e as medidas de dispersão (variância e desvio padrão). Essas medidas, hoje tão comuns e simples, tiveram um lento e complexo desenvolvimento ao longo de muitos séculos. A noção de que a média poderia representar os dados só surgiu com os trablahos de Galileu por volta de 1632 (Sthal, 2006 ) e o termo desvio padrão só foi cunhado em 1892 pelo estatístico Karl Person (Magnello, 1996). Essas medidas são os blocos fundamentais da estatística moderna e é imprescindível saber usá-las e interpretá-las adequadamente.
Parte 1 - Carregamento do dataset mpg
Para experimentarmos usar as diversas funções estatísticas do R, vamos primeiro carregar um conjunto de dados que vem junto com o pacote ggplot2. Se você já instalou o pacote tidyverse então o ggplot2 já foi instalado. Você pode também instalar o pacote ggplot2 isoladamente se desejar. O comando para instalar os pacotes é o install.packages(). Lembre-se de que a instalação de um pacote deve ser sempre feita no console e nunca num R script ou num R Notebook.
Para instalar o pacote tidyverse, use o comando abaixo no console: (recomendado)
1 > install.packages("tidyverse")
Caso prefira, instalar oggplot2 isoladamente, use o comando abaixo no console:
1 > install.packages("ggplot2")
ATENÇÃO: Se você já instalou esses pacotes, não é necessário instalar novamente.
Com os pacote ggplot2 instalado podemos agora usar os datasets que vem junto com esse pacote. para isso é necessário primeiro carregar o pacote ggplot2 na memória do computador, o que é feito com a função library(ggplot2).
Atenção: observe que ao usar a função library() não precisamos usar as aspas.
Com o pacote ggplot2 estão carregados na memória e podemos usar os datasets que vem junto com esse pacote. Vamos usar o dataset mpg para nosso treinamento de estatística descritiva no R. O acrônimo mpg significa Miles Per Gallon - uma medida de quantas milhas um carro pode viajar se você colocar apenas um galão de gasolina ou diesel em seu tanque (1 galão equivale a 3.79 litros e uma milha equivale a 1.6km).
Esta medida padronizada serve comparar carros com base na sua eficiência. O conjunto de dados mpg que vem junto com o ggplot2 é apenas um subconjunto dos dados de economia de combustível que a EPA (Enviroment Protection Agency - USA) disponibiliza em http://fueleconomy.gov. O conjunto completo dos dados podem ser obtidos nesse site, no link seguir:
http://fueleconomy.gov/feg/download.shtml.
Em primeiro lugar, abra um novo Script para deixar todos os comandos gravados. Escolha um nome para seu Script e salve regularmente esse Script para não perder os dados. Digite os comandos a seguir em seu Script e não no console. Para executar um comando do Script coloque o cursor no final da linha de comandos e clique em Command+Return (no mac) ou Control+Return (no Windows).
No início de seu Script é que você deve colocar os comandos library, como a seguir:
1 library(tidyverse)
Para facilitar essa aula, vamos usar simplesmente o dataset mpg que já vem com o ggplot2. Para carregar esse dataset basta usar o comando abaixo:
1 data(mpg)
Com a função class() podemos verificar que esse dataset é um data frame do R.
1 > class(mpg)
2 [1] "tbl_df" "tbl" "data.frame"
Em primeiro lugar, vamos visualizar as primeiras linhas desse dataset com a função head():
1 > head(mpg)
2
3 # A tibble: 6 x 11
4 manufacturer model displ year cyl trans drv cty hwy fl class
5 <chr> <chr> <dbl> <int> <int> <chr> <chr> <int> <int> <chr> <chr>
6 1 audi a4 1.8 1999 4 auto(l5) f 18 29 p compact
7 2 audi a4 1.8 1999 4 manual(m5) f 21 29 p compact
8 3 audi a4 2.0 2008 4 manual(m6) f 20 31 p compact
9 4 audi a4 2.0 2008 4 auto(av) f 21 30 p compact
10 5 audi a4 2.8 1999 6 auto(l5) f 16 26 p compact
11 6 audi a4 2.8 1999 6 manual(m5) f 18 26 p compact
Com esse comando você pode visualizar as primeiras linhas tabela do dataset mpg.
Podemos também usar o comando str() para visualizarmos a estrutura desse data frame, as variáveis e seus tipos:
1 > str(mpg)
2
3 Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 234 obs. of 11 variables:
4 $ manufacturer: chr "audi" "audi" "audi" "audi" ...
5 $ model : chr "a4" "a4" "a4" "a4" ...
6 $ displ : num 1.8 1.8 2 2 2.8 2.8 3.1 1.8 1.8 2 ...
7 $ year : int 1999 1999 2008 2008 1999 1999 2008 1999 1999 2008 ...
8 $ cyl : int 4 4 4 4 6 6 6 4 4 4 ...
9 $ trans : chr "auto(l5)" "manual(m5)" "manual(m6)" "auto(av)" ...
10 $ drv : chr "f" "f" "f" "f" ...
11 $ cty : int 18 21 20 21 16 18 18 18 16 20 ...
12 $ hwy : int 29 29 31 30 26 26 27 26 25 28 ...
13 $ fl : chr "p" "p" "p" "p" ...
14 $ class : chr "compact" "compact" "compact" "compact" ...
Esse dataset possui 243 linhas (observações) com 11 variáveis. O significado de cada variável está descrito na documentação de ajuda do dataset mpg e pode ser visualizado com o comando ?mpg no console. A tabela abaixo mostra o significado de cada variável:
| variável | significado |
|---|---|
| manufacturer | marca |
| model | modelo |
| displ | cilindradas (Engine Displacement) |
| year | ano de fabricação |
| cyl | número de cilindros |
| trans | tipo de marcha: automática / manual |
| drv | tração: f=frontal, r=traseira, 4=4x4 |
| cty | milhas por galão na cidade |
| hwy | milhas por galão na estrada |
| fl | tipo de combustível: r=regular, p=premium, d=diesel, e=ethanol, c=CNG (gás) |
| class | tipo de carro |
Parte 2 - Tabelas de frequências
Em estatística, uma distribuição de frequências é uma tabela ou gráfico que mostra a frequência das variáveis categóricas (nominais ou ordinais) de uma amostra, ou sejam, o número de ocorrências dessas variáveis. Variáveis numéricas podem também ser mostradas em tabelas de frequencias, nesse caso, é necessário classificar as variáveis numéricas em intervalos. Cada entrada na tabela contém a frequência ou a contagem de ocorrências dentro de um grupo ou intervalo específico. Ou seja, uma tabela de frequências resume a distribuição dos valores da amostra.
Use a função table() para criar tabelas de frequências das variáveis categóricas dessa pesquisa (marca, ano, número de cilindros, tipo de marcha, tipo de combustível, tipo de carro). A função table() mostra as frequencias absolutas de cada uma das classes da variável. Por exemplo, para saber quantos carros nessa amostra tem 4 cilindros, quantos tem 5 cilindros, quantos tem 6 cilindros e quantos tem 8 cilindros podemos usar a função table(), inserindo como argumento a variável cyl, como mostrado abaixo:
1 > table(mpg$cyl)
2
3 4 5 6 8
4 81 4 79 70
Essa tabela pode ficar mais compreensível se nomearmos o conjunto de dados. Nesse caso, a variável cylrepresenta o nº de cilindros dos carros, logo:
1 > table(cilindros=mpg$cyl)
2
3 cilindros
4 4 5 6 8
5 81 4 79 70
Podemos também verificar as proporções relativas de cada variável com a função prop.table().
1 > prop.table(table(cilindros=mpg$cyl))
2
3 cilindros
4 4 5 6 8
5 0.34615385 0.01709402 0.33760684 0.29914530
Caso se deseje expressar as proporções em percentuais, basta multiplicar a tabela por 100
1 > prop.table(table(cilindros=mpg$cyl))*100
2
3 cilindros
4 4 5 6 8
5 34.615385 1.709402 33.760684 29.914530
E para arrendar as casas decimais, usamos a função round(). Veja no exemplo abaixo o uso dessa função arrendondando o percentual para 2 casas decimais.
1 > round(prop.table(table(cilindros=mpg$cyl))*100,2)
2
3 cilindros
4 4 5 6 8
5 34.62 1.71 33.76 29.91
Podemos também usar a função table() para construir tabelas de duas ou mais dimensões. Para isso basta incluir as outras variáveis como argumentos da função. Lembre-se que nomear as variáveis pode tornar a tabela mais compreensível.
1 > table(montadora=mpg$manufacturer, cilindros=mpg$cyl)
2
3 cilindros
4 montadora 4 5 6 8
5 audi 8 0 9 1
6 chevrolet 2 0 3 14
7 dodge 1 0 15 21
8 ford 0 0 10 15
9 honda 9 0 0 0
10 hyundai 8 0 6 0
11 jeep 0 0 3 5
12 land rover 0 0 0 4
13 lincoln 0 0 0 3
14 mercury 0 0 2 2
15 nissan 4 0 8 1
16 pontiac 0 0 4 1
17 subaru 14 0 0 0
18 toyota 18 0 13 3
19 volkswagen 17 4 6 0
Nesse caso, a primeira variável será colocadas nas linhas e a segunda variável será colocadas nas colunas da tabela.
Quando temos tabelas de frequências de duas dimensões, podemos extrair as frequencias relativas tanto por linhas como por colunas, para isso basta inserir mais um argumento na função prop.table():
1 - para calcular as frequencias relativas em cada linha
2 - para calcular as frequencias relativas em cada coluna
1 # frequencias relativas calculadas em cada linha
2 > prop.table(table(montadora=mpg$manufacturer, cilindros=mpg$cyl),1)
3
4 cilindros
5 montadora 4 5 6 8
6 audi 0.44444444 0.00000000 0.50000000 0.05555556
7 chevrolet 0.10526316 0.00000000 0.15789474 0.73684211
8 dodge 0.02702703 0.00000000 0.40540541 0.56756757
9 ford 0.00000000 0.00000000 0.40000000 0.60000000
10 honda 1.00000000 0.00000000 0.00000000 0.00000000
11 hyundai 0.57142857 0.00000000 0.42857143 0.00000000
12 jeep 0.00000000 0.00000000 0.37500000 0.62500000
13 land rover 0.00000000 0.00000000 0.00000000 1.00000000
14 lincoln 0.00000000 0.00000000 0.00000000 1.00000000
15 mercury 0.00000000 0.00000000 0.50000000 0.50000000
16 nissan 0.30769231 0.00000000 0.61538462 0.07692308
17 pontiac 0.00000000 0.00000000 0.80000000 0.20000000
18 subaru 1.00000000 0.00000000 0.00000000 0.00000000
19 toyota 0.52941176 0.00000000 0.38235294 0.08823529
20 volkswagen 0.62962963 0.14814815 0.22222222 0.00000000
Mais uma vez, podemos usar a função round para arrendondar os dados. Nesse caso, para facilitar a compreensão do código, podemos fazer cada etapa separadamente, como abaixo:
1 # criando uma tabela 2x2 com montadoras x nº de cilindros - frequencias absolutas
2 > tabela.1 <- table(montadora=mpg$manufacturer, cilindros=mpg$cyl)
3 > tabela.1
4
5 cilindros
6 montadora 4 5 6 8
7 audi 8 0 9 1
8 chevrolet 2 0 3 14
9 dodge 1 0 15 21
10 ford 0 0 10 15
11 honda 9 0 0 0
12 hyundai 8 0 6 0
13 jeep 0 0 3 5
14 land rover 0 0 0 4
15 lincoln 0 0 0 3
16 mercury 0 0 2 2
17 nissan 4 0 8 1
18 pontiac 0 0 4 1
19 subaru 14 0 0 0
20 toyota 18 0 13 3
21 volkswagen 17 4 6 0
1 # calculandoas frequencias relativas NAS LINHAS, em percentuais da tabela recém \
2 criada
3 > tabela.2 <- prop.table(tabela.1,1)*100
4 > tabela.2
5
6 cilindros
7 montadora 4 5 6 8
8 audi 44.444444 0.000000 50.000000 5.555556
9 chevrolet 10.526316 0.000000 15.789474 73.684211
10 dodge 2.702703 0.000000 40.540541 56.756757
11 ford 0.000000 0.000000 40.000000 60.000000
12 honda 100.000000 0.000000 0.000000 0.000000
13 hyundai 57.142857 0.000000 42.857143 0.000000
14 jeep 0.000000 0.000000 37.500000 62.500000
15 land rover 0.000000 0.000000 0.000000 100.000000
16 lincoln 0.000000 0.000000 0.000000 100.000000
17 mercury 0.000000 0.000000 50.000000 50.000000
18 nissan 30.769231 0.000000 61.538462 7.692308
19 pontiac 0.000000 0.000000 80.000000 20.000000
20 subaru 100.000000 0.000000 0.000000 0.000000
21 toyota 52.941176 0.000000 38.235294 8.823529
22 volkswagen 62.962963 14.814815 22.222222 0.000000
1 # observe que a soma de cada linha deverá ser 100
2 # arredondando os valores para 1 casa decimal.
3 > tabela.3 <- round(tabela.2,1)
4 > tabela.3
5
6 cilindros
7 montadora 4 5 6 8
8 audi 44.4 0.0 50.0 5.6
9 chevrolet 10.5 0.0 15.8 73.7
10 dodge 2.7 0.0 40.5 56.8
11 ford 0.0 0.0 40.0 60.0
12 honda 100.0 0.0 0.0 0.0
13 hyundai 57.1 0.0 42.9 0.0
14 jeep 0.0 0.0 37.5 62.5
15 land rover 0.0 0.0 0.0 100.0
16 lincoln 0.0 0.0 0.0 100.0
17 mercury 0.0 0.0 50.0 50.0
18 nissan 30.8 0.0 61.5 7.7
19 pontiac 0.0 0.0 80.0 20.0
20 subaru 100.0 0.0 0.0 0.0
21 toyota 52.9 0.0 38.2 8.8
22 volkswagen 63.0 14.8 22.2 0.0
Variáveis cagtegóricas são usualmente resumidas com tabelas de frequências como fizemos acima. Variáveis numéricas podem se resumidas em tabelas, desde que seus valores sejam categorizados em classes ou intervalos. Entretanto, no caso de variáveis numéricas, podemos resumir os dados de outras formas, usando medidas numéricas de centralidade e de dispersão desses dados, como veremos a seguir.
Parte 3 - Medidas de Tendência Central
Média e Mediana
A medida mais frequentemente investigada num conjunto de dados é seu centro, ou o ponto no qual as observações tendem a se concentrar. Medidas de tendência central são as estatísticas que descrevem um conjunto de dados pela sua posição central.
Existem várias medidas (estatísticas) que identificam a posição central de um conjunto de dados. As principais estatísticas que resumem um conjunto de dados pela posição central são a média, a mediana e a moda. A média e a mediana são facilmente calculadas no R através das funções mean() e median().
Vamos avaliar a média e a mediana do consumo dos carros na cidade e na estrada, lembrando que esses dados estão na variável cty e hwydo dataset mpg. Lembre-se que para acessar uma variável de um data frame usamos o operador $ da seguinte maneira: nome.do.data.frame$nome.da.variável.
Calculando a média e a mediana do número de milhas percorridas na cidade por galão :
1 > mean(mpg$cty)
2 [1] 16.85897
3
4 > median(mpg$cty)
5 [1] 17
Calculando a média e a mediana do número de milhas percorridas na estrada por galão :
1 > mean(mpg$hwy)
2 [1] 23.44017
3
4 > median(mpg$hwy)
5 [1] 24
Podemos visualizar esses dados num gráfico de barras com as médias de consumo na estrada e na cidade.
1 medias.consumo <- data.frame(cidade=mean(mpg$cty), estrada=mean(mpg$hwy))
2 medias.long <- gather(medias.consumo, local, milhas, cidade, estrada)
3 ggplot(medias.long, aes(x=local, y=milhas)) +
4 geom_col(fill = "cornflowerblue") +
5 ggtitle("Consumo em milhas por galão: cidade x estrada") +
6 geom_text(aes(label=round(milhas,2)), vjust=-0.5)
7 rm(medias.consumo,medias.long)
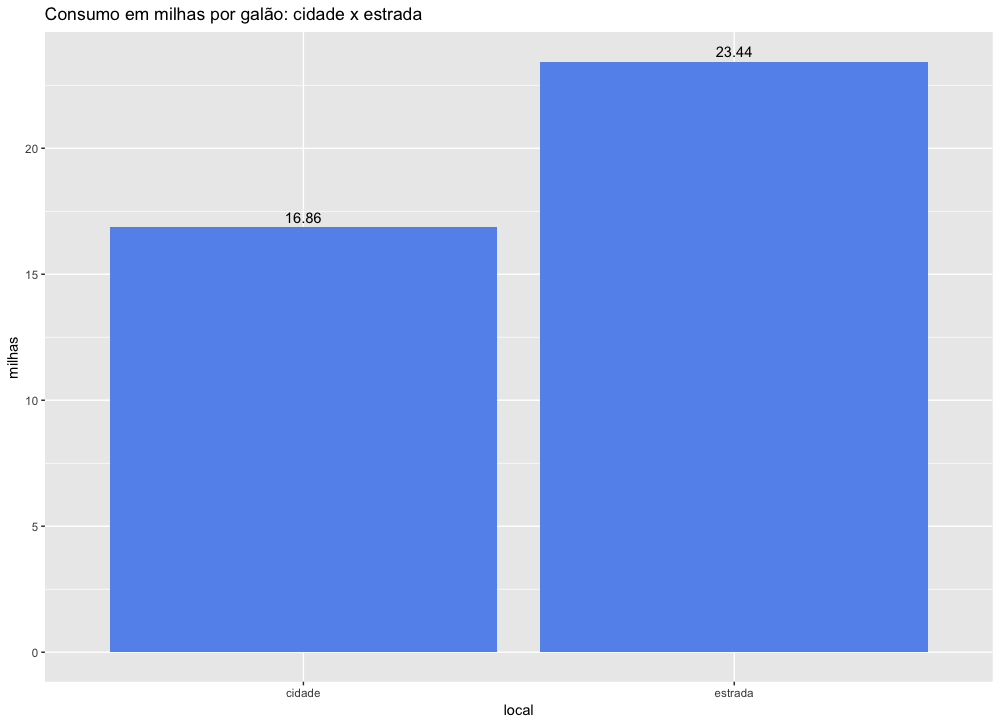
Podemos ver que a quantidade média de milhas percorridas na estrada, com um galão, é bem maior. ou seja, com a mesma quantidade de combustível (um galão) os carros percorrem mais milhas na estrada do que na cidade.
Entretanto, examinar apenas a média ou a mediana desses valores não é suficiente. Uma situação pessoal vivida pelo biólogo Stephen Jay Gould nos mostra como a média é apenas uma parte da história. Em julho de 1982 Gould foi diagnosticado com um Mesotelioma abadominal, uma forma rara e grave de câncer, cuja média de expectativa de vida na ocasião era de 8 meses. Uma leitura superficial desses dados poderia fazer Gould pensar que iria morrer em 8 meses. Entretanto, tendo um sólido conhecimento biológico e estatístico, Gould não se satisfez em conhecer apenas o dados da mediana (ou da média) e procurou descobrir qual seria a variação desses dados, quanto alguém poderia viver com esse tipo de câncer? O que Gould descobriu depois sobre esse câncer é que algumas pessoas conseguiam sobreviver por muitos anos depois do diagnóstico, ou seja, a curva de distribuição da sobrevida era muito assimétrica à direita. Nas palavras de Gould,
Portanto, para analisar de forma adequada um conjunto de dados, precisamos conhecer mais do que apenas a média e a mediana, precisamos conhecer a distribuição dos dados. Vamos ver como estão distribuídos os dados do rendimento dos carros na cidade.
1 ggplot(data=mpg) +
2 geom_density(aes(x=cty), fill= "cornflowerblue", col="blue", alpha=0.5) +
3 xlab("milhas por galão") +
4 ylab("frequencia") +
5 geom_vline(xintercept = mean(mpg$cty), col="red") +
6 labs(title = "Distribuição do rendimento dos carros na cidade",
7 subtitle = "Milhas por galão de combustível",
8 caption = "Fonte: dataset mpg do pacote ggplot2")
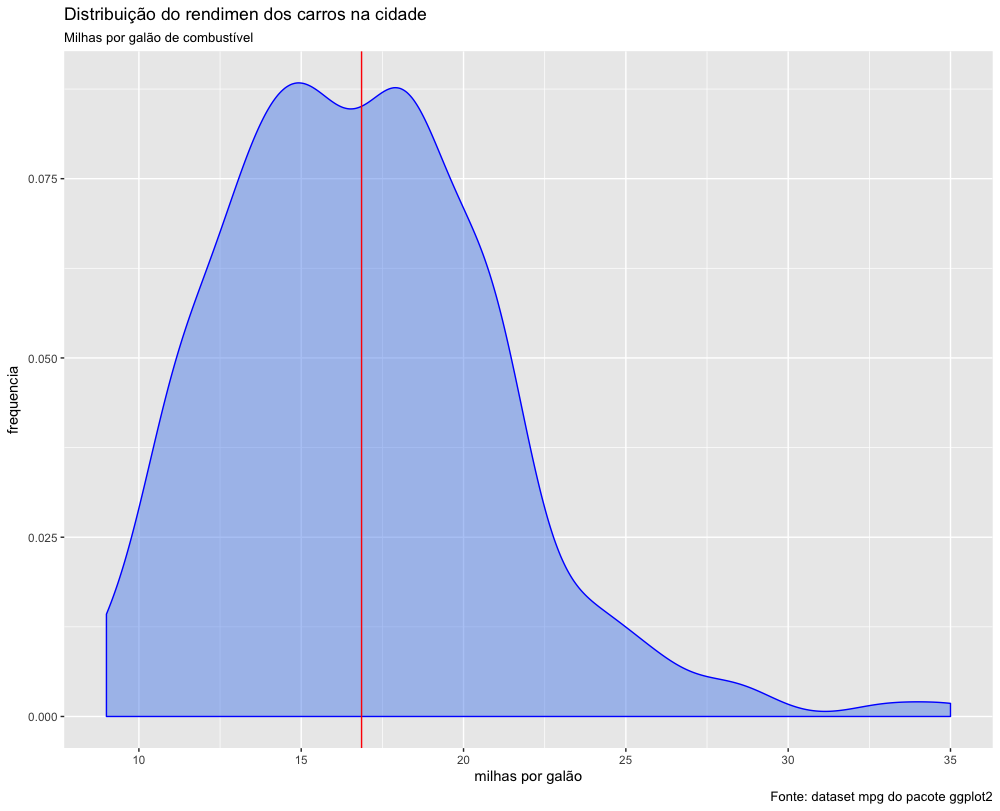
Podemos ver que a média conta apenas uma parte da história, pois existem carros que percorrem menos de 10 milhas com um galão, e alguns poucos carros que percorrem até 35 milhas com um galão de combustível.
Vamos visualizar agora as duas distribuições do rendimento, na cidade e na estrada, sobrepostas uma na outra. As linhas verticais representam as médias da quantidade de milhas percorridas na cidade e na estrada. Não se preocupe em tentar entender esse código agora. Você pode simplesmente copiar e colar esse código em seu script:
1 mpg.long <- mpg %>%
2 select(cty, hwy) %>%
3 gather(key=local, value = distancia, cty, hwy)
4
5 ggplot(data=mpg.long) +
6 geom_density(aes(x=distancia, fill=local), alpha=0.5) +
7 xlab("miles per gallon") + ylab("frequencia") +
8 geom_vline(xintercept = mean(mpg$cty), col="red") +
9 geom_vline(xintercept = mean(mpg$hwy), col="cyan4") +
10 labs(title = "Distribuição do consumo dos carros",
11 subtitle = "Milhas por galão de combustível: cidade x estrada",
12 caption = "Fonte: dataset mpg do pacote ggplot2")
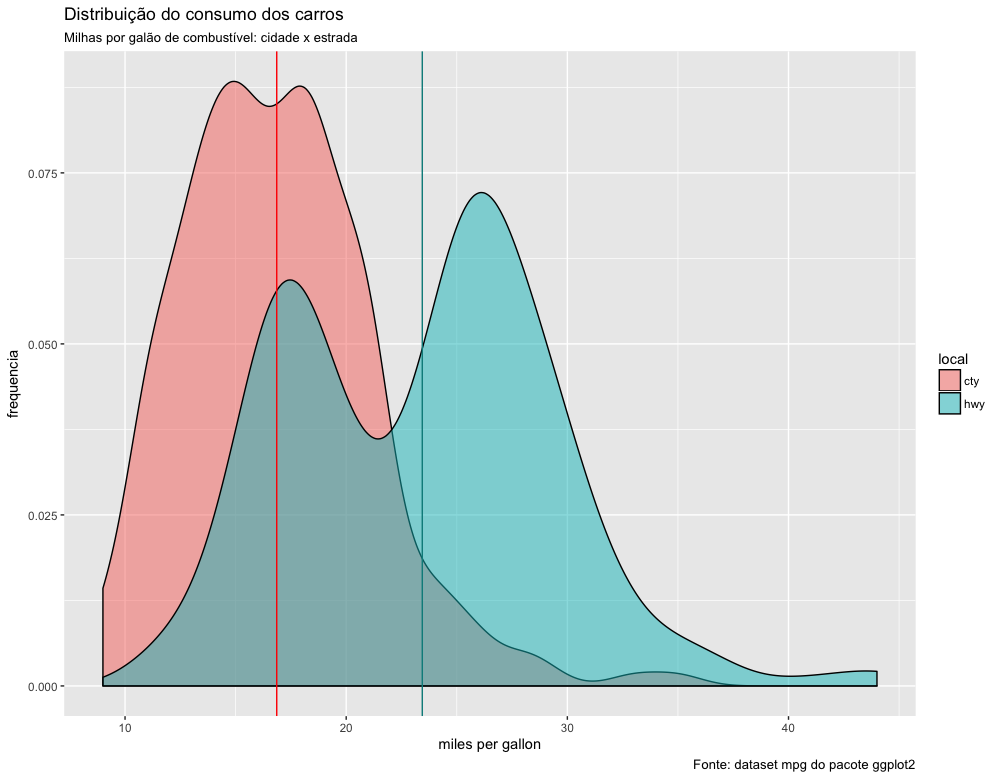
Podemos ver que existe uma grande sopreposição das curvas de distribuição. Não podemos dizer, portanto, que a quantidade de milhas percorridas na cidade será sempre menor que na estrada. Isso só será verdade se estivermos comparando um mesmo tipo de carro. Entretanto, alguns carros conseguem percorrer na cidade mais milhas que outros conseguem percorrer na estrada.
A distribuição dos dados ao redor da média é assimétrica à direita em ambos os conjuntos de dados, pois os valores mais extremos estão à direita.
Observe também que ambas as distribuições têm dois picos, mais evidentes na distribuição do consumo na estrada. Essa distribuição é chamada de bimodal devido a isso.
Vamos analisar agora a distribuição das cilindradas dos veículos, calculando inicialmente a média e a mediana (variável é displ).
1 > mean(mpg$displ) # media das cilindradas
2 [1] 3.471795
3
4 > median(mpg$displ) # mediana das cilindradas
5 [1] 3.3
A mediana é um pouco diferente da média, ligeiramente inferior à média. Se a distribuição desse dados fosse simétrica seria esperado que a média e a mediana fossem iguais, o que não é o caso. Vamos analisar visualmente a distribuição das cilindradas com o código abaixo:
1 ggplot() +
2 geom_density(data=mpg, aes(x=displ),
3 fill="green",
4 color="darkblue",
5 alpha=0.5) +
6 geom_vline(xintercept = mean(mpg$displ),
7 col="red") +
8 geom_vline(xintercept = median(mpg$displ),
9 col="blue") +
10 xlab("cilindradas") +
11 ylab("frequencia") +
12 labs(title = "Distribuição das Cilindradas dos Carros",
13 subtitle = "azul:mediana, vermelho:media",
14 caption = "Fonte: dataset mpg do pacote ggplot2")
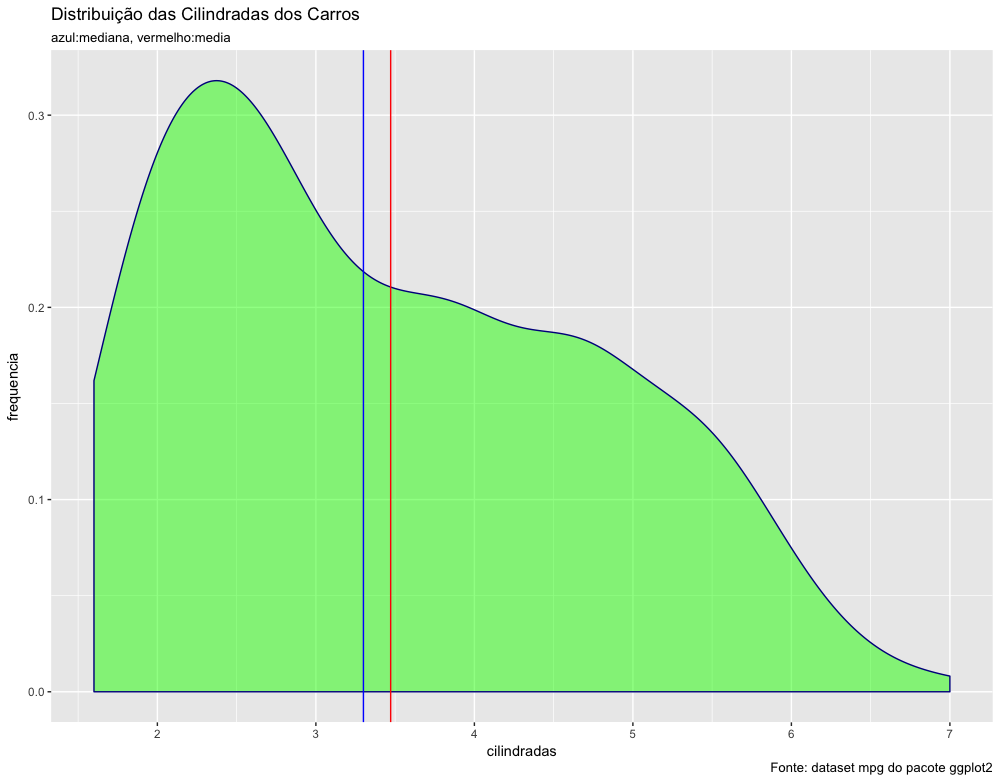
Veja que a distribuição é assimétrica à direita, ou seja, tem valores mais extremos à direita. Esses valores aumentam o valor da média. A mediana, por outro lado, é menos afetada por valores extremos. Você pode verificar no gráfico acima que a mediana (azul) é menor que a média (vermelho).
Visualizar num gráfico a distribuição dos dados é uma etapa chave da análise descritiva de uma pesquisa. Mas precisamos também conhecer as medidas estatísticas usadas para resumir a variação (ou dispersão) dos dados. Essas medidas são o objeto do próximo tópico.
Parte 4 - Medidas de Dispersão
1. Amplitude (range)
2. Amplitude interquartil (IQR = interquartile range)
3. Percentis (quantiles)
4. Variância
5. Desvio padrão (sd = standard deviation)
Como vimos, conhecer o ponto central de uma distribuição não é suficiente para descrever completamente um conjunto de dados. Precisamos saber também como esses dados estão distribuídos. Alguns conjuntos de dados podem ter a mesma média e serem bastante diferentes. Veja nos gráficos abaixo alguns exemplos de dados com a mesma média, mas com grande diferença no que se refere à dispersão dos dados ao redor da média.
1 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 \
2 e desvio padrão=5
3 c1 <- rnorm(1000, mean = 100, sd = 5)
4 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 \
5 e desvio padrão=10
6 c2 <- rnorm(1000, mean = 100, sd = 10)
7 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 \
8 e desvio padrão=20
9 c3 <- rnorm(1000, mean = 100, sd = 20)
10 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 \
11 e desvio padrão=40
12 c4 <- rnorm(1000, mean = 100, sd = 40)
13 # indica que iremos colocar os gráficos num grid 2x2
14 par(mfrow=c(2,2))
15
16 # gerando os histogramas coloridos.
17
18 hist(c1,
19 col = "orange",
20 breaks = 15,
21 xlim = c(-50, 250),
22 main = "Média = 100 \nDesvio padrão = 5")
23
24 hist(c2,
25 col = "darkorange",
26 breaks = 15,
27 xlim = c(-50, 250),
28 main = "Média = 100 \nDesvio padrão = 10")
29
30 hist(c3,
31 col = "brown",
32 breaks = 15,
33 xlim = c(-50, 250),
34 main = "Média = 100 \nDesvio padrão = 15")
35
36 hist(c4,
37 col = "red",
38 breaks = 15,
39 xlim = c(-50, 250),
40 main = "Média = 100 \nDesvio padrão = 40")
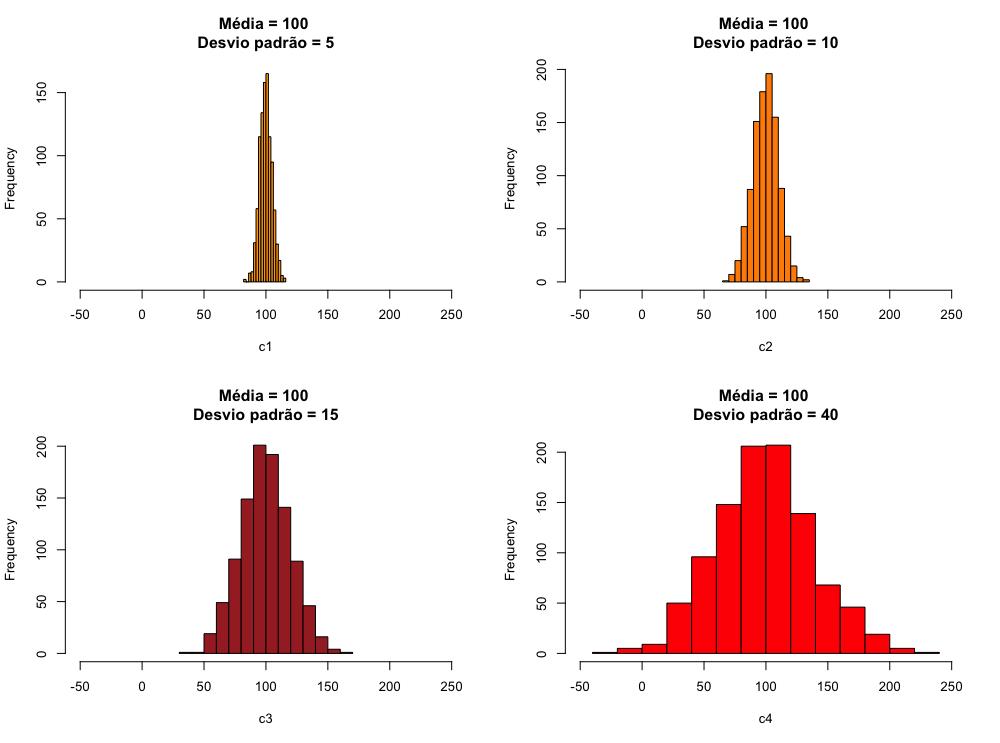
A necessidade descrever melhor um conjunto de dados tornou necessária a criação de medidas que descrevessem a dispersão dos dados ao redor da média.
Amplitude
A medida mais simples de dispersão dos dados é amplitude (range em ingles). A amplitude é a diferença entre o valor máximo e o valor mínimo. Veja no exemplo abaixo uma ilustração visual do significado dessa medida. Copie e cole esse código no seu script R para ver o gráfico.
1 a <- c(1, 1.2, 1.5, 1.7, 1.8, 1.9, 2.2, 2.3, 2.6, 2.7, 8)
2 b <- c(1, 2, 2.5, 4, 4.5, 5.5, 6, 6.4, 7, 7.5, 8)
3
4 tabela <- data.frame(a, b) %>% gather(key = conjunto, value = valores, a, b)
5
6 ggplot(tabela) +
7 geom_dotplot(aes(x=valores, fill=conjunto)) +
8 facet_wrap(~conjunto, ncol=1) +
9 ggtitle("Distribuição dos dados dos conjuntos a e b") +
10 theme(legend.position="none")
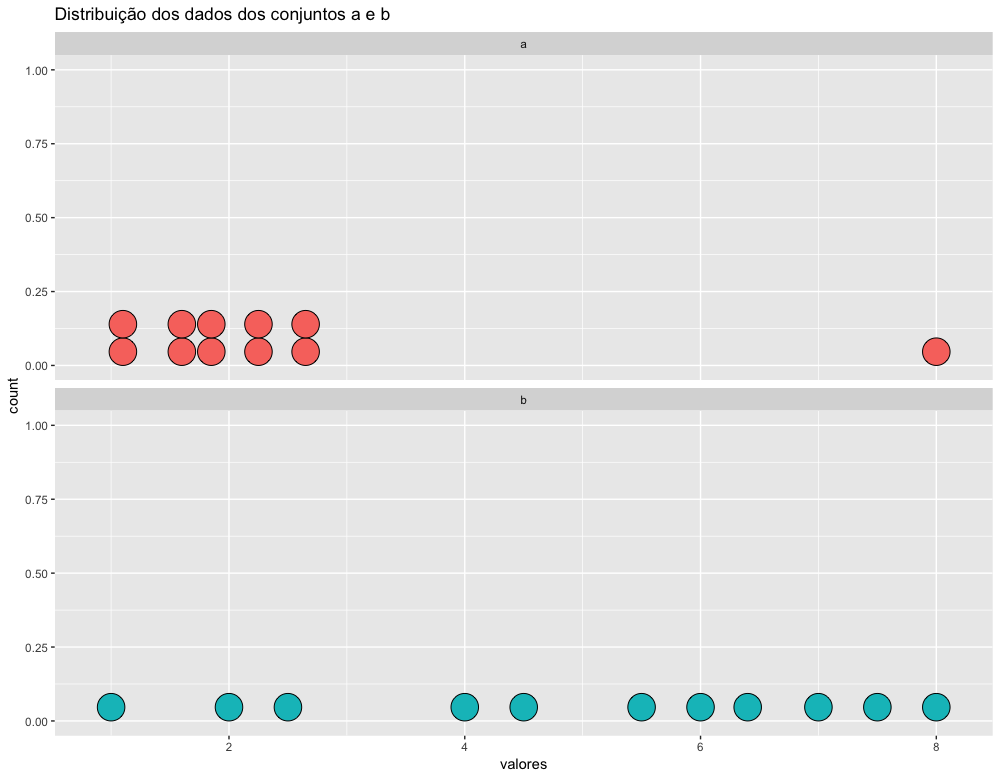
Podemos ver no gráfico acima que ambos os conjuntos tem 1 como valor mínimo e 8 como valor máximo, ou seja, ambos conjuntos de dados tem amplitude igual a 7. A medida da amplitude é simplemente a diferença entre os valores máximo e mínimo. Embora os limites sejam idênticos e a amplitude seja a mesma, esses dois conjuntos tem distribuições muito diferentes.
Podemos saber quais os valores maximos e mínimos com a função range(). Essa função mostra os valores máximo e mínimo de um conjunto de dados.
1 > range(conjunto_1)
2 [1] 1 8
3
4 > range(conjunto_2)
5 [1] 1 8
Vamos descobrir quais limites superiores e inferiores da distancia percorrida pelos carros, com um galão de combustível, na cidade, usando a função range():
1 > range(mpg$cty)
2 [1] 9 35
Podemos ver que existem carros que percorrem apenas 9 milhas com um galão e outros que percorrem 35 milhas com um galão. Ou seja, a amplitude dessa amostra é de 35-9 = 26 milhas.
Entretanto, essa informação é uma medida muito grosseira, pois a amplitude é calculada usando apenas 2 dados do conjunto, os valores máximo e mínimo.
Quartis, Percentil, Qualtil e Amplitude Interquartil
A amplitude interquartil é uma medida de variabilidade, baseada na divisão de um conjunto de dados em quartis. Os quartis dividem um conjunto de dados ordenados em quatro partes iguais. Os valores que separam partes são chamados de primeiro, segundo e terceiro quartis, e são denotados por Q1, Q2 e Q3, respectivamente. O primeiro quartil (Q1) é o valor abaixo do qual estão 25% dos dados, o segundo quartil (Q2) é o valor abaixo do qual estão 50% do dados e o terceiro quartil (Q3) é o valor abaixo do qual estão 75% dos dados.
A divisão dos conjunto de dados em percentuais é o que se denomina de percentil. Os percentis mais famosos são:
- 1º quartil ( = percentil 25%)
- 2º quartil ( = percentil 50% = mediana)
- 3º quartil (= percentil 75%).
Em estatística é comum usar o termo quantil para se referir ao percentil. A única diferença é que o quando usamos percentil usamos o número em sua forma de porcentagem (percentil 50%) e quando usamos o termo quantil usamos o número em sua forma decimal (quantil 0.5). O R tem uma função denominada quantile() para que você possa saber o quantil (ou percentil) que desejar.
Vamos calcular os quantis mais importantes, que são o primeiro, segundo e terceiro quartis: Q1, Q2 e Q3 no conjunto de dados da cilindrada dos carros no dataset mpg.
1 > Q1 <- quantile(mpg$displ, probs = 0.25)
2 > Q2 <- quantile(mpg$displ, probs = 0.50)
3 > Q3 <- quantile(mpg$displ, probs = 0.75)
4
5 > Q1
6 25%
7 2.4
8
9 > Q2
10 50%
11 3.3
12
13 > Q3
14 75%
15 4.6
Podemos ver que o 2º quartil é exatamente a própria mediana. O gráfico abaixo ajuda a visualizar o significado dos quartis. O código abaixo plota um gráfico para continuar nossa análise:
1 ggplot() +
2 geom_density(data=mpg,
3 aes(x=displ),
4 fill="lightblue",
5 color="darkblue")+
6 geom_vline(xintercept = Q1,
7 col="blue") +
8 geom_vline(xintercept = Q2,
9 col="blue") +
10 geom_vline(xintercept = Q3,
11 col="blue") +
12 theme(plot.title = element_text(lineheight=0.8)) +
13 annotate("text",
14 x=2,
15 y=0.1,
16 label= "25%",
17 color="black",
18 fontface=2,
19 size=4) +
20 annotate("text",
21 x=3,
22 y=0.1,
23 label= "25%",
24 color="black",
25 fontface=2,
26 size=4) +
27 annotate("text", x=4,
28 y=0.1,
29 label= "25%",
30 color="black",
31 fontface=2,
32 size=4) +
33 annotate("text",
34 x=5,
35 y=0.1,
36 label= "25%",
37 color="black",
38 fontface=2,
39 size=4) +
40 labs(title = "Distribuição das Cilindradas com os quartis",
41 subtitle = "cada quartil tem 25% dos carros \n Q1=2.4 Q2=3.3 Q3=4.6",
42 caption = "Fonte: dataset mpg do pacote ggplot2")
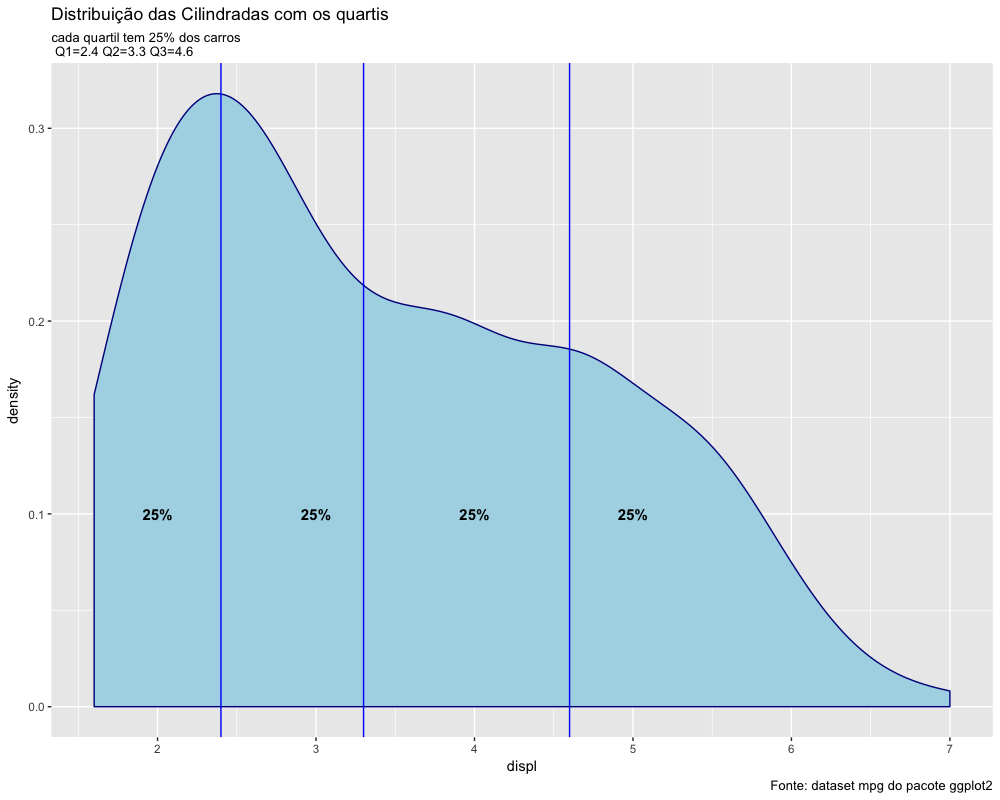
Na estatística descritiva, a amplitude interquartil (IQR) é uma medida de dispersão estatística, sendo igual à diferença entre o quartil superior (Q3) e quartil inferior (Q1). É também chamada de midspread ou middle 50%, ou H-spread.
IQR = Q3 - Q1.
Em outras palavras, a amplitude interquartil (IQR) é 3º quartil menos o 1º quartil. Para compreender o que é o IQR observe os seguintes conjuntos de dados:
1 a <- c(1, 1.2, 1.5, 1.7, 1.8, 1.9, 2.2, 2.3, 2.6, 2.7, 8)
2 b <- c(1, 2, 2.5, 4, 4.5, 5.5, 6, 6.4, 7, 7.5, 8)
Esses dados tem a mesma amplitude, mas seu IQR é bastante diferente e pode ser visualizado num gráfico de boxplot como abaixo:
1 boxplot(a,b,col="lightblue")
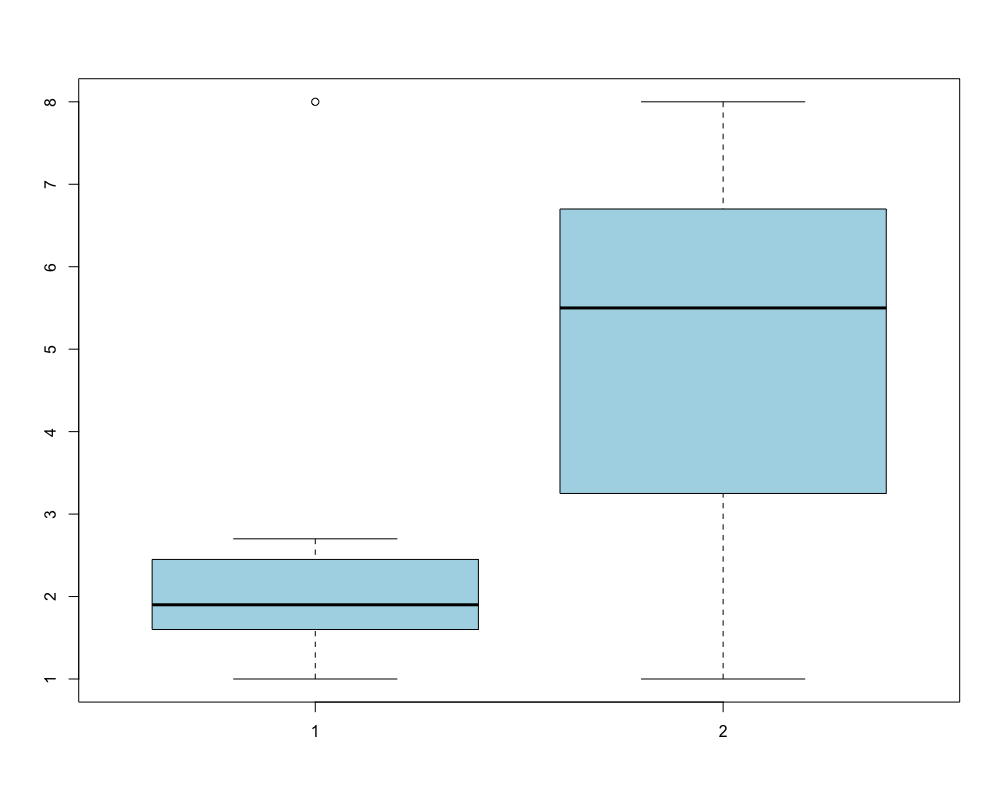
Num boxplot, a caixa representa os 50% dos dados centrais do conjunto, ou seja, os limites das caixas de um boxplot são o 1º e o 3º quartis.
A medida IQR (amplitude interquartil) é mais robusta que a amplitude simples, pois desconsidera os 25% de dados superiores e os 25 inferiores.
Agora vamos criar um grafico de densidade e um boxplot com os dados da cilindrada para visualizarmos essas medidas. O código abaixo gera os gráficos e coloca esses gráficos nos objetos plot1 e plot2:
1 plot1 <- ggplot() +
2 geom_density(data=mpg,
3 aes(x=displ),
4 fill="lightblue",
5 color="darkblue") +
6 xlab("Cilindrada") +
7 geom_vline(xintercept = Q1, col="red") +
8 geom_vline(xintercept = Q3, col="red") +
9 geom_vline(xintercept = Q2, col="blue") +
10 theme(plot.title =element_text(lineheight=0.8)) +
11 ggtitle("Densidade de Probabilidade")
12
13 plot2 <- ggplot() +
14 geom_boxplot(data=mpg,
15 aes(x=0,y=displ),
16 fill="lightblue",
17 color="darkblue") +
18 ylab("Cilindrada") +
19 ggtitle("BoxPlot") +
20 coord_flip()
Para plotar os gráficos apenas digite os nomes dos objetos como abaixo:
1 plot1
2 plot2
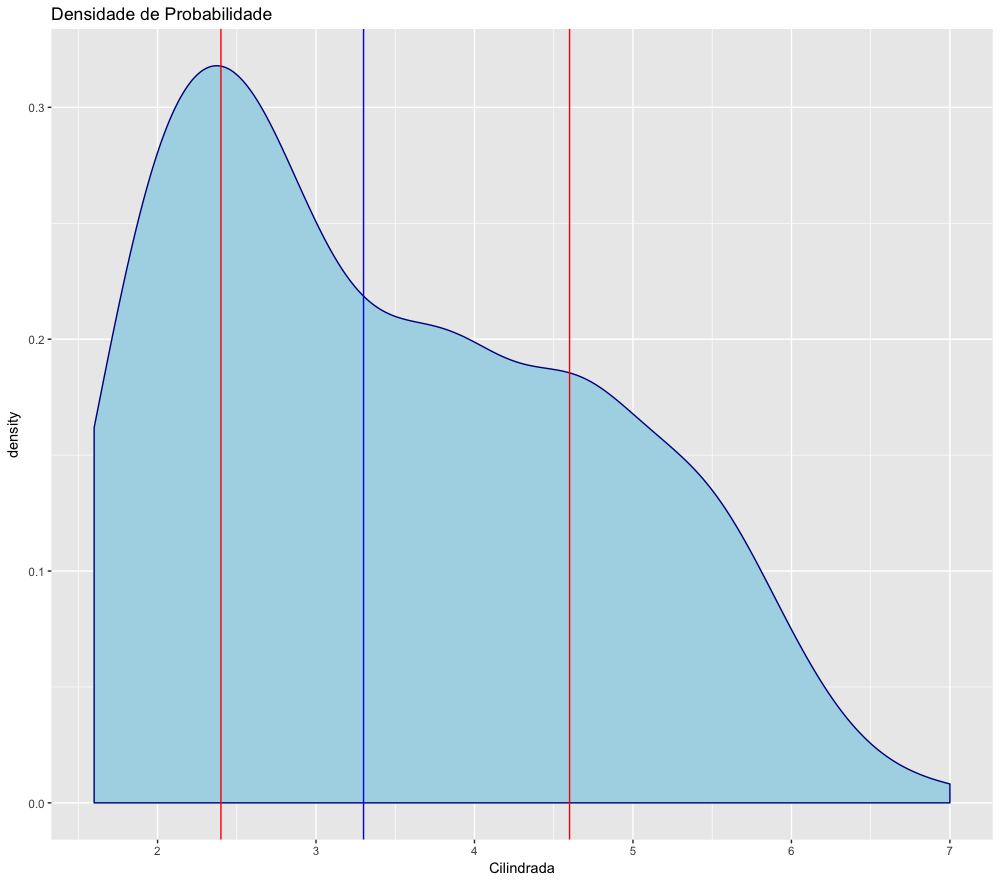
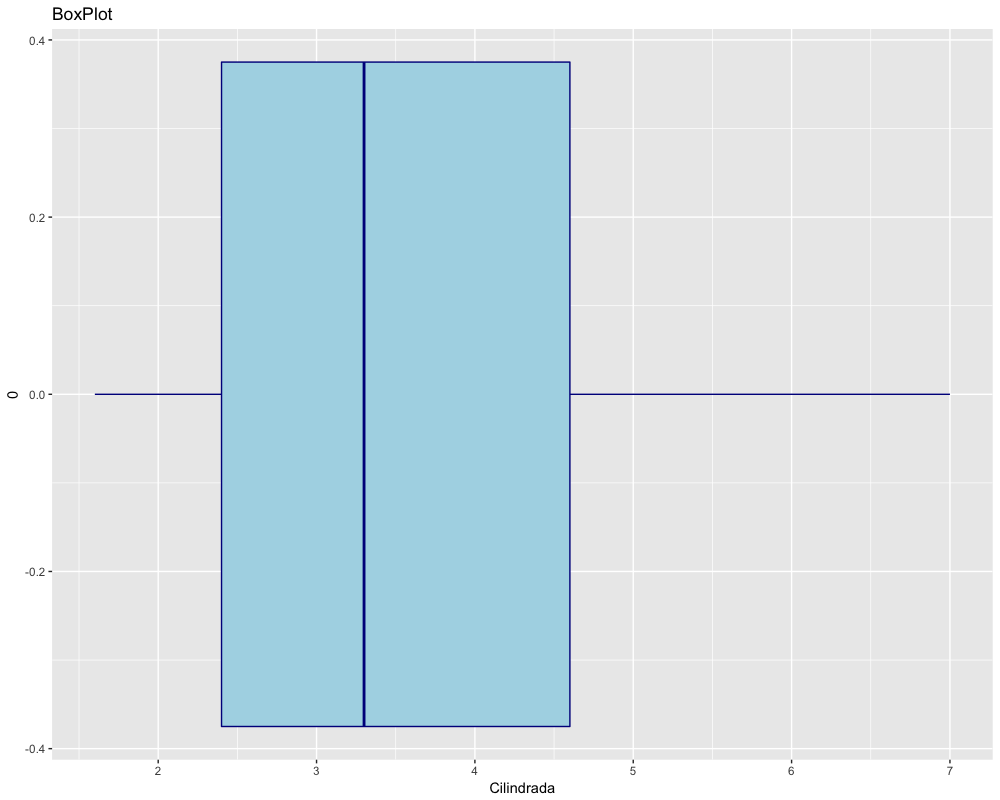
O R tem funções para calcular o percentil que você desejar, mas como é um software estatístico, a função é quantil() e o não percentil. Para obter o valor correspondente ao quantil desejado, é preciso fornecer como argumento da função o objeto com os dados e o quantil desejado. O resultado é o valor que corresponde àquele quantil.
Vamos testar calculando o quantil 0.5, que o mesmo que a mediana, usando os dados das cilindradas:
Calculando o quantil 0.5 (= percentil 50% = mediana):
1 > quantile(mpg$displ, 0.5)
2 50%
3 3.3
Calculando a mediana, para verificarmos que o resultado é o mesmo:
1 > median(mpg$displ)
2 [1] 3.3
O significado da mediana = 3.3
- 50% dos carros nesse dataset tem sua cilindrada acima de 3.3
- 50% dos carros nesse dataset tem sua cilindrada abaixo de 3.3
Variância e Desvio Padrão
Como vimos, a amplitude interquartil (IQR) é uma medida mais interessante que a mera amplitude, pois descarta os valores extremos, sendo assim menos sensível a outliers, ou seja, é uma medida considerada mais robusta que a simples amplitude. entretanto, o IQR também sofre do mesmo problema que a amplitude: é um cálculo que só usa dois dados, deixando muitos dados fora da análise.
Precisamos encontrar uma nova medida que represente melhor a dispersão do conjunto de dados, usando todos os dados desse conjunto.
Uma forma de fazer isso é analisar a distância de cada dado em relação à média, somar todas essas distâncias e dividir o valor encontrado pelo número de elementos do conjunto de dados (234 no nosso caso do dataset mpg). Entretanto, essa simples soma iria resultar sempre em zero, pois esse conjunto de distâncias de cada dado em relação à média iria conter valores positivos e negativos que iriam se cancelar totalmente. Vamos testar isso com o R no conjunto de dados do consumo dos carros na cidade do dataset mpg.
1 desvios <- (mpg$cty - mean(mpg$cty))
2 > resultado <- sum(desvios)/234
3 > resultado
4 [1] 1.275333e-15
Para visualizarmos esse número da forma usual usamos a função format():
1 > format(resultado, scientific = FALSE)
2 [1] "0.000000000000001275333"
O resultado dessa conta no R não foi exatamente ZERO devido a problemas de arredondamento. Mas, teoricamente, se não houvessem erros de arredondamente, o valor seria exatamente sempre ZERO. Logo, essa medida é inútil.
Uma possibilidade alternativa é somarmos os módulos das distâncias, para que os valores não se cancelem, podemos fazer isso no R usando a função abs().
1 > resultado2 <- sum(abs(desvios))/234
2 > resultado2
3 [1] 3.347359
Entretanto, a operação de módulo (ou valor absoluto) é uma operação matemática com muitas limitações. Existe um outro modo melhor de evitarmos valores negativos nas distancias calculadas: podemos usar o quadrado das distâncias. Essa é a medida conhecida como variância.
Variância
Calculando a dispersão elevando ao quadrado para evitar valores negativos:
1 > resultado3 <- sum((desvios)^2)/234
2 > resultado3
3 [1] 18.03567
É preciso, entretanto, fazer uma observação sobre o denominador desse fórmula. Quando calculamos a variância de uma população usando todos os dados da população o denominador é justamente o tamanho dessa população.
Entretanto, na maioria das vezes, trabalhamos apenas com uma amostra da população. Uma das principais funções da estatística é fazer inferências sobre a população usando como referência uma amostra. Nesse caso, quando estamos analisando uma amostra, o denominador da variância precisa de um pequeno ajuste, ao invés de n, o deve ser n-1. Ou seja, no caso de nossa amostra de 234 carros, usaremos no denominador o valor 233 (=234-1).
1 > resultado4 <- sum((desvios)^2)/233
2 > resultado4
3 [1] 18.11307
Essa é a medida denominada de variância amostral. E o R tem uma função própria para isso^ a função var():
1 > var(mpg$cty)
2 18.11307
A variância encontrada foi de 18.11307 milhas ao quadrado.
Veja que o resultado da operação var(mpg$cty) foi idêntico ao calculado acima passo-a-passo. Ou seja, a fórmula da função var() utiliza no denominador o valor n-1. Para calcular a variância populacional deveríamos usar n no denominador, mas o R não tem essa função.
Para pensar: como você pode fazer para obter o valor da variância populacional a partir da função var( ) do R? Podemos encontrar o resultado desejado simplesmente multiplicando o resultado encontrado por (n-1)/n
A variância, calculada com a nova fórmula de variância populacional, é de 18.03567 milhas ao quadrado.
Desvio Padrão
Apesar da importância da variância, essa medida tem um pequeno probleminha: ao elevar ao quadrado, a unidade de medida dos dados também foi elevada ao quadrado (milhas ao quadrado). Portanto, se nossa amostra se refere à altura em metros, a unidade da variância é metros ao quadrado, se a unidade de nossa medida são dias, horas, centímetros, a unidade de medida da variância será dias2 , horas2 , cm2 . Essas medidas são de difícil interpretação, daí a necessidade de ajustarmos essas medidas.
O modo mais simples de fazer isso é justamente fazendo a raiz quadrada da variância Desse modo, a unidade de medida volta a ser a original. A raiz quadrada da variância foi nomeada de desvio padrão, por ser a medida mais usada (padrão) de desvio dos dados, ou seja, de quanto os dados se desviam da medida central (média).
O R tem uma função preparada para o cálculo do desvio padrão: sd(). Lembre-se que na língua inglesa desvio padrão se escreve standard deviation, daí sd(). Vamos calcular o desvio padrão do consumo dos carros na cidade:
1 > sd(mpg$cty)
2 [1] 4.255946
Observe que o desvio padrão calculado acima é o desvio padrão amostral, com n-1 no denominador. Caso se pretenda calcular o desvio padrão populacional o resultado acima deve ser multiplicado por (n-1)/n (no caso especifico acima, devemos multiplicar por 233/234.
Propriedades do Desvio Padrão
O desvio padrão é a medida de dispersão mais comum na estatística, que utiliza em seus cálculos todos os dados. Devido ao fato de uma das etapas do cálculo do desvio padrão envolver a operação de elevar ao quadrado, o desvio padrão será sempre um valor positivo (ou zero). Se todos os valores dos dados forem iguais, o desvio padrão será ZERO. Uma das vantagens do desvio padrão é que a unidade de medida é a mesma dos dados da amostra, ao contrário da variância, na qual a unidade de medida é o quadrado da unidade original.
Ao analisar o desvio padrão, é preciso ter em mente que desvios pequenos indicam que os dados se agrupam em torno da média e desvios grandes indicam que os dados estão dispersos numa grande amplitude. Finalmente, como o cálculo do desvio padrão leva em conta todos os elementos do conjunto de dados, o resultado é que o desvio padrão é sensível aos outliers (valores extremos).
Conclusões finais
Nesse capítulo estudamos as medidas estatísticas de tendência central e de dispersão. Vimos também que essas medidas numéricas são melhor compreendidas quando associadas a gráficos que ilustrem o que os números indicam. A próxima etapa da análise descritiva é justamente aprender a criar gráficos que ilustrem os dados.
Referências
1. Stephen Few. Now You See it. Simple Visualization Techniques for Quantitative Analisys. Analytics Press, 2009.
2. Stephen Jay Gould. The Median Isn’t the Message. American Medical Association Journal of Ethics, January 2013, 15(1):77-81.