População e amostra

No capítulo anterior vimos que os dados de uma pesquisa se distribuem de diversos modos, que a principal distribuição é a distribuição normal e que uma das razões da importância dessa distribuição é o fato de diversas medidas na natureza terem uma distribuição normal. Mas veremos a seguir que existe também uma razão matemática para a importância dessa distribuição. Mas primeiramente precisamos desenvolver a noção de amostra e população.

Grande parte das pesquisas científicas visa criar um conhecimento a ser aplicado a uma população a partir de dados de um conjunto menor dessa população, ou seja, de uma amostra. Uma pesquisa de intenção de votos faz justamente isso, visa inferir qual será o resultado da votação de toda população a partir de uma amostra dessa população. Um das etapas mais importantes desse tipo de pesquisa é exatamente a forma de escolher a amostra. É importante que a amostra seja representativa da população para a qual se pretende fazer a inferência. Por exemplo, para uma pesquisa de intenção de votos para prefeito será necessário amostrar moradores da cidade, de forma que todos os bairros estejam representados, todas as classes sociais, etc. Numa pesquisa de votos para presidente será necessária uma amostra com moradores de todos os estados do Brasil, de forma que todos estejam representados, todas classes sociais, sexos, etc. Fazer uma amostragem realmente representativa é uma etapa essencial em qualquer pesquisa mas essas técnicas não serão discutidas nesse manual. O foco desse capítulo é discutir as sutilezas do definição de amostra e população.

Vamos imaginar uma pesquisa que pretenda conhecer a altura dos brasileiros. Será necessário escolher representantes de várias regiões do Brasil, de ambos os sexos, de várias idades. Feito isso, são tomadas as medidas de altura de todos os participantes da pesquisa (amostra). Com esses dados coletados podemos descrever a altura da população em termos de sua média, desvio padrão, etc. As medidas que são calculadas a partir desses dados são chamadas de estatísticas da amostra. A média das alturas é um exemplo de uma estatística da amostra, quaisquer outras medidas calculadas com base nos dados dessa amostra serão também estatísticas. É importante salientar que o valor de uma estatística depende da amostra particular. Se essa mesma pesquisa for realizada com outra amostra o resultado da média das alturas será certamente sempre um pouco diferente.

Usando o exemplo anterior, vimos que a população eram os brasileiros, e os participantes da pesquisa eram a amostra. Mas precisamos avaliar agora a estatística da amostra: a média das alturas. Nossa estatística, a média calculada, é também uma amostra. Nossa estatística, nossa média, é apenas uma das médias entre todas as possíveis médias que poderiam ter sido calculadas. Para cada possível conjunto de participantes haveria uma média diferente. Esse imenso conjunto de possíveis médias é a população de onde saiu nossa média. Essa população, esse conjunto de todas médias possíveis é o que se denomina de distribuição amostral

Distribuição amostral

A compreensão do que é uma distribuição amostral e de suas características é fundamental para a realização e interpretação dos testes estatísticos, pois é nessa distribuição especial que são calculadas as probabilidades que o pesquisador busca conhecer sobre seus dados.

Distribuições amostrais podem ser construídas com quaisquer medidas estatísticas. Entretanto, para facilitar a discussão, iremos nos ater ao tipo mais usual: a distribuição amostral de médias. O conjunto das médias de todas as amostras possíveis, de um mesmo tamanho, retiradas de uma mesma população, é que se denomina de distribuição amostral de médias. Se pudessemos fazer um número inifinito de pesquisas, cada uma com uma amostra do mesmo tamanho, a distribuição das médias dessas amostras seria uma distribuição amostral de médias. O problema é que isso é inviável. Pesquisas são caras, demoradas, trabalhosas. Portanto, na prática o pesquisador só tem os dados de sua amostra. Entretanto, como veremos adiante, todo cálculo estatístico depende de conhecer os parâmetros (média e desvio padrão) da curva de distribuição amostral do problema que está sendo estudado. Como resolver esse problema, como conhecer a média e o desvio padrão da curva de distribuição amostral se temos apenas uma amostra e não um número infinito de amostras?

A solução dessa questão foi um processo lento de desenvolvimento ao longo de mais de um século, desde início de 1810 até por volta de 1935, ao longo do qual os mais importantes matemáticos da história moderna foram aos poucos concebendo o que finalmente conhecemos como Teorema do Limite Central (Central Limit Theorem - CLT).

Vamos verificar essas relações em dois exemplo prático. Com o R iremos simular um conjunto de dados de altura de uma população, construir a distribuição desses dados. Em seguida vamos construir uma distribuição amostral a partir desses dados, retirando um conjunto de amostras do mesmo tamanho. O conjunto das médias dessas amostras servirá como sendo nossa distribuição amostral.

Uma das mais importantes questões da estatística é justamente a seguinte: como será a distribuição dessas médias, qual será a média e o desvio padrão da distribuição amostral?

Exemplo 1:

Vamos inicialmente examinar o que é uma distribuição amostral usando como exemplo população bem reduzida, de apenas 6 elementos. Suponha que nossas dados sejam referentes a alguma medida dessas 6 pessoas e que essa seja nossa população.

1 pop <- c(97, 98, 99, 101, 102, 103)

A média das alturas dessa população pode ser facilmente calculada:

1 mean(pop)
2 [1] 100

Mas numa pesquisa nunca temos acesso a toda população, apenas a amostras dessa população. Como nossa amostra é pequena, podemos é factível listar todas as possíveis amostras de determinado tamanho (n). Nesse exemplo, vamos listar todas as amostras possíveis com n=3. Isso pode ser facilmente conseguido no R com a função combn(), que gera uma matriz com todas as combinações de m elementos retirados de um determinado vetor, colocando cada conjunto de 3 elementos numa coluna.

 1 all.combinations <- combn(pop,3)
 2 all.combinations
 3     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [\
 4 ,15] [,16] [,17] [,18] [,19] [,20]
 5 [1,]   97   97   97   97   97   97   97   97   97    97    98    98    98    98 \
 6    98    98    99    99    99   101
 7 [2,]   98   98   98   98   99   99   99  101  101   102    99    99    99   101 \
 8   101   102   101   101   102   102
 9 [3,]   99  101  102  103  101  102  103  102  103   103   101   102   103   102 \
10   103   103   102   103   103   103

Podemos facilmente calcular a média de cada um desses conjuntos de 3 elementos. Para isso basta usar a função colMeans() que calcula as médias de cada coluna de uma matrix.

1 dist.amostral <- colMeans(all.combinations)

Esse conjunto de médias de todas as combinações possíveis de amostras de 3 elementos obtidos da população é um exemplo de distribuição amostral, nesse caso uma distribuição amostral de médias.

Vamos agora calcular a média da distribuição amostral:

1 mean(dist.amostral)
2 [1] 100

A média da distribuição amostral foi exatamente igual à média da distribuição da população original. Isso não é coincidência. O Teorema do Limite Central afirma justamente isso, que a média da distribuição amostral é exatamente igual à média da distribuição da população original. Além da relação entre as médias, esse teorema também descreve a relação entre o desvio padrão da população e da distribuição amostral.

Vamos comparar os desvios padrões dessas duas distribuições.

1 sd(pop)
2 sd(dist.amostral)
3 [1] 2.366432
4 [1] 0.9911893

Podemos ver que o desvio padrão da distribuição amostral é bem menor.

Segundo o Teorema do Limite Central (CLT), o desvio padrão da distribuição amostral e sempre menor que o da população. Mas além disso, de de acordo com esse teorema, à medida que o tamanho da amostra aumenta, o desvio padrão da distribuição amostral tende a se aproximar cada vez mais do valor do desvio padrão da população dividido pela raiz quadrada do tamanho da amostra.

[
\text{Desvio padrão da distribuição amostral}=\frac{\text{Desvio padrão da população}}{\text{raiz quadrada do tamanho da amostra}}
]

[
\sigma_\bar{X}=\frac{\sigma_p}{\sqrt{n}}
]

[
SE_\bar{X}=\frac{\sigma_p}{\sqrt{n}}
]

Entretanto, em nosso exemplo a amostra é muito pequena, teve apenas 3 elementos. Para visualizarmos melhor essa relação será necessário usar um exemplo mais realístico. Faremos isso no próximo tópico.

Preparando a população
Numa pesquisa da ANAC (Agência Nacional de Aviação Civil) de 2009, na qual foram avaliados os dados antropométricos de 5305 brasileiros entre 15-87 anos de idade em 20 aeroportos do Brasil, a altura média da amostra foi de 173.1cm e o desvio padrão foi de 7.3cm (SILVA & MONTEIRO, 2009). Além disso, a literatura demonstra que medidas de estatura de uma população tendem a possuir uma distribuição normal. Portanto, vamos simular nossa população usando uma aproximação desses dados com a função rnorm().

Simulando um conjunto de milhão de medidas de alturas, distribuídas de forma normal, com média de 173cm e desvio padrão de 7cm.

1 set.seed(1)
2 pop <- rnorm(n = 1000000, mean = 173, sd = 7)
3 pop.df <- data.frame(altura = pop)

Preparando as amostras
Uma distribuição amostral deveria ser composta de todas as amostras possíveis, entretando, precisamos estipular algum limite razoável para que nossos computadores executem esses cálculos num tempo razoável. Dependendo da capacidade seu computador, talvez seja necessário até reduzir a quantidade de amostras ou o tamanho da amostra. Iremos fazer uma simulação de mil amostras de 100 elementos em cada.

1 amostras <- data.frame(replicate(1000, sample(pop, size = 100)))

Preparando a distribuição amostral
Vamos agora calcular a média de cada amostra de 100 elementos criada acima com a função apply(). O primeiro termo dessa função indica o nome do data frame com os dados, o segundo termo dessa função, 2 , indica que a função a ser calculada será aplicada nas colunas do data.frame. O terceito termo indica a função que será utilizada, nesse caso será a função mean, para calcular a média. Iremos colocar essas médias num data frame que chamaremos de medias.

1 medias <- data.frame(media=apply(amostras, 2, mean))
2 head(medias)
3      media
4 X1 173.5902
5 X2 173.5943
6 X3 172.6597
7 X4 172.9608
8 X5 172.3325
9 X6 173.4830

Vamos verificar visualmente essas distribuições no gráfico abaixo.

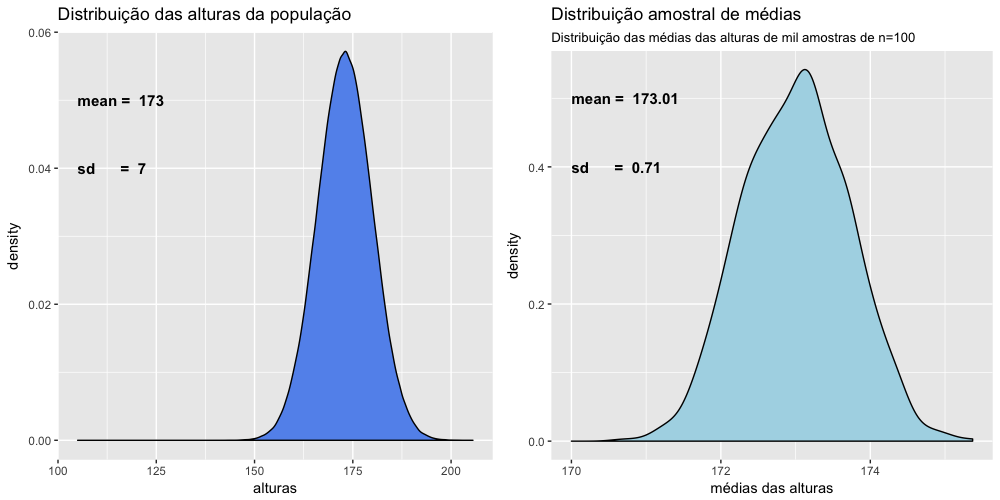
Analisando esses gráficos podemos verificar que as duas distribuições são aproximadamente normais, as médias das duas distribuições são praticamente iguais, e o desvio padrão da distribuição amostral é 10 vezes menor. Como o desvio padrão representa a dispersão dos dados, a curva de distribuição amostral deveria ser mais estreita que a curva de distribuição das alturas da população. É difícil perceber isso com os esses gráficos lado a lado como na figura acima, pois a escala dos dois gráficos é diferente. Observe os eixos x e y e poderá se certificar disso.

O gráfico abaixo mostra essas duas curvas sobrepostas e agora fica mais claro que não apenas que as médias são iguais, mas também o quanto a curva de distribuição amostral das médias tem realmente um desvio padrão bem menor que a curva de distribuição das alturas da população original.

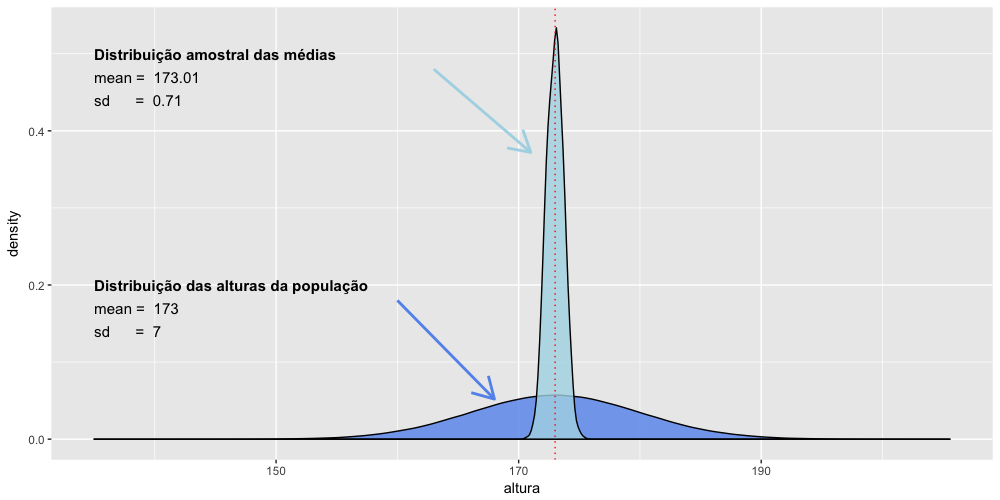
A distribuição amostral tem um pico muito mais alto por uma questão puramente matemática: numa curva de distribuição a área abaixo da curva é sempre igual a 1, portanto, quanto menor o desvio padrão mais alta será a curva, pois a área de ambas tem de ser sempre igual a 1. O importante nesse gráfico é verificarmos que as curvas tem a mesma média, mas a curva de distribuição amostral é realmente bem mais estreita, ou seja, tem um desvio padrão bem menor. Se observarmos bem, o desvio padrão da curva de distribuição amostral é exatamente dez vezes menor que a da população. Veremos adiante a razão disso.

Resumindo o que foi observado:
- A distribuição amostral teve um formato aproximadamente normal.
- A média da distribuição amostral foi a mesma da população original.
- O desvio padrão da distribuição amostral foi bem menor que o da população original.

Essas três observações acima representam o teorema fundamental da estatística, denominado “Teorema do Limite Central”, usado praticamente todas as vezes em que se faz um teste de hipóteses científicas. A grande utilidade desse teorema pode ser compreendida logo em sua definição:

dadas certas condições…, quando o tamanho da amostra aumenta, a distribuição amostral aproxima-se cada vez mais de uma distribuição normal, não importando se a distribuição da população seja normal ou não.

Ou seja, não importa se a distribuição da medida de interesse na população é normal ou não, uma distribuição amostral dessa medida será normal. Isso é o que torna a distribuição normal tão importante, pois os teste estatísticos são sempre realizados sempre numa distribuição amostral que, por sua vez, será sempre normal. O gráfico abaixo ajudará a visualizar melhor essa relação.

Além disso, o Teorema do Limite Central (CLT) relaciona a média e o desvio padrão da população e da distribuição amostral:

a média da distribuição amostral é a mesma da população.
o desvio padrão da distribuição amostral é o desvio padrão da população dividido pela raiz quadrada no tamanho da amostra.

As nossas amostras tinham 100 participantes (n=100), logo, como a raiz quadrada de 100 é igual a 10, o desvio padrão da distribuição amostral foi exatamente o da população dividido por 10:

- desvio padrão da população era 7cm.
- desvio padrão da distribuição amostral foi de 0.7cm.

Referências

1. Saul Stahl. The Evolution of the Normal Distribution. Mathematics Magazine, 79(2), April 2006.

2. Sue Gordon. The Normal Distribution.

3. M. Eileen Magnello. Karl Pearson’s Gresham Lectures: W. F. R. Weldon, Speciation and the Origins of
Pearsonian Statistics. The British Journal for the History of Science, Vol. 29, No. 1 (Mar., 1996), pp. 43- 63

4. Silva S, Monteiro W. Levantamento do Perfil antropométrico da População Brasileira Usuária do Transporte Aéreo Nacional–Projeto Conhecer, ANAC. Publicação técnica do acervo da ANAC, 2009.