Distribuições de probabilidade
carregando os pacotes necessários para o capítulo
1 > library(ggplot2)
2 > library(gridExtra) # necessário para usar a função grid.arrange
Introdução
Variation is the hard reality, not a set of imperfect measures for a central tendency.
Stephen Jay Gould
A medicina trabalha com incertezas, cada paciente responde de um determinado modo a uma doença ou a um tratamento. A variabilidade é a regra. Como disse Stephen Gould, a variação é a realidade. E é justamente essa variação nas repostas é que faz com que os dados de qualquer pesquisa estejam distribuídos de alguma forma. Entretanto, apesar dessa variabilidade, apesar dessa aleatoriedade, podemos notar padrões em muitos eventos aleatórios da natureza. O estudo das distribuições de probabilidade é justamente o estudo da análise desses padrões aleatórios.
A questão importante é responder à seguinte pergunta: qual será o padrão da distribuição de frequências dos resultados de uma experiência se repetirmos essa experiência infinitas vezes?.
Uma distribuição de frequências relativas de um número infinito de experimentos representa a probabilidade real de cada evento do experimento e é usualmente chamada de distribuição de probabilidades. Distribuições de probabilidades representam, portanto, a forma como os resultados (dados) de um determinado fenômeno (ou experimento) se distribuem quando o fenômeno (ou experimento) ocorre de forma totalmente aleatória (ou randomizada). Mas como nunca podemos fazer um número infinito de experimentos, toda distribuição de probabilidades é um modelo matemático teórico que representa essa situação.
Veremos adiantes que existem distribuições de probabilidade discretas e contínuas. As distribuições de probabilidade discretas são representadas graficamente por um histograma e as distribuições de probabilidade contínuas são representadas graficamente por uma curva, chamada curva de distribuição.
Mas, afinal de contas, o que é uma curva de distribuição de probabilidade?
Tecnicamente, uma curva de distribuição de probabilidade criada por uma função matemática, cuja área total abaixo da curva seja exatamente igual a 1. Essa curva, ou seja, esse gráfico, é uma representação teórica da probabilidade dos eventos ou dos dados de um estudo. A probabilidade total ou 100% é representada pela área total abaixo da curva, que é, portanto, sempre igual a 1.
A probabilidade de dados maiores que um certo valor é a área abaixo da curva à direita daquele ponto.
A probabilidade de dados menores que um certo valor é a área abaixo da curva à esquerda daquele ponto.
A probabilidade de dados entre dois valores é justamente a área abaixo da curva entre esses dois pontos.
Em termos simples, essa curva serve como uma representação da probabilidade teórica de ocorrência dos diferentes valores de um conjunto de resultados.
A Distribuição uniforme e um jogo de dados
Vamos ver como podemos encontrar padrões em eventos aleatórios começando com um exemplo muito simples: jogando um dado. Ao jogar um dado, qual a probabilidade do resultado ser o nº 6? ou 5? Se o dado não estiver viciado, a probabilidade de qualquer um dos seis resultados é igual a 1/6. Se chamarmos de **n** o nº de possibilidades, a probabilidade de qualquer dos resultados será 1/n. Nesse exemplo, 1/6.
Entretanto, se jogarmos o dado 60 vezes, será muito pouco provável obtermos exatamente a mesma proporção de cada um dos seis números do dado. Por outro lado, se jogarmos o dado 6 milhões de vezes, provavelmente cada face do dado irá ser obtida aproximadamente 1 milhão de vezes. Vamos ver como esse padrão vai se formando à medida que aumentando o nº de vezes que fazemos nosso experimento.
O R nos permite facilmente simular uma dado. A primeira coisa a fazer é criar um objeto com as propriedades de um dado que nos interessam, ou seja, possuir valores de 1 a 6. Veja que, no nosso modelo de dado, só nos interessa essa propriedade. Como já comentamos no capítulo passado, um modelo é útil justamente por nos ajudar a focar a atenção nos aspectos considerados mais importantes.
Para criar um dado no R. Simplesmente atribuímos a esse objeto os valores de 1 a 6.
1 > dado <- c(1:6)
2 > dado
3 [1] 1 2 3 4 5 6
O que precisamos fazer agora é simular a jogada do dado. Para fazer isso precisamos apenas entender uma abstração: o que significa jogar um dado? Ao jogar um dado podemos ter apenas 6 resultados válidos: 1, 2, 3, 4, 5, 6. Ou seja, jogar um dado equivale a retirar aleatoriamente uma das possibilidades de conjunto com esses 6 valores.
O R, sendo um software estatístico, tem uma função própria para isso. A função sample() tem como argumentos um conjunto e o nº de ítens desse conjunto que iremos retirar. No nosso caso o conjunto é o objeto dado que criamos. Nesse exemplo, iremos retirar apenas 1 amostra do conjunto de 6 possibilidades. Em outras palavras, ao simular uma jogada de um dado teremos UM único resultado dentre os 6 possível. A simulação, portanto, é de retirar ao acaso uma das 6 possibilidades.
1 > sample(dado, size=1)
2 [1] 3
A cada vez que essa linha de código fore executada o R irá escolher de forma aleatória uma das 6 possibilidades. Experimente executar esse código inúmeras vezes e verá que o resultado se modifica aleatoriamente.
A questão é: existe um padrão nesses resultados?
Vamos fazer um experimento jogando nosso dado 20 vezes, para verificarmos qual a frequência com que cada número irá aparecer. Para isso, basta informar como argumento da função sample size=20 e replace=TRUE. O argumento replace=TRUE indica que o a amostragem será feita com reposição, ou seja, o número que foi sorteado poderá ser sorteado novamente (o que é o que acontece num jogo de dados. Usarei a função table() e a função prop.table() para criar uma tabela com as frequências relativas de cada resultado.
1 > amostra1 <- prop.table(table(sample(dado, size=20, replace = TRUE)))
2 > amostra1
3
4 1 2 3 4 5 6
5 0.15 0.25 0.15 0.20 0.05 0.20
A cada vez que esse código for executado a proporção de cada face do dado se modifica. Não parece haver ainda um padrão.
Mas a visualização ficará ainda mais interessante se fizermos um gráfico de barras dessas frequências relativas:{r}
amostra1 <- prop.table(table(sample(dado, size=20, replace = TRUE)))
barplot(amostra1, xlab = "Faces do dado", ylab = "Frequencia relativa", col = "dodgerblue4", ylim= c(0,1))
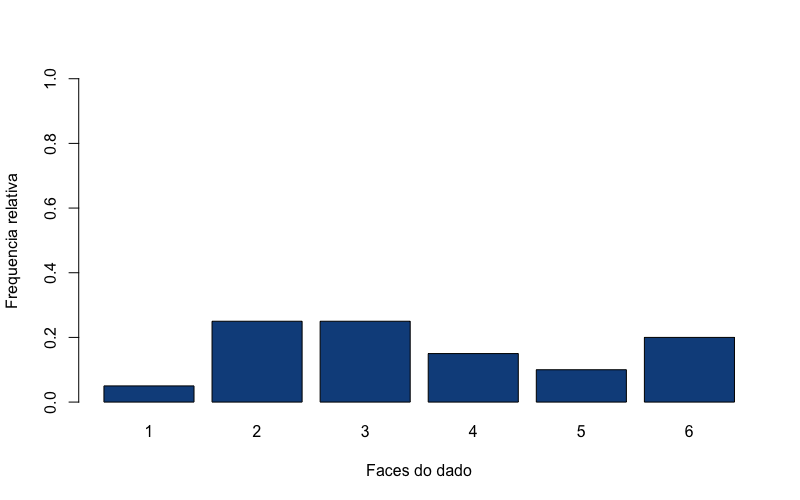
Se você repetir esse código várias vezes verá que não parece haver um padrão de respostas. A frequência dos resultados de cada face do dado varia muito.
A questão é: existirá um padrão se jogarmos o dado mil vezes, um milhão de vezes, infinitas vezes?
Se desejarmos repetir essa jogada mil de vezes, podemos usar o mesmo comando sample(), mas alterando o argumento size para size=1000, o que indica o tamanho de nossa amostra (mil jogadas do dado). Vamos colocar o resultado dessas jogadas num outro objeto, que chamaremos de amostra2. O código a seguir cria uma amostra de mil jogadas, em seguida cria uma tabela de frequências absolutas de cada face do dado, transforma a tabela numa tabela de frequências relativas, e finalmente, gera um gráfico de barras com esses dados. Você pode clicar no botão play diversas vezes, toda vez que clicar no botão play esse código será executado.
1 > amostra2 <- sample(dado, size=1000, replace = TRUE)
2 > tabela2 <- table(amostra2)
3 > tabela2 <- prop.table(tabela2)
4 > barplot(tabela2, xlab = "Faces do dado", ylab = "Frequencia relativa", col = "\5 dodgerblue4", ylim= c(0,0.5))
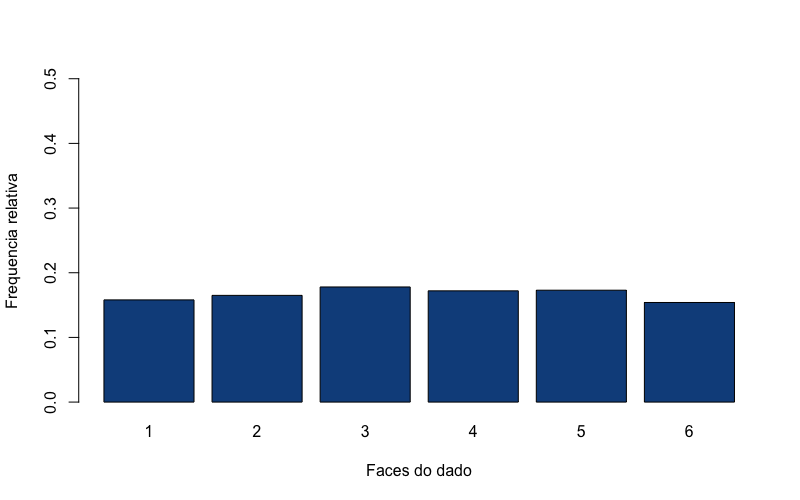
A cada vez que esse código é executado o gráfico apresenta ligeiras diferenças. Ou seja, a frequência de cada face se altera muito menos com uma amostra de mil jogadas de dados. Se nossa amostra for aumentada para cem mil jogadas, você poderá ver que as frequências de cada face são praticamente as mesmas.
1 > amostra3 <- sample(dado, size=100000, replace = TRUE)
2 > tabela3 <- table(amostra3)
3 > tabela3 <- prop.table(tabela3)
4 > barplot(tabela3, xlab = "Faces do dado", ylab = "Frequência relativa", col = "\5 dodgerblue4", ylim= c(0,0.5))
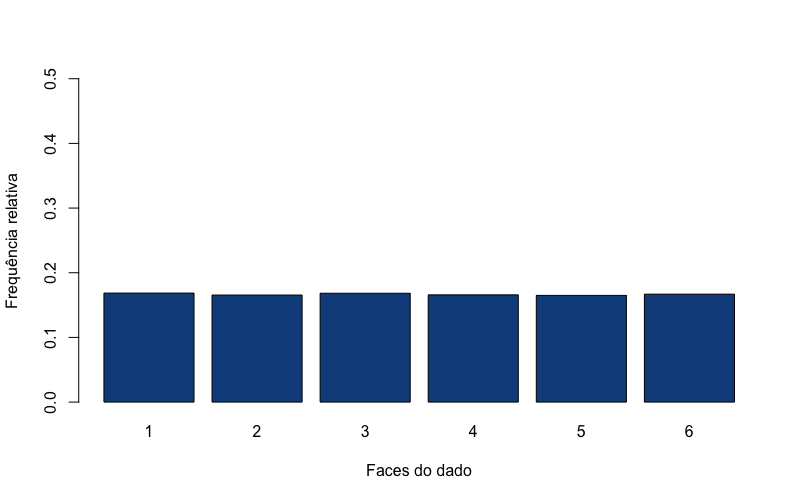
Precisamos agora imaginar um gráfico de frequências relativas como esses, mas feito a partir de um número infinitamente grande de jogadas. À medida que o nº de jogadas aumenta a distribuição de frequências converge para o que se chama de uma distribuição de probabilidade. Ou seja, uma distribuição de probabilidades é em sua essencia uma distribuição de frequências de um número infinito de jogadas, ou de eventos.
Existem inúmeros tipos de distribuição de probabilidade, cada uma com um nome, cada uma representando uma situação diferente. A distribuição de probabilidades criada acima é a que denominamos de Distribuição Uniforme Discreta. Uma distribuição uniforme discreta é uma distribuição de probabilidade simétrica, na qual um número finito de valores têm a mesma probabilidade de serem observados. O exemplo mais simples de uma distribuição uniforme discreta é justamente o nosso exemplo de jogar um dado. Os valores possíveis são 1, 2, 3, 4, 5, 6 e cada vez que o dado é lançado, a probabilidade de um qualquer resultado é 1/6. Uma distribuição uniforme pode ser também contínua se os valores possíveis estão dentro de um continuum numérico.
Existem diversas outras situações nas quais a frequência de cada possibilidade é diferente e cada uma dessas situações pode ter sua distribuição modelada matematicamente. O que é preciso sempre manter em mente é que o termo distribuição de probabilidade se refere a um modelo matemático teórico que pretende simular uma determinada distribuição de resultados.
A distribuição normal
Sem dúvida alguma a mais importante das distribuições de probabilidade teóricas é a distribuição normal.
Diversas fenômenos na natureza seguem um padrão de distribuição simétrico e em forma de sino. Devido a essa forma, essa distribuição de frequências ficou conhecida como distribuição em sino (bell shaped). Como tantos fenômenos são distribuídos dessa forma, a busca por um modelo matemático para modelar essa distribuição tem uma longa trajetória na ciência. A busca por essa equação é uma parte fascinante da história da ciência, envolvendo diversos grande matemáticos. O modelo matemático dessa curva se originou por volta do ano de 1733 com o trabalho do matemático Abraham Demoivre, quando buscava modelos para prever resultados de jogos de azar. Essa curva também foi derivado de forma independente em 1786 por Pierre Laplace, um astrônomo e matemático. No entanto, a curva normal como modelo para a distribuição de erros na teoria científica é mais comumente associada a um astrônomo e matemático alemão, Karl Friedrich Gauss, que encontrou uma nova derivação da fórmula para a curva em 1809 (Gordon, 2006). Por esse motivo, a curva normal às vezes é referido como a curva “gaussiana”. Em 1835, outro matemático e astrônomo, Lambert Qutelet, usou o modelo para descrever características fisiológicas e sociais humanas. Quetelet acreditava que “normal” significava média e que os desvios da média eram os erros da natureza e foi o primeiro matemático a extender o uso da curva de distribuição normal para os campos das ciências sociais e biomédicas (Stahl, 2006).
A famosa equação da curva de distribuição normal ou Gaussiana, que envolve o uso das mais importantes constantes matemáticas, $\pi$ e $e$.
p(x) = \frac{1}{\sqrt{2\pi}} \text{e}^{-x^2/2}{format: latex}
Essa equação só chegou em sua forma atual com o trabalho do estatístico Karl Pearson, que foi o primeiro a escrever essa equação em termos de desvio padrão e, posteriormente, com o trabalho de Fisher, que adicionou os parâmetros de localização (média), culminando na forma moderna dessa equação, com os parâmetros $\sigma$ (desvio padrão) e $\mu$ (média).
p(x) = \frac{1}{\sigma \sqrt{2\pi}} \text{e}^{-1/2(\frac{x-\mu}{\sigma})^2}{format: latex}
Não é preciso decorar essa fórmula. Ela só está aí para que você possa conhecer uma das mais importantes equações da estatística. Uma Precisamos compreender o que é uma distribuição normal e saber utilizá-la adequadamente. Isso é o fundamental num curso introdutório de estatística.
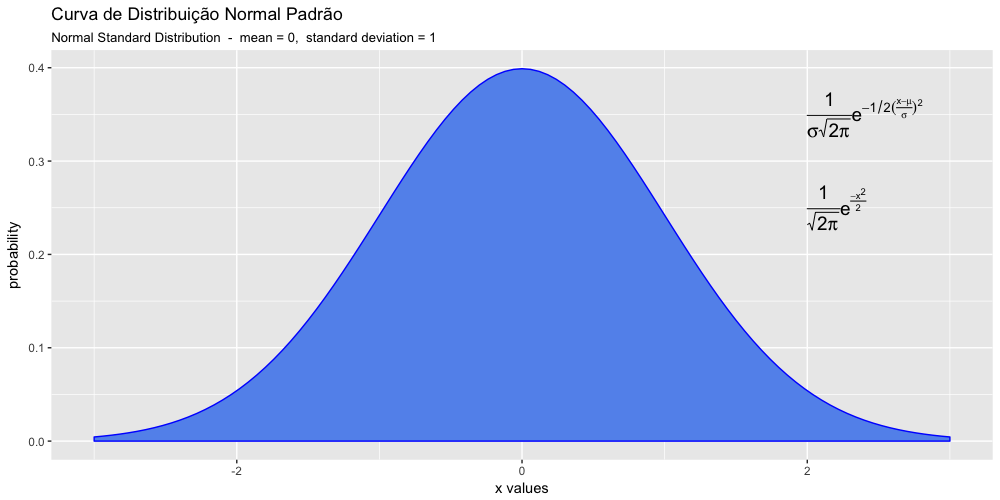
Aqui vale a pena relembrar que uma curva de distribuição de probabilidade é criada por uma função matemática, cuja área total abaixo da curva é exatamente igual a 1 e a área abaixo da curva entre dois pontos é a medida da probabilidade dos eventos ou resultados entre esses dois pontos.
- A probabilidade de dados maiores que um certo valor é a área abaixo da curva à direita daquele ponto.
- A probabilidade de dados menores que um certo valor é a área abaixo da curva à esquerda daquele ponto.
- A probabilidade de dados entre dois valores é justamente a área abaixo da curva entre esses dois pontos.
Vamos visualizar a relação entre área abaixo da curva e a probabilidade de ocorrências dos dados nos gráficos abaixo:
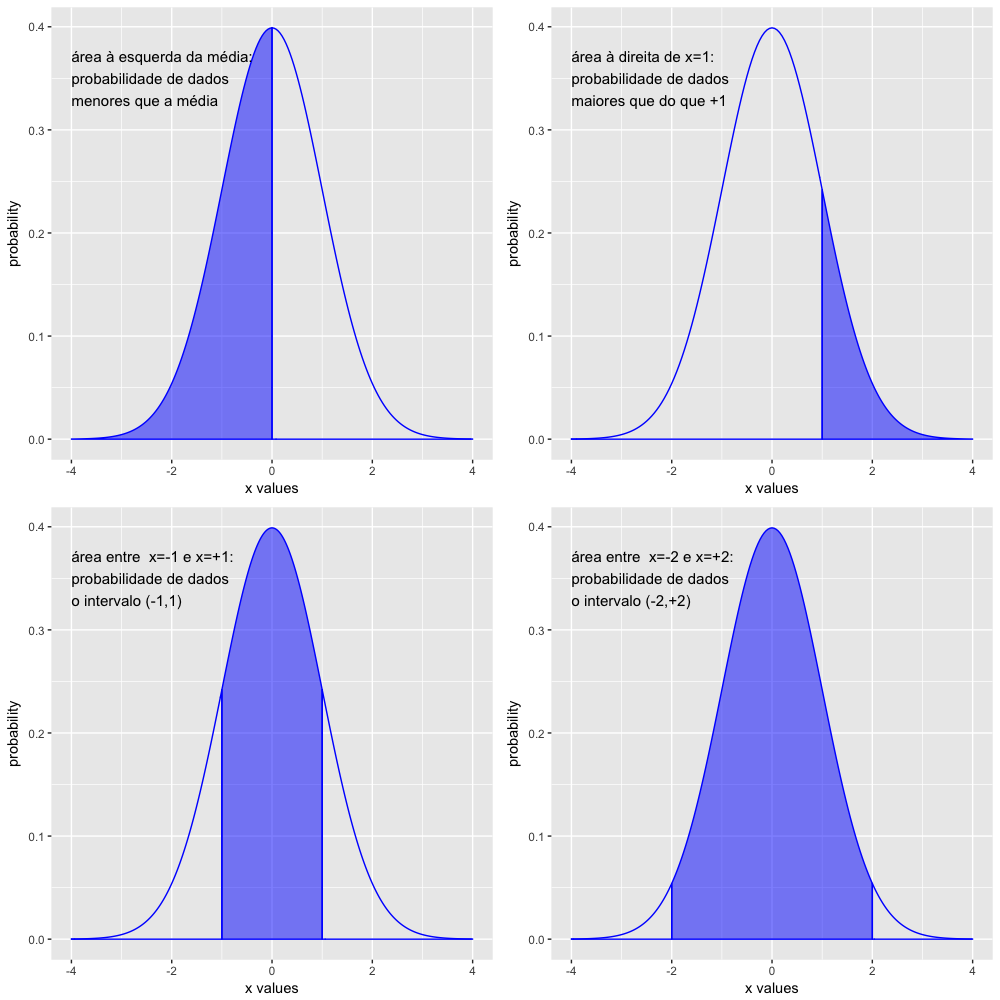
A curva normal padrão
Se você observar com a atenção, verá que nos gráficos acima a média foi sempre igual a ZERO. Além disso, nesses gráficos o desvio padrão foi igual a UM em todos. Esses parâmetros (média = 0 e desvio padrão = 1) definem uma curva normal padrão. Ou seja, a curva normal padrão é aquela cuja média é 0 e o desvio padrão é 1.
Muitas vezes temos de comparar os dados de diferentes experimentos, cada um representado por uma curva normal diferente. Mas aí surge um problema, como comparar dados de curvas com parâmetros diferentes? Podemos fazer isso transformando todos os valores do eixo x em z-scores. Veremos a seguir o que é um z-score e como fazer essa transformação.
A normalização e os z-scores.
Um z-score indica quantos desvios padrões um determinado valor se distancia da média.
Na estatística o score z é uma medida padronizada do quanto um valor se distancia da média em termos de desvios padrões. Ou seja, um score z mede quantos desvios padrões um determinado valor se distancia da média. A unidade do z-score é, portanto, o desvio padrão. Um z-score de +3 significa que o valor está 3 desvios padrões acima da média. Um z-score de -3 significa que o valor está a 3 desvios padrões abaixo da média.
Transformarmos todos os valores da pesquisa (eixo x) em z-scores equivale a transformar a curva normal numa curva normal padrão. A média é transformada em ZERO e o desvio padrão é transformado em 1. Desse modo podemos comparar diferentes curvas. Esse procedimento é o que se denomina normalização.
Normalização: procedimento para transformar os dados brutos de uma pesquisa em z-scores.
Equaçao de normalização
z = \frac{x-\mu}{\sigma}{format: latex}
Interpretando o z-score:
- z-score = 0 → o valor é igual à média
- z-score < 0 → valor é menor que a média
- z-score > 0 → valor é maior que a média
Além disso:
- z-score = 1 → 1 desvio padrão maior que a média
- z-score = 2 → 2 desvios padrão maior que a média
- z-score = -1 → 1 desvio padrão menor que a média
- z-score = -2 → 2 desvios padrão menor que a média
Calculando as probabilidades - parte 1: pnorm(x)
Na curva normal padrão é muito fácil calcular a probabilidade da ocorrência dos dados com a função pnorm(). essa função recebe esse nome pela junção de p de probabilidades com norm de curva normal: daí pnorm(): probabilidades na curva normal. Essa função calcula por padrão a área abaixo da curva à esquerda do ponto indicado. Como a área total abaixo de uma curva de distribuição de probabilidade é sempre igual a 1, basta subtrairmos pnorm(x) de 1, ou seja, 1-pnorm(x). Mas podemos também modificar o comportamento da função pnorm() alterando o parâmetro lower.tail para false.
Vamos calcular a probabilidade de ocorrência dados iguais ou menores que ZERO, ou seja, menores que a média, lembrando que na curva normal padrão a média é 0 e o desvio padrão é igual a 1. Além disso, lembre-se que numa curva normal padrão os valores do eixo x representam o z-score, ou seja, representam os desvios padrões.
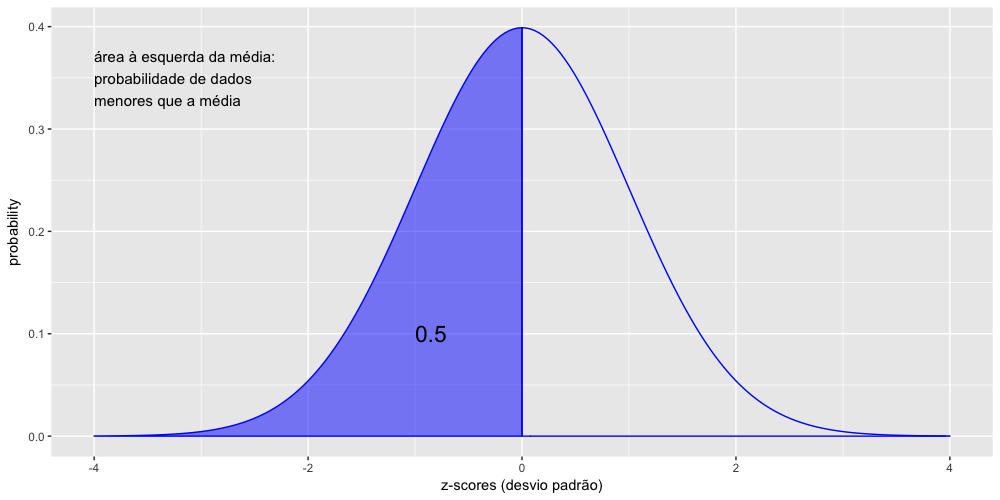
1 > pnorm(0, mean=0, sd=1)
2 [1] 0.5
O resultado é o esperado, pois como a curva normal é simétrica, 50% dos resultados estão abaixo da média e 50% dos resultados estão acima da média. Logo a probabilidade de encontrarmos resultados abaixo da média é 50% (ou 0.5).
Além de calcular por default a área à esquerda do ponto indicado, a função pnorm() têm também como valores default os parâmetros da curva normal padrão, ou seja, se não informarmos esses argumentos a função irá considerar que a média = 0 e o desvio padrão = 1. Então, se estivermos trabalhando com a curva normal padrão, podemos simplificar o cálculo acima para apenas pnorm(0).
1 > pnorm(0)
2 [1] 0.5
Lembre-se que numa curva normal padrão os valores do eixo x representam o desvio padrão. Vamos fazer alguns cálculos de probabilidades nessa curva normal padrão.
Vamos calcular agora a probabilidade de dados maiores ou iguais a 1 desvio padrão acima da média, ou seja, à direita de z = +1.
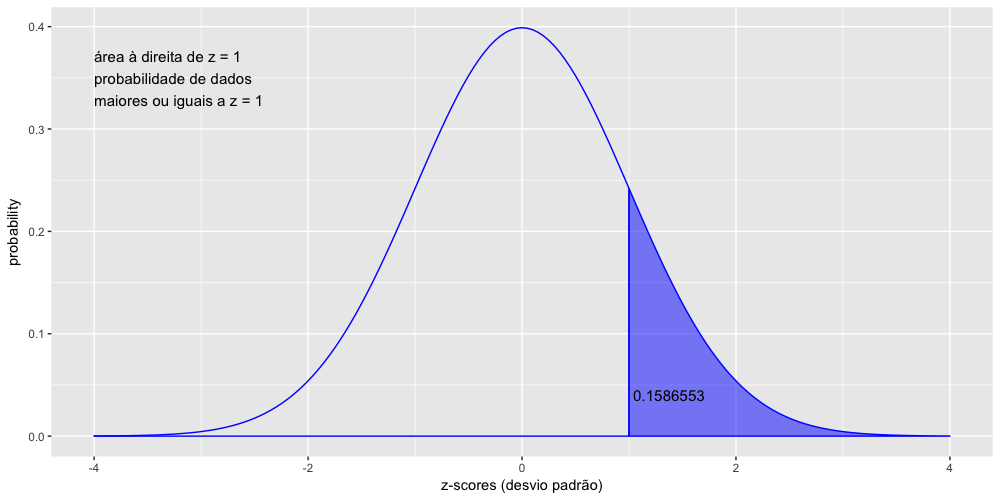
Como a função pnorm() calcula por default a área abaixo da curva à esquerda do ponto indicado, temos de subtrair essa área da área total do gráfico. Como a área total abaixo de uma curva de distribuição de probabilidade é sempre igual a 1, basta subtrairmos de 1, como feito abaixo:
1 > 1-pnorm(1)
2 [1] 0.1586553
Mas podemos também modificar o comportamento da função pnorm() alterando o parâmetro lower.tail para FALSE. Veja que o resultado é o mesmo do cálculo anterior.
1 > pnorm(1, lower.tail = FALSE)
2 [1] 0.1586553
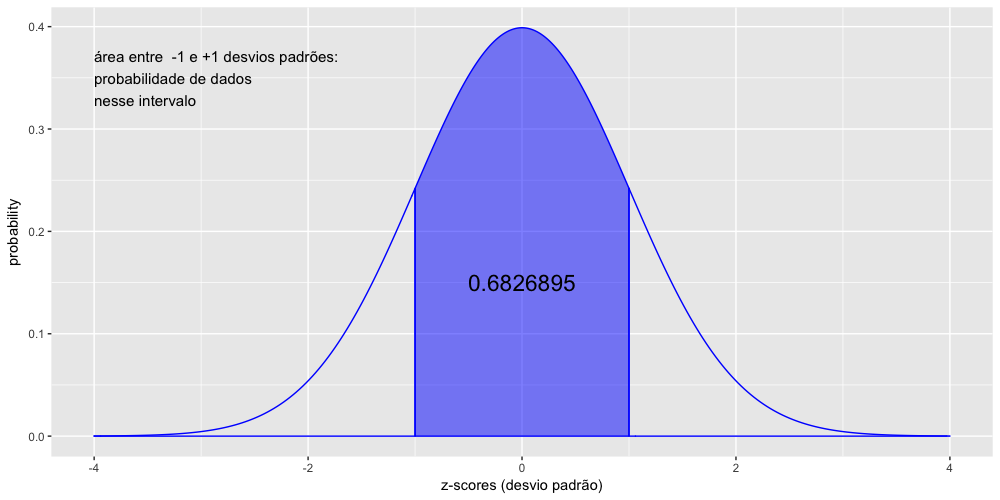
Vamos calcular agora a probabilidade de dados entre -1 e +1 desvios padrões, ou seja 1 desvio padrão ao redor da média.
1 # 1 desvio padrão ao redor da média
2 > pnorm(1) - pnorm(-1)
3 [1] 0.6826895
O resultado acima indica que, numa curva normal, aproximadamente 68% dos dados estão entre -1 e +1 desvios padrões. Esse resultado é válido não apenas para a curva normal padrão, mas para qualquer curva normal, pois calculamos a área usando desvios padrões.
Vamos calcular agora a probabilidade de dados entre -2 e 2 desvios padrões
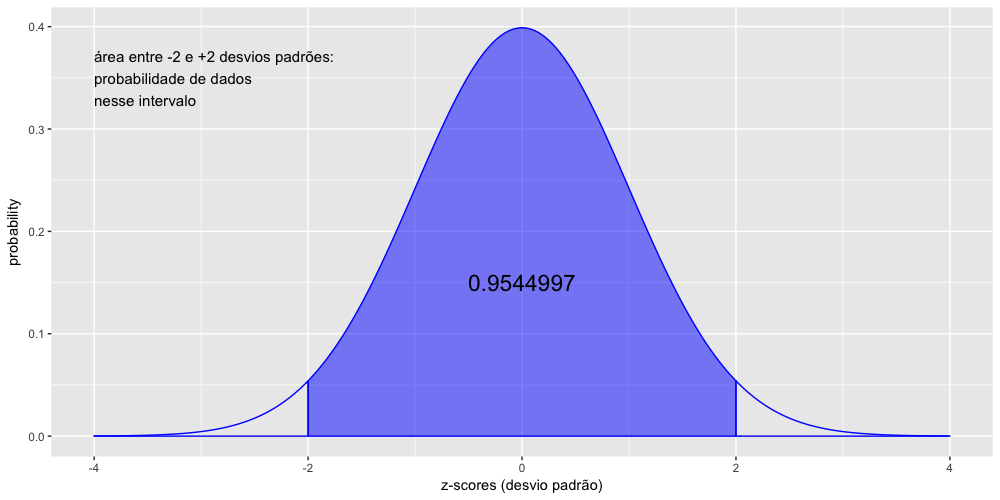
1 > pnorm(2) - pnorm(-2)
2 [1] 0.9544997
O resultado acima indica que, numa curva normal, aproximadamente 95% dos dados estão entre -2 e +2 desvios padrões. Esse resultado é válido não apenas para a curva normal padrão, mas para qualquer curva normal.
Vamos calcular agora a probabilidade de dados entre -3 e +3 desvios padrões, ou seja, 3 desvios padrões ao redor da média.
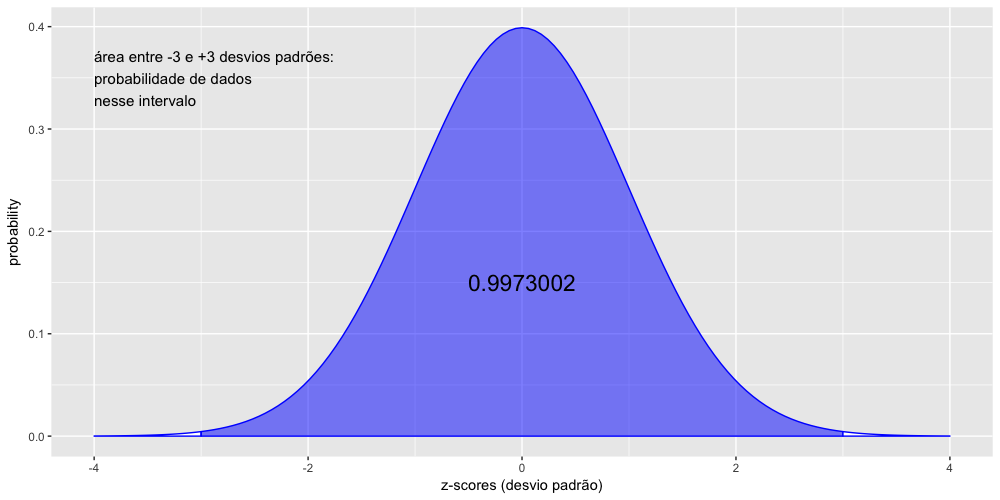
1 > pnorm(3) - pnorm(-3)
2 [1] 0.9973002
O resultado acima indica que, numa curva normal, aproximadamente 99,7% dos dados estão entre -3 e +3 desvios padrões. Esse resultado é válido não apenas para a curva normal padrão, mas para qualquer curva normal.
Os cálculos acima são usalmente conhecidos como a regra do 68-95-99.7 e servem para nos ajudar a calcular probabilidades sem necessidade de uso de computadores ou calculadoras.
Os parâmetros da curva normal - média e desvio padrão
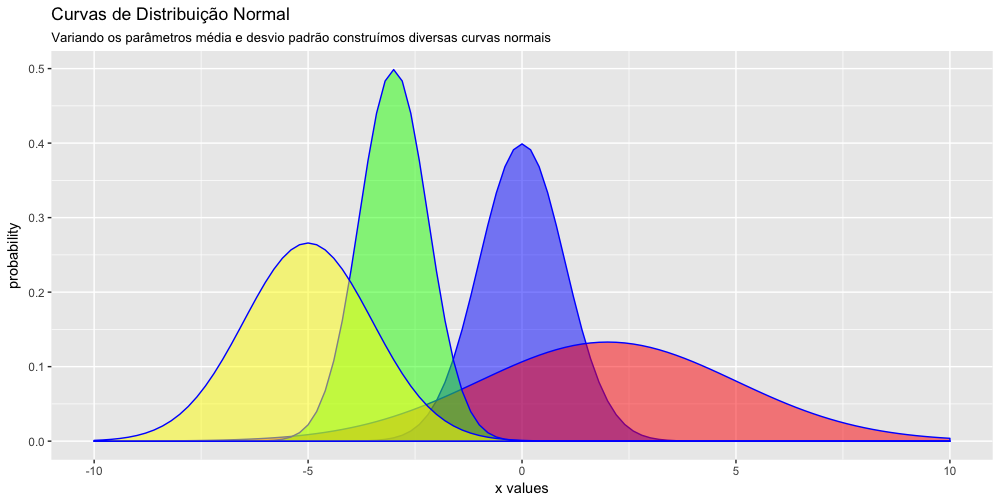
A média e o desvio padrão, são os parâmetros da curva normal, ou seja, as medidas que definem a curva. Alterando esses parâmetros podemos construir uma infinidade de curvas normais. Veja que esses dois parâmetros fazem parte da equação moderna da curva normal, desde sua introdução por Pearson e Fisher.
p(x) = \frac{1}{\sigma \sqrt{2\pi}} \text{e}^{\frac{-(x-\mu)^2}{2\sigma^2}}{format:latex}
Alterando esse parâmetros podemos construir uma infinidade de curvas normais.
Calculando as probabilidades - parte 2: pnorm(x, mean= , sd= )
A função pnorm() pode ser usada também para calcular probabilidades em situações nas quais a curva normal não é padrão. Para isso basta inserir na funcão pnorm() os argumentos mean= e sd=. Vamos experimentar fazer esses cálculos num exemplo.
Calcule o percentual de homens com altura superior a 180cm numa população cuja média de altura dos homens seja 170cm e cujo desvio padrão seja 10cm.
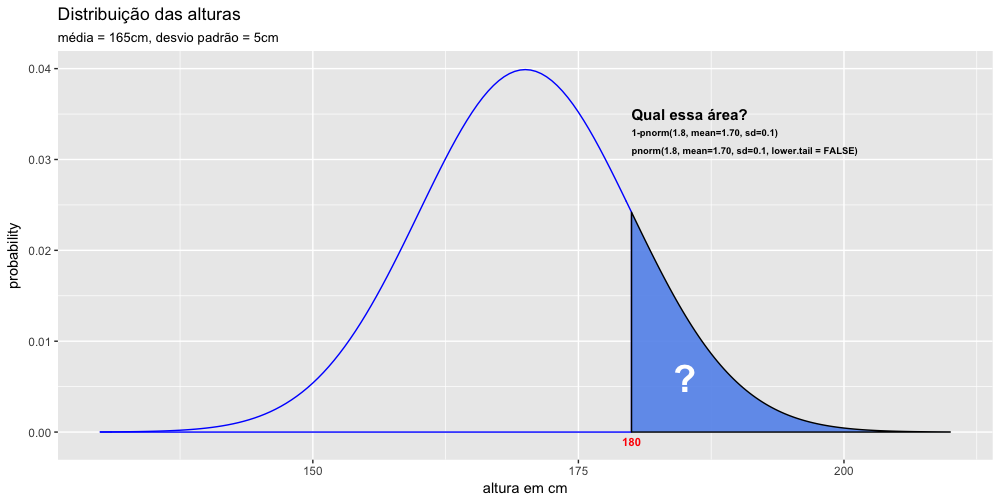
1 > 1-pnorm(180, mean=170, sd=10)
2 [1] 0.1586553
Ou então:{r}
> pnorm(180, mean=170, sd=10, lower.tail = FALSE)
[1] 0.1586553
Interpretando esse resultado: Nessa população, aproximadamente 16% dos homens tem altura igual ou superior a 180cm.
Calcule o percentual de homens com altura inferior a 1.50m numa população cuja média de altura dos homens seja 1.70m e cujo desvio padrão seja 0.1m.
1 > pnorm(1.5, mean=1.70, sd=0.1)
2 [1] 0.02275013
Interpretando esse resultado: Nessa população, aproximadamente 2.3% dos homens tem altura menor ou igual a 1.50m.
Calculando probabilidades parte 3 - a função qnorm()
Frequentemente nos deparamos com o problema inverso do que foi feito nas seções anteriores. Às vezes temos a área abaixo da curva e desejamos saber os pontos no eixo x que correspondem aos limites dessa área. Para isso usamos a função qnorm(). Podemos usar a função qnorm() com seus valores default para responder à seguinte questão: qual o z-score de determinado quantile da distribuição normal?
O principal argumento da função qnorm() são os quantiles, que equivalem às áreas abaixo da curva à esquerda de determinado ponto (o ponto que desejamos descobrir).
Vejamos num exemplo. Qual o valor do z-score da mediana? Lembre-se que a mediana represnta o percentil 50%, que é o mesmo que quantil 0.5. Portanto:
1 > qnorm(0.5)
2 [1] 0
O resultado acima é o z-score do quantil 0.5, ou seja, o z-score da mediana. O resultado é o esperado, pois numa distribuição normal o z-score da mediana é ZERO, tendo em vista que a distribuição é simétrica.
Um outro exemplo.
Numa população de mulheres cuja altura tem média 165cm e desvio padrão de 5cm, qual a altura (o ponto do eixo x) a abaixo do qual se encontram 80% das mulheres? Para responder à essa questão precisamos entender que o quantil desejado é 0.8. Veja representação gráfica dessa questão.
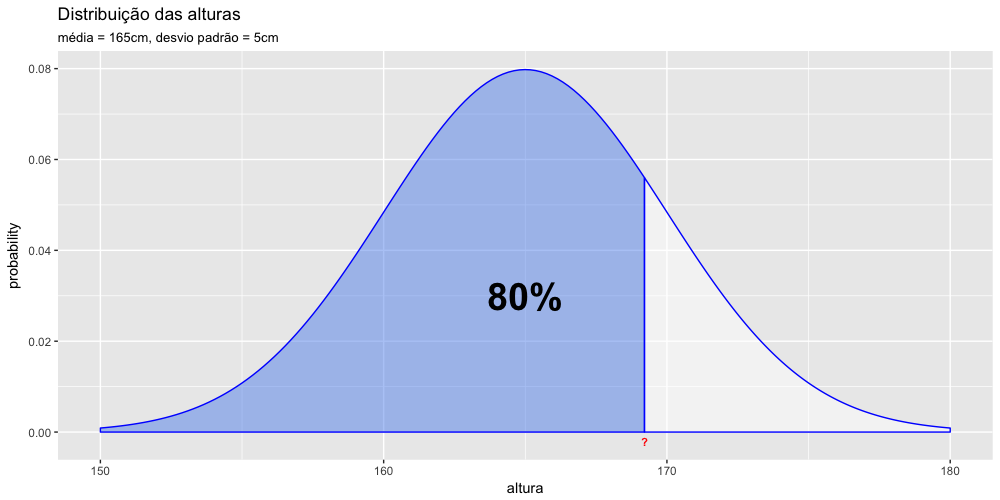
A partir daí basta inserir os argumentos na função qnorm().
1 > qnorm(0.8, mean=165, sd=5 )
2 [1] 169.2081
O resultado acima indica que 80% das mulheres tem menos de 169.2cm de altura.
Simulando uma distribuição normal
Frequentemente precisamos fazer simulações estatísticas. Para isso existem os modelos estatísticos e a equação da curva normal nos permite simular quaisquer tipos de distribuições normais desejadas.
Quando desejamos simular uma distribuição normal no R usamos a função rnorm(). random + normal = rnorm. Ou seja, essa função gera uma série de números aleatórios distribuidos de forma normal padrão: com média=0 e desvio padrão = 1. Entretanto, podemos modificar esses parâmetros e indicar a média (mean) e o desvio padrão (sd) que desejamos (lembre-se que o termo em ingles para desvio padrão é “standard deviation”, por isso “sd”).
Vamos simular os dados de altura uma população de 1000 de habitantes com média de altura de 175cm e um desvio padrão de 5cm. Iremos colocar esses valores num objeto (numa variável) que chamaremos de pop.altura, pois esses dados irão representar a altura de nossa população.
1 # criando um conjunto com 1 milhão de números distribuídos de forma normal
2 # com média = 175 e desvio padrão =5
3 > altura <- rnorm(1000, mean = 175, sd = 5)
4
5 # Colocando esse conjunto de dados num data frame:
6 > df.altura <- data.frame(altura)
Verificando a normalidade.
Nas seções anteriores fizemos diversos cálculos usando o modelo teórico da distribuição normal. Mas para usarmos esse modelo na vida real precisamos nos certificar que os dados da pesquisa realmente seguem uma distribuição normal. Usar o modelo da distribuição normal para dados que não estão normalmente distribuídos é um erro grave.
Uma forma usual de se verificar a normalidade dos dados é através da simples inspeção do gráfico de densidade de probabilidade.
Outra forma é através dos gráficos qqplot, ou quantile-quantile plot. Um gráfico qqplot é na verdade um scatter plot de quantiles de dois conjuntos de dados: os dados reais da pesquisa e os dados teóricos. com esse gráfico podemos verificar se os dados da pesquisa tem uma distribuição normal. Se os dados da pesquisa estiverem distribuídos de forma normal, ao plotar o gráfico iremos ver uma linha diagonal perfeita, indicando uma forte correlação entre os dados da pesquisa e os valores de uma distribuição normal.
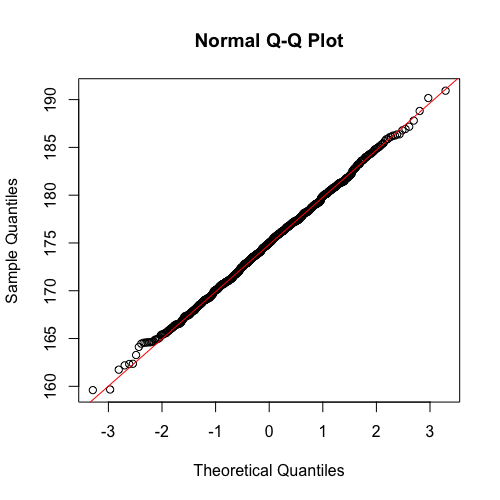
No R a função para gerar esse gráfico é a qqnorm(). Geralmente plotamos também uma linha de regressão nesse gráfico, o que é feito no r com a função qqline(). Frequentemente essas duas funções são usadas em conjunto como no gráfico abaixo.
Você poderá ver no gráfico abaixo que o eixo y representa os dados da amostra a serem testados e o eixo x representa os dados de uma distribuição normal. Se os dados da amostra estiverem distribuídos de forma normal os pontos do scatter plot estatão alinhados junto à reta inclinada no gráfico. No gráfico abaixo, com 1000 de dados, apenas um número muito pequeno de dados está fora do alinhamento, demonstrando que os dados estão realmente distribuídos de forma normal.
1 > qqnorm(altura)
2 > qqline(altura, col="red")