Teste de Hipóteses

Introdução

O que atualmente se conhece como teste de hipótese é um procedimento estatístico ainda bastante rudimentar e ainda alvo de muitas críticas. Os procedimentos desses teste são muito recentes, tendo se originado por volta de 1925, quando o estatístico Ronald Fisher publicou sua obra “Statistical Methods for Research Workers”. As idéias de Fisher revolucionaram os métodos estatísticos e são até hoje usados rotineiramente, apesar de suas imperfeições. O modelo atual de um teste estatístico é, na verdade, uma combinação das idéias de Fisher e Neynman, dois dos mais importantes estatísticos do século XX, mas que nunca concordaram um com o outro e muito menos em combinar seus procedimentos numa única teoria. Apesar de ano após ano aparecerem artigos criticando essa forma de teste de hipótese, é até hoje essa amalgama das teorias desses dois estatísticos que está sedimentada em livros textos e que compõe grande parte dos testes estatísticos na área da saúde.

Um teste de hipóteses envolve um procedimente estatístico que tenta escolher uma dentre duas hipóteses de uma pesquisa, tais como a hipótese de que o medicamento não funciona e a hipótese de que funciona. O procedimento padrão de um teste é que, logo em seu início, sejam estipuladas essas duas hipóteses, que recebem os nomes de hipótese nula e hipótese alternativa.

A hipótese alternativa

Denomina-se hipótese alternativa a hipótese que o pesquisador deseja tentar confirmar, é a suposição do pesquisador de que determinado agente tem realmente um efeito, de que os fenômenos estudados tem alguma relação de causa e efeito.

Na estatística a hipótese nula é geralmente simbolizada por H1 ou H₁.

A hipótese nula

Hipótese nula é o oposto da hipótese alternativa. Denomina-se hipótese nula de uma pesquisa a hipótese de que o agente em estudo não tem efeito. Por exemplo, de que a dieta não funciona, de que o medicamento não funciona, de que a vacina não funciona. Ou seja, é a hipótese de que não há nenhuma relação de causalidade entre os dois fenômenos estudados.

Em outras palavras, hipótese nula é a hipótese de que o acaso sozinho é responsável pela variação encontrada nos resultados e, consequentemente, quaisquer diferenças encontradas entre os grupos testados se devem meramente ao acaso, não havendo, portanto, nenhuma diferença real entre os grupos.

Na estatística a hipótese nula geralmente é simbolizada por H0 ou H₀.

A forma como os dados estão distribuídos nessa situação é chamada de distribuição sob a hipótese nula, ou simplesmente de distribuição nula.

Distribuição nula

Nos capítulos passados vimos que as distribuições teóricas de probabilidades são modelos matemáticos que podem servir para prever ou antecipar resultados de eventos ou experimentos cientíticos. Um outro uso importante das distribuições de probabilidade é servirem de modelos teóricos de como os dados deveriam estar distribuídos em determinadas situações. Esses modelos teóricos ideais são usados rotineiramente para fins de comparação em pesquisas científicas.

Por exemplo, para sabermos se uma dieta funciona, não basta termos os resultados dos efeitos, precisamos saber como seriam esses resultados se a dieta não funcionasse. Precisamos lembrar que, ainda que uma dieta não tenha efeito, quando testada em um grande conjunto de pessoas, certamente haverá mudanças no peso devidas ao acaso. Algumas pessoas poderão até mesmo engordar, outras emagrecer. Mas, se a dieta não funciona, espera-se que a maior parte não mude muito o peso. O que os pesquisadores precisam é saber como estarão distribuidos os pesos dos participantes se a dieta não funciona. Ou seja, precisamos comparar os resultados encontrados na pesquisa com um modelo teórico no qual a dieta não funciona. Precisamos saber como estariam distribuídos os dados na hipótese da dieta não ter efeito. Essa distribuição dos dados causada apenas pelos os efeitos do acaso é conhecida na estatística pelo nome de distribuição nula.

O termo distribuição nula se refere a um modelo teórico que mostra como os dados estarão distribuídos se apenas os efeitos do acaso estiverem atuando sobre os resultados. Quando um pesquisador pretende mostrar que determinado agente tem um efeito real, será necessário demonstrar que os dados encontrados estão distribuídos de forma significativamente diferente da distribuição nula.

O conceito de distribuição nula foi cunhado por Ronald Fisher e exposto pela primeira por volta de 1935 em seu livro The Design of Experiments. Nesse livro Fisher descreve os passos para um curioso experimento: Há alguma diferença no saber de um chá se o leite for adicionado à xícara de chá depois e não antes do se colocar o chá. Esse experimento é fruto de um evento real na vida de Fisher relatado num interessante livro sobre a história da estatística “The Lady Tasting Tea” de David Salsburg (2001). Segundo conta a história, a senhora Muriel Bristou alegava que o sabor do chá era melhor se o leite fosse adicionado depois que o já tivesse siddo colocado na xícara e que, caso fossem colocados na ordem inversa (leite primeiro e chá depois), o sabor não seria o mesmo. Diante dessa situação, Fisher idealizou um experimento no qual seria testada estatisticamente a possibilidade de diferenciar o sabor do chá nas duas condições descritas. Foram preparadas 4 xícaras com chá primeiro e leite adicionado posteriormente e outras 4 da forma inversa.

Uma distribuição nula desse experimento deveria representar a probabilidade de cada resultado possível ter ocorrido meramente por acaso. Por exemplo, acertar por acaso as 4 xícaras nas quais o leite foi adicionado depois do chá equivale a uma probabilidade de 1/70, ou seja, 1.4% de probabilidade disso ocorrer puramente por acaso. Acertar exatamente 3 xícaras equivale a uma probabilidade de 16/70, ou seja, 22.9% de probabilidade disso ocorrer por acaso. A distribuição das probabilidades de cada resultado ocorrer por acase é o que se denomina de distribuição nula.

Segundo o relato de David Salburg no livro “The Lady Tasting Tea” (2001, pag.8), a Sra. Muriel identificou corretamente as 4 xícaras nas quais o leite havia sido colocado depois do chá. Esse resultado pode ter sido por acaso? Sim! pode! Existe uma probabilidade de 1.4% de que ela tenha acertado por acaso. Mas o que fazer com esse resultado? Acreditamos na capacidade dela distinguir ou acreditamos que foi um mero acaso?

Podemos percever que um teste de hipóteses nunca prova uma relação entre os fatores estudados, apenas dá evidências probabilisticas dessa relação. É justamente essa avaliação da probabilidade que serve de parâmetro para a escolha de uma das duas hipóteses (nula ou alternativa).

Por isso mesmo o resultado de um teste estatístico geralmente é expresso em termos de rejeição ou não rejeição da hipótese nula, e nunca se diz que uma das hipóteses seja a verdadeira.

Segundo Fisher, a hipótese nula nunca pode provada, mas pode ser rejeitada no decorrer do experimento.

In relation to any experiment we may speak of this hypothesis as the null hypothesis, and it should be noted that the null hypothesis is never proved or established, but is possible disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
Ronald Fisher - The Design of Experiments

Nível de significância do teste

Os testes estatísticos nunca nos dão certeza dos resultados, podendo produzir resultados que não representam a verdade. Podemos acreditar que um medicamento funciona quando na verdade não funciona ou podemos acreditar que não funciona quando funciona.

Como nunca temos certeza se o resultado de um teste estatístico representa a verdade ou não, é preciso sempre analisar também qual a probabilidade do resultado encontrado ser falso.

Essa probabilidade do resultado encontrado ser falso depende de uma escolha arbitrária do próprio pesquisador. Vamos analisar o experimento de Fisher sobre a capacidade da Sra. Muriel discernir as diferenças no sabor do chá. A questão é: quantos acertos serão necessários podermos aceitar que Muriel seja realmente capaz de perceber a diferença no sabor? Quantos acertos vão convencer o pesquisador dessa capacidade? Veja o quanto essa decisão é subjetiva. Definir esse ponto de corte, significa decidir a partir de que ponto poderemos considerar que o resultado não foi devido apenas à sorte ou ao acaso, mas sim a uma real diferença de sabor entre os dois tipos de amostras. O resultado obtido (acertar as 4 xícaras) tem 1.4% de probabilidade de ter ocorrido por acaso. O que fazer com esse resultado é a questão. Acreditamos na capacidade dela distinguir ou acreditamos que foi um mero acaso?

Esse limite, esse ponto subjetivo, a partir do qual aceitamos uma hipótese e rejeitamos a outra é denominado na literatura científica de nível de significância. Tem sido uma prática tadicional da ciência aceitar que um resultado que corresponda a aproximadamente 1 chance em 20 possa ser considerado significativo, ou seja, podemos considerar que não deve ter ocorrido por acaso. Em termos percentuais isso significa dizer que se a probabilidade de um evento ocorrer foi menor que 5%, quando nos depararmos com essa ocorrência, podemos acreditar que não deve ter ocorrido por acaso. Usando esse ponto de corte, passamos a acreditar que a Sra. Muriel realmente consegue distinguir as xícaras.

it is a convenient convention to take twice the standard error as the limit of significance; this is roughly equivalent to the corresponding limit P = ·05
Ronald Fisher, Statistical Methods for Research Workers, 5ed. 1934. p.113

…it is convenient to take this point (p=0.05) as a limit in judging whether a deviation is to be considered significant or not.
Ronald Fisher, Statistical Methods for Research Workers, 5ed. 1934. p.43

Entrentanto, não podemos deixar de ter em conta que existe ainda uma possibilidade dela ter acertado meramente por acaso. Esse é o papel do nível de significância, determinar previamente o ponto de corte a partir do qual o pesquisador irá considerar que o resultado não foi por acaso.

A probabilidade de encontrarmos um resultado positivo (de que há diferenças ou de que o medicamento faz efeito) e esse resultado na verdade ser falso é denotado por alpha ($\alpha$). A probabilidade de encontrarmos um resultado falso negativo (rejeitarmos a hipótese nula quando ela é verdadeira) é denotada por beta ($\beta$).

Essa medida denotada por alpha ($\alpha$) é chamada de nível de significância do teste. Mas afinal de contas o que significa isso?

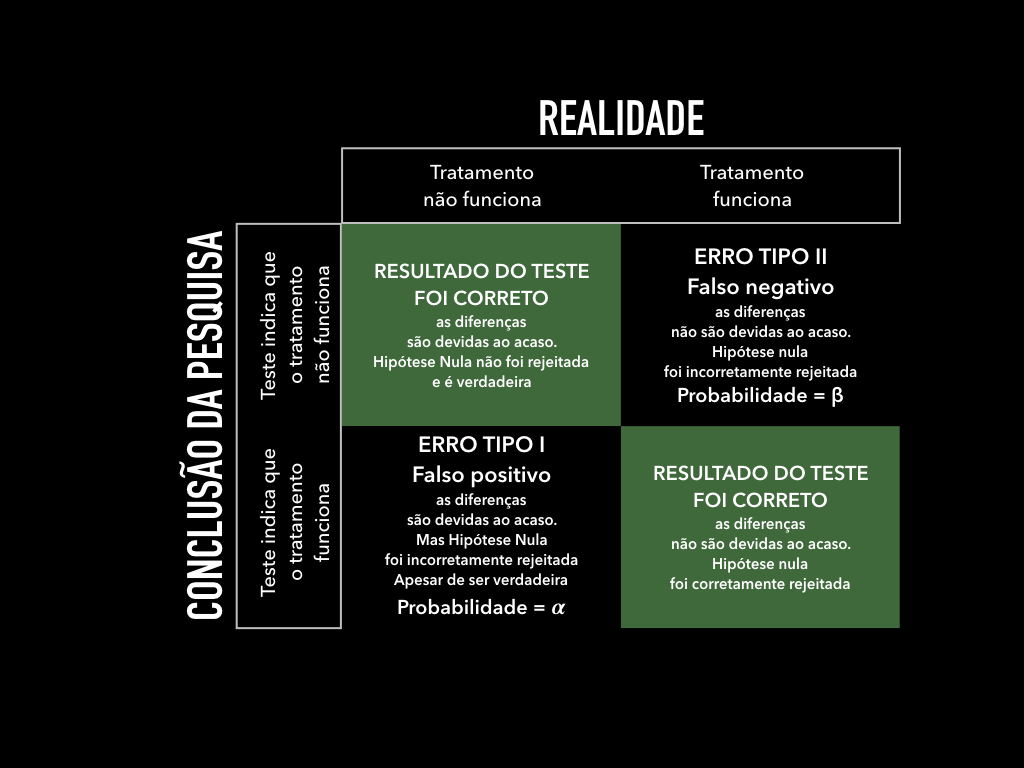
Erros tipo I e tipo II

Um ponto que precisa ser enfatizado é que o resultado de um teste de hipóteses, sendo meramente probabilístico, pode ser errado. Nenhum pesquisador tem acesso à verdade absoluta, mas apenas aos resultados de seus testes. Portanto, toda pesquisa pode ter um resultado que não representa a verdade. Essa situação é tão comum estima-se que cerca de metade dos resultados da literatura científica médica são falsos (Ioannidis, 2005).

Existem duas maneiras pelas quais os resultados de uma pesquisa pode ser falso: Uma pesquisa pode rejeitar a hipótese nula quando na verdade ela é a verdadeira. Ou então, por outro lado, uma pesquisa pode não conseguir rejeitar a hipótese nula quando na verdade ela é falsa. Resumindo podemos errar de duas formas:

• rejeitar uma hipótese nula que é verdadeira (um falso positivo).
• não rejeitar uma hipótese nula que é falsa (um falso negativo).

Esses dois tipos de resultados errados recebem nomes especiais na literatura científica:

• Erro tipo I (falso positivo): rejeitar uma hipótese nula que é verdadeira
• Erro tipo II (falso negativo): falhar em rejeitar uma hipótese nula que é falsa.

Teste unicaudal ou bicaudal

Antes de iniciarmos os procedimentos do teste propriamente dito precisamos definir mais uma questão acerca das hipóteses nula e alternativa: a direção do teste.

Às vezes uma pesquisa pretende demonstrar que um determinado medicamento reduz algo como, por exemplo, um medicamento que reduz a pressão arterial. Outras vezes pretende demonstrar que um medicamento aumenta algo como, por exemplo, um medicamento para aumentar a concentração nos estudos. No primeiro exemplo poderíamos fazer um teste para saber se o medicamento reduz a pressão arterial. No segundo caso, poderíamos fazer um teste para saber se o medicamento aumenta a concentração nos estudos. Nesses dois exemplos é feito apenas em uma direção, sendo então denominado unicaudal.

Entretanto, como frequentemente não podemos ter certeza dos efeitos do medicamento ou do agente em estudo, temos de ter em mente sempre a possibilidade de haver um efeito oposto ao que esperávamos acontecer. Pode ser que um determinado medicamento que supostamente aumente a concentração tenha na verdade o efeito contrário. Por isso mesmo considera-se que um testes estatísticos mais robusto sejam aqueles nos quais são consideradas essas duas possibilidades, nesse caso o teste é denominado bicaudal. Nesse tipo de teste é avaliado se o medicamento (ou agente em estudo) produz algum efeito, seja aumentando ou seja diminuindo alguma coisa. Esse teste que leve em conta a possibilidade desses dois desfechos é chamado de teste bicaudal.

p-values

Nas seções anteriores vimos que um pesquisador tem de definir o nível de significância de sua pesquisa e que esse nível de significância tem sido estabelecido habitualmente em 5% (0.05). Sendo esse o ponto de corte, o ponto que define o limite para decisão de rejeitar ou não a hipótese nula. Ou seja, habitualmente a hipótese nula é rejeitada se os dados encontrados na pesquisa tem uma probabilidade menor que 5% (0.05) de terem ocorrido por acaso.

Para podermos tomar a decisão de rejeitar ou não a hipótese nula precisamos de dois ítens:

1. O nível de significância, usualmente convencionado como sendo 5% (0.05) e indicado nos artigos científicos simplesmente por: ($\alpha = 0.05$).
2. O cálculo da probabilidade de de encontrarmos, meramente por acaso, dados iguais ou mais extremos que os que foram encontrados na pesquisa. Esse resultado, o valor da probabilidade, é o chamado valor de p (p-value) e denotado na literatura científica apenas por $p$.

Conclusão

Levando em conta o resultado encontrado no exemplo das de Fisher, o resultado poderia ser simplesmente escrito da seguinte maneira:

$\alpha = 0.05$
$p = 0.0143$

Como o valor de p foi menor que 0.05, rejeitamos a hipótese nula e aceitamos a evidência de que realmente há diferença no sabor do chá dependendo a ordem em que os ingredientes são colocados (chá e leite) e que essa diferença pode ser percebida pela Sra. Muriel.

Referências

1. Ronald Fisher. The Design of Experiments. Hafner Publishing Company: New York, 1971.
2. David Salsburg. The Lady Tasting Tea. How Statistics Revolutionized Science in the Twentieth Century. Holt Paperbacks: New York, 2001.
3. John P. A. Ioannidis Why most published research findings are false. PLoS Med, v. 2, n. 8, p. e124, 2005.