30. Newton’s definition of density

Newton’s definition 1 in the Principia:

Quantity of matter is a measure of matter that arises from its density and volume jointly.

In Definition 1 Newton uses Kepler’s Rule to define density in a cryptic way. He labels the constant of density 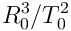“mass” and neglects to clarify that 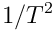is frequency squared.

This is Newton’s greatest discovery. He was the first person to realize the fundamental nature of Kepler’s Rule.

In order to brand Kepler’s Rule as his own discovery Newton associated it with two superfluous terms: force and mass. If Newton were to use Kepler’s Rule as is with only radius and period he would have glorified Kepler and reduced himself to a mere astronomer. As a marketing genius and a megalomaniacal worlbuilder Newton chose to brand Kepler’s Rule as Newton’s laws and made it the foundation of his System of the World.

Force and mass are decorative terms Newton superimposed on Kepler’s Rule and are not supported by observations. They do not exist in operational formulas. Observations reject the existence of mass (matter) but in order to save Newton’s authority physicists – instead of dropping the word mass – invented the concept of zero mass, e.g., the photon.

Force too is redundant. Einstein showed that force is unphysical. Once again, in order to save Newton’s sacred authority physicists do not let go of Newton’s occult force. They keep writing “F” in their derivations in order to cancel it in the next line.

Based on the above I propose the following propositions:

• Kepler’s Rule is fundamental
  • discovered in a database of observations
  • proven to work in the solar system
  • proven to work in binary stars and other systems
  • takes only two terms — radius and period of an orbit
  • is independent of any laws and ideologies, such as Newtonism
• Kepler’s Rule is the definition of density
  • For a given frequency and volume density is constant
• Newtonism is a branding of Kepler’s Rule
  • newtonian mechanics is Kepler’s Rule written with standard units and constants
  • mathematical formalisms of newtonian mechanics - Lagrange, Hamilton - are Kepler’s Rule expressed with calculus notation