Leanpub: Publish Early, Publish Often

6. Kepler’s Rule and Newton’s Laws

What is the difference between

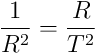
$\frac{1}{R^2} = \frac{R}{T^2}$

and

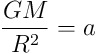
$\frac{GM}{R^2} = a$

To me GM/R² = a is Kepler’s rule

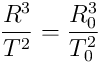
$\frac{R^3}{T^2} = \frac{R_0^3}{T_0^2}$

written with Newtonian units where

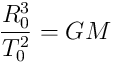
$\frac{R_0^3}{T_0^2} = GM$

The symbol a is a proxy for R/T². Therefore, we can equally ask, what is the difference between

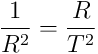
$\frac{1}{R^2} = \frac{R}{T^2}$

and

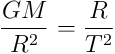
$\frac{GM}{R^2} = \frac{R}{T^2}$

Let’s combine like terms on one side

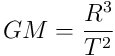
$GM = \frac{R^3}{T^2}$

If we define 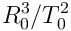${R_0^3/T_0^2}$ as the constant term in Kepler’s Rule then we have

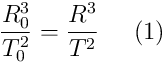
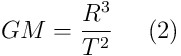
$\frac{R_0^3}{T_0^2} = \frac{R^3}{T^2} \; \; \; \; \; (1)$ $GM = \frac{R^3}{T^2} \; \; \; \; \; (2)$

Therefore (1) and (2) are the same Kepler’s Rule. In (2) the unit term is

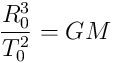
$\frac{R_0^3}{T_0^2} = GM$

We can also set the unit term to unity

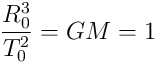
$\frac{R_0^3}{T_0^2} = GM = 1$

and then we would have

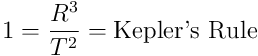
$1 = \frac{R^3}{T^2} = \textup{Kepler's Rule}$

I see

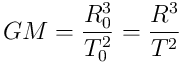
$GM = \frac{R_0^3}{T_0^2} = \frac{R^3}{T^2}$

as Kepler’s Rule written with the conventional unit GM.

Physicists read the same in two ways

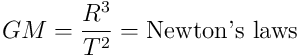
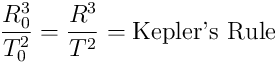
$GM = \frac{R^3}{T^2} = \textup{Newton's laws}$ $\frac{R_0^3}{T_0^2} = \frac{R^3}{T^2} = \textup{Kepler's Rule}$

They then substitute

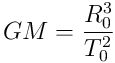
$GM = \frac{R_0^3}{T_0^2}$

in Kepler’s Rule and call this substitution “deriving Kepler’s law from Newton’s laws.”

So in physics writing Kepler’s Rule with a unit called “Newton’s constant G” turns Kepler’s rule into Newton’s law.

But the way I see it

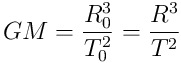
$GM = \frac{R_0^3}{T_0^2} = \frac{R^3}{T^2}$

is one expression. This is Kepler’s Rule. This expression has nothing to do with Newton’s laws or Newtonian mechanics.

All evidence shows that Kepler’s Rule came first. Kepler’s Rule was discovered in observations. Physicists agree on this.

The claim physicists make is that Newton discovered the underlying dynamic law in Kepler’s geometric rule.

But this is not true.

Even if Newton made the claim that the Newtonian force was the underlying dynamical quantity of the geometric Kepler’s rule today physics tells us that Newton’s force is unphysical and does not exist.

If Newton’s force has been shown to be unphysical by physicists themselves why do they still talk about a dynamical foundation of Kepler’s rule discovered by Newton?

The only claim for dynamical terms must be G and M.

But neither G nor M nor GM are dynamical quantities.

G was not written by Newton. Newton did not use constants, he worked with proportions, not with equations.

Mass is the constant term 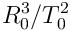R_0^3/T_0^2 . This is how Newton defined mass.

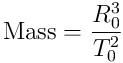
$\textup{Mass} = \frac{R_0^3}{T_0^2}$

R and T are geometric therefore mass as defined by Newton is the name of the unit term in Kepler’s Rule.

Once again we see that Newton labelled Kepler’s Rule with Newtonian labels and his followers reified Newton’s labels.

My conclusion is that Newton’s followers to this day insist on copying Newton’s labels blindly.

Then what to do?

What is the correct way to read

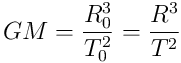
$GM = \frac{R_0^3}{T_0^2} = \frac{R^3}{T^2}$

Is this a dynamic or geometric expression?

Is this Kepler’s Rule or Newton’s laws?

How can we decide?

Is there an independent authority outside physics who can evaluate this expression independent of Newtonian dogma?

Why is it that writing Kepler’s rule with a conventional unit turn it into Newton’s dynamical law?

If the Newtonian force has been shown to be unphysical why is it that physicists still insist that Newton’s force is the dynamical and true law, not Kepler’s geometric rule?

The stakes are very high. Physicists will never concede that orbits are independent of Newton’s force and therefore orbits are independent of force with no ifs and buts. Physicists will always come up with rationalizations to keep Newton’s force associated with orbits at least on pedagogical level. Otherwise that would be the end of Newtonian physics. Physicists is not ready for that yet.

But suppose that the last paragraph is my opinion. What kind of evidence is needed so that physicists will finally stop calling Kepler’s Rule Newton’s law? Is that possible?

What evidence do we need to offer to prove that orbits are independent of Newtonian force?

Is it possible that physicists will stop arguing both that orbits are independent of force and not? At present they use sophistry to argue that orbits are defined by general relativity and therefore independent of Newtonian force and that orbits are dependent on force as needed.

The sophistry doesn’t work because if orbits are independent of force than physicists must accept that there are no dynamical terms in Kepler’s Rule.

What is curious to me is that Newton’s laws, Newton’s mechanics, force, mass are no longer used in astronomy. Yet physicists are unwilling to give up their absolute faith in Newton’s authority. Doesn’t make sense.