5. Variation
The variance
Watch this video before beginning.
Recall that the mean of distribution was a measure of its center. The variance, on the other hand, is a measure of spread. To get a sense, the plot below shows a series of increasing variances.
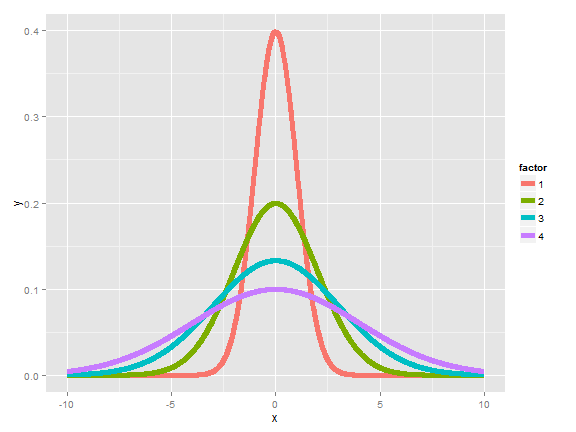
We saw another example of how variances changed in the last chapter when we looked at the distribution of averages; they were always centered at the same spot as the original distribution, but are less spread out. Thus, it is less likely for sample means to be far away from the population mean than it is for individual observations. (This is why the sample mean is a better estimate than the population mean.)
If 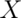 is a random variable with mean
is a random variable with mean 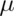 , the variance of
, the variance of
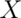 is defined as
is defined as
![Var(X) = E[(X - \mu)^2] = E[X^2] - E[X]^2.](/preview_site_images/LittleInferenceBook/leanpub_equation_158.png)
The rightmost equation is the shortcut formula that is almost always used
for calculating variances in practice.
Thus the variance is the expected (squared) distance from the mean. Densities
with a higher variance are more spread out than densities with
a lower variance. The square root of the variance is called the
standard deviation. The main benefit of working with standard deviations
is that they have the same units as the data, whereas the variance has the
units squared.
In this class, we’ll only cover a few basic examples for calculating a variance. Otherwise, we’re going to use the ideas without the formalism. Also remember, what we’re talking about is the population variance. It measures how spread out the population of interest is, unlike the sample variance which measures how spread out the observed data are. Just like the sample mean estimates the population mean, the sample variance will estimate the population variance.
Example
What’s the variance from the result of a toss of a die? First recall that ![E[X] = 3.5](/preview_site_images/LittleInferenceBook/leanpub_equation_159.png) , as we discussed in the previous lecture.
Then let’s calculate the other bit of information that we need,
, as we discussed in the previous lecture.
Then let’s calculate the other bit of information that we need, ![E[X^2]](/preview_site_images/LittleInferenceBook/leanpub_equation_160.png) .
.
![E[X^2] = 1 ^ 2 \times \frac{1}{6} + 2 ^ 2 \times \frac{1}{6} + 3 ^ 2 \times \frac{1}{6} + 4 ^ 2 \times \frac{1}{6} + 5 ^ 2 \times \frac{1}{6} + 6 ^ 2 \times \frac{1}{6} = 15.17](/preview_site_images/LittleInferenceBook/leanpub_equation_161.png)
Thus now we can calculate the variance as:
![Var(X) = E[X^2] - E[X]^2 \approx 2.92.](/preview_site_images/LittleInferenceBook/leanpub_equation_162.png)
Example
What’s the variance from the result of the toss of a
(potentially biased) coin with probability of heads (1) of 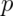 ? First recall that
? First recall that
![E[X] = 0 \times (1 - p) + 1 \times p = p.](/preview_site_images/LittleInferenceBook/leanpub_equation_164.png) Secondly, recall that since
Secondly, recall that since 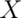 is either 0 or 1,
is either 0 or 1,
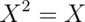 . So we know that:
. So we know that:
![E[X^2] = E[X] = p.](/preview_site_images/LittleInferenceBook/leanpub_equation_167.png)
Thus we can now calculate the variance of a coin flip as
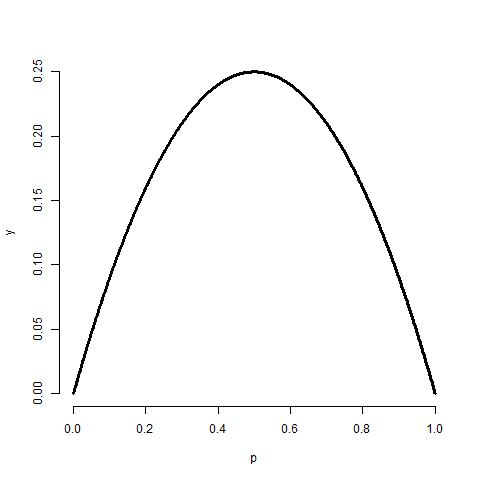
![Var(X) = E[X^2] - E[X]^2 = p - p^2 = p(1 - p).](/preview_site_images/LittleInferenceBook/leanpub_equation_168.png) This is a well known formula, so it’s worth committing
to memory. It’s interesting to note that this function is
maximized at
This is a well known formula, so it’s worth committing
to memory. It’s interesting to note that this function is
maximized at 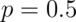 . The plot below shows this by
plotting
. The plot below shows this by
plotting 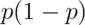 by
by 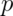 .
.
= seq(0 , 1, length = 1000)
y = p * (1 - p)
plot(p, y, type = "l", lwd = 3, frame = FALSE)
The sample variance
The sample variance is the estimator of the population variance. Recall that the population variance is the expected squared deviation around the population mean. The sample variance is (almost) the average squared deviation of observations around the sample mean. It is given by
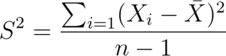
The sample standard deviation is the square root of the sample variance.
Note again that
the sample variance is almost, but not quite, the average squared deviation from
the sample mean since we divide by  instead of
instead of
 . Why do we do this you might ask? To answer that question
we have to think in the terms of simulations. Remember that the
sample variance is a random variable, thus it has a distribution
and that distribution has an associated population mean. That
mean is the population variance that we’re trying to estimate
if we divide by
. Why do we do this you might ask? To answer that question
we have to think in the terms of simulations. Remember that the
sample variance is a random variable, thus it has a distribution
and that distribution has an associated population mean. That
mean is the population variance that we’re trying to estimate
if we divide by  rather than
rather than  .
.
It is also nice that as we collect more data the distribution of the sample variance gets more concentrated around the population variance that it’s estimating.
Simulation experiments
Watch this video before beginning.
Simulating from a population with variance 1
Let’s try simulating collections of standard normals and taking the variance. If we repeat this over and over, we get a sense of the distribution of sample variances variances.
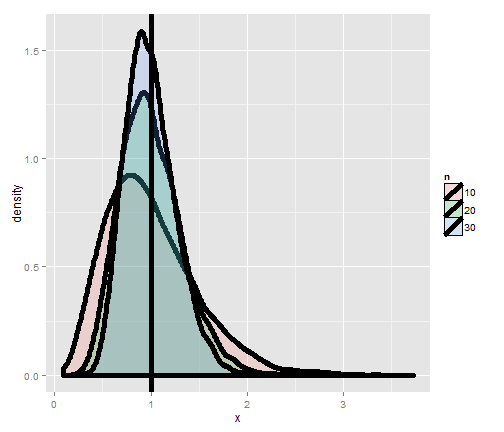
Notice that these histograms are always centered in the same spot, 1. In other words, the sample variance is an unbiased estimate of the population variances. Notice also that they get more concentrated around the 1 as more data goes into them. Thus, sample variances comprised of more observations are less variable than sample variances comprised of fewer.
Variances of x die rolls
Let’s try the same thing, now only with die rolls instead of simulating standard normals. In this experiment, we simulated samples of die rolls, took the variance and then repeated that process over and over. What is plotted are histograms of the collections of sample variances.
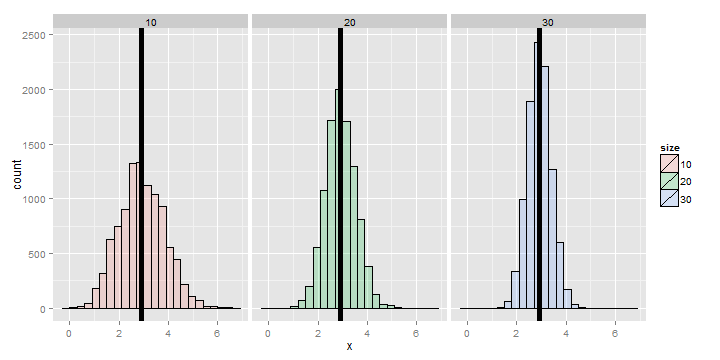
Recall that we calculated the variance of a die roll as 2.92 earlier on in this chapter. Notice each of the histograms are centered there. In addition, they get more concentrated around 2.92 as more the variances are comprised of more dice.
The standard error of the mean
At last, we finally get to a perhaps very surprising (and useful) fact:
how to estimate the variability of the mean of a sample, when we only get to observe
one realization. Recall that the average of random sample from a population
is itself a random variable having a distribution, which in simulation
settings we can explore by repeated sampling averages. We know that this
distribution is centered around the population mean,
![E[\bar X] = \mu](/preview_site_images/LittleInferenceBook/leanpub_equation_177.png) . We also know the variance of the distribution
of means of random samples.
. We also know the variance of the distribution
of means of random samples.
The variance of the sample mean is: 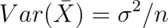 where
where 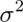 is the variance of the population being sampled
from.
is the variance of the population being sampled
from.
This is very useful, since we don’t have repeat sample means
to get its variance directly using the data. We already know a good estimate of
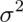 via the sample variance. So, we can get a good estimate
of the variability of the mean, even though we only get to observe 1 mean.
via the sample variance. So, we can get a good estimate
of the variability of the mean, even though we only get to observe 1 mean.
Notice also this explains why in all of our simulation experiments the variance of the sample mean kept getting smaller as the sample size increased. This is because of the square root of the sample size in the denominator.
Often we take the square root of the variance of the mean to get the standard deviation of the mean. We call the standard deviation of a statistic its standard error.
Summary notes
- The sample variance,
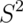 , estimates the population variance,
, estimates the population variance, 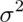 .
. - The distribution of the sample variance is centered around
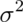 .
. - The variance of the sample mean is
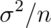 .
.
- Its logical estimate is
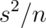 .
. - The logical estimate of the standard error is
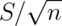 .
.
- Its logical estimate is
-
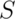 , the standard deviation, talks about how variable the population is.
, the standard deviation, talks about how variable the population is. -
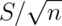 , the standard error, talks about how variable averages of random
samples of size
, the standard error, talks about how variable averages of random
samples of size 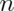 from the population are.
from the population are.
Simulation example 1: standard normals
Watch this video before beginning.
Standard normals have variance 1. Let’s try sampling
means of 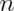 standard normals. If our theory is correct, they should
have standard deviation
standard normals. If our theory is correct, they should
have standard deviation 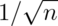
> nosim <- 1000
> n <- 10
## simulate nosim averages of 10 standard normals
> sd(apply(matrix(rnorm(nosim * n), nosim), 1, mean))
[1] 0.3156
## Let's check to make sure that this is sigma / sqrt(n)
> 1 / sqrt(n)
[1] 0.3162
So, in this simulation, we simulated 1000 means of 10 standard normals. Our
theory says the standard deviation of averages of 10 standard normals must
be 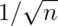 . Taking the standard deviation of the 10000 means yields
nearly exactly that. (Note that it’s only close, 0.3156 versus 0.31632.
To get it to be exact, we’d have to simulate
infinitely many means.)
. Taking the standard deviation of the 10000 means yields
nearly exactly that. (Note that it’s only close, 0.3156 versus 0.31632.
To get it to be exact, we’d have to simulate
infinitely many means.)
Simulation example 2: uniform density
Standard uniforms have variance 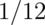 . Our theory mandates
that means of random samples of
. Our theory mandates
that means of random samples of 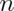 uniforms
have sd
uniforms
have sd 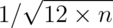 . Let’s try it with a simulation.
. Let’s try it with a simulation.
> nosim <- 1000
> n <- 10
> sd(apply(matrix(runif(nosim * n), nosim), 1, mean))
[1] 0.09017
> 1 / sqrt(12 * n)
[1] 0.09129
Simulation example 3: Poisson
Poisson(4) random variables have variance 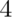 . Thus means of
random samples of
. Thus means of
random samples of 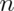 Poisson(4)
should have standard deviation
Poisson(4)
should have standard deviation 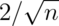 . Again let’s try it out.
. Again let’s try it out.
> nosim <- 1000
> n <- 10
> sd(apply(matrix(rpois(nosim * n, 4), nosim), 1, mean))
[1] 0.6219
> 2 / sqrt(n)
[1] 0.6325
Simulation example 4: coin flips
Our last example is an important one. Recall that the variance of a
coin flip is 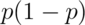 . Therefore the standard deviation of the average
of
. Therefore the standard deviation of the average
of 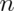 coin flips should be
coin flips should be 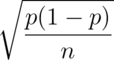 .
.
Let’s just do the simulation with a fair coin. Such coin
flips have variance 0.25. Thus means of
random samples of 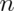 coin flips have sd
coin flips have sd 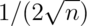 .
Let’s try it.
.
Let’s try it.
> nosim <- 1000
> n <- 10
> sd(apply(matrix(sample(0 : 1, nosim * n, replace = TRUE),
nosim), 1, mean))
[1] 0.1587
> 1 / (2 * sqrt(n))
[1] 0.1581
Data example
Now let’s work through a data example to show how the standard error of the
mean is used in practice. We’ll use the father.son height data from Francis
Galton.
library(UsingR); data(father.son);
x <- father.son$sheight
n<-length(x)
Here’s a histogram of the sons’ heights from the dataset. Let’ calculate different variances and interpret them in this context.
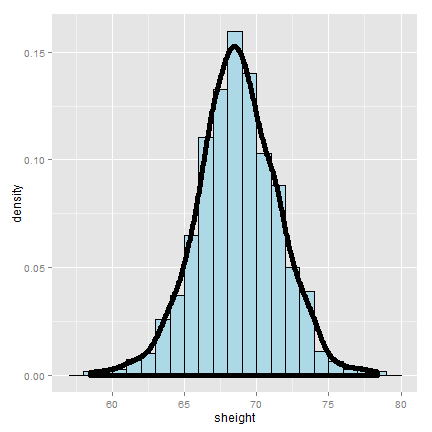
>round(c(var(x), var(x) / n, sd(x), sd(x) / sqrt(n)),2)
[1] 7.92 0.01 2.81 0.09
The first number, 7.92, and its square root, 2.81, are the estimated variance
and standard deviation of the sons’ heights. Therefore, 7.92 tells us exactly how variable
sons’ heights were in the data and estimates how variable sons’ heights are
in the population. In contrast 0.01, and the square root 0.09, estimate how
variable averages of  sons’ heights are.
sons’ heights are.
Therefore, the smaller numbers discuss the precision of our estimate of the mean of sons’ heights. The larger numbers discuss how variable sons’ heights are in general.
Summary notes
- The sample variance estimates the population variance.
- The distribution of the sample variance is centered at what its estimating.
- It gets more concentrated around the population variance with larger sample sizes.
- The variance of the sample mean is the population variance
divided by
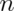 .
.
- The square root is the standard error.
- It turns out that we can say a lot about the distribution of averages from random samples, even though we only get one to look at in a given data set.
Exercises
- If I have a random sample from a population, the sample variance is an estimate of?
- The population standard deviation.
- The population variance.
- The sample variance.
- The sample standard deviation.
- The distribution of the sample variance of a random sample from a population is centered at what?
- The population variance.
- The population mean.
- I keep drawing samples of size
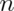 from a population with variance
from a population with variance 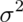 and taking their average. I do this thousands of times. If I were to take the variance of the collection of averages, about what would it be?
and taking their average. I do this thousands of times. If I were to take the variance of the collection of averages, about what would it be? - You get a random sample of
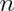 observations from a population and take their average. You would like to estimate the variability of averages of $$n$$ observations from this population to better understand how precise of an estimate it is. Do you need to repeated collect averages to do this?
observations from a population and take their average. You would like to estimate the variability of averages of $$n$$ observations from this population to better understand how precise of an estimate it is. Do you need to repeated collect averages to do this?
- No, we can multiply our estimate of the population variance by
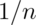 to get a good estimate of the variability of the average.
to get a good estimate of the variability of the average. - Yes, you have to get repeat averages.
- No, we can multiply our estimate of the population variance by
- A random variable takes the value -4 with probability .2 and 1 with probability .8. What is the variance of this random variable? Watch a video solution to this problem. and look at a version with a worked out solution.
- If
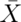 and
and 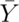 are comprised of n iid random variables arising from distributions
having means
are comprised of n iid random variables arising from distributions
having means 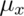 and
and 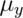 , respectively and common variance
, respectively and common variance
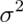 what is the variance
what is the variance 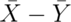 ?
Watch a video solution to this problem here and see a typed up solution here
?
Watch a video solution to this problem here and see a typed up solution here
- Let
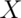 be a random variable having standard deviation
be a random variable having standard deviation  . What can
be said about the variance of
. What can
be said about the variance of 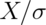 ? Watch a video solution to this
problem here and
typed up solutions here.
? Watch a video solution to this
problem here and
typed up solutions here. - Consider the following pmf given in R by the code
p <- c(.1, .2, .3, .4)and ‘x <- 2 : 5`. What is the variance? Watch a video solution to this problem here and here is the problem worked out. - If you roll ten standard dice, take their average, then repeat this process over and over and construct a histogram, what would be its variance expressed to 3 decimal places? Watch a video solution here and see the text here.