6. Some common distributions
The Bernoulli distribution
The Bernoulli distribution arises as the result of a binary outcome, such
as a coin flip. Thus, Bernoulli random variables take (only)
the values 1 and 0 with probabilities of (say) 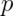 and
and  ,
respectively. Recall that the
PMF for a Bernoulli random variable
,
respectively. Recall that the
PMF for a Bernoulli random variable 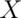 is
is
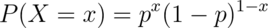 .
.
The mean of a Bernoulli random variable is 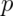 and the variance is
and the variance is
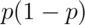 . If we let
. If we let 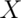 be a Bernoulli random variable,
it is typical to call
be a Bernoulli random variable,
it is typical to call 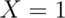 as a “success” and
as a “success” and 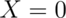 as a “failure”.
as a “failure”.
If a random variable follows a Bernoulli distribution with success probability
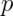 we write that
we write that 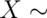 Bernoulli
Bernoulli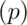 .
.
Bernoulli random variables are commonly used for modeling any binary trait for a random sample. So, for example, in a random sample whether or not a participant has high blood pressure would be reasonably modeled as Bernoulli.
Binomial trials
The binomial random variables are obtained as the sum of iid Bernoulli trials. So if a Bernoulli trial is the result of a coin flip, a binomial random variable is the total number of heads.
To write it out as mathematics, let  be iid
Bernoulli
be iid
Bernoulli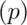 , then
, then 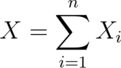 is a
binomial random variable. We write out that
is a
binomial random variable. We write out that
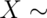 Binomial
Binomial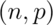 . The binomial mass function is
. The binomial mass function is
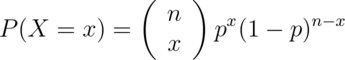
where 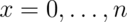 . Recall that the notation
. Recall that the notation
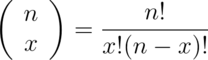
(read “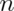 choose
choose 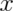 ”) counts the number of ways of
selecting
”) counts the number of ways of
selecting 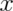 items out of
items out of 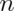 without replacement disregarding the order of the items. It turns out
that
without replacement disregarding the order of the items. It turns out
that 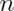 choose 0 is 1 and
choose 0 is 1 and 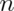 choose 1 and
choose 1 and
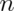 choose
choose  are both
are both 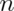 .
.
Example
Suppose a friend has 8 children, 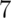 of which are girls and none are
twins. If each gender has an independent
of which are girls and none are
twins. If each gender has an independent 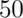 % probability for each
birth, what’s the probability of getting
% probability for each
birth, what’s the probability of getting 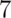 or more girls out of
or more girls out of
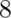 births?
births?

> choose(8, 7) * 0.5^8 + choose(8, 8) * 0.5^8
[1] 0.03516
> pbinom(6, size = 8, prob = 0.5, lower.tail = FALSE)
[1] 0.03516
The normal distribution
Watch this video before beginning
The normal distribution is easily the handiest distribution in all of statistics. It can be used in an endless variety of settings. Moreover, as we’ll see later on in the course, sample means follow normal distributions for large sample sizes.
Remember the goal of probability modeling. We are assuming a probability
distribution for our population as a way of parsimoniously characterizing
it. In fact, the normal distribution only requires two numbers to characterize
it. Specifically,
a random variable is said to follow a normal or Gaussian
distribution with mean 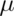 and variance
and variance 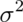 if the associated density is:
if the associated density is:
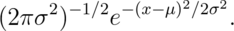
If 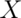 is a RV with this density then
is a RV with this density then ![E[X] = \mu](/preview_site_images/LittleInferenceBook/leanpub_equation_257.png) and
and
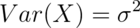 . That is, the normal distribution is characterized
by the mean and variance. We write
. That is, the normal distribution is characterized
by the mean and variance. We write 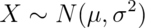 to denote
a normal random variable. When
to denote
a normal random variable. When 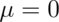 and
and  the resulting distribution is called the standard normal distribution.
Standard normal RVs are often labeled
the resulting distribution is called the standard normal distribution.
Standard normal RVs are often labeled 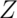
Consider an example, if we say that intelligence quotients are normally
distributed with a mean of 100 and a standard deviation of 15. Then, we
are saying that if we randomly sample a person from this population, the
probability that they have an IQ of say 120 or larger, is governed by a
normal distribution with a mean of 100 and a variance of 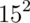 .
.
Taken another way, if we know that the population is normally distributed then to estimate everything about the population, we need only estimate the population mean and variance. (Estimated by the sample mean and the sample variance.)
Reference quantiles for the standard normal
The normal distribution is so important that it is useful to memorize
reference probabilities and quantiles. The image below shows reference lines
at 0, 1, 2 and 3 standard deviations above and below 0. This is for the standard
normal; however, all of the rules apply to non standard normals as 0, 1, 2
and 3 standard deviations above and below 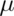 , the population mean.
, the population mean.
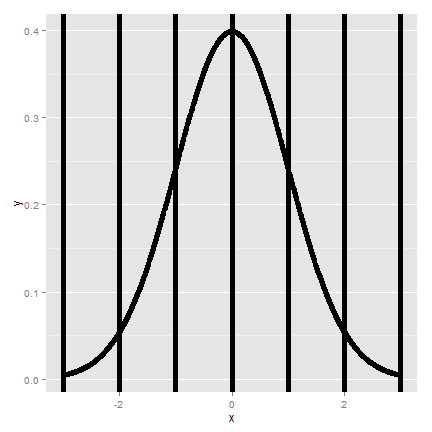
The most relevant probabilities are.
- Approximately 68\%, 95\% and 99\% of the normal density lies within 1, 2 and 3 standard deviations from the mean, respectively.
- -1.28, -1.645, -1.96 and -2.33 are the
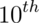 ,
, 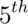 ,
,
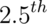 and
and 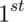 percentiles of the standard normal
distribution, respectively.
percentiles of the standard normal
distribution, respectively. - By symmetry, 1.28, 1.645, 1.96 and 2.33 are the
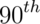 ,
,
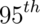 ,
, 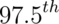 and
and 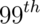 percentiles of the
standard normal distribution, respectively.
percentiles of the
standard normal distribution, respectively.
Shifting and scaling normals
Since the normal distribution is characterized by only the mean and variance,
which are a shift and a scale, we can transform normal random variables to
be standard normals and vice versa. For example If
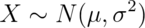 then:
then:
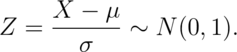
If 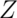 is standard normal
is standard normal
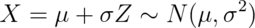
then 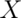 is
is 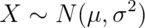 . We can use these facts
to answer questions about non-standard normals by relating them back to
the standard normal.
. We can use these facts
to answer questions about non-standard normals by relating them back to
the standard normal.
Example
What is the 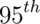 percentile of a
percentile of a 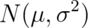 distribution?
Quick answer in R
distribution?
Quick answer in R qnorm(.95, mean = mu, sd = sigma). Alternatively, because
we have the standard normal quantiles memorized,
and we know that 1.645 is its 95th percentile, the answer has to be
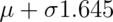 .
.
In general, 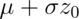 where
where 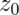 is the appropriate standard normal quantile.
is the appropriate standard normal quantile.
To put some context on our previous setting, population
mean BMI for men is reported as
29 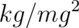 with a
standard deviation of 4.73. Assuming normality of BMI, what is the population
with a
standard deviation of 4.73. Assuming normality of BMI, what is the population
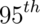 percentile? The answer is then:
percentile? The answer is then:
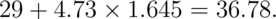
Or alternatively, we could simply type r qnorm(.95, 29, 4.73) in R.
Now let’s reverse the process. Imaging asking what’s the probability that a randomly drawn subject from this population has a BMI less than 24.27? Notice that
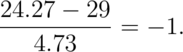
Therefore, 24.27 is 1 standard deviation below the mean. We know that 16% lies
below or above 1 standard deviation from the mean. Thus 16% lies below.
Alternatively, pnorm(24.27, 29, 4.73) yields the result.
Example
Assume that the number of daily ad clicks for a company is (approximately) normally distributed with a mean of 1020 and a standard deviation of 50. What’s the probability of getting more than 1,160 clicks in a day? Notice that:
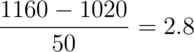
Therefore, 1,160 is 2.8 standard deviations above the mean. We know from our
standard normal quantiles that the probability of being larger
than 2 standard deviation is 2.5% and 3 standard deviations is far in the tail.
Therefore, we know that the probability has to be smaller than 2.5% and should
be very small. We can obtain it
exactly as r pnorm(1160, 1020, 50, lower.tail = FALSE) which is 0.3%. Note
that we can also obtain the probability as r pnorm(2.8, lower.tail = FALSE).
Example
Consider the previous example again. What number of daily ad clicks would represent the one where 75% of days have fewer clicks (assuming days are independent and identically distributed)? We can obtain this as:
> qnorm(0.75, mean = 1020, sd = 50)
[1] 1054
The Poisson distribution
Watch this video before beginning.
The Poisson distribution is used to model counts. It is perhaps only second to the normal distribution usefulness. In fact, the Bernoulli, binomial and multinomial distributions can all be modeled by clever uses of the Poisson.
The Poisson distribution is especially useful for modeling unbounded
counts or counts per unit of time (rates).
Like the number of clicks on advertisements, or the number of
people who show up at a bus stop. (While these are in principle bounded,
it would be hard to actually put an upper limit on it.) There is
also a deep connection between the Poisson distribution and popular models
for so-called event-time data. In addition, the Poisson distribution is
the default model for so-called contingency table data, which is simply
tabulations of discrete characteristics. Finally, when 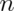 is large
and
is large
and 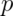 is small, the Poisson is an accurate approximation to the
binomial distribution.
is small, the Poisson is an accurate approximation to the
binomial distribution.
The Poisson mass function is:
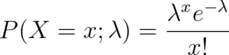
for 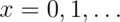 . The mean of this distribution is
. The mean of this distribution is
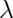 . The variance of this distribution is also
. The variance of this distribution is also 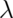 .
Notice that
.
Notice that 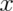 ranges from 0 to
ranges from 0 to 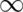 . Therefore,
the Poisson distribution is especially useful for modeling unbounded counts.
. Therefore,
the Poisson distribution is especially useful for modeling unbounded counts.
Rates and Poisson random variables
The Poisson distribution is useful for rates, counts that occur
over units of time. Specifically, if 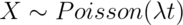 where
where ![\lambda = E[X / t]](/preview_site_images/LittleInferenceBook/leanpub_equation_298.png) is the expected count per unit of time
and
is the expected count per unit of time
and 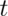 is the total monitoring time.
is the total monitoring time.
Example
The number of people that show up at a bus stop is Poisson with a mean of 2.5 per hour. If watching the bus stop for 4 hours, what is the probability that $3$ or fewer people show up for the whole time?
> ppois(3, lambda = 2.5 * 4)
[1] 0.01034
Therefore, there is about a 1% chance that 3 or fewer people show up. Notice the multiplication by four in the function argument. Since lambda is specified as events per hour we have to multiply by four to consider the number of events that occur in 4 hours.
Poisson approximation to the binomial
When 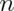 is large and
is large and 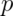 is small the Poisson distribution
is an accurate approximation to the binomial distribution. Formally, if
is small the Poisson distribution
is an accurate approximation to the binomial distribution. Formally, if
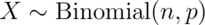 then
then 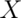 is approximately
Poisson where
is approximately
Poisson where 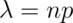 provided that
provided that 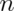 is large
is large
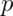 is small.
is small.
Example, Poisson approximation to the binomial
We flip a coin with success probability 0.01 five hundred times. What’s the probability of 2 or fewer successes?
> pbinom(2, size = 500, prob = 0.01)
[1] 0.1234
> ppois(2, lambda = 500 * 0.01)
[1] 0.1247
So we can see that the probabilities agree quite well. This approximation is often done as the Poisson model is a more convenient model in many respects.
Exercises
- Your friend claims that changing the font to comic sans will result in more ad revenue on your web sites. When presented in random order, 9 pages out of 10 had more revenue when the font was set to comic sans. If it was really a coin flip for these 10 sites, what’s the probability of getting 9 or 10 out of 10 with more revenue for the new font?
- A software company is doing an analysis of documentation errors of their products. They sampled their very large codebase in chunks and found that the number of errors per chunk was approximately normally distributed with a mean of 11 errors and a standard deviation of 2. When randomly selecting a chunk from their codebase, whats the probability of fewer than 5 documentation errors?
- The number of search entries entered at a web site is Poisson at a rate of 9 searches per minute. The site is monitored for 5 minutes. What is the probability of 40 or fewer searches in that time frame?
- Suppose that the number of web hits to a particular site are approximately normally distributed with a mean of 100 hits per day and a standard deviation of 10 hits per day. What’s the probability that a given day has fewer than 93 hits per day expressed as a percentage to the nearest percentage point? Watch a video solution and see the problem.
- Suppose that the number of web hits to a particular site are approximately normally distributed with a mean of 100 hits per day and a standard deviation of 10 hits per day. What number of web hits per day represents the number so that only 5% of days have more hits? Watch a video solution and see the problem and solution.
- Suppose that the number of web hits to a particular site are approximately normally distributed with a mean of 100 hits per day and a standard deviation of 10 hits per day. Imagine taking a random sample of 50 days. What number of web hits would be the point so that only 5% of averages of 50 days of web traffic have more hits? Watch a video solution and see the problem and solution.
- You don’t believe that your friend can discern good wine from cheap. Assuming that you’re right, in a blind test where you randomize 6 paired varieties (Merlot, Chianti, …) of cheap and expensive wines. What is the change that she gets 5 or 6 right? Watch a video solution and see the original problem.
- The number of web hits to a site is Poisson with mean 16.5 per day. What is the probability of getting 20 or fewer in 2 days? Watch a video solution and see a written solution.