10. P-values

Introduction to P-values

Watch this video before beginning.

P-values are the most common measure of statistical significance. Their ubiquity, along with concern over their interpretation and use makes them controversial among statisticians. The following manuscripts are interesting reads about P-values.

What is a P-value?

The central idea of a P-value is to assume that the null hypothesis is true and calculate how unusual it would be to see data (in the form of a test statistic) as extreme as was seen in favor of the alternative hypothesis. The formal definition is:

A P-value is the probability of observing a test statistic as or more extreme in favor of the alternative than was actually obtained, where the probability is calculated assuming that the null hypothesis is true.

A P-value then requires a few steps. 1. Decide on a statistic that evaluates support of the null or alternative hypothesis. 2. Decide on a distribution of that statistic under the null hypothesis (null distribution). 3. Calculate the probability of obtaining a statistic as or more extreme as was observed using the distribution in 2.

The way to interpret P-values is as follows. If the P-value is small, then either 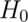H_0 is true and we have observed a rare event or 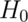H_0 is false (or possibly the null model is incorrect).

Let’s do a quick example. Suppose that you get a t statistic of 2.5 for 15 degrees of freedom testing 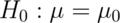H_0:\mu = \mu_0 versus 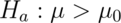H_a : \mu > \mu_0. What’s the probability of getting a t statistic as large as 2.5?

P-value calculation in R.
> pt(2.5, 15, lower.tail = FALSE)
[1] 0.01225

Therefore, the probability of seeing evidence as extreme or more extreme than that actually obtained under 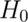H_0 is 0.0123. So, (assuming our model is correct) either we observed data that was pretty unlikely under the null, or the null hypothesis if false.

The attained significance level

Recall in a previous chapter that our test statistic was 2 for 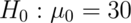H_0 : \mu_0 = 30 versus 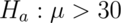H_a:\mu > 30 using a normal test (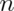n was 100). Notice that we rejected the one sided test when 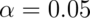\alpha = 0.05, would we reject if 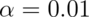\alpha = 0.01, how about 0.001?

The smallest value for alpha that you still reject the null hypothesis is called the attained significance level. This is mathematically equivalent, but philosophically a little different from, the P-value. Whereas the P-value is interpreted in the terms of how probabilistically extreme our test statistic is under the null, the attained significance level merely conveys what the smallest level of 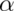\alpha that one could reject at.

This equivalence makes P-values very convenient to convey. The reader of the results can perform the test at whatever \alpha he or she choses. This is especially useful in multiple testing circumstances.

Here’s the two rules for performing hypothesis tests with P-values. * If the P-value for a test is less than 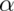\alpha you reject the null hypothesis * For two sided hypothesis test, double the smaller of the two one sided hypothesis test Pvalues

Binomial P-value example

Suppose a friend has 8 children, 7 of which are girls and none are twins. If each gender has an independent 50% probability for each birth, what’s the probability of getting 7 or more girls out of 8 births?

This calculation is a P-value where the statistic is the number of girls and the null distribution is a fair coin flip for each gender. We want to test 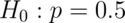H_0: p=0.5 versus 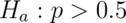H_a: p > 0.5, where 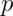p is the probability of having a girl for each birth.

Recall here’s the calculation:

Example of a Binomial P-value calculation in R.
> pbinom(6, size = 8, prob = 0.5, lower.tail = FALSE)
[1] 0.03516

Since our P-value is less than 0.05 we would reject at a 5% error rate. Note, however, if we were doing a two sided test, we would have to double the P-value and thus would then fail to reject.

Poisson example

Watch this video before beginning.

Suppose that a hospital has an infection rate of 10 infections per 100 person/days at risk (rate of 0.1) during the last monitoring period. Assume that an infection rate of 0.05 is an important benchmark.

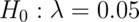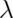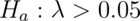Given a Poisson model, could the observed rate being larger than 0.05 be attributed to chance? We want to test H_0: \lambda = 0.05 where \lambda is the rate of infections per person day so that 5 would be the rate per 100 days. Thus we want to know if 9 events per 100 person/days is unusual with respect to a Poisson distribution with a rate of 5 events per 100. Consider H_a: \lambda > 0.05.

Poisson P-value calculation.
> ppois(9, 5, lower.tail = FALSE)
[1] 0.03183

Again, since this P-value is less than 0.05 we reject the null hypothesis. The P-value would be 0.06 for two sided hypothesis (double) and so we would fail to reject in that case.

Exercises

  1. P-values are probabilities that are calculated assuming which hypothesis is true?
    • the alternative
    • the null
  2. You get a P-value of 0.06. Would you reject for a type I error rate of 0.05?
    • Yes you would reject the null
    • No you would not reject the null
    • It depends on information not given
  3. The proposed procedure for getting a two sided P-value for the exact binomial test considered here is what?
    • Multiplying the one sided P-value by one half
    • Doubling the larger of the two one sided P-values
    • Doubling the smaller of the two one sided P-values
    • No procedure exists
  4. Consider again the mtcars dataset. Use a two group t-test to test the hypothesis that the 4 and 6 cyl cars have the same mpg. Use a two sided test with unequal variances. Give a P-value. Watch the video here and see the text here
  5. You believe the coin that you’re flipping is biased towards heads. You get 55 heads out of 100 flips. Give an exact P-value for the hypothesis that the coin is fair. Watch a video solution and see the text.
  6. A web site was monitored for a year and it received 520 hits per day. In the first 30 days in the next year, the site received 15,800 hits. Assuming that web hits are Poisson. Give an exact one sided P-value to the hypothesis that web hits are up this year over last. Do you reject? Watch the video solutions and see the problem text.
  7. Suppose that in an AB test, one advertising scheme led to an average of 10 purchases per day for a sample of 100 days, while the other led to 11 purchases per day, also for a sample of 100 days. Assuming a common standard deviation of 4 purchases per day. Assuming that the groups are independent and that they days are iid, perform a Z test of equivalence. Give a P-value for the test? Watch a video solution and see the text.
  8. Consider the mtcars data set.
    • Give the p-value for a t-test comparing MPG for 6 and 8 cylinder cars assuming equal variance, as a proportion to 3 decimal places.
    • Give the associated P-value for a z test.
    • Give the common standard deviation estimate for MPG across cylinders to 3 decimal places.
    • Would the t test reject at the two sided 0.05 level (0 for no 1 for yes)? Watch a video solution and see the text.

Up next

11. Power