Table of Contents
The author has used good faith effort in preparation of this book, but makes no expressed or implied warranty of any kind and disclaims without limitation all responsibility for errors or omissions. No liability is assumed for incidental or consequential damages in connection with or arising out of the use of the information or programs contained herein. Use of the information and instructions in this book is at your own risk.
The cover image is in the public domain and available from the New York Public Library. The cover font is Open Sans Condensed, released by Steve Matteson under the Apache License version 2.0.
1. Introduction
With the enthusiasm of youth, the QuantLib web site used to state that QuantLib aimed at becoming “the standard free/open-source financial library.” By interpreting such statement a bit loosely, one might say that it has somewhat succeeded—albeit by employing the rather devious trick of being the first, and thus for some time the only open-source financial library1.
Standard or not, the project is thriving; at the time of this writing, each new release is downloaded a few thousand times, there is a steady stream of contributions from users, and the library seems to be used in the real world—as far as I can guess through the usual shroud of secrecy used in the financial world. All in all, as a project administrator, I can declare myself a happy camper.
But all the more for that, the lack of proper documentation shows. Although a detailed class reference is available (that was an easy task, since it can be generated automatically) it doesn’t let one see the forest for the trees; so that a new user might get the impression that the QuantLib developers share the views of the Bellman from Lewis Carroll’s Hunting of the Snark:
“What use are Mercator’s North Poles and Equators,
Tropics, Zones and Meridian Lines?”
So the Bellman would cry: and the crew would reply,
“They are merely conventional signs!”
The purpose of this book is to fill a part of the existing void. It is a report on the design and implementation of QuantLib, alike in spirit—but, hopefully, with less frightening results—to the How I did it book2 prominently featured in Mel Brooks’ Young Frankenstein. If you are—or want to be—a QuantLib user, you will find here useful information on the design of the library that might not be readily apparent when reading the code. If you’re working in quantitative finance, even if not using QuantLib, you can still read it as a field report on the design of a financial library. You will find that it covers issues that you might also face, as well as some possible solutions and their rationale. Based on your constraints, it is possible—even likely—that you will choose other solutions; but you might profit from this discussion just the same.
In my descriptions, I’ll also point out shortcomings in the current implementation; not to disparage the library (I’m pretty much involved in it, after all) but for more useful purposes. On the one hand, describing the existing pitfalls will help developers avoid them; on the other hand, it might show how to improve the library. Indeed, it already happened that reviewing the code for this book caused me to go back and modify it for the better.
For reasons of both space and time, I won’t be able to cover every aspect of the library. In the first half of the book, I’ll describe a few of the most important classes, such as those modeling financial instruments and term structures; this will give you a view of the larger architecture of the library. In the second half, I’ll describe a few specialized frameworks, such as those used for creating Monte Carlo or finite-differences models. Some of those are more polished than others; I hope that their current shortcomings will be as interesting as their strong points.
The book is primarily aimed at users wanting to extend the library with their own instruments or models; if you desire to do so, the description of the available class hierarchies and frameworks will provide you with information about the hooks you need to integrate your code with QuantLib and take advantage of its facilities. If you’re not this kind of user, don’t close the book yet; you can find useful information too. However, you might want to look at the QuantLib Python Cookbook instead. It can be useful to C++ users, too.
And now, as is tradition, a few notes on the style and requirements of this book.
Knowledge of both C++ and quantitative finance is assumed. I’ve no pretense of being able to teach you either one, and this book is thick enough already. Here, I just describe the implementation and design of QuantLib; I’ll leave it to other and better authors to describe the problem domain on one hand, and the language syntax and tricks on the other.
As you already noticed, I’ll write in the first person singular. True, it might look rather self-centered—as a matter of fact, I hope you still haven’t put down the book in annoyance—but we would feel rather pompous if we were to use the first person plural. The author of this book feels the same about using the third person. After a bit of thinking, I opted for a less formal but more comfortable style (which, as you noted, also includes a liberal use of contractions). For the same reason, I’ll be addressing you instead of the proverbial acute reader. The use of the singular will also help to avoid confusion; when I use the plural, I describe work done by the QuantLib developers as a group.
I will describe the evolution of a design when it is interesting on its own, or relevant for the final result. For the sake of clarity, in most cases I’ll skip over the blind alleys and wrong turns taken; put together design decisions which were made at different times; and only show the final design, sometimes simplified. This will still leave me with plenty to say: in the words of the Alabama Shakes, “why” is an awful lot of question.
I will point out the use of design patterns in the code I describe. Mind you, I’m not advocating cramming your code with them; they should be applied when they’re useful, not for their own sake.3 However, QuantLib is now the result of several years of coding and refactoring, both based on user feedback and new requirements being added over time. It is only natural that the design evolved toward patterns.
I will apply to the code listings in the book the same conventions used in the library and outlined in appendix B. I will depart from them in one respect: due to the limitations on line length, I might drop the std and boost namespaces from type names. When the listings need to be complemented by diagrams, I will be using UML; for those not familiar with this language, a concise guide can be found in Fowler, 2003.
And now, let’s dive.
2. Financial instruments and pricing engines
The statement that a financial library must provide the means to price financial instruments would certainly have appealed to Monsieur de La Palisse. However, that is only a part of the whole problem; a financial library must also provide developers with the means to extend it by adding new pricing functionality.
Foreseeable extensions are of two kinds, and the library must allow either one. On the one hand, it must be possible to add new financial instruments; on the other hand, it must be feasible to add new means of pricing an existing instrument. Both kinds have a number of requirements, or in pattern jargon, forces that the solution must reconcile. This chapter details such requirements and describes the design that allows QuantLib to satisfy them.
2.1 The Instrument class
In our domain, a financial instrument is a concept in its own right. For this reason alone, any self-respecting object-oriented programmer will code it as a base class from which specific instruments will be derived.
The idea, of course, is to be able to write code such as
for (i = portfolio.begin(); i != portfolio.end(); ++i)
totalNPV += i->NPV();
where we don’t have to care about the specific type of each
instrument. However, this also prevents us from knowing what
arguments to pass to the NPV method, or even what methods to
call. Therefore, even the two seemingly harmless lines above tell us
that we have to step back and think a bit about the interface.
2.1.1 Interface and requirements
The broad variety of traded assets—which range from the simplest to
the most exotic—implies that any method specific to a given class of
instruments (say, equity options) is bound not to make sense for some
other kind (say, interest-rate swaps). Thus, very few methods were
singled out as generic enough to belong to the Instrument
interface. We limited ourselves to those returning its present value
(possibly with an associated error estimate) and indicating whether or
not the instrument has expired; since we can’t specify what arguments
are needed,4 the methods take none; any needed input will
have to be stored by the instrument. The resulting interface is shown
in the listing below.
Instrument class.class Instrument {
public:
virtual ~Instrument();
virtual Real NPV() const = 0;
virtual Real errorEstimate() const = 0;
virtual bool isExpired() const = 0;
};
As is good practice, the methods were first declared as pure virtual ones; but—as Sportin’ Life points out in Gershwin’s Porgy and Bess—it ain’t necessarily so. There might be some behavior that can be coded in the base class. In order to find out whether this was the case, we had to analyze what to expect from a generic financial instrument and check whether it could be implemented in a generic way. Two such requirements were found at different times, and their implementation changed during the development of the library; I present them here in their current form.
One is that a given financial instrument might be priced in different ways (e.g., with one or more analytic formulas or numerical methods) without having to resort to inheritance. At this point, you might be thinking “Strategy pattern”. It is indeed so; I devote section 2.2 to its implementation.
The second requirement came from the observation that the value of a financial instrument depends on market data. Such data are by their nature variable in time, so that the value of the instrument varies in turn; another cause of variability is that any single market datum can be provided by different sources. We wanted financial instruments to maintain links to these sources so that, upon different calls, their methods would access the latest values and recalculate the results accordingly; also, we wanted to be able to transparently switch between sources and have the instrument treat this as just another change of the data values.
We were also concerned with a potential loss of efficiency. For instance, we could monitor the value of a portfolio in time by storing its instruments in a container, periodically poll their values, and add the results. In a simple implementation, this would trigger recalculation even for those instruments whose inputs did not change. Therefore, we decided to add to the instrument methods a caching mechanism: one that would cause previous results to be stored and only recalculated when any of the inputs change.
2.1.2 Implementation
The code managing the caching and recalculation of the instrument value was written for a generic financial instrument by means of two design patterns.
When any of the inputs change, the instrument is notified by means of the Observer pattern (Gamma et al, 1995). The pattern itself is briefly described5 in appendix A; I describe here the participants.
Obviously enough, the instrument plays the role of the observer while
the input data play that of the observables. In order to have access
to the new values after a change is notified, the observer needs to
maintain a reference to the object representing the input. This might
suggest some kind of smart pointer; however, the behavior of a pointer
is not sufficient to fully describe our problem. As I already
mentioned, a change might come not only from the fact that values from
a data feed vary in time; we might also want to switch to a different
data feed. Storing a (smart) pointer would give us access to the
current value of the object pointed; but our copy of the pointer,
being private to the observer, could not be made to point to a
different object. Therefore, what we need is the smart equivalent of a
pointer to pointer. This feature was implemented in QuantLib as a
class template and given the name of Handle. Again, details are
given in appendix A; relevant to this discussion is the
fact that copies of a given Handle share a link to an
object. When the link is made to point to another object, all copies
are notified and allow their holders to access the new
pointee. Furthermore, Handles forward any notifications from
the pointed object to their observers.
Finally, classes were implemented which act as observable data and can
be stored into Handles. The most basic is the Quote
class, representing a single varying market value. Other inputs for
financial instrument valuation can include more complex objects such
as yield or volatility term structures.6
Another problem was to abstract out the code for storing and
recalculating cached results, while still leaving it to derived
classes to implement any specific calculations.
In earlier versions of QuantLib, the functionality was included in the
Instrument class itself; later, it was extracted and coded into
another class—somewhat unsurprisingly called LazyObject—which is
now reused in other parts of the library. An outline of the class is
shown in the following listing.
LazyObject class.class LazyObject : public virtual Observer,
public virtual Observable {
protected:
mutable bool calculated_;
virtual void performCalculations() const = 0;
public:
void update() { calculated_ = false; }
virtual void calculate() const {
if (!calculated_) {
calculated_ = true;
try {
performCalculations();
} catch (...) {
calculated_ = false;
throw;
}
}
}
};
The code is not overly complex. A boolean data member calculated_ is
defined which keeps track of whether results were calculated and still
valid. The update method, which implements the Observer
interface and is called upon notification from observables, sets such
boolean to false and thus invalidates previous results.
The calculate method is implemented by means of the Template Method
pattern (Gamma et al, 1995), sometimes also called
non-virtual interface. As explained in the Gang of Four book, the
constant part of the algorithm (in this case, the management of the cached
results) is implemented in the base class; the varying parts (here,
the actual calculations) are delegated to a virtual method, namely,
performCalculations, which is called in the body of the
base-class method. Therefore, derived classes will only implement
their specific calculations without having to care about caching: the
relevant code will be injected by the base class.
The logic of the caching is simple. If the current results are no longer valid, we let the derived class perform the needed calculations and flag the new results as up to date. If the current results are valid, we do nothing.
However, the implementation is not as simple. You might
wonder why we had to insert a try block setting
calculated_ beforehand and a handler rolling back the change
before throwing the exception again. After all, we could have written
the body of the algorithm more simply—for instance, as in the
following, seemingly equivalent code, that doesn’t catch and rethrow
exceptions:
if (!calculated_) {
performCalculations();
calculated_ = true;
}
The reason is that there are cases (e.g., when the lazy object is a
yield term structure which is bootstrapped lazily) in which
performCalculations happens to recursively call
calculate. If calculated_ were not set to true,
the if condition would still hold and performCalculations
would be called again, leading to infinite recursion. Setting such
flag to true prevents this from happening; however, care must
now be taken to restore it to false if an exception is
thrown. The exception is then rethrown so that it can be caught by the
installed error handlers.
A few more methods are provided in LazyObject which enable
users to prevent or force a recalculation of the results. They are not
discussed here. If you’re interested, you can heed the advice often
given by master Obi-Wan Kenobi: “Read the source, Luke.”
The Instrument class inherits from LazyObject. In order
to implement the interface outlined earlier,
it decorates the calculate method with code specific to
financial instruments. The resulting method is shown in
the listing below, together with other bits of supporting
code.
Instrument class.class Instrument : public LazyObject {
protected:
mutable Real NPV_;
public:
Real NPV() const {
calculate();
return NPV_;
}
void calculate() const {
if (isExpired()) {
setupExpired();
calculated_ = true;
} else {
LazyObject::calculate();
}
}
virtual void setupExpired() const {
NPV_ = 0.0;
}
};
Once again, the added code follows the Template Method pattern to
delegate instrument-specific calculations to derived classes. The
class defines an NPV_ data member to store the result of the
calculation; derived classes can declare other data members to store
specific results.7 The body of the calculate method calls
the virtual isExpired method to check whether the instrument is an
expired one. If this is the case, it calls another virtual method,
namely, setupExpired, which has the responsibility of giving
meaningful values to the results; its default implementation sets
NPV_ to 0 and can be called by derived classes. The calculated_
flag is then set to true. If the instrument is not expired, the
calculate method of LazyObject is called instead, which in turn
will call performCalculations as needed. This imposes a contract on
the latter method, namely, its implementations in derived classes are
required to set NPV_ (as well as any other instrument-specific data
member) to the result of the calculations. Finally, the NPV method
ensures that calculate is called before returning the answer.
2.1.3 Example: interest-rate swap
I end this section by showing how a specific financial instrument can be implemented based on the described facilities.
The chosen instrument is the interest-rate swap. As you surely know, it is a contract which consists in exchanging periodic cash flows. The net present value of the instrument is calculated by adding or subtracting the discounted cash-flow amounts depending on whether the cash flows are paid or received.
Not surprisingly, the swap is implemented8 as a new class
deriving from Instrument. Its outline is shown in
the following listing.
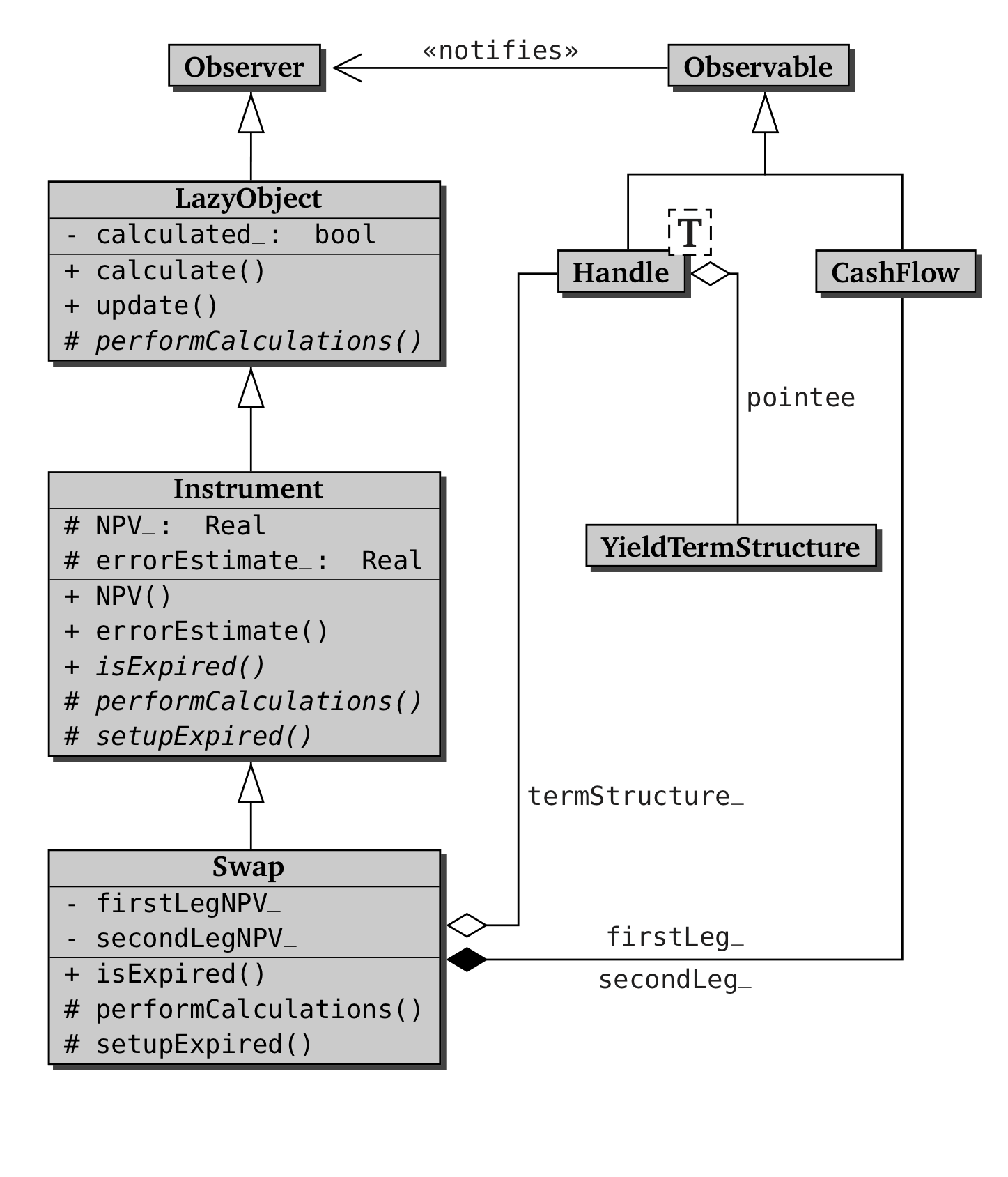
Swap class.class Swap : public Instrument {
public:
Swap(const vector<shared_ptr<CashFlow> >& firstLeg,
const vector<shared_ptr<CashFlow> >& secondLeg,
const Handle<YieldTermStructure>& termStructure);
bool isExpired() const;
Real firstLegBPS() const;
Real secondLegBPS() const;
protected:
// methods
void setupExpired() const;
void performCalculations() const;
// data members
vector<shared_ptr<CashFlow> > firstLeg_, secondLeg_;
Handle<YieldTermStructure> termStructure_;
mutable Real firstLegBPS_, secondLegBPS_;
};
It contains as data members the objects
needed for the calculations—namely, the cash flows on the first and
second leg and the yield term structure used to discount their
amounts—and two variables used to store additional
results. Furthermore, it declares methods implementing the
Instrument interface and others returning the swap-specific
results. The class diagram of Swap and the related classes is shown
in the figure below.
Swap class.The fitting of the class to the Instrument framework is done in
three steps, the third being optional depending on the derived class;
the relevant methods are shown in the next listing.
Swap class.Swap::Swap(const vector<shared_ptr<CashFlow> >& firstLeg,
const vector<shared_ptr<CashFlow> >& secondLeg,
const Handle<YieldTermStructure>& termStructure)
: firstLeg_(firstLeg), secondLeg_(secondLeg),
termStructure_(termStructure) {
registerWith(termStructure_);
vector<shared_ptr<CashFlow> >::iterator i;
for (i = firstLeg_.begin(); i!= firstLeg_.end(); ++i)
registerWith(*i);
for (i = secondLeg_.begin(); i!= secondLeg_.end(); ++i)
registerWith(*i);
}
bool Swap::isExpired() const {
Date settlement = termStructure_->referenceDate();
vector<shared_ptr<CashFlow> >::const_iterator i;
for (i = firstLeg_.begin(); i!= firstLeg_.end(); ++i)
if (!(*i)->hasOccurred(settlement))
return false;
for (i = secondLeg_.begin(); i!= secondLeg_.end(); ++i)
if (!(*i)->hasOccurred(settlement))
return false;
return true;
}
void Swap::setupExpired() const {
Instrument::setupExpired();
firstLegBPS_= secondLegBPS_ = 0.0;
}
void Swap::performCalculations() const {
NPV_ = - Cashflows::npv(firstLeg_,**termStructure_)
+ Cashflows::npv(secondLeg_,**termStructure_);
errorEstimate_ = Null<Real>();
firstLegBPS_ = - Cashflows::bps(firstLeg_, **termStructure_);
secondLegBPS_ = Cashflows::bps(secondLeg_, **termStructure_);
}
Real Swap::firstLegBPS() const {
calculate();
return firstLegBPS_;
}
Real Swap::secondLegBPS() const {
calculate();
return secondLegBPS_;
}
The first step is performed in the class constructor, which takes as arguments (and copies into the corresponding data members) the two sequences of cash flows to be exchanged and the yield term structure to be used for discounting their amounts. The step itself consists in registering the swap as an observer of both the cash flows and the term structure. As previously explained, this enables them to notify the swap and trigger its recalculation each time a change occurs.
The second step is the implementation of the required interface. The
logic of the isExpired method is simple enough; its body loops
over the stored cash flows checking their payment dates. As soon as it
finds a payment which still has not occurred, it reports the swap as
not expired. If none is found, the instrument has expired. In this
case, the setupExpired method will be called. Its
implementation calls the base-class one, thus taking care of the data
members inherited from Instrument; it then sets to 0 the
swap-specific results.
The last required method is performCalculations. The calculation is
performed by calling two external functions from the Cashflows
class.9 The first one, namely, npv, is a straightforward
translation of the algorithm outlined above: it cycles on a sequence
of cash flows adding the discounted amount of its future cash flows.
We set the NPV_ variable to the difference of the results from the
two legs. The second one, bps, calculates the basis-point
sensitivity (BPS) of a sequence of cash flows. We call it once per leg
and store the results in the corresponding data members. Since the
result carries no numerical error, the errorEstimate_ variable is
set to Null<Real>()—a specific floating-point value which is used
as a sentinel value indicating an invalid number.10
The third and final step only needs to be performed if—as in this
case—the class defines additional results. It consists in writing
corresponding methods (here, firstLegBPS and
secondLegBPS) which ensure that the calculations are (lazily)
performed before returning the stored results.
The implementation is now complete. Having been written on top of the
Instrument class, the Swap class will benefit from its
code. Thus, it will automatically cache and recalculate results
according to notifications from its inputs—even though no related
code was written in Swap except for the registration calls.
2.1.4 Further developments
You might have noticed a shortcoming in my treatment of the previous
example and of the Instrument class in general. Albeit
generic, the Swap class we implemented cannot manage
interest-rate swaps in which the two legs are paid in different
currencies. A similar problem would arise if you wanted to add the
values of two instruments whose values are not in the same currency;
you would have to convert manually one of the values to the
currency of the other before adding them together.
Such problems stem from a single weakness of the implementation: we
used the Real type (i.e., a simple floating-point number) to
represent the value of an instrument or a cash flow. Therefore, such
results miss the currency information which is attached to them in the
real world.
The weakness might be removed if we were to express such results by
means of the Money class. Instances of such class contain
currency information; moreover, depending on user settings, they are
able to automatically perform conversion to a common currency upon
addition or subtraction.
However, this would be a major change, affecting a large part of the code base in a number of ways. Therefore, it will need some serious thinking before we tackle it (if we do tackle it at all).
Another (and more subtle) shortcoming is that the Swap class
fails to distinguish explicitly between two components of the
abstraction it represents. Namely, there is no clear separation
between the data specifying the contract (the cash-flow specification)
and the market data used to price the instrument (the current discount
curve).
The solution is to store in the instrument only the first group of data (i.e., those that would be in its term sheet) and keep the market data elsewhere.11 The means to do this are the subject of the next section.
2.2 Pricing engines
We now turn to the second of the requirements I stated in the previous section. For any given instrument, it is not always the case that a unique pricing method exists; moreover, one might want to use multiple methods for different reasons. Let’s take the classic textbook example—the European equity option. One might want to price it by means of the analytic Black-Scholes formula in order to retrieve implied volatilities from market prices; by means of a stochastic volatility model in order to calibrate the latter and use it for more exotic options; by means of a finite-difference scheme in order to compare the results with the analytic ones and validate one’s finite-difference implementation; or by means of a Monte Carlo model in order to use the European option as a control variate for a more exotic one.
Therefore, we want it to be possible for a single instrument to be
priced in different ways. Of course, it is not desirable to give
different implementations of the performCalculations method,
as this would force one to use different classes for a single
instrument type. In our example, we would end up with a base
EuropeanOption class from which AnalyticEuropeanOption,
McEuropeanOption and others would be derived. This is wrong in
at least two ways. On a conceptual level, it would introduce different
entities when a single one is needed: a European option is a European
option is a European option, as Gertrude Stein said. On a usability
level, it would make it impossible to switch pricing methods at
run-time.
The solution is to use the Strategy pattern, i.e., to let the
instrument take an object encapsulating the computation to be
performed. We called such an object a pricing engine. A given
instrument would be able to take any one of a number of available
engines (of course corresponding to the instrument type), pass the
chosen engine the needed arguments, have it calculate the value of the
instrument and any other desired quantities, and fetch the results.
Therefore, the performCalculations method would be
implemented roughly as follows:
void SomeInstrument::performCalculations() const {
NPV_ = engine_->calculate(arg1, arg2, ... , argN);
}
where we assumed that a virtual calculate method is defined in
the engine interface and implemented in the concrete engines.
Unfortunately, the above approach won’t work as such. The problem is,
we want to implement the dispatching code just once, namely, in the
Instrument class. However, that class doesn’t know the number
and type of arguments; different derived classes are likely to have
data members differing wildly in both number and type. The same goes
for the returned results; for instance, an interest-rate swap might
return fair values for its fixed rate and floating spread, while the
ubiquitous European option might return any number of Greeks.
An interface passing explicit arguments to the engine through a method, as the one outlined above, would thus lead to undesirable consequences. Pricing engines for different instruments would have different interfaces, which would prevent us from defining a single base class; therefore, the code for calling the engine would have to be replicated in each instrument class. This way madness lies.
The solution we chose was that arguments and results be passed and
received from the engines by means of opaque structures aptly called
arguments and results. Two structures derived from those
and augmenting them with instrument-specific data will be stored in
any pricing engine; an instrument will write and read such data in
order to exchange information with the engine.
The listing below shows the interface of the resulting
PricingEngine class, as well as its inner argument and
results classes and a helper GenericEngine class
template. The latter implements most of the PricingEngine
interface, leaving only the implementation of the calculate
method to developers of specific engines. The arguments and
results classes were given methods which ease their use as drop
boxes for data: arguments::validate is to be called after input
data are written to ensure that their values lie in valid ranges,
while results::reset is to be called before the engine starts
calculating in order to clean previous results.
PricingEngine and of related classes.class PricingEngine : public Observable {
public:
class arguments;
class results;
virtual ~PricingEngine() {}
virtual arguments* getArguments() const = 0;
virtual const results* getResults() const = 0;
virtual void reset() const = 0;
virtual void calculate() const = 0;
};
class PricingEngine::arguments {
public:
virtual ~arguments() {}
virtual void validate() const = 0;
};
class PricingEngine::results {
public:
virtual ~results() {}
virtual void reset() = 0;
};
// ArgumentsType must inherit from arguments;
// ResultType from results.
template<class ArgumentsType, class ResultsType>
class GenericEngine : public PricingEngine {
public:
PricingEngine::arguments* getArguments() const {
return &arguments_;
}
const PricingEngine::results* getResults() const {
return &results_;
}
void reset() const { results_.reset(); }
protected:
mutable ArgumentsType arguments_;
mutable ResultsType results_;
};
Armed with our new classes, we can now write a generic
performCalculation method. Besides the already mentioned
Strategy pattern, we will use the Template Method pattern to allow any
given instrument to fill the missing bits. The resulting
implementation is shown in the next listing. Note that an
inner class Instrument::result was defined; it inherits
from PricingEngine::results and contains the results that have
to be provided for any instrument12
Instrument class.class Instrument : public LazyObject {
public:
class results;
virtual void performCalculations() const {
QL_REQUIRE(engine_, "null pricing engine");
engine_->reset();
setupArguments(engine_->getArguments());
engine_->getArguments()->validate();
engine_->calculate();
fetchResults(engine_->getResults());
}
virtual void setupArguments(
PricingEngine::arguments*) const {
QL_FAIL("setupArguments() not implemented");
}
virtual void fetchResults(
const PricingEngine::results* r) const {
const Instrument::results* results =
dynamic_cast<const Value*>(r);
QL_ENSURE(results != 0, "no results returned");
NPV_ = results->value;
errorEstimate_ = results->errorEstimate;
}
template <class T> T result(const string& tag) const;
protected:
shared_ptr<PricingEngine> engine_;
};
class Instrument::results
: public virtual PricingEngine::results {
public:
Value() { reset(); }
void reset() {
value = errorEstimate = Null<Real>();
}
Real value;
Real errorEstimate;
};
As for performCalculation, the actual work is split between a
number of collaborating classes—the instrument, the pricing engine,
and the arguments and results classes. The dynamics of such a
collaboration (described in the following paragraphs) might be best
understood with the help of the UML sequence diagram shown in
the first of the next two figures; the static relationship between the
classes (and a possible concrete instrument) is shown in
the second.
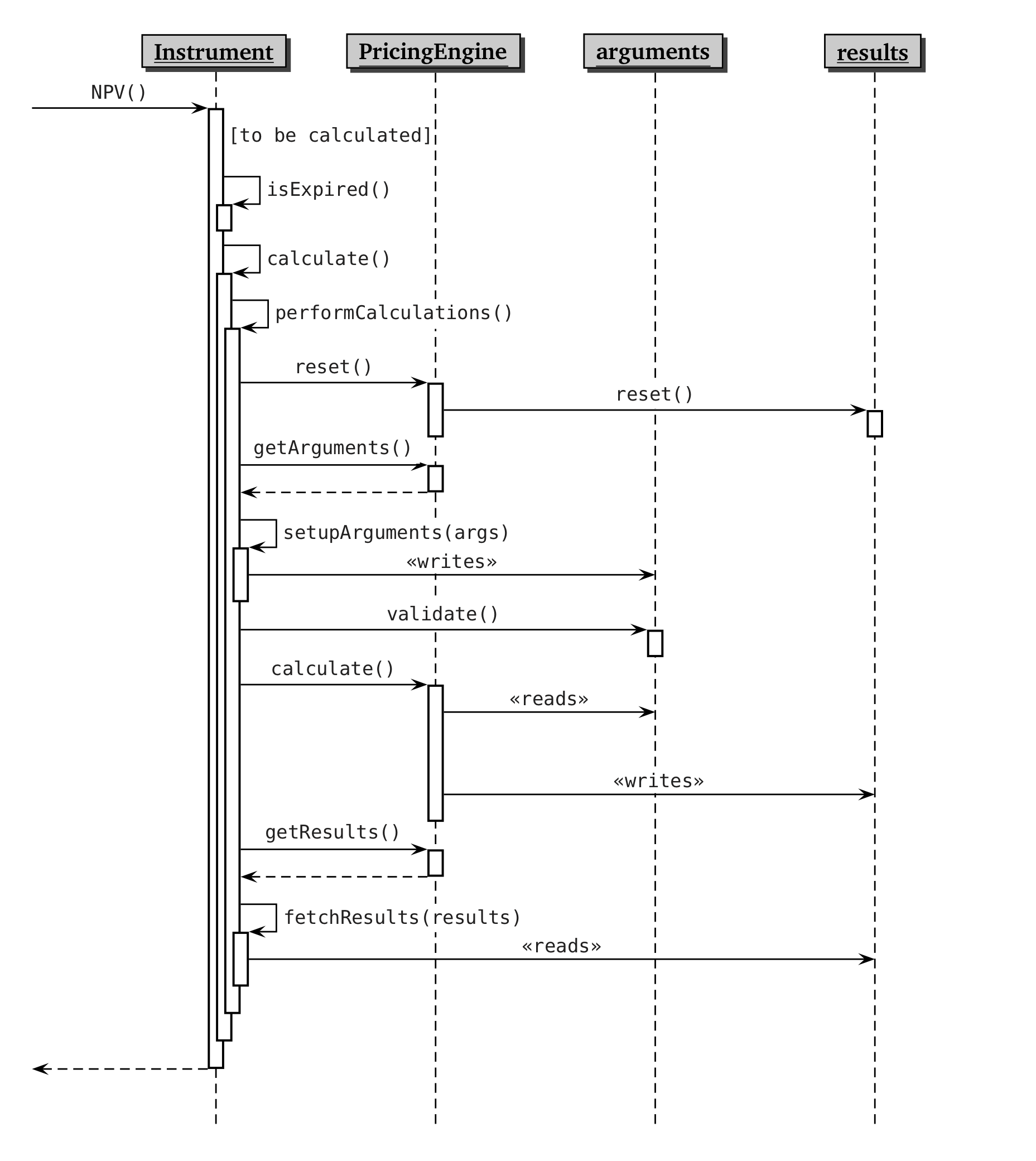
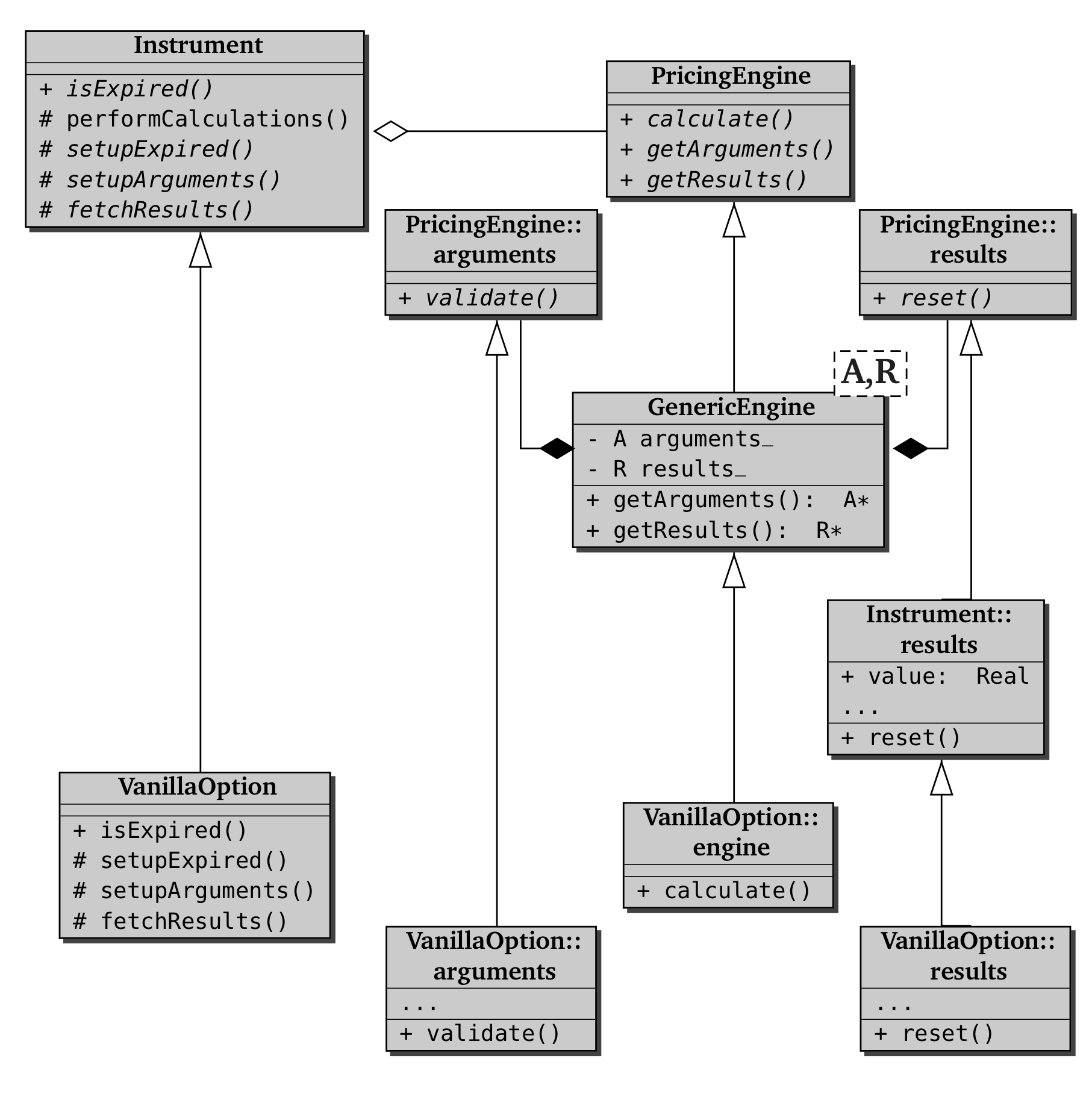
Instrument, PricingEngine, and related classes
including a derived instrument class.A call to the NPV method of the instrument eventually triggers
(if the instrument is not expired and the relevant quantities need to
be calculated) a call to its performCalculations method. Here
is where the interplay between instrument and pricing engine
begins. First of all, the instrument verifies that an engine is
available, aborting the calculation if this is not the case. If one is
found, the instrument prompts it to reset itself. The message is
forwarded to the instrument-specific result structure by means of its
reset method; after it executes, the structure is a clean slate
ready for writing the new results.
At this point, the Template Method pattern enters the scene. The
instrument asks the pricing engine for its argument structure, which
is returned as a pointer to arguments. The pointer is then
passed to the instrument’s setupArguments method, which acts as
the variable part in the pattern. Depending on the specific
instrument, such method verifies that the passed argument is of the
correct type and proceeds to fill its data members with the correct
values. Finally, the arguments are asked to perform any needed checks
on the newly-written values by calling the validate method.
The stage is now ready for the Strategy pattern. Its arguments set,
the chosen engine is asked to perform its specific calculations,
implemented in its calculate method. During the processing,
the engine will read the inputs it needs from its argument structure
and write the corresponding outputs into its results structure.
After the engine completes its work, the control returns to the
Instrument instance and the Template Method pattern continues
unfolding. The called method, fetchResults, must now ask the
engine for the results, downcast them to gain access to the contained
data, and copy such values into its own data members. The
Instrument class defines a default implementation which fetches
the results common to all instruments; derived classes might extend it
to read specific results.
2.2.1 Example: plain-vanilla option
At this point, an example is necessary. A word of
warning, though: although a class exists in QuantLib which implements
plain-vanilla options—i.e., simple call and put equity options with
either European, American or Bermudan exercise—such class is
actually the lowermost leaf of a deep class hierarchy. Having the
Instrument class at its root, such hierarchy specializes it
first with an Option class, then again with a
OneAssetOption class generalizing options on a single
underlying, passing through another class or two until it finally
defines the VanillaOption class we are interested in.
There are good reasons for this; for instance, the code
in the OneAssetOption class can naturally be reused for, say,
Asian options, while that in the Option class lends itself for
reuse when implementing all kinds of basket options. Unfortunately,
this causes the code for pricing a plain option to be spread among all
the members of the described inheritance chain, which would not make
for an extremely clear example. Therefore, I will describe a simplified
VanillaOption class with the same implementation as the one in
the library, but inheriting directly from the Instrument class;
all code implemented in the intermediate classes will be
shown as if it were implemented in the example
class rather than inherited.
The listing below shows the interface of our
vanilla-option class. It declares the required methods from the
Instrument interface, as well as accessors for additional
results, namely, the greeks of the options; as pointed out in the
previous section, the corresponding data members are declared as
mutable so that their values can be set in the logically constant
calculate method.
VanillaOption class.class VanillaOption : public Instrument {
public:
// accessory classes
class arguments;
class results;
class engine;
// constructor
VanillaOption(const shared_ptr<Payoff>&,
const shared_ptr<Exercise>&);
// implementation of instrument method
bool isExpired() const;
void setupArguments(Arguments*) const;
void fetchResults(const Results*) const;
// accessors for option-specific results
Real delta() const;
Real gamma() const;
Real theta() const;
// ...more greeks
protected:
void setupExpired() const;
// option data
shared_ptr<Payoff> payoff_;
shared_ptr<Exercise> exercise_;
// specific results
mutable Real delta_;
mutable Real gamma_;
mutable Real theta_;
// ...more
};
Besides its own data and methods, VanillaOption declares a
number of accessory classes: that is, the specific argument and result
structures and a base pricing engine. They are defined as
inner classes to highlight the relationship between them and the
option class; their interface is shown in the next listing.
VanillaOption inner classes.class VanillaOption::arguments
: public PricingEngine::arguments {
public:
// constructor
arguments();
void validate() const;
shared_ptr<Payoff> payoff;
shared_ptr<Exercise> exercise;
};
class Greeks : public virtual PricingEngine::results {
public:
Greeks();
Real delta, gamma;
Real theta;
Real vega;
Real rho, dividendRho;
};
class VanillaOption::results : public Instrument::results,
public Greeks {
public:
void reset();
};
class VanillaOption::engine
: public GenericEngine<VanillaOption::arguments,
VanillaOption::results> {};
Two comments can be made on such accessory classes. The first is that,
making an exception to what I said in my introduction to the example,
I didn’t declare all data members into the results class. This
was done in order to point out an implementation detail. One might
want to define structures holding a few related and commonly used
results; such structures can then be reused by means of inheritance,
as exemplified by the Greeks structure that is here composed
with Instrument::results to obtain the final structure. In
this case, virtual inheritance from PricingEngine::results must
be used to avoid the infamous inheritance diamond (see, for instance,
Stroustrup, 2013; the name is in the index).
The second comment is that, as shown, it is sufficient to inherit from
the class template GenericEngine (instantiated with the right
argument and result types) to provide a base class for
instrument-specific pricing engines. We will see that derived classes
only need to implement their calculate method.
We now turn to the implementation of the VanillaOption class,
shown in the following listing.
VanillaOption class.VanillaOption::VanillaOption(
const shared_ptr<StrikedTypePayoff>& payoff,
const shared_ptr<Exercise>& exercise)
: payoff_(payoff), exercise_(exercise) {}
bool VanillaOption::isExpired() const {
Date today = Settings::instance().evaluationDate();
return exercise_->lastDate() < today;
}
void VanillaOption::setupExpired() const {
Instrument::setupExpired();
delta_ = gamma_ = theta_ = ... = 0.0;
}
void VanillaOption::setupArguments(
PricingEngine::arguments* args) const {
VanillaOption::arguments* arguments =
dynamic_cast<VanillaOption::arguments*>(args);
QL_REQUIRE(arguments != 0, "wrong argument type");
arguments->exercise = exercise_;
arguments->payoff = payoff_;
}
void VanillaOption::fetchResults(
const PricingEngine::results* r) const {
Instrument::fetchResults(r);
const VanillaOption::results* results =
dynamic_cast<const VanillaOption::results*>(r);
QL_ENSURE(results != 0, "wrong result type");
delta_ = results->delta;
... // other Greeks
}
Real VanillaOption::delta() const {
calculate();
QL_ENSURE(delta_ != Null<Real>(), "delta not given");
return delta_;
}
Its constructor takes a few objects defining the instrument. Most of them will be described in later chapters or in appendix A. For the time being, suffice to say that the payoff contains the strike and type (i.e., call or put) of the option, and the exercise contains information on the exercise dates and variety (i.e., European, American, or Bermudan). The passed arguments are stored in the corresponding data members. Also, note that they do not include market data; those will be passed elsewhere.
The methods related to expiration are straightforward; isExpired
checks whether the latest exercise date is passed, while
setupExpired calls the base-class implementation and sets the
instrument-specific data to 0.
The setupArguments and fetchResults methods are a bit
more interesting. The former starts by downcasting the generic
argument pointer to the actual type required, raising an
exception if another type was passed; it then turns to the actual
work. In some cases, the data members are just copied verbatim into
the corresponding argument slots. However, it might be the case that
the same calculations (say, converting dates into times) will be
needed by a number of engines; setupArguments provides a place
to write them just once.
The fetchResults method is the dual of
setupArguments. It also starts by downcasting the passed
results pointer; after verifying its actual type, it
copies the results into his own data members.
Any method that returns additional results, such as delta, will do
as NPV does: it will call calculate, check that the corresponding
result was cached (because any given engine might or might not be able
to calculate it) and return it.
The above implementation is everything we needed to have a working instrument—working, that is, once it is set an engine which will perform the required calculations. Such an engine is sketched in the listing below and implements the analytic Black-Scholes-Merton formula for European options.
VanillaOption class.class AnalyticEuropeanEngine
: public VanillaOption::engine {
public:
AnalyticEuropeanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&
process)
: process_(process) {
registerWith(process);
}
void calculate() const {
QL_REQUIRE(
arguments_.exercise->type() == Exercise::European,
"not an European option");
shared_ptr<PlainVanillaPayoff> payoff =
dynamic_pointer_cast<PlainVanillaPayoff>(
arguments_.payoff);
QL_REQUIRE(process, "Black-Scholes process needed");
... // other requirements
Real spot = process_->stateVariable()->value();
... // other needed quantities
BlackCalculator black(payoff, forwardPrice,
stdDev, discount);
results_.value = black.value();
results_.delta = black.delta(spot);
... // other greeks
}
private:
shared_ptr<GeneralizedBlackScholesProcess> process_;
};
Its constructor takes (and registers itself with) a Black-Scholes
stochastic process that contains market-data information about the
underlying including present value, risk-free rate, dividend yield,
and volatility. Once again, the actual calculations are hidden behind
the interface of another class, namely, the BlackCalculator
class. However, the code has enough detail to show a few relevant
features.
The method starts by verifying a few preconditions. This might come as
a surprise, since the arguments of the calculations were already
validated by the time the calculate method is called. However,
any given engine can have further requirements to be fulfilled before
its calculations can be performed. In the case of our engine, one such
requirement is that the option is European and that the payoff is a
plain call/put one, which also means that the payoff will be cast down
to the needed class.13
In the middle section of the method, the engine extracts from the passed arguments any information not already presented in digested form. Shown here is the retrieval of the spot price of the underlying; other quantities needed by the engine, e.g., the forward price of the underlying and the risk-free discount factor at maturity, are also extracted.14
Finally, the calculation is performed and the results are stored in
the corresponding slots of the results structure. This concludes both
the calculate method and the example.
A. Odds and ends
A number of basic issues with the usage of QuantLib have been glossed over in the previous chapters, in order not to undermine their readability (if any) with an accumulation of technical details; as pointed out by Douglas Adams in the fourth book of its Hitchhiker trilogy,15
[An excessive amount of detail] is guff. It doesn’t advance the action. It makes for nice fat books such as the American market thrives on, but it doesn’t actually get you anywhere.
This appendix provides a quick reference to some such issues. It is not meant to be exhaustive nor systematic;16 if you need that kind of documentation, check the QuantLib reference manual, available at the QuantLib web site.
Basic types
The library interfaces don’t use built-in types; instead, a number of
typedefs are provided such as Time, Rate,
Integer, or Size. They are all mapped to basic types
(we talked about using full-featured types, possibly with range
checking, but we dumped the idea). Furthermore, all floating-point
types are defined as Real, which in turn is defined as
double. This makes it possible to change all of them
consistently by just changing Real.
In principle, this would allow one to choose the desired level of
accuracy; but to this, the test-suite answers “Fiddlesticks!” since
it shows a few failures when Real is defined as float or
long double. The value of the typedefs is really in making the
code more clear—and in allowing dimensional analysis for those who,
like me, were used to it in a previous life as a physicist; for
instance, expressions such as exp(r) or r+s*t can be
immediately flagged as fishy if they are preceded by Rate r,
Spread s, and Time t.
Of course, all those fancy types are only aliases to double and
the compiler doesn’t really distinguish between them. It would nice
if they had stronger typing; so that, for instance, one could overload
a method based on whether it is passed a price or a volatility.
One possibility would be the BOOST_STRONG_TYPEDEF macro, which is one
of the bazillion utilities provided by Boost. It is used as, say,
BOOST_STRONG_TYPEDEF(double, Time)
BOOST_STRONG_TYPEDEF(double, Rate)
and creates a corresponding proper class with appropriate conversions to and from the underlying type. This would allow overloading methods, but has the drawbacks that not all conversions are explicit. This would break backward compatibility and make things generally awkward.17
Also, the classes defined by the macro overload all operators: you can happily add a time to a rate, even though it doesn’t make sense (yes, dimensional analysis again). It would be nice if the type system prevented this from compiling, while still allowing, for instance, to add a spread to a rate yielding another rate or to multiply a rate by a time yielding a pure number.
How to do this in a generic way, and ideally with no run-time costs, was shown first by Barton and Nackman, 1995; a variation of their idea is implemented in the Boost.Units library, and a simpler one was implemented once by yours truly while still working in Physics.18 However, that might be overkill here; we don’t have to deal with all possible combinations of length, mass, time and so on.
The ideal compromise for a future library might be to implement wrapper classes (à la Boost strong typedef) and to define explicitly which operators are allowed for which types. As usual, we’re not the first ones to have this problem: the idea has been floating around for a while, and at some point a proposal was put forward (Brown, 2013) to add to C++ a new feature, called opaque typedefs, which would have made it easier to define this kind of types.
A final note: among these types, there is at least one which is not
determined on its own (like Rate or Time) but depends on
other types. The volatility of a price and the volatility of a rate
have different dimensions, and thus should have different types.
In short, Volatility should be a template type.
Date calculations
Date calculations are among the basic tools of quantitative finance. As can be expected, QuantLib provides a number of facilities for this task; I briefly describe some of them in the following subsections.
Dates and periods
An instance of the Date class represents a specific day such as
November 15th, 2014. This class provides a number of methods for
retrieving basic information such as the weekday, the day of the
month, or the year; static information such as the minimum and maximum
date allowed (at this time, January 1st, 1901 and December 31st, 2199,
respectively) or whether or not a given year is a leap year; or other
information such as a date’s Excel-compatible serial number or whether
or not a given date is the last date of the month. The complete list
of available methods and their interface is documented in the
reference manual. No time information is included (unless you enable
an experimental compilation switch).
Capitalizing on C++ features, the Date class also overloads a
number of operators so that date algebra can be written in a natural
way; for example, one can write expressions such as ++d, which
advances the date d by one day; d + 2, which yields the
date two days after the given date; d2 - d1, which yields the
number of days between the two dates; d - 3*Weeks, which yields
the date three weeks before the given date (and incidentally, features
a member of the available TimeUnit enumeration, the other
members being Days, Months, and Years); or
d1 < d2, which yields true if the first date is earlier
than the second one. The algebra implemented in the Date class
works on calendar days; neither bank holidays nor business-day
conventions are taken into account.
The Period class models lengths of time such as two days, three
weeks, or five years by storing a TimeUnit and an integer. It
provides a limited algebra and a partial ordering. For the non
mathematically inclined, this means that two Period instances
might or might not be compared to see which is the shorter; while it
is clear that, say, 11 months are less than one year, it is not
possible to determine whether 60 days are more or less than two months
without knowing which two months. When the comparison cannot
be decided, an exception is thrown.
And of course, even when the comparison seems obvious, we managed to sneak in a few surprises. For instance, the comparison
Period(7,Days) == Period(1,Weeks)
returns true. It seems correct, right? Hold that thought.
Calendars
Holidays and business days are the domain of the Calendar
class. Several derived classes exist which define holidays for a
number of markets; the base class defines simple methods for
determining whether or not a date corresponds to a holiday or a
business day, as well as more complex ones for performing tasks such
as adjusting a holiday to the nearest business day (where “nearest”
can be defined according to a number of business-day conventions,
listed in the BusinessDayConvention enumeration) or advancing a
date by a given period or number of business days.
It might be interesting to see how the behavior of a calendar changes
depending on the market it describes. One way would have been to
store in the Calendar instance the list of holidays for the
corresponding market; however, for maintainability we wanted to code
the actual calendar rules (such as “the fourth Thursday in November”
or “December 25th of every year”) rather than enumerating the
resulting dates for a couple of centuries. Another obvious way would
have been to use polymorphism and the Template Method pattern; derived
calendars would override the isBusinessDay method, from which
all others could be implemented. This is fine, but it has the
shortcoming that calendars would need to be passed and stored in
shared_ptrs. The class is conceptually simple, though, and is
used frequently enough that we wanted users to instantiate it and pass
it around more easily—that is, without the added verbosity of
dynamic allocation.
The final solution was the one shown in the listing below. It is a variation of the pimpl idiom, also reminiscent of the Strategy or Bridge patterns; these days, the cool kids might call it type erasure, too (Becker,2007).
Calendar class.class Calendar {
protected:
class Impl {
public:
virtual ~Impl() {}
virtual bool isBusinessDay(const Date&) const = 0;
};
shared_ptr<Impl> impl_;
public:
bool isBusinessDay(const Date& d) const {
return impl_->isBusinessDay(d);
}
bool isHoliday(const Date& d) const {
return !isBusinessDay(d);
}
Date adjust(const Date& d,
BusinessDayConvention c = Following) const {
// uses isBusinessDay() plus some logic
}
Date advance(const Date& d,
const Period& period,
BusinessDayConvention c = Following,
bool endOfMonth = false) const {
// uses isBusinessDay() and possibly adjust()
}
// more methods
};
Long story short: Calendar declares a polymorphic inner class Impl
to which the implementation of the business-day rules is delegated and
stores a pointer to one of its instances. The non-virtual
isBusinessDay method of the Calendar class forwards to the
corresponding method in Calendar::Impl; following somewhat the
Template Method pattern, the other Calendar methods are also
non-virtual and implemented (directly or indirectly) in terms of
isBusinessDay.19
Coming back to this after all these years, though, I’m thinking that
we might have implemented all public methods in terms of
isHoliday instead. Why? Because all calendars are defined
by stating which days are holidays (e.g., Christmas on December 25th
in a lot of places, or MLK Day on the third Monday in January in the
United States). Having isBusinessDay in the Impl
interface instead forces all derived classes to negate that logic
instead of implementing it directly. It’s like having them implement
isNotHoliday.
Derived calendar classes can provide specialized behavior by defining
an inner class derived from Calendar::Impl; their constructor
will create a shared pointer to an Impl instance and store it
in the impl_ data member of the base class. The resulting
calendar can be safely copied by any class that need to store a
Calendar instance; even when sliced, it will maintain the
correct behavior thanks to the contained pointer to the polymorphic
Impl class. Finally, we can note that instances of the same
derived calendar class can share the same Impl instance. This
can be seen as an implementation of the Flyweight pattern—bringing
the grand total to about two and a half patterns for one deceptively
simple class.
Enough with the implementation of Calendar, and back to its
behavior. Here’s the surprise I mentioned in the previous section.
Remember Period(1,Weeks) being equal to Period(7,Days)?
Except that for the advance method of a calendar, 7 days means 7
business days. Thus, we have a situation in which two periods
p1 and p2 are equal (that is, p1 == p2 returns
true) but calendar.advance(p1) differs from
calendar.advance(p2). Yay, us.
I’m not sure I have a good idea for a solution here. Since we want
backwards compatibility, the current uses of Days must keep
working in the same way; so it’s not possible, say, to start
interpreting calendar.advance(7, Days) as 7 calendar days.
One way out might be to keep the current situation, introduce two new
enumeration cases BusinessDays and CalendarDays that
remove the ambiguity, and deprecate Days. Another is to just
remove the inconsistency by dictating that a 7-days period do not, in
fact, equal one week; I’m not overly happy about this one.
As I said, no obvious solution. If you have any other suggestions, I’m all ears.
Day-count conventions
The DayCounter class provides the means to calculate the
distance between two dates, either as a number of days or a fraction
of an year, according to different conventions. Derived classes such
as Actual360 or Thirty360 exist; they implement
polymorphic behavior by means of the same technique used by the
Calendar class and described in the previous section.
Unfortunately, the interface has a bit of a rough edge. Instead of
just taking two dates, the yearFraction method is declared as
Time yearFraction(const Date&,
const Date&,
const Date& refPeriodStart = Date(),
const Date& refPeriodEnd = Date()) const;
The two optional dates are required by one specific day-count convention (namely, the ISMA actual/actual convention) that requires a reference period to be specified besides the two input dates. To keep a common interface, we had to add the two additional dates to the signature of the method for all day counters (most of which happily ignore them). This is not the only mischief caused by this day counter; you’ll see another in the next section.
Schedules
The Schedule class, shown in the next listing, is
used to generate sequences of coupon dates.
Schedule class.class Schedule {
public:
Schedule(const Date& effectiveDate,
const Date& terminationDate,
const Period& tenor,
const Calendar& calendar,
BusinessDayConvention convention,
BusinessDayConvention terminationDateConvention,
DateGeneration::Rule rule,
bool endOfMonth,
const Date& firstDate = Date(),
const Date& nextToLastDate = Date());
Schedule(const std::vector<Date>&,
const Calendar& calendar = NullCalendar(),
BusinessDayConvention convention = Unadjusted,
... /* `other optional parameters` */);
Size size() const;
bool empty() const;
const Date& operator[](Size i) const;
const Date& at(Size i) const;
const_iterator begin() const;
const_iterator end() const;
const Calendar& calendar() const;
const Period& tenor() const;
bool isRegular(Size i) const;
Date previousDate(const Date& refDate) const;
Date nextDate(const Date& refDate) const;
... // other inspectors and utilities
};
Following practice and ISDA conventions, this class has to accept a lot of parameters; you can see them as the argument list of its constructor. (Oh, and you’ll forgive me if I don’t go and explain all of them. I’m sure you can guess what they mean.) They’re probably too many, which is why the library uses the Named Parameter Idiom (already described in chapter 4) to provide a less unwieldy factory class. With its help, a schedule can be instantiated as
Schedule s = MakeSchedule().from(startDate).to(endDate)
.withFrequency(Semiannual)
.withCalendar(TARGET())
.withNextToLastDate(stubDate)
.backwards();
Other methods include on the one hand, inspectors for the stored data;
and on the other hand, methods to give the class a sequence interface,
e.g., size, operator[], begin, and end.
The Schedule class has a second constructor, taking a
precomputed vector of dates and a number of optional parameters, which
might be passed to help the library use the resulting schedule
correctly. Such information includes the date generation rule or
whether the dates are aligned to the end of the month, but mainly,
you’ll probably need to pass the tenor and an isRegular
vector of bools, about which I need to spend a couple of words.
What does “regular” mean? The boolean isRegular(i) doesn’t refer to
the i-th date, but to the i-th interval; that is, the one between
the i-th and (i+1)-th dates. When a schedule is built based on a
tenor, most intervals correspond to the passed tenor (and thus are
regular) but the first and last intervals might be shorter or longer
depending on whether we passed an explicit first or next-to-last date.
We might do this, e.g., when we want to specify a short first coupon.
If we build the schedule with a precomputed set of dates, we don’t have the tenor information and we can’t tell if a given interval is regular unless those pieces of information are passed to the schedule.20 In turn, this means that using that schedule to build a sequence of coupons (by passing it, say, to the constructor of a fixed-rate bond) might give us the wrong result. And why, oh, why does the bond needs this missing info in order to build the coupons? Again, because the day-count convention of the bond might be ISMA actual/actual, which needs a reference period; and in order to calculate the reference period, we need to know the coupon tenor. In absence of this information, all the bond can do is assume that the coupon is regular, that is, that the distance between the passed start and end dates of the coupon also corresponds to its tenor.
Finance-related classes
Given our domain, it is only to be expected that a number of classes directly model financial concepts. A few such classes are described in this section.
Market quotes
There are at least two possibilities to model quoted values. One is to model quotes as a sequence of static values, each with an associated timestamp, with the current value being the latest; the other is to model the current value as a quoted value that changes dynamically.
Both views are useful; and in fact, both were implemented in the
library. The first model corresponds to the TimeSeries class,
which I won’t describe in detail here; it is basically a map between
dates and values, with methods to retrieve values at given dates and
to iterate on the existing values, and it was never really used in
other parts of the library. The second resulted in the Quote
class, shown in the following listing.
Quote class.class Quote : public virtual Observable {
public:
virtual ~Quote() {}
virtual Real value() const = 0;
virtual bool isValid() const = 0;
};
Its interface is slim enough. The class inherits from the
Observable class, so that it can notify its dependent objects
when its value change. It declares the isValid method, that
tells whether or not the quote contains a valid value (as opposed to,
say, no value, or maybe an expired value) and the value method,
which returns the current value.
These two methods are enough to provide the needed behavior. Any other object whose behavior or value depends on market values (for example, the bootstrap helpers of chapter 2) can store handles to the corresponding quotes and register with them as an observer. From that point onwards, it will be able to access the current values at any time.
The library defines a number of quotes—that is, of implementations
of the Quote interface. Some of them return values which are
derived from others; for instance, ImpliedStdDevQuote turns
option prices into implied-volatility values. Others adapt other
objects; ForwardValueQuote returns forward index fixings as the
underlying term structures change, while LastFixingQuote
returns the latest value in a time series.
At this time, only one implementation is an genuine source of external
values; that would be the SimpleQuote class, shown in
the next listing.
SimpleQuote class.class SimpleQuote : public Quote {
public:
SimpleQuote(Real value = Null<Real>())
: value_(value) {}
Real value() const {
QL_REQUIRE(isValid(), "invalid SimpleQuote");
return value_;
}
bool isValid() const {
return value_!=Null<Real>();
}
Real setValue(Real value) {
Real diff = value-value_;
if (diff != 0.0) {
value_ = value;
notifyObservers();
}
return diff;
}
private:
Real value_;
};
It is simple in the sense that it
doesn’t implement any particular data-feed interface: new values are
set manually by calling the appropriate method. The latest value
(possibly equal to Null<Real>() to indicate no value) is stored
in a data member. The Quote interface is implemented by having
the value method return the stored value, and the
isValid method checking whether it’s null. The method used to
feed new values is setValue; it takes the new value, notifies
its observers if it differs from the latest stored one, and returns
the increment between the old and new values.21
I’ll conclude this post with a few short notes. The first is that
the type of the quoted values is constrained to Real. This has
not been a limitation so far, and besides, it’s now too late to define
Quote as a class template; so it’s unlikely that this will ever
change.
The second is that the original idea was that the Quote
interface would act as an adapter to actual data feeds, with different
implementations calling the different API and allowing QuantLib to use
them in a uniform way. So far, however, nobody provided such
implementations; the closer we got was to use data feeds in Excel and
set their values to instances of SimpleQuote.
The last (and a bit longer) note is that the interface of
SimpleQuote might be modified in future to allow more advanced
uses. When setting new values to a group of related quotes (say, the
quotes interest rates used for bootstrapping a curve) it would be
better to only trigger a single notification after all values are set,
instead of having each quote send a notification when it’s updated.
This behavior would be both faster, since chains of notifications turn
out to be quite the time sink, and safer, since no observer would risk
to recalculate after only a subset of the quotes are updated. The
change (namely, an additional silent parameter to
setValue that would mute notifications when equal to
true) has already been implemented in a fork of the library,
and could be added to QuantLib too.
Interest rates
The InterestRate class (shown in the listing that follows)
encapsulates general interest-rate calculations. Instances of this
class are built from a rate, a day-count convention, a compounding
convention, and a compounding frequency (note, though, that the value
of the rate is always annualized, whatever the frequency). This
allows one to specify rates such as “5%, actual/365, continuously
compounded” or “2.5%, actual/360, semiannually compounded.” As can be
seen, the frequency is not always needed. I’ll return to this later.
InterestRate class.enum Compounding { Simple, // 1+rT
Compounded, // (1+r)^T
Continuous, // e^{rT}
SimpleThenCompounded
};
class InterestRate {
public:
InterestRate(Rate r,
const DayCounter&,
Compounding,
Frequency);
// inspectors
Rate rate() const;
const DayCounter& dayCounter();
Compounding compounding() const;
Frequency frequency() const;
// automatic conversion
operator Rate() const;
// implied discount factor and compounding after a given time
// (or between two given dates)
DiscountFactor discountFactor(Time t) const;
DiscountFactor discountFactor(const Date& d1,
const Date& d2) const;
Real compoundFactor(Time t) const;
Real compoundFactor(const Date& d1,
const Date& d2) const;
// other calculations
static InterestRate impliedRate(Real compound,
const DayCounter&,
Compounding,
Frequency,
Time t);
... // same with dates
InterestRate equivalentRate(Compounding,
Frequency,
Time t) const;
... // same with dates
};
Besides the obvious inspectors, the class provides a number of
methods. One is the conversion operator to Rate, i.e., to
double. On afterthought, this is kind of risky, as the
converted value loses any day-count and compounding information; this
might allow, say, a simply-compounded rate to slip undetected where a
continuously-compounded one was expected. The conversion was added
for backward compatibility when the InterestRate class was
first introduced; it might be removed in a future revision of the
library, dependent on the level of safety we want to force on
users.22
Other methods complete a basic set of calculations. The
compoundFactor returns the unit amount compounded for a time
\(t\) (or equivalently, between two dates \(d_1\) and
\(d_2\)) according to the given interest rate; the
discountFactor method returns the discount factor between two dates
or for a time, i.e., the reciprocal of the compound factor; the
impliedRate method returns a rate that, given a set of conventions,
yields a given compound factor over a given time; and the
equivalentRate method converts a rate to an equivalent one with
different conventions (that is, one that results in the same
compounded amount).
Like the InterestRate constructor, some of these methods take a
compounding frequency. As I mentioned, this doesn’t always make
sense; and in fact, the Frequency enumeration has a
NoFrequency item just to cover this case.
Obviously, this is a bit of a smell. Ideally, the frequency should be
associated only with those compounding conventions that need it, and
left out entirely for those (such as Simple and
Continuous) that don’t. If C++ supported it, we would write
something like
enum Compounding { Simple,
Compounded(Frequency),
Continuous,
SimpleThenCompounded(Frequency)
};
which would be similar to algebraic data types in functional
languages, or case classes in Scala;23 but unfortunately
that’s not an option. To have something of this kind, we’d have to go
for a full-featured Strategy pattern and turn Compounding into
a class hierarchy. That would probably be overkill for the needs of
this class, so we’re keeping both the enumeration and the smell.
Indexes
Like other classes such as Instrument and TermStructure,
the Index class is a pretty wide umbrella: it covers concepts
such as interest-rate indexes, inflation indexes, stock indexes—you
get the drift.
Needless to say, the modeled entities are diverse enough that the
Index class has very little interface to call its own. As
shown in the following listing, all its methods have to do with
index fixings.
Index class.class Index : public Observable {
public:
virtual ~Index() {}
virtual std::string name() const = 0;
virtual Calendar fixingCalendar() const = 0;
virtual bool isValidFixingDate(const Date& fixingDate)
const = 0;
virtual Real fixing(const Date& fixingDate,
bool forecastTodaysFixing = false)
const = 0;
virtual void addFixing(const Date& fixingDate,
Real fixing,
bool forceOverwrite = false);
void clearFixings();
};
The isValidFixingDate method tells us whether a
fixing was (or will be made) on a given date; the
fixingCalendar method returns the calendar used to determine
the valid dates; and the fixing method retrieves a fixing for a
past date or forecasts one for a future date. The remaining methods
deal specifically with past fixings: the name method, which
returns an identifier that must be unique for each index, is used to
index (pun not intended) into a map of stored fixings; the
addFixing method stores a fixing (or many, in other overloads
not shown here); and the clearFixing method clears all stored
fixings for the given index.
Why the map, and where is it in the Index class? Well, we started
from the requirement that past fixings should be shared rather than
per-instance; if one stored, say, the 6-months Euribor fixing for a
date, we wanted the fixing to be visible to all instances of the same
index,24 and not just the particular one whose addFixing
method we called. This was done by defining and using an
IndexManager singleton behind the curtains. Smelly? Sure, as all
singletons. An alternative might have been to define static class
variables in each derived class to store the fixings; but that would
have forced us to duplicate them in each derived class with no real
advantage (it would be as much against concurrency as the singleton).
Since the returned index fixings might change (either because their
forecast values depend on other varying objects, or because a newly
available fixing is added and replaces a forecast) the Index
class inherits from Observable so that instruments can register
with its instances and be notified of such changes.
At this time, Index doesn’t inherit from Observer,
although its derived classes do (not surprisingly, since forecast
fixings will almost always depend on some observable market quote).
This was not an explicit design choice, but rather an artifact of the
evolution of the code and might change in future
releases. However, even if we were to inherit Index from Observer,
we would still be forced to have some code duplication in derived
classes, for a reason which is probably worth describing in more
detail.
I already mentioned that fixings can change for two reasons. One is
that the index depends on other observables to forecast its fixings;
in this case, it simply registers with them (this is done in each
derived class, as each class has different observables). The other
reason is that a new fixing might be made available, and that’s more
tricky to handle. The fixing is stored by a call to addFixing
on a particular index instance, so it seems like no external
notification would be necessary, and that the index can just call the
notifyObservers method to notify its observers; but that’s not
the case. As I said, the fixings is shared; if we store today’s
3-months Euribor fixing, it will be available to all instances of such
index, and thus we want all of them to be aware of the
change. Moreover, instruments and curves might have registered with
any of those Index instances, so all of them must send in turn
a notification.
The solution is to have all instances of the same index communicate by
means of a shared object; namely, we used the same IndexManager
singleton that stores all index fixings. As I said,
IndexManager maps unique index tags to sets of fixings; also,
by making the sets instances of the ObservableValue class, it
provides the means to register and receive notification when one or
more fixings are added for a specific tag (this class is described
later in this appendix. You don’t need the details here).
All pieces are now in place. Upon construction, any Index
instance will ask IndexManager for the shared observable
corresponding to the tag returned by its name method. When
we call addFixings on, say, some particular 6-months Euribor
index, the fixing will be stored into IndexManager; the
observable will send a notification to all 6-months Euribor indexes
alive at that time; and all will be well with the world.
However, C++ still throws a small wrench in our gears. Given the above, it would be tempting to call
registerWith(IndexManager::instance().notifier(name()));
in the Index constructor and be done with it. However, it
wouldn’t work; for the reason that in the constructor of the base
class, the call to the virtual method name wouldn’t be
polymorphic.25 From here stems the code
duplication I mentioned a few paragraphs earlier; in order to work,
the above method call must be added to the constructor of each derived
index class which implements or overrides the name
method. The Index class itself doesn’t have a constructor
(apart from the default one that the compiler provides).
As an example of a concrete class derived from Index, the next
listing sketches the InterestRateIndex class.
InterestRateIndex class.class InterestRateIndex : public Index, public Observer {
public:
InterestRateIndex(const std::string& familyName,
const Period& tenor,
Natural settlementDays,
const Currency& currency,
const Calendar& fixingCalendar,
const DayCounter& dayCounter);
: familyName_(familyName), tenor_(tenor), ... {
registerWith(Settings::instance().evaluationDate());
registerWith(
IndexManager::instance().notifier(name()));
}
std::string name() const;
Calendar fixingCalendar() const;
bool isValidFixingDate(const Date& fixingDate) const {
return fixingCalendar().isBusinessDay(fixingDate);
}
Rate fixing(const Date& fixingDate,
bool forecastTodaysFixing = false) const;
void update() { notifyObservers(); }
std::string familyName() const;
Period tenor() const;
... // other inspectors
Date fixingDate(const Date& valueDate) const;
virtual Date valueDate(const Date& fixingDate) const;
virtual Date maturityDate(const Date& valueDate) const = 0;
protected:
virtual Rate forecastFixing(const Date& fixingDate)
const = 0;
std::string familyName_;
Period tenor_;
Natural fixingDays_;
Calendar fixingCalendar_;
Currency currency_;
DayCounter dayCounter_;
};
std::string InterestRateIndex::name() const {
std::ostringstream out;
out << familyName_;
if (tenor_ == 1*Days) {
if (fixingDays_==0) out << "ON";
else if (fixingDays_==1) out << "TN";
else if (fixingDays_==2) out << "SN";
else out << io::short_period(tenor_);
} else {
out << io::short_period(tenor_);
}
out << " " << dayCounter_.name();
return out.str();
}
Rate InterestRateIndex::fixing(
const Date& d,
bool forecastTodaysFixing) const {
QL_REQUIRE(isValidFixingDate(d), ...);
Date today = Settings::instance().evaluationDate();
if (d < today) {
Rate pastFixing =
IndexManager::instance().getHistory(name())[d];
QL_REQUIRE(pastFixing != Null<Real>(), ...);
return pastFixing;
}
if (d == today && !forecastTodaysFixing) {
Rate pastFixing = ...;
if (pastFixing != Null<Real>())
return pastFixing;
}
return forecastFixing(d);
}
Date InterestRateIndex::valueDate(const Date& d) const {
QL_REQUIRE(isValidFixingDate(d) ...);
return fixingCalendar().advance(d, fixingDays_, Days);
}
As you might expect, such class
defines a good deal of specific behavior besides what it inherits from
Index. To begin with, it inherits from Observer, too,
since Index doesn’t. The InterestRateIndex constructor
takes the data needed to specify the index: a family name, as in
“Euribor”, common to different indexes of the same family such as,
say, 3-months and 6-months Euribor; a tenor that specifies a
particular index in the family; and additional information such as the
number of settlement days, the index currency, the fixing calendar,
and the day-count convention used for accrual.
The passed data are, of course, copied into the corresponding data
members; then the index registers with a couple of observables. The
first is the global evaluation date; this is needed because, as I’ll
explain shortly, there’s a bit of date-specific behavior in the class
that is triggered when an instance is asked for today’s fixing. The
second observable is the one which is contained inside
IndexManager and provides notifications when new fixings are
stored. We can identify this observable here: the
InterestRateIndex class has all the information needed to
determine the index, so it can implement the name method and
call it. However, this also means that classes deriving from
InterestRateIndex must not override name; since the
overridden method would not be called in the body of this constructor
(as explained earlier), they would register with
the wrong notifier. Unfortunately, this can’t be enforced in C++,
which doesn’t have a keyword like final in Java or
sealed in C#; but the alternative would be to require
that all classes derived from InterestRateIndex register with
IndexManager, which is equally not enforceable, probably more
error-prone, and certainly less convenient.
The other methods defined in InterestRateIndex have different
purposes. A few implement the required Index and
Observer interfaces; the simplest are update, which
simply forwards any notification, fixingCalendar, which returns
a copy of the stored calendar instance, and isValidFixingDate,
which checks the date against the fixing calendar.
The name method is a bit more complicated. It stitches
together the family name, a short representation of the tenor, and the
day-count convention to get an index name such as “Euribor 6M
Act/360” or “USD Libor 3M Act/360”; special tenors such as
overnight, tomorrow-next and spot-next are detected so that the
corresponding acronyms are used.
The fixing method contains the most logic. First, the required
fixing date is checked and an exception is raised if no fixing was
supposed to take place on it. Then, the fixing date is checked
against today’s date. If the fixing was in the past, it must be among
those stored in the IndexManager singleton; if not, an
exception is raised since there’s no way we can forecast a past
fixing. If today’s fixing was requested, the index first tries
looking for the fixing in the IndexManager and returns it if
found; otherwise, the fixing is not yet available. In this case, as
well as for a fixing date in the future, the index forecasts the value
of the fixing; this is done by calling the forecastFixing
method, which is declared as purely virtual in this class and
implemented in derived ones. The logic in the fixing method is
also the reason why, as I mentioned, the index registers with the
evaluation date; the behavior of the index depends on the value of
today’s date, so it need to be notified when it changes.
Finally, the InterestRateIndex class defines other methods that
are not inherited from Index. Most of them are inspectors that
return stored data such as the family name or the tenor; a few others
deal with date calculations. The valueDate method takes a
fixing date and returns the starting date for the instrument that
underlies the rate (for instance, the deposit underlying a
LIBOR, which for most currencies starts two business days
after the fixing date); the maturityDate method takes a value
date and returns the maturity of the underlying instrument (e.g., the
maturity of the deposit); and the fixingDate method is the
inverse of valueDate, taking a value date and returning the
corresponding fixing date. Some of these methods are virtual, so that
their behavior can be overridden; for instance, while the default
behavior for valueDate is to advance the given number of fixing
days on the given calendar, LIBOR index mandates first to
advance on the London calendar, then to adjust the resulting date on
the calendar corresponding to the index currency. For some reason,
fixingDate is not virtual; this is probably an oversight that
should be fixed in a future release.
Exercises and payoffs
I’ll close this section with a couple of domain-related classes used in the definitions of a few instruments.
First, the Exercise class, shown in the listing below.
Exercise class and its derived classes.class Exercise {
public:
enum Type {
American, Bermudan, European
};
explicit Exercise(Type type);
virtual ~Exercise();
Type type() const;
Date date(Size index) const;
const std::vector<Date>& dates() const;
Date lastDate() const;
protected:
std::vector<Date> dates_;
Type type_;
};
class EarlyExercise : public Exercise {
public:
EarlyExercise(Type type,
bool payoffAtExpiry = false);
bool payoffAtExpiry() const;
};
class AmericanExercise : public EarlyExercise {
public:
AmericanExercise(const Date& earliestDate,
const Date& latestDate,
bool payoffAtExpiry = false);
};
class BermudanExercise : public EarlyExercise {
public:
BermudanExercise(const std::vector<Date>& dates,
bool payoffAtExpiry = false);
};
class EuropeanExercise : public Exercise {
public:
EuropeanExercise(const Date& date);
};
As you would expect, the base class declares methods to retrieve
information on the date, or dates, of the exercise. Quite a few of
them, actually. There’s a dates method that returns the set of
exercise dates, a date method that returns the one at a particular
index, and a convenience method lastDate that, as you might have
guessed, returns the last one; so there’s some redundancy
there.26 Also, there’s a type method that is leaving me
scratching my head as I look at the code again.
The type method returns the kind of exercise, picking its value from
a set (European, Bermudan, or American) declared in an inner
enumeration Exercise::Type. This is not puzzling per se, but it
goes somewhat against what we did next, which is to use inheritance to
declare AmericanExercise, BermudanExercise, and EuropeanExercise
classes. On the one hand, the use of a virtual destructor in the base
Exercise class seems to suggest that inheritance is the way to go if
one wants to define new kind of exercises. On the other hand,
enumerating the kind of exercises in the base class seems to go
against this kind of extension, since inheriting a new exercise class
would also require one to add a new case to the enumeration. For
inheritance, one can also argue that the established idiom around the
library is to pass around smart pointers to the Exercise class; and
against inheritance, that the class doesn’t define any virtual method
except the destructor, and the behavior of an instance of any derived
class is only given by the value of the data members stored in the
base class. In short: it seems that, when we wrote this, we were even
more confused than I am now.
Were I to write it now, I’d probably keep the enumeration and make it
a concrete class: the derived classes might either create objects that
can be safely sliced to become Exercise instances when passed
around, or they could be turned into functions returning
Exercise instances directly. As much as this might irk
object-oriented purists, there are a number of places in the code
where the type of the exercise need to be checked, and having an
enumeration is probably the pragmatic choice when compared to using
casts or some kind of visitor pattern. The absence of specific
behavior in derived classes seems another hint to me.
As I wrote this, it occurred to me that an exercise might also be an
Event, as described in chapter 4. However,
this doesn’t always match what the Exercise class models. In
the case of a European exercise, we could also model it as an
Event instance; in the case of a Bermudan exercise, the
Exercise instance would probably correspond to a set of
Event instances; and in the case of an American exercise, what
we’re really modeling here is an exercise range—and as a matter of
fact, the meaning of the interface also changes in this case, since
the dates method no longer returns the set of all possible
exercise dates, but just the first and last date in the range. As
often happens, the small things that seem obvious turn out to be
difficult to model soundly when looked up close.
Onwards to the Payoff class, shown in the next listing together with
a few of its derived classes.
Payoff class and a few derived classes.class Payoff : std::unary_function<Real,Real> {
public:
virtual ~Payoff() {}
virtual std::string name() const = 0;
virtual std::string description() const = 0;
virtual Real operator()(Real price) const = 0;
virtual void accept(AcyclicVisitor&);
};
class TypePayoff : public Payoff {
public:
Option::Type optionType() const;
protected:
TypePayoff(Option::Type type);
};
class FloatingTypePayoff : public TypePayoff {
public:
FloatingTypePayoff(Option::Type type);
Real operator()(Real price) const;
// more Payoff interface
};
class StrikedTypePayoff : public TypePayoff {
public:
Real strike() const;
// more Payoff interface
protected:
StrikedTypePayoff(Option::Type type,
Real strike);
};
class PlainVanillaPayoff : public StrikedTypePayoff {
public:
PlainVanillaPayoff(Option::Type type,
Real strike);
Real operator()(Real price) const;
// more Payoff interface
};
Its interface includes an operator(), returning the value of the
payoff given the value of the underlying, an accept method to
support the Visitor pattern, and a couple of inspectors (name and
description) which can be used for reporting—and are probably one
too many.
In hindsight, we tried to model the class before having a grasp of
enough use cases. Unfortunately, the resulting interface stuck. The
biggest problem is the dependency of operator() on a single
underlying, which excludes payoffs based on multiple underlying
values.27 Another one is the over-reliance on inheritance.
For instance, we have a TypePayoff class that adds a type (Call or
Put, which again might be restrictive) and the corresponding
inspector; a StrikedTypePayoff which adds a strike; and, finally,
PlainVanillaPayoff, which models a simple call or put payoff and
ends up removed from the Payoff class by three levels of
inheritance: probably too many, considering that this is used to
implement a textbook option and will be looked up by people just
starting with the library.
Another misstep we might have made is to add a pointer to a
Payoff instance to the Option class as a data member,
with the intent that it should contain the information about the
payoff. This led us to classes such as FloatingTypePayoff,
also shown in the listing. It’s used in the implementation of
floating lookback options, and stores the information about the type
(as in, call or put); but since the strike is fixed at the maturity of
the option, it can’t specify it and can’t implement the payoff with
the interface we specified. Its operator() throws an exception
if invoked. In this case, we might as well do without the payoff and
just pass the type to the lookback option; that is, if its base
Option class didn’t expect a payoff.
Math-related classes
The library also needs some mathematical tools, besides those provided by the C++ standard library. Here is a brief overview of some of them.
Interpolations
Interpolations belong to a kind of class which is not common in QuantLib: namely, the kind that might be unsafe to use.
The base class, Interpolation, is shown in the listing below. It
interpolates two underlying random-access sequences of \(x\) and
\(y\) values, and provides an operator() that returns the
interpolated values as well as a few other convenience methods. Like
the Calendar class we saw in a previous
section, it implements polymorphic behavior
by means of the pimpl idiom: it declares an inner Impl class whose
derived classes will implement specific interpolations and to which
the Interpolation class forwards its own method calls. Another inner
class template, templateImpl, implements the common machinery and
stores the underlying data.
Interpolation class.class Interpolation : public Extrapolator {
protected:
class Impl {
public:
virtual ~Impl() {}
virtual void update() = 0;
virtual Real xMin() const = 0;
virtual Real xMax() const = 0;
virtual Real value(Real) const = 0;
virtual Real primitive(Real) const = 0;
virtual Real derivative(Real) const = 0;
};
template <class I1, class I2>
class templateImpl : public Impl {
public:
templateImpl(const I1& xBegin, const I1& xEnd,
const I2& yBegin);
Real xMin() const;
Real xMax() const;
protected:
Size locate(Real x) const;
I1 xBegin_, xEnd_;
I2 yBegin_;
};
shared_ptr<Impl> impl_;
public:
typedef Real argument_type;
typedef Real result_type;
bool empty() const { return !impl_; }
Real operator()(Real x, bool extrapolate = false) const {
checkRange(x,extrapolate);
return impl_->value(x);
}
Real primitive(Real x, bool extrapolate = false) const;
Real derivative(Real x, bool extrapolate = false) const;
Real xMin() const;
Real xMax() const;
void update();
protected:
void checkRange(Real x, bool extrapolate) const;
};
As you can see, templateImpl doesn’t copy the \(x\) and \(y\)
values; instead, it just provides a kind of view over them by storing
iterators into the two sequences. This is what makes interpolations
unsafe: on the one hand, we have to make sure that the lifetime of an
Interpolation instance doesn’t exceed that of the underlying
sequences, to avoid pointing into a destroyed object; and on the other
hand, any class that stores an interpolation instance will have
to take special care of copying.
The first requirement is not a big problem. An interpolation is seldom used on its own; it is usually stored as a data member of some other class, together with its underlying data. This takes care of the lifetime issues, as the interpolation and the data live and die together.
The second is not a big problem, either: but whereas the first issue
is usually taken care of automatically, this one requires some action
on the part of the developer. As I said, the usual case is to have an
Interpolation instance stored in some class together with its
data. The compiler-generated copy constructor for the container class
would make new copies of the underlying data, which is correct; but it
would also make a new copy of the interpolation that would still be
pointing at the original data (since it would store copies of the
original iterators). This is, of course, not correct.
To avoid this, the developer of the host class needs to write a
user-defined copy constructor that not only copies the data, but also
regenerates the interpolation so that it points to the new
sequences—which might not be so simple. An object holding an
Interpolation instance can’t know its exact type (which is
hidden in the Impl class) and thus can’t just rebuild it to
point somewhere else.
One way out of this would have been to give interpolations some kind of
virtual clone method to return a new one of the same type, or a
virtual rebind method to change the underlying iterators once
copied. However, that wasn’t necessary, as most of the times we
already have interpolation traits laying around.
What’s that, you say? Well, it’s those Linear or LogLinear classes
I’ve been throwing around while I was explaining interpolated term
structures in chapter 3. An example is
in the following listing, together with its corresponding
interpolation class.
LinearInterpolation class and of its traits class.template <class I1, class I2>
class LinearInterpolationImpl
: public Interpolation::templateImpl<I1,I2> {
public:
LinearInterpolationImpl(const I1& xBegin, const I1& xEnd,
const I2& yBegin)
: Interpolation::templateImpl<I1,I2>(xBegin, xEnd, yBegin),
primitiveConst_(xEnd-xBegin), s_(xEnd-xBegin) {}
void update();
Real value(Real x) const {
Size i = this->locate(x);
return this->yBegin_[i] + (x-this->xBegin_[i])*s_[i];
}
Real primitive(Real x) const;
Real derivative(Real x) const;
private:
std::vector<Real> primitiveConst_, s_;
};
class LinearInterpolation : public Interpolation {
public:
template <class I1, class I2>
LinearInterpolation(const I1& xBegin, const I1& xEnd,
const I2& yBegin) {
impl_ = shared_ptr<Interpolation::Impl>(
new LinearInterpolationImpl<I1,I2>(xBegin, xEnd,
yBegin));
impl_->update();
}
};
class Linear {
public:
template <class I1, class I2>
Interpolation interpolate(const I1& xBegin, const I1& xEnd,
const I2& yBegin) const {
return LinearInterpolation(xBegin, xEnd, yBegin);
}
static const bool global = false;
static const Size requiredPoints = 2;
};
The LinearInterpolation class doesn’t have a lot of logic: its only method is
a template constructor (the class itself is not a template) that
instantiates an inner implementation class. The latter inherits
from templateImpl and is the one that does the heavy lifting,
implementing the actual interpolation formulas (with the help of
methods, such as locate, defined in its base class).
The Linear traits class defines some static information,
namely, that we need at least two points for a linear interpolation,
and that changing a point only affects the interpolation locally; and
also defines an interpolate method that can create an
interpolation of a specific type from a set of iterators into \(x\) and
\(y\). The latter method is implemented with the same interface by all
traits (when an interpolation, such as splines, needs more parameters,
they are passed to the traits constructor and stored) and is the one
that’s going to help in our copying problem. If you look, for
instance, at the listing of the InterpolatedZeroCurve class back in
chapter 3, you’ll see that
we’re storing an instance of the traits class (it’s called
interpolator_ there) together with the interpolation and the
underlying data. If we do the same in any class that stores an
interpolation, we’ll be able to use the traits to create a new one in
the copy constructor.
Unfortunately, though, we have no way at this time to enforce writing
a copy constructor in a class that stores an interpolation, so its
developer will have to remember it. We have no way, that is, without
making the Interpolation class non-copyable and thus also
preventing useful idioms (like returning an interpolation from a
method, as traits do). In C++11, we’d solve this by making it
non-copyable and movable.
A final note: the interpolation stores iterators into the original
data, but this is not enough to keep it up to date when any of the
data changes. When this happens, its update method must be called
so that the interpolation can refresh its state; this is the
responsibility of the class that contains the interpolation and the
data (and which, probably, is registered as an observer with whatever
may change.) This holds also for those interpolations, such as
linear, that might just read the data directly: depending on the
implementation, they might precalculate some results and store them as
state to be kept updated. (The current LinearInterpolation
implementation does this for the slopes between the points, as well as
the values of its primitive at the nodes.28 Depending on how
frequently the data are updated, this might be either an optimization
or a pessimization.)
One-dimensional solvers
Solvers were used in the bootstrap routines described in chapter 3, the yield calculations mentioned in chapter 4, and any code that needs a calculated value to match a target; i.e, that needs, given a function \(f\), to find the \(x\) such that \(f(x) = \xi\) within a given accuracy.
The existing solvers will find the \(x\) such that \(f(x) = 0\); of course, this doesn’t make them any less generic, but it requires you to define the additional helper function \(g(x) \equiv f(x)-\xi\). There are a few of them, all based on algorithms which were taken from Numerical Recipes in C (Press et al, 1992) and duly reimplemented.29
The following listing shows the interface of the class template
Solver1D, used as a base by the available solvers.
Solver1D class template and of a few derived classes.template <class Impl>
class Solver1D : public CuriouslyRecurringTemplate<Impl> {
public:
template <class F>
Real solve(const F& f,
Real accuracy,
Real guess,
Real step) const;
template <class F>
Real solve(const F& f,
Real accuracy,
Real guess,
Real xMin,
Real xMax) const;
void setMaxEvaluations(Size evaluations);
void setLowerBound(Real lowerBound);
void setUpperBound(Real upperBound);
};
class Brent : public Solver1D<Brent> {
public:
template <class F>
Real solveImpl(const F& f,
Real xAccuracy) const;
};
class Newton : public Solver1D<Newton> {
public:
template <class F>
Real solveImpl(const F& f,
Real xAccuracy) const;
};
It provides some boilerplate code, common to all of them: one overload
of the solve method looks for lower and upper values of \(x\)
that bracket the solution, while the other checks that the solution is
actually bracketed by the passed minimum and maximum values. In both
cases, the actual calculation is delegated to the solveImpl method
defined by the derived class and implementing a specific algorithm.
Other methods allow you to set constraints on the explored range, or
the number of function evaluations.
The forwarding to solveImpl is implemented using the Curiously
Recurring Template Pattern, already described in chapter
7. When we wrote these classes, we were at the
height of our template craze (did I mention we even had an
implementation of expression templates? (Veldhuizen,
2000)) so you might suspect that the choice
was dictated by the fashion of that time. However, it wouldn’t have
been possible to use dynamic polymorphism. We wanted the solvers to
work with any function pointer or function object, and
boost::function wasn’t around yet, which forced us to use a template
method. Since the latter couldn’t be virtual, CRTP was the only way
to put the boilerplate code in the base class and let it call a method
defined in derived ones.
A few notes to close this subsection. First: if you want to write a
function that takes a solver, the use of CRTP forces you to make it a
template, which might be awkward. To be honest, most of the times we
didn’t bother and just hard-coded an explicit choice of solver. I
won’t blame you if you do the same. Second: most solvers only use the
passed f by calling f(x), so they work with anything that can be
called as a function, but Newton and NewtonSafe also require that
f.derivative(x) be defined. This, too, might have been awkward if
we used dynamic polymorphism. Third, and last: the Solver1D
interface doesn’t specify if the passed accuracy \(\epsilon\)
should apply to \(x\) (that is, if the returned
\(\tilde{x}\) should be within \(\epsilon\) of the true
root) or to \(f(x)\) (that is, if \(f(\tilde{x})\) should be
within \(\epsilon\) of 0). However, all existing solvers treat
it as the accuracy on \(x\).
Optimizers
Multi-dimensional optimizers are more complex than 1-D solvers. In a nutshell, they find the set of variables \(\tilde{\mathbf{x}}\) for which the cost function \(f(\mathbf{x})\) returns its minimum value; but of course, there’s a bit more to it.
Unlike solvers, optimizers don’t use templates. They inherit from the
base class OptimizationMethod, shown in the next listing.
OptimizationMethod class.class OptimizationMethod {
public:
virtual ~OptimizationMethod() {}
virtual EndCriteria::Type minimize(
Problem& P,
const EndCriteria& endCriteria) = 0;
};
Its only method, apart from the virtual
destructor, is minimize. The method takes a reference to a
Problem instance, which in turn contains references to the function
to minimize and to any constraints, and performs the calculations; at
the end of which, it has the problem of having too many things to
return. Besides the best-solution array \(\tilde{\mathbf{x}}\),
it must return the reason for exiting the calculation (did
it converge, or are we returning our best guess after
the maximum number of evaluations?) and it would be nice to return
\(f(\tilde{\mathbf{x}})\) as well, since
it’s likely that it was already calculated.
In the current implementation, the method returns the reason for
exiting and stores the other results inside the Problem
instance. This is also the reason for passing the problem as a
non-const reference; an alternative solution might have been to
leave the Problem instance alone and to return all required
values in a structure, but I see how this might be seen as more
cumbersome. On the other hand, I see no reason for minimize
itself to be non-const: my guess is that it was an oversight on
our part (I’ll get back to this later).
Onward to the Problem class, shown in the listing below.
Problem class.class Problem {
public:
Problem(CostFunction& costFunction,
Constraint& constraint,
const Array& initialValue = Array());
Real value(const Array& x);
Disposable<Array> values(const Array& x);
void gradient(Array& grad_f, const Array& x);
// ... other calculations ...
Constraint& constraint() const;
// ... other inspectors ...
const Array& currentValue();
Real functionValue() const;
void setCurrentValue(const Array& currentValue);
Integer functionEvaluation() const;
// ... other results ...
};
As I mentioned, it groups together arguments such as the cost function to minimize, the constraints, and an optional guess. It provides methods that call the underlying cost function while keeping track of the number of evaluation, and that I’ll describe when talking about cost functions; a few inspectors for its components; and methods to retrieve the results (as well as to set them; the latter are used by the optimizers).
The problem (no pun intended) is that it takes and stores its
components as non-const references. I’ll talk later about
whether they might be const instead. The fact that they’re
reference is an issue in itself, since it puts the responsibility on
client code to make sure that their lifetimes last at least as much as
that of the Problem instance.
In an alternative implementation in which the optimizer returned its
results in a structure, the issue might be moot: we might do away with
the Problem class and pass its components directly to the
minimize method. This would sidestep the lifetime issue, since
they wouldn’t be stored. The disadvantage would be that each
optimizer would have to keep track of the number of function
evaluations, causing some duplication in the code base.
Also unlike for 1-D solvers, the cost function is not a template
parameter for the minimization method. It needs to inherit from the
CostFunction class, shown in the next listing.
CostFunction class.class CostFunction {
public:
virtual ~CostFunction() {}
virtual Real value(const Array& x) const = 0;
virtual Array values(const Array& x) const = 0;
virtual void gradient(Array& grad, const Array& x) const;
virtual Real valueAndGradient(Array& grad,
const Array& x) const;
virtual void jacobian(Matrix &jac, const Array &x) const;
virtual Array valuesAndJacobian(Matrix &jac,
const Array &x) const;
};
Unsurprisingly, its interface declares the value method, which
returns, well, the value of the function for the given array of
arguments;30 but it also declares a
values method returning an array, which is a bit more
surprising until you remember that optimizers are often used for
calibrating over a number of quotes. Whereas value returns the
total error to minimize (let’s say, the sum of the squares of the
errors, or something like it), values returns the set of errors
over each quote; there are algorithms that can make use of this
information to converge more quickly.
Other methods return the derivatives of the value, or the values, for
use by some specific algorithms: gradient calculates the
derivative of value with respect to each variable and stores it
in the array passed as first argument, jacobian does the same
for values filling a matrix, and the valueAndGradient
and valuesAndJacobian methods calculate both values and
derivatives at the same time for efficiency. They have a default
implementation that calculates numerical derivatives; but of course
that’s costly, and derivative-based algorithms should only be used if
you can override the method with an analytic calculation.
A note: checking the interface of CostFunction shows that all
its methods are declared as const, so passing it as non-{const}
reference to the Problem constructor was probably a goof.
Changing it to const would widen the contract of the
constructor, so it should be possible without breaking backward
compatibility.
Finally, the Constraint class, shown in the following listing.
Constraint class.class Constraint {
protected:
class Impl;
public:
bool test(const Array& p) const;
Array upperBound(const Array& params) const;
Array lowerBound(const Array& params) const;
Real update(Array& p,
const Array& direction,
Real beta);
Constraint(const shared_ptr<Impl>& impl =
shared_ptr<Impl>());
};
It works as a base class for constraints to be applied to the domain
of the cost function; the library also defines a few predefined ones,
not shown here, as well as a CompositeConstraint class that can be
used to merge a number of them into a single one.
Its main method is test, which takes an array of variables and
returns whether or not they satisfy the constraint; that is, if the
array belongs to the domain we specified as valid. It also defines
the upperBound and lowerBound methods, which in theory should
specify the maximum and minimum value of the variables but in practice
can’t always specify them correctly; think of the case in which the
domain is a circle, and you’ll see that there are cases in which
\(x\) and \(y\) are both between their upper and lower bounds
but the resulting point is outside the domain.
A couple more notes. First, the Constraint class also defines an
update method. It’s not const, which would make sense if it
updated the constraint; except it doesn’t. It takes an array of
variables and a direction, and extends the original array in the given
direction until it satisfies the constraint. It should have been
const, it should have been named differently, and as the kids say I
can’t even. This might be fixed, though. Second, the class uses the
pimpl idiom (see a previous section) and the
default constructor also takes an optional pointer to the
implementation. Were I to write the class today, I’d have a default
constructor taking no arguments and an additional constructor taking
the implementation and declared as protected and to be used by derived
classes only.
Some short final thoughts on the const-correctness of these classes.
In summary: it’s not great, with some methods that can be fixed and
some others that can’t. For instance, changing the minimize
method would break backwards compatibility (since it’s a virtual
method, and constness is part of its signature) as well as a few
optimizers, that call other methods from minimize and use data
members as a way to transfer information between
methods.31 We could have avoided this if we had put some more
effort in reviewing code before version 1.0. Let this be a lesson for
you, young coders.
Statistics
The statistics classes were written mostly to collect samples from Monte Carlo simulations (you’ll remember them from chapter 6). The full capabilities of the library are implemented as a series of decorators, each one adding a layer of methods, instead of a monolith; as far as I can guess, that’s because you can choose one of two classes at the bottom of the whole thing. A layered design gives you the possibility to build more advanced capabilities just once, based on the common interface of the bottom layer.
The first class you can choose, shown below, is called
IncrementalStatistics, and has the interface you would more or
less expect: it can return the number of samples, their combined
weight in case they were weighed, and a number of statistics results.
IncrementalStatisticsclass.class IncrementalStatistics {
public:
typedef Real value_type;
IncrementalStatistics();
Size samples() const;
Real weightSum() const;
Real mean() const;
Real variance() const;
Real standardDeviation() const;
Real errorEstimate() const;
// skewness, kurtosis, min, max...
void add(Real value, Real weight = 1.0);
template <class DataIterator>
void addSequence(DataIterator begin, DataIterator end);
};
Samples can be added one by one or as a sequence delimited by two iterators. The shtick of this class is that it doesn’t store the data it gets passed, but instead it updates the statistics on the fly; the idea was to save the memory that would be otherwise used for the storage, and in the year 2000 (when a computer might have 128 or 256 MB of RAM) it was a bigger concern than it is now. The implementation used to be homegrown; nowadays it’s written in terms of the Boost accumulator library.
The second class, GeneralStatistics, implements the same
interface and adds a few other methods, made possible by the fact that
it stores (and thus can return) the passed data; for instance, it can
return percentiles or sort its data. It also provides a template
expectationValue method that can be used for bespoke
calculations; if you’re interested, there’s more on that in the aside
at the end of this section.
GeneralStatistics class.class GeneralStatistics {
public:
// ... same as IncrementalStatistics ...
const std::vector<std::pair<Real,Real> >& data() const;
template <class Func, class Predicate>
std::pair<Real,Size>
expectationValue(const Func& f,
const Predicate& inRange) const;
Real percentile(Real y) const;
// ... other inspectors ...
void sort() const;
void reserve(Size n) const;
};
Next, the outer layers. The first ones add statistics associated with
risk, like expected shortfall or value at risk; the problem being that
you usually need the whole set of samples for those. In the case of
incremental statistics, therefore, we have to forgo the exact
calculation and look for approximations. One possibility is to take
the mean and variance of the samples, suppose they come from a
Gaussian distribution with the same moments, and get analytic results
based on this assumption; that’s what the
GenericGaussianStatistics class does.
GaussianStatistics class.template<class S>
class GenericGaussianStatistics : public S {
public:
typedef typename S::value_type value_type;
GenericGaussianStatistics() {}
GenericGaussianStatistics(const S& s) : S(s) {}
Real gaussianDownsideVariance() const;
Real gaussianDownsideDeviation() const;
Real gaussianRegret(Real target) const;
Real gaussianPercentile(Real percentile) const;
Real gaussianValueAtRisk(Real percentile) const;
Real gaussianExpectedShortfall(Real percentile) const;
// ... other measures ...
};
typedef GenericGaussianStatistics<GeneralStatistics>
GaussianStatistics;
As I mentioned, and as you can see, it’s implemented as a decorator; it
takes the class to decorate as a template parameter, inherits from it
so that it still has all the methods of its base class, and adds the
new methods. The library provides a default instantiation,
GaussianStatistics, in which the template parameter is
GeneralStatistics. Yes, I would have expected the incremental
version, too, but there’s a reason for this; bear with me for a
minute.
When the base class stores the full set of samples, we can write a
decorator that calculates the actual risk measures; that would be the
GenericRiskStatistics class. As for the Gaussian statistics, I
won’t discuss the implementation (you can look them up in the
library).
RiskStatistics class.template <class S>
class GenericRiskStatistics : public S {
public:
typedef typename S::value_type value_type;
Real downsideVariance() const;
Real downsideDeviation() const;
Real regret(Real target) const;
Real valueAtRisk(Real percentile) const;
Real expectedShortfall(Real percentile) const;
// ... other measures ...
};
typedef GenericRiskStatistics<GaussianStatistics>
RiskStatistics;
As you can see, the layers can be combined; the default
instantiation provided by the library, RiskStatistics, takes
GaussianStatistics as its base and thus provides both Gaussian
and actual measures. This was also the reason why
GeneralStatistics was used as the base for the latter.
On top of it all, it’s possible to have other decorators; the library
provides a few, but I won’t show their code here. One is
SequenceStatistics, that can be used when a sample is an array
instead of a single number, uses internally a vector of instances of
scalar statistics classes, and also adds the calculation of the
correlation and covariance between the elements of the samples; it is
used, for instance, in the LIBOR market model, where each
sample usually collects cash flows at different times. Other two are
ConvergenceStatistics and DiscrepancyStatistics; they
provide information on the properties of the sequence of samples,
aren’t used anywhere else in the library, but at least we had the
decency of writing unit tests for both of them.
Linear algebra
I don’t have a lot to write about the current implementation of the
Array and Matrix classes, shown in the following listing.
Array and Matrix classes.class Array {
public:
explicit Array(Size size = 0);
// ... other constructors ...
Array(const Array&);
Array(const Disposable<Array>&);
Array& operator=(const Array&);
Array& operator=(const Disposable<Array>&);
const Array& operator+=(const Array&);
const Array& operator+=(Real);
// ... other operators ...
Real operator[](Size) const;
Real& operator[](Size);
void swap(Array&);
// ... iterators and other utilities ...
private:
boost::scoped_array<Real> data_;
Size n_;
};
Disposable<Array> operator+(const Array&, const Array&);
Disposable<Array> operator+(const Array&, Real);
// ... other operators and functions ...
class Matrix {
public:
Matrix(Size rows, Size columns);
// ... other constructors, assignment operators etc. ...
const_row_iterator operator[](Size) const;
row_iterator operator[](Size);
Real& operator()(Size i, Size j) const;
// ... iterators and other utilities ...
};
Disposable<Matrix> operator+(const Matrix&, const Matrix&);
// ... other operators and functions ...
Their interface is what you would expect:
constructors and assignment operators, element access (the
Array class provides the a[i] syntax; the Matrix
class provides both m[i][j] and m(i,j), because we aim
to please), a bunch of arithmetic operators, all working element by
element as usual,32 and a few utilities. There are no
methods for resizing, or for other operations suited for containers,
because this classes are not meant to be used as such; they’re
mathematical utilities. Storage is provided by a
scoped_ptr, which manages the lifetime of the underlying memory.
In the case of Array, we also provide a few functions such as
Abs, Log and their like; being good citizens, we’re not
overloading the corresponding functions in namespace std
because that’s forbidden by the standard. More complex functionality
(such as matricial square root, or various decompositions) can be
found in separate modules.
In short, a more or less straightforward implementation of arrays and
matrices. The one thing which is not obvious is the presence of the
Disposable class template, which I’ll describe in more detail
in a further section of this appendix; for the time being, let me just
say that it’s a pre-C++11 attempt at move semantics.
The idea was to try and reduce the abstraction penalty. Operator
overloading is very convenient—after all, c = a+b is much
easier to read than understand than add(a,b,c)—but
doesn’t come for free: declaring addition as
Array operator+(const Array& a, const Array& b);
means that the operator must create and return a new Array
instance, that is, must allocate and possibly copy its memory. When
the number of operations increases, so does the overhead.
In the first versions of the library, we tried to mitigate the problem
by using expression templates. The idea (that I will only describe
very roughly, so I suggest you read (Veldhuizen,
2000) for details) is that operators don’t
return an array, but some kind of parse tree holding references to the
terms of the expression; so, for instance, 2*a+b won’t actually
perform any calculation but only create a small structure with the
relevant information. It is only when assigned that the expression is
unfolded; and at that point, the compiler would examine the whole
thing and generate a single loop that both calculates the result and
copies it into the array being assigned.
The technique is still relevant today (possibly even more so, given
the progress in compiler technology) but we abandoned it after a few
years. Not all compilers were able to process it, forcing us to
maintain both expression templates and the simpler implementation, and
it was difficult to read and maintain (compare the current
declaration of operator+ with
VectorialExpression<
BinaryVectorialExpression<
Array::const_iterator, Array::const_iterator, Add> >
operator+(const Array& v1, const Array& v2);
for a taste of what the code was like); therefore, when the C++ community
started talking of move semantics and some ideas for implementations
began to appear, we took the hint and switched to Disposable.
As I said, compilers progressed a lot during these years; nowadays,
I’m guessing that all of them would support an expression-template
implementation, and the technique itself has probably improved.
However, if I were to write the code today (or if I started to change
things) the question might be whether to write classes such as
Array or Matrix at all. At the very least, I’d consider
implementing them in terms of std::valarray, which is supposed
to provide facilities for just such a task. In the end, though, I’d
probably go for some existing library such as uBLAS: it is
available in Boost, it’s written by actual experts in numerical code,
and we already use it in some parts of the library for specialized
calculations.
Global settings
The Settings class, outlined in the listing below, is
a singleton (see later) that holds information
global to the whole library.
Settings class.class Settings : public Singleton<Settings> {
private:
class DateProxy : public ObservableValue<Date> {
DateProxy();
operator Date() const;
...
};
... // more implementation details
public:
DateProxy& evaluationDate();
const DateProxy& evaluationDate() const;
boost::optional<bool>& includeTodaysCashFlows();
boost::optional<bool> includeTodaysCashFlows() const;
...
};
Most of its data are flags that you can look up in the official documentation, or that you can simply live without; the one piece of information that you’ll need to manage is the evaluation date, which defaults to today’s date and is used for the pricing of instruments and the fixing of any other quantity.
This poses a challenge: instruments whose value can depend on the
evaluation date must be notified when the latter changes. This is
done by returning the corresponding information indirectly, namely,
wrapped inside a proxy class; this can be seen from the signature of
the relevant methods. The proxy inherits from the
ObservableValue class template (outlined in
the next listing) which is implicitly convertible to
Observable and overloads the assignment operator in order to
notify any changes. Finally, it allows automatic conversion of the
proxy class to the wrapped value.
ObservableValue class template.template <class T>
class ObservableValue {
public:
// initialization and assignment
ObservableValue(const T& t)
: value(t), observable_(new Observable) {}
ObservableValue<T>& operator=(const T& t) {
value_ = t;
observable_->notifyObservers();
return *this;
}
// implicit conversions
operator T() const { return value_; }
operator shared_ptr<Observable>() const {
return observable_;
}
private:
T value_;
shared_ptr<Observable> observable_;
};
This allows one to use the facility with a natural syntax. On the one hand, it is possible for an observer to register with the evaluation date, as in:
registerWith(Settings::instance().evaluationDate());
on the other hand, it is possible to use the returned value just like
a Date instance, as in:
Date d2 =
calendar.adjust(Settings::instance().evaluationDate());
which triggers an automatic conversion; and on the gripping hand, an assignment can be used for setting the evaluation date, as in:
Settings::instance().evaluationDate() = d;
which will cause all observers to be notified of the date change.
Of course, the elephant in the room is the fact that we have a global
evaluation date at all. The obvious drawback is that one can’t
perform two parallel calculations with two different evaluation dates,
at least in the default library configuration; but while this is true,
it is also not the whole story. On the one hand, there’s a
compilation flag that allows a program to have one distinct
Settings instance per thread (with a bit of work on the part of
the user) but as we’ll see, this doesn’t solve all the issues. On the
other hand, the global data may cause unpleasantness even in a
single-threaded program: even if one wanted to evaluate just an
instrument on a different date, the change will trigger recalculation
for every other instrument in the system when the evaluation date is
set back to its original value.
This clearly points (that is, quite a few smart people had the same idea when we talked about it) to some kind of context class that should replace the global settings. But how would one select a context for any given calculation?
It would be appealing to add a setContext method to the
Instrument class, and to arrange things so that during
calculation the instrument propagates the context to its engine and in
turn to any term structures that need it. However, I don’t think this
can be implemented easily.
First, the instrument and its engine are not always aware of all the term structures that are involved in the calculation. For instance, a swap contains a number of coupons, any of which might or might not reference a forecast curve. We’re not going to reach them unless we add the relevant machinery to all the classes involved. I’m not sure that we want to set a context to a coupon.
Second, and more important, setting the context for an engine would be
a mutating operation. Leaving it to the instrument during
calculations would execute it at some point during the call to its
NPV method, which is supposed to be const. This would
make it way too easy to trigger a race condition; for instance with a
harmless-looking operation such as using the same discount curve for
two instruments and evaluating them at different dates. If you have a
minimum of experience in parallel programming, you wouldn’t dream of, say,
relinking the same handle in two concurrent threads; but when the
mutation is hidden inside a const method, you might not be
aware of it. (But wait, you say. Aren’t there other mutating
operations possibly being done during the call to NPV? Good
catch: see the aside at the end of this section.)
So it seems that we have to set up the context before starting the calculation. This rules out driving the whole thing from the instrument (because, again, we would be hiding the fact that setting a context to an instrument could undo the work done by another that shared a term structure with the first) and suggests that we’d have to set the context explicitly on the several term structures. On the plus side, we no longer run the risk of a race in which we unknowingly try to set the same context to the same object. The drawbacks are that our setup just got more complex, and that we’d have to duplicate curves if we want to use them concurrently in different contexts: two parallel calculations on different dates would mean, for instance, two copies of the overnight curve for discounting. And if we have to do this, we might as well manage with per-thread singletons.
Finally, I’m skipping over the scenario in which the context is passed but not saved. It would lead to method calls like
termStructure->discount(t, context);
which would completely break caching, would cause discomfort to all parties involved, and if we wanted stuff like this we’d write in Haskell.
To summarize: I hate to close the section on a gloomy note, but all is not well. The global settings are a limitation, but I don’t have a solution; and what’s worse, the possible changes increase complexity. We would not only tell first-time users looking for the Black-Scholes formula that they needs term structures, quotes, an instrument and an engine: we’d also put contexts in the mix. A little help here?
Utilities
In QuantLib, there are a number of classes and functions which don’t model a financial concept. They are nuts and bolts, used to build some of the scaffolding for the rest of the library. This section is devoted to some of these facilities.
Smart pointers and handles
The use of run-time polymorphism dictates that many, if not most, objects be allocated on the heap. This raises the problem of memory management—a problem solved in other languages by built-in garbage collection, but left in C++ to the care of the developer.
I will not dwell on the many issues in memory management, especially since they are now mostly a thing of the past. The difficulty of the task (especially in the presence of exceptions) was enough to discourage manual management; therefore, ways were found to automate the process.
The weapons of choice in the C++ community came to be smart pointers:
classes that act like built-in pointers but that can take care of the
survival of the pointed objects while they are still needed and of
their destruction when this is no longer the case. Several
implementations of such classes exist which use different techniques;
we chose the smart pointers from the Boost libraries (most notably
shared_ptr, now included in the ANSI/ISO C++ standard). Don’t
look for boost::shared_ptr in the library, though: the relevant
classes are imported in an internal QuantLib namespace and used, e.g.,
as ext::shared_ptr. This will allow us to switch to the C++11
implementation painlessly when the time comes.
I won’t go into details on shared pointers; you can browse the Boost
site for documentation. Here, I’ll just mention that
their use in QuantLib completely automated memory management. Objects
are dynamically allocated all over the place; however, there is not
one single delete statement in all the tens of thousands of lines of
which the library consists.
Pointers to pointers (if you need a quick refresher, see the aside at the end of the section for their purpose and semantics) were also replaced by smart equivalents. We chose not to just use smart pointers to smart pointers; on the one hand, because having to write
ext::shared_ptr<ext::shared_ptr<YieldTermStructure> >
gets tiresome very quickly—even in Emacs; on the other hand, because
the inner shared_ptr would have to be allocated dynamically,
which just didn’t felt right; and on the gripping hand, because it
would make it difficult to implement observability. Instead, a class
template called Handle was provided for this purpose. Its
implementation, shown in the listing that follows, relies on an
intermediate inner class called Link which stores a smart
pointer. In turn, the Handle class stores a smart pointer to a
Link instance, decorated with methods that make it easier to
use it. Since all copies of a given handle share the same link, they
are all given access to the new pointee when any one of them is linked
to a new object.
Handle class template.template <class Type>
class Handle {
protected:
class Link : public Observable, public Observer {
public:
explicit Link(const shared_ptr<Type>& h =
shared_ptr<Type>());
void linkTo(const shared_ptr<Type>&);
bool empty() const;
void update() { notifyObservers(); }
private:
shared_ptr<Type> h_;
};
shared_ptr<Link<Type> > link_;
public:
explicit Handle(const shared_ptr<Type>& h =
shared_ptr<Type>());
const shared_ptr<Type>& operator->() const;
const shared_ptr<Type>& operator*() const;
bool empty() const;
operator shared_ptr<Observable>() const;
};
template <class Type>
class RelinkableHandle : public Handle<Type> {
public:
explicit RelinkableHandle(const shared_ptr<Type>& h =
shared_ptr<Type>());
void linkTo(const shared_ptr<Type>&);
};
The contained shared_ptr<Link> also gives the handle the means
to be observed by other classes. The Link class is both an
observer and an observable; it receives notifications from its pointee
and forwards them to its own observers, as well as sending its own
notification each time it is made to point to a different
pointee. Handles take advantage of this behavior by defining an
automatic conversion to shared_ptr<Observable> which simply
returns the contained link. Thus, the statement
registerWith(h);
is legal and works as expected; the registered observer will receive notifications from both the link and (indirectly) the pointed object.
You might have noted that the means of relinking a handle (i.e., to
have all its copies point to a different object) were not given to the
Handle class itself, but to a derived RelinkableHandle
class. The rationale for this is to provide control over which handle
can be used for relinking—and especially over which handle can’t.
In the typical use case, a Handle instance will be instantiated
(say, to store a yield curve) and passed to a number of instruments,
pricing engines, or other objects that will store a copy of the handle
and use it when needed. The point is that an object (or client code
getting hold of the handle, if the object exposes it via an inspector)
must not be allowed to relink the handle it stores, whatever the
reason; doing so would affect a number of other object.33
The link should only be changed from the original handle—the main handle, if you like.
Given the frailty of human beings, we wanted this to be enforced by
the compiler. Making the linkTo method a const one and
returning const handles from our inspectors wouldn’t work;
client code could simply make a copy to obtain a non-const
handle. Therefore, we removed linkTo from the Handle
interface and added it to a derived class. The type system works
nicely to our advantage. On the one hand, we can instantiate the
main handle as a RelinkableHandle and pass it to any object
expecting a Handle; automatic conversion from derived to base
class will occur, leaving the object with a sliced but fully
functional handle. On the other hand, when a copy of a Handle
instance is returned from an inspector, there’s no way to downcast it
to RelinkableHandle.
Error reporting
There are a great many places in the library where some condition must be checked. Rather than doing it as
if (i >= v.size())
throw Error("index out of range");
we wanted to express the intent more clearly, i.e., with a syntax like
require(i < v.size(), "index out of range");
where on the one hand, we write the condition to be satisfied and not
its opposite; and on the other hand, terms such as require,
ensure, or assert—which have a somewhat canonical
meaning in programming—would tell whether we’re checking a
precondition, a postcondition, or a programmer error.
We provided the desired syntax with macros. “Get behind thee,” I hear you say. True, macros have a bad name, and in fact they caused us a problem or two, as we’ll see below. But in this case, functions had a big disadvantage: they evaluate all their arguments. Many times, we want to create a moderately complex error message, such as
require(i < v.size(),
"index " + to_string(i) + " out of range");
If require were a function, the message would be built whether
or not the condition is satisfied, causing a performance hit that
would not be acceptable. With a macro, the above is textually
replaced by something like
if (!(i < v.size()))
throw Error("index " + to_string(i) + " out of range");
which builds the message only if the condition is violated.
The next listing shows the current version of one of the
macros, namely, QL_REQUIRE; the other macros are defined in a
similar way.
QL_REQUIRE macro.#define QL_REQUIRE(condition,message) \
if (!(condition)) { \
std::ostringstream _ql_msg_stream; \
_ql_msg_stream << message; \
throw QuantLib::Error(__FILE__,__LINE__, \
BOOST_CURRENT_FUNCTION, \
_ql_msg_stream.str()); \
} else
Its definition has a few more bells and whistles that
might be expected. Firstly, we use an ostringstream to build the
message string. This allows one to use a syntax like
QL_REQUIRE(i < v.size(),
"index " << i << " out of range");
to build the message (you can see how that works by replacing the
pieces in the macro body). Secondly, the Error instance is
passed the name of the current function as well as the line and file
where the error is thrown. Depending on a compilation flag, this
information can be included in the error message to help developers;
the default behavior is to not include it, since it’s of little
utility for users. Lastly, you might be wondering why we added an
else at the end of the macro. That is due to a common macro
pitfall, namely, its lack of a lexical scope. The else is
needed by code such as
if (someCondition())
QL_REQUIRE(i < v.size(), "index out of bounds");
else
doSomethingElse();
Without the else in the macro, the above would not work as
expected. Instead, the else in the code would pair with
the if in the macro and the code would translate into
if (someCondition()) {
if (!(i < v.size()))
throw Error("index out of bounds");
else
doSomethingElse();
}
which has a different behavior.
As a final note, I have to describe a disadvantage of these macros. As they are now, they throw exceptions that can only return their contained message; no inspector is defined for any other relevant data. For instance, although an out-of-bounds message might include the passed index, no other method in the exception returns the index as an integer. Therefore, the information can be displayed to the user but would be unavailable to recovery code in catch clauses—unless one parses the message, that is; but that is hardly worth the effort. There’s no planned solution at this time, so drop us a line if you have one.
Disposable objects
The Disposable class template was an attempt to implement move
semantics in C++03 code. To give credit where it’s due, we took the
idea and technique from an article by Andrei Alexandrescu
(Alexandrescu, 2003) in which he described how
to avoid copies when returning temporaries.
The basic idea is the one that was starting to float around in those
years and that was given its final form in C++11: when passing a
temporary object, copying it into another one is often less efficient
than swapping its contents with those of the target. You want to move
a temporary vector? Copy into the new object the pointer to its
storage, instead of allocating a new one and copying the elements. In
modern C++, the language itself supports move semantics with the
concept of rvalue reference (Hinnant et al, 2006); the
compiler knows when it’s dealing with a temporary, and we can use
std::move in the few cases when we want to turn an object into one.
In our implementation, shown in the following listing, we don’t
have such support; you’ll see the consequences of this in a minute.
Disposable class template.template <class T>
class Disposable : public T {
public:
Disposable(T& t) {
this->swap(t);
}
Disposable(const Disposable<T>& t) : T() {
this->swap(const_cast<Disposable<T>&>(t));
}
Disposable<T>& operator=(const Disposable<T>& t) {
this->swap(const_cast<Disposable<T>&>(t));
return *this;
}
};
The class itself is not much to look at. It relies on the template
argument implementing a swap method; this is where any resource
contained inside the class are swapped (hopefully in a cheap way)
instead of copied. The constructors and the assignment operator all
use this to move stuff around without copies—with a difference,
depending on what is passed. When building a Disposable from
another one, we take it by const reference because we want the
argument to bind to temporaries; that’s what most disposables will be.
This forces us to use a const_cast in the body, when it’s time
to call swap and take the resources from the disposable. When
building a Disposable from a non-disposable object, instead, we
take is as a non-const reference; this is to prevent ourselves
from triggering unwanted destructive conversions and from finding
ourselves with the empty husk of an object when we thought to have a
usable one. This, however, has a disadvantage; I’ll get to it in a
minute.
The next listing shows how to retrofit Disposable to a
class; Array, in this case.
Disposable class template in the Array class.Array::Array(const Disposable<Array>& from)
: data_((Real*)(0)), n_(0) {
swap(const_cast<Disposable<Array>&>(from));
}
Array& Array::operator=(const Disposable<Array>& from) {
swap(const_cast<Disposable<Array>&>(from));
return *this;
}
void Array::swap(Array& from) {
data_.swap(from.data_);
std::swap(n_,from.n_);
}
As you see, we need to add a
constructor and an assignment operator taking a Disposable (in
C++11, they would be a move constructor and a move assignment
operators taking an rvalue reference) as well as the swap
method that will be used in all of them. Again, the constructors take
the Disposable by const reference and cast it later, in
order to bind to temporaries—although now that I think of it, they
could take it by copy, adding another cheap swap.
Finally, the way Disposable is used is by returning it from
function, like in the following code:
Disposable<Array> ones(Size n) {
Array result(n, 1.0);
return result;
}
Array a = ones(10);
Returning the array causes it to be converted to Disposable,
and assigning the returned object causes its contents to be swapped
into a.
Now, you might remember that I talked about a disadvantage when I
showed you the Disposable constructor being safe and taking an
object by non-const reference. It’s that it can’t bind to temporaries; therefore, the function above can’t be written more simply as:
Disposable<Array> ones(Size n) {
return Array(n, 1.0);
}
because that wouldn’t compile. This forces us to take the more verbose route and give the array a name.34
Nowadays, of course, we’d use rvalue references and move constructors
and forget all about the above. To tell the truth, I’ve a nagging
suspicion that Disposable might be getting in the way of the
compiler and doing more harm than good. Do you know the best way to
write code like the above and avoid abstraction penalty in modern
C++? It’s this one:
Array ones(Size n) {
return Array(n, 1.0);
}
Array a = ones(10);
In C++17, the copies that might have been done when returning the
array and when assigning it are guaranteed to be elided (that is, the
compiler will generate code that builds the returned array directly
inside the one we’re assigning); most recent compilers have been doing
that for a while, without waiting for the standard to bind them. It’s
called RVO, for Return Value Optimization, and using
Disposable prevents it and thus might make the code slower
instead of faster.
Design patterns
A few design patterns were implemented in QuantLib. You can refer to the Gang of Four book (Gamma et al, 1995) for a description of such patterns; so why do I write about them? Well, as once noted by G. K. Chesterton,
[p]oets have been mysteriously silent on the subject of cheese
and the Gang was just as silent on a number of issues that come up when you write actual implementations—through no fault of them, mind you. The variations are almost limitless, and they were only four.
Thus, I will use this final section to point out a few ways in which our implementations were tailored to the requirements of the library.
The Observer pattern
The use of the Observer pattern in the QuantLib library is widespread; you’ve seen it used in chapter 2 and chapter 3 to let financial instruments and term structures keep track of changes and recalculate when needed.
Our version of the pattern (sketched in the next listing) is close enough to that described in the Gang of Four book; but as I mentioned, there are questions and problems that weren’t discussed there.
Observable and Observer classes.class Observable {
friend class Observer;
public:
void notifyObservers() {
for (iterator i=observers_.begin();
i!=observers_.end(); ++i) {
try {
(*i)->update();
} catch (std::exception& e) {
// store information for later
}
}
}
private:
void registerObserver(Observer* o) {
observers_.insert(o);
}
void unregisterObserver(Observer*);
list<Observer*> observers_;
};
class Observer {
public:
virtual ~Observer() {
for (iterator i=observables_.begin();
i!=observables_.end(); ++i)
(*i)->unregisterObserver(this);
}
void registerWith(const shared_ptr<Observable>& o) {
o->registerObserver(this);
observables_.insert(o);
}
void unregisterWith(const shared_ptr<Observable>&);
virtual void update() = 0;
private:
list<shared_ptr<Observable> > observables_;
};
For instance: what information should we include in the notification?
In our implementation, we went for minimalism—all that an observer
gets to know is that something changed. It would have been possible to
provide more information (e.g., by having the update method
take the notifying observable as an argument) so that observers could
select what to recalculate and save a few cycles; but I don’t think
that this feature was worth the added complexity.
Another question: what happens if an observer raises an exception from
its update method? This would happen when an observable is
sending a notification, i.e., while the observable is iterating over
its observers, calling update on each one. If the exception
were to propagate, the loop would be aborted and a number of observers
would not receive the notification—bad. Our solution was to catch
any such exception, complete the loop, and raise an exception at the
end if anything went wrong. This causes the original exceptions to be
lost, which is not good either; however, we felt this to be the lesser
of the two evils.
Onwards to the third issue: that is, copy behavior. It is not very clear what should happen when an observer or an observable are copied. Currently, what seemed a sensible choice is implemented: on the one hand, copying an observable results in the copy not having any observer; on the other hand, copying an observer results in the copy being registered with the same observables as the original. However, other behaviors might be considered; as a matter of fact, the right choice might be to inhibit copying altogether.
The big problems, however, were two. First: we obviously had to make sure that the lifetimes of the observer and observables were managed properly, meaning that no notification should be sent to an already deleted object. To do so, we had observers store shared pointers to their observables, which ensures that no observable is deleted before an observer is done with it. The observers will unregister with any observable before being deleted, which in turn makes it safe for observables to store a list of raw pointers to their observers.
This, however, is only guaranteed to work in a single-threaded setting; and we are exporting QuantLib bindings to C# and Java, where unfortunately there is always another thread where the garbage collector is busy deleting stuff. Every once in a while, this caused random crashes as a notification was sent to a half-deleted object. Once the problem was understood, it was fixed (hi, Klaus); however, the fix slows down the code, so it’s inactive by default and can be enabled by a compilation switch. Use it if you need the C# or Java bindings.
The second big problem is35 that, like in the Jerry Lee Lewis’
song, there’s a whole lotta notifyin’ going on. A change of date can
easily trigger tens or hundreds of notifications; and even if most of
the update methods only set a flag and forward the call, the time
adds up.
People using QuantLib in applications where calculation time is
paramount, such as CVA/XVA (hi, Peter) have worked
around the problem by disabling notifications and recalculating
explicitly. A step towards reducing notification time would be to
remove the middlemen, and shorten the chains of notifications;
however, this is not possible due to the ubiquitous presence of the
Handle class in the chains. Handles can be relinked, and thus
chains of dependencies can change even after objects are built.
In short, the problem is still not solved. You know where to find us if you have any bright ideas.
The Singleton pattern
The Gang of Four devoted the first part of their book to creational patterns. While logically sound, this choice turned out to have an unfortunate side effect: all too often, overzealous programmers would start to read the book and duly proceed to sprinkle their code with abstract factories and singletons. Needless to say, this does less than intended for the clarity of the code.
You might suspect the same reason for the presence of a
Singleton class template in QuantLib. (Quite maliciously, I
might add. Shame on you.) Fortunately, we can base our defense on
version-control logs; such class was added to the library later than,
say, Observer (a behavioral pattern) or Composite (a structural one).
Our default implementation is shown in the following listing.
Singleton class template.template <class T>
class Singleton : private noncopyable {
public:
static T& instance();
protected:
Singleton();
};
#if defined(QL_ENABLE_SESSIONS)
// the definition must be provided by the user
Integer sessionId();
#endif
template <class T>
T& Singleton<T>::instance() {
static map<Integer, shared_ptr<T> > instances_;
#if defined(QL_ENABLE_SESSIONS)
Integer id = sessionId();
#else
Integer id = 0;
#endif
shared_ptr<T>& instance = instances_[id];
if (!instance)
instance = shared_ptr<T>(new T);
return *instance;
}
It’s based on the Curiously Recurring Template Pattern, that I
described in chapter 7; to be a singleton, a class C
needs to inherit from Singleton<C>, to provide a private constructor
taking on arguments, and to make Singleton<C> a friend so that it
can use it. You can see an example in the Settings
class.
As suggested by Scott Meyers (Meyers, 2005), the map
holding the instances (bear with me) is defined as a static variable
inside the instance method. This prevents the so-called static
initialization order fiasco, in which the variable is used before
being defined, and in C++11 it has the additional guarantee that the
initialization is thread-safe (even though that’s not the whole story,
as we’ll see).
Now, you might have a few questions; e.g., why a map of instances if
this is supposed to be a singleton? Well, that’s because having a
single instance might be limiting; for instance—no pun
intended—you might want to perform simultaneous calculations on
different evaluation dates. Thus, we tried to mitigate the problem by
allowing one Singleton instance per thread. This is enabled by
a compilation flag, and causes the instance method to use the
#if branch in which it gets an id from a sessionId
function and uses it to index into the map. If you enable per-thread
singletons, you must also provide the latter function; it will
probably be something like
Integer sessionId() {
return /* `some unique thread id from your system API` */ ;
}
in which you will identify the thread using the functions made
available by your operating system (or some threading library), turn
the identifier into a unique integer, and return it. In turn, this
will cause the instance method to return a unique instance per each
thread. If you don’t enable the feature, instead, the id will always
ever be 0 and you’ll always get the same instance. In this case,
you probably don’t want to use threads at all—and in the other case,
you obviously do, but you have to be careful anyway: see the
discussion in the section on global settings.
You might also be asking yourself why I said that this is our
default implementation. Nice catch. There are others, which I
won’t show here and which are enabled by a number of compilation
flags. On the one hand, it turned out that the static-variable
implementation didn’t work when compiled as managed C++ code under
.NET (at least with older Visual Studio compilers), so in
that case we switch it with one in which the map is a static class
variable. On the other hand, if you want to use a global
Singleton instance in a multi-threaded setting, you want to
make sure that the initialization of the Singleton instance is
thread-safe (I’m talking about the instance itself, not the map
containing it; it’s where the new T is executed). This
requires locks, mutexes and stuff, and we don’t want to go near any of
that in the default single-threaded setting; therefore, that code is
behind yet another compilation flag. You can look at it in the
library, if you’re interested.
Your last question might be whether we should have a Singleton class
at all—and it’s a tough one. Again, I refer you to the previous
discussion of global settings. At this time, much like democracy
according to Winston Churchill, it seems to be the worst solution
except for all the others.
The Visitor pattern
Our implementation, shown in the next listing, follows the
Acyclic Visitor pattern (Martin, 1997) rather than
the one in the Gang of Four book: we defined a degenerate
AcyclicVisitor class, to be used in the interfaces, and a class
template Visitor which defines the pure virtual visit method for
its template argument.
AcyclicVisitor class and of the Visitor class template.class AcyclicVisitor {
public:
virtual ~AcyclicVisitor() {}
};
template <class T>
class Visitor {
public:
virtual ~Visitor() {}
virtual void visit(T&) = 0;
};
The pattern also needs support from any class hierarchy that we want to be visitable; an example is shown in the listing that follows.
void Event::accept(AcyclicVisitor& v) {
Visitor<Event>* v1 = dynamic_cast<Visitor<Event>*>(&v);
if (v1 != 0)
v1->visit(*this);
else
QL_FAIL("not an event visitor");
}
void CashFlow::accept(AcyclicVisitor& v) {
Visitor<CashFlow>* v1 =
dynamic_cast<Visitor<CashFlow>*>(&v);
if (v1 != 0)
v1->visit(*this);
else
Event::accept(v);
}
void Coupon::accept(AcyclicVisitor& v) {
Visitor<Coupon>* v1 = dynamic_cast<Visitor<Coupon>*>(&v);
if (v1 != 0)
v1->visit(*this);
else
CashFlow::accept(v);
}
Each of the classes in the hierarchy (or at least, those that we want
to be specifically visitable) need to define an accept method
that takes a reference to AcyclicVisitor. Each of the methods
tries to cast the passed visitor to the specific Visitor
instantiation for the corresponding class. A successful cast means
that the visitor defines a visit method taking this specific
class, so we invoke it. A failed cast means that we have to look for
an fallback. If the class is not the root of the hierarchy (like
CashFlow or Coupon in the listing) we can call the
base-class implementation of accept, which in turn will try the
cast. If we’re at the root, like the Event class, we have no
further fallback and we raise an exception.36
Finally, a visitor is implemented as the BPSCalculator class in
chapter 4. It inherits from
AcyclicVisitor, so that it can be passed to the various accept
methods, as well as from an instantiation of the Visitor template
for each class for which it will provide a visit method. It will be
passed to the accept method of some instance, which will eventually
call one of the visit methods or raise an exception.
I already discussed the usefulness of the Visitor pattern in chapter 4, so I refer you to it (the unsurprising summary: it depends). Therefore, I will only spend a couple of words on why we chose Acyclic Visitor.
In short, the Gang-of-Four version of Visitor might be a bit faster,
but it’s a lot more intrusive; in particular, every time you add a new
class to the visitable hierarchy you’re also forced to go and add the
corresponding visit method to each existing visitor (where by
“forced” I mean that your code wouldn’t compile if you didn’t). With
Acyclic Visitor, you don’t need to do it; the accept method in your
new class will fail the cast and fallback to its base class.37
Mind you, this is convenient but not necessarily a good thing (like a
lot of things in life, I might add): you should review existing
visitors anyway, check whether the fallback implementation makes sense
for your class, and add a specific one if it doesn’t. But I think
that the disadvantage of not having the compiler warn you is more than
balanced by the advantage of not having to write a visit method for
each cash-flow class when, as in BPSCalculator, a couple will
suffice.
B. Code conventions
Every programmer team has a number of conventions to be used while writing code. Whatever the conventions (several exist, which provides a convenient casus belli for countless wars) adhering to them helps all developers working on the same project,38 as they make it easier to understand the code; a reader familiar with their use can distinguish at a glance between a macro and a function, or between a variable and a type name.
The following listing briefly illustrates the conventions used throughout the QuantLib library. Following the advice in Sutter and Alexandrescu, 2004, we tried to reduce their number at a minimum, enforcing only those conventions which enhance readability.
#define SOME_MACRO
typedef double SomeType;
class SomeClass {
public:
typedef Real* iterator;
typedef const Real* const_iterator;
};
class AnotherClass {
public:
void method();
Real anotherMethod(Real x, Real y) const;
Real member() const; // getter, no "get"
void setMember(Real); // setter
private:
Real member_;
Integer anotherMember_;
};
struct SomeStruct {
Real foo;
Integer bar;
};
Size someFunction(Real parameter,
Real anotherParameter) {
Real localVariable = 0.0;
if (condition) {
localVariable += 3.14159;
} else {
localVariable -= 2.71828;
}
return 42;
}
Macros are in all uppercase, with words separated by underscores. Type
names start with a capital and are in the so-called camel case; words
are joined together and the first letter of each word is
capitalized. This applies to both type declarations such as
SomeType and class names such as SomeClass and
AnotherClass. However, an exception is made for type
declarations that mimic those found in the C++ standard library;
this can be seen in the declaration of the two iterator types in
SomeClass. The same exception might be made for inner classes.
About everything else (variables, function and method names, and
parameters) are in camel case and start with a lowercase
character. Data members of a class follow the same convention, but are
given a trailing underscore; this makes it easier to distinguish them
from local variables in the body of a method (an exception is often
made for public data members, especially in structs or struct-like
classes). Among methods, a further convention is used for getters and
setters. Setter names are created by adding a leading set to
the member name and removing the trailing underscore. Getter names
equal the name of the returned data member without the trailing
underscore; no leading get is added. These conventions are
exemplified in AnotherClass and SomeStruct.
A much less strict convention is that the opening brace after a
function declaration or after an if, else, for,
while, or do keyword are on the same line as the
preceding declaration or keyword; this is shown in
someFunction. Moreover, else keywords are on the same
line as the preceding closing brace; the same applies to the
while ending a do statement. However, this is more a
matter of taste than of readability; therefore, developers are free to
use their own conventions if they cannot stand this one. The shown
function exemplifies another convention aimed at improving
readability, namely, that function and method arguments should be
aligned vertically if they do not fit a single line.
QuantLib license
QuantLib is
- © 2000, 2001, 2002, 2003 RiskMap srl
- © 2001, 2002, 2003 Nicolas Di Césaré
- © 2001, 2002, 2003 Sadruddin Rejeb
- © 2002, 2003, 2004 Decillion Pty(Ltd)
- © 2002, 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2014, 2015 Ferdinando Ametrano
- © 2003, 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2014, 2016, 2017, 2018, 2019 StatPro Italia srl
- © 2003, 2004, 2007 Neil Firth
- © 2003, 2004 Roman Gitlin
- © 2003 Niels Elken Sønderby
- © 2003 Kawanishi Tomoya
- © 2004 FIMAT Group
- © 2004 M-Dimension Consulting Inc.
- © 2004 Mike Parker
- © 2004 Walter Penschke
- © 2004 Gianni Piolanti
- © 2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019 Klaus Spanderen
- © 2004 Jeff Yu
- © 2005, 2006, 2008 Toyin Akin
- © 2005 Sercan Atalik
- © 2005, 2006 Theo Boafo
- © 2005, 2006, 2007, 2009 Piter Dias
- © 2005, 2013 Gary Kennedy
- © 2005, 2006, 2007 Joseph Wang
- © 2005 Charles Whitmore
- © 2006, 2007 Banca Profilo S.p.A.
- © 2006, 2007 Marco Bianchetti
- © 2006 Yiping Chen
- © 2006 Warren Chou
- © 2006, 2007 Cristina Duminuco
- © 2006, 2007 Giorgio Facchinetti
- © 2006, 2007 Chiara Fornarola
- © 2006 Silvia Frasson
- © 2006 Richard Gould
- © 2006, 2007, 2008, 2009, 2010 Mark Joshi
- © 2006, 2007, 2008 Allen Kuo
- © 2006, 2007, 2008, 2009, 2012 Roland Lichters
- © 2006, 2007 Katiuscia Manzoni
- © 2006, 2007 Mario Pucci
- © 2006, 2007 François du Vignaud
- © 2007 Affine Group Limited
- © 2007 Richard Gomes
- © 2007, 2008 Laurent Hoffmann
- © 2007, 2008, 2009, 2010, 2011 Chris Kenyon
- © 2007 Gang Liang
- © 2008, 2009, 2014, 2015, 2016 Jose Aparicio
- © 2008 Yee Man Chan
- © 2008, 2011 Charles Chongseok Hyun
- © 2008 Piero Del Boca
- © 2008 Paul Farrington
- © 2008 Lorella Fatone
- © 2008, 2009 Andreas Gaida
- © 2008 Marek Glowacki
- © 2008 Florent Grenier
- © 2008 Frank Hövermann
- © 2008 Simon Ibbotson
- © 2008 John Maiden
- © 2008 Francesca Mariani
- © 2008, 2009, 2010, 2011, 2012, 2014 Master IMAFA - Polytech’Nice Sophia - Université de Nice Sophia Antipolis
- © 2008, 2009 Andrea Odetti
- © 2008 J. Erik Radmall
- © 2008 Maria Cristina Recchioni
- © 2008, 2009, 2012, 2014 Ralph Schreyer
- © 2008 Roland Stamm
- © 2008 Francesco Zirilli
- © 2009 Nathan Abbott
- © 2009 Sylvain Bertrand
- © 2009 Frédéric Degraeve
- © 2009 Dirk Eddelbuettel
- © 2009 Bernd Engelmann
- © 2009, 2010, 2012 Liquidnet Holdings, Inc.
- © 2009 Bojan Nikolic
- © 2009, 2010 Dimitri Reiswich
- © 2009 Sun Xiuxin
- © 2010 Kakhkhor Abdijalilov
- © 2010 Hachemi Benyahia
- © 2010 Manas Bhatt
- © 2010 DeriveXperts SAS
- © 2010, 2014 Cavit Hafizoglu
- © 2010 Michael Heckl
- © 2010 Slava Mazur
- © 2010, 2011, 2012, 2013 Andre Miemiec
- © 2010 Adrian O’ Neill
- © 2010 Robert Philipp
- © 2010 Alessandro Roveda
- © 2010 SunTrust Bank
- © 2011, 2013, 2014 Fabien Le Floc’h
- © 2012, 2013 Grzegorz Andruszkiewicz
- © 2012, 2013, 2014, 2015, 2016, 2017, 2018 Peter Caspers
- © 2012 Mateusz Kapturski
- © 2012 Simon Shakeshaft
- © 2012 Édouard Tallent
- © 2012 Samuel Tebege
- © 2013 BGC Partners L.P.
- © 2013, 2014 Cheng Li
- © 2013 Yue Tian
- © 2014, 2017 Francois Botha
- © 2014, 2015 Johannes Goettker-Schnetmann
- © 2014 Michal Kaut
- © 2014, 2015 Bernd Lewerenz
- © 2014, 2015, 2016 Paolo Mazzocchi
- © 2014, 2015 Thema Consulting SA
- © 2014, 2015, 2016 Michael von den Driesch
- © 2015 Riccardo Barone
- © 2015 CompatibL
- © 2015, 2016 Andres Hernandez
- © 2015 Dmitri Nesteruk
- © 2015 Maddalena Zanzi
- © 2016 Nicholas Bertocchi
- © 2016 Stefano Fondi
- © 2016, 2017 Fabrice Lecuyer
- © 2016, 2019 Eisuke Tani
- © 2017 BN Algorithms Ltd
- © 2017 Paul Giltinan
- © 2017 Werner Kuerzinger
- © 2017 Oleg Kulkov
- © 2017 Joseph Jeisman
- © 2018 Tom Anderson
- © 2018 Alexey Indiryakov
- © 2018 Jose Garcia
- © 2018 Matthias Groncki
- © 2018 Matthias Lungwitz
- © 2018 Sebastian Schlenkrich
- © 2018 Roy Zywina
- © 2019 Aprexo Limited
- © 2019 Wojciech Slusarski
QuantLib includes code taken from Peter Jäckel’s book “Monte Carlo Methods in Finance”.
QuantLib includes software developed by the University of Chicago, as Operator of Argonne National Laboratory.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
- Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
- Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
- Neither the names of the copyright holders nor the names of the QuantLib Group and its contributors may be used to endorse or promote products derived from this software without specific prior written permission.
This software is provided by the copyright holders and contributors “as is” and any express or implied warranties, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose are disclaimed. In no event shall the copyright holders or contributors be liable for any direct, indirect, incidental, special, exemplary, or consequential damages (including, but not limited to, procurement of substitute goods or services; loss of use, data, or profits; or business interruption) however caused and on any theory of liability, whether in contract, strict liability, or tort (including negligence or otherwise) arising in any way out of the use of this software, even if advised of the possibility of such damage.
Bibliography
D. Abrahams, Want Speed? Pass by Value. In C++ Next, 2009.
D. Adams, So Long, and Thanks for all the Fish. 1984.
A. Alexandrescu, Move Constructors. In C/C++ Users Journal, February 2003.
F. Ametrano and M. Bianchetti, Everything You Always Wanted to Know About Multiple Interest Rate Curve Bootstrapping but Were Afraid to Ask. SSRN working papers series n.2219548, 2013.
J. Barton and L.R. Nackman, Dimensional Analysis. In C++ Report, January 1995.
T. Becker, On the Tension Between Object-Oriented and Generic Programming in C++. 2007.
Boost C++ libraries. http://boost.org.
M. K. Bowen and R. Smith, Derivative formulae and errors for non-uniformly spaced points. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, volume 461, pages 1975–1997. The Royal Society, 2005.
D. Brigo and F. Mercurio, Interest Rate Models –— Theory and Practice, 2nd edition. Springer, 2006.
Mel Brooks (director), Young Frankenstein. Twentieth Century Fox, 1974.
W.E. Brown, Toward Opaque Typedefs for C++1Y, v2. C++ Standards Committee Paper N3741, 2013.
L. Carroll, The Hunting of the Snark. 1876.
G.K. Chesterton, Alarms and Discursions. 1910.
M.P. Cline, G. Lomow and M. Girou, C++ FAQs, 2nd edition. Addison-Wesley, 1998.
J.O. Coplien, A Curiously Recurring Template Pattern. In S.B. Lippman, editor, C++ Gems. Cambridge University Press, 1996.
C.S.L. de Graaf. Finite Difference Methods in Derivatives Pricing under Stochastic Volatility Models. Master’s thesis, Mathematisch Instituut, Universiteit Leiden, 2012.
C. Dickens, Great Expectations. 1860.
P. Dimov, H.E. Hinnant and D. Abrahams, The Forwarding Problem: Arguments. C++ Standards Committee Paper N1385, 2002.
M. Dindal (director), The Emperor’s New Groove. Walt Disney Pictures, 2000.
D.J. Duffy, Finite Difference Methods in Financial Engineering: A Partial Differential Equation Approach. John Wiley and Sons, 2006.
M. Fowler, UML Distilled: A Brief Guide to the Standard Object Modeling Language, 3rd edition. Addison-Wesley, 2003.
M. Fowler, Fluent Interface. 2005.
M. Fowler, K. Beck, J. Brant, W. Opdyke and D. Roberts, Refactoring: Improving the Design of Existing Code. Addison-Wesley, 1999.
E. Gamma, R. Helm, R. Johnson and J. Vlissides, Design Patterns: Element of Reusable Object-Oriented Software. Addison-Wesley, 1995.
P. Glasserman, Monte Carlo Methods in Financial Engineering. Springer, 2003.
D. Gregor, A Brief Introduction to Variadic Templates. C++ Standards Committee Paper N2087, 2006.
H.E. Hinnant, B. Stroustrup and B. Kozicki, A Brief Introduction to Rvalue References. C++ Standards Committee Paper N2027, 2006.
A. Hunt and D. Thomas, The Pragmatic Programmer: From Journeyman to Master. Addison-Wesley, 1999.
International Standards Organization, Programming Languages — C++. International Standard ISO/IEC 14882:2014.
International Swaps and Derivatives Associations, Financial products Markup Language.
P. Jäckel, Monte Carlo Methods in Finance. John Wiley and Sons, 2002.
J. Kerievsky, Refactoring to Patterns. Addison-Wesley, 2004.
R. Kleiser (director), Grease. Paramount Pictures, 1978.
H.P. Lovecraft, The Call of Cthulhu. 1928.
R.C. Martin, Acyclic Visitor. In Pattern Languages of Program Design 3. Addison-Wesley, 1997.
S. Meyers, Effective C++, 3rd edition. Addison-Wesley, 2005.
N.C. Myers, Traits: a new and useful template technique. In The C++ Report, June 1995.
G. Orwell, Animal Farm. 1945.
W.H. Press, S.A. Teukolsky, W.T. Vetterling and B.P. Flannery, Numerical Recipes in C, 2nd edition. Cambridge University Press, 1992.
QuantLib. http://quantlib.org.
E. Queen, The Roman Hat Mystery. 1929.
V. Simonis and R. Weiss, Exploring Template Template Parameters. In Perspectives of System Informatics, number 2244 in Lecture Notes in Computer Science. Springer Berlin / Heidelberg, 2001.
B. Stroustrup, The C++ Programming Language, 4th edition. Addison-Wesley, 2013.
H. Sutter, You don’t know const and mutable. In Sutter’s Mill, 2013.
H. Sutter and A. Alexandrescu, C++ Coding Standards. Addison-Wesley, 2004.
T. Veldhuizen, Techniques for Scientific C++. Indiana University Computer Science Technical Report TR542, 2000.
H.G. Wells, The Shape of Things to Come. 1933.
P.G. Wodehouse, My Man Jeeves. 1919.
Notes
1A few gentle users happened to refer to our library as “the QuantLib.” As much as I like the expression, modesty and habit have so far prevented me from using it.↩
2In this case, of course, it would be “How we did it.”↩
3A more thorough exposition of this point can be found in Kerievsky, 2004.↩
4Even fancy new C++11 stuff like variadic templates won’t help.↩
5This does not excuse you from reading the Gang of Four book.↩
6Most likely, such objects ultimately depend on Quote
instances, e.g., a yield term structure might depend on the quoted
deposit and swap rates used for bootstrapping.↩
7The Instrument class also defines an errorEstimate_
member, which is omitted here for clarity of exposition. The
discussion of NPV_ applies to both.↩
8The implementation shown in this section is somewhat outdated. However, I’m still using it here since it provides a simpler example.↩
9If you happen to feel slightly cheated, consider that the point of this example is to show how to package calculations into a class—not to show how to implement the calculations. Your curiosity will be satisfied in a later chapter devoted to cash flows and related functions.↩
10NaN might be a better choice, but the means of
detecting it are not portable. Another possibility still to be
investigated would be to use boost::optional.↩
11Beside being conceptually clearer, this would prove useful to external functions implementing serialization and deserialization of the instrument—for instance, to and from the FpML format.↩
12The Instrument::results class also contains a
std::map where pricing engines can store additional results. The
relevant code is here omitted for clarity.↩
13dynamic_pointer_cast is
the equivalent of dynamic_cast for shared pointers.↩
14You can find the full code of the engine in the QuantLib sources.↩
15No, it’s not a mistake. It is an inaccurately-named trilogy of five books. It’s a long story.↩
16Nor automatic, nor hydromatic. That would be the Grease Lightning.↩
17For instance, a simple expression like Time t = 2.0;
wouldn’t compile. You’d also have to write f(Time(1.5)) instead
of just f(1.5), even if f wasn’t overloaded.↩
18I won’t explain it here, but go read it. It’s almost insanely cool.↩
19The same technique is used in a number of other classes,
such as DayCounter in the next section or Parameter from
chapter 5.↩
20Well, we could use heuristics, but it could get ugly fast.↩
21The choice to return the latest increment is kind of unusual; the idiomatic choice in C and C++ would be to return the old value.↩
22There are different views on safety among the core developers, ranging from “babysit the user and don’t let him hurt himself” to “give him his part of the inheritance, pat him on his back, and send him to find his place in the world.”↩
23Both support pattern matching on an object, which is like a
neater switch on steroids. Go have a look when you have some
time.↩
24Note that by “instances of the same index” I mean here
instances of the same specific index, not of the same class (which
might group different indexes); for instance, USDLibor(3*Months)
and USDLibor(6*Months) are not instances of the same index;
two different USDLibor(3*Months) are.↩
25If you’re not familiar with the darker corners of C++: when the constructor of a base class is executed, any data members defined in derived classes are not yet built. Since any behavior specific to the derived class is likely to depend on such yet-not-existing data, C++ bails out and uses the base-class implementation of any virtual method called in the base-class constructor body.↩
26Lovers of encapsulation will probably prefer the version taking an index to the one returning a vector, since the latter reveals more than necessary about the internal storage of the class.↩
27This also constrains how we model payoffs based on multiple fixings of an underlying; for instance, Asian options are passed the payoff for a plain option and the average of the fixings is done externally, before passing it to the payoff. One might want the whole process to be described as “the payoff”.↩
28The presence of the primitive and derivative methods
is a bit of implementation leak. They were required by
interpolated interest-rate curves in order to pass from zero rates
to forwards and back.↩
29This also goes for a few multi-dimensional optimizers. In that case, apart from the obvious copyright issues, we also rewrote them in order to use idiomatic C++ and start indexing arrays from 0.↩
30Although you might be a bit surprised that it
doesn’t declare operator() instead.↩
31Some of them declare those data members as
mutable, suggesting the methods might have been
const in the past. As I write this, I haven’t investigated
this further.↩
32It always bothered me that a*b returns the element-wise
product and not the dot product, but I seem to be alone among
programmers.↩
33This is not as far-fetched as it might seem; we’ve been bitten by it.↩
34Well, it doesn’t actually force us, but writing
return Disposable<Array>(Array(n, 10)) is even uglier than the
alternative.↩
35Notice that I didn’t say was.↩
36Another alternative would be to do nothing, but we preferred not to fail silently.↩
37In fact, you’re not even required to define an accept
method; you could just inherit it. However, this would prevent
visitors to target this specific class.↩
38However, the QuantLib developers are human. As such, they sometimes fail to follow the rules I am describing.↩
