Sumário
- Dedicatória
- Capa
- Prefácio
- Introdução
- R - uma linguagem para análise de dados e gráficos
- A importância da Estatística na Medicina
- Breve História do R
- Instalação do R e do RStudio
- RStudio - primeiros passos
- Variáveis no R
- Tipos de Dados
- Funções no R
- Pacotes do R
- Data Frames
- Lendo Dados
- RStudio Projects
- Estatística Descritiva no R
- Manipulando dados no R
-
Visualizando dados - Gráficos básicos do R
- Introdução
- Parte 1 - Visualizando dados categóricos.
- Gráficos de Pizza - picharts
- Parte 2 - Visualizando dados numéricos
- Histogramas
- Gráficos de densidade
- Boxplots
- Parte 3 - Visualizando relações entre variáveis
- Correlação entre uma variável numérica e uma variável categórica
- Correlação entre duas variáveis numéricas
- Correlação
- Modelos Científicos
-
Distribuições de probabilidade
- Introdução
- A Distribuição uniforme e um jogo de dados
- A distribuição normal
- A curva normal padrão
- A normalização e os z-scores.
- Calculando as probabilidades - parte 1: pnorm(x)
- Os parâmetros da curva normal - média e desvio padrão
- Calculando as probabilidades - parte 2: pnorm(x, mean= , sd= )
- Calculando probabilidades parte 3 - a função qnorm()
- Simulando uma distribuição normal
- Verificando a normalidade.
- População e amostra
- Distribuição nula
- Teste de Hipóteses
- p-values
- Notes
Dedicatória
À minha esposa Esther
E aos meus filhos Gustavo e Leo
Capa
Photo “Flat Lay Black Coffee” by Ronaldo Arthur Vidal, Published on February 18, 2016 on Unsplash
Prefácio
Introdução
Esse manual foi desenvolvido para ser usado em cursos introdutórios de estatística e análise de dados na área de saúde.
Faz parte de um projeto de incentivo à utilização da linguagem R e do ambiente RStudio como ferramentas nas aulas de estatística em cursos das áreas de saúde, tendo sido desenvolvido com o propósito de auxiliar o aprendizado e o uso desses softwares por estudantes sem nenhuma formação em ciência da computação ou linguagens de programação.
Não se pretende fazer uma imersão profunda na linguagem R e de todas suas potencialidade, pelo contrário, o que esse manual almeja é fazer uma introdução à linguagem R de forma simples e, na medida do possível, agradável, sem sobrecarregar o estudante.
Também não se pretende aqui discutir ou analisar fórmulas estatísticas, mas sim desenvolver os conceitos básicos da análise descritiva e inferencial com o uso da linguagem R.
Esse é um trabalho em construção, ainda em um estágio inicial, sugestões e correções são muito bem vindas.
R - uma linguagem para análise de dados e gráficos
Aprender uma linguagem computacional de estatística pode parecer inicialmente assustador para alunos de graduação da área da saúde. Entretanto, estamos aprendendo novas línguas a todo momento e uma linguagem computacional nada mais é do que uma nova língua.
Todo ramo da ciência tem sua língua própria, muitas vezes incompreensível para quem não foi iniciado naquela disciplina. A medicina tem seu próprio vocabulário, com inúmeros termos obscuros até mesmo para médicos de especialidades diferentes. Todos os ramos do conhecimento têm seu próprio vocabuário e seu modo próprio de fazer a comunicação da informação. A linguagem de sinais tem em seus gestos a forma de expressar a linguagem, a música tem uma notação gráfica para expressar toda suas notas, melodias, ritmos. Até mesmo jogos tem uma linguagem própria. O xadrez tem vários sistemas de notação para expressar os movimentos do jogo.
Não apenas os ramos da ciência têm sua língua, mas também cada equipamento, cada máquina, seja um carro, um microondas, um computador ou um smartphone, tem também sua própria linguagem. Cada aparelho só compreende aquilo que foi projetado para compreender. Uma torradeira só sabe esquentar e a forma de comunicarmos a ela o momento de fazer isso é apertando um botão. Um microondas é capaz de se aquecer de várias formas, dependendo da informação que é inserida em seu painel. Um smartphone consegue fazer uma infinidade de procedimentos, todos dependentes das informação que é inserida na tela pelo seu proprietário. Quanto mais sofisticado um equipamento, mais funções ele pode realizar, maior vocabulário necessário para essa interação.
Mas, então,como pode alguém sem nenhuma formação em engenharia ou computação, conseguir fazer um equipamento tão sofisticado como um smartphone encontrar a localização de uma cidade, mostrar na tela a imagem de uma rua da cidade, traçar uma rota de sua posição até esse local? Conseguimos isso porque a forma como os seres humanos se comunicam com os equipamentos evoluiu de forma impressionante no último século. Há alguns poucos anos era preciso aprender um código morse para transmitir uma informação pelo telégrafo, hoje com um conhecimento muito mais simples podemos nos comunicar com todo o planeta através da internet num smartphone.
Da mesma forma, as linguagem computacionais evoluiram substancialmente desde sua criação. As primeiras linguagems de programação eram tão obscuras que só apenas umas poucos iniciados eram capazes de usar um computador. Mas cada ano surgem novas linguagens, cada vez mais simples de serem usadas. Atualmente, até mesmo crianças se tornam exímias programadoras.
As linguagens computacionais modernas permitem a comunicação entre um ser humano e um computador de uma forma que cada vez mais simples. E a linguagem R é justamente a ponte entre a linguagem da estatística e a linguagem humana. O R foi criado para ser justamente uma uma linguagem para análise de dados e produção de gráficos (IHAKA, 1996). A linguagem R tornou possível executarmos complexos cálculos matemáticos de forma fácil e rápida e criarmos gráficos complexos com simples comandos.
A importância da Estatística na Medicina
A estatística é uma das áreas fundamentais das ciências da saúde. Em um dos primeiros artigos sobre o ensino da estatística para estudantes de medicina, num editorial do British Medical Journal de 1937, Bradford Hill já salientava que para poder ler de forma crítica a literatura científica o médico precisava dominar os conceitos estatísticos (Hill, 1965). Entretanto, o ensino da estatística só se tornou compulsório nas escolas médicas de Londres a partir de 1975 e em muitos países europeus apenas dez anos mais tarde (Altman e Bland, 1991). Nas últimas duas décadas a Organização Mundial de Saúde tem buscado estratégias para melhorar o ensino da estatística para os profissionais de saúde, tendo em vista que essas habilidades são úteis não apenas para aqueles que desejam se tornar pesquisadores, mas para todos que trabalham com a saúde, pois favorecem o pensamento crítico, lógico e científico, facilitando os processos de tomada de decisão, de análise de riscos e de avaliação das evidências científicas (Lwanga et al., 1999). A falta do conhecimento estatístico coloca em risco todo o projeto de uma prática baseada em evidências, cujo ponto fundamental é justamente a capacidade de uma leitura crítica da literatura científica (Sackett e Rosenberg, 1995).
A importância desse conhecimento se torna ainda mais relevante quando levamos em conta a imensa quantidade de erros estatísticos básicos na literatura médica (Altman e Bland, 1991) e baixa qualidade da literatura científica que, infelizmente, é muito menos confiável do que nossa intuição imagina. Em um dos artigos mais citados de 2005, Ioannidis alerta que cerca de metade dos resultados da literatura científica médica não são verdadeiros (Ioannidis, 2005) e, mais recentemente, que a maioria dos estudos clínicos não são úteis (Ioannidis, 2016). Ou seja, não apenas a maioria dos resultados são falsos, como a maioria dos resultados verdadeiros não são úteis (Ioannidis, 2016). O médico, consumidor principal dessa literatura, precisa mais do que nunca saber analisar de forma crítica esses artigos e, para tanto, a formação sólida em métodos estatísticos é de suma importância.
Entretanto, existem barreiras reais ao ensino da estatística para estudantes das áreas da saúde. A mera menção da palavra “estatística” é suficiente para evocar fortes reações emocionais de rejeição na maioria das pessoas (Hill, 1947). Estudantes de medicina muitas vezes preferem evitar disciplinas com conteúdo matemático e, via de regra, os cursos de estatística ou bioestatística não são muito populares entre esses alunos (Altman e Bland, 1991). Além disso, alunos das áreas de saúde usualmente tem dificuldade em perceber a importância dessa disciplina, não veem razão para estudar metodologia da pesquisa científica e não se sentem motivados para aprender os difíceis conceitos matemáticos fundamentais (Clarke et al., 1980; Altman e Bland, 1991). Essas barreiras podem comprometer seriamente o aprendizado da estatística pelos estudantes de medicina e, como resultado disso, fazer com que muitos médicos sejam incapazes de uma leitura crítica da literatura científica.
A performance do aprendizado de um estudante está diretamente relacionada a diversos fatores, tais como o seu grau de engajamento, ao prazer em estudar o conteúdo, ao seu sentimento de confiança na capacidade de aprender, a sua determinação para aprender. Assim, devem ser buscados mecanismos que possibilitem aumentar esses fatores. Um desses fatores é o uso de softwares estatísticos adequados. O uso de um software em cursos introdutórios de estatística deve levar em consideração uma série de fatores: disponibilidade, custo, facilidade de uso, possibilidade de geração de gráficos e imagens, facilidade de acesso a literatura sobre o software, documentação do software, disponibilidades de pacotes auxiliares, utilidade futura do software na vida acadêmica.
A linguagem estatística R associada à interface do RStudio preenchem da melhor forma possível os requisitos necessários para essa função.
Breve História do R
A origem do R é a Linguagem S, que foi desenvolvida por John Chambers em 1976, enquanto trabalhana nos laboratórios da empresa de telefonia AT&T Bell Labs. No início da década de 90, a linguagem S foi incrementada com uma notação para modelos estatísticos, resultado numa significativa economia de esforço de programação para análise estatística de dados. No final da década de 90 o S foi revisado e se tornou uma linguagem de alto padrão totalmente baseada em programação por objetos. Essa é versão atual da linguagem S, que deu origem ao R.
A linguagem R foi criada por volta de 1993 por Robert Gentleman e Ross Ihaka, na universidade de Auckland, na Nova Zelândia, como uma ferramenta para ensino nos cursos introdutórios de estatística desses professores (Ihaka, 98).
O R é o produto de uma colaboração entre estatísticos para criação de um ambiente computacional poderoso, programável, portátil e aberto, aplicável aos problemas mais complexos e sofisticados, bem como análises “rotineiras”, sem restrições de acesso ou uso, executável em diversos sistemas operacionais (macOS, Windows, Linux).
O R é uma linguagem de código aberto e livre, publicado sob a licença pública GNU, mantido pela R Foundation. Sua estrutura de código aberto e de software público e gratuito atraiu um grande número de desenvolvedores.
A popularidade do R tem crescido ininterruptamente, principalmente nos últimos 5 anos (Robinson, 2017). Atualmente o R é um dos principais softwares estatísticos usados em pesquisas acadêmicas, principalmente em pesquisas na área médica, pois o R é “a ferramente de escolha para muitos métodos estatísticos necessários nos estudos clínicos” (Robinson, 2017). O R é atualmente o principal repositório de funções estatísticas validadas (Revolutions, 2017b).
“R has really become the second language for people coming out of grad school now, and there’s an amazing amount of code being written for it,” said Max Kuhn, associate director of nonclinical statistics at Pfizer (Vance, 2009).
Nos últimos anos o uso do R como ferramenta para aulas de estatísticas cresceu muito e surgiram vários pacotes específicos para uso como ferramentas de ensino da estatística, tais como o mosaic, Teachingdemos, simpleR, uwIntroStats. Foram lançados nos últimos anos diversos livros textos introdutórios de estatística baseados no uso do R: Introductory Statistics with R, Discovering Statistics Using R, Learn Statistics Using R, An R Introduction to Statistics, Introduction to probability and Statistics Using R, OpenIntro Statistics e diversos outros manuais introdutórios disponíveis livremente na internet. Em 2014, durante o New England Statistics Symposium, foi lançado o site StatsTeachR, um site open-access, repositório de módulos de ensino da estatística usando o R.
O R possui uma rica documentação, inúmeros tutoriais gratuitos disponíveis na internet, uma grande e crescente comunidade de suporte. Recentes levantamentos têm revelado que o uso do R tem crescido vertiginosamente nas últimas décadas, sendo atualmente o software estatístico com maior projeção de crescimento.
Timeline
- 1993: Research project in Auckland, New Zealand
- 1995: R Released as open-source software
- 1997: R core group formed
- 2000: R 1.0.0 released (February 29)
- 2003: R Foundation founded
- 2004: First international user conference in Vienna
- 2015: R Consortium founded
-
(fonte: http://blog.revolutionanalytics.com/2016/03/16-years-of-r-history.html)
Comprehensive R Archive Network, CRAN.
O CRAN (Comprehensive R Archive Network) é um repositório onde qualquer pessoa pode contribuir com uma extensão para R (chamadas de “pacote” - packages), desde que atenda aos requisitos de qualidade e licenciamento estabelecidos pelos mantenedores do CRAN. Em janeiro de 2017, graças à comunidade extremamente ativa de desenvolvedores que contribuem para o R diariamente, o CRAN atingiu a marca de 10.000 pacotes disponíveis para download (Revolutions, 2017a).
Popularidade do R
O R tem se tornado cada vez mais popular na pesquisa científica. Em 2009 o jornal New York Times publicou uma reportagem acerca da popularidade o R entre os cientistas. Segundo o New York Times, o R tem se tornado a segunda língua dos pesquisadores.
Numa pesquisa realizada em 2015 pela Rexer Analytics Survey o R foi o mais usado entre 1220 cientistas avaliados.
RStudio
RStudio é um Ambiente de Desenvolvimento Integrado (IDE - Integrated Development Enviroment) para uso da linguagem estatística R. Um IDE é um software com ferramentas de apoio ao desenvolvimento do trabalho e facilita incrivelmente trabalhar com o R. O RStudio foi lançado ao público em 2008 e já conta hoje com um grande número de usuários. Atualmente o Rstudio 'é usado pela NASA, Eli Lilly, AstraZeneca, Samsung, Honda, Hyunday, Walmart, Nestle, General Eletric, Santander, Universidade de Oxford, Universidade de Toronto e inúmeras outras instituições.
A versão gratuita do Rstudio é perfeitamente adequada para os usos acadêmicos, tornando totalmente dispensável o uso de softwares pagos e com custo elevado.
Referências.
1. Ross Ihaka.R : Past and Future History.A Draft of a Paper for Interface ’98. Disponível em: https://www.stat.auckland.ac.nz/~ihaka/downloads/Interface98.pdf. Acessado em 07/01/2018.
2. David Robinson. The Impressive Growth of R. October 10, 2017. Stackoverflow Blog. Disponível em: https://stackoverflow.blog/2017/10/10/impressive-growth-r. Acessado em 07/01/2018.
3. Revolutions. CRAN now has 10,000 R packages. Here's how to find the ones you need. Revolutions Analitics Blog. January 27, 2017. Disponível em: http://blog.revolutionanalytics.com/2017/01/cran-10000.html. Acessado em 07/01/2018.
4. Revolutions. R's remarkable growth. October 10, 2017. Disponível em: http://blog.revolutionanalytics.com/2017/10/rs-remarkable-growth.html. Acessado em 07/01/2018.
5. Ashlee Vance.Data Analysts Captivated by R’s Power. New York Times - Business Computing. January 6, 2009. Disponível em: http://www.nytimes.com/2009/01/07/technology/business-computing/07program.html?pagewanted=1. Acessado em: 07/01/2018.
Instalação do R e do RStudio
Instalando o R
O R pode ser baixado para instalação no site do CRAN:
https://cran.r-project.org/index.html
Instalando o RStudio
O RStudio pode ser instalado a partir do site do RStudio:
Video da instalação no Youtube
Há um pequeno video de instalação do R e do RStudio no Mac no link a seguir:
RStudio - primeiros passos
O R é uma linguagem, uma linguagem escrita. Da mesma forma que precisamos de um papel ou um processador de texto para escrevermos uma carta, também precisamos de um meio onde escrever nossos comandos na linguagem R. Qualquer editor de textos simples poderia servir para escrevermos na linguagem R, o TextEdit no Mac. Entretanto, usar um software específico para escrevermos comandos na linguagem R facilita muito o trabalho. O RStudio é justamente isso e muito mais. E um ambiente completo para escrever todo um projeto de análises estatísticas com a linguagem R.
Os Painéis do RStudio
O Painel Console
O console é o painel no qual podemos digitar e executar comando, e onde os resultados também irão ser exibidos.
O Painel Editor
O Editor é o painel no qual serão exibidos os editores de texto do RStudio. No Editor podemos criar arquivos de Script ou de Notebooks (veremos adiantes esses tipos de arquivos).
O Painel Ambiente
O painel Ambiente possui várias abas: Environment, History, Connections.
A primeira, chamada de Enviroment (ambiente), exibe as variáveis e objetos que estão na memória durante uma sessão do RStudio.
A segunda aba, chamada de History, contém a lista de todos os comandos que foram executados pelo R nas últimas sessões.
A terceira aba, Connections, é usada em projetos mais avançados, para mostrar as conexões do RStudio com bancos de dados. Não usaremos essa aba nesse curso.
O Painel Files
O painel Files também possui várias abas: Files, Plots, Packages, Help e Viewer.
A aba Files mostra a pasta atual do R e os arquivos dessa pasta.
A aba Plots mostra os gráficos criados na sessão do R. Essa aba permite tanto a visualização como a exportação dos gráficos no formato de imagem ou pdf.
A aba Packages mostra os pacotes do R que foram instalados e permite a atualização desses pacotes.
A aba Help mostra o arquivo help do R.
A aba Viewer serve para visualização de arquivos da web. Não usaremos essa aba nesse curso.
R Script
No cinema ou no teatro um script é o texto escrito do diálogos dos personagens. Na ciência da computação um script é um texto escrito em alguma linguagem de programação. No nosso caso, R Script é um texto com comandos da linguagem R. Ou seja, em última análise, um script é nada mais que um documento de texto, que pode ser salvo, assim como podemos salvar documentos que escrevemos com o uso de processadores de texto. Tal como salvamos documentos do Word, também podemos salvar os Scripts escritos no RStudio.
Um script contém a sequencia de comandos que desejamos que sejam executados pelo R. Podemos também escrever os comandos diretamente no console, entretanto os comando assim escritos não podem ser salvos. A vantagem de escrever os comandos num documento de texto é justamente poder salvar esse documento para uso posterior. Em computação é usual denominarmos os comandos num documento de texto como nosso código. Em especial, quando esse código está escrito na linguagem R, é usual denominar esses comando de código em R ou simplesmente de R code.
R Notebook
O R Notebook é um documento de texto mais sofisticado que um R Script. Um documento do tipo R Notebook é um misto de texto e códigos. O texto de um R Notebook é escrito no formato mais usado em ciência chamado de Markdown, intercalado com trechos de código (chamados de code chunks). Essa mistura de texto com code chunks proporciona criar documentos com toda nossa análise estatística de forma muito mais simples. Além disso, um R Notebook pode ser gravado em diferentes formatos (word, pdf ou html) o que simplifica os processos de transferência de arquivos entre colaboradores.
Video Aula
Link para video aula de primeiros passos com o RStudio:
Variáveis no R
Objetos no R
“Everything that exists is an object” “Everything that happens is a function”
John Chambers, Creator of the S programming language
O R é uma linguagem de programação de alto nível e como tal, usa do conceito de objetos. As linguagens de programação desse tipo são chamadas de linguagens orientadas a objetos. Essa abstração simplifica muito a programação e torna muito mais fácil resolver problemas complexos. Os objetos mais comuns do R são chamados de variáveis.
Variáveis no R
Uma variável é um objeto que armazena dados, tais como valores numéricos, datas, caracteres, palavras, valores lógicos (veremos isso adiante) etc.
Operador de Atribuição
Para armazenar um dado numa variável usamos um operador especial, denominado de operador de atribuição:
1 <-
O operador de atribuição serve para atribuirmos um dado a um objeto e tem a forma de uma seta para esquerda, formada pelo sinal de menor imediatamente seguida do sinal de menos <-.
Isso forma uma seta, indicando que o resultado da operação será colocado no objeto à esquerda da seta.
1 > x <- 2
2 > y <- 3
3 > z <- "Maria"
Observe que ao criar uma variável para armazenar uma palavra ou um caractere, é necessário colocar essa palavra entre aspas. O R entende que está entre aspas é uma palavra ou um texto e não um número.
Operadores Aritméticos
Os operadores mais comuns do R são os aritméticos:
| operador | ação |
|---|---|
| + | somar |
| - | subtrair |
| / | dividir |
| * | multiplicar |
| ^ | elevar à uma potência |
Veja nos exemplos abaixo algumas operações matemáticas simples:
1 > x <- 2
2 > y <- 3
3 > z <- (x + y)^2
Precedência de Operações
Assim como na matemática, também no R existem regras de precedência de operações com um detalhe: os parênteses sempre tem preferência, ou precedência, sendo usados para colocarmos as operações na ordem desejada. ou seja, as operações entre parênteses tem prioridade sobre outras operações. Veja o exemplo abaixo
1 < 4 * 3 + 2
2 [1] 14
3
4 > (4 * 3) + 2
5 [1] 14
6
7 > 4 * (3 + 2)
8 [1] 20
Comentários no R
Um outro símbolo importante no R é o hashtag #. Esse símbolo indica que o texto a seguir é um comentário, ou seja, é um texto para ser lido por humanos e que o computador simplesmente ignora.
1 # atribuindo o valor de 30 (anos) a variável idade
2 > idade <- 30
3
4 # Calculando a idade em meses e armazenando
5 # esse novo dado na variável idade.meses
6 > idade.meses <- 30 * 12
Estilos de nomeação de variáveis e objetos
Como você deve ter notado, variáveis devem ter nomes fáceis de serem compreendidos, nomes que mostrem o que significam. Se uma variável serve para armazenar a glicemia é mais adequado que essa variável seja denominada glicemia do que apenas x. Por outro lado, devemos usar nomes sucintos e evitar nomes grandes, glicemia é mais apropriado do que niveis.de.glicose.dos.pacientes, que é demasiadamente extenso.
Nomes compostos
Entretanto, quando houver necessidade de usar nomes compostos, o modo adequado é usar um ponto separando as palavras, tais como: glico.fem ou idade.media.
Evite usar o underline em variáveis, a separação de palavras pelo o underline é geralmente usado para nomear arquivos tais como: research_results_fase_1.csv.
Evite usar maiúsculas para separar as palavras de uma variável, pois esse estilo geralmente é usado para nomear funções, tal como em “solveEquation”. Veja que as palavras são separadas pelo uso de uma maiúscula no início das palavras, exceto a primeira. Esse modo criar nomes é geralmente usado para nomearmos funções, portanto, vamos evitar fazer isso ao criarmos nomes de variáveis.
Regras para criação de nomes de objetos
Além dessa dica, existem regras formais para criar nomes de variáveis:
1. O nome de uma variável deve SEMPRE começar com uma letra
2. O nome de uma variável NÃO pode começar com números ou caracteres especiais
3. O nome de uma variável NÃO pode conter espaços
4. O nome de uma variável NÃO pode conter caracteres com acentos gramaticais.
Case Sensitive
Um ponto importante: o R é case sensitive, ou seja, maiúsculas e minúsculas são considerados caracteres diferentes: portanto as variáveis idade e Idade são diferentes. A dica é evitar usar maiúsculas em nomes de variáveis, para não criar confusão.
Vetores no R
Vetores são objetos fundamentais de todas linguagens computacionais. Um vetor é um conjunto de elementos da mesma natureza. Por exemplo, um conjunto de números, um conjunto de palavras, etc.
A forma mais comum de criar um vetor no R é através do uso do comando c que signific acombine, como mostrado a seguir.
1 # criando um vetor numérico com idades dos pacientes
2 > idades <- c(45, 32, 24, 23, 55, 56)
3
4 # criando um vetor com nomes dos pacientes:
5 > nomes <- c("Eduardo", "José", "Antônio", "Pedro", "Maria", "Gustavo")
Tipos de Dados
A ciência depende de dados, que são gerados a partir de alguma forma de coleta. Tudo que for quantificado será armazenado numa variável. Uma variável deve ser entendida como um objeto que contém os resultados dessa coleta de dados.
Mas dados podem ser coletados de difentes modos: algumas dados são provenientes de algo que foi contado, outros dados provém de algo que foi medido. Contar e medir fornecem diferentes tipos de dados. Podemos por exemplo, contar o nº de pessoas com AIDS, o nº de eleitores de um determinado político, o nº de óbitos, de nascimentos etc. Por outro lado, podemos medir o perímetro cefálico de crianças recém-nascidas, o nível pressórico ou de glicemia de um grupo de pacientes, etc.
Variáveis com dados provenientes de contagem são denominadas variáveis categóricas, também chamadas de variáveis qualitativas, pois podem expressar uma qualidade (qual o nº de asiáticos no brasil)
Variáveis com dados provenientes de medidas são denominadas variáveis numéricas, também chamadas de variáveis quantitativas.
As variáveis categóricas (ou qualitativas) se dividem em nominais e ordinais.
As variáveis numéricas por sua vez são tradicionalmente divididas em variáveis numéricas discretas e numéricas contínuas.
A necessidade de classificarmos as variáveis em diferentes tipos é devido ao fato de que o tipo de variável determina os tipos de operações matemáticas que podem ser realizadas e, consequentemente, as medidas estatísticas e os testes estatísticos que podem ser realizados.
Variáveis categóricas (qualitativas)
Algumas variáveis são nomes que expressão uma qualidade (que podem ter ou não uma ordenação). Em estatística essas variáveis são chamadas categóricas e podem se dividir em nominais ou ordinais. Variáveis nominais expressam qualidades, mas sem uma ordenação. Variáveis ordinais também expressão qualidades, mas tem uma ordenação. As variáveis categóricas não podem ser usadas em operações aritiméticas. Não podemos, por exemplo, calcular a média desse tipo de variável. O que podemos fazer com variáveis categóricas é construir tabelas de frequências de cada categoria.
No R as variáveis categóricas são chamados de factor.
Os dados das variáveis que não possuem nenhuma ordenação, são chamadas de variáveis categóricas nominais. Quando uma variável categórica tem uma ordenação ela recebe o nome de variável ordinal. O R não tem nomes distintos para esses dois tipos de variáveis categóricas, sendo ambas classificadas no R como sendo do tipo factor.
Entretanto, é possível indicar para o R que a ordenação de uma variável é importante. A função factor() permite atribuir uma ordem às variáveis nominais, tornando-as assim variáveis ordinais. Isso é feito configurando o parâmetro de ordem para TRUE e atribuindo um vetor com a hierarquia de nível desejada. Sem essa ordenação vamos ter problemas ao fazer gráficos que precisam de uma ordem, pois não controlamos a ordem que será colocada no gráfico.
A linguagem R trabalha com diferentes tipos de variáveis para armazenar as diferentes categorias de dados. As variáveis no R podem ser classificadas como numéricas (para armazenar dados numéricos), caracteres (para armazenar palavras), datas etc. Para verificar o tipo de dado de uma variável ou vetor, basta usar a função class( ). Vejamos alguns exemplos.
1 > nomes <- c("Henris", "Leo", "Gustavo")
2 > class(nomes)
3 [1] "character"
Variáveis quantitativas (numéricas)
As variáveis quantitativas (numéricas) são resultado de alguma medida realizada. Podem ser números inteiros (discretas) ou reais (contínuas). A grande diferença dessas variáveis com as qualitativas é que com as variáveis numéricas podemos fazer todas operações matemáticas: somar, dividir, calcular a média, a variância, o desvio padrão etc.
1 > idade <- c(45,10,12)
2 > class(idade)
3 [1] "numeric"
Variáveis Lógicas
Existem variáveis chamadas de lógicas. Variáveis lógicas armazenam o resultado de uma operação lógica. Operações lógicas são aquelas realizadas através de operadores lógicos: igual, maior, maior ou igual, menor, menor ou igual, etc.
| operador | significado |
|---|---|
| < | menor que .. |
| <= | menor ou igual a … |
| > | maior que … |
| >= | maior ou igual a … |
| == | extamente igual a … |
| ! | não / negação |
| != | não igual ou diferente de … |
| OR | |
| & | AND |
Variáveis lógicas são aquelas que armazenam resultados de operações lógicas. No exemplo uma operação lógica é realizada e seu resultado é colocado numa variável.
1 > resultado.1 <- (4 < 5)
2 > resultado.1
3 [1] TRUE
4
5 > resultado.2 <- (10 < 5)
6 > resultado.2
7 [1] FALSE
Veja que o valor da variável resultado.1 é TRUE, pois quatro é realmente menor que cinco. Da mesma forma o valor da variável resultado.2 é FALSE, pois 10 não é menor que 5.
Usando a função class( ), podemos verificar que as variáveis resultado.1 e resultado.2 são do tipo logical (lógico).
1 > class(resultado.1)
2 [1] "logical"
3
4 > class(resultado.2)
5 [1] "logical"
Um ponto importante a ser memorizado é que é usual em linguagens de programação que TRUE tenha o valor de 1 e FALSE tenha o valor de 0.
portanto:
1 > resultado.1 * 5
2 [1] 5
3
4 > resultado.2 * 5
5 [1] 0
NA Values
É muito frequente que faltem dados em pesquisas. Às vezes uma questão de um questionário deixou de ser respondida, às vezes um dado não foi encontrado etc. Esses dados são representados no R como NA, que significa NOT AVAILABLE. É importante reconhecer a existência desses dados faltantes pois a presença desses dados faltantes pode impedir que sejam executados cálculos matemáticos. Afinal de contas, o que poderia significar 3*NA? Experimente fazer essa conta no R.
Funções no R
As funções são a base de uma linguagem de programação. Assim como uma função matemática, na computação uma função recebe um conjunto de dados, processa esses dados e retorna um resultado.
Uma função y=2x recebe como input um valor e dá como resultado o dobro desse valor.
A função y=sen(x) recebe como input um determinado valor numérico e dá como resultado o seno desse valor.
A linguagem R tem inúmeras funções estatísticas que executam os inúmeros cálculos matemáticos necessários para resolvermos problemas estatísticos, desde os mais básicos até os mais complexos, facilitando bastante o ensino e a aprendizagem da estatística.
Argumentos de uma função
Toda função no R tem a seguinte estrutura: nome(argumentos). Ou seja, o nome da função, entre parênteses, os argumentos da função. Observe que não há espaços entre o nome da função e os parênteses com os argumentos.
Denominam-se argumentos de uma função os dados que são inseridos na função para o cálculo desejado. Vejamos como exemplo função para extrair a raiz quadrada de um número: sqrt().
O nome da função é sqrt, é uma abreviação de square root, ou raiz quadrada. Entre parênteses colocamos os argumentos, nesse caso, o número que desejamos que seja extraída a raiz quadrada. Portanto, para obter a raiz quadrada de 225 basta usar a função sqrt() com o argumento 225:
1 > sqrt(225)
2 [1] 15
Uma função pode ter mais de um argumento, o que é o mais comum na verdade. E alguns argumentos servem para indicar como a função deve se comportar. Uma função fundamental do R é a que lê os arquivos com dados, para que possamos fazer nossos cálculos. Um argumento dessa função é o nome do arquivo, outros argumentos são: se esse arquivo contém cabeçalho, se os dados estão separados por vírgula ou ponto e vírgula, se o decimal é uma vírgula ou um ponto etc. Para usar essa função devemos informar todos esses argumentos.
No exemplo abaixo, mostramos a função read.csv( ) e como essa função pode ser usada para ler um arquivo chamado resultados.csv, que contem cabeçalhos, cujos dados estão separados por vírgulas e cujos valores decimais são separados por um ponto:
1 read.csv(file ="resultados.csv",
2 header = TRUE,
3 sep = ",",
4 dec = ".")
na.rm = TRUE
Um argumento importante de muitas funções é o na.rm = TRUE. a expressão na.rm é uma abreviação de REMOVE NOT AVAILABLE DATA, ou seja, remova os dados faltantes. Ao indicarmos que esse argumento é verdadeiro (TRUE), o R irá desconsiderar dados em branco ou faltantes ao fazer os cálculos. Sem esse argumento, frequentemente os cálculos não são realizados.
Algumas funções matemáticas comuns:
| função | ação |
|---|---|
sqrt() |
calcula a raiz quadrada |
log() |
calcula o logaritmo natural |
abs() |
retorna o valor absoluto |
Algumas funções estatísticas comuns:
| função | ação |
|---|---|
mean() |
calcula a média de um conjunto de valores |
median() |
calcula a mediana de um conjunto de valores |
sum() |
calcula a soma de um conjunto de valores |
min() |
retorna o valo mínimo de um conjunto de valores |
max() |
retorna o valor máximo de um conjunto de valores |
var() |
calcula a variância de um conjunto de valores |
sd() |
calcula o desvio padrão de um conjunto de valores |
Pacotes do R
Uma das maiores forças da linguagem R é o seu excelente conjunto de pacotes (packages). Pacotes são conjuntos de funções criadas por outras pessoas que contribuem para o desenvolvimento da linguagem R. Como o R é uma linguagem aberta, qualquer pessoa pode contribuir criando pacotes. Atualmente o R é um dos mais importantes repositórios de funções estatísticas, sendo muito comum que teses de mestrado na área da estatística se tornem pacotes do R.
Na verdade, uma das principais razões do sucesso do R são os pacotes extremamente versáteis que a linguagem hoje dispõe. O R tem hoje mais de 10.000 pacotes só no site do CRAN, além de milhares de outros em diferentes sites.
Dentre esses tantos pacotes, alguns se destacam pela sua extrema versatilidade e um nome se destaca no universo da estatística: Hadley Wickham, um estatístico neozelandês, é o responsável pela criação dos pacotes mais famosos do R, entre eles o ggplot2 para geração de gráficos é o dplyr para manipulação de dados.
O pacote ggplot2 é o pacote gráfico mais importante do R, já tendo sido baixado mais de 10 milhões de vezes do site do CRAN. O código abaixo mostra o total de downloads do ggplot2:
1 library(tidyverse)
2 library(dlstats)
3 stat.ggplot <- cran_stats(c("ggplot2"))
4 downloads.gg <- stat.ggplot %<%
5 select(downloads) %<%
6 sum
O pacote dplyr, por sua vez, já foi baixado mais de 6 milhões de vezes do site do CRAN, sendo um dos pacotes mais usados para manipulação de dados.
Esses dois pacotes e vários outros podem ser instalados mais facilmente através da instalação do pacote tidyverse. O tidyverse é uma coleção de pacotes, instalando automaticamente uma série de pacotes úteis em análises de dados, entres eles o dplyr, ggplot2 e outros, sendo o modo mais prático de instalar esses pacotes, pois com um único comando são instalados diversos pacotes. Mais informações sobre o pacote tidyverse podem ser encontradas em https://www.tidyverse.org.
Para instalar um pacote, você pode usar a função install.packages() no console. É importante salientar que um pacote deve ser sempre instalado a partir do console e nunca a partir de um script ou de qualquer outro documento de texto. Além disso, vale a pena lembrar que um pacote só precisa ser instalado uma única vez. Por outro lado, sempre que desejamos usar o pacote precisamos carregar esse pacote na memória (na sessão do R) com o comando library(). Esse carregamento do pacote na sessão deve ser feito toda vez que formos usar o pacote, de preferência no início da sessão. Em geral o comando library( ) deve ser um dos primeiros comandos de um script.
Por exemplo, para instalar o pacote tidyverse usamos o comando install.packages() no console, como mostrado abaixo:
1 > install.packages("tidyverse")
Observe que o comando install.packages() exige que o nome do pacote a ser instalado esteja entre aspas.
Ao executar esse comando você verá que o R instala diversos pacotes.
Para carregar o pacote tidyverse em sua sessão R atual, use o comando library() no início de seu script ou de seu R Notebook, como mostrado abaixo.
1 library(tidyverse)
Observe que no comando library() o nome do pacote não precisa ser escrito entre aspas.
Data Frames
Data frames são as estruturas de dados mais importantes do R e uma das principais razões do uso crescente da linguagem R. Superficialmente um data frame é como uma planilha do Excel, com colunas e linhas.
Cada coluna de um data frame é uma variável, ou melhor, um vetor.
Cada linha de um data frame é uma observação.
Por exemplo, numa pesquisa com 50 pacientes, na qual são coletados dados de nome, idade, sexo, estado civil, profissão e diagnóstico, nosso data frame consistiria de 50 linhas (cada linha para um paciente) e 6 colunas (nome, idade, sexo, estado civil, profissão e diagnóstico).
Um modo de criar um data frame é com a função data.frame(), como a seguir:
1 > nome <- c("Henrique", "Antônio", "Fabiano")
2 > idade <- c(45, 40, 48)
3 > mydata <- data.frame(nome, idade)
A última linha acima criou o data frame, com as colunas nome e idade e com 3 linhas, uma para cada paciente.
O Operador $
O operador $ é usado para acessarmos as colunas de um data frame. Para acessarmos a coluna com as idades basta usarmos mydata$idade, como abaixo:
1 > mydata$idade
2 [1] 45 40 48
Para calcular a média das idades dos pacientes no data frame acima basta usar a função mean, colocando mydata$idade como argumento da função, como abaixo:
1 > mean(mydata$idade)
2 [1] 44.33333
Datasets do R
O R possui vários datasets (conjuntos de dados) para facilitar o aprendizado. Para saber mais sobre os datasets inclusos no R digite no console o comando abaixo:
1 > data( )
Podemos carregar os datasets já inclusos no R com a função mesma função data( ), mas incluindo como argumento o nome do dataset desejado. No exemplo a seguir iremos carregar o dataset USArrests. Este dataset contém estatísticas das prisões por 100.000 habitantes por assalto, assassinato e estupro em cada um dos 50 estados dos EUA em 1973, como também a porcentagem da população urbana.
1 > data("USArrests")
Como esse dataset carregado podemos agora visualizar os dados simplesmente digitando o nome do dataset no console
1 > USArrests
Experimente também usar a função str(), que mostra a estrutura dos dados de um objeto, para verificar a estrutura e o tipo de objeto é esse dataset:
1 > str(USArrests)
Você deverá obter como resultado que o dataset USArrests é um data frame com 50 observações (50 linhas) e 4 variáveis (Murder, Assalt, UrbanPop e Rape), como mostrado abaixo:
1 'data.frame': 50 obs. of 4 variables:
2 $ Murder : num 13.2 10 8.1 8.8 9 7.9 3.3 5.9 15.4 17.4 ...
3 $ Assault : int 236 263 294 190 276 204 110 238 335 211 ...
4 $ UrbanPop: int 58 48 80 50 91 78 77 72 80 60 ...
5 $ Rape : num 21.2 44.5 31 19.5 40.6 38.7 11.1 15.8 31.9 25.8 ...
Observe que antes de cada variável se encontra o operador $, que é o modo de acessar cada uma dessas variáveis. Experimente digitar o comando abaixo para acessar a variável Murder:
1 > USArrests$Murder
Datasets externos
Os datasets inclusos no R servem apenas para treinamento do uso. O mais importante numa análise estatística é poder usar seu próprio conjunto de dados, proveniente de sua pesquisa. Para isso é necessário ler um arquivo externo e carregar esse arquivo na sessão do R. O RStudio possui uma função para importação de arquivos dentro da aba File -> Import Dataset. Entretanto, devemos SEMPRE EVITAR importar arquivos por esse meio. O método mais indicado para importar um arquivo é fazer isso dentro do próprio Script, usando as funções de leitura de dados como mostrado no próximo capítulo.
Lendo Dados
Para podermos efetivamente usar o R, uma etapa inicial é justamente carregarmos os dados a serem analisados. Existem diversos formatos de arquivos para armazenar dados, cada um apropriado para ser lido por determinados aplicativos. Vejamos:
| formato | Tipo de dados | software para ler os dados |
|---|---|---|
| .txt | texto | Qualquer leitor de texto |
| .doc | texto | Word (microsoft) |
| .docx | texto | Word (microsoft) |
| .xls | planilha | Excel (microsoft) |
| .ppt | slides | PowerPoint (microsoft) |
| documento portátil | Qualquer leitor de PDF (ex: Acrobat) | |
| .pages | texto | Pages (Apple) |
| .numbers | planilha | Numbers (Apple) |
| .key | slides | Keynote (Apple) |
| .csv | dados | Qualquer leitor de texto |
Alguns formatos de arquivos dependem de um software específico para sua leitura. Outros formatos são menos expecíficos, podendo ser lidos por um grande número de softwares, como é o caso dos arquivos .txte dos arquivos .pdf. Esses formatos são mais universais, sendo padrões comuns para comunicação de informações textuais.
Quando essa troca de dados se refere não um texto propriamente dito, mas um conjunto de dados, tais como tabelas com dados, um dos formatos mais universais é o .csv (comma separated values = valores separados por virgulas).
A estrutura desse arquivo é bastante simples: existem várias linhas, cada linha com vários dados, separados por vírgulas. Existem, entretanto variações nesse formato, por exemplo, no Brasil as casas decimais são separadas por vírgulas, nesse caso o delimitador dos valores não poderia ser a vírgula e é usado então o ponto e vírgula. Ao ler dados no formato .csv é sempre importante informar se os dados são separados por , ou ; e se o separador do decimal é a virgula , ou o ponto final .. Caso contrário a leitura dos dados poderá ser corrompida.
Para ler dados no R o ideal é que os dados estejam, de preferência, no formato separado por vírgulas, chamado de “comma separated values” ou, simplesmente de csv. A extensão .csv no final do nome de um arquivo indica que esse é um arquivo de dados no formato separado por vírgulas. Todo software de planilhas, tal como o Excel ou Numbers (do Mac) são capazes de salvar os dados nesse formato.
O R tem uma função especial para ler esses tipos de dados: read.csv( ).
Os argumentos dessa função já foram mostrados no capítulo sobre as funções:
| argumentos | valor default | valor que necessita ser ajustado |
|---|---|---|
file = |
não possui | “nome do arquivo a ser lido.csv” |
na.strings |
NA | trocar para o que estiver sendo usado no arquivo |
header |
FALSE |
trocar para TRUE se houver cabeçalho no arquivo |
sep |
espaço | trocar para "," ou ";" conforme o usado no arquivo |
dec |
”.” | usar o default ou trocar por "," se for o caso |
O código de exemplo abaixo lê um arquivo de dados chamado pesquisa.csv, no formato .csv, no qual há há um cabeçalho (header= TRUE) , cujos valores estão separadads por vírgula (sep = ",") e o separador decimal é o ponto final (dec = ".")
1 read.csv(file = "pesquisa.csv",
2 header = TRUE,
3 sep = ",",
4 dec = ".")
Argumentos default
Caso o arquivo esteja no formato .csv com as especificações acima, podemos usar essa mesma função informando apenas o nome do arquivo, pois a função read.csv() assume como valores default essas especificações, bastando indicar o nome do arquivo: a função read.csv().
1 read.csv(file = "pesquisa.csv")
Ou seja, com os dados no formato padrão, a leitura dos dados é extremamente fácil com o comando acima. Esse comando lê o arquivo chamado pesquisa.csv. Mas falta ainda um detalhe: é preciso colocar os dados lidos numa variável. O comando correto deve ser parecido com a linha abaixo. É lógico que você pode mudar o nome da variável que vai receber os dados. No caso abaixo a variável, ou melhor, o objeto, que vai receber os dados foi chamado de mydata e os dados estão sendo lidos de um arquivo chamado pesquisa.csv.
1 mydata <- read.csv(file = "pesquisa.csv")
Agora sim, os dados são lidos e colocados na variável mydata. Você verá que, ao ler um arquivo de dados dessa forma, o objeto mydata será um data frame, com linhas representado cada paciente (observação) e colunas representando as variáveis da pesquisa.
RStudio Projects
Working Directory
Toda sessão de trabalho com R tem uma diretório de trabalho associado. Para que o R possa ler um arquivo, é necessário que esse arquivo esteja na pasta do diretório de trabalho da sessão do R. Se o arquivo a ser lido estiver em outra pasta, será invisível para o RStudio.
Podemos indicar ao R que diretório da sessão de trabalho seja o diretório da aba Files. Para isso, clique em Session (no menu do RStudio) e em seguida em
Set Working Directory -> To Files Pane Location.
Entretanto, esse é um método muito arcaico e desajeitado e trabalhoso para fazer toda vez que formos usar o RStudio.
A melhor forma de resolver esse problema é usar sempre um Project do RStudio.
Projects do RStudio
Um trabalho de análises estatísticas geralmente depende de um arquivo com os dados a serem lidos, de arquivos de R Scripts ou R Notebooks, com os códigos da análise culminando na geração de arquivos de resultados, tais como pdfs ou imanes para serem salvos. O ideal é que todos esses arquivos estejam numa mesma pasta no computador.
O RStudio possibilita a criação de um Project, que torna uma pasta no computador o diretório de trabalho de uma sessão do R sempre que esse Project for aberto.
Quando um Project é aberto, o RStudio cria uma nova sessão de trabalho e define que a pasta do Projeto se torne o diretório de trabalho do R, automatizando o processo de definição do diretório de trabalho e ajudando a organizar a sessão do R.
Criando um Projeto
Antes de criar um projeto, crie primeiro a pasta que servirá de diretório de trabalho em seu computador e salve nessa pasta os arquivos com os dados a serem analisados.
Para criar um projeto (project) clique em Project (na parte superior à direta do RStudio) e em seguida em New Project. A seguir, escolha a opção
Existing Directory - Associate a project with an existing directory.
E, em seguida, clique em Browse para encontrar a pasta existente e associá-la ao seu projeto. Finalmente, clique em Create Project para finalizar o processo de criação de seu projeto.
Video de Criação de Projetos no RStudio
Estatística Descritiva no R
Introdução
Veremos nesse capítulo as medidas mais importantes para descrever uma conjunto de dados: as medidas de localização central (média e mediana) e as medidas de dispersão (variância e desvio padrão). Essas medidas, hoje tão comuns e simples, tiveram um lento e complexo desenvolvimento ao longo de muitos séculos. A noção de que a média poderia representar os dados só surgiu com os trablahos de Galileu por volta de 1632 (Sthal, 2006 ) e o termo desvio padrão só foi cunhado em 1892 pelo estatístico Karl Person (Magnello, 1996). Essas medidas são os blocos fundamentais da estatística moderna e é imprescindível saber usá-las e interpretá-las adequadamente.
Parte 1 - Carregamento do dataset mpg
Para experimentarmos usar as diversas funções estatísticas do R, vamos primeiro carregar um conjunto de dados que vem junto com o pacote ggplot2. Se você já instalou o pacote tidyverse então o ggplot2 já foi instalado. Você pode também instalar o pacote ggplot2 isoladamente se desejar. O comando para instalar os pacotes é o install.packages(). Lembre-se de que a instalação de um pacote deve ser sempre feita no console e nunca num R script ou num R Notebook.
Para instalar o pacote tidyverse, use o comando abaixo no console: (recomendado)
1 > install.packages("tidyverse")
Caso prefira, instalar oggplot2 isoladamente, use o comando abaixo no console:
1 > install.packages("ggplot2")
ATENÇÃO: Se você já instalou esses pacotes, não é necessário instalar novamente.
Com os pacote ggplot2 instalado podemos agora usar os datasets que vem junto com esse pacote. para isso é necessário primeiro carregar o pacote ggplot2 na memória do computador, o que é feito com a função library(ggplot2).
Atenção: observe que ao usar a função library() não precisamos usar as aspas.
Com o pacote ggplot2 estão carregados na memória e podemos usar os datasets que vem junto com esse pacote. Vamos usar o dataset mpg para nosso treinamento de estatística descritiva no R. O acrônimo mpg significa Miles Per Gallon - uma medida de quantas milhas um carro pode viajar se você colocar apenas um galão de gasolina ou diesel em seu tanque (1 galão equivale a 3.79 litros e uma milha equivale a 1.6km).
Esta medida padronizada serve comparar carros com base na sua eficiência. O conjunto de dados mpg que vem junto com o ggplot2 é apenas um subconjunto dos dados de economia de combustível que a EPA (Enviroment Protection Agency - USA) disponibiliza em http://fueleconomy.gov. O conjunto completo dos dados podem ser obtidos nesse site, no link seguir:
http://fueleconomy.gov/feg/download.shtml.
Em primeiro lugar, abra um novo Script para deixar todos os comandos gravados. Escolha um nome para seu Script e salve regularmente esse Script para não perder os dados. Digite os comandos a seguir em seu Script e não no console. Para executar um comando do Script coloque o cursor no final da linha de comandos e clique em Command+Return (no mac) ou Control+Return (no Windows).
No início de seu Script é que você deve colocar os comandos library, como a seguir:
1 library(tidyverse)
Para facilitar essa aula, vamos usar simplesmente o dataset mpg que já vem com o ggplot2. Para carregar esse dataset basta usar o comando abaixo:
1 data(mpg)
Com a função class() podemos verificar que esse dataset é um data frame do R.
1 > class(mpg)
2 [1] "tbl_df" "tbl" "data.frame"
Em primeiro lugar, vamos visualizar as primeiras linhas desse dataset com a função head():
1 > head(mpg)
2
3 # A tibble: 6 x 11
4 manufacturer model displ year cyl trans drv cty hwy fl class
5 <chr> <chr> <dbl> <int> <int> <chr> <chr> <int> <int> <chr> <chr>
6 1 audi a4 1.8 1999 4 auto(l5) f 18 29 p compact
7 2 audi a4 1.8 1999 4 manual(m5) f 21 29 p compact
8 3 audi a4 2.0 2008 4 manual(m6) f 20 31 p compact
9 4 audi a4 2.0 2008 4 auto(av) f 21 30 p compact
10 5 audi a4 2.8 1999 6 auto(l5) f 16 26 p compact
11 6 audi a4 2.8 1999 6 manual(m5) f 18 26 p compact
Com esse comando você pode visualizar as primeiras linhas tabela do dataset mpg.
Podemos também usar o comando str() para visualizarmos a estrutura desse data frame, as variáveis e seus tipos:
1 > str(mpg)
2
3 Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 234 obs. of 11 variables:
4 $ manufacturer: chr "audi" "audi" "audi" "audi" ...
5 $ model : chr "a4" "a4" "a4" "a4" ...
6 $ displ : num 1.8 1.8 2 2 2.8 2.8 3.1 1.8 1.8 2 ...
7 $ year : int 1999 1999 2008 2008 1999 1999 2008 1999 1999 2008 ...
8 $ cyl : int 4 4 4 4 6 6 6 4 4 4 ...
9 $ trans : chr "auto(l5)" "manual(m5)" "manual(m6)" "auto(av)" ...
10 $ drv : chr "f" "f" "f" "f" ...
11 $ cty : int 18 21 20 21 16 18 18 18 16 20 ...
12 $ hwy : int 29 29 31 30 26 26 27 26 25 28 ...
13 $ fl : chr "p" "p" "p" "p" ...
14 $ class : chr "compact" "compact" "compact" "compact" ...
Esse dataset possui 243 linhas (observações) com 11 variáveis. O significado de cada variável está descrito na documentação de ajuda do dataset mpg e pode ser visualizado com o comando ?mpg no console. A tabela abaixo mostra o significado de cada variável:
| variável | significado |
|---|---|
| manufacturer | marca |
| model | modelo |
| displ | cilindradas (Engine Displacement) |
| year | ano de fabricação |
| cyl | número de cilindros |
| trans | tipo de marcha: automática / manual |
| drv | tração: f=frontal, r=traseira, 4=4x4 |
| cty | milhas por galão na cidade |
| hwy | milhas por galão na estrada |
| fl | tipo de combustível: r=regular, p=premium, d=diesel, e=ethanol, c=CNG (gás) |
| class | tipo de carro |
Parte 2 - Tabelas de frequências
Em estatística, uma distribuição de frequências é uma tabela ou gráfico que mostra a frequência das variáveis categóricas (nominais ou ordinais) de uma amostra, ou sejam, o número de ocorrências dessas variáveis. Variáveis numéricas podem também ser mostradas em tabelas de frequencias, nesse caso, é necessário classificar as variáveis numéricas em intervalos. Cada entrada na tabela contém a frequência ou a contagem de ocorrências dentro de um grupo ou intervalo específico. Ou seja, uma tabela de frequências resume a distribuição dos valores da amostra.
Use a função table() para criar tabelas de frequências das variáveis categóricas dessa pesquisa (marca, ano, número de cilindros, tipo de marcha, tipo de combustível, tipo de carro). A função table() mostra as frequencias absolutas de cada uma das classes da variável. Por exemplo, para saber quantos carros nessa amostra tem 4 cilindros, quantos tem 5 cilindros, quantos tem 6 cilindros e quantos tem 8 cilindros podemos usar a função table(), inserindo como argumento a variável cyl, como mostrado abaixo:
1 > table(mpg$cyl)
2
3 4 5 6 8
4 81 4 79 70
Essa tabela pode ficar mais compreensível se nomearmos o conjunto de dados. Nesse caso, a variável cylrepresenta o nº de cilindros dos carros, logo:
1 > table(cilindros=mpg$cyl)
2
3 cilindros
4 4 5 6 8
5 81 4 79 70
Podemos também verificar as proporções relativas de cada variável com a função prop.table().
1 > prop.table(table(cilindros=mpg$cyl))
2
3 cilindros
4 4 5 6 8
5 0.34615385 0.01709402 0.33760684 0.29914530
Caso se deseje expressar as proporções em percentuais, basta multiplicar a tabela por 100
1 > prop.table(table(cilindros=mpg$cyl))*100
2
3 cilindros
4 4 5 6 8
5 34.615385 1.709402 33.760684 29.914530
E para arrendar as casas decimais, usamos a função round(). Veja no exemplo abaixo o uso dessa função arrendondando o percentual para 2 casas decimais.
1 > round(prop.table(table(cilindros=mpg$cyl))*100,2)
2
3 cilindros
4 4 5 6 8
5 34.62 1.71 33.76 29.91
Podemos também usar a função table() para construir tabelas de duas ou mais dimensões. Para isso basta incluir as outras variáveis como argumentos da função. Lembre-se que nomear as variáveis pode tornar a tabela mais compreensível.
1 > table(montadora=mpg$manufacturer, cilindros=mpg$cyl)
2
3 cilindros
4 montadora 4 5 6 8
5 audi 8 0 9 1
6 chevrolet 2 0 3 14
7 dodge 1 0 15 21
8 ford 0 0 10 15
9 honda 9 0 0 0
10 hyundai 8 0 6 0
11 jeep 0 0 3 5
12 land rover 0 0 0 4
13 lincoln 0 0 0 3
14 mercury 0 0 2 2
15 nissan 4 0 8 1
16 pontiac 0 0 4 1
17 subaru 14 0 0 0
18 toyota 18 0 13 3
19 volkswagen 17 4 6 0
Nesse caso, a primeira variável será colocadas nas linhas e a segunda variável será colocadas nas colunas da tabela.
Quando temos tabelas de frequências de duas dimensões, podemos extrair as frequencias relativas tanto por linhas como por colunas, para isso basta inserir mais um argumento na função prop.table():
1 - para calcular as frequencias relativas em cada linha
2 - para calcular as frequencias relativas em cada coluna
1 # frequencias relativas calculadas em cada linha
2 > prop.table(table(montadora=mpg$manufacturer, cilindros=mpg$cyl),1)
3
4 cilindros
5 montadora 4 5 6 8
6 audi 0.44444444 0.00000000 0.50000000 0.05555556
7 chevrolet 0.10526316 0.00000000 0.15789474 0.73684211
8 dodge 0.02702703 0.00000000 0.40540541 0.56756757
9 ford 0.00000000 0.00000000 0.40000000 0.60000000
10 honda 1.00000000 0.00000000 0.00000000 0.00000000
11 hyundai 0.57142857 0.00000000 0.42857143 0.00000000
12 jeep 0.00000000 0.00000000 0.37500000 0.62500000
13 land rover 0.00000000 0.00000000 0.00000000 1.00000000
14 lincoln 0.00000000 0.00000000 0.00000000 1.00000000
15 mercury 0.00000000 0.00000000 0.50000000 0.50000000
16 nissan 0.30769231 0.00000000 0.61538462 0.07692308
17 pontiac 0.00000000 0.00000000 0.80000000 0.20000000
18 subaru 1.00000000 0.00000000 0.00000000 0.00000000
19 toyota 0.52941176 0.00000000 0.38235294 0.08823529
20 volkswagen 0.62962963 0.14814815 0.22222222 0.00000000
Mais uma vez, podemos usar a função round para arrendondar os dados. Nesse caso, para facilitar a compreensão do código, podemos fazer cada etapa separadamente, como abaixo:
1 # criando uma tabela 2x2 com montadoras x nº de cilindros - frequencias absolutas
2 > tabela.1 <- table(montadora=mpg$manufacturer, cilindros=mpg$cyl)
3 > tabela.1
4
5 cilindros
6 montadora 4 5 6 8
7 audi 8 0 9 1
8 chevrolet 2 0 3 14
9 dodge 1 0 15 21
10 ford 0 0 10 15
11 honda 9 0 0 0
12 hyundai 8 0 6 0
13 jeep 0 0 3 5
14 land rover 0 0 0 4
15 lincoln 0 0 0 3
16 mercury 0 0 2 2
17 nissan 4 0 8 1
18 pontiac 0 0 4 1
19 subaru 14 0 0 0
20 toyota 18 0 13 3
21 volkswagen 17 4 6 0
1 # calculandoas frequencias relativas NAS LINHAS, em percentuais da tabela recém cria\
2 da
3 > tabela.2 <- prop.table(tabela.1,1)*100
4 > tabela.2
5
6 cilindros
7 montadora 4 5 6 8
8 audi 44.444444 0.000000 50.000000 5.555556
9 chevrolet 10.526316 0.000000 15.789474 73.684211
10 dodge 2.702703 0.000000 40.540541 56.756757
11 ford 0.000000 0.000000 40.000000 60.000000
12 honda 100.000000 0.000000 0.000000 0.000000
13 hyundai 57.142857 0.000000 42.857143 0.000000
14 jeep 0.000000 0.000000 37.500000 62.500000
15 land rover 0.000000 0.000000 0.000000 100.000000
16 lincoln 0.000000 0.000000 0.000000 100.000000
17 mercury 0.000000 0.000000 50.000000 50.000000
18 nissan 30.769231 0.000000 61.538462 7.692308
19 pontiac 0.000000 0.000000 80.000000 20.000000
20 subaru 100.000000 0.000000 0.000000 0.000000
21 toyota 52.941176 0.000000 38.235294 8.823529
22 volkswagen 62.962963 14.814815 22.222222 0.000000
1 # observe que a soma de cada linha deverá ser 100
2 # arredondando os valores para 1 casa decimal.
3 > tabela.3 <- round(tabela.2,1)
4 > tabela.3
5
6 cilindros
7 montadora 4 5 6 8
8 audi 44.4 0.0 50.0 5.6
9 chevrolet 10.5 0.0 15.8 73.7
10 dodge 2.7 0.0 40.5 56.8
11 ford 0.0 0.0 40.0 60.0
12 honda 100.0 0.0 0.0 0.0
13 hyundai 57.1 0.0 42.9 0.0
14 jeep 0.0 0.0 37.5 62.5
15 land rover 0.0 0.0 0.0 100.0
16 lincoln 0.0 0.0 0.0 100.0
17 mercury 0.0 0.0 50.0 50.0
18 nissan 30.8 0.0 61.5 7.7
19 pontiac 0.0 0.0 80.0 20.0
20 subaru 100.0 0.0 0.0 0.0
21 toyota 52.9 0.0 38.2 8.8
22 volkswagen 63.0 14.8 22.2 0.0
Variáveis cagtegóricas são usualmente resumidas com tabelas de frequências como fizemos acima. Variáveis numéricas podem se resumidas em tabelas, desde que seus valores sejam categorizados em classes ou intervalos. Entretanto, no caso de variáveis numéricas, podemos resumir os dados de outras formas, usando medidas numéricas de centralidade e de dispersão desses dados, como veremos a seguir.
Parte 3 - Medidas de Tendência Central
Média e Mediana
A medida mais frequentemente investigada num conjunto de dados é seu centro, ou o ponto no qual as observações tendem a se concentrar. Medidas de tendência central são as estatísticas que descrevem um conjunto de dados pela sua posição central.
Existem várias medidas (estatísticas) que identificam a posição central de um conjunto de dados. As principais estatísticas que resumem um conjunto de dados pela posição central são a média, a mediana e a moda. A média e a mediana são facilmente calculadas no R através das funções mean() e median().
Vamos avaliar a média e a mediana do consumo dos carros na cidade e na estrada, lembrando que esses dados estão na variável cty e hwydo dataset mpg. Lembre-se que para acessar uma variável de um data frame usamos o operador $ da seguinte maneira: nome.do.data.frame$nome.da.variável.
Calculando a média e a mediana do número de milhas percorridas na cidade por galão :
1 > mean(mpg$cty)
2 [1] 16.85897
3
4 > median(mpg$cty)
5 [1] 17
Calculando a média e a mediana do número de milhas percorridas na estrada por galão :
1 > mean(mpg$hwy)
2 [1] 23.44017
3
4 > median(mpg$hwy)
5 [1] 24
Podemos visualizar esses dados num gráfico de barras com as médias de consumo na estrada e na cidade.
1 medias.consumo <- data.frame(cidade=mean(mpg$cty), estrada=mean(mpg$hwy))
2 medias.long <- gather(medias.consumo, local, milhas, cidade, estrada)
3 ggplot(medias.long, aes(x=local, y=milhas)) +
4 geom_col(fill = "cornflowerblue") +
5 ggtitle("Consumo em milhas por galão: cidade x estrada") +
6 geom_text(aes(label=round(milhas,2)), vjust=-0.5)
7 rm(medias.consumo,medias.long)
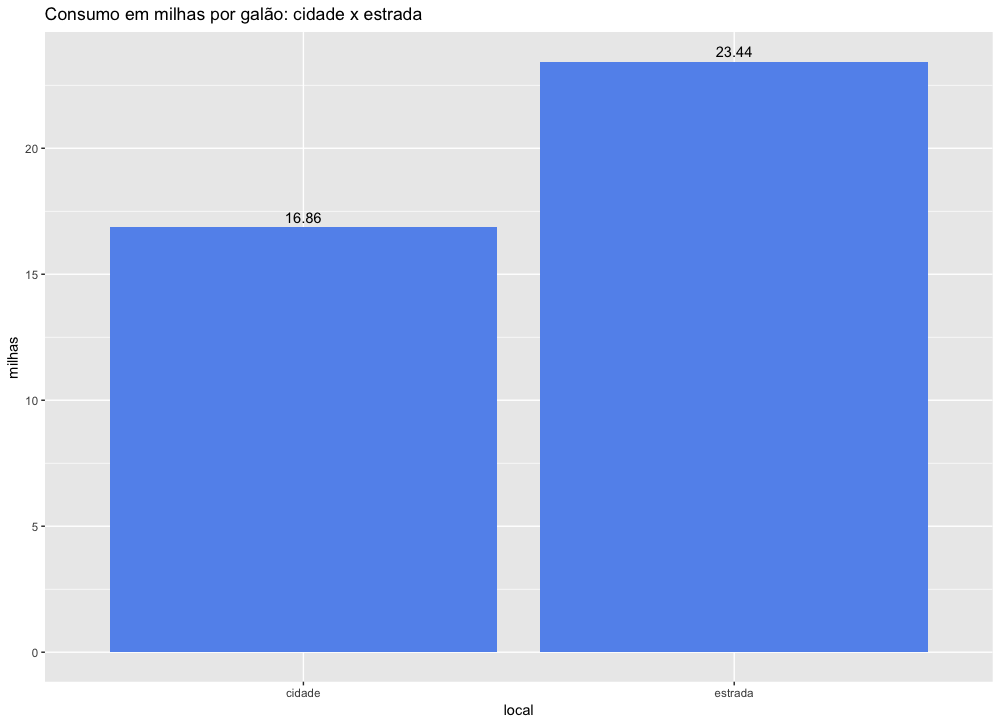
Podemos ver que a quantidade média de milhas percorridas na estrada, com um galão, é bem maior. ou seja, com a mesma quantidade de combustível (um galão) os carros percorrem mais milhas na estrada do que na cidade.
Entretanto, examinar apenas a média ou a mediana desses valores não é suficiente. Uma situação pessoal vivida pelo biólogo Stephen Jay Gould nos mostra como a média é apenas uma parte da história. Em julho de 1982 Gould foi diagnosticado com um Mesotelioma abadominal, uma forma rara e grave de câncer, cuja média de expectativa de vida na ocasião era de 8 meses. Uma leitura superficial desses dados poderia fazer Gould pensar que iria morrer em 8 meses. Entretanto, tendo um sólido conhecimento biológico e estatístico, Gould não se satisfez em conhecer apenas o dados da mediana (ou da média) e procurou descobrir qual seria a variação desses dados, quanto alguém poderia viver com esse tipo de câncer? O que Gould descobriu depois sobre esse câncer é que algumas pessoas conseguiam sobreviver por muitos anos depois do diagnóstico, ou seja, a curva de distribuição da sobrevida era muito assimétrica à direita. Nas palavras de Gould,
Portanto, para analisar de forma adequada um conjunto de dados, precisamos conhecer mais do que apenas a média e a mediana, precisamos conhecer a distribuição dos dados. Vamos ver como estão distribuídos os dados do rendimento dos carros na cidade.
1 ggplot(data=mpg) +
2 geom_density(aes(x=cty), fill= "cornflowerblue", col="blue", alpha=0.5) +
3 xlab("milhas por galão") +
4 ylab("frequencia") +
5 geom_vline(xintercept = mean(mpg$cty), col="red") +
6 labs(title = "Distribuição do rendimento dos carros na cidade",
7 subtitle = "Milhas por galão de combustível",
8 caption = "Fonte: dataset mpg do pacote ggplot2")
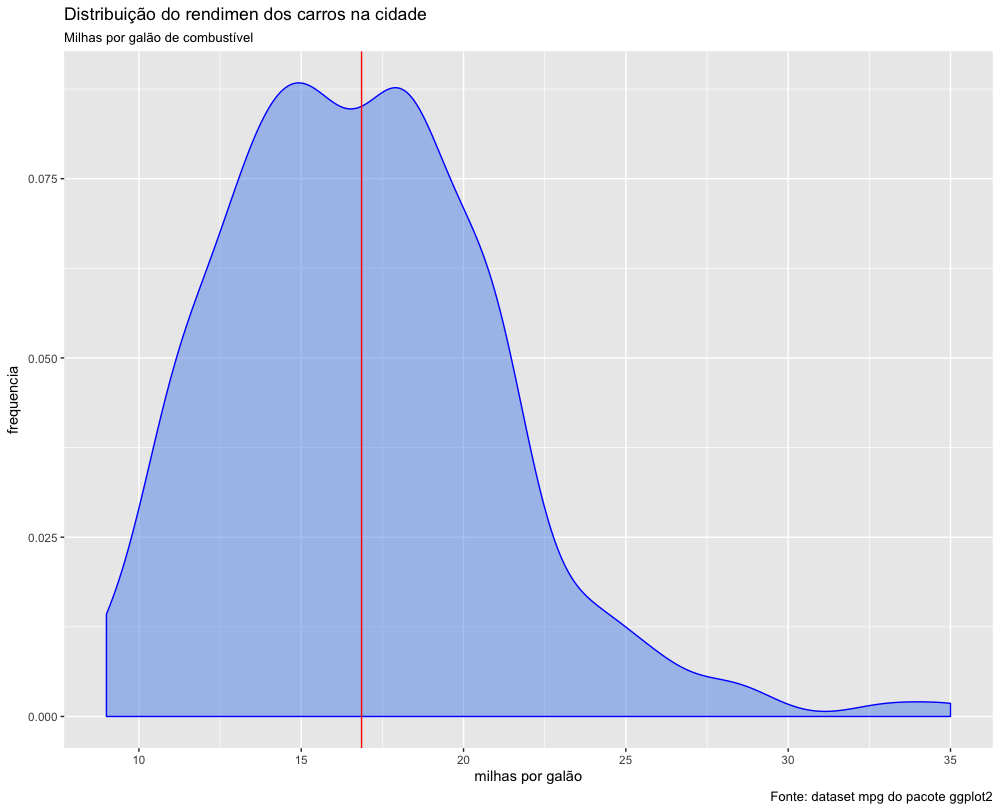
Podemos ver que a média conta apenas uma parte da história, pois existem carros que percorrem menos de 10 milhas com um galão, e alguns poucos carros que percorrem até 35 milhas com um galão de combustível.
Vamos visualizar agora as duas distribuições do rendimento, na cidade e na estrada, sobrepostas uma na outra. As linhas verticais representam as médias da quantidade de milhas percorridas na cidade e na estrada. Não se preocupe em tentar entender esse código agora. Você pode simplesmente copiar e colar esse código em seu script:
1 mpg.long <- mpg %>%
2 select(cty, hwy) %>%
3 gather(key=local, value = distancia, cty, hwy)
4
5 ggplot(data=mpg.long) +
6 geom_density(aes(x=distancia, fill=local), alpha=0.5) +
7 xlab("miles per gallon") + ylab("frequencia") +
8 geom_vline(xintercept = mean(mpg$cty), col="red") +
9 geom_vline(xintercept = mean(mpg$hwy), col="cyan4") +
10 labs(title = "Distribuição do consumo dos carros",
11 subtitle = "Milhas por galão de combustível: cidade x estrada",
12 caption = "Fonte: dataset mpg do pacote ggplot2")
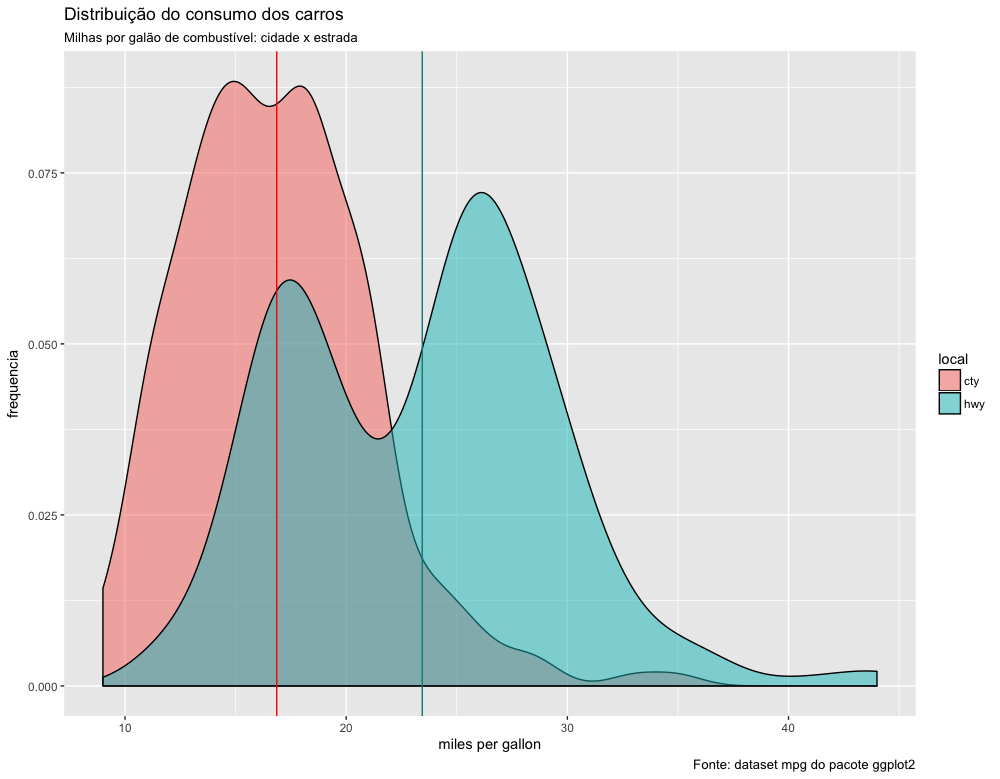
Podemos ver que existe uma grande sopreposição das curvas de distribuição. Não podemos dizer, portanto, que a quantidade de milhas percorridas na cidade será sempre menor que na estrada. Isso só será verdade se estivermos comparando um mesmo tipo de carro. Entretanto, alguns carros conseguem percorrer na cidade mais milhas que outros conseguem percorrer na estrada.
A distribuição dos dados ao redor da média é assimétrica à direita em ambos os conjuntos de dados, pois os valores mais extremos estão à direita.
Observe também que ambas as distribuições têm dois picos, mais evidentes na distribuição do consumo na estrada. Essa distribuição é chamada de bimodal devido a isso.
Vamos analisar agora a distribuição das cilindradas dos veículos, calculando inicialmente a média e a mediana (variável é displ).
1 > mean(mpg$displ) # media das cilindradas
2 [1] 3.471795
3
4 > median(mpg$displ) # mediana das cilindradas
5 [1] 3.3
A mediana é um pouco diferente da média, ligeiramente inferior à média. Se a distribuição desse dados fosse simétrica seria esperado que a média e a mediana fossem iguais, o que não é o caso. Vamos analisar visualmente a distribuição das cilindradas com o código abaixo:
1 ggplot() +
2 geom_density(data=mpg, aes(x=displ),
3 fill="green",
4 color="darkblue",
5 alpha=0.5) +
6 geom_vline(xintercept = mean(mpg$displ),
7 col="red") +
8 geom_vline(xintercept = median(mpg$displ),
9 col="blue") +
10 xlab("cilindradas") +
11 ylab("frequencia") +
12 labs(title = "Distribuição das Cilindradas dos Carros",
13 subtitle = "azul:mediana, vermelho:media",
14 caption = "Fonte: dataset mpg do pacote ggplot2")
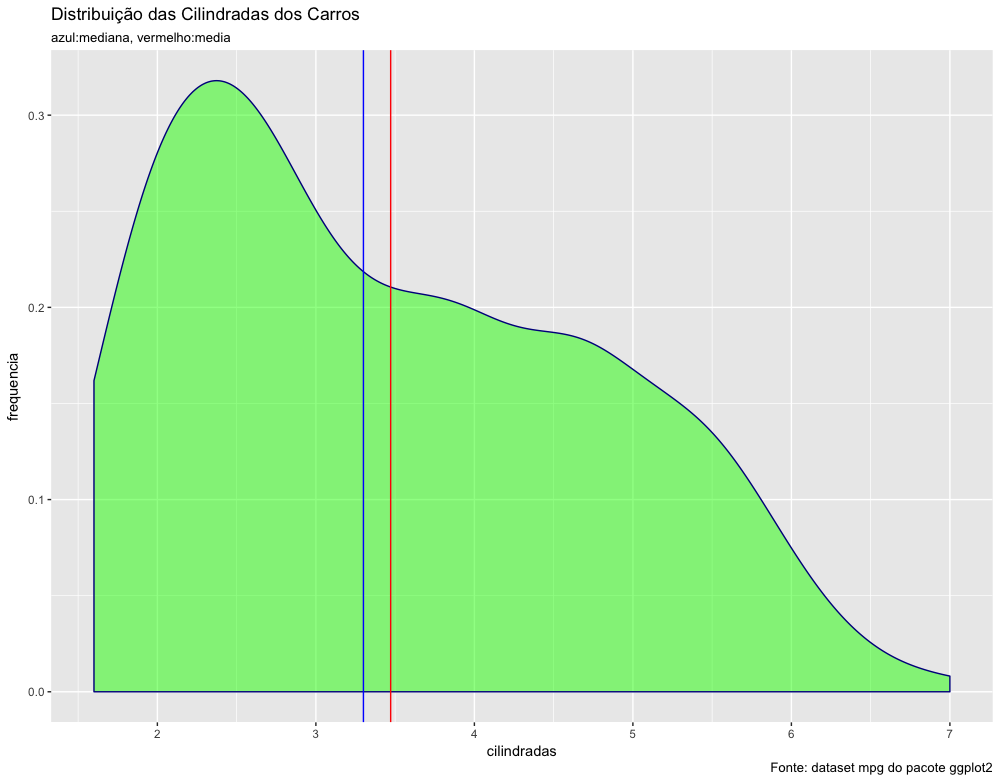
Veja que a distribuição é assimétrica à direita, ou seja, tem valores mais extremos à direita. Esses valores aumentam o valor da média. A mediana, por outro lado, é menos afetada por valores extremos. Você pode verificar no gráfico acima que a mediana (azul) é menor que a média (vermelho).
Visualizar num gráfico a distribuição dos dados é uma etapa chave da análise descritiva de uma pesquisa. Mas precisamos também conhecer as medidas estatísticas usadas para resumir a variação (ou dispersão) dos dados. Essas medidas são o objeto do próximo tópico.
Parte 4 - Medidas de Dispersão
1. Amplitude (range)
2. Amplitude interquartil (IQR = interquartile range)
3. Percentis (quantiles)
4. Variância
5. Desvio padrão (sd = standard deviation)
Como vimos, conhecer o ponto central de uma distribuição não é suficiente para descrever completamente um conjunto de dados. Precisamos saber também como esses dados estão distribuídos. Alguns conjuntos de dados podem ter a mesma média e serem bastante diferentes. Veja nos gráficos abaixo alguns exemplos de dados com a mesma média, mas com grande diferença no que se refere à dispersão dos dados ao redor da média.
1 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 e de\
2 svio padrão=5
3 c1 <- rnorm(1000, mean = 100, sd = 5)
4 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 e de\
5 svio padrão=10
6 c2 <- rnorm(1000, mean = 100, sd = 10)
7 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 e de\
8 svio padrão=20
9 c3 <- rnorm(1000, mean = 100, sd = 20)
10 # cria um conjunto com 1000 números distribuidos de forma normal, com média 100 e de\
11 svio padrão=40
12 c4 <- rnorm(1000, mean = 100, sd = 40)
13 # indica que iremos colocar os gráficos num grid 2x2
14 par(mfrow=c(2,2))
15
16 # gerando os histogramas coloridos.
17
18 hist(c1,
19 col = "orange",
20 breaks = 15,
21 xlim = c(-50, 250),
22 main = "Média = 100 \nDesvio padrão = 5")
23
24 hist(c2,
25 col = "darkorange",
26 breaks = 15,
27 xlim = c(-50, 250),
28 main = "Média = 100 \nDesvio padrão = 10")
29
30 hist(c3,
31 col = "brown",
32 breaks = 15,
33 xlim = c(-50, 250),
34 main = "Média = 100 \nDesvio padrão = 15")
35
36 hist(c4,
37 col = "red",
38 breaks = 15,
39 xlim = c(-50, 250),
40 main = "Média = 100 \nDesvio padrão = 40")
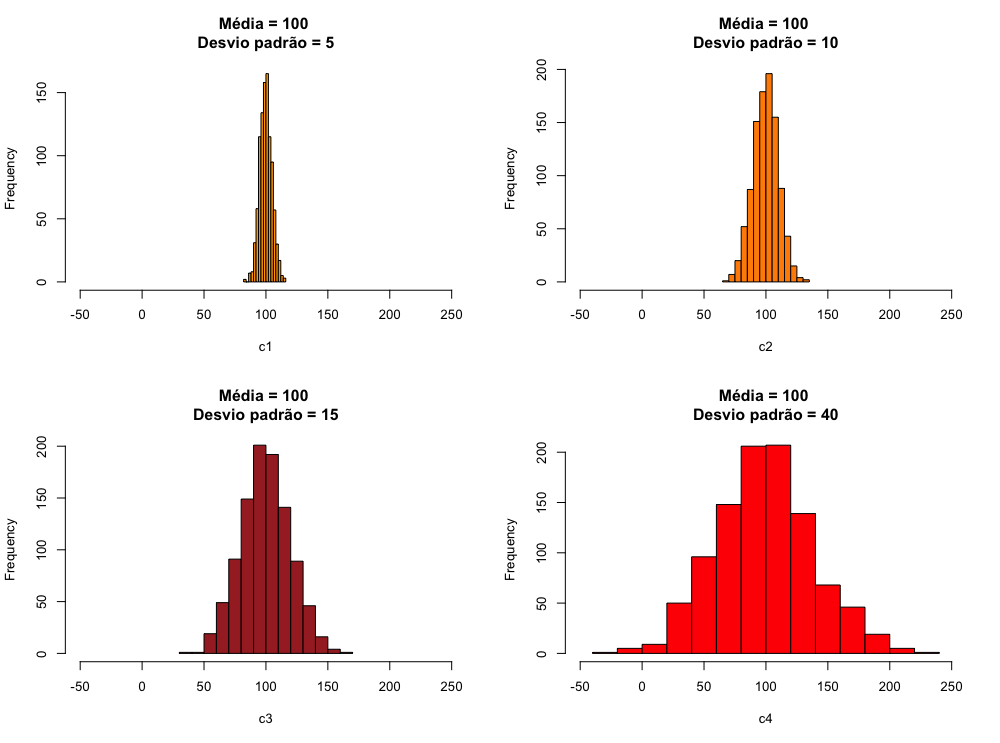
A necessidade descrever melhor um conjunto de dados tornou necessária a criação de medidas que descrevessem a dispersão dos dados ao redor da média.
Amplitude
A medida mais simples de dispersão dos dados é amplitude (range em ingles). A amplitude é a diferença entre o valor máximo e o valor mínimo. Veja no exemplo abaixo uma ilustração visual do significado dessa medida. Copie e cole esse código no seu script R para ver o gráfico.
1 a <- c(1, 1.2, 1.5, 1.7, 1.8, 1.9, 2.2, 2.3, 2.6, 2.7, 8)
2 b <- c(1, 2, 2.5, 4, 4.5, 5.5, 6, 6.4, 7, 7.5, 8)
3
4 tabela <- data.frame(a, b) %>% gather(key = conjunto, value = valores, a, b)
5
6 ggplot(tabela) +
7 geom_dotplot(aes(x=valores, fill=conjunto)) +
8 facet_wrap(~conjunto, ncol=1) +
9 ggtitle("Distribuição dos dados dos conjuntos a e b") +
10 theme(legend.position="none")
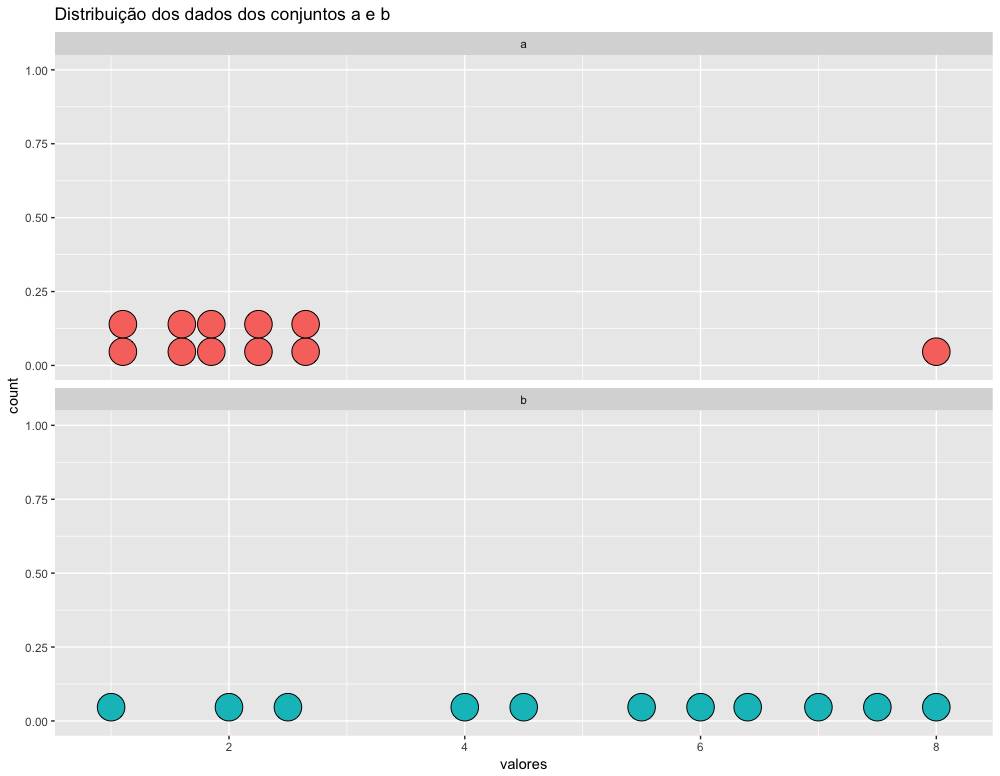
Podemos ver no gráfico acima que ambos os conjuntos tem 1 como valor mínimo e 8 como valor máximo, ou seja, ambos conjuntos de dados tem amplitude igual a 7. A medida da amplitude é simplemente a diferença entre os valores máximo e mínimo. Embora os limites sejam idênticos e a amplitude seja a mesma, esses dois conjuntos tem distribuições muito diferentes.
Podemos saber quais os valores maximos e mínimos com a função range(). Essa função mostra os valores máximo e mínimo de um conjunto de dados.
1 > range(conjunto_1)
2 [1] 1 8
3
4 > range(conjunto_2)
5 [1] 1 8
Vamos descobrir quais limites superiores e inferiores da distancia percorrida pelos carros, com um galão de combustível, na cidade, usando a função range():
1 > range(mpg$cty)
2 [1] 9 35
Podemos ver que existem carros que percorrem apenas 9 milhas com um galão e outros que percorrem 35 milhas com um galão. Ou seja, a amplitude dessa amostra é de 35-9 = 26 milhas.
Entretanto, essa informação é uma medida muito grosseira, pois a amplitude é calculada usando apenas 2 dados do conjunto, os valores máximo e mínimo.
Quartis, Percentil, Qualtil e Amplitude Interquartil
A amplitude interquartil é uma medida de variabilidade, baseada na divisão de um conjunto de dados em quartis. Os quartis dividem um conjunto de dados ordenados em quatro partes iguais. Os valores que separam partes são chamados de primeiro, segundo e terceiro quartis, e são denotados por Q1, Q2 e Q3, respectivamente. O primeiro quartil (Q1) é o valor abaixo do qual estão 25% dos dados, o segundo quartil (Q2) é o valor abaixo do qual estão 50% do dados e o terceiro quartil (Q3) é o valor abaixo do qual estão 75% dos dados.
A divisão dos conjunto de dados em percentuais é o que se denomina de percentil. Os percentis mais famosos são:
- 1º quartil ( = percentil 25%)
- 2º quartil ( = percentil 50% = mediana)
- 3º quartil (= percentil 75%).
Em estatística é comum usar o termo quantil para se referir ao percentil. A única diferença é que o quando usamos percentil usamos o número em sua forma de porcentagem (percentil 50%) e quando usamos o termo quantil usamos o número em sua forma decimal (quantil 0.5). O R tem uma função denominada quantile() para que você possa saber o quantil (ou percentil) que desejar.
Vamos calcular os quantis mais importantes, que são o primeiro, segundo e terceiro quartis: Q1, Q2 e Q3 no conjunto de dados da cilindrada dos carros no dataset mpg.
1 > Q1 <- quantile(mpg$displ, probs = 0.25)
2 > Q2 <- quantile(mpg$displ, probs = 0.50)
3 > Q3 <- quantile(mpg$displ, probs = 0.75)
4
5 > Q1
6 25%
7 2.4
8
9 > Q2
10 50%
11 3.3
12
13 > Q3
14 75%
15 4.6
Podemos ver que o 2º quartil é exatamente a própria mediana. O gráfico abaixo ajuda a visualizar o significado dos quartis. O código abaixo plota um gráfico para continuar nossa análise:
1 ggplot() +
2 geom_density(data=mpg,
3 aes(x=displ),
4 fill="lightblue",
5 color="darkblue")+
6 geom_vline(xintercept = Q1,
7 col="blue") +
8 geom_vline(xintercept = Q2,
9 col="blue") +
10 geom_vline(xintercept = Q3,
11 col="blue") +
12 theme(plot.title = element_text(lineheight=0.8)) +
13 annotate("text",
14 x=2,
15 y=0.1,
16 label= "25%",
17 color="black",
18 fontface=2,
19 size=4) +
20 annotate("text",
21 x=3,
22 y=0.1,
23 label= "25%",
24 color="black",
25 fontface=2,
26 size=4) +
27 annotate("text", x=4,
28 y=0.1,
29 label= "25%",
30 color="black",
31 fontface=2,
32 size=4) +
33 annotate("text",
34 x=5,
35 y=0.1,
36 label= "25%",
37 color="black",
38 fontface=2,
39 size=4) +
40 labs(title = "Distribuição das Cilindradas com os quartis",
41 subtitle = "cada quartil tem 25% dos carros \n Q1=2.4 Q2=3.3 Q3=4.6",
42 caption = "Fonte: dataset mpg do pacote ggplot2")
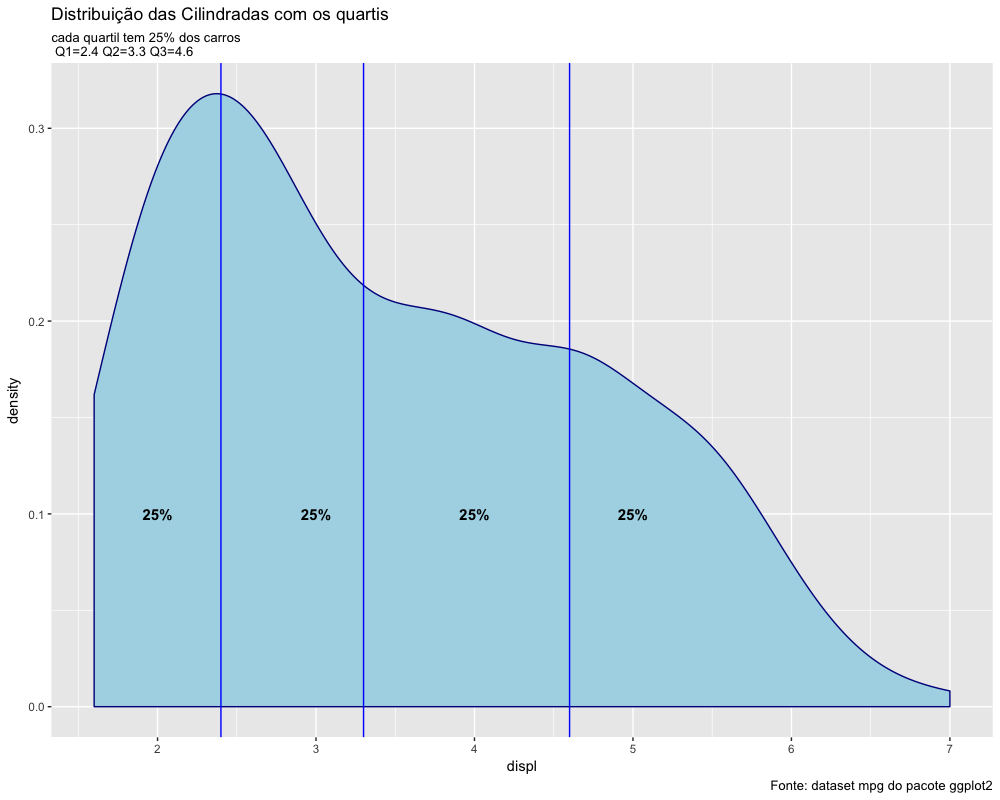
Na estatística descritiva, a amplitude interquartil (IQR) é uma medida de dispersão estatística, sendo igual à diferença entre o quartil superior (Q3) e quartil inferior (Q1). É também chamada de midspread ou middle 50%, ou H-spread.
IQR = Q3 - Q1.
Em outras palavras, a amplitude interquartil (IQR) é 3º quartil menos o 1º quartil. Para compreender o que é o IQR observe os seguintes conjuntos de dados:
1 a <- c(1, 1.2, 1.5, 1.7, 1.8, 1.9, 2.2, 2.3, 2.6, 2.7, 8)
2 b <- c(1, 2, 2.5, 4, 4.5, 5.5, 6, 6.4, 7, 7.5, 8)
Esses dados tem a mesma amplitude, mas seu IQR é bastante diferente e pode ser visualizado num gráfico de boxplot como abaixo:
1 boxplot(a,b,col="lightblue")
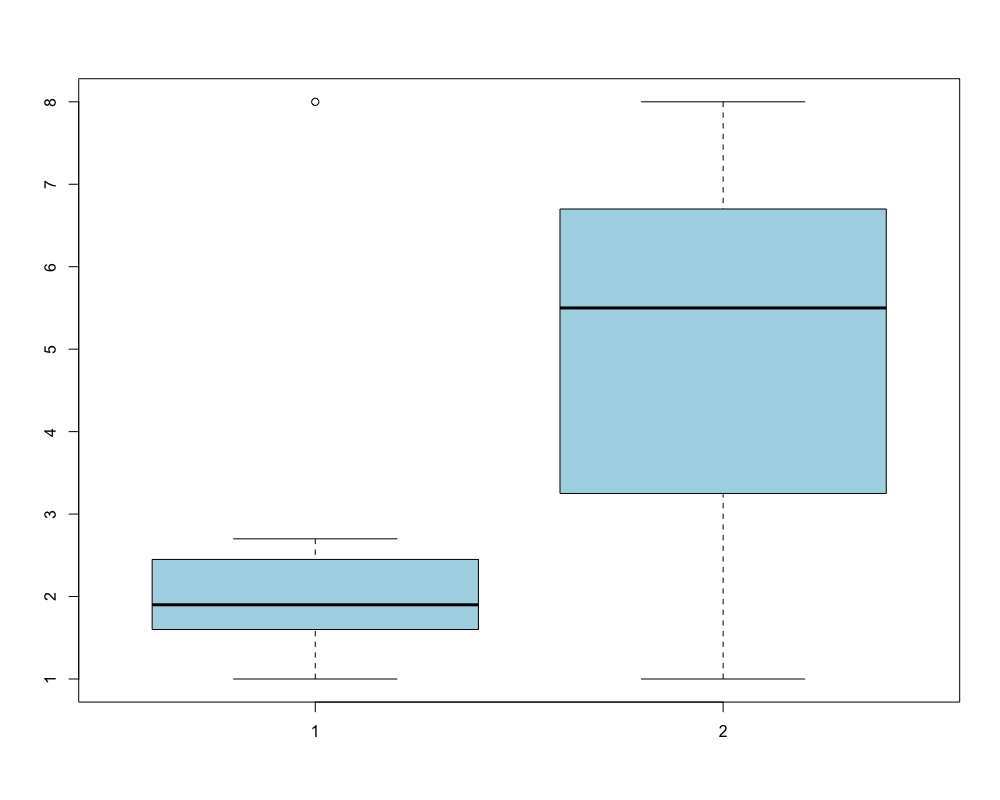
Num boxplot, a caixa representa os 50% dos dados centrais do conjunto, ou seja, os limites das caixas de um boxplot são o 1º e o 3º quartis.
A medida IQR (amplitude interquartil) é mais robusta que a amplitude simples, pois desconsidera os 25% de dados superiores e os 25 inferiores.
Agora vamos criar um grafico de densidade e um boxplot com os dados da cilindrada para visualizarmos essas medidas. O código abaixo gera os gráficos e coloca esses gráficos nos objetos plot1 e plot2:
1 plot1 <- ggplot() +
2 geom_density(data=mpg,
3 aes(x=displ),
4 fill="lightblue",
5 color="darkblue") +
6 xlab("Cilindrada") +
7 geom_vline(xintercept = Q1, col="red") +
8 geom_vline(xintercept = Q3, col="red") +
9 geom_vline(xintercept = Q2, col="blue") +
10 theme(plot.title =element_text(lineheight=0.8)) +
11 ggtitle("Densidade de Probabilidade")
12
13 plot2 <- ggplot() +
14 geom_boxplot(data=mpg,
15 aes(x=0,y=displ),
16 fill="lightblue",
17 color="darkblue") +
18 ylab("Cilindrada") +
19 ggtitle("BoxPlot") +
20 coord_flip()
Para plotar os gráficos apenas digite os nomes dos objetos como abaixo:
1 plot1
2 plot2
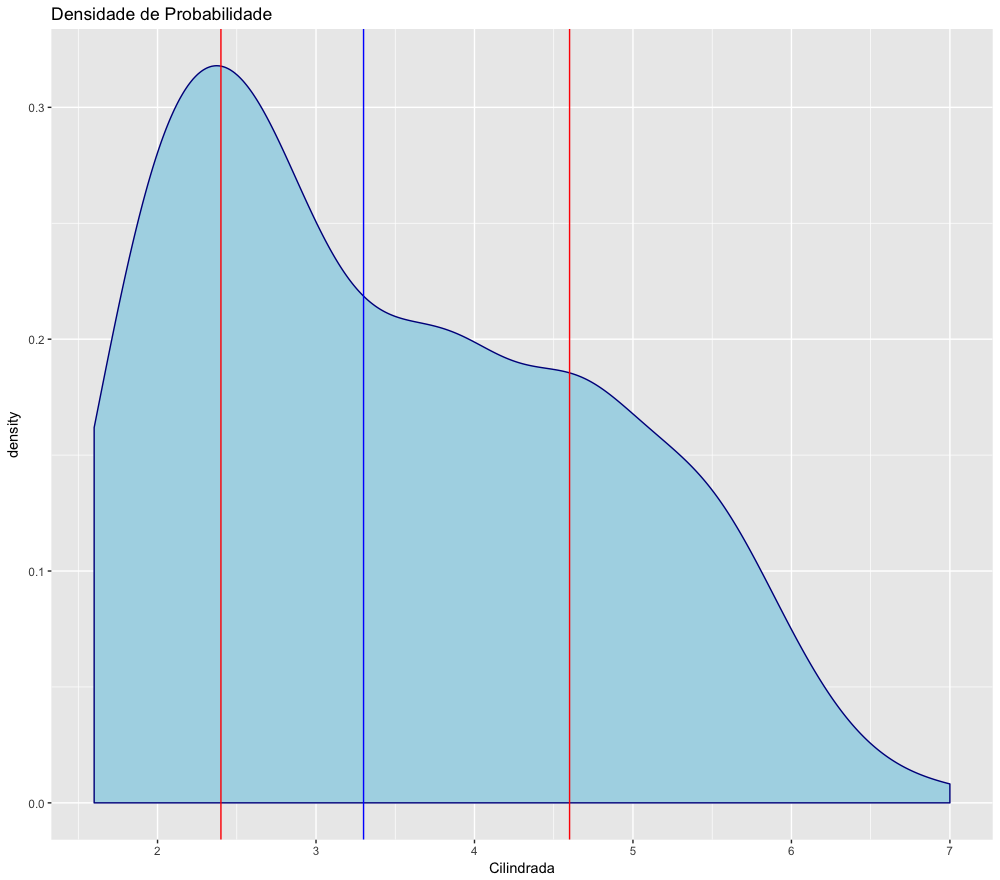
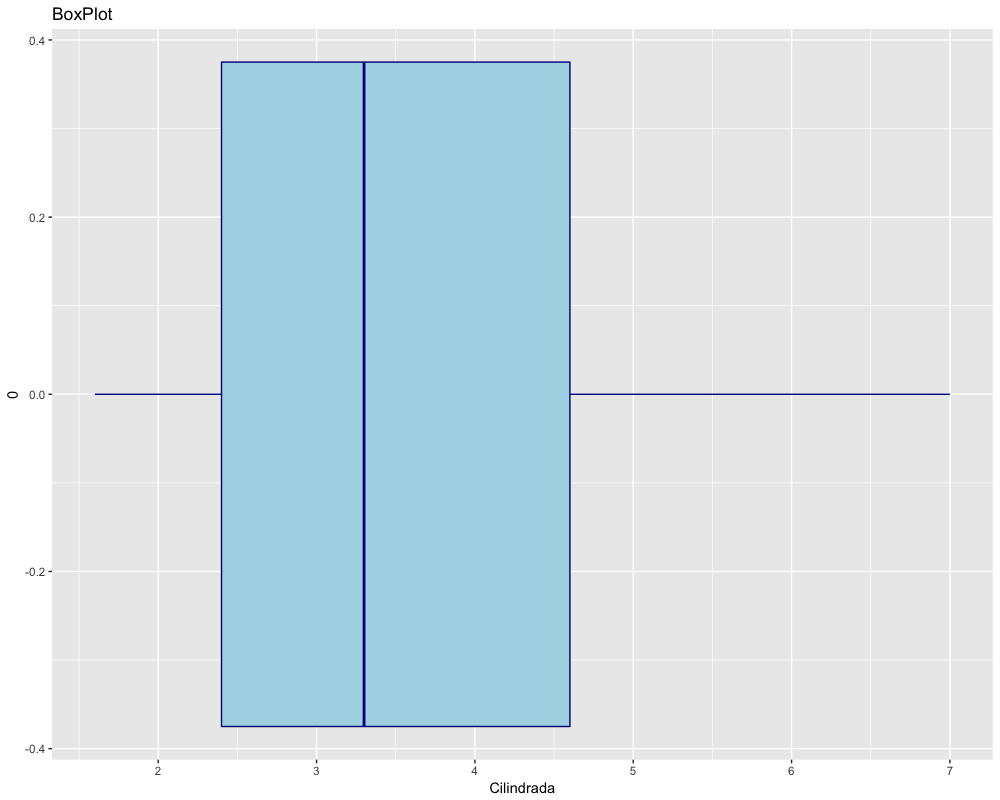
O R tem funções para calcular o percentil que você desejar, mas como é um software estatístico, a função é quantil() e o não percentil. Para obter o valor correspondente ao quantil desejado, é preciso fornecer como argumento da função o objeto com os dados e o quantil desejado. O resultado é o valor que corresponde àquele quantil.
Vamos testar calculando o quantil 0.5, que o mesmo que a mediana, usando os dados das cilindradas:
Calculando o quantil 0.5 (= percentil 50% = mediana):
1 > quantile(mpg$displ, 0.5)
2 50%
3 3.3
Calculando a mediana, para verificarmos que o resultado é o mesmo:
1 > median(mpg$displ)
2 [1] 3.3
O significado da mediana = 3.3
- 50% dos carros nesse dataset tem sua cilindrada acima de 3.3
- 50% dos carros nesse dataset tem sua cilindrada abaixo de 3.3
Variância e Desvio Padrão
Como vimos, a amplitude interquartil (IQR) é uma medida mais interessante que a mera amplitude, pois descarta os valores extremos, sendo assim menos sensível a outliers, ou seja, é uma medida considerada mais robusta que a simples amplitude. entretanto, o IQR também sofre do mesmo problema que a amplitude: é um cálculo que só usa dois dados, deixando muitos dados fora da análise.
Precisamos encontrar uma nova medida que represente melhor a dispersão do conjunto de dados, usando todos os dados desse conjunto.
Uma forma de fazer isso é analisar a distância de cada dado em relação à média, somar todas essas distâncias e dividir o valor encontrado pelo número de elementos do conjunto de dados (234 no nosso caso do dataset mpg). Entretanto, essa simples soma iria resultar sempre em zero, pois esse conjunto de distâncias de cada dado em relação à média iria conter valores positivos e negativos que iriam se cancelar totalmente. Vamos testar isso com o R no conjunto de dados do consumo dos carros na cidade do dataset mpg.
1 desvios <- (mpg$cty - mean(mpg$cty))
2 > resultado <- sum(desvios)/234
3 > resultado
4 [1] 1.275333e-15
Para visualizarmos esse número da forma usual usamos a função format():
1 > format(resultado, scientific = FALSE)
2 [1] "0.000000000000001275333"
O resultado dessa conta no R não foi exatamente ZERO devido a problemas de arredondamento. Mas, teoricamente, se não houvessem erros de arredondamente, o valor seria exatamente sempre ZERO. Logo, essa medida é inútil.
Uma possibilidade alternativa é somarmos os módulos das distâncias, para que os valores não se cancelem, podemos fazer isso no R usando a função abs().
1 > resultado2 <- sum(abs(desvios))/234
2 > resultado2
3 [1] 3.347359
Entretanto, a operação de módulo (ou valor absoluto) é uma operação matemática com muitas limitações. Existe um outro modo melhor de evitarmos valores negativos nas distancias calculadas: podemos usar o quadrado das distâncias. Essa é a medida conhecida como variância.
Variância
Calculando a dispersão elevando ao quadrado para evitar valores negativos:
1 > resultado3 <- sum((desvios)^2)/234
2 > resultado3
3 [1] 18.03567
É preciso, entretanto, fazer uma observação sobre o denominador desse fórmula. Quando calculamos a variância de uma população usando todos os dados da população o denominador é justamente o tamanho dessa população.
Entretanto, na maioria das vezes, trabalhamos apenas com uma amostra da população. Uma das principais funções da estatística é fazer inferências sobre a população usando como referência uma amostra. Nesse caso, quando estamos analisando uma amostra, o denominador da variância precisa de um pequeno ajuste, ao invés de n, o deve ser n-1. Ou seja, no caso de nossa amostra de 234 carros, usaremos no denominador o valor 233 (=234-1).
1 > resultado4 <- sum((desvios)^2)/233
2 > resultado4
3 [1] 18.11307
Essa é a medida denominada de variância amostral. E o R tem uma função própria para isso^ a função var():
1 > var(mpg$cty)
2 18.11307
A variância encontrada foi de 18.11307 milhas ao quadrado.
Veja que o resultado da operação var(mpg$cty) foi idêntico ao calculado acima passo-a-passo. Ou seja, a fórmula da função var() utiliza no denominador o valor n-1. Para calcular a variância populacional deveríamos usar n no denominador, mas o R não tem essa função.
Para pensar: como você pode fazer para obter o valor da variância populacional a partir da função var( ) do R? Podemos encontrar o resultado desejado simplesmente multiplicando o resultado encontrado por (n-1)/n
A variância, calculada com a nova fórmula de variância populacional, é de 18.03567 milhas ao quadrado.
Desvio Padrão
Apesar da importância da variância, essa medida tem um pequeno probleminha: ao elevar ao quadrado, a unidade de medida dos dados também foi elevada ao quadrado (milhas ao quadrado). Portanto, se nossa amostra se refere à altura em metros, a unidade da variância é metros ao quadrado, se a unidade de nossa medida são dias, horas, centímetros, a unidade de medida da variância será dias2 , horas2 , cm2 . Essas medidas são de difícil interpretação, daí a necessidade de ajustarmos essas medidas.
O modo mais simples de fazer isso é justamente fazendo a raiz quadrada da variância Desse modo, a unidade de medida volta a ser a original. A raiz quadrada da variância foi nomeada de desvio padrão, por ser a medida mais usada (padrão) de desvio dos dados, ou seja, de quanto os dados se desviam da medida central (média).
O R tem uma função preparada para o cálculo do desvio padrão: sd(). Lembre-se que na língua inglesa desvio padrão se escreve standard deviation, daí sd(). Vamos calcular o desvio padrão do consumo dos carros na cidade:
1 > sd(mpg$cty)
2 [1] 4.255946
Observe que o desvio padrão calculado acima é o desvio padrão amostral, com n-1 no denominador. Caso se pretenda calcular o desvio padrão populacional o resultado acima deve ser multiplicado por (n-1)/n (no caso especifico acima, devemos multiplicar por 233/234.
Propriedades do Desvio Padrão
O desvio padrão é a medida de dispersão mais comum na estatística, que utiliza em seus cálculos todos os dados. Devido ao fato de uma das etapas do cálculo do desvio padrão envolver a operação de elevar ao quadrado, o desvio padrão será sempre um valor positivo (ou zero). Se todos os valores dos dados forem iguais, o desvio padrão será ZERO. Uma das vantagens do desvio padrão é que a unidade de medida é a mesma dos dados da amostra, ao contrário da variância, na qual a unidade de medida é o quadrado da unidade original.
Ao analisar o desvio padrão, é preciso ter em mente que desvios pequenos indicam que os dados se agrupam em torno da média e desvios grandes indicam que os dados estão dispersos numa grande amplitude. Finalmente, como o cálculo do desvio padrão leva em conta todos os elementos do conjunto de dados, o resultado é que o desvio padrão é sensível aos outliers (valores extremos).
Conclusões finais
Nesse capítulo estudamos as medidas estatísticas de tendência central e de dispersão. Vimos também que essas medidas numéricas são melhor compreendidas quando associadas a gráficos que ilustrem o que os números indicam. A próxima etapa da análise descritiva é justamente aprender a criar gráficos que ilustrem os dados.
Referências
- Stephen Few. Now You See it. Simple Visualization Techniques for Quantitative Analisys. Analytics Press, 2009.
- Stephen Jay Gould. The Median Isn’t the Message. American Medical Association Journal of Ethics, January 2013, 15(1):77-81.
Manipulando dados no R
No capítulo passado aprendemos a usar as funções estatísticas para calcular os pontos centrais e a dispersão dos dados:
- média - mean()
- mediana - median()
- amplitude - range()
- quantiles (percentis) - quantile()
- variância - var()
- desvio padrão - sd()
O conjunto de pacotes tidyverse
Precisamos agora aprender a usar as funções de manipulação de dados do pacote dplyr. Instalar o tidyverse é o modo mais fácil de ter acesso a esse pacote, pois o dplyr faz parte do conjuto de pacotes do tidyverse.
A primeira etapa é instalar o pacote tidyverse, caso ainda não tenha feito isso. Se você já instalou esse pacote, passe para a próxima etapa. Lembre-se, que um pacote só precisa ser instalado uma única vez.
A segunda etapa é carregar o pacote na sessão. Isso é feito com o comando library(). O carregamento dos pacotes necesssários deve ser feito sempre no início de seu script.
1 library(tidyverse)
O pacote dplyr
O dplyr é um pacote para manipulação de dados, escrito e mantido por Hadley Wickham, com funções úteis e fáceis de usar para exploração dos dados. As principais funções desse pacote são:
| função | ação |
|---|---|
| filter() | seleciona linhas de acordo com argumentos lógicos |
| select() | seleciona variáveis (colunas) |
A função `filter()
As linhas de um data frame representam as diferentes observações. Por exemplo, em pesquisas na área de saúde, geralmente cada linha representa um participante da pesquisa.
Frequentemente precisamos acessar subgrupos desse grande conjunto de participantes, ou seja, precisamos selecionar subgrupos nos quais desejamos fazer nossa análise. Isso é feito no R com a função filter() do pacote {dplyr}.
O modo de usar a função filter()é muito simples: o primeiro argumento é o data frame a ser usado, em seguida as expressões lógicas para filtrar/selecionar as linhas do data.frame, como mostaremos a seguir, usando novamente o dataset mpg do pacote ggplot2 (Esse pacote também faz parte do tidyverse).
Vamos carregar esses dados com a função data():
1 data(mpg)
Relembrando o significado de cada variável:
| variável | significado |
|---|---|
| manufacturer | marca |
| model | modelo |
| displ | cilindradas (Engine Displacement) |
| year | ano de fabricação |
| cyl | número de cilindros |
| trans | tipo de marcha: automática / manual |
| drv | tração: f=frontal, r=traseira, 4=4x4 |
| cty | milhas por galão na cidade |
| hwy | milhas por galão na estrada |
| fl | tipo de combustível: r=regular, p=premium, d=diesel, e=ethanol, c=CNG (gás) |
| class | tipo de carro |
Sabemos que para acessar uma variável de um data frame usamos o operador $ e que a variável com os nomes das montadores é manufacturer. Vamos então checar quais são as montadoras dos carros dessa pacote com o comando unique().
1 unique(mpg$manufacturer)
O resultado do comando acima é a lista de todos as montadoras no dataset, sem repetição:
1 > unique(mpg$manufacturer)
2 "audi" "chevrolet" "dodge" "ford"
3 "honda" "hyundai" "jeep" "land rover"
4 "lincoln" "mercury" "nissan" "pontiac"
5 "subaru" "toyota" "volkswagen"
Como podemos ver, esse banco de dados tem carros de várias montadoras. Em análises estatísticas que é frequentemente necessário separar os dados de acordo com alguma regra, por exemplo, de acordo com a montadora.
Para separar um grupo, com base em alguma regra, usamos a função filter(). Podemos, por exemplo querer analisar apenas os carros das montadoras audi, toyota, ford, chevrolet. Vamos fazer um novo data frame com cada uma dessas montadoras e calcular a média e o desvio padrão do desempenho/consumo na cidade (milhas percorridas com um galão) de cada uma dessas montadoras.
Filtrando os carros da Audi:
1 audi <- filter(mpg, manufacturer == "audi")
2 mean(audi$cty)
3 sd(audi$cty)
O resultado dos comandos acima é:
1 > mean(audi$cty)
2 [1] 17.61111
3
4 > sd(audi$cty)
5 [1] 1.974511
Filtrando os carros da Toyota:
1 toyota <- filter(mpg, manufacturer == "toyota")
2 mean(toyota$cty)
3 sd(toyota$cty)
O resultado dos comandos acima é:
1 > mean(toyota$cty)
2 [1] 18.52941
3
4 > sd(toyota$cty)
5 [1] 4.046961
Filtrando os carros da Ford:
1 ford <- filter(mpg, manufacturer == "ford")
2 mean(ford$cty)
3 sd(ford$cty)
O resultado dos comandos acima é:
1 > mean(ford$cty)
2 [1] 14
3
4 > sd(ford$cty)
5 [1] 1.914854
Filtrando os carros da Chevrolet:
1 chev <- filter(mpg, manufacturer == "chevrolet")
2 mean(chev$cty)
3 sd(chev$cty)
O resultado dos comandos acima é:
1 > mean(chev$cty)
2 [1] 15
3
4 > sd(chev$cty)
5 [1] 2.924988
Podemos ver com essa análise inicial que os carros da Audi e da Toyota percorrem mais milhas com um galão que os carros da Chevrolet e da Ford. Podemos ver também que os carros da Audi, apesar de terem uma média de milhas percorridas menor que os carros da Toyota, a performance da Audi tem um desvio padrão menor, indicando que seus carros estão com o consumo consistentemente perto da média. A Toyota, por outro lado, tem um desvio padrão maior, o que indica que alguns carros tem um consumo bem mais inferior que a média e outros carros tem um consumo bem maior que a média.
É interessante também podermos comparar visualmente essas quatro marcas que foram nosso interesse. Para isso vamos usar a função filter() novamente, dessa vez construindo um único data frame com essas quatro montadoras, que nomearei de atfc (iniciais de audi, toyota, ford e chevrolet). Para isso devemos substituir o operador de igualdade (==)
pelo operador (%in%) e criar um vetor com as montadoras que quero no meu novo data frame:
1 atfc <- filter(mpg, manufacturer %in% c("audi", "toyota", "ford", "chevrolet"))
2 boxplot(cty~manufacturer, data=atfc, col="lightblue")
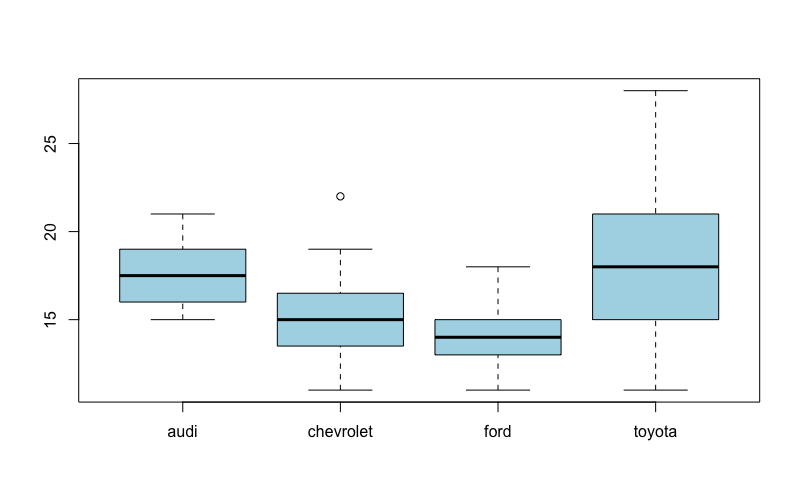
Podemos usar o comando filter() para filtramos os dados de acordo com regras numéricas. Podemos por exemplo separar os carros abaixo de 2.0 cilindradas, aqueles entre 2.0 e 3.0 cilindradas e os carros com 4.0 ou mais cilindradas. Vamos ver se as cilindradas influenciam no quanto um carro é capaz de percorrer com um galão. Lembre-se de que as cilindradas estão na variável displ, que é uma abreviação de Engine Displacement.
1 cilin.1a2 <- filter(mpg, displ<=2)
2 cilin.2a3 <- filter(mpg, displ>2 & displ<4)
3 cilin.4a7 <- filter(mpg, displ>=4)
Agora podemos calcular as médias das distâncias percorridas na cidade em cada um desses grupos:
1 mean(cilin.1a2$cty)
2 mean(cilin.2a3$cty)
3 mean(cilin.4a7$cty)
O resultado dos comandos acima é:
1 > mean(cilin.1a2$cty)
2 [1] 22.34884
3
4 > mean(cilin.2a3$cty)
5 [1] 17.79048
6
7 > mean(cilin.4a7$cty)
8 [1] 12.97674
Podemos ver que à medida que as cilindradas aumentam, diminui-se a distância percorridas com um galão de combustível. Isso pode ser mais facilmente visualizado num gráfico de dispersão, usualmente chamado de scatter plot:
1 ggplot(mpg, aes(x=displ, y=cty)) +
2 geom_jitter() +
3 geom_smooth(method = "lm")
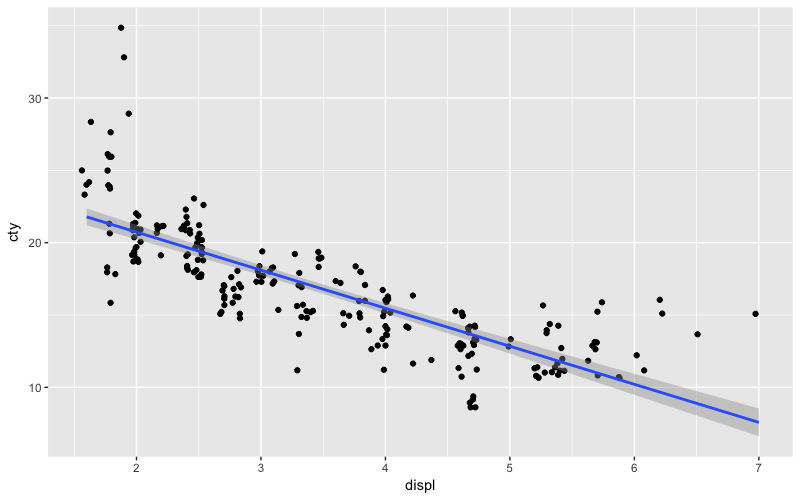
Com esse gráfico podemos ver que existe uma correlação negativa entre as cilindradas e a distância percorrida com um galão de combustível: quanto maior a cilindrada, menor a distância média percorrida. Em outras palavras: um carro 1.0 é mais econômico que um carro 4.0.
A função select()
A função select() possibilita selecionar as variáveis que interessam e criar novos data frames apenas com os dados selecionados. Como exemplo, vamos imaginar a situação na qual só interessam as variáveis modelo, distância percorrida na cidade e na estrada. Vamos criar um novo data frame chamado new.df só com essas variáveis. A função select() é usada da seguinte maneira:
select(data.frame, variável1, variável2, …)
1 new.df <- select(mpg, model, cty, hwy)
2 str(new.df)
1 Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 234 obs. of 3 variables:
2 $ model: chr "a4" "a4" "a4" "a4" ...
3 $ cty : int 18 21 20 21 16 18 18 18 16 20 ...
4 $ hwy : int 29 29 31 30 26 26 27 26 25 28 ...
Veja que esse novo data frame só tem 3 variáveis: model, cty e hwy.
Existem muitas outros modos de usar essa função, para mais detalhes digite ?select no console.
Visualizando dados - Gráficos básicos do R
Introdução
Nos capítulos passado aprendemos a usar as funções estatísticas para descrever um conjunto de dados, através de tabelas de frequência, a calcular os pontos centrais, as medidas de dispersão dos dados e a manipular um conjunto de dados através das funções filter() e select() do pacote dplyr. Essas medidas estatísticas servem para resumir um grande conjunto de dados com poucos números. Entretanto, essas medidas numéricas são bastante limitadas e tornam a apreciação dos conjunto de dados muito maçante e bastante técnica. Por outro lado, a análise visual dos dados, além de mais atrativa, é muitas vezes mais compreensiva. Na palavras de John Tukey:
“A grande virtude da representação gráfica é que ela serve para mostrar de forma clara e efetiva a mensagem por trás de quantidades cjuos cálculos ou observações estão longe de serem simples”
“One great virtue of good graphical representation is that it can serve to display clearly and effectively a message carried by quantities whose calculation is far from simple”
Nossa habilidade de pensar é grandemente aprimorada quando representamos quantidades numéricas de forma visual. Mas, apesar da criação de gráficos ser uma arte bem antiga, seu uso científico para representação de dados numéricos tem uma história relativamente recente. O uso de gráficos para apresentação de dados só se tornau uma prática comum depois dos trabalhos de William Playfair no final do século 19 e início do século 19 (Friendly & Denis, 2005; Fienberg, 1979).
Construir um gráfico nos séculos 18 e 19 era um árduo trabalho artístico e intelectual. Nos quase 200 anos desde que gráficos passaram a ser usados, sua construção deixou de ser uma tarefa de manual e se tornou um trabalho computacional. Com o advento das capacidades gráficas dos computadores, a partir do século 20, é que a criação dos mais variados tipos de gráficos estatísticos se tornou algo simples de ser realizado.
A linguagem R, desde seu início, foi criada com essa pretensão de ser uma linguagem estatística voltara para a construção de gráficos (Ihaka & Gentleman, 1996). Mas somente por volta de 2005 é que se tornou clara a noção do que é de fato um gráfico, como descrever um gráfico e como criar um gráfico. Foi com o trabalho entitulado “The grammar of graphics”, de Leland Wilkinson em 2005, que se tornou possível construir uma verdadeira linguagem computacional para os gráficos. E essa linguagem atingiu seu pleno potencial quando a gramática dos gráficos foi implementada no R com o pacote ggplot2, desenvolvido por Hadley Wickham em 2005 (Wickham, 2009).
Entretanto, essa aparente simplicidade pode ser enganosa. Numa pesquisa de 2012, foram detectados erros em 30% dos gráficos da revista Science, uma das mais prestigiadas revistas científicas do mundo (Cleveland, 2012). Atualmente, mais importante do que gerar um gráfico, é saber qual gráfico mais adequado usar e como interpretar corretamente as informações de um gráfico científico.
Objetivos de aprendizagem
Capacitar os alunos a criarem gráficos com as funções básicas do R. A criação de gráficos com o pacote ggplot será tema de outro capítulo.
Carregamento dos dados
Para facilitar essa aula, vamos usar o dataset mpg que já vem com o ggplot2.
A primeira etapa é instalar o pacote tidyverse, que contém o ggplot2. Se você já instalou esse pacote, passe para a próxima etapa. Lembre-se, que um pacote só precisa ser instalado uma única vez, se você já fez isso, não precisa fazer novamente.
A segunda etapa é carregar o pacote tidyverse na sessão. Isso é feito com o comando library(). O carregamento dos pacotes necesssários deve ser feito sempre no início de seu script.
1 > library(tidyverse)
A terceira etapa é carregar o dataset mpg. Para isso basta usar o comando abaixo:
1 > data(mpg)
Esse dataset já foi analisado numericamente nos capítulos passados, e possui 243 linhas (observações) com 11 variáveis. O significado de cada variável está descrito na documentação de ajuda do dataset mpg e pode ser visualizado com o comando ?mpg no console. A tabela abaixo mostra o significado de cada variável:
| variável | significado |
|---|---|
| manufacturer | marca |
| model | modelo |
| displ | cilindradas (Engine Displacement) |
| year | ano de fabricação |
| cyl | número de cilindros |
| trans | tipo de marcha: automática / manual |
| drv | tração: f=frontal, r=traseira, 4=4x4 |
| cty | milhas por galão na cidade |
| hwy | milhas por galão na estrada |
| fl | tipo de combustível: r=regular, p=premium, d=diesel, e=ethanol, c=CNG (gás) |
| class | tipo de carro: compact, midsize, suv, 2seater, minivan, pickup ou subcompact |
Parte 1 - Visualizando dados categóricos.
Variáveis categóricas podem ser representadas por gráficos de barras, gráficos de pizza.
Gráficos de Pizza - picharts
Gráfico de Pizza, também chamado de gráfico de torta ou de setor, é um diagrama circular fatiado como uma pizza, cujos valores de cada categoria são proporcionais à área de cada fatia. Ou seja, um gráfico de pizza é uma representação gráfica de uma tabela de frequências. Portanto, a criação da tabela de frequências deve sempre preceder a criação de um gráfico de pizza.
Mas é preciso ressaltar que gráficos de pizza tem um uso bastante restrito:
- São usados apenas para variáveis categóricas nominais, não são adequados para variáveis ordinais.
- São usados para explicitar a dominância de uma categoria sobre as outras
- Não servem para distinguir pequenas diferenças entre as categorias.
- Não são adequados para representar variáveis com mais de 5 níveis, pois o gráfico fica confuso.
Algumas dicas ajudam a criar gráficos de pizza adequados: jamais use efeitos de 3D em seus gráficos, nem mesmo nos gráficos de pizza; evita usar muitas cores, mas pode-se sar uma cor diferente para destacar o segmento de interesse.
O R tem uma função extremamente simples para criar gráficos de pizza: pie().
Vejamos como podemos usar um gráfico de pizza para representar o quanto é mais comum o uso de combustível regular pelos carros de nossa amostra:
1 # Criamos a tabela de frequencias com a função table
2 > tab.1 <- table(mpg$fl)
3
4 # geramos o gráfico com a tabela como argumento da função pie()
5 > pie(tab.1)
Ou simplesmente:
1 > pie(table(mpg$fl))
Um gráfico deve ter a função de simplificar a compreensão dos dados, portanto, é sempre adequado colocar títulos e legendas. Isso pode ser feito com os argumentos da função das funções gráficas no R.
main = "título"labels = c("nome do segmentos 1", "nome do segmento 2", ...)
1 > pie(table(mpg$fl),
2 main = "Combustíveis usados",
3 labels = c(c="Gás Veícular - CNG", d="diesel", e="etanol", p="premium", r="regu\
4 lar"))
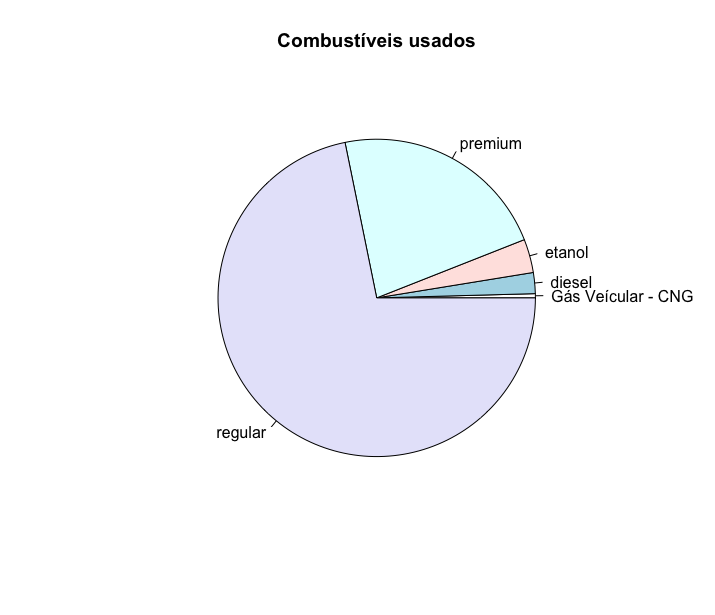
Se é do interesse do gráfico mostrar que a gasolina regular é mais frequentes que as outras, então podemos colorir de forma diferente o setor de interesse com o argumento col= c("cor do segmentos 1", "cor do segmento 2", ...).
1 > pie(table(mpg$fl),
2 main = "Combustíveis usados",
3 labels = c(c="gás Veícular - CNG", d="diesel", e="etanol", p="premium", r="regu\
4 lar"),
5 col = c(c="gray", d="gray", e="gray", p="gray", r="dodg\
6 erblue"))
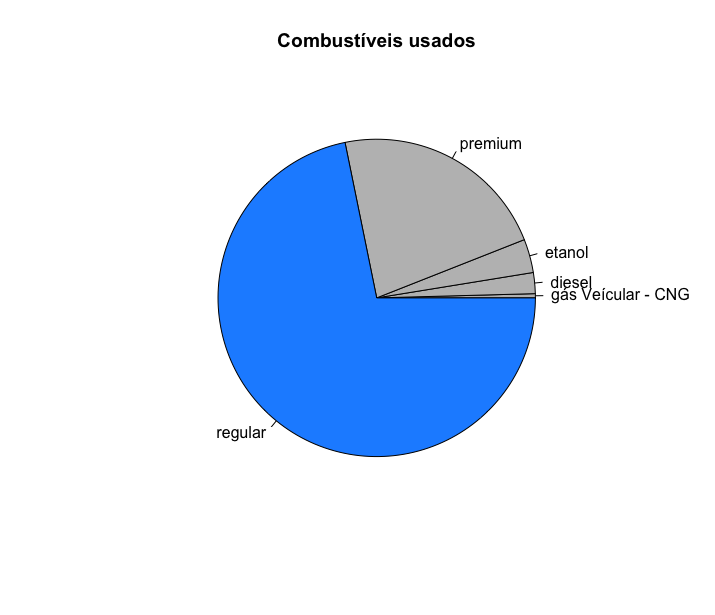
Finalmente, veja que num gráfico de pizza com muitos setores é difícil comparar as diferentes áreas, e portanto, o gráfico perde sua função de esclarecer os dados. Existem cerca de 7 diferentes tipos de carros nesse dataset, usar um gráfico de pizza para mostrar as frequencias de cada tipo não é uma boa idéia. Como você poderá ver, é muito difícil avaliar as diferentes áreas das fatias da pizza e portanto, não sabemos ao certo quais as frequencias dos carros: Existem mais pickups ou subcompactos ou midsizes?
1 > pie(table(mpg$class))
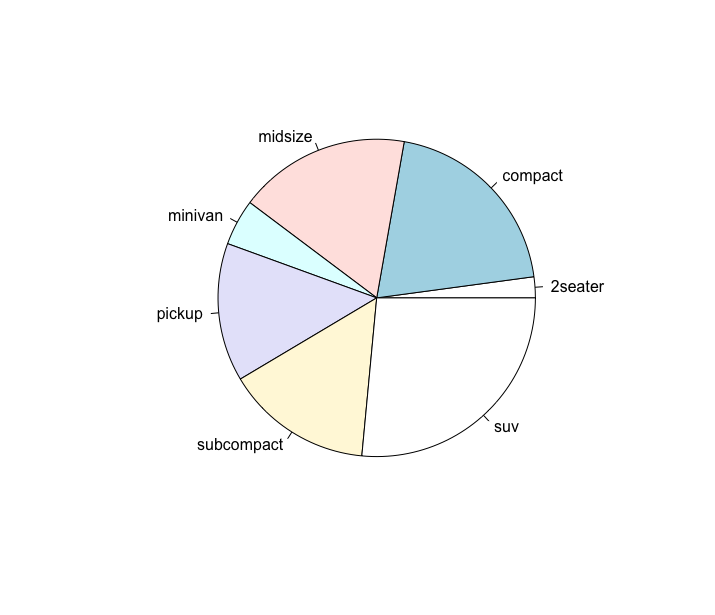
A forma mais adequada de representar as frequências de mais de 4 ou 5 categorias é através de um gráfico de barras, como veremos a seguir.
Gráficos de Barra - barplot
Um gráfico de barras é também uma representação gráfica de uma tabela de frequências. Portanto, a criação da tabela de frequências também deve sempre preceder a criação de um gráfico de barras. Num gráfico de barras o comprimento (ou área) das barras é proporcional aos valores que representam e podem ser desenhadas verticalmente ou horizontalmente.
Gráficos de barras tem uma utilização mais ampla, pois são fáceis de serem lidos, servem para representar frequências de variáveis categóricas nominais ou ordinais, são mais fáceis quando temos de comparar diferenças entre categorias, ainda que pequenas.
Algumas dicas ajudam a criar gráficos de barra adequados: jamais use efeitos de 3D em seus gráficos, evita usar muitas cores, mas pode-se usar uma cor diferente para destacar o segmento de interesse. Isso é mais útil do que colocar cada segmento com uma cor.
O R tem uma função extremamente simples para criar gráficos de barra: barplot().
Vejamos como podemos usar um gráfico de pizza para representar as frequências das categorias dos carros de nossa amostra:
1 > barplot(table(mpg$class))
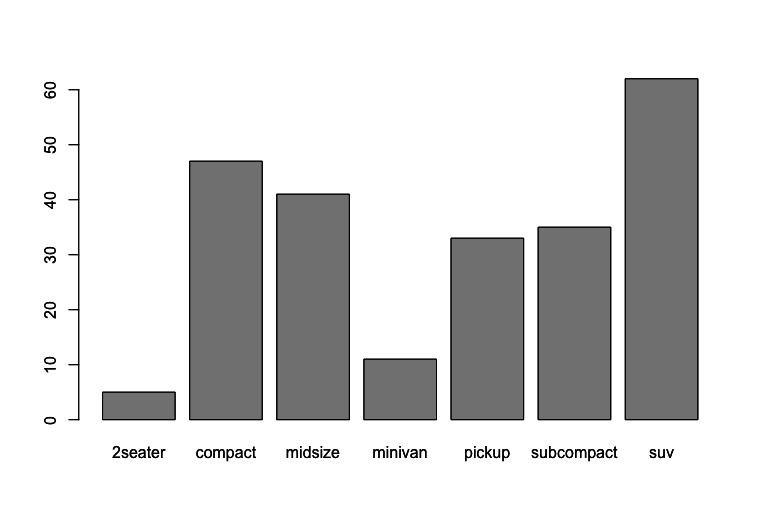
Assim como fizemos no gráfico de pizza, devemos também colocar o título, com o mesmo argumento que usamos anteriormente:main = "título".
Nos gráficos de barplot() podemos usar os argumentos xlab() e ylab() para nomear os eixos x e y do gráfico, como fizemos no gráfico a seguir. Podemos também reduzir o tamanho da fonte usada no eixo x com o argumento cex.names=, para que os nomes das categorias caibam embaixo das barras.
1 > barplot(table(mpg$class),
2 main = "Frequencia das categorias dos carros da amostra",
3 xlab = "Tipos de carros",
4 ylab = "Frequencia",
5 cex.names = 0.8)
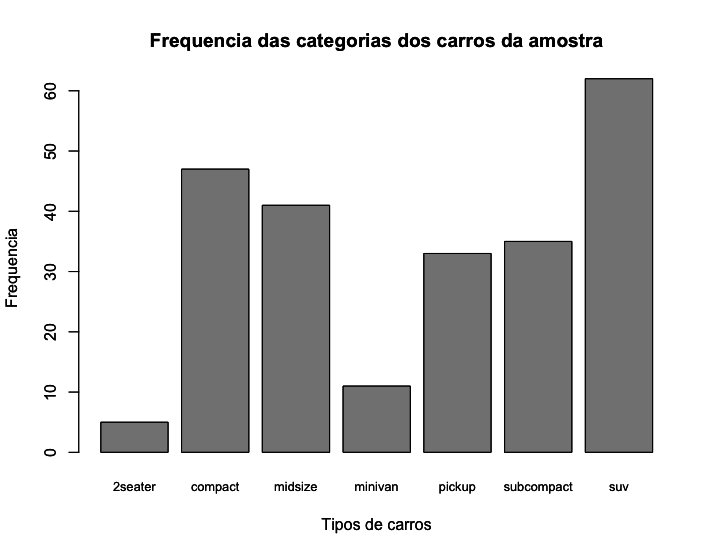
Podemos também colocar os nomes das categorias do eixo x na vertical, pois às vezes isso facilita a leitura dos nomes. Para fazer isso, basta inserir o argumento las=2 como fizemos abaixo. No caso abaixo, o texto do eixo x iria se sobrepor aos nomes dos tipos de carros, por isso deletei o argumento xlabs e coloquei o argumento sub = "subtítulo", pois o subtítulo fica um pouco mais abaixo na tabela e não se sobrepoe aos nomes das categorias.
1 > barplot(table(mpg$class),
2 main = "Frequencia das categorias dos carros da amostra",
3 sub = "Tipos de carros",
4 ylab = "Frequencia",
5 cex.names = 0.8,
6 las=2)
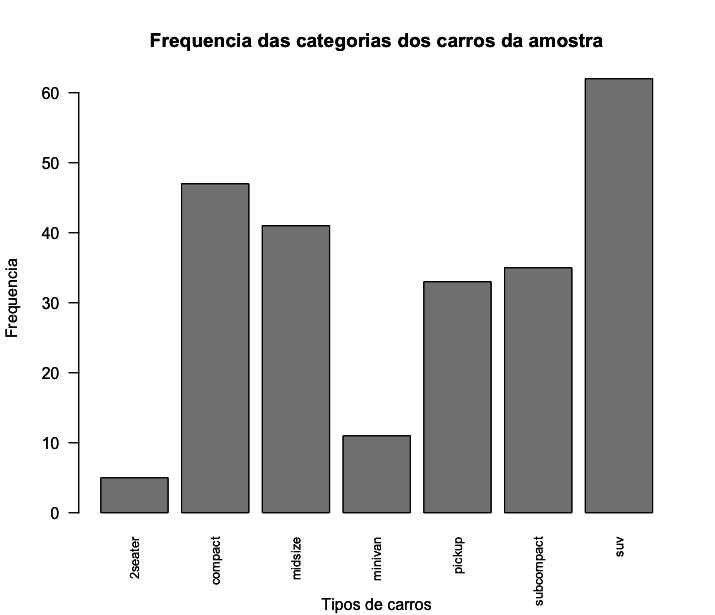
Muitas vezes é interessante, num gráfico de barras ordenar as barras de acordo com a frequência. Mas é preciso atentar para um ponto importante, isso só deve ser feito se a variável é nominal. No caso de variáveis ordinais, não devemos alterar a sequencia. Essa ordenação pode ser feita com a função sort() aplicada na tabela de frequencias criada antes de gerar o gráfico.
1 # criamos a tabela de frequências
2 > tabela_1 <- table(mpg$class)
3
4 # ordenamos a tabela criada acima
5 > tabela_ordenada <- sort(tabela_1)
6
7 # agora sim, plotamos a tabela ordenada
8 > barplot(tabela_ordenada, las=2)
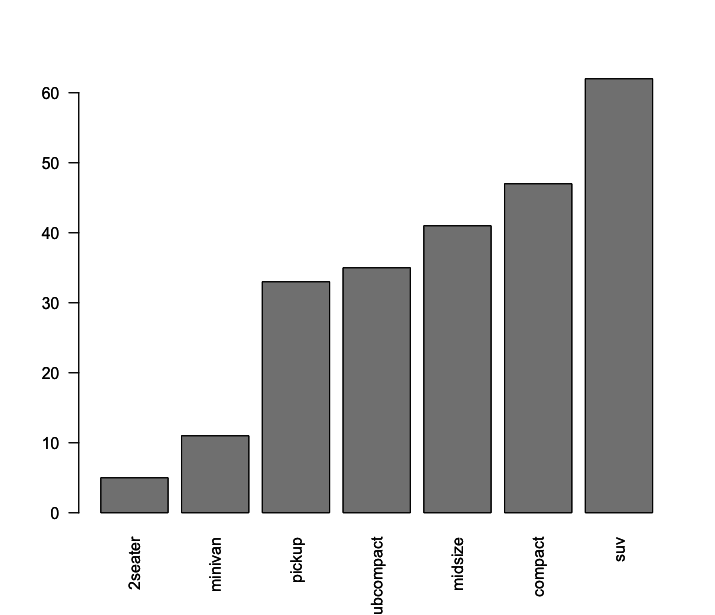
Podemos também ordenar de forma decrescente, para isso precisamos inserir o argumento decreasing=TRUE na função sort():
1 # criamos a tabela de frquencias
2 > tabela_1 <- table(mpg$class)
3
4 # ordenamos a tabela criada acima
5 > tabela_ordenada <- sort(tabela_1, decreasing = TRUE)
6
7 # agora sim, plotamos a tabela ordenada
8 > barplot(tabela_ordenada, las=2)
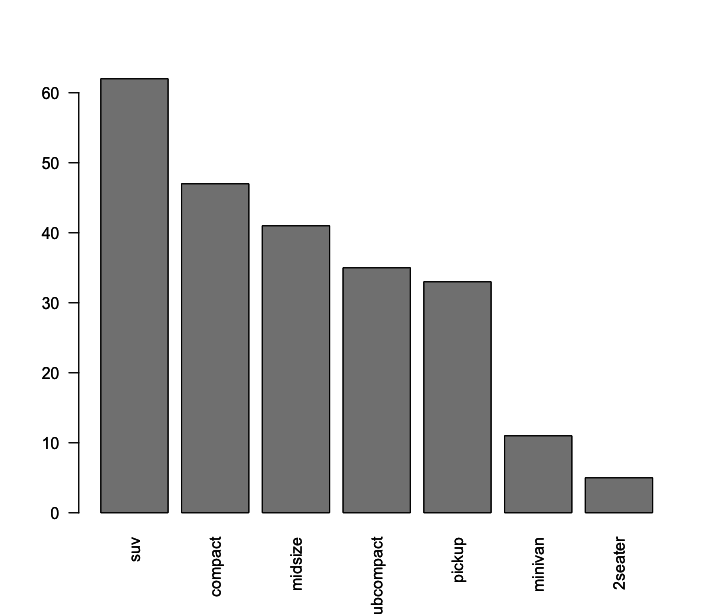
Podemos da mesma forma destacar a categoria de interesse modificando a cor conforme desejamos, com o argumento col=. Nesse exemplo aproveitei para mostrar como podemos colorir apenas a barra de nosso interesse e também mostrar como toda operação de criar a tabela de frequências e ordenar essa tabela pode ser colocado dentro da própria função barplot(), sem a necessidade de criar variáveis intermediárias.
1 > barplot(sort(table(mpg$class), decreasing = TRUE),
2 col = c("firebrick", "gray", "gray", "gray", "gray", "gray", "gray"),
3 las=2)
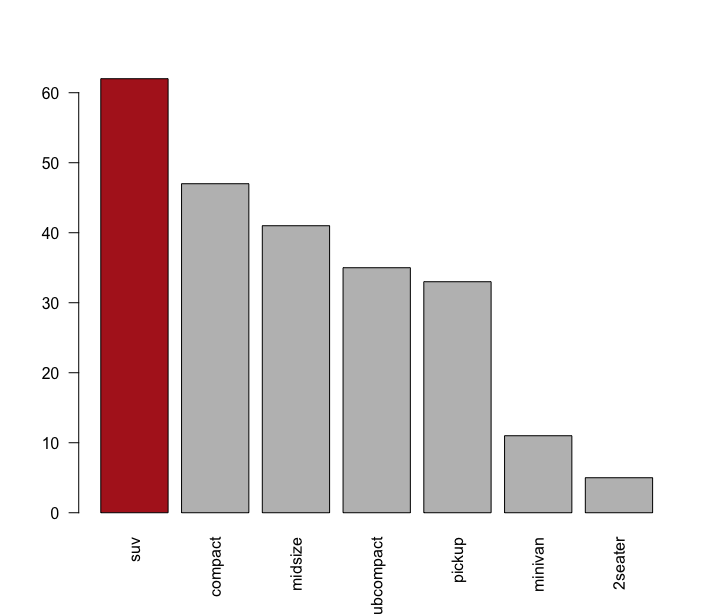
Podemos colocar as barras na horizontal com o argumento horiz=TRUE. No exemplo a seguir foi usado também o argumento las = 1 para colocar o nome de cada categoria de carros na horizontal.
1 > barplot(sort(table(mpg$class), decreasing = TRUE),
2 main = "Frequencia dos tipos de carros da amostra",
3 las = 1,
4 horiz=TRUE)
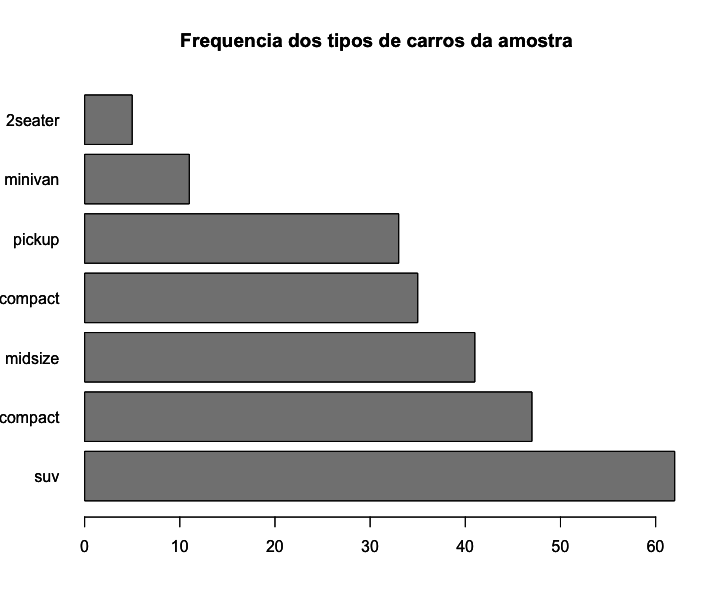
Finalmente, ao contrário de gráficos de pizza, num gráfico de barras podemos colocar muitas categorias. Veja como um gráfico de barras é bem mais adequado para representar variáveis com muitas categorias, tal como as montadoras dessa amostra (15 categorias).
1 # o comando par(mfrow=c(1,2)) indica que os dois gráficos devem ser plotados juntos,\
2 numa mesma linha com duas colunas
3 > par(mfrow=c(1,2))
4
5 # cria o grafico de barras com as montadoras
6 > barplot(sort(table(mpg$manufacturer), decreasing = TRUE),
7 cex.names = 0.7,
8 horiz = TRUE,
9 las=1)
10
11 # cria o gráfico de pizza com as montadoras
12 > pie(table(mpg$manufacturer), cex=0.7)
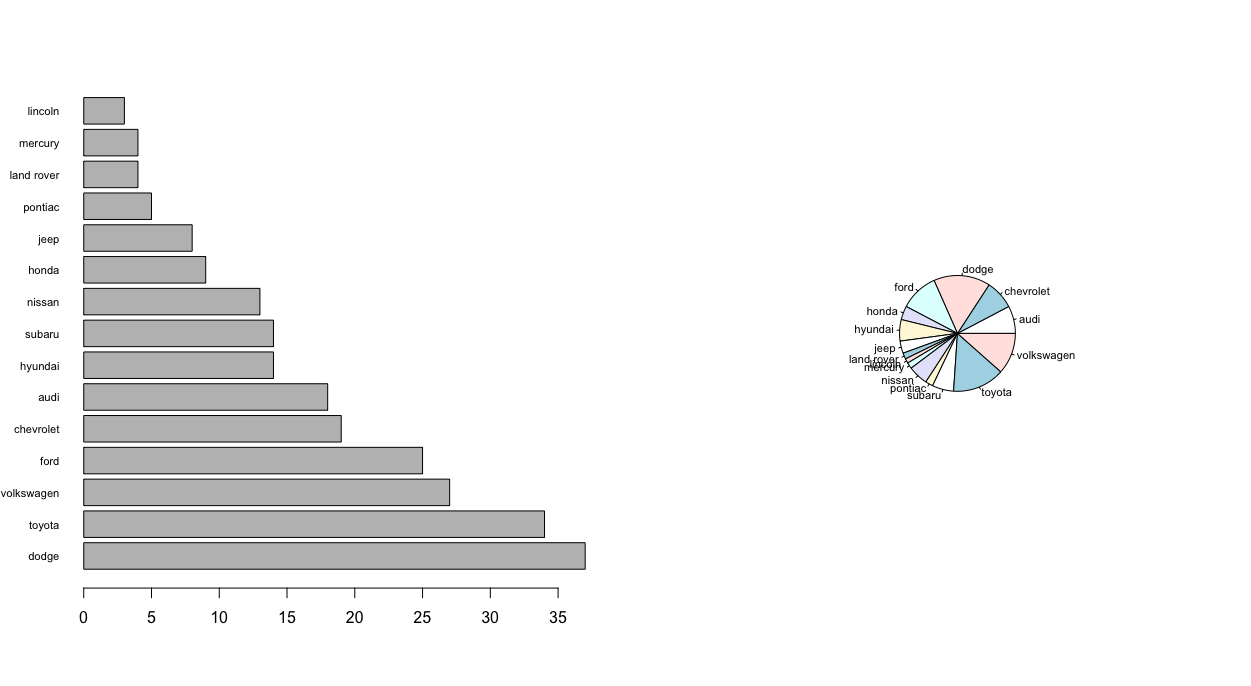
Parte 2 - Visualizando dados numéricos
Variáveis numéricas podem ter sua distribuição representada graficamente através de histogramas, gráficos de densidade de probabilidade e boxplots. Vamos ver cada um desses tipos de gráficos.
Histogramas
Um histograma é um gráfico de distribuição de frequências de dados numéricos (quantitativos). O objetivo de um histograma é resumir graficamente a distribuição de um conjunto de dados de uma única variável, permitindo visualizar o centro dessa distribuição, a moda, a dispersão dos dados, a presença de outliers e a forma da distribuição. A etapa mais importante na criação de um histograma é a divisão dos dados em classes, o que determina quantas colunas (bins) terá o histograma. Existem diversos modos de fazer esse cálculo, mas isso é totalmente dispensável com o R, pois o R faz isso automaticamente.
Apesar de se parecer um um gráfico de barras, um histograma é um gráfico totalmente diferente. Em primeiro lugar um gráfico de barras representa valores de variáveis categóricas enquanto um histograma representa a distribuição de valores de variáveis numéricas. Em segundo lugar, enquanto podemos reposicionar as barras num gráfico de barras, isso jamais pode ser feito num histograma, pois esse reposicionamento não faz sentido algum num conjunto numérico de dados. Para evitar que se confundam, um gráfico de barras deve sempre ter espaços entre as barras o que nunca deve acontecer num histograma. Assim, apenas pela a inspeção visual superficial, já podemos saber se o gráfico é um histograma ou um gráfico de barras.
Criar um histograma no R é extremamente fácil. Ao contrários dos gráficos de pizza e de barra, para criar um histograma no R não é necessário fazer nenhuma tabela de frequências, basta inserir o próprio vetor com os dados como argumento da função. A função para criar um histograma é hist().
No exemplo a seguir faremos um histograma dos dados numéricos do consumo dos carros na cidade (variável é cty).
1 > hist(mpg$cty)
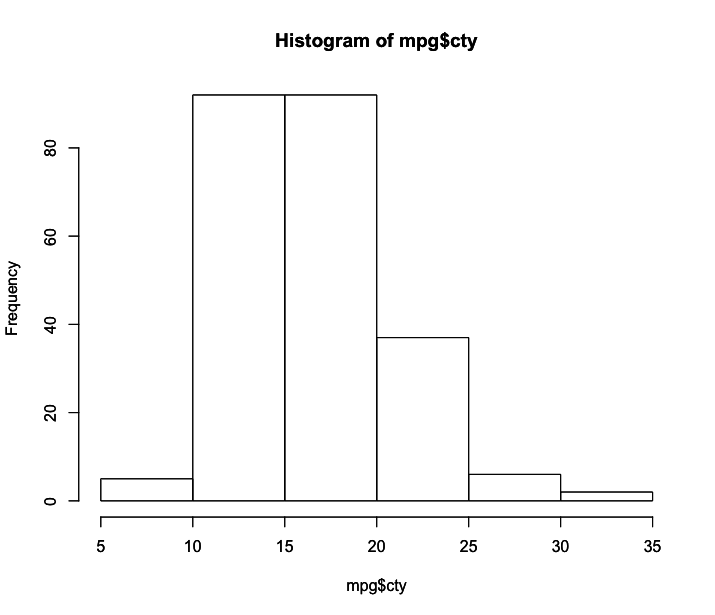
Veja que para construir o histograma tudo que fizemos foi inserir a variável cty como argumento da função hist(). O R calculou automaticamente a quantidade de colunas do histograma. Entretanto, podemos escolher manualmente quantas colunas desejamos, para que o gráfico se adeque melhor aos nossos interesses. Para isso basta alterar o argumento breaks, que define a quantidade de break points no gráfico. Você irá perceber que o número de colunas não corresponde exatamente ao número de break points, devido à maneira como R executa seu algoritmo para dividir os dados, mas o resultado é geralmente o que se pretende. Vamos testar refazer o histograma anterior indicando que desejamos 10 break points, e também colorindo as barras para melhorar o aspecto visual com o argumento col=.
1 > hist(mpg$cty, breaks = 10, col = "cornflowerblue")
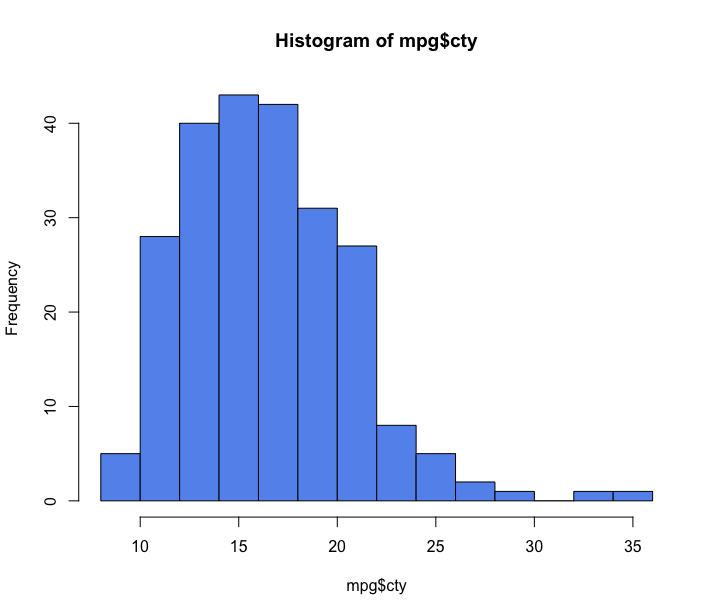
Podemos também melhorar esse histograma inserindo o título, e os nomes dos eixos com os mesmos argumentos usados anteriormente: main=, xlab=, ylab=.
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequência")
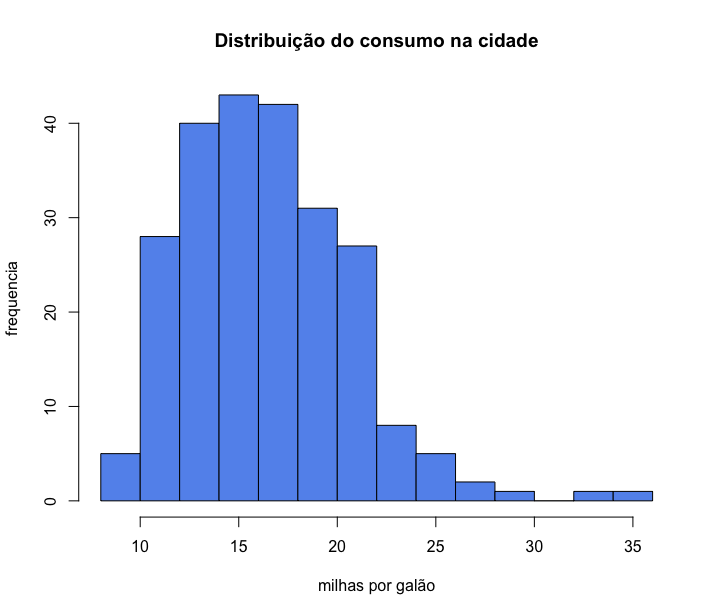
Veja que no gráfico acima os eixos x e y não comtemplam todo a amplitude de dados. Podemos ajustar os limites dos eixos x e y com os argumentos xlim e ylim:
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequencia",
7 xlim = c(0,40),
8 ylim = c(0,50))
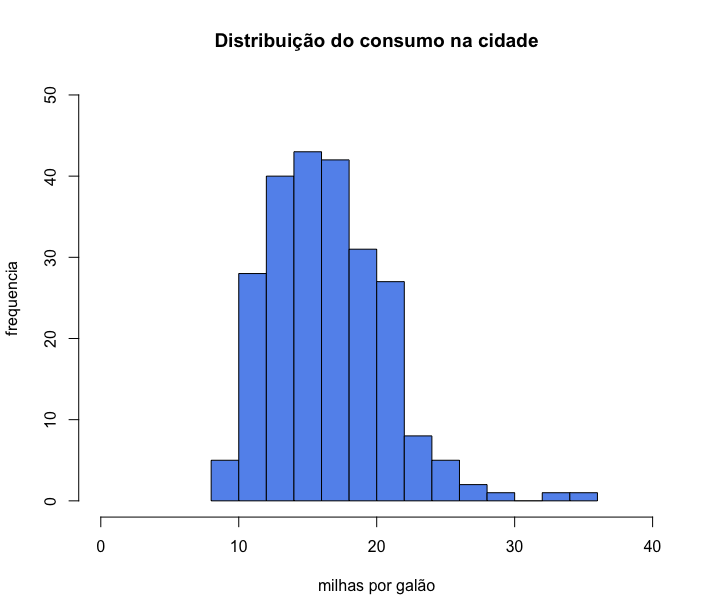
Uma das grandes vantagens do R é ser uma linguagem orientada a objetos. Tudo no R é um objeto, até um histograma. Assim, um objeto no R pode até mesmo armazenar o histograma. E ao fazer isso, podemos verificar vários detalhes do histograma.
1 > myhistogram <- hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequência",
7 xlim = c(0,40),
8 ylim = c(0,50))
Depois de armazenar o histograma num objeto, basta digitar o nome desse objeto para ter acesso aos detalhes do histograma.
1 > myhistogram
2
3 $breaks
4 [1] 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36
5
6 $counts
7 [1] 5 28 40 43 42 31 27 8 5 2 1 0 1 1
8
9 $density
10 [1] 0.010683761 0.059829060 0.085470085 0.091880342 0.089743590
11 [6] 0.066239316 0.057692308 0.017094017 0.010683761 0.004273504
12 [11] 0.002136752 0.000000000 0.002136752 0.002136752
13
14 $mids
15 [1] 9 11 13 15 17 19 21 23 25 27 29 31 33 35
16
17 $xname
18 [1] "mpg$cty"
19
20 $equidist
21 [1] TRUE
22
23 attr(,"class")
24 [1] "histogram"
Caso seja necessário acessar alguns desses dados isoladamente, basta usar o operador $, como fazedemos um data frame. Por exemplo, para acessar o valor de cada coluna, basta acessar counts.
1 > myhistogram$counts
2 [1] 5 28 40 43 42 31 27 8 5 2 1 0 1 1
Podemos ver que a primeira barra tem 5 carros, a segunda 28 carros, a terceira 40 carros etc.
Podemos também fazer um histograma com a densidade de probabilidade ao invés da contagem absoluta, para isso basta alterar o argumento freq para FALSE: freq = FALSE. Nesse caso, temos de ter cuidado de não usar o argumento ylim e sim deixar o R usar os limites adequados no eixo y.
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequencia",
7 xlim = c(0,40),
8 freq = FALSE)
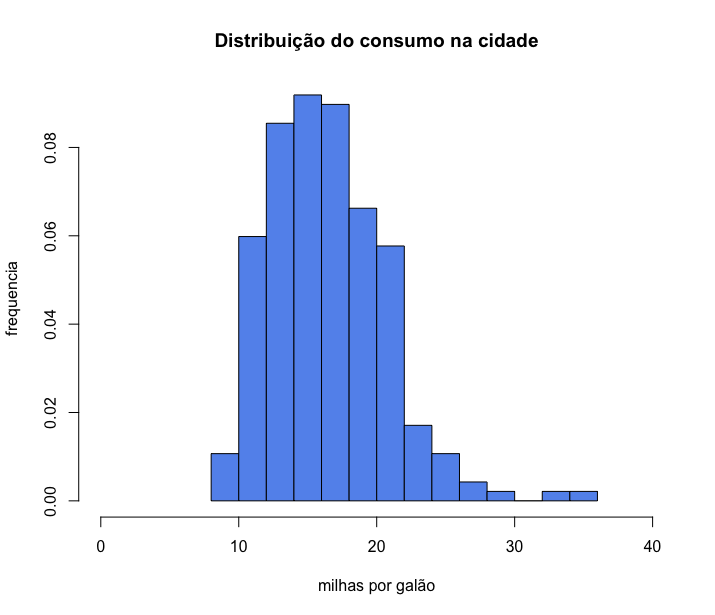
Até então nosso eixo y representava os valores absolutos, a contagem absoluta dos carros. No exemplo acima fizemos uma mudança no argumento freq e eixo y passou a representar as probabilidades. Nesse caso, se nosso histograma estiver usando probabilidades, podemos, então, inserir também uma linha de densidade com a função lines(). Observe que só podemos inserir essa linha de densidade se o histograma tiver sido criado com probabilidades, ou seja, se o indicarmos nos argumentos do histograma freq = FALSE.
1 > hist(mpg$cty,
2 breaks = 10,
3 col = "cornflowerblue",
4 main = "Distribuição do consumo na cidade",
5 xlab = "milhas por galão",
6 ylab = "frequencia",
7 xlim = c(0,40),
8 freq = FALSE)
9 > lines(density(mpg$cty))
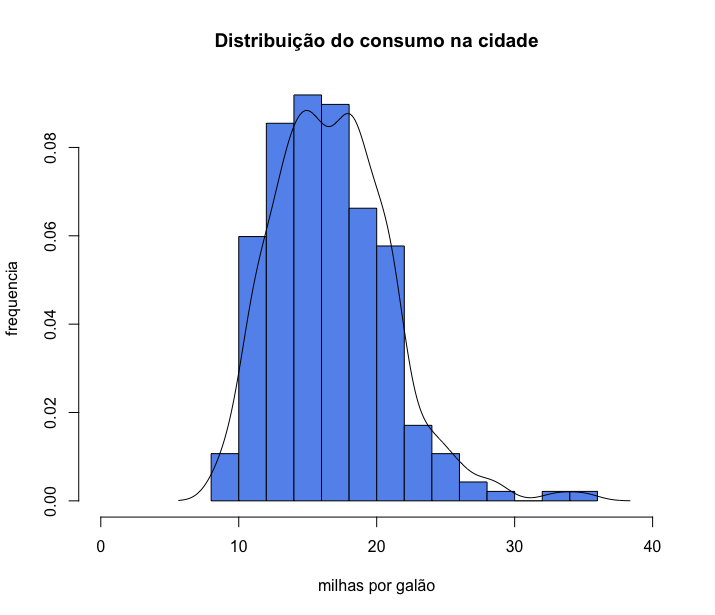
Gráficos de densidade
Um gráfico de densidade é uma variação de um histograma. Enquanto os histogramas vizualizam os dados em intervalos, um gráfico de densidade de probabilidade visualiza a distribuição dos dados num continuum. Uma vantagem dos gráficos de densidade sobre histogramas é que são melhores na determinação da forma da distribuição, pois não são afetados pelo número de barras usadas. Os picos de um gráfico de densidade ajudam a exibir onde os valores estão concentrados ao longo do intervalo. Veja que no último histograma plotado não era visivel que a curva seria bimodal, o que só ficou claro quando fizemos a sobreposição com a curva de densidade de probabilidade.
Quando geramos gráficos de barras ou de pizza foi necessário primeiro criar tabelas de frequencias dos dados. Do mesmo modo, para criar gráficos de densidade precisamos primeiro gerar os pontos do gráfico, o que é feito com a função density(). Depois, basta inserir esses dados como argumentos da função plot().
1 > densitypoints <- density(mpg$cty)
2 > plot(densitypoints,
3 main = "Densidade do consumo dos carros na cidade ")
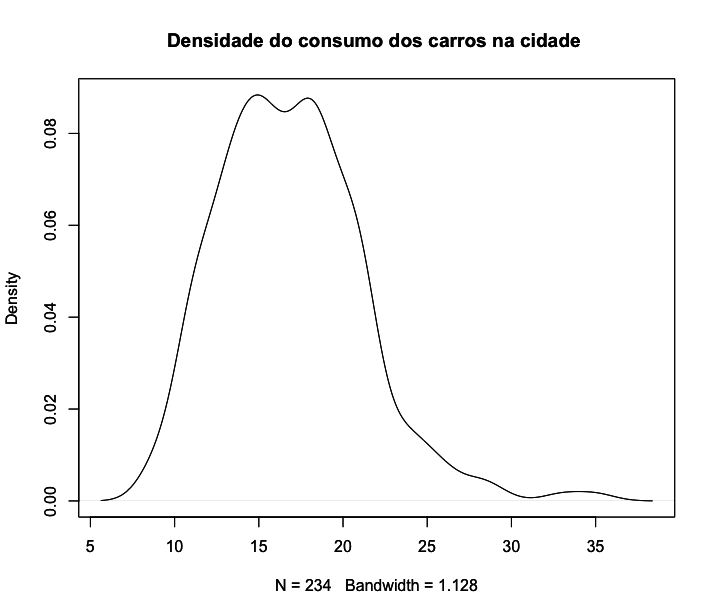
Boxplots
Um boxplot, também chamado de diagrama de caixa, é um gráfico para representar a variação (dispersão) de dados numéricos e seus quartis, sendo uma maneira padronizada de exibir a distribuição de dados com base em cinco números: mínimo, primeiro quartil, mediana, terceiro quartil e máximo.
O retângulo central de um box plot abrange o primeiro quartil para o terceiro quartil (intervalo interquartil ou IQR), correspondendo a 50% das medidas e a linha dentro do retângulo representa a mediana.
Num boxplot simples os “bigodes” (whiskers) nas extremidades da caixa mostram as localizações do mínimo e máximo. Entretanto, é mais comum que esses bigodes sirvam para separar valores extremos e outliers dos valores mais comuns do conjunto de dados.
REVER ESSE PARÁGRAFO:
Outliers são 3 × IQR acima do terceiro quartil ou 3 × IQR abaixo do primeiro quartil. Valores extremos são versões ligeiramente mais centrais de outliers: 1,5 × IQR acima do terceiro quartil ou 1,5 × IQR abaixo do primeiro quartil. Se houver valores como esses, o lado do lado apropriado é levado para 1,5 × IQR do quartil (a “cerca interna”) em vez do máximo ou mínimo, e os pontos de dados independentes individuais são exibidos como círculos preenchidos (por suspeitos de valores atípicos ) ou círculos cheios (para outliers). (A “cerca externa” é 3 × IQR do quartil).
Criar um boxplot no R é muito simples com a função boxplot(). Vamos criar um boxplot dos mesmos dados do consumo na cidade, para podermos comparar com os gráficos de histograma e de densidade feitos acima. Assim como no caso de um histograma, não é necessário criar tabelas antes de criar o gráfico, basta inserir o vetor com os dados na função boxplot().
1 > boxplot(mpg$cty)
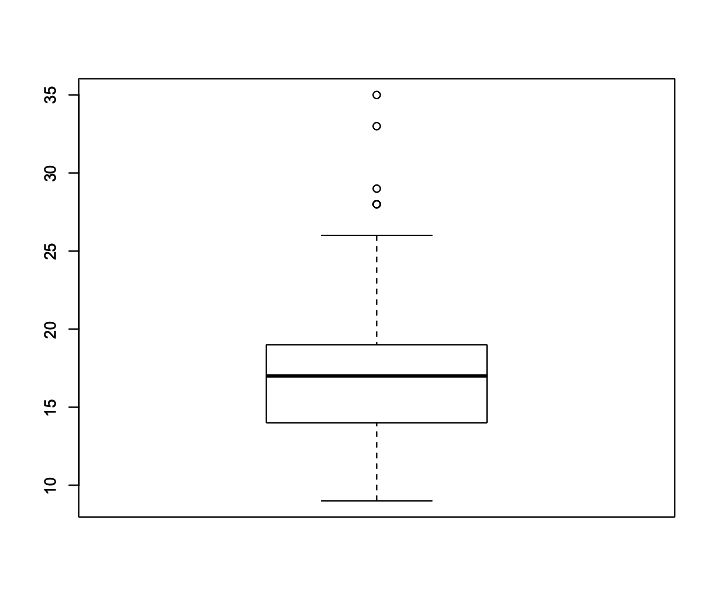
Da mesma forma que fizemos com os gráficos de histograma, podemos inserir o título, subtítulos e nomes dos eixos.
1 > boxplot(mpg$cty,
2 col = "cornflowerblue",
3 main = "Consumo de combustível",
4 ylab = "milhas por galão",
5 xlab = "cidade")
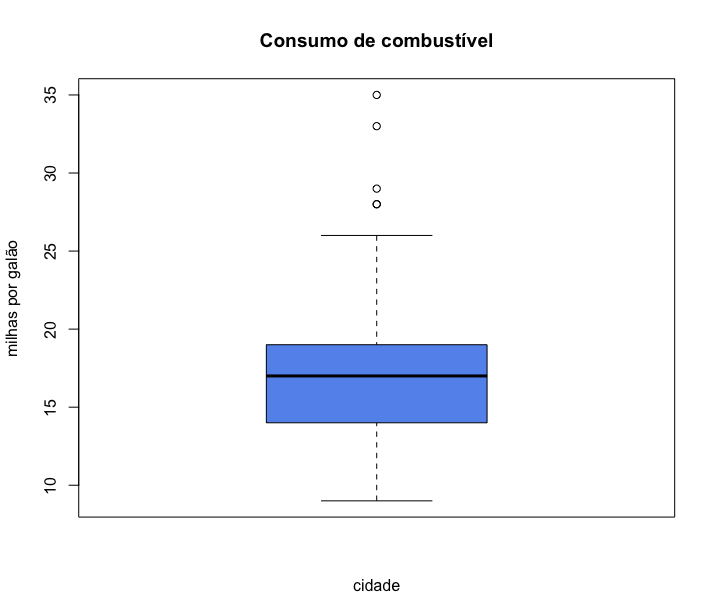
Uma das grandes vantagens do boxplot é que serve para podermos facilmente compararmos diferentes conjuntos de dados. Podemos por exemplo visualizar lado a lado a distribuição do consumo na cidade e do consumo na estrada. Nesse caso, quando temos mais de um boxplot, usamos o argumento names para nomearmos cada boxplot separadamente, como feito abaixo. Nesse caso é desnecessário nomear o eixo x e por isso não usei o argumento xlab.
1 > boxplot(mpg$cty, mpg$hwy,
2 col = "cornflowerblue",
3 main = "Distribuição do consumo de combustível",
4 ylab = "milhas por galão",
5 names=c("cidade","estrada"))
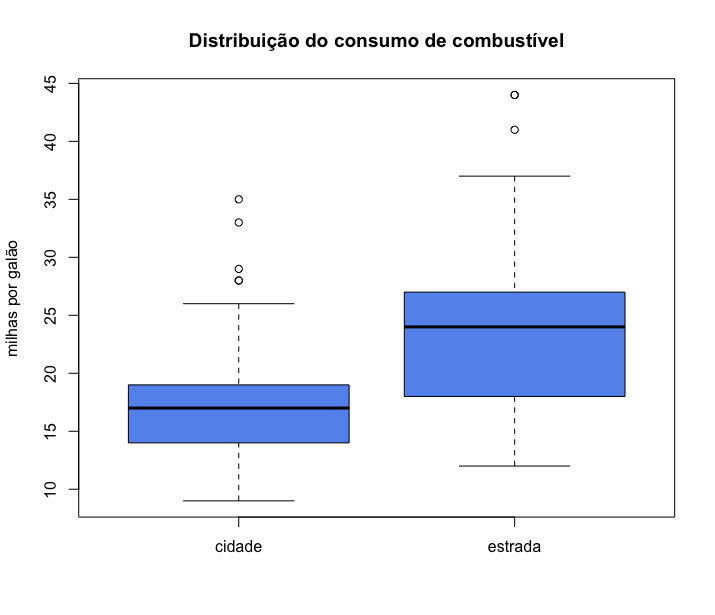
Parte 3 - Visualizando relações entre variáveis
Correlação entre uma variável numérica e uma variável categórica
A análise visual da relação entre uma variável categórica e uma variável numérica é geralmente feita através da plotagem de um gráfico de boxplot múltipo, como feito no último exemplo, no qual comparamos a distribuição do desempenho (variável numérica - milhas percorridas com um galão) com o local de trânsito (variável categórica: cidade ou estrada). Um outro gráfico comum é o de dotplot com margem de erro de cada média. Entretanto, esse tipo de gráfico é muito complexo para ser plotado com as funções básicas do R e não será analisado nessa aula. O pacote ideal para plotar gráficos mais complexos é o ggplot2.
Correlação entre duas variáveis numéricas
Gráficos de dispersão, ou scatter plots são gráficos nos quais duas variáveis numéricas são plotadas, uma em cada eixo, para que se possa analisar a relação entre elas. Através de um scatter plot podemos visualizar se existe uma correlação matemática entre essas variáveis. Podemos nos perguntar por exemplo, se existe alguma correlação entre as cililndradas e o consumo do carro? Um gráfico de dispersão (scatter plot) proporciona uma representaçõa visual bastante adequada para essa pergunta.
A função básica no R para gerar um scatter plot é simplemente plot(). Esse comando é bastante versátil e pode ser usado para plotar vários tipos de gráficos, inclusive de barras ou histograma, pois o comando plot() interpreta automaticamente o tipo de dado e escolhe o gráfico adequado. Entretanto, nunca é indicado deixar o que o R faça essa escolha, é sempre mais indicado usar os comando apropriados para cada tipo de gráfico.
Para usar o comando plot() para plotar um grafico de dispersão precisamos informar os dois conjuntos de dados a serem plotados. Para isso precisamos usar o operador $ para acessarmos cada variável a ser usada.
1 > plot(mpg$cty, mpg$displ)
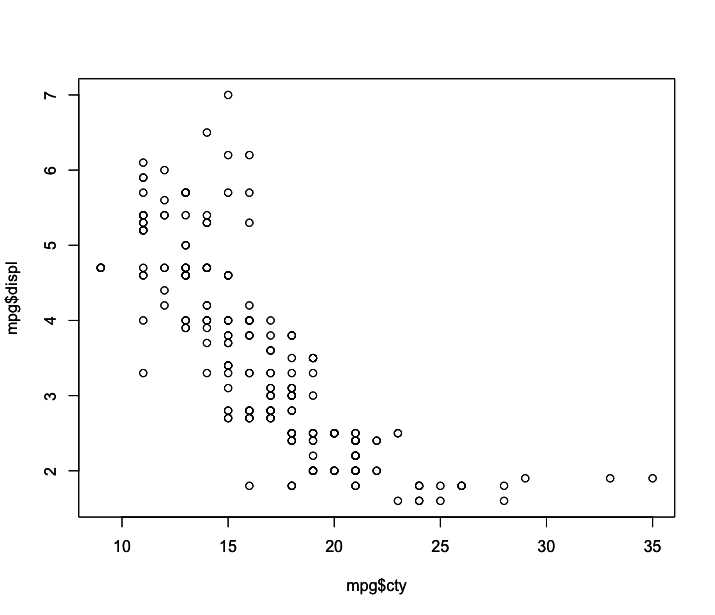
Como você pode observar, a primeira variável fica no eixo x e a segunda no eixo y. Podemos deixar indicado de forma explícita qual variável desejamos colocar em cada eixo.
1 > plot(x=mpg$cty, y=mpg$displ)
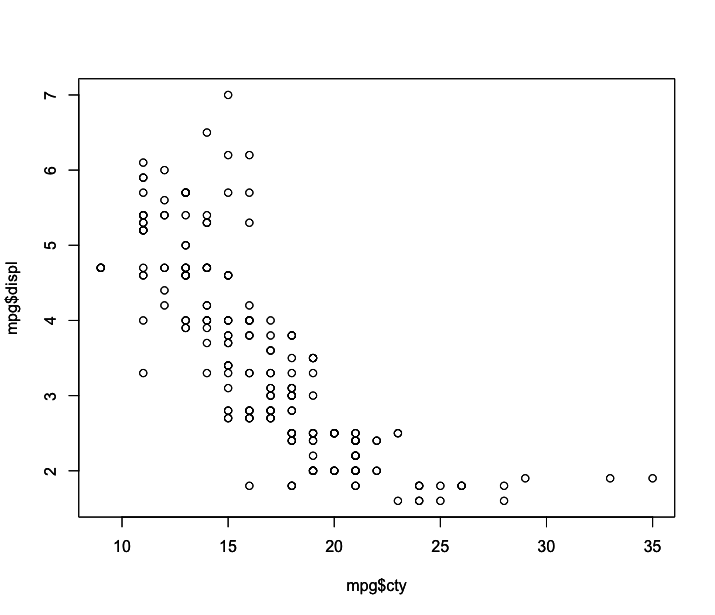
Podemos acrescentar o título e nomes dos eixos com os argumentos main, xlab e ylab, da mesma forma como fizemos com os gráficos anteriores.
1 > plot(x=mpg$displ, y=mpg$cty, # variáveis a serem plotadas
2 main = "Corelação entre cilindradas e consumo", # título
3 xlab = "milhas por galão", # nome do eixo x
4 ylab = "cilindradas") # nome do eixo y
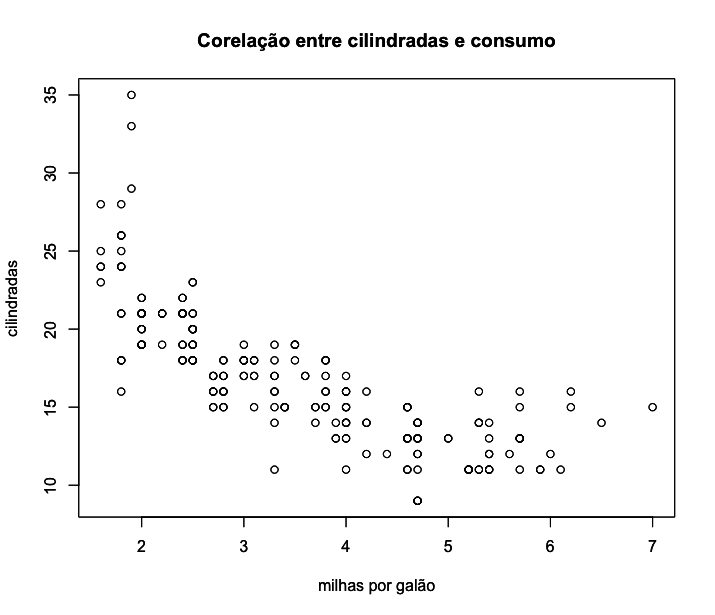
Podemos mudar o tipo de ponto no desenho com a o argumento pch, variando de 1 a 25. Experimente mudar o valor de pch para ver as alterações no gráfico.
1 > plot(x=mpg$displ, y=mpg$cty, # variáveis a serem plotadas
2 main = "Corelação entre cilindradas e consumo", # título
3 xlab = "milhas por galão", # nome do eixo x
4 ylab = "cilindradas", # nome do eixo y
5 pch = 20)
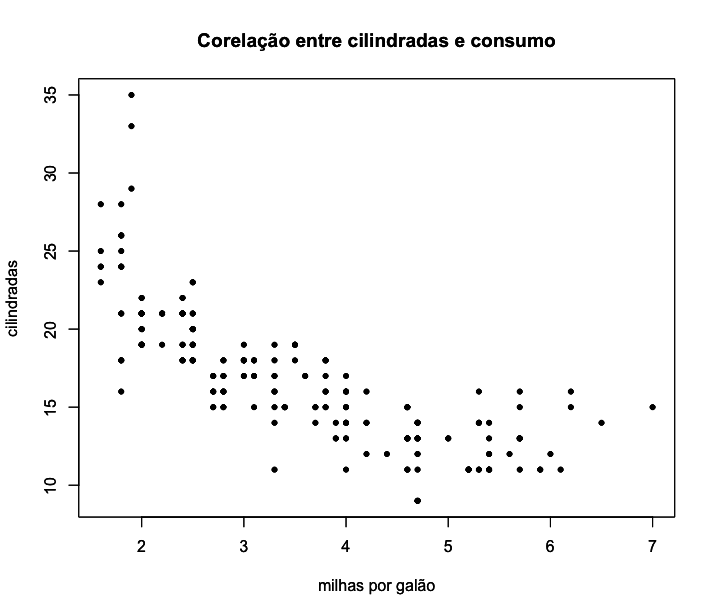
Um scatter plot server para visualizarmos a relação entre duas variáveis numéricas. Entretanto, a melhor e mais usual forma de visualizar essa correlação linear é através da inserção no gráfico de uma linha que represente a melhor relação linear possível entre essas duas variáveis (chamada de reta de regressão).
Podemos facilmente acrescentar uma reta de regressão linear no gráfico. Para isso teremos de usar uma função matemática lm(y~x) (linear model) para calcular a reta de regressão linear e depois pedir para plotar essa linha no gráfico usando a função abline(). Atenção para o fato de que a primeira variável na função lm() é a variável dependente e a segunda é a independente. Logo, a fórmula abaixo cty~displ indica que a variável cty (milhas percorridas) é a variável dependente de disp (cilindradas).
1 > plot(x=mpg$displ, y=mpg$cty, # variáveis a serem plo\
2 tadas
3 main = "Corelação entre cilindradas e consumo", # título
4 xlab = "milhas por galão", # nome do eixo x
5 ylab = "cilindradas", # nome do eixo y
6 pch = 20)
7 > retaRegressao <- lm(cty~displ, data = mpg ) # cálculo da reta de regres\
8 são linear
9 > abline(retaRegressao, col = "red") # insere a reta no gráfico \
10 de cor "red"
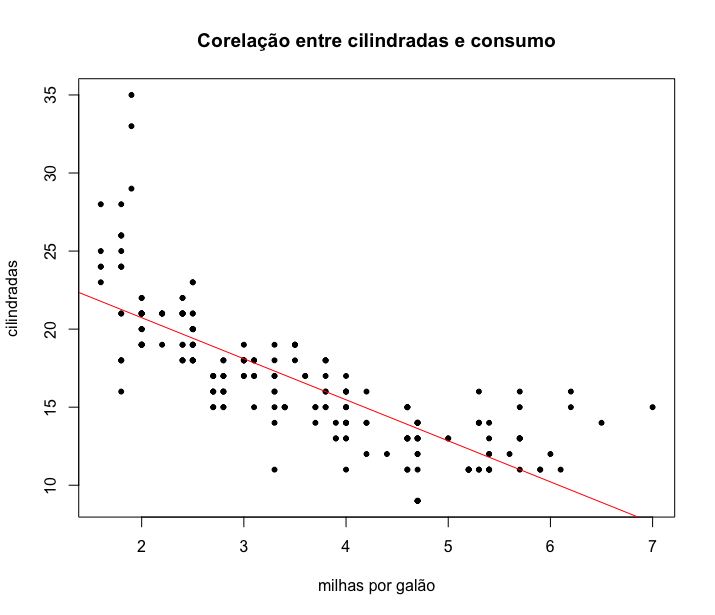
Através desse gráfico podemos verificar que parece haver uma relação negativa entre as cilindradas e as milhas percorridas, ou seja, quanto menor as cilindradas, maior a quantidade de milhas percorridas com um galão de combustível.
Mas além da inspeção visual, podemos também calcular a força dessa correlação. A medida estatística mais comum para mensurar a força da correlação entre duas variáveis numéricas é o Coeficiente de Correlação de Pearson - denotado por r.
O coeficiente de correlação é uma medida da força e direção da correlação linear entre duas variáveis. Ou seja, só serve para analisar correlações lineares.
A linguagem R tem uma função específica para calcular o coeficiente de correlação linear de Pearson (r) entre duas variáveis numéricas. A função cor() - de correlação - calcula o valor desse coeficiente com o sinal correto (positivo ou negativo). Para usar essa função basta inserir como argumentos as duas variáveis numéricas para as quais se deseja calcular o coeficiente.
1 > cor(mpg$displ, mpg$cty)
2 [1] -0.798524
A função lm() usada na criação da linha de regressão também faz o cálculo desse coeficiente de correlação, além de inúmeros cálculos matemáticos. Esse valor pode ser obtido na própria variável que criamos retaRegressao. Vejamos
1 > summary(retaRegressao)
2
3 Call:
4 lm(formula = cty ~ displ, data = mpg)
5
6 Residuals:
7 Min 1Q Median 3Q Max
8 -6.3109 -1.4695 -0.2566 1.1087 14.0064
9
10 Coefficients:
11 Estimate Std. Error t value Pr(>|t|)
12 (Intercept) 25.9915 0.4821 53.91 <2e-16 ***
13 displ -2.6305 0.1302 -20.20 <2e-16 ***
14 ---
15 Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
16
17 Residual standard error: 2.567 on 232 degrees of freedom
18 Multiple R-squared: 0.6376, Adjusted R-squared: 0.6361
19 F-statistic: 408.2 on 1 and 232 DF, p-value: < 2.2e-16
Veja que um dos valores calculados é o R-squared (ou seja, o r ao quadrado). Se desejarmos obter especificamente o valor de R-squared basta usar o operador $ como abaixo:
1 > summary(retaRegressao)$r.squared
2 [1] 0.6376405
E, finalmente, para obter o valor do coeficiente de correlação, basta extrair a raiz quadrada desse valor acima:
1 > r_squared <- summary(retaRegressao)$r.squared
2 > r <- sqrt(r_squared)
3 > r
4 [1] 0.798524
Podemos também fazer todo esse cálculo acima em apenas uma linha.
1 > sqrt(summary(retaRegressao)$r.squared)
2 [1] 0.798524
Veja que o coeficiente de correlação calculado acima foi positivo. Entretanto, lembre-se que esse resultado acima veio de uma extração de raiz quadrada e o resultado de uma operação de extração de raiz quadrada poderia tanto ser positivo ou negativo. No exemplo acima, sabemos que esse valor é na verdade negativo, pois já verificamos que a relação entre as variáveis cilindradas e milhas percorridas é negativa. Por outro lado, o valor absoluto encontrado indica que essa é uma correlação forte (correlação negativa forte).
A mensagem é clara: se deseja economizar combustível, prefira carros 1.0.
Referências
- Hadley Wickham. ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag, New York, 2009.
- Michael Friendly and Daniel Denis. The early origins and development of the scatterplot. Journal of the History of the Behavioral Sciences, Vol. 41(2), 103–130 Spring 2005.
- Stephen E. Fienberg. Graphical Methods in Statistics. The American Statistician, Vol. 33(4): 165-178, 1979.
- William S. Cleveland.Graphs in Scientific Publications. The American Statistician,
Vol. 38(4): 261-269, 1984 - Ross Ihaka; Robert Gentleman. R: a language for data analysis and graphics. Journal of computational and graphical statistics, Vol. 5(3): 299-314, 1996.
- Hadley Wickham. A layered grammar of graphics. Journal of Computational and Graphical Statistics, Vol. 19(1):3–28, 2010.
Correlação
Introdução.
No capítulo anterior aprendemos como gerar gráficos de dispersão - scatter plots - para analisar a relação entre duas variáveis numéricas. Vimos, resumidamente, que podemos calcular o coeficiente de correlação entre duas variáveis numérica. Precisamos, agora, aprofundar esse importante tópico.
O conceito de correlação se originou por volta de 1888, nos trabalhos do estatístico inglês Francis Galton (Stigler, 1989). Os estatísticos da era Vitorina estavam fascinados com a noção da hereditariedade e desejavam conseguir quantificar as influências genéticas no ser humano. Uma das pesquisas mais importantes dessa busca foi o estudo para quantificar as relações entre as alturas de pais e filhos. Galton e seu discípulo Karl Pearson coletaram uma grande quantidade de dados de alturas de pais e filhos para suas análises e, foi analisando esses dados que Galton concebeu a idéia de correlação (Galton, 1888 - 1889). E foi também Galton deu os primeiros passos na direção da construção do que hoje entendemos por um gráfico de dispersão ou scatter plot (Friendly & Denis, 2005).
O scatter plot, também chamado de gráfico de dispersão, ou diagrama de dispersão, é um dos gráficos mais usados na ciência. Estima-se que os scatter plots correspondam a cerca de 70-80% dos gráficos usados em publicações científicas (Tuft, 1983 APUD Friendly & Denis, 2005). Isso se deve à importância dessa análise de correlação e do gráfico de dispersão na busca da causa de eventos, na compreensão da causalidade dos fenômenos. Através da análise da correlação, buscamos compreender como uma variável afeta outra, se um determinada coisa afeta outra (Few, 2009). Esse tipo de conhecimento é fundamental na medicina, pois se sabemos que o uso de cigarro se correlaciona com o aumento do risco de câncer de pulmão podemos tentar evitar esse desfecho com campanhas anti-tabagismo; se sabemos que o uso de ácido fólico na gravidez se relaciona com a redução do risco de espinha bífida podemos então indicar o uso dessa substância para grávidas. Com isso já podemos perceber a importância de descobrirmos relações de causalidade e de como a interpretação da correlação é um tema de fundamental importância na medicina.
Entretanto, correlação não implica necessariamente em causalidade. Quando encontramos uma correlação entre duas variáveis, isso pode se dever a vários fatores:
- há uma relação de causalidade, uma das variáveis afeta a outra
- nenhuma das variáveis afeta a outra, as duas são afetadas por um outro ou mais fatores em comum
- nenhuma das variáveis afeta a outra, mas ambas podem estar conectadas por uma outra variável.
- a aparente correlação na verdade é resultado de um erro devido a uma amostra insuficiente ou enviesada.
É sempre válido reforçar que correlação não implica causalidade. A simples verificação de uma forte correlação entre duas variáveis não é suficiente para determinar a relação de causalidade entre elas. Tanto a correlação percebida visualmente como através da medida do coeficiente de correlação podem ocorrer entre variáveis que não tem nenhuma relação entre si. Esse tipo de correlação é chamdo de correlação espúria. Para maiores exemplos de correlações espurias veja o site http://www.tylervigen.com/spurious-correlations, de onde foi obtida a imagem abaixo, que mostra um exemplo de correlação meramente espúria.
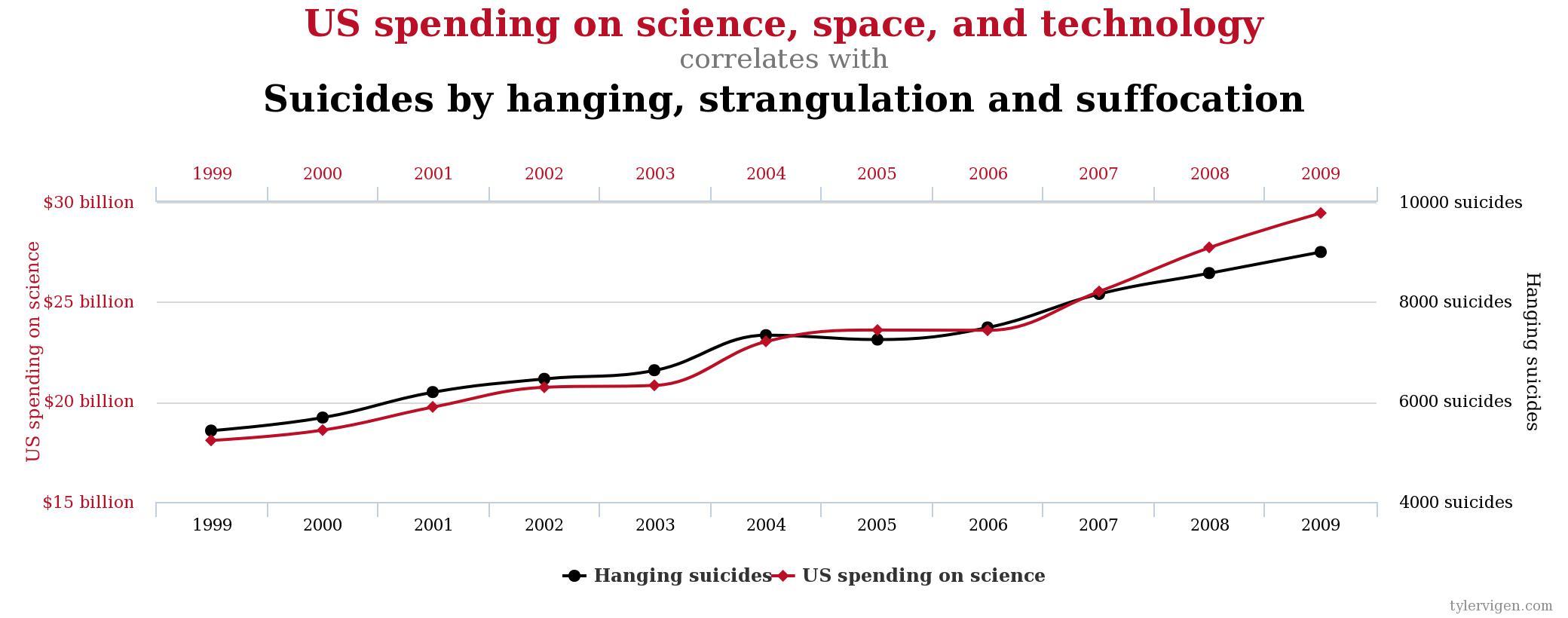
Esteja especialmente atento a correlações entre variáveis que evoluem no tempo. Muito frequentemente duas variáveis se modificam ao longo do tempo por motivos totalmente diversos e não por uma relação de causalidade entre uma e outra.
Carregamento dos pacotes necessários
Para esse capítulos serão necessários alguns pacotes do R. Se, ao usar a função library() para carregar esses pacotes, você receber a mensagem que algum pacote não existe, faça a instalação desse pacote e, depois, tente novamente usar a função library().
Será necessário já ter instalado os seguintes pacotes:
- tidyverse
- dplyr
- gridExtra
- HistData
Após a instalação é necessário carregar os pacotes com o comando library().
1 library(tidyverse)
2 library(dplyr)
3 library(gridExtra)
4 library(HistData)
Análise Univariada e Bivariada
Antes de iniciar o tema da correlação, é importante resumir dois termos comuns na estatística: análise univariada e análise bivariada.
A análise univariada é a forma mais simples de análise estatística. O que caracateriza a análise univariada é que apenas uma variável está envolvida. Dependendo do tipo dessa variável, poderemos fazer diversas análises descritivas ou inferenciais. No caso da análise descritiva de uma variável não numérica (nominal ou oridinal) podemos descrever a frequência de cada nível da variável e podemos construir gráficos de barra ou de pizza com essas frequências. Para variáveis numéricas, podemos descrever o aspecto visual da distribuição (a forma da distribuição), calcular a moda, a média, a mediana, a amplitude, o IQR, os quartis, a variância e desvio padrão. A análise inferencial de uma única variável (análise inferencial univariada) é o conjunto de análises, de inferências, sobre uma população a partir de uma amostra.
A análise bivariada é o nome dado às técnicas de análise da relação entre duas variáveis. Frequentemente essa análise serve para determinar a relação entre duas variáveis numéricas, sendo uma delas a variável explanatória (variável preditora ou independente) e a outra a variável de resposta (de desfecho ou variável dependente). Por convenção, quando representamos graficamente essas variáveis, plotamos a variável explanatória (preditora/independente) no eixo x e a variável de reposta (de desfecho ou dependente) no eixo y. A representação gráfica usual de uma relação entre duas variáveis numéricas é o scatter plot, também chamado de gráfico de dispersão.
Um scatter plot mostra as características da relação entre duas variáveis, os padrões dessa relação. Em uma avaliação da relação de duas variáveis através de um scatter plot geralmente devemos avaliar 4 características:
- forma do gráfico (linear ou não linear)
- direção da tendência (positiva ou negativa)
- força da relação (grau de disperção)
- presença de outliers. (pontos fora do padrão)
Forma
Forma diz respeito à forma que os pontos formam no gráfico, podendo ser, em resumo, linear ou não linear. Essa é uma análise visual.
Direção
Essa análise pode ser apenas visual ou calculada pelo que se chama de covariância: ou seja, o quanto as variáveis variam de forma conjunta. Quando ambas as variáveis variam na mesma direção, ou seja, uma aumenta quando a outra aumenta, ou uma diminui quando a outra diminui, a direção da variação é positiva, ou seja, a covariância é positiva.
A direção é negativa quando uma aumenta quando a outra diminui. Nesse caso a covariância é dita negativa.
Analisaremos a covariância logo a seguir.
Força
A força da relação diz respeito quão forte é a correlação, o que é mensurado pelo grau de dispersão dos pontos do gráfico. A força de uma correlação linear é mensurada pelo coeficiente de correlação.
Analisaremos o coeficiente de correlação logo a seguir.
Outliers
A presença de outliers pode influenciar enormemente a medida da força da correlação (o coeficiente de correlação), logo, é sempre importante verificar visualmente se existem outliers no gráfico de scatter plot.
Um scatter plot histórico
A título de exemplo, vamos recriar um scatter plot com dados da pesquisa de Francis Galton e Karl Pearson de 1888. Esses dados estão disponíveis no pacote HistData. Para ter acesso a esses dados é necessário já ter instalado esse pacote e já ter feito uso do comando library(HistData) para carregar esse pacote na sessão atual do R.
Para carregar os dados de Galton e Pearson use o comando abaixo:
1 data("Galton")
para ter uma idéia do dataset, use o comando str(Galton):
1 str(Galton)
2 'data.frame': 928 obs. of 2 variables:
3 $ parent: num 1.79 1.74 1.66 1.64 1.63 ...
4 $ child : num 1.57 1.57 1.57 1.57 1.57 ...
Podemos ver que esse é um data frame com 928 observações, com as alturas de pais e filhos. Entretanto, as medidas de altura desse dataset estão em polegadas (inches). É interessante converter essas as medidas para metros, unidade com a qual estamos mais acostumados a usar.
1 Galton$parent <- Galton$parent* 0.0254
2 Galton$child <- Galton$child * 0.0254
Vamos então gerar um scatter plot com o ggplot2:
1 ggplot(data=Galton, aes(x=parent, y=child)) +
2 geom_jitter(color="blue", size=1, alpha=0.5) +
3 geom_smooth(method = "lm", color = "red", fullrange = TRUE) +
4 ggtitle(label="Correlação da altura de pais e filhos",
5 subtitle ="Galton e Pearson - 1888") +
6 xlab("Altura dos pais (m)") +
7 ylab("Altura dos filhos (m)") +
8 xlim(c(1.5,2)) +
9 ylim(c(1.5,2))
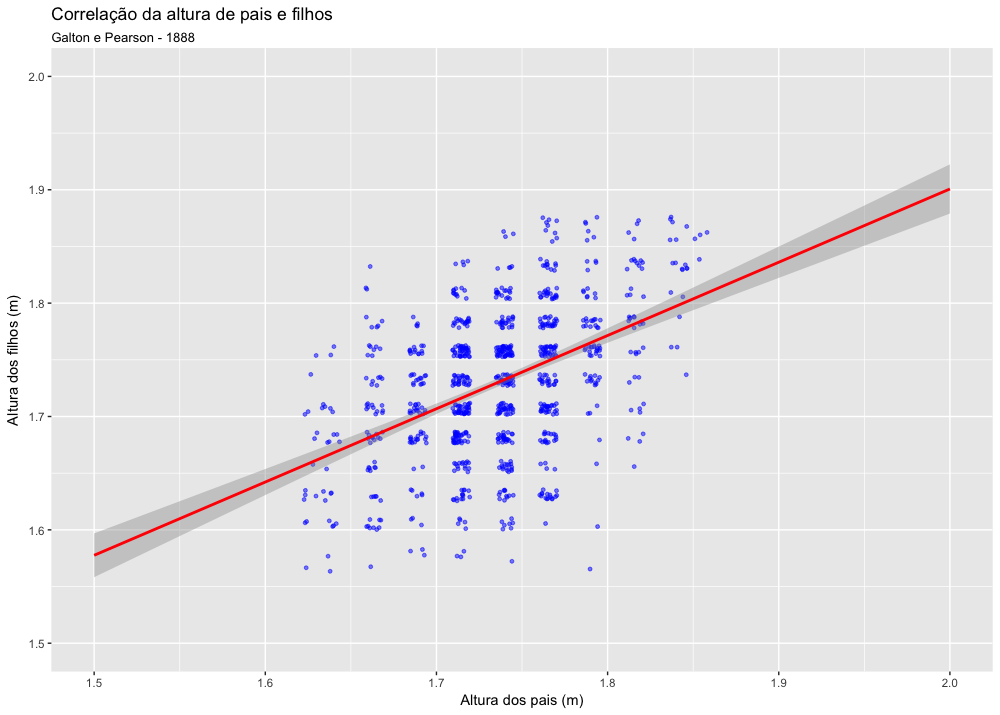
Covariância
A covariância de duas variáveis x e y em um conjunto de dados mede como esses dois estão relacionados linearmente. A covariância da amostra é definida em termos da amostra como:
cov_{x,y}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{n}{format: latex}
Observando a fórmula acima com atenção você poderá verificar que a covariância é o somatório da multiplicação de todos os desvios de cada variável. Ou seja, é calcula-se o desvio de cada dado em relação à sua média em cada eixo, multiplicam-se esses dois desvios e, finalment, faz-se o somatório de todos essas multiplicações.
Mas não se assuste com essa fórmula. Todos esses cálculos serão feitos automaticamente pelo R. O importante aqui é entender que quando os desvios são no mesmo sentido o sinal será positivo, quando os desvios são em sentidos diferentes o resultado será negativo. Ou seja, uma covariância positiva indica uma relação linear positiva entre as variáveis, e uma covariância negativa indica o oposto. Os gráficos abaixo ajudarão a compreender o que significa uma covariância positiva e negativa.
Vamos criar alguns conjuntos de dados de exemplo para plotarmos alguns gráficos de dispersão (scatter plots) e vamos calcular as covariâncias entres pares desses conjuntos de dados.
1 set.seed(0)
2 x = c(1:60)
3 A = 2*x
4 B = c(seq(from = 120,to = 2, by= -2))
5 C = x
6 D = (x^3)/1000
7 E = runif(60, 1, 120)
8
9 dat <- data.frame(x, A,B, C, D, E)
10
11 covA <- round(cov(dat$x,dat$A),2)
12 covB <- round(cov(dat$x,dat$B),2)
13 covC <- round(cov(dat$x,dat$C),2)
14 covD <- round(cov(dat$x,dat$D),2)
15 covE <- round(cov(dat$x,dat$E),2)
Agora vamos plotar alguns gráficos com esses dados para melhor compreensão do que é a covariância e interpretar o que é uma covariância positiva ou negativa.
1 plot1 <- ggplot(data = dat) +
2 geom_point(aes(x=x,y=A)) +
3 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
4 ggtitle("A \nCorrelação positiva perfeita") +
5 annotate("text", x=0, y=100, label= paste("cov=", covA), color="black", fontface=1\
6 , size=4, hjust = 0)
7
8 plot2 <- ggplot(data = dat) +
9 geom_point(aes(x=x,y=B)) +
10 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
11 ggtitle("B \nCorrelação negativa perfeita") +
12 annotate("text", x=45, y=100, label= paste("cov=", covB), color="black", fontface=\
13 1, size=4, hjust = 0)
14
15 grid.arrange(plot1, plot2, ncol = 2, nrow=1)
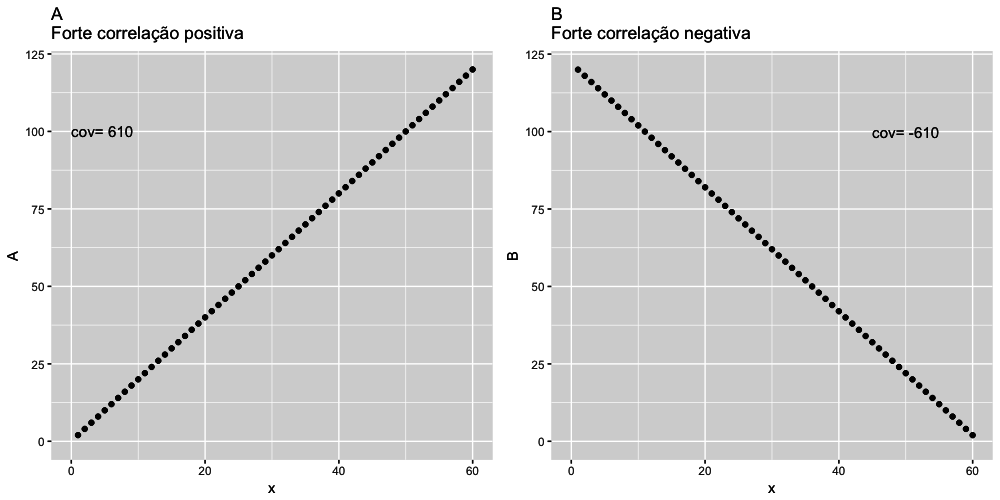
Analisando os gráficos A e B acima pode-se perceber que em ambos há uma correlação perfeita entre as variáveis dos eixos x e y e, além disso, podemos ver que a covariância serve para indicar a direção da correlação. No gráfico A as variáveis estão correlacionados de forma positiva: quando uma aumenta a outra aumenta, portanto a correlação é positiva (+610). No gráfico B as variáveis estão correlacionadas de forma negativa, quando a variável no eixo aumenta, a variável no eixo y diminui, portanto a medida da correlação é negativa (-610). Entretanto, o valor absoluto da covariância não tem muito valor para compararmos diferentes gráficos de dispersão. Veja no exemplo abaixo que duas correlações perfeitas podem ter covariâncias bastante diferentes.
1 # apesar de ser desnecessário, repeti aqui o código do plot1 para melhor compreensão\
2 desse code chunk
3 plot1 <- ggplot(data = dat) +
4 geom_point(aes(x=x,y=A)) +
5 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
6 ggtitle("A \nCorrelação positiva perfeita") +
7 annotate("text", x=0, y=100, label= paste("cov=", covA), color="black", fontface=1\
8 , size=4, hjust = 0)
9
10 plot3 <- ggplot(data = dat) +
11 geom_point(aes(x=x,y=C)) +
12 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
13 ggtitle("C \nCorrelação positiva perfeita") +
14 annotate("text", x=0, y=100, label= paste("cov=", covC), color="black", fontface=1\
15 , size=4, hjust = 0)
16
17 grid.arrange(plot1, plot3, ncol = 2, nrow=1)
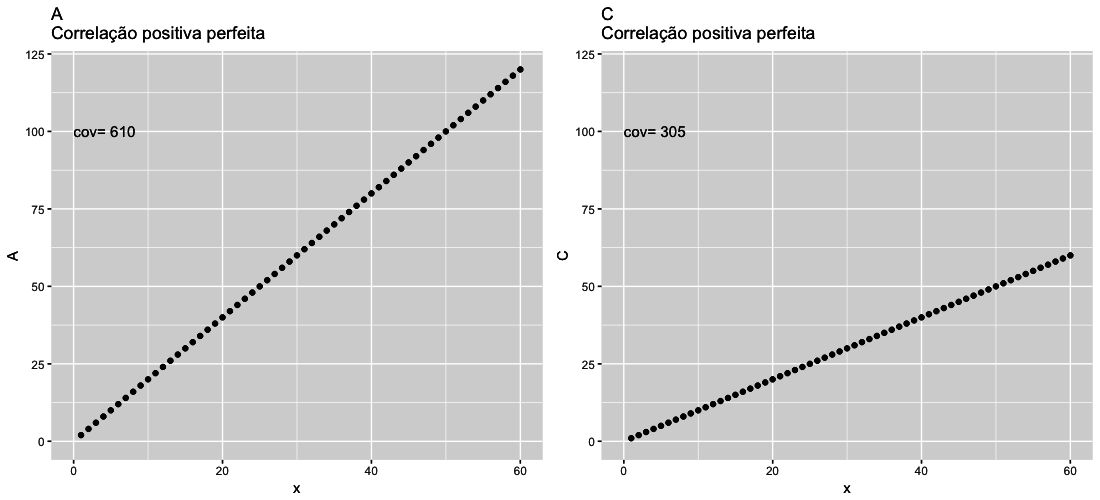
Analisando os gráficos A e C acima pode-se perceber que apesar da covariância servir para indicar a direção da correlação, ela não uma boa medida para comparar a força da correlação entre conjuntos diferentes de dados. Veja que os gráficos A e C tem uma correlação perfeita entre suas variáveis, entretanto, o valor da covariância entre os dois gráficos é muito diferente, sendo duas vezes maior no gráfico A. Essa diferença enorme entre os valores torna difícil usar a covariância como uma medida para comparar a força da correlação entre diferentes conjuntos de dados. Isso nos mostra que a medida da covariância não é adequada para comparar a força da correlação entre conjuntos diferentes de dados. Para isso, vamos precisar de outro tipo de medida.
Para podermos comparar a força da correlação entre diferentes gráficos ou diferentes conjuntos de dados, precisamos de uma medida normalizada. Para essa finalidade usamos o coeficiente de correlação.
Coeficiente de Correlação
O coeficiente de correlação é uma medida da força da correlação linear entre duas variáveis. Essa medida, que se originou dos trabalhos de Galton, teve seu desenvolvimento matemático feito por Karl Pearson. Devido a isso o coeficiente de correlação linear é também conhecido como coeficiente de correlação de Pearson e é denotado pela letra r.
O coeficiente de correlação é a versão normalizada da covariância, ou seja, o coeficiente de correlação de duas variáveis é simplesmente a covariância dessas variáveis dividida pelo produto dos desvios padrões de cada uma dessas variáveis. Essa divisão faz a normalização do coeficiente de correlação e possibilita sua comparação entre diferentes conjuntos de dados. Com isso, o coeficiente de correlação passa a ter uma varição de -1 até +1, sendo o sinal a indicação da direção da correlação e o valor absoluto desse coeficiente e indica a magnitude da relação linear entre essas duas variáveis. Como varia sempre de -1 a 1, possibilita a comparação de diferentes conjuntos de dados. Mas lembre-se, o coeficiente de correlação é uma medida da força e direção da correlação linear entre duas variáveis. Ou seja, só serve para analisar correlações lineares.
Direção da correlação linear
- correlação linear positiva -> coeficiente é positivo
- correlação linear negativa -> coeficiente é negativo
Força da correlação linear
- próxima de -1 ou +1 : correlação linear total
- próxima de -0.75 ou +0.75: correlação linear forte
- próximo de -0.50 ou +0.50: correlação linear moderada
- próximo de -0.20 ou +0.20: correlação linearfraca
- próxima de 0: não há correlação linear
Cuidados com a interpretacão do coeficiente de correlação
Cuidado com a interpretação de um coeficiente de correlação com valor absoluto pequeno. Isso não quer dizer que não há correlação entre as variáveis, mas sim que não há uma correlação linear. É importante salientar que duas variáveis podem ter uma forte correlação não linear e, logicamente, nenhuma correlação linear. Nesse caso o coeficiente de correlação não é uma medida útil, pois só mede a força da correlação não linear. Portanto, lembre-se, o coeficiente de correlação (linear) só é útil para analisar correlações lineares entre duas variáveis.
Além disso, cuidado com a interpretação de um coeficiente de correlação forte. Isso pode ser enganoso também. Um conjunto de dados pode ter um forte coeficiente de correlação apesar de não apresentarem nenhuma correlação real.
Calculando o coeficiente de correlação no R
A fórmula do coeficiente de correlação é:
r_{x,y}=\frac{cov_{x,y}}{\sigma_{x}\sigma{y}}{format: latex}
Mas não se assuste com essa fórmula, o R tem uma função para realizar esses cálculos: cor(x,y). A função cor(x, y) calcula o coeficiente de correlação de Pearson entre as variáveis x e y. Uma vez que esta quantidade é simétrica em relação a x e y, não importa em que ordem você colocar as variáveis.
Ao mesmo tempo, a função cor() é muito conservadora quando encontra dados faltantes (por exemplo NA). Quando essa função encontra algum dado NA o resultado será sempre NA. Usamos o argumento "use=pairwise.complete.obs" para alterar esse comportamento padrão de retornar NA sempre que qualquer um dos valores encontrados. Esse argumento, definido dessa forma, permite que a função cor() calcule o coeficiente de correlação para aquelas observações onde os valores de x e y não estão faltando, ou seja, levando em conta apenas os pares completos de observações.
O metodo default da função cor() é calcular o coeficiente de correlação de Pearson. Mas a função cor() pode calcular também outros coeficientes de correlação, tal como o de “kendall” ou de “spearman”. Para isso basta informar nos argumentos da função o método desejado:
1 cor(dat$x, dat$A, method = "pearson") # default: deve ser usado quando os dados estã\
2 o normalmente distribuídos
3 cor(dat$x, dat$A, method = "kendal")
4 cor(dat$x, dat$A, method = "spearman") # usado quando os dados não estão normalmente\
5 distribuídos
6 [1] 1
7 [1] 1
8 [1] 1
Ao analisar o coeficiente de correlação de duas variáveis, é sempre importante fazer também uma inspeção visual dos gráficos. Vamos ver nos gráficos abaixo a importância dessa inspeção visual.
1 corA <- round(cor(dat$x,dat$A),2)
2 corB <- round(cor(dat$x,dat$B),2)
3 corC <- round(cor(dat$x,dat$C),2)
4 corD <- round(cor(dat$x,dat$D),2)
5 corE <- round(cor(dat$x,dat$E),2)
6
7 plot1a <- ggplot(data = dat) +
8 geom_point(aes(x=x,y=A)) +
9 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
10 ggtitle("A \nCorrelação positiva perfeita") +
11 annotate("text", x=0, y=115, label= paste("r=", corA), color="black", fontface=1, \
12 size=4, hjust = 0)
13
14 plot2a <- ggplot(data = dat) +
15 geom_point(aes(x=x,y=B)) +
16 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
17 ggtitle("B \nCorrelação negativa perfeita") +
18 annotate("text", x=45, y=115, label= paste("r=", corB), color="black", fontface=1,\
19 size=4, hjust = 0)
20
21 plot4 <- ggplot(data = dat) +
22 geom_point(aes(x=x,y=D)) +
23 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
24 ggtitle("D \nAusência de correlação linear\nCorrelação não linear perfeita") +
25 annotate("text", x=5, y=115, label= paste("r=", corD), color="black", fontface=1, \
26 size=4, hjust = 0)
27
28
29 plot5 <- ggplot(data = dat) +
30 geom_point(aes(x=x,y=E)) +
31 coord_cartesian(xlim=c(0, 60), ylim=c(0, 120)) +
32 ggtitle("E \nAusência de correlação\nNão há nenhum tipo de correlação") +
33 annotate("text", x=40, y=115, label= paste("r=", corE), color="black", fontface=1,\
34 size=4, hjust = 0)
35
36
37 grid.arrange(plot1a, plot2a, plot4, plot5, ncol = 2, nrow=2)
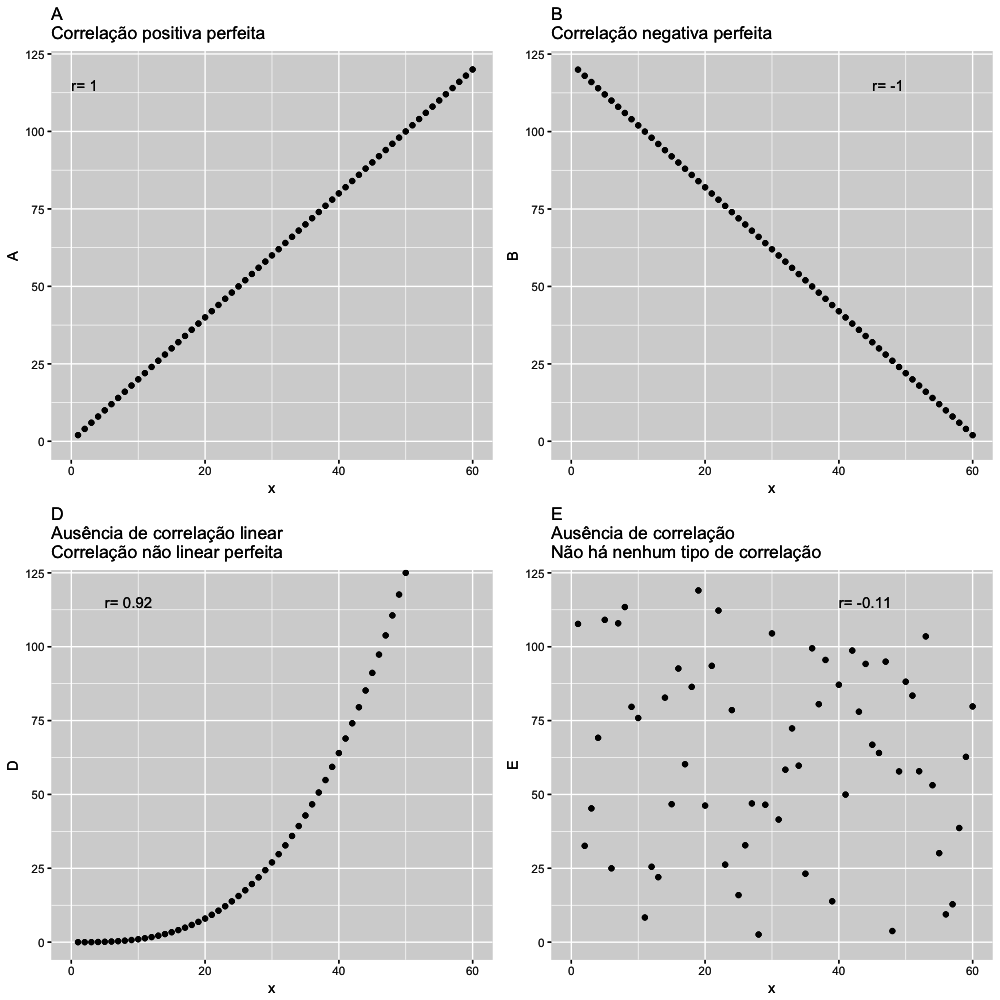
Analisando os gráficos acima podemos ver que os dados dos gráficos A e B tem uma correlação perfeita, respectivamente positiva e negativa. Em ambos esses gráficos o coeficiente de correlação tem o valor absoluto de 1, indicando uma correlação perfeita.
No gráfico D, apesar de um alto valor do coeficiente de correlação, na verdade a correlação entre as variáveis desse gráfico é perfeitamente não linear. A análise apenas do coeficiente de correlação linear poderia ser enganosa. A inspeção visual foi importante para podermos perceber não haver sentido em tentar calcular um coeficiente de correlação linear para esses dados.
No Gráfico E a ausência completa de correlação linear foi corretamente indentificada pelo valor de r= -0.11. O valor absoluto desse coeficiente, sendo tão próximo de zero é compatível a inspeção visual do gráfico.
Vamos analisar alguns exemplos de scatter plots interessantes de um conjunto de dados publicado por F. J. Anscombe em 1973 na revista The American Statistician (Vol. 27, No. 1, pp. 17-21). O objetivo desses gráficos é justamente mostrar que, juntamente com os cálculos numéricos dos dados, a inspeção visual dos dados é etapa fundamental na análise de dados. O conjunto de dados de F. J. Anscombe já faz parte do R e pode ser facilmente acessado no dataset anscombe.
1 anscombe
2 x1 x2 x3 x4 y1 y2 y3 y4
3 1 10 10 10 8 8.04 9.14 7.46 6.58
4 2 8 8 8 8 6.95 8.14 6.77 5.76
5 3 13 13 13 8 7.58 8.74 12.74 7.71
6 4 9 9 9 8 8.81 8.77 7.11 8.84
7 5 11 11 11 8 8.33 9.26 7.81 8.47
8 6 14 14 14 8 9.96 8.10 8.84 7.04
9 7 6 6 6 8 7.24 6.13 6.08 5.25
10 8 4 4 4 19 4.26 3.10 5.39 12.50
11 9 12 12 12 8 10.84 9.13 8.15 5.56
12 10 7 7 7 8 4.82 7.26 6.42 7.91
13 11 5 5 5 8 5.68 4.74 5.73 6.89
Vamos inicialmente calcular as medidas estatísticas do conjunto de dados de Anscombe. Calculando a média, desvio padrão e o coeficiente de correlação em cada um desses conjuntos de dados com o código abaixo.
1 # preparando os dados para melhor utilização
2 Anscombe <- with(anscombe, data.frame(x = c(x1, x2, x3, x4),
3 y = c(y1, y2, y3, y4),
4 group = gl(4, nrow(anscombe))))
5
6 Anscombe %>%
7 group_by(group) %>%
8 summarise(mean = mean(y),
9 std_dev = sd(y),
10 correlation = cor(x, y))
11
12 # A tibble: 4 x 4
13 group mean std_dev correlation
14 <fctr> <dbl> <dbl> <dbl>
15 1 1 7.500909 2.031568 0.8164205
16 2 2 7.500909 2.031657 0.8162365
17 3 3 7.500000 2.030424 0.8162867
18 4 4 7.500909 2.030579 0.8165214
Veja que as medidas estatísticas desse 4 pares de dados são extremamente parecidas. A simples análise desses números poderia indicar que se tratam de conjuntos muitos similares, com as mesmas médias, os mesmos desvios padrões e, inclusive, o mesmo coeficiente de correlação entre cada par de variáveis. Entretanto, como veremos, a análise visual desses dados mostra uma história basante diferente.
1 # plotando os 4 gráficos de Anscombe
2 ggplot(Anscombe, aes(x, y)) +
3 geom_point() +
4 geom_smooth(method='lm', se=FALSE) +
5 facet_wrap(~ group) +
6 annotate("text",
7 x=16,
8 y=5.2,
9 label= "mean = 7.5\nsd = 2.0\nr = 0.82",
10 color="black",
11 fontface=2,
12 size=3,
13 hjust = 0)
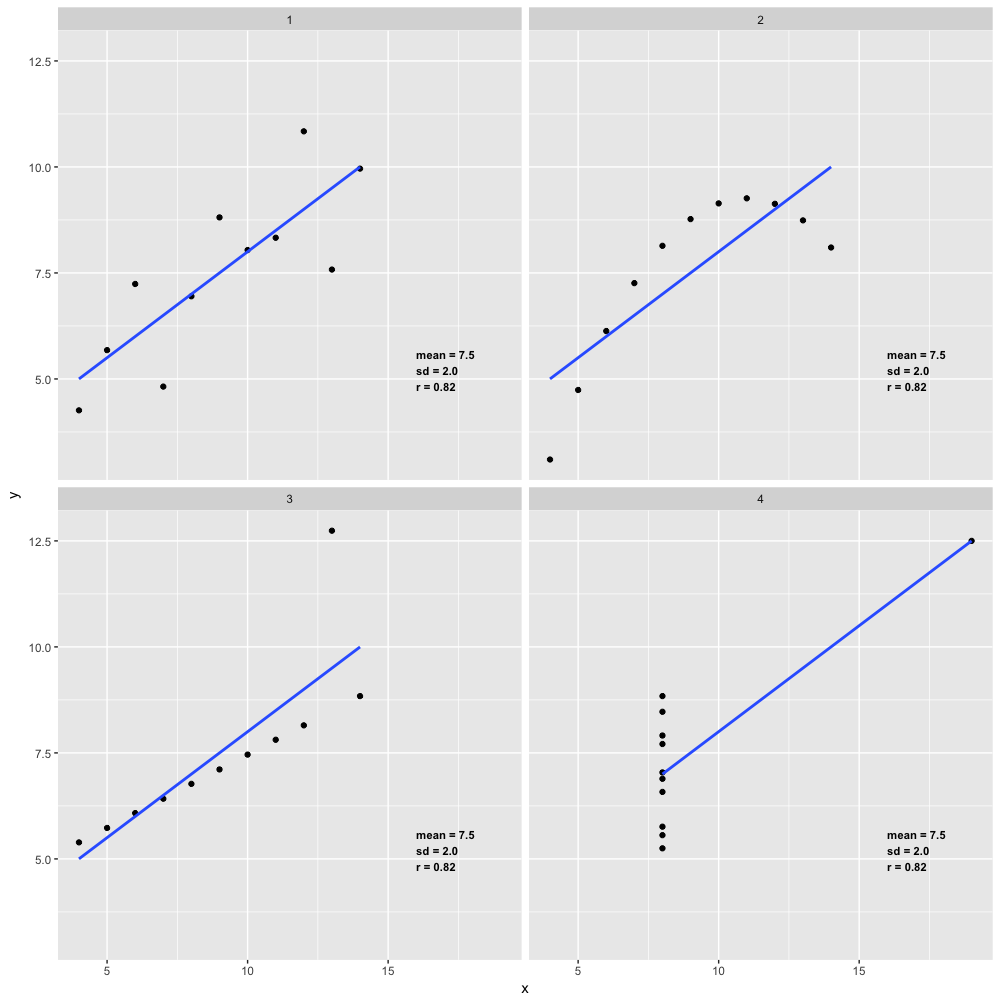
Veja que nesses 4 gráficos a linha de regressão é muito parecida. Na verdade é idêntica.
Veja também que a média dos dados, o desvio padrão e o coeficiente de correlação também são idênticos. Entretanto, apesar dessas estatísticas idênticas, é fácil verificar visualmente que os dados são bastante diferentes.
Os dados do grupo 1 tem uma forte correlação linear
Os dados do grupo 2, apesar de terem um coeficiente de correlação alto, na verdade tem uma correlação não linear.
Os dados do grupo 3 apresentam uma correlação linear quase absoluta, a não ser por um outlier.
Os dados do grupo 4 não apresentam correlação alguma, nem linear nem de qualquer outra forma.
Com esses exemplos de Anscombe podemos ver que as medidas estatísticas tradicionais não descrevem completamente os dados e que a visualização gráfica dos dados é extremamente importante.
\newpage
## Linha de Regressão - the best fit line
Em muitos gráficos do tipo scatter plot é comum haver uma linha reta que representa a correlação linear desses dados, a reta de regressão. Essa é reta que melhor representa os pontos (best fit line) e é calculada através do método de least squares.
Essa linha, denominada de least square regression line ou simplesmente linha de regressão, pode ser facilmente calculada no R através da função geom_smooth(). Para isso devemos especificar o argumento method="lm". lm significa linear model. Por padrão a linha será desenhada em azul com uma sombra de cinza ao redor, indicado o intrevalo de confiança de 95%. Se desejarmos NÃO plotar esse intervalo de confiança basta incluir o argumento se=FALSE. se significa standard error.
Vamos usar novamente alguns dados do dataset mpg que já vem junto com o ggplot2 R para criar essa linha de regressão, calcular a covariância e o coeficiente de correlação.
Vamos inicialmente verificar esses dados:
1 str(mpg)
2
3 Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 234 obs. of 11 variables:
4 $ manufacturer: chr "audi" "audi" "audi" "audi" ...
5 $ model : chr "a4" "a4" "a4" "a4" ...
6 $ displ : num 1.8 1.8 2 2 2.8 2.8 3.1 1.8 1.8 2 ...
7 $ year : int 1999 1999 2008 2008 1999 1999 2008 1999 1999 2008 ...
8 $ cyl : int 4 4 4 4 6 6 6 4 4 4 ...
9 $ trans : chr "auto(l5)" "manual(m5)" "manual(m6)" "auto(av)" ...
10 $ drv : chr "f" "f" "f" "f" ...
11 $ cty : int 18 21 20 21 16 18 18 18 16 20 ...
12 $ hwy : int 29 29 31 30 26 26 27 26 25 28 ...
13 $ fl : chr "p" "p" "p" "p" ...
14 $ class : chr "compact" "compact" "compact" "compact" ...
Esse dataset já foi analisado numericamente e graficamente nos capítulos passados, e possui 243 linhas (observações) com 11 variáveis. O significado de cada variável está descrito na documentação de ajuda do dataset mpg e pode ser visualizado com o comando ?mpg no console. A tabela abaixo mostra o significado de cada variável:
| variável | significado |
|---|---|
| manufacturer | marca |
| model | modelo |
| displ | cilindradas (Engine Displacement) |
| year | ano de fabricação |
| cyl | número de cilindros |
| trans | tipo de marcha: automática / manual |
| drv | tração: f=frontal, r=traseira, 4=4x4 |
| cty | milhas por galão na cidade |
| hwy | milhas por galão na estrada |
| fl | tipo de combustível: r=regular, p=premium, d=diesel, e=ethanol, c=CNG (gás) |
| class | tipo de carro: compact, midsize, suv, 2seater, minivan, pickup ou subcompact |
Vamos plotar novamente os dados de cilindradas e desempenho (milhas por galão) para uma inspeção visual inicial, mas dessa vez vamos usar o pacote ggplot2 para criar gráficos mais profissionais.
1 ggplot(data=mpg, aes(cty, displ)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 xlab("milhas por galão") +
5 ylab("cilindradas")
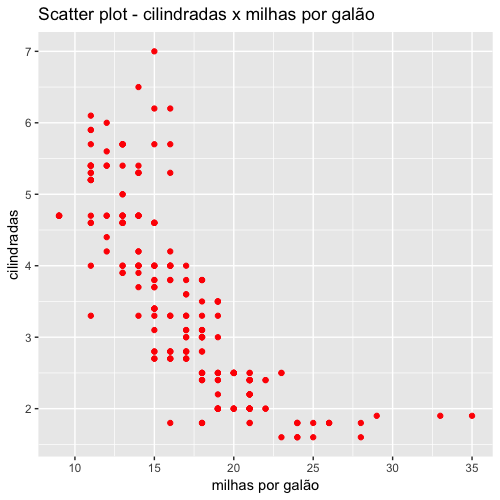
No capítulo passado adicionamos uma reta de regressão a esse gráfico com as funções gráficas básicas do R. Para efeitos didáticos, vamos novamente adicionar uma reta de regressão nesse gráfico, mas agora usando o ggplot2.
Com o ggplot2 é muito simples adicionar uma reta de regressão aos pontos do gráfico. Para isso, basta usar a função geom_smooth(method="lm"). O argumento method="lm" indica que a linha a ser incluida no gráfico será calculada pelo método de modelo linear (linear model = lm). Veja que essa função adiciona por padrão o intervalo de confiança de 95% do redor da reta.
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 geom_smooth(method=lm) # Add linear regression line
7 # (by default includes 95% confidence region)
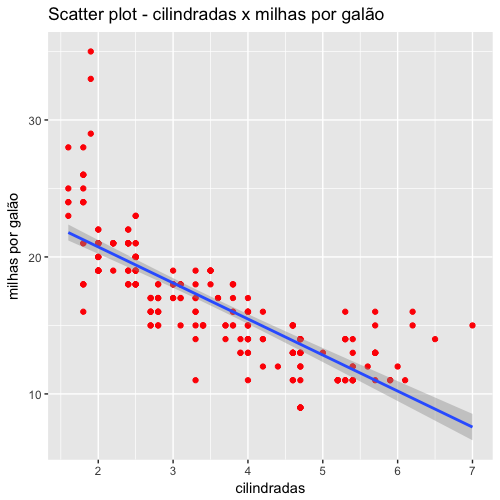
Já sabemos também calcular o coeficiente de correlação linear entre esses dados com a função cor().
1 cor(mpg$displ, mpg$cty)
2 [1] -0.798524
Veja que o coeficiente de correlação foi negativo e, em valores absolutos, teve um valor alto. Isso indica que há uma forte correlação negativa entre essas variáveis (cilindradas e milhas percorridas por galão), corroborando nossa hipótese anterior de que carros 1.0 são mais econômicos.
O pacote gráfico ggplot2 possui também funções que permitem facilmente inserir linhas curvas - não lineares - que melhor se ajustam aos pontos do gráfico. Na verdade esse é o comportamento padrão da função geom_smooth. Se usarmos essa função com seus valores default será inserida uma linha curva e não uma linha de regressão linear.
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 geom_smooth() # (by default includes 95% confidence region)
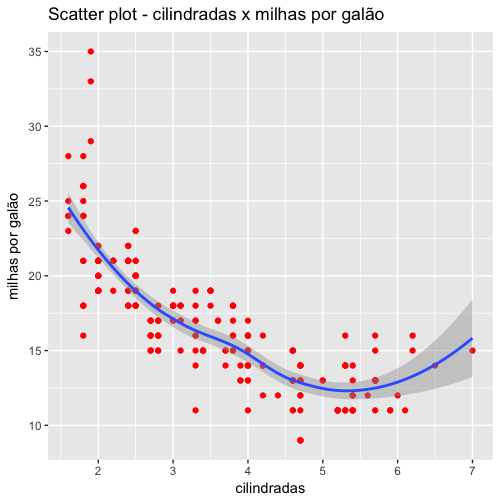
\newpage
Vamos analisar outro conjunto de dados que já vem no R: O dataset Indometh já faz parte do R e contém dados da farmacocinética do antibiótico indometacina. A primeira coluna do data frame é o nº do paciente (6 no total), a segunda coluna é o tempo da coleta do sangue e a terceira coluna é a concentração sérica do antibiótico no sangue.
Vamos inicialmente verificar esses dados:
1 str(Indometh)
2
3 Classes ‘nfnGroupedData’, ‘nfGroupedData’, ‘groupedData’ and 'data.frame': 66 obs. o\
4 f 3 variables:
5 $ Subject: Ord.factor w/ 6 levels "1"<"4"<"2"<"5"<..: 1 1 1 1 1 1 1 1 1 1 ...
6 $ time : num 0.25 0.5 0.75 1 1.25 2 3 4 5 6 ...
7 $ conc : num 1.5 0.94 0.78 0.48 0.37 0.19 0.12 0.11 0.08 0.07 ...
8 - attr(*, "formula")=Class 'formula' language conc ~ time | Subject
9 .. ..- attr(*, ".Environment")=<environment: R_EmptyEnv>
10 - attr(*, "labels")=List of 2
11 ..$ x: chr "Time since drug administration"
12 ..$ y: chr "Indomethacin concentration"
13 - attr(*, "units")=List of 2
14 ..$ x: chr "(hr)"
15 ..$ y: chr "(mcg/ml)"
Plotando os dados
1 ggplot(data=Indometh, aes(x=time, y=conc)) +
2 geom_point()
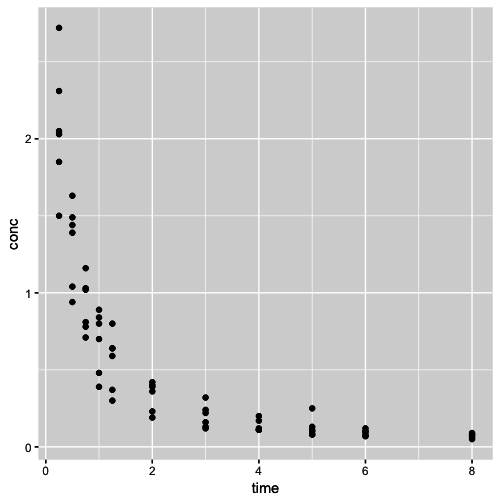
Podemos verificar visualmente que a relação entre o tempo e a concentração sérica não é linear. Vamos plotar a reta de regressão para mostrar como essa reta não se ajusta bem aos dados e, em seguida, calcular o coeficiente de correlação linear de Pearson.
1 ggplot(data=Indometh, aes(x=time, y=conc)) +
2 geom_point() +
3 geom_smooth(method = "lm")
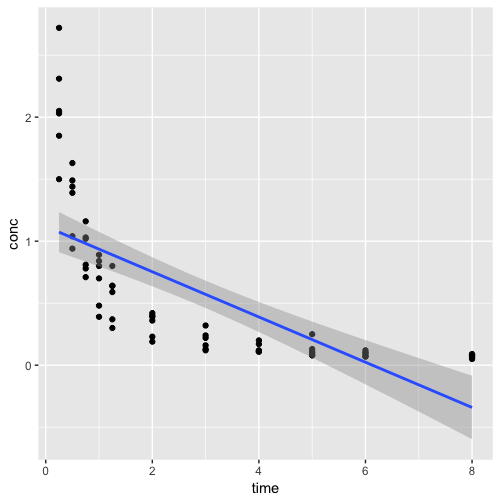
Calculando o coeficiente de correlação:
1 cor(Indometh$time, Indometh$conc)
2 [1] -0.7104719
Veja que o coeficiente foi negativo indicando haver uma relação negativa entre o tempo e a medida da concentração sérica, o que é bastante plausíve, pois a concentração sérica se reduz com o passar do tempo. Entretanto, o valor absoluto do coeficiente de correlação foi muito alto. Isso demonstra mais uma vez a inadequação de calcular o coeficiente de correlação num conjunto de dados que tem uma relação claramente não linear.
Como já vimos, o R nos permite facilmente plotar também linhas curvas para representar relações não lineares com a função geom_smooth() do pacote ggplot2. Se deixarmos a funçãp geom_smooth usar seu comportamento default, iremos gerar uma gráfico com uma curva que se ajusta aos dados da melhor forma possível.
1 ggplot(data=Indometh, aes(x=time, y=conc)) +
2 geom_point() +
3 geom_smooth()
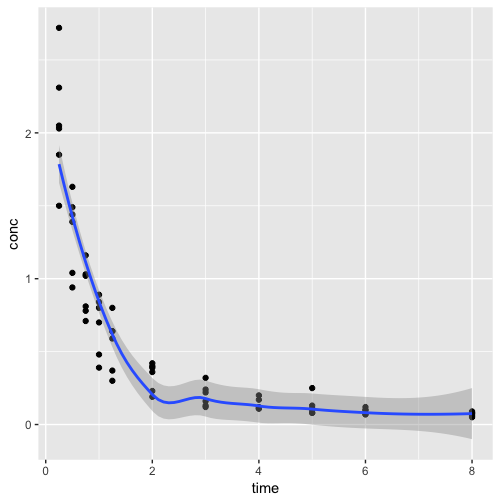
Apêndice Extra - Transformações logarítmicas
Existem diversas técnicas para conseguirmos para modelarmos de forma mais adequada a relação entre duas variáveis. Uma forma simples é através da transformação logaritmica dos dados. Isso pode ser feito facilmente no R com a função log que calcula o logarítmo natural dos dados. Vamos experimentar fazer uma transformação logarítmica em ambas as variáveis e verificar o resultado.
1 # criando um novo data frame chamado log.Indometh
2 log.Indometh <- Indometh
3
4 # Fazendo a transformação logarítmica das variáveis desse data frame
5 log.Indometh$conc <- log(Indometh$conc)
6 log.Indometh$time <- log(Indometh$time)
7
8 #plotando o gráfico com a linha de regressão (linear model)
9 ggplot(data=log.Indometh, aes(x=time, y=conc)) +
10 geom_point() +
11 geom_smooth(method = "lm")
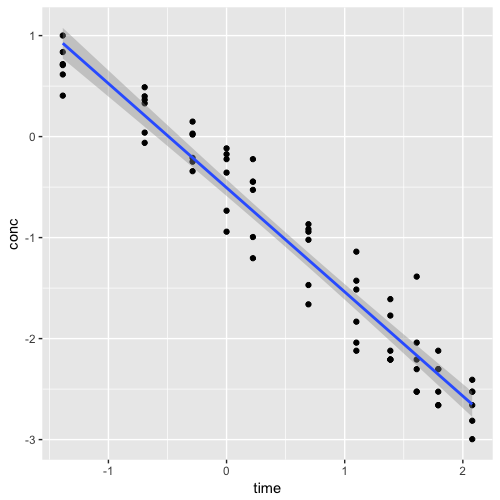
Vamos agora calcular o coeficiente de correlação dessas variáveis após a transformação logaritmica.
1 cor(log.Indometh$time, log.Indometh$conc)
2 [1] -0.9671346
Veja que o novo valor do coeficiente de correlação foi muitíssimo forte, indicando que a relação entre essas variáveis é melhor explicada por uma relação logarítmica e não por uma relação linear.
Referências
- Stigler, Stephen M. Francis Galton’s Account of the Invention of Correlation.
Statist. Sci. 4 (1989), no. 2, 73–79. doi:10.1214/ss/1177012580. https://projecteuclid.org/euclid.ss/1177012580 - Francis Galton. Co-Relations and Their Measurement, Chiefly from Anthropometric Data. Proceedings of the Royal Society of London. Vol. 45 (1888 - 1889), pp. 135-145. Disponível em: https://www.york.ac.uk/depts/maths/histstat/galton_corr.pdf.
- Friendly, M. and Denis, D. (2005). The early origins and development of the scatterplot. J. Hist. Behav. Sci., 41: 103–130. doi:10.1002/jhbs.20078
- Stephen Few. Now You See It. Simple Visualization Techniques for Quantitative Analysis. Analytic Press: Oakland, 2009.
-
-
- Anscombe. Graphs in Statistical Analysis. The American Statistician. 1973, Vol. 27, No. 1, pp. 17-21.
-
Modelos Científicos
1 > library(tidyverse)
Introdução
O que é um modelo científico?
Um modelo é qualquer forma de representação simplificada a realidade que seja útil para analisamos e compreendermos os fenômenos em sua essência.
Um modelo pode ser um objeto físico, tal como um protótipo em miniatura de um avião ou uma peça de resina como um fêmur humano; pode ser uma teoria, tal como o modelo atômico de Bohr; pode ser um ser vivo, como nas situações em que um ratinho de laboratório é usado para testar os efeitos de um medicamento. Pode ser uma equação matemática, como a equação de uma reta de regressão linear. Um modelo pode ser também uma combinação de objetos físicos e softwares, tal como o manequim do SymMan, que simula as respostas biológicas humanas. Modelos nos ajudam a compreender os fenômenos pois ajudam a focar nossa atenção nos aspectos considerados mais importantes. O uso de simulações através de modelos tecnológicos é atualmente prática cada vez mais comum no ensino da medicina.
Modelos de relação linear no R
No capítulo anterior estudamos como o conceito de correlação é importante para a determinação da interação entre uma variável explanatória (independente) e uma variável de reposta (dependente). Vimos também que uma das etapas do estudo de correlação é a criação de uma reta de regressão, que é a reta que melhor se ajusta aos dados.
Precisamos agora relembrar que toda reta é definida por uma equação matemática muito simples:
[
y = mx + n
]
Na equação acima, m é chamado de coeficiente angular e representa a inclinação da reta e n é chamado de coeficiente linear da reta (ou intercept), sendo definido como o ponto em que a reta intercepta o eixo y.Com essa equação, dada uma coordenada no eixo x, podemos determinar qual será a coordenada no eixo y, bastando saber o valor dos coeficientes m e n. Toda reta é definida por essa simples equação, inclusive a reta de regressão linear. Ou seja, a geração da reta de regressão num gráfico depende apenas de conhecermos esses coeficientes. O processo de descobrir esses coeficientes depende de um processo conhecido na estatística como método dos quadrados mínimos. Entretanto, não precisamos nos preocupar com esse método num curso introdutório de estatística. O importante é saber que o R faz todos esses cálculos automaticamente e gera a reta de regressão como já vimos. Vamos repetir esse gráfico agora, mas extendendo os eixos um pouco mais para podermos ver os pontos de interceptação da reta nos eixos.
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 xlim(c(-1,11)) +
7 ylim(c(-1,40)) +
8 geom_vline(xintercept=0) +
9 geom_hline(yintercept=0) +
10 geom_smooth(method=lm, fullrange = TRUE) # Add linear regression line
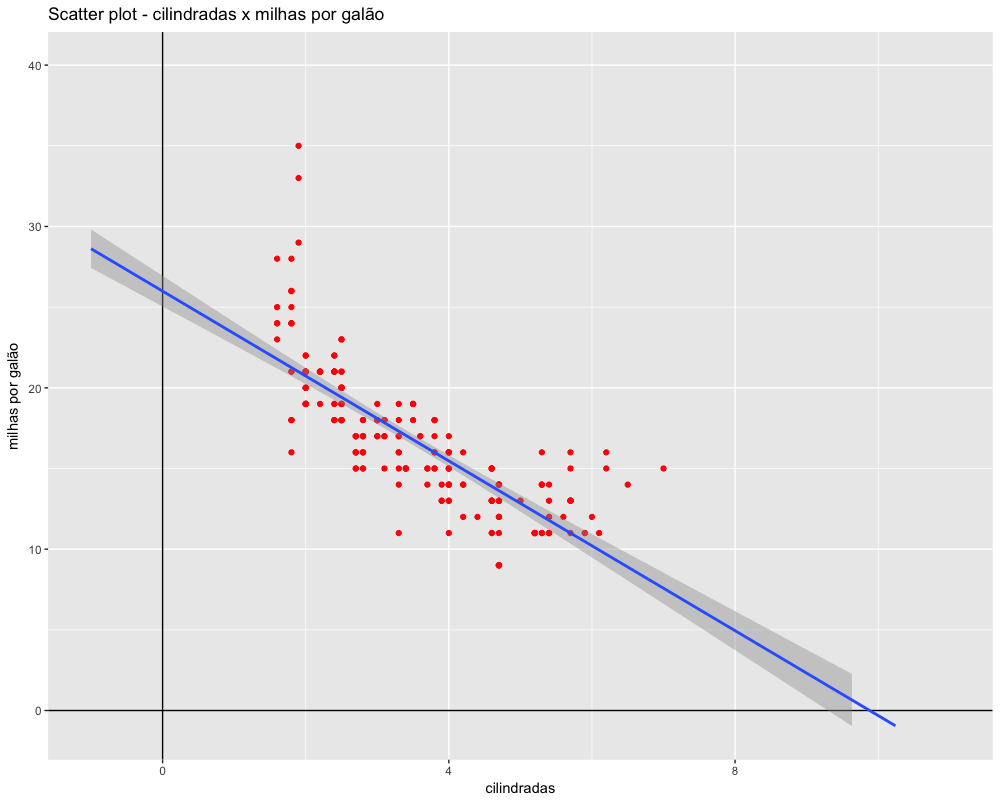
Observe no gráfico acima que a reta cruza o eixo y um pouco acima de 25 milhas e que a reta tem uma inclinação negativa. Ao calcularmos os valores exatos desses coeficientes você verá que eles coincidem com o gráfico. Calcular os coeficientes dessa reta é o próprio processo de criação de um modelo linear. Para obter os valores exatos dos coeficientes precisamos apenas pedir ao r para criar um modelo de relação liner com os dados que desejarmos. A função para criação de um modelo linear no R e lm()de linear model. Essa função tem a forma lm(y~x, data) que é interpretada pelo R como y depende de x. Observe que a fórmula inserida na função lm() deve ser na sequência:
variável_de_desfecho ~ variável_preditora
Vamos testar essa função usando os mesmos dados do gráfico acima: cilindradas como variável independente (explanatória ou independente) e milhas por galão como variável dependente (de desfecho ou dependente).
1 > lm(cty~displ, mpg)
2
3 Call:
4 lm(formula = cty ~ displ, data = mpg)
5
6 Coefficients:
7 (Intercept) displ
8 25.99 -2.63
Podemos ver no resultado acima a fórmula que foi usada no cálculo dos coeficientes e, logo abaixo, os coeficientes.
O valor mostrado logo abaixo de (intercept) é o coeficiente linear n = 25.99, o ponto do eixo y no qual a reta cruza o eixo vertical, ou seja, o ponto de interceptação da reta no eixo y. Veja que esse valor corresponde ao que havíamos notado no gráfico.
O outro valor é o coeficiente angular da reta m = -2.63.
Com isso temos tudo que precisamos para construir a reta de regressão. Ou seja, temos agora um modelo matemático para podermos prever qual será a distância percorrida por um carro, bastando saber suas cilindradas.
Vamos analisar os valores das cilindradas de nossa amostras:
1 > sort(unique(mpg$displ))
2
3 [1] 1.6 1.8 1.9 2.0 2.2 2.4 2.5 2.7 2.8 3.0 3.1 3.3 3.4 3.5 3.6 3.7 3.8 3.9
4 [19] 4.0 4.2 4.4 4.6 4.7 5.0 5.2 5.3 5.4 5.6 5.7 5.9 6.0 6.1 6.2 6.5 7.0
Veja que nessa amostra não temos carros de 3.2 cilindradas. Mas podemos usar nosso modelo (m = -2.63, n = 25.99) para prever quantas milhas esse carro irá percorrer com um galão de gasolina. Nossa fórmula será a seguinte:
1 > milhas_percorridas = -2.63 * 3.2 + 25.99
2 > milhas_percorridas
3 [1] 17.574
Vamos verificar que esse resultado no gráfico abaixo:
1 ggplot(data=mpg, aes(displ, cty)) +
2 geom_point(color = "red") +
3 ggtitle("Scatter plot - cilindradas x milhas por galão") +
4 ylab("milhas por galão") +
5 xlab("cilindradas") +
6 scale_x_continuous(breaks = seq(min(-1), max(15), by=0.5)) +
7 scale_y_continuous(breaks = seq(min(-1), max(40), by=1)) +
8 geom_vline(xintercept=0) +
9 geom_hline(yintercept=0) +
10 geom_vline(xintercept=3.2, color="blue", linetype="dotted") +
11 geom_hline(yintercept=17.574, color="blue", linetype="dotted") +
12 geom_smooth(method=lm, fullrange = TRUE) # Add linear regression line
13 # (by default includes 95% confidence region)
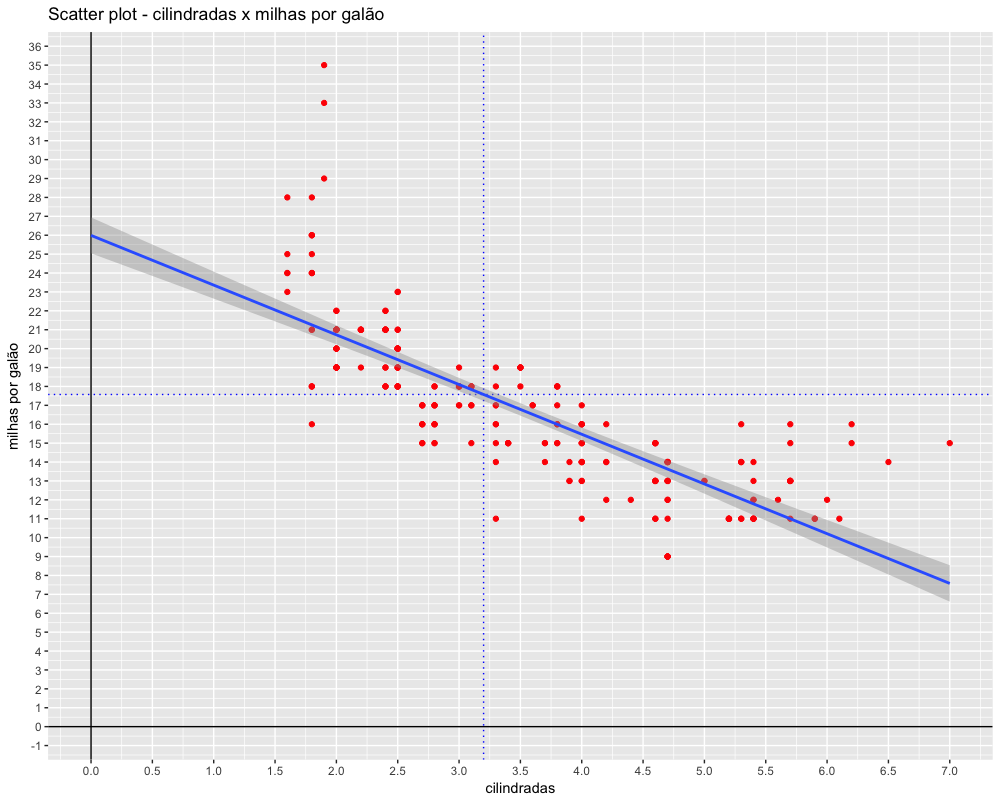
O Coeficiente de Determinação - magnitude do efeito
A função lm() tem muito mais dados do que apenas os coeficiente da reta. Para acessarmos esses dados completos basta usar a função summary() como abaixo:
1 > summary(lm(cty~displ, mpg))
2
3 Call:
4 lm(formula = cty ~ displ, data = mpg)
5
6 Residuals:
7 Min 1Q Median 3Q Max
8 -6.3109 -1.4695 -0.2566 1.1087 14.0064
9
10 Coefficients:
11 Estimate Std. Error t value Pr(>|t|)
12 (Intercept) 25.9915 0.4821 53.91 <2e-16 ***
13 displ -2.6305 0.1302 -20.20 <2e-16 ***
14 ---
15 Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
16
17 Residual standard error: 2.567 on 232 degrees of freedom
18 Multiple R-squared: 0.6376, Adjusted R-squared: 0.6361
19 F-statistic: 408.2 on 1 and 232 DF, p-value: < 2.2e-16
Veja que um dos resultados apresentados é o que se chama de R-Squared (R2). Essa medida é o coeficiente de determinação calculado pelo R para esse modelo linear. Esse coeficiente indica a proporção da variação da variável dependente pode ser explicada pela variável dependente. Nesse nosso exempplo o valor de R2 de 0.64 indica que 64% da variação do nº de milhas percorridas depende das cilindradas e o restante depende de outros fatores não analisados. Esse coeficiente indica a magnitude do efeito da variável independente (cilindradas) sobre a variável dependente (milhas percorridas).
A raiz quadrada desse coeficiente é justamente o coeficiente de correlação de Pearson que vimos no capítulo passado.
As limitações e utilidades dos modelos
Na seção anterior vimos que uma equação de uma reta servia como um modelo matemático da relação entre as cilindradas e a quantidade de milhas percorridas. Com esse modelo foi possivel inferir a quantidade de milhas percorridas com um galão por um carro de 3.2 cilindradas. É obvio que esse modelo é apenas uma simplificação da realidade. O resultado certamente irá depender de uma série de outras variáveis, tais como, por exemplo, o combustível usado, a idade do carro, os pneus usados, o tipo de asfalto e até mesmo o modo de condução do motorista. Modelos científicos serão sempre reducionistas, mas isso não é um defeito. Na verdade o papel do modelos não é representar a realidade em todos seus detalhes, o que seria impossível, mas simplificar a realidade de forma útil.
Modelos podem ser representações de um fenômeno natural mas também podem ser representações de um conjunto de dados. Existem diversos modelos matemáticos para representar distribuições de dados. Esses modelos teóricos de distribuição de dados são chamados de “Distribuições de Probabilidade”. Existe um número enorme de distribuições de probabilidade, cada uma apropriada para representar um tipo diferente de distribuição de dados. Esse é o tema do próximo capítulo.
Distribuições de probabilidade
carregando os pacotes necessários para o capítulo
1 > library(ggplot2)
2 > library(gridExtra) # necessário para usar a função grid.arrange
Introdução
Variation is the hard reality, not a set of imperfect measures for a central tendency.
Stephen Jay Gould
A medicina trabalha com incertezas, cada paciente responde de um determinado modo a uma doença ou a um tratamento. A variabilidade é a regra. Como disse Stephen Gould, a variação é a realidade. E é justamente essa variação nas repostas é que faz com que os dados de qualquer pesquisa estejam distribuídos de alguma forma. Entretanto, apesar dessa variabilidade, apesar dessa aleatoriedade, podemos notar padrões em muitos eventos aleatórios da natureza. O estudo das distribuições de probabilidade é justamente o estudo da análise desses padrões aleatórios.
A questão importante é responder à seguinte pergunta: qual será o padrão da distribuição de frequências dos resultados de uma experiência se repetirmos essa experiência infinitas vezes?.
Uma distribuição de frequências relativas de um número infinito de experimentos representa a probabilidade real de cada evento do experimento e é usualmente chamada de distribuição de probabilidades. Distribuições de probabilidades representam, portanto, a forma como os resultados (dados) de um determinado fenômeno (ou experimento) se distribuem quando o fenômeno (ou experimento) ocorre de forma totalmente aleatória (ou randomizada). Mas como nunca podemos fazer um número infinito de experimentos, toda distribuição de probabilidades é um modelo matemático teórico que representa essa situação.
Veremos adiantes que existem distribuições de probabilidade discretas e contínuas. As distribuições de probabilidade discretas são representadas graficamente por um histograma e as distribuições de probabilidade contínuas são representadas graficamente por uma curva, chamada curva de distribuição.
Mas, afinal de contas, o que é uma curva de distribuição de probabilidade?
Tecnicamente, uma curva de distribuição de probabilidade criada por uma função matemática, cuja área total abaixo da curva seja exatamente igual a 1. Essa curva, ou seja, esse gráfico, é uma representação teórica da probabilidade dos eventos ou dos dados de um estudo. A probabilidade total ou 100% é representada pela área total abaixo da curva, que é, portanto, sempre igual a 1.
A probabilidade de dados maiores que um certo valor é a área abaixo da curva à direita daquele ponto.
A probabilidade de dados menores que um certo valor é a área abaixo da curva à esquerda daquele ponto.
A probabilidade de dados entre dois valores é justamente a área abaixo da curva entre esses dois pontos.
Em termos simples, essa curva serve como uma representação da probabilidade teórica de ocorrência dos diferentes valores de um conjunto de resultados.
A Distribuição uniforme e um jogo de dados
Vamos ver como podemos encontrar padrões em eventos aleatórios começando com um exemplo muito simples: jogando um dado. Ao jogar um dado, qual a probabilidade do resultado ser o nº 6? ou 5? Se o dado não estiver viciado, a probabilidade de qualquer um dos seis resultados é igual a 1/6. Se chamarmos de **n** o nº de possibilidades, a probabilidade de qualquer dos resultados será 1/n. Nesse exemplo, 1/6.
Entretanto, se jogarmos o dado 60 vezes, será muito pouco provável obtermos exatamente a mesma proporção de cada um dos seis números do dado. Por outro lado, se jogarmos o dado 6 milhões de vezes, provavelmente cada face do dado irá ser obtida aproximadamente 1 milhão de vezes. Vamos ver como esse padrão vai se formando à medida que aumentando o nº de vezes que fazemos nosso experimento.
O R nos permite facilmente simular um dado. A primeira coisa a fazer é criar um objeto com as propriedades de um dado que nos interessam, ou seja, possuir valores de 1 a 6. Veja que, no nosso modelo de dado, só nos interessa essa propriedade. Como já comentamos no capítulo passado, um modelo é útil justamente por nos ajudar a focar a atenção nos aspectos considerados mais importantes.
Para criar um dado no R. Simplesmente atribuímos a esse objeto os valores de 1 a 6.
1 > dado <- c(1:6)
2 > dado
3 [1] 1 2 3 4 5 6
O que precisamos fazer agora é simular a jogada do dado. Para fazer isso precisamos apenas entender uma abstração: o que significa jogar um dado? Ao jogar um dado podemos ter apenas 6 resultados válidos: 1, 2, 3, 4, 5, 6. Ou seja, jogar um dado equivale a retirar aleatoriamente uma das possibilidades de conjunto com esses 6 valores.
O R, sendo um software estatístico, tem uma função própria para isso. A função sample() tem como argumentos um conjunto e o nº de ítens desse conjunto que iremos retirar. No nosso caso o conjunto é o objeto dado que criamos. Nesse exemplo, iremos retirar apenas 1 amostra do conjunto de 6 possibilidades. Em outras palavras, ao simular uma jogada de um dado teremos UM único resultado dentre os 6 possível. A simulação, portanto, é de retirar ao acaso uma das 6 possibilidades.
1 > sample(dado, size=1)
2 [1] 3
A cada vez que essa linha de código fore executada o R irá escolher de forma aleatória uma das 6 possibilidades. Experimente executar esse código inúmeras vezes e verá que o resultado se modifica aleatoriamente.
A questão é: existe um padrão nesses resultados?
Vamos fazer um experimento jogando nosso dado 20 vezes, para verificarmos qual a frequência com que cada número irá aparecer. Para isso, basta informar como argumento da função sample size=20 e replace=TRUE. O argumento replace=TRUE indica que o a amostragem será feita com reposição, ou seja, o número que foi sorteado poderá ser sorteado novamente (o que é o que acontece num jogo de dados. Usarei a função table() e a função prop.table() para criar uma tabela com as frequências relativas de cada resultado.
1 > amostra1 <- prop.table(table(sample(dado, size=20, replace = TRUE)))
2 > amostra1
3
4 1 2 3 4 5 6
5 0.15 0.25 0.15 0.20 0.05 0.20
A cada vez que esse código for executado a proporção de cada face do dado se modifica. Não parece haver ainda um padrão.
Mas a visualização ficará ainda mais interessante se fizermos um gráfico de barras dessas frequências relativas:{r}
amostra1 <- prop.table(table(sample(dado, size=20, replace = TRUE)))
barplot(amostra1, xlab = "Faces do dado", ylab = "Frequencia relativa", col = "dodgerblue4", ylim= c(0,1))
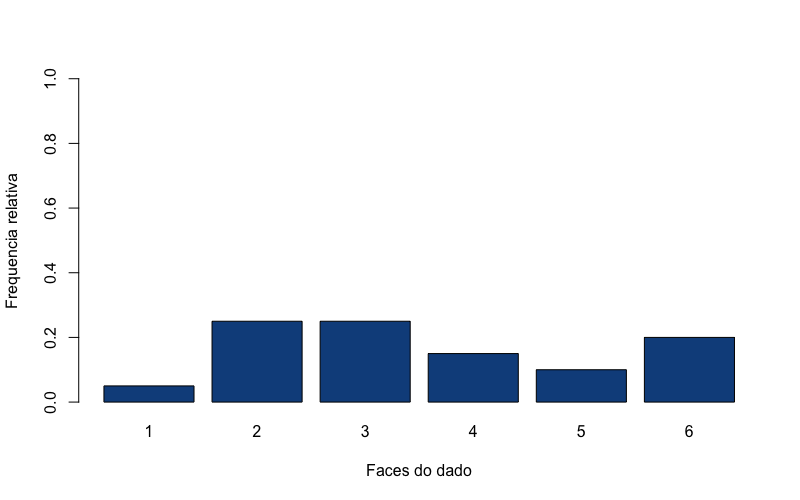
Se você repetir esse código várias vezes verá que não parece haver um padrão de respostas. A frequência dos resultados de cada face do dado varia muito.
A questão é: existirá um padrão se jogarmos o dado mil vezes, um milhão de vezes, infinitas vezes?
Se desejarmos repetir essa jogada mil de vezes, podemos usar o mesmo comando sample(), mas alterando o argumento size para size=1000, o que indica o tamanho de nossa amostra (mil jogadas do dado). Vamos colocar o resultado dessas jogadas num outro objeto, que chamaremos de amostra2. O código a seguir cria uma amostra de mil jogadas, em seguida cria uma tabela de frequências absolutas de cada face do dado, transforma a tabela numa tabela de frequências relativas, e finalmente, gera um gráfico de barras com esses dados. Você pode clicar no botão play diversas vezes, toda vez que clicar no botão play esse código será executado.
1 > amostra2 <- sample(dado, size=1000, replace = TRUE)
2 > tabela2 <- table(amostra2)
3 > tabela2 <- prop.table(tabela2)
4 > barplot(tabela2, xlab = "Faces do dado", ylab = "Frequencia relativa", col = "dodg\5 erblue4", ylim= c(0,0.5))
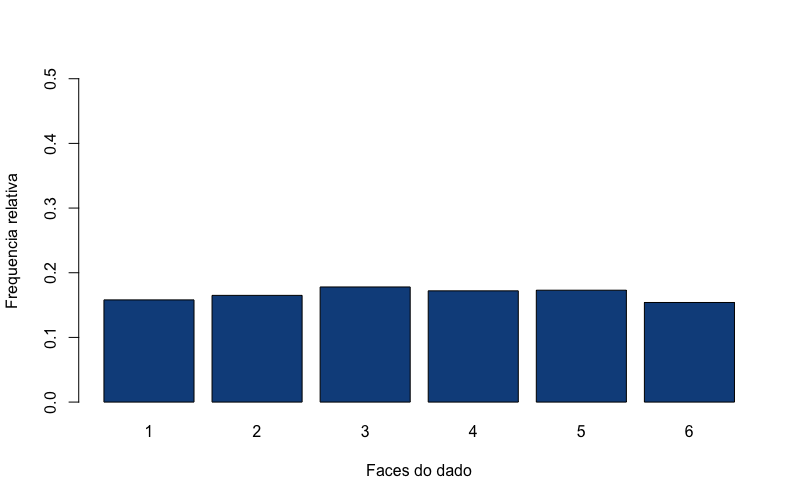
A cada vez que esse código é executado o gráfico apresenta ligeiras diferenças. Ou seja, a frequência de cada face se altera muito menos com uma amostra de mil jogadas de dados. Se nossa amostra for aumentada para cem mil jogadas, você poderá ver que as frequências de cada face são praticamente as mesmas.
1 > amostra3 <- sample(dado, size=100000, replace = TRUE)
2 > tabela3 <- table(amostra3)
3 > tabela3 <- prop.table(tabela3)
4 > barplot(tabela3, xlab = "Faces do dado", ylab = "Frequência relativa", col = "dodg\5 erblue4", ylim= c(0,0.5))
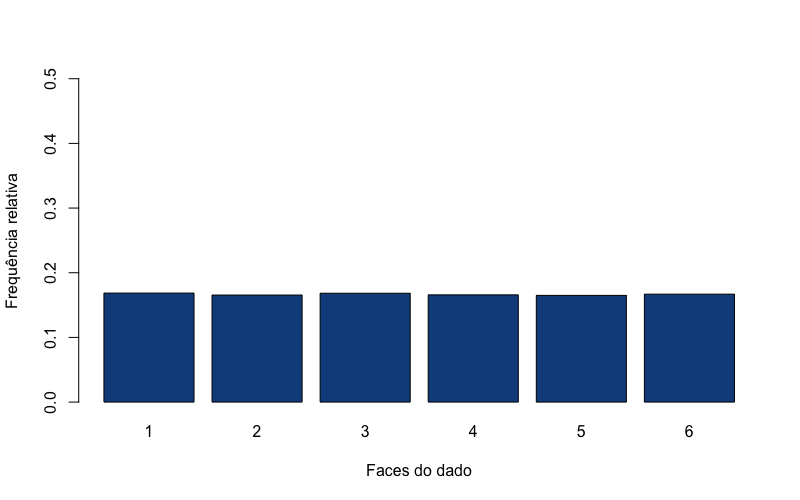
Precisamos agora imaginar um gráfico de frequências relativas como esses, mas feito a partir de um número infinitamente grande de jogadas. À medida que o nº de jogadas aumenta a distribuição de frequências converge para o que se chama de uma distribuição de probabilidade. Ou seja, uma distribuição de probabilidades é em sua essência uma distribuição de frequências de um número infinito de jogadas, ou de eventos.
Existem inúmeros tipos de distribuição de probabilidade, cada uma com um nome, cada uma representando uma situação diferente. A distribuição de probabilidades criada acima é a que denominamos de Distribuição Uniforme Discreta. Uma distribuição uniforme discreta é uma distribuição de probabilidade simétrica, na qual um número finito de valores tem a mesma probabilidade de serem observados. O exemplo mais simples de uma distribuição uniforme discreta é justamente o nosso exemplo de jogar um dado. Os valores possíveis são 1, 2, 3, 4, 5, 6 e cada vez que o dado é lançado, a probabilidade de um qualquer resultado é 1/6. Uma distribuição uniforme pode ser também contínua se os valores possíveis estão dentro de um continuum numérico.
Existem diversas outras situações nas quais a frequência de cada possibilidade é diferente e cada uma dessas situações pode ter sua distribuição modelada matematicamente. O que é preciso sempre manter em mente é que o termo distribuição de probabilidade se refere a um modelo matemático teórico que pretende simular uma determinada distribuição de resultados.
A distribuição normal
Sem dúvida alguma a mais importante das distribuições de probabilidade teóricas é a distribuição normal.
Diversos fenômenos na natureza seguem um padrão de distribuição simétrico e em forma de sino. Devido a essa forma, essa distribuição de frequências ficou conhecida como distribuição em sino (bell shaped). Como tantos fenômenos são distribuídos dessa forma, a busca por um modelo matemático para modelar essa distribuição tem uma longa trajetória na ciência. A busca por essa equação é uma parte fascinante da história da ciência, envolvendo diversos grandes matemáticos. O modelo matemático dessa curva se originou por volta do ano de 1733 com o trabalho do matemático Abraham Demoivre, quando buscava modelos para prever resultados de jogos de azar. Essa curva também foi derivada de forma independente em 1786 por Pierre Laplace, um astrônomo e matemático. No entanto, a curva normal como modelo para a distribuição de erros na teoria científica é mais comumente associada a um astrônomo e matemático alemão, Karl Friedrich Gauss, que encontrou uma nova derivação da fórmula para a curva em 1809 (Gordon, 2006). Por esse motivo, a curva normal às vezes é referida como a curva “gaussiana”. Em 1835, outro matemático e astrônomo, Lambert Qutelet, usou o modelo para descrever características fisiológicas e sociais humanas. Quetelet acreditava que “normal” significava média e que os desvios da média eram os erros da natureza e foi o primeiro matemático a estender o uso da curva de distribuição normal para os campos das ciências sociais e biomédicas (Stahl, 2006).
A famosa equação da curva de distribuição normal ou Gaussiana, que envolve o uso das mais importantes constantes matemáticas, $\pi$ e $e$.
p(x) = \frac{1}{\sqrt{2\pi}} \text{e}^{-x^2/2}{format: latex}
Essa equação só chegou em sua forma atual com o trabalho do estatístico Karl Pearson, que foi o primeiro a escrever essa equação em termos de desvio padrão e, posteriormente, com o trabalho de Fisher, que adicionou os parâmetros de localização (média), culminando na forma moderna dessa equação, com os parâmetros $\sigma$ (desvio padrão) e $\mu$ (média).
p(x) = \frac{1}{\sigma \sqrt{2\pi}} \text{e}^{-1/2(\frac{x-\mu}{\sigma})^2}{format: latex}
Não é preciso decorar essa fórmula. Ela só está aí para que você possa conhecer uma das mais importantes equações da estatística. O importante é compreender o que é uma distribuição normal e saber utilizá-la adequadamente. Isso é o fundamental num curso introdutório de estatística.
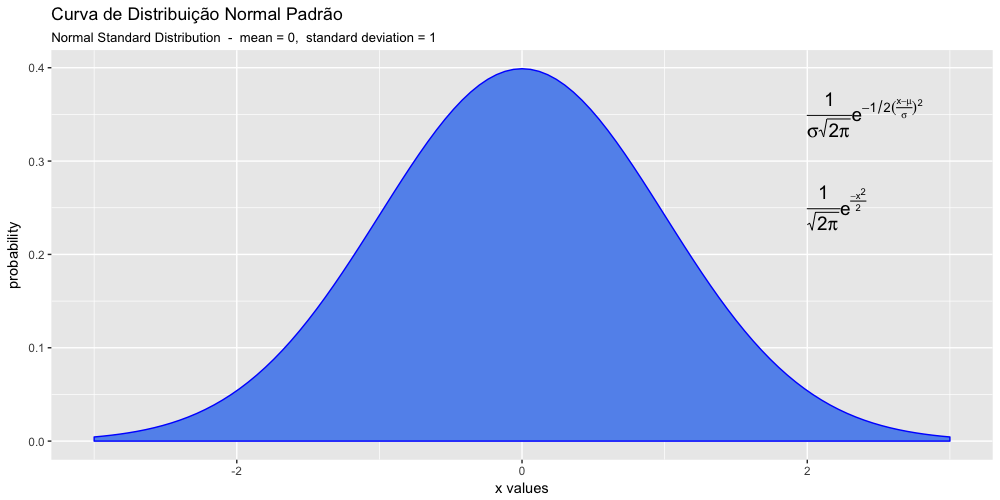
Aqui vale a pena relembrar que uma curva de distribuição de probabilidade é criada por uma função matemática, cuja área total abaixo da curva é exatamente igual a 1 e a área abaixo da curva entre dois pontos é a medida da probabilidade dos eventos ou resultados entre esses dois pontos.
- A probabilidade de dados maiores que um certo valor é a área abaixo da curva à direita daquele ponto.
- A probabilidade de dados menores que um certo valor é a área abaixo da curva à esquerda daquele ponto.
- A probabilidade de dados entre dois valores é justamente a área abaixo da curva entre esses dois pontos.
Vamos visualizar a relação entre área abaixo da curva e a probabilidade de ocorrências dos dados nos gráficos abaixo:
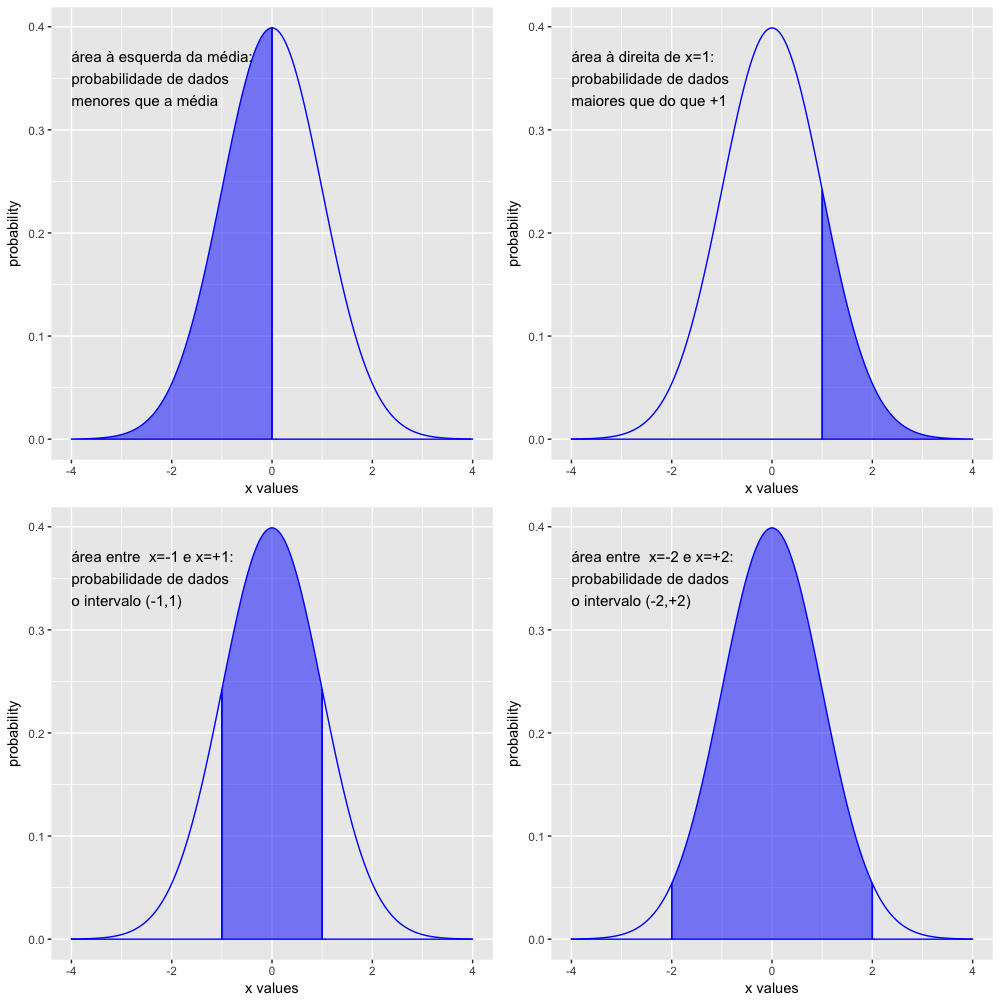
A curva normal padrão
Se você observar com a atenção, verá que nos gráficos acima a média foi sempre igual a ZERO. Além disso, nesses gráficos o desvio padrão foi igual a UM em todos. Esses parâmetros (média = 0 e desvio padrão = 1) definem uma curva normal padrão. Ou seja, a curva normal padrão é aquela cuja média é 0 e o desvio padrão é 1.
Muitas vezes temos de comparar os dados de diferentes experimentos, cada um representado por uma curva normal diferente. Mas aí surge um problema, como comparar dados de curvas com parâmetros diferentes? Podemos fazer isso transformando todos os valores do eixo x em z-scores. Veremos a seguir o que é um z-score e como fazer essa transformação.
A normalização e os z-scores.
Um z-score indica quantos desvios padrões um determinado valor se distancia da média.
Na estatística o score z é uma medida padronizada do quanto um valor se distancia da média em termos de desvios padrões. Ou seja, um score z mede quantos desvios padrões um determinado valor se distancia da média. A unidade do z-score é, portanto, o desvio padrão. Um z-score de +3 significa que o valor está 3 desvios padrões acima da média. Um z-score de -3 significa que o valor está a 3 desvios padrões abaixo da média.
Transformarmos todos os valores da pesquisa (eixo x) em z-scores equivale a transformar a curva normal numa curva normal padrão. A média é transformada em ZERO e o desvio padrão é transformado em 1. Desse modo podemos comparar diferentes curvas. Esse procedimento é o que se denomina normalização.
Normalização: procedimento para transformar os dados brutos de uma pesquisa em z-scores.
Equação de normalização
z = \frac{x-\mu}{\sigma}{format: latex}
Interpretando o z-score:
- z-score = 0 → o valor é igual à média
- z-score < 0 → valor é menor que a média
- z-score > 0 → valor é maior que a média
Além disso:
- z-score = 1 → 1 desvio padrão maior que a média
- z-score = 2 → 2 desvios padrão maior que a média
- z-score = -1 → 1 desvio padrão menor que a média
- z-score = -2 → 2 desvios padrão menor que a média
Calculando as probabilidades - parte 1: pnorm(x)
Na curva normal padrão é muito fácil calcular a probabilidade da ocorrência dos dados com a função pnorm(). essa função recebe esse nome pela junção de p de probabilidades com norm de curva normal: daí pnorm(): probabilidades na curva normal. Essa função calcula por padrão a área abaixo da curva à esquerda do ponto indicado. Como a área total abaixo de uma curva de distribuição de probabilidade é sempre igual a 1, basta subtrairmos pnorm(x) de 1, ou seja, 1-pnorm(x). Mas podemos também modificar o comportamento da função pnorm() alterando o parâmetro lower.tail para false.
Vamos calcular a probabilidade de ocorrência dados iguais ou menores que ZERO, ou seja, menores que a média, lembrando que na curva normal padrão a média é 0 e o desvio padrão é igual a 1. Além disso, lembre-se que numa curva normal padrão os valores do eixo x representam o z-score, ou seja, representam os desvios padrões.
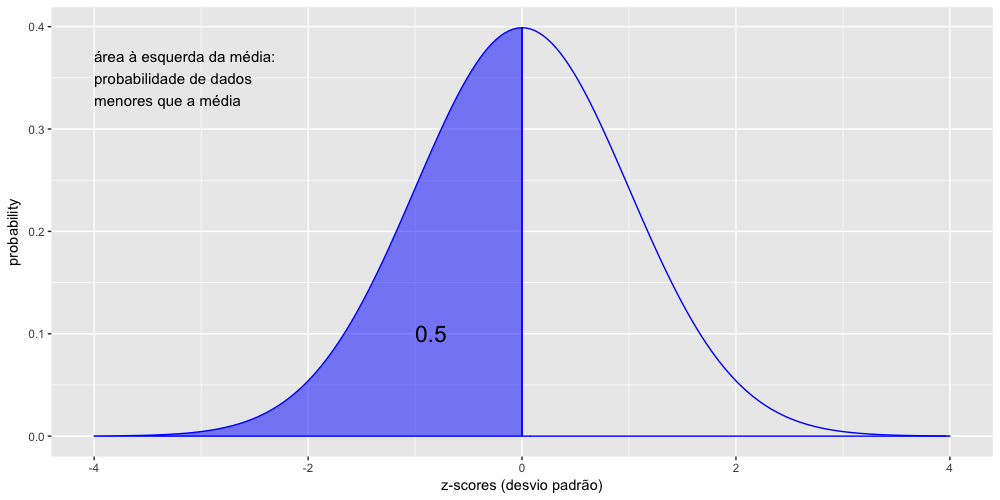
1 > pnorm(0, mean=0, sd=1)
2 [1] 0.5
O resultado é o esperado, pois como a curva normal é simétrica, 50% dos resultados estão abaixo da média e 50% dos resultados estão acima da média. Logo a probabilidade de encontrarmos resultados abaixo da média é 50% (ou 0.5).
Além de calcular por default a área à esquerda do ponto indicado, a função pnorm() têm também como valores default os parâmetros da curva normal padrão, ou seja, se não informarmos esses argumentos a função irá considerar que a média = 0 e o desvio padrão = 1. Então, se estivermos trabalhando com a curva normal padrão, podemos simplificar o cálculo acima para apenas pnorm(0).
1 > pnorm(0)
2 [1] 0.5
Lembre-se que numa curva normal padrão os valores do eixo x representam o desvio padrão. Vamos fazer alguns cálculos de probabilidades nessa curva normal padrão.
Vamos calcular agora a probabilidade de dados maiores ou iguais a 1 desvio padrão acima da média, ou seja, à direita de z = +1.
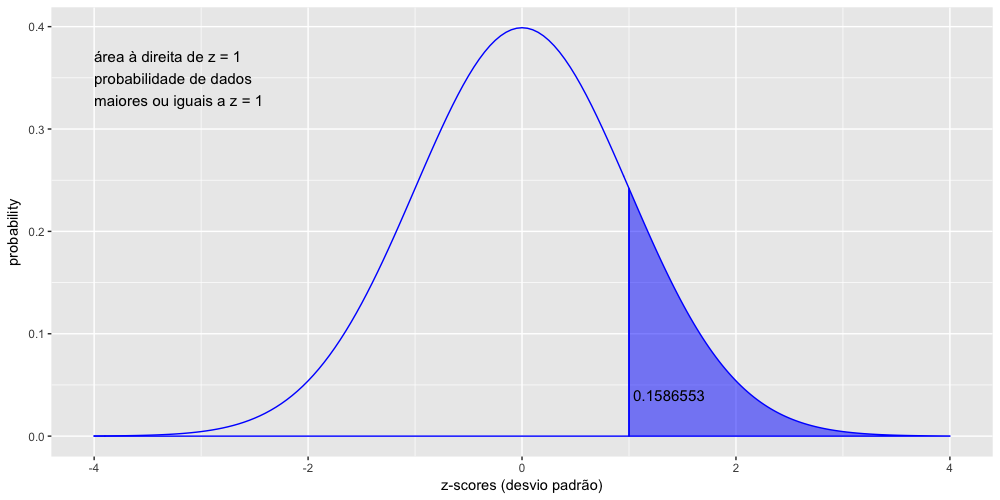
Como a função pnorm() calcula por default a área abaixo da curva à esquerda do ponto indicado, temos de subtrair essa área da área total do gráfico. Como a área total abaixo de uma curva de distribuição de probabilidade é sempre igual a 1, basta subtrairmos de 1, como feito abaixo:
1 > 1-pnorm(1)
2 [1] 0.1586553
Mas podemos também modificar o comportamento da função pnorm() alterando o parâmetro lower.tail para FALSE. Veja que o resultado é o mesmo do cálculo anterior.
1 > pnorm(1, lower.tail = FALSE)
2 [1] 0.1586553
Vamos calcular agora a probabilidade de dados entre -1 e +1 desvios padrões, ou seja 1 desvio padrão ao redor da média.
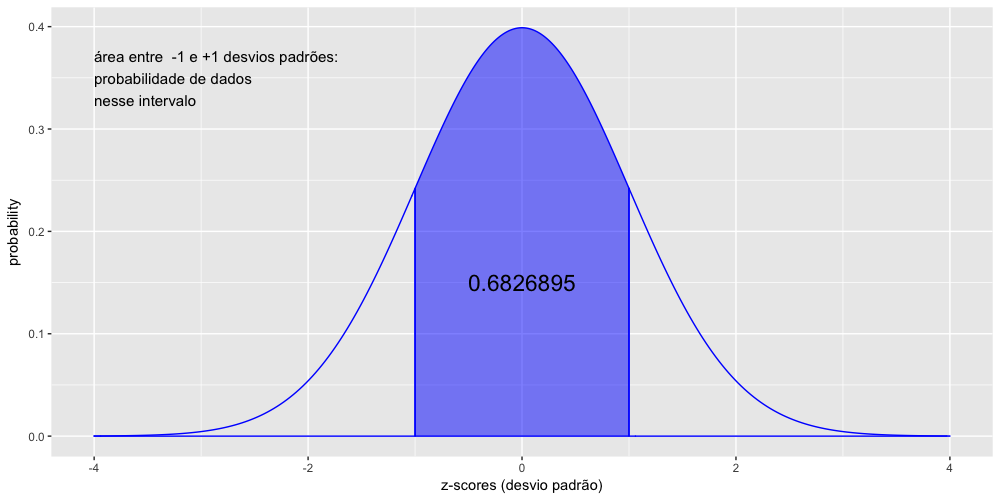
1 # 1 desvio padrão ao redor da média
2 > pnorm(1) - pnorm(-1)
3 [1] 0.6826895
O resultado acima indica que, numa curva normal, aproximadamente 68% dos dados estão entre -1 e +1 desvios padrões. Esse resultado é válido não apenas para a curva normal padrão, mas para qualquer curva normal, pois calculamos a área usando desvios padrões.
Vamos calcular agora a probabilidade de dados entre -2 e 2 desvios padrões
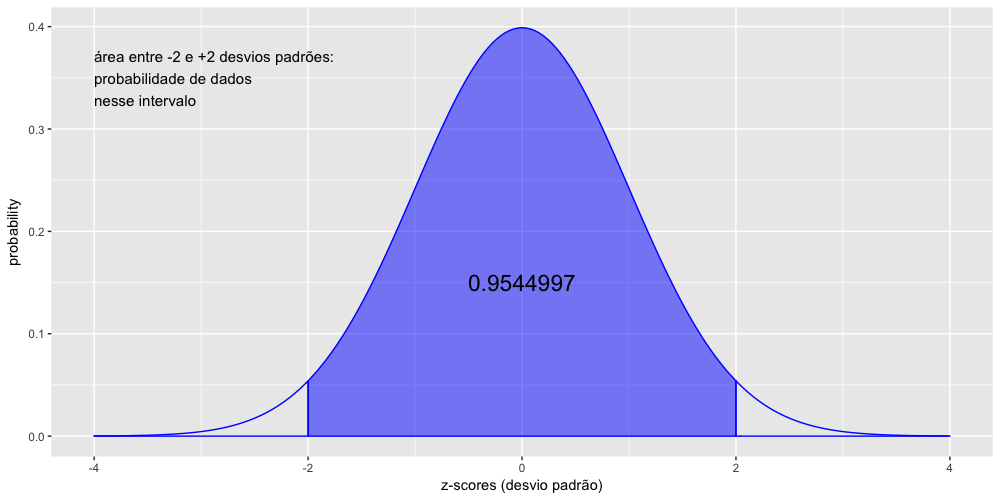
1 > pnorm(2) - pnorm(-2)
2 [1] 0.9544997
O resultado acima indica que, numa curva normal, aproximadamente 95% dos dados estão entre -2 e +2 desvios padrões. Esse resultado é válido não apenas para a curva normal padrão, mas para qualquer curva normal.
Vamos calcular agora a probabilidade de dados entre -3 e +3 desvios padrões, ou seja, 3 desvios padrões ao redor da média.
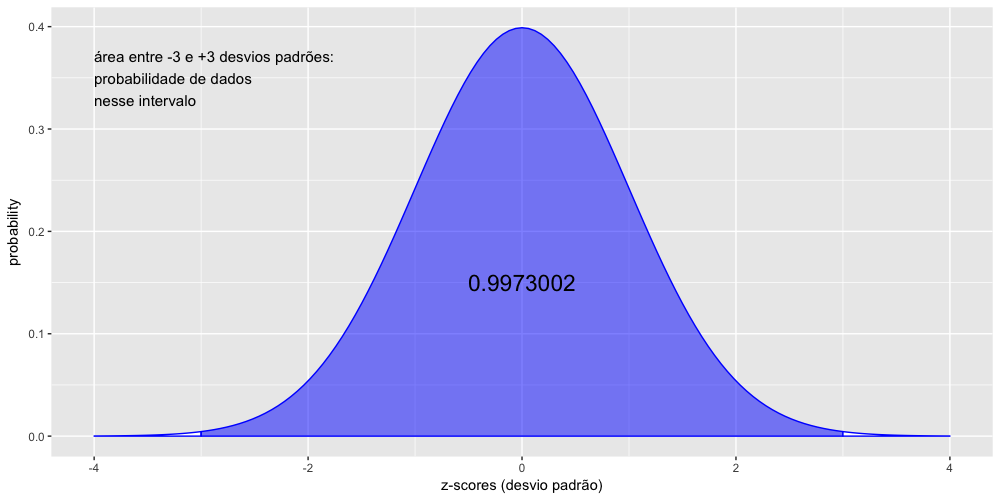
1 > pnorm(3) - pnorm(-3)
2 [1] 0.9973002
O resultado acima indica que, numa curva normal, aproximadamente 99,7% dos dados estão entre -3 e +3 desvios padrões. Esse resultado é válido não apenas para a curva normal padrão, mas para qualquer curva normal.
Os cálculos acima são usualmente conhecidos como a regra do 68-95-99.7 e servem para nos ajudar a calcular probabilidades sem necessidade de uso de computadores ou calculadoras.
Os parâmetros da curva normal - média e desvio padrão
A média e o desvio padrão, são os parâmetros da curva normal, ou seja, as medidas que definem a curva. Alterando esses parâmetros podemos construir uma infinidade de curvas normais. Veja que esses dois parâmetros fazem parte da equação moderna da curva normal, desde sua introdução por Pearson e Fisher.
p(x) = \frac{1}{\sigma \sqrt{2\pi}} \text{e}^{\frac{-(x-\mu)^2}{2\sigma^2}}{format:latex}
Alterando esse parâmetros podemos construir uma infinidade de curvas normais.
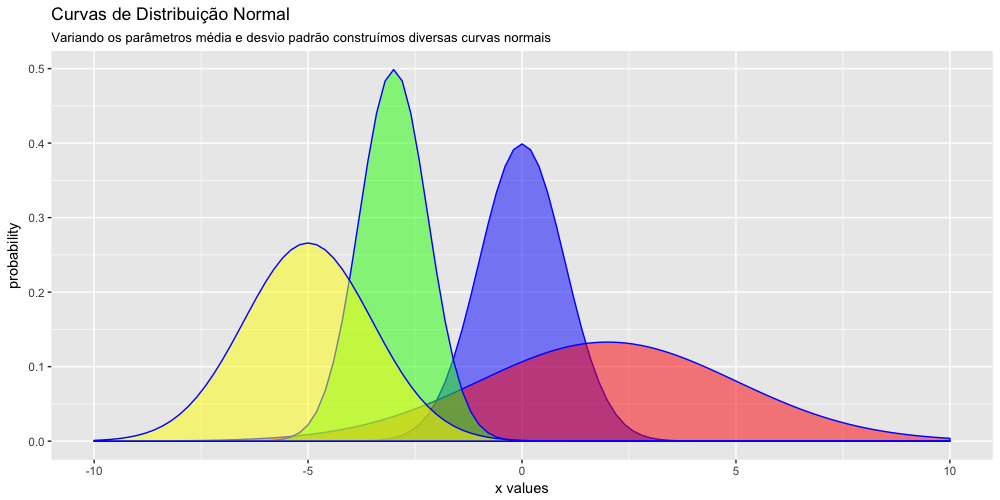
Calculando as probabilidades - parte 2: pnorm(x, mean= , sd= )
A função pnorm() pode ser usada também para calcular probabilidades em situações nas quais a curva normal não é padrão. Para isso basta inserir na funcão pnorm() os argumentos mean= e sd=. Vamos experimentar fazer esses cálculos num exemplo.
Calcule o percentual de homens com altura superior a 180cm numa população cuja média de altura dos homens seja 170cm e cujo desvio padrão seja 10cm.
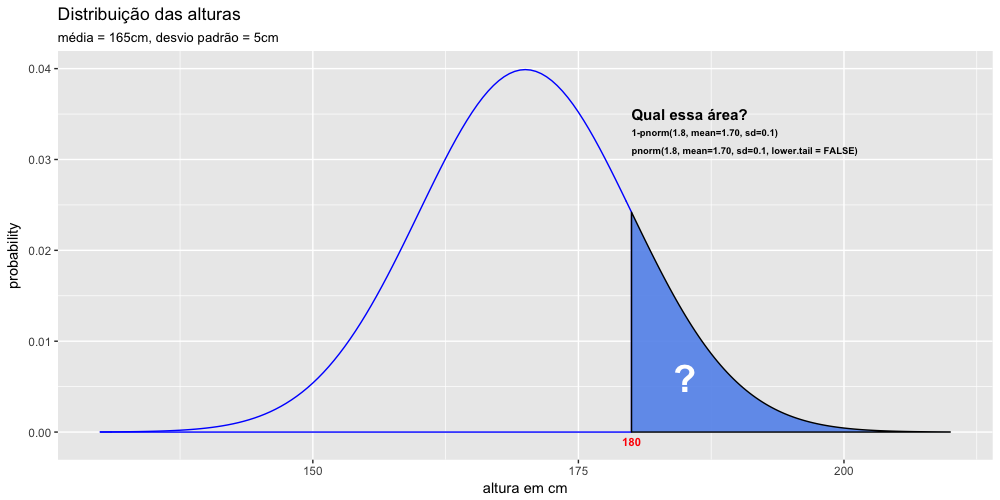
1 > 1-pnorm(180, mean=170, sd=10)
2 [1] 0.1586553
Ou então:{r}
> pnorm(180, mean=170, sd=10, lower.tail = FALSE)
[1] 0.1586553
Interpretando esse resultado: Nessa população, aproximadamente 16% dos homens tem altura igual ou superior a 180cm.
Calcule o percentual de homens com altura inferior a 1.50m numa população cuja média de altura dos homens seja 1.70m e cujo desvio padrão seja 0.1m.
1 > pnorm(1.5, mean=1.70, sd=0.1)
2 [1] 0.02275013
Interpretando esse resultado: Nessa população, aproximadamente 2.3% dos homens tem altura menor ou igual a 1.50m.
Calculando probabilidades parte 3 - a função qnorm()
Frequentemente nos deparamos com o problema inverso do que foi feito nas seções anteriores. Às vezes temos a área abaixo da curva e desejamos saber os pontos no eixo x que correspondem aos limites dessa área. Para isso usamos a função qnorm(). Podemos usar a função qnorm() com seus valores default para responder à seguinte questão: qual o z-score de determinado quantile da distribuição normal?
O principal argumento da função qnorm() são os quantiles, que equivalem às áreas abaixo da curva à esquerda de determinado ponto (o ponto que desejamos descobrir).
Vejamos num exemplo. Qual o valor do z-score da mediana? Lembre-se que a mediana representa o percentil 50%, que é o mesmo que quantil 0.5. Portanto:
1 > qnorm(0.5)
2 [1] 0
O resultado acima é o z-score do quantil 0.5, ou seja, o z-score da mediana. O resultado é o esperado, pois numa distribuição normal o z-score da mediana é ZERO, tendo em vista que a distribuição é simétrica.
Um outro exemplo.
Numa população de mulheres cuja altura tem média 165cm e desvio padrão de 5cm, qual a altura (o ponto do eixo x) a abaixo do qual se encontram 80% das mulheres? Para responder à essa questão precisamos entender que o quantil desejado é 0.8. Veja representação gráfica dessa questão.
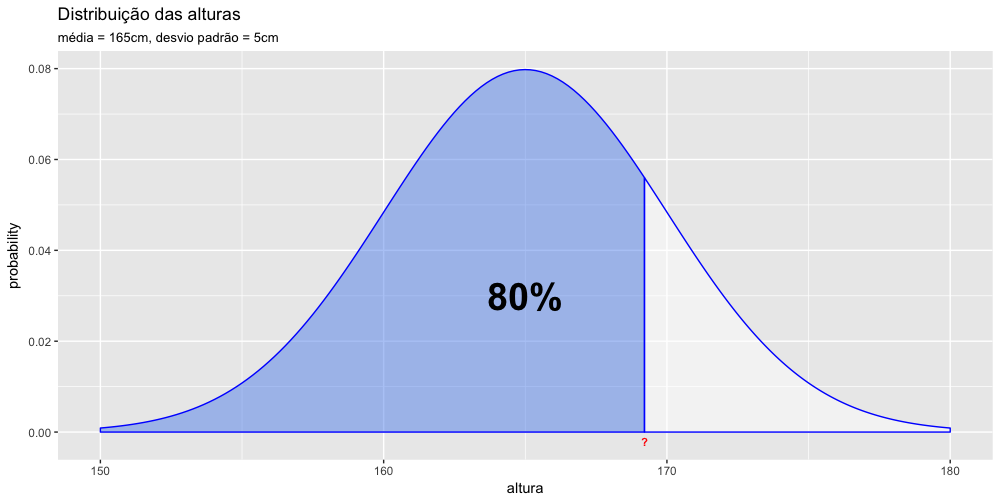
A partir daí basta inserir os argumentos na função qnorm().
1 > qnorm(0.8, mean=165, sd=5 )
2 [1] 169.2081
O resultado acima indica que 80% das mulheres tem menos de 169.2cm de altura.
Simulando uma distribuição normal
Frequentemente precisamos fazer simulações estatísticas. Para isso existem os modelos estatísticos e a equação da curva normal nos permite simular quaisquer tipos de distribuições normais desejadas.
Quando desejamos simular uma distribuição normal no R usamos a função rnorm(). random + normal = rnorm. Ou seja, essa função gera uma série de números aleatórios distribuídos de forma normal padrão: com média=0 e desvio padrão = 1. Entretanto, podemos modificar esses parâmetros e indicar a média (mean) e o desvio padrão (sd) que desejamos (lembre-se que o termo em inglês para desvio padrão é “standard deviation”, por isso “sd”).
Vamos simular os dados de altura uma população de 1000 de habitantes com média de altura de 175cm e um desvio padrão de 5cm. Iremos colocar esses valores num objeto (numa variável) que chamaremos de pop.altura, pois esses dados irão representar a altura de nossa população.
1 # criando um conjunto com 1 milhão de números distribuídos de forma normal
2 # com média = 175 e desvio padrão =5
3 > altura <- rnorm(1000, mean = 175, sd = 5)
4
5 # Colocando esse conjunto de dados num data frame:
6 > df.altura <- data.frame(altura)
Verificando a normalidade.
Nas seções anteriores fizemos diversos cálculos usando o modelo teórico da distribuição normal. Mas para usarmos esse modelo na vida real precisamos nos certificar que os dados da pesquisa realmente seguem uma distribuição normal. Usar o modelo da distribuição normal para dados que não estão normalmente distribuídos é um erro grave.
Uma forma usual de se verificar a normalidade dos dados é através da simples inspeção do gráfico de densidade de probabilidade.
Outra forma é através dos gráficos qqplot, ou quantile-quantile plot. Um gráfico qqplot é na verdade um scatter plot de quantiles de dois conjuntos de dados: os dados reais da pesquisa e os dados teóricos. Com esse gráfico podemos verificar se os dados da pesquisa têm uma distribuição normal. Se os dados da pesquisa estiverem distribuídos de forma normal, ao plotar o gráfico iremos ver uma linha diagonal perfeita, indicando uma forte correlação entre os dados da pesquisa e os valores de uma distribuição normal.
No R a função para gerar esse gráfico é a qqnorm(). Geralmente plotamos também uma linha de regressão nesse gráfico, o que é feito no r com a função qqline(). Frequentemente essas duas funções são usadas em conjunto como no gráfico abaixo.
Você poderá ver no gráfico abaixo que o eixo y representa os dados da amostra a serem testados e o eixo x representa os dados de uma distribuição normal. Se os dados da amostra estiverem distribuídos de forma normal os pontos do scatter plot estarão alinhados junto à reta inclinada no gráfico. No gráfico abaixo, com 1000 de dados, apenas um número muito pequeno de dados está fora do alinhamento, demonstrando que os dados estão realmente distribuídos de forma normal.
1 > qqnorm(altura)
2 > qqline(altura, col="red")
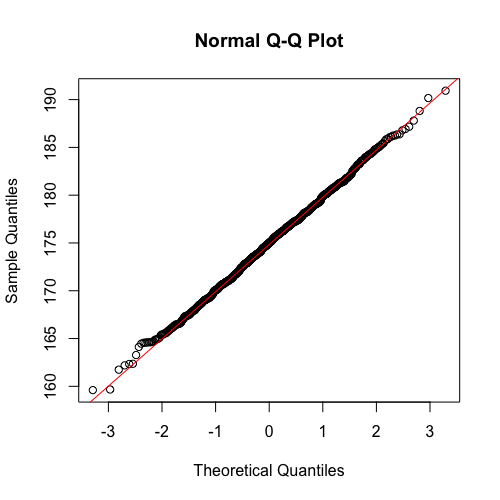
População e amostra
No capítulo anterior vimos que os dados de uma pesquisa se distribuem de diversos modos, que a principal distribuição é a distribuição normal e que uma das razões da importância dessa distribuição é o fato de diversas medidas na natureza terem uma distribuição normal. Mas veremos a seguir que existe também uma razão matemática para a importância dessa distribuição. Mas primeiramente precisamos desenvolver a noção de amostra e população.
Grande parte das pesquisas científicas visa criar um conhecimento a ser aplicado a uma população a partir de dados de um conjunto menor dessa população, ou seja, de uma amostra. Uma pesquisa de intenção de votos faz justamente isso, visa inferir qual será o resultado da votação de toda população a partir de uma amostra dessa população. Uma das etapas mais importantes desse tipo de pesquisa é exatamente a forma de escolher a amostra. É importante que a amostra seja representativa da população para a qual se pretende fazer a inferência. Por exemplo, para uma pesquisa de intenção de votos para prefeito será necessário amostrar moradores da cidade, de forma que todos os bairros estejam representados, todas as classes sociais, etc. Numa pesquisa de votos para presidente será necessária uma amostra com moradores de todos os estados do Brasil, de forma que todos estejam representados, todas classes sociais, sexos, etc. Fazer uma amostragem realmente representativa é uma etapa essencial em qualquer pesquisa, mas essas técnicas não serão discutidas nesse manual. O foco desse capítulo é discutir as sutilezas do definição de amostra e população.
Vamos imaginar uma pesquisa que pretenda conhecer a altura dos brasileiros. Será necessário escolher representantes de várias regiões do Brasil, de ambos os sexos, de várias idades. Feito isso, são tomadas as medidas de altura de todos os participantes da pesquisa (amostra). Com esses dados coletados podemos descrever a altura da população em termos de sua média, desvio padrão, etc. As medidas que são calculadas a partir desses dados são chamadas de estatísticas da amostra. A média das alturas é um exemplo de uma estatística da amostra, quaisquer outras medidas calculadas com base nos dados dessa amostra serão também estatísticas. É importante salientar que o valor de uma estatística depende da amostra particular. Se essa mesma pesquisa for realizada com outra amostra o resultado da média das alturas será certamente sempre um pouco diferente.
Usando o exemplo anterior, vimos que a população eram os brasileiros, e os participantes da pesquisa eram a amostra. Mas precisamos avaliar agora a estatística da amostra: a média das alturas. Nossa estatística, a média calculada, é também uma amostra. Nossa estatística, nossa média, é apenas uma das médias entre todas as possíveis médias que poderiam ter sido calculadas. Para cada possível conjunto de participantes haveria uma média diferente. Esse imenso conjunto de possíveis médias é a população de onde saiu nossa média. Essa população, esse conjunto de todas médias possíveis é o que se denomina de distribuição amostral
Distribuição amostral
A compreensão do que é uma distribuição amostral e de suas características é fundamental para a realização e interpretação dos testes estatísticos, pois é nessa distribuição especial que são calculadas as probabilidades que o pesquisador busca conhecer sobre seus dados.
Distribuições amostrais podem ser construídas com quaisquer medidas estatísticas. Entretanto, para facilitar a discussão, iremos nos ater ao tipo mais usual: a distribuição amostral de médias. O conjunto das médias de todas as amostras possíveis, de um mesmo tamanho, retiradas de uma mesma população, é que se denomina de distribuição amostral de médias. Se pudéssemos fazer um número infinito de pesquisas, cada uma com uma amostra do mesmo tamanho, a distribuição das médias dessas amostras seria uma distribuição amostral de médias. O problema é que isso é inviável. Pesquisas são caras, demoradas, trabalhosas. Portanto, na prática o pesquisador só tem os dados de sua amostra. Entretanto, como veremos adiante, todo cálculo estatístico depende de conhecer os parâmetros (média e desvio padrão) da curva de distribuição amostral do problema que está sendo estudado. Como resolver esse problema, como conhecer a média e o desvio padrão da curva de distribuição amostral se temos apenas uma amostra e não um número infinito de amostras?
A solução dessa questão foi um processo lento de desenvolvimento ao longo de mais de um século, desde início de 1810 até por volta de 1935, ao longo do qual os mais importantes matemáticos da história moderna foram aos poucos concebendo o que finalmente conhecemos como Teorema do Limite Central (Central Limit Theorem - CLT).
Vamos verificar essas relações em dois exemplos práticos. Com o R iremos simular um conjunto de dados de altura de uma população, construir a distribuição desses dados. Em seguida vamos construir uma distribuição amostral a partir desses dados, retirando um conjunto de amostras do mesmo tamanho. O conjunto das médias dessas amostras servirá como sendo nossa distribuição amostral.
Uma das mais importantes questões da estatística é justamente a seguinte: como será a distribuição dessas médias, qual será a média e o desvio padrão da distribuição amostral?
Exemplo 1:
Vamos inicialmente examinar o que é uma distribuição amostral usando como exemplo população bem reduzida, de apenas 6 elementos. Suponha que nossas dados sejam referentes a alguma medida dessas 6 pessoas e que essa seja nossa população.
1 pop <- c(97, 98, 99, 101, 102, 103)
A média das alturas dessa população pode ser facilmente calculada:
1 mean(pop)
2 [1] 100
Mas numa pesquisa nunca temos acesso a toda população, apenas a amostras dessa população. Como nossa amostra é pequena, podemos é factível listar todas as possíveis amostras de determinado tamanho (n). Nesse exemplo, vamos listar todas as amostras possíveis com n=3. Isso pode ser facilmente conseguido no R com a função combn(), que gera uma matriz com todas as combinações de m elementos retirados de um determinado vetor, colocando cada conjunto de 3 elementos numa coluna.
1 all.combinations <- combn(pop,3)
2 all.combinations
3 [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15]\
4 [,16] [,17] [,18] [,19] [,20]
5 [1,] 97 97 97 97 97 97 97 97 97 97 98 98 98 98 9\
6 8 98 99 99 99 101
7 [2,] 98 98 98 98 99 99 99 101 101 102 99 99 99 101 10\
8 1 102 101 101 102 102
9 [3,] 99 101 102 103 101 102 103 102 103 103 101 102 103 102 10\
10 3 103 102 103 103 103
Podemos facilmente calcular a média de cada um desses conjuntos de 3 elementos. Para isso basta usar a função colMeans() que calcula as médias de cada coluna de uma matriz.
1 dist.amostral <- colMeans(all.combinations)
Esse conjunto de médias de todas as combinações possíveis de amostras de 3 elementos obtidos da população é um exemplo de distribuição amostral, nesse caso uma distribuição amostral de médias.
Vamos agora calcular a média da distribuição amostral:
1 mean(dist.amostral)
2 [1] 100
A média da distribuição amostral foi exatamente igual à média da distribuição da população original. Isso não é coincidência. O Teorema do Limite Central afirma justamente isso, que a média da distribuição amostral é exatamente igual à média da distribuição da população original. Além da relação entre as médias, esse teorema também descreve a relação entre o desvio padrão da população e da distribuição amostral.
Vamos comparar os desvios padrões dessas duas distribuições.
1 sd(pop)
2 sd(dist.amostral)
3 [1] 2.366432
4 [1] 0.9911893
Podemos ver que o desvio padrão da distribuição amostral é bem menor.
Segundo o Teorema do Limite Central (CLT), o desvio padrão da distribuição amostral e sempre menor que o da população. Mas além disso, de de acordo com esse teorema, à medida que o tamanho da amostra aumenta, o desvio padrão da distribuição amostral tende a se aproximar cada vez mais do valor do desvio padrão da população dividido pela raiz quadrada do tamanho da amostra.
[
\text{Desvio padrão da distribuição amostral}=\frac{\text{Desvio padrão da população}}{\text{raiz quadrada do tamanho da amostra}}
]
[
\sigma_\bar{X}=\frac{\sigma_p}{\sqrt{n}}
]
[
SE_\bar{X}=\frac{\sigma_p}{\sqrt{n}}
]
Entretanto, em nosso exemplo a amostra é muito pequena, teve apenas 3 elementos. Para visualizarmos melhor essa relação será necessário usar um exemplo mais realístico. Faremos isso no próximo tópico.
Preparando a população
Numa pesquisa da ANAC (Agência Nacional de Aviação Civil) de 2009, na qual foram avaliados os dados antropométricos de 5305 brasileiros entre 15-87 anos de idade em 20 aeroportos do Brasil, a altura média da amostra foi de 173.1cm e o desvio padrão foi de 7.3cm (SILVA & MONTEIRO, 2009). Além disso, a literatura demonstra que medidas de estatura de uma população tendem a possuir uma distribuição normal. Portanto, vamos simular nossa população usando uma aproximação desses dados com a função rnorm().
Simulando um conjunto de milhão de medidas de alturas, distribuídas de forma normal, com média de 173cm e desvio padrão de 7cm.
1 set.seed(1)
2 pop <- rnorm(n = 1000000, mean = 173, sd = 7)
3 pop.df <- data.frame(altura = pop)
Preparando as amostras
Uma distribuição amostral deveria ser composta de todas as amostras possíveis, entretanto, precisamos estipular algum limite razoável para que nossos computadores executem esses cálculos num tempo razoável. Dependendo da capacidade seu computador, talvez seja necessário até reduzir a quantidade de amostras ou o tamanho da amostra. Iremos fazer uma simulação de mil amostras de 100 elementos em cada.
1 amostras <- data.frame(replicate(1000, sample(pop, size = 100)))
Preparando a distribuição amostral
Vamos agora calcular a média de cada amostra de 100 elementos criada acima com a função apply(). O primeiro termo dessa função indica o nome do data frame com os dados, o segundo termo dessa função, 2 , indica que a função a ser calculada será aplicada nas colunas do data.frame. O terceiro termo indica a função que será utilizada, nesse caso será a função mean, para calcular a média. Iremos colocar essas médias num data frame que chamaremos de medias.
1 medias <- data.frame(media=apply(amostras, 2, mean))
2 head(medias)
3 media
4 X1 173.5902
5 X2 173.5943
6 X3 172.6597
7 X4 172.9608
8 X5 172.3325
9 X6 173.4830
Vamos verificar visualmente essas distribuições no gráfico abaixo.
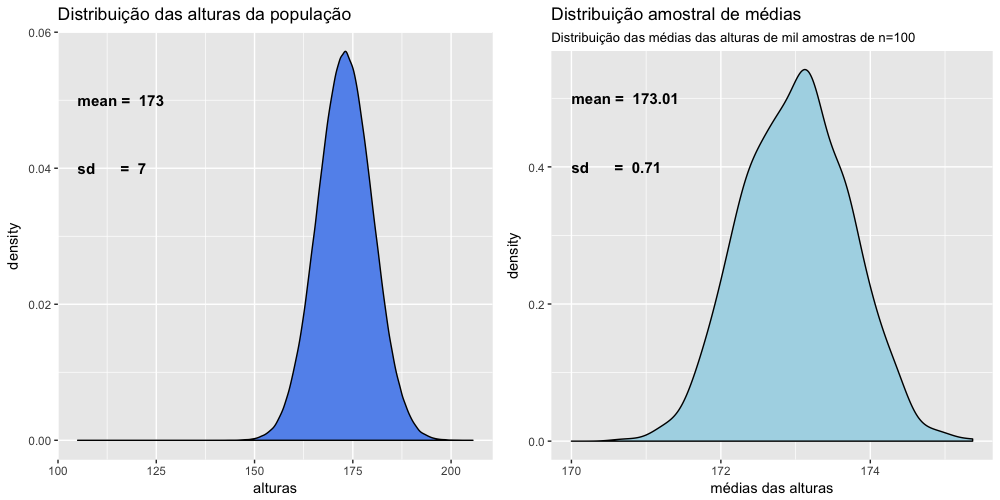
Analisando esses gráficos podemos verificar que as duas distribuições são aproximadamente normais, as médias das duas distribuições são praticamente iguais, e o desvio padrão da distribuição amostral é 10 vezes menor. Como o desvio padrão representa a dispersão dos dados, a curva de distribuição amostral deveria ser mais estreita que a curva de distribuição das alturas da população. É difícil perceber isso com os esses gráficos lado a lado como na figura acima, pois a escala dos dois gráficos é diferente. Observe os eixos x e y e poderá se certificar disso.
O gráfico abaixo mostra essas duas curvas sobrepostas e agora fica mais claro que não apenas que as médias são iguais, mas também o quanto a curva de distribuição amostral das médias tem realmente um desvio padrão bem menor que a curva de distribuição das alturas da população original.
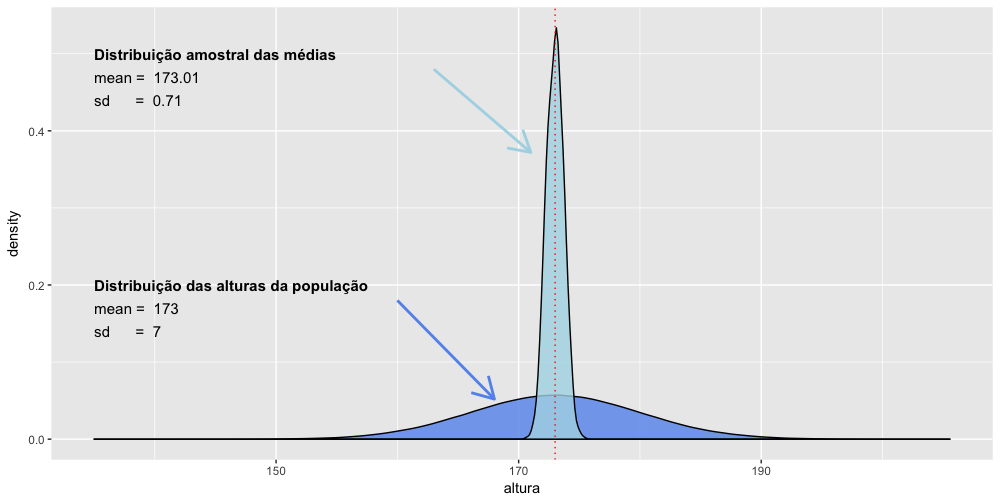
A distribuição amostral tem um pico muito mais alto por uma questão puramente matemática: numa curva de distribuição a área abaixo da curva é sempre igual a 1, portanto, quanto menor o desvio padrão mais alta será a curva, pois a área de ambas tem de ser sempre igual a 1. O importante nesse gráfico é verificarmos que as curvas têm a mesma média, mas a curva de distribuição amostral é realmente bem mais estreita, ou seja, tem um desvio padrão bem menor. Se observarmos bem, o desvio padrão da curva de distribuição amostral é exatamente dez vezes menor que a da população. Veremos adiante a razão disso.
Resumindo o que foi observado:
- A distribuição amostral teve um formato aproximadamente normal.
- A média da distribuição amostral foi a mesma da população original.
- O desvio padrão da distribuição amostral foi bem menor que o da população original.
Essas três observações acima representam o teorema fundamental da estatística, denominado “Teorema do Limite Central”, usado praticamente todas as vezes em que se faz um teste de hipóteses científicas. A grande utilidade desse teorema pode ser compreendida logo em sua definição:
dadas certas condições…, quando o tamanho da amostra aumenta, a distribuição amostral aproxima-se cada vez mais de uma distribuição normal, não importando se a distribuição da população seja normal ou não.
Ou seja, não importa se a distribuição da medida de interesse na população é normal ou não, uma distribuição amostral dessa medida será normal. Isso é o que torna a distribuição normal tão importante, pois os teste estatísticos são sempre realizados sempre numa distribuição amostral que, por sua vez, será sempre normal. O gráfico abaixo ajudará a visualizar melhor essa relação.
Além disso, o Teorema do Limite Central (CLT) relaciona a média e o desvio padrão da população e da distribuição amostral:
a média da distribuição amostral é a mesma da população.
o desvio padrão da distribuição amostral é o desvio padrão da população dividido pela raiz quadrada no tamanho da amostra.
As nossas amostras tinham 100 participantes (n=100), logo, como a raiz quadrada de 100 é igual a 10, o desvio padrão da distribuição amostral foi exatamente o da população dividido por 10:
- desvio padrão da população era 7cm.
- desvio padrão da distribuição amostral foi de 0.7cm.
Referências
- Saul Stahl. The Evolution of the Normal Distribution. Mathematics Magazine, 79(2), April 2006.
- Sue Gordon. The Normal Distribution.
-
- Eileen Magnello. Karl Pearson’s Gresham Lectures: W. F. R. Weldon, Speciation and the Origins of
Pearsonian Statistics. The British Journal for the History of Science, Vol. 29, No. 1 (Mar., 1996), pp. 43- 63
- Eileen Magnello. Karl Pearson’s Gresham Lectures: W. F. R. Weldon, Speciation and the Origins of
- Silva S, Monteiro W. Levantamento do Perfil antropométrico da População Brasileira Usuária do Transporte Aéreo Nacional–Projeto Conhecer, ANAC. Publicação técnica do acervo da ANAC, 2009.
Distribuição nula
Nos capítulos passados vimos que as distribuições teóricas de probabilidades são modelos matemáticos que podem servir para prever ou antecipar resultados de eventos ou experimentos científicos. Um outro uso importante das distribuições de probabilidade é servirem de modelos teóricos de como os dados deveriam estar distribuídos em determinadas situações. Esses modelos teóricos ideais são usados rotineiramente para fins de comparação em pesquisas científicas.
Por exemplo, para sabermos se uma dieta funciona, não basta termos os resultados dos efeitos, precisamos saber como seriam esses resultados se a dieta não funcionasse. Precisamos lembrar que, ainda que uma dieta não tenha efeito, quando testada em um grande conjunto de pessoas, certamente haverá mudanças no peso devidas ao acaso. Algumas pessoas poderão até mesmo engordar, outras emagrecer. Mas, se a dieta não funciona, espera-se que a maior parte não mude muito o peso. O que os pesquisadores precisam é saber como estarão distribuidos os pesos dos participantes se a dieta não funciona. Ou seja, precisamos comparar os resultados encontrados na pesquisa com um modelo teórico no qual a dieta não funciona. Precisamos saber como estariam distribuídos os dados na hipótese da dieta não ter efeito. Essa distribuição dos dados causada apenas pelos os efeitos do acaso é conhecida na estatística pelo nome de distribuição nula.
O termo distribuição nula se refere a um modelo teórico que mostra como os dados estarão distribuídos se apenas os efeitos do acaso estiverem atuando sobre os resultados. Quando um pesquisador pretende mostrar que determinado agente tem um efeito real, será necessário demonstrar que os dados encontrados estão distribuídos de forma significativamente diferente da distribuição nula.
O conceito de distribuição nula foi cunhado por Ronald Fisher e exposto pela primeira por volta de 1935 em seu livro The Design of Experiments1. Nesse livro Fisher descreve os passos para um curioso experimento: Há alguma diferença no saber de um chá se o leite for adicionado à xícara de chá depois e não antes do se colocar o chá. Esse experimento é fruto de um evento real na vida de Fisher relatado num interessante livro sobre a história da estatística “The Lady Tasting Tea” de David Salsburg (2001). Segundo conta a história, a senhora Muriel Bristou alegava que o sabor do chá era melhor se o leite fosse adicionado depois que o já tivesse sido colocado na xícara e que, caso fossem colocados na ordem inversa (leite primeiro e chá depois), o sabor não seria o mesmo. Diante dessa situação, Fisher idealizou um experimento no qual seria testada estatisticamente a possibilidade de diferenciar o sabor do chá nas duas condições descritas. Foram preparadas 4 xícaras com chá primeiro e leite adicionado posteriormente e outras 4 da forma inversa.
Uma distribuição nula desse experimento deveria representar a probabilidade de cada resultado possível ter ocorrido meramente por acaso. Por exemplo, acertar por acaso as 4 xícaras nas quais o leite foi adicionado depois do chá equivale a uma probabilidade de 1/70, ou seja, 1.4% de probabilidade disso ocorrer puramente por acaso. Acertar exatamente 3 xícaras equivale a uma probabilidade de 16/70, ou seja, 22.9% de probabilidade disso ocorrer por acaso. A distribuição das probabilidades de cada resultado ocorrer por acaso é o que se denomina de distribuição nula.
Segundo o relato de David Salburg no livro “The Lady Tasting Tea” (2001, pag.8), a Sra. Muriel identificou corretamente as 4 xícaras nas quais o leite havia sido colocado depois do chá. Esse resultado pode ter sido por acaso? Sim! pode! Existe uma probabilidade de 1.4% de que ela tenha acertado por acaso. Mas o que fazer com esse resultado? Acreditamos na capacidade dela distinguir ou acreditamos que foi sorte, que foi um mero acaso?
Podemos perceber que um teste de hipóteses nunca prova uma relação entre os fatores estudados, apenas dá evidências probabilísticas dessa relação. É justamente essa avaliação da probabilidade que serve de parâmetro para a escolha de uma das duas hipóteses (nula ou alternativa).
Por isso mesmo o resultado de um teste estatístico geralmente é expresso em termos de rejeição ou não rejeição da hipótese nula, e nunca se diz que uma das hipóteses seja a verdadeira.
Segundo Fisher, a hipótese nula nunca pode provada, mas pode ser rejeitada no decorrer do experimento.
In relation to any experiment we may speak of this hypothesis as the null hypothesis, and it should be noted that the null hypothesis is never proved or established, but is possible disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
Ronald Fisher - The Design of Experiments
Teste de Hipóteses
Introdução
O que atualmente se conhece como teste de hipótese é um procedimento estatístico ainda bastante rudimentar e ainda alvo de muitas críticas. Os procedimentos desses testes são muito recentes, tendo se originado por volta de 1925, quando o estatístico Ronald Fisher publicou sua obra “Statistical Methods for Research Workers”. As idéias de Fisher revolucionaram os métodos estatísticos e são até hoje usados rotineiramente, apesar de suas imperfeições. O modelo atual de um teste estatístico é, na verdade, uma combinação das ideias de Fisher e Neynman, dois dos mais importantes estatísticos do século XX, mas que nunca concordaram um com o outro e muito menos em combinar seus procedimentos numa única teoria. Apesar de ano após ano aparecerem artigos criticando essa forma de teste de hipótese, é até hoje essa amalgama das teorias desses dois estatísticos que está sedimentada em livros textos e que compõe grande parte dos testes estatísticos na área da saúde.
Um teste de hipóteses envolve um procedimento estatístico que tenta escolher uma dentre duas hipóteses de uma pesquisa, tais como a hipótese de que o medicamento não funciona e a hipótese de que funciona. O procedimento padrão de um teste é que, logo em seu início, sejam estipuladas essas duas hipóteses, que recebem os nomes de hipótese nula e hipótese alternativa.
A hipótese alternativa
Denomina-se hipótese alternativa a hipótese que o pesquisador deseja tentar confirmar, é a suposição do pesquisador de que determinado agente tem realmente um efeito, de que os fenômenos estudados tem alguma relação de causa e efeito.
Na estatística a hipótese nula é geralmente simbolizada por H1 ou H1.
A hipótese nula
Hipótese nula é o oposto da hipótese alternativa. Denomina-se hipótese nula de uma pesquisa a hipótese de que o agente em estudo não tem efeito. Por exemplo, de que a dieta não funciona, de que o medicamento não funciona, de que a vacina não funciona. Ou seja, é a hipótese de que não há nenhuma relação de causalidade entre os dois fenômenos estudados.
Em outras palavras, hipótese nula é a hipótese de que o acaso sozinho é responsável pela variação encontrada nos resultados e, consequentemente, quaisquer diferenças encontradas entre os grupos testados se devem meramente ao acaso, não havendo, portanto, nenhuma diferença real entre os grupos.
Na estatística a hipótese nula geralmente é simbolizada por H0 ou H0.
A forma como os dados estão distribuídos nessa situação é chamada de distribuição sob a hipótese nula, ou simplesmente de distribuição nula.
Distribuição nula
Nos capítulos passados vimos que as distribuições teóricas de probabilidades são modelos matemáticos que podem servir para prever ou antecipar resultados de eventos ou experimentos científicos. Um outro uso importante das distribuições de probabilidade é servirem de modelos teóricos de como os dados deveriam estar distribuídos em determinadas situações. Esses modelos teóricos ideais são usados rotineiramente para fins de comparação em pesquisas científicas.
Por exemplo, para sabermos se uma dieta funciona, não basta termos os resultados dos efeitos, precisamos saber como seriam esses resultados se a dieta não funcionasse. Precisamos lembrar que, ainda que uma dieta não tenha efeito, quando testada em um grande conjunto de pessoas, certamente haverá mudanças no peso devidas ao acaso. Algumas pessoas poderão até mesmo engordar, outras emagrecer. Mas, se a dieta não funciona, espera-se que a maior parte não mude muito o peso. O que os pesquisadores precisam é saber como estarão distribuídos os pesos dos participantes se a dieta não funciona. Ou seja, precisamos comparar os resultados encontrados na pesquisa com um modelo teórico no qual a dieta não funciona. Precisamos saber como estariam distribuídos os dados na hipótese da dieta não ter efeito. Essa distribuição dos dados causada apenas pelos efeitos do acaso é conhecida na estatística pelo nome de distribuição nula.
O termo distribuição nula se refere a um modelo teórico que mostra como os dados estarão distribuídos se apenas os efeitos do acaso estiverem atuando sobre os resultados. Quando um pesquisador pretende mostrar que determinado agente tem um efeito real, será necessário demonstrar que os dados encontrados estão distribuídos de forma significativamente diferente da distribuição nula.
O conceito de distribuição nula foi cunhado por Ronald Fisher e exposto pela primeira por volta de 1935 em seu livro The Design of Experiments. Nesse livro Fisher descreve os passos para um curioso experimento: Há alguma diferença no saber de um chá se o leite for adicionado à xícara de chá depois e não antes do se colocar o chá. Esse experimento é fruto de um evento real na vida de Fisher relatado num interessante livro sobre a história da estatística “The Lady Tasting Tea” de David Salsburg (2001). Segundo conta a história, a senhora Muriel Bristou alegava que o sabor do chá era melhor se o leite fosse adicionado depois que o já tivesse sido colocado na xícara e que, caso fossem colocados na ordem inversa (leite primeiro e chá depois), o sabor não seria o mesmo. Diante dessa situação, Fisher idealizou um experimento no qual seria testada estatisticamente a possibilidade de diferenciar o sabor do chá nas duas condições descritas. Foram preparadas 4 xícaras com chá primeiro e leite adicionado posteriormente e outras 4 da forma inversa.
Uma distribuição nula desse experimento deveria representar a probabilidade de cada resultado possível ter ocorrido meramente por acaso. Por exemplo, acertar por acaso as 4 xícaras nas quais o leite foi adicionado depois do chá equivale a uma probabilidade de 1/70, ou seja, 1.4% de probabilidade disso ocorrer puramente por acaso. Acertar exatamente 3 xícaras equivale a uma probabilidade de 16/70, ou seja, 22.9% de probabilidade disso ocorrer por acaso. A distribuição das probabilidades de cada resultado ocorrer por acaso é o que se denomina de distribuição nula.
Segundo o relato de David Salburg no livro “The Lady Tasting Tea” (2001, pag.8), a Sra. Muriel identificou corretamente as 4 xícaras nas quais o leite havia sido colocado depois do chá. Esse resultado pode ter sido por acaso? Sim! pode! Existe uma probabilidade de 1.4% de que ela tenha acertado por acaso. Mas o que fazer com esse resultado? Acreditamos na capacidade dela distinguir ou acreditamos que foi um mero acaso?
Podemos perceber que um teste de hipóteses nunca prova uma relação entre os fatores estudados, apenas dá evidências probabilísticas dessa relação. É justamente essa avaliação da probabilidade que serve de parâmetro para a escolha de uma das duas hipóteses (nula ou alternativa).
Por isso mesmo o resultado de um teste estatístico geralmente é expresso em termos de rejeição ou não rejeição da hipótese nula, e nunca se diz que uma das hipóteses seja a verdadeira.
Segundo Fisher, a hipótese nula nunca pode provada, mas pode ser rejeitada no decorrer do experimento.
In relation to any experiment we may speak of this hypothesis as the null hypothesis, and it should be noted that the null hypothesis is never proved or established, but is possible disproved, in the course of experimentation. Every experiment may be said to exist only in order to give the facts a chance of disproving the null hypothesis.
Ronald Fisher - The Design of Experiments
Nível de significância do teste
Os testes estatísticos nunca nos dão certeza dos resultados, podendo produzir resultados que não representam a verdade. Podemos acreditar que um medicamento funciona quando na verdade não funciona ou podemos acreditar que não funciona quando funciona.
Como nunca temos certeza se o resultado de um teste estatístico representa a verdade ou não, é preciso sempre analisar também qual a probabilidade do resultado encontrado ser falso.
Essa probabilidade do resultado encontrado ser falso depende de uma escolha arbitrária do próprio pesquisador. Vamos analisar o experimento de Fisher sobre a capacidade da Sra. Muriel discernir as diferenças no sabor do chá. A questão é: quantos acertos serão necessários podermos aceitar que Muriel seja realmente capaz de perceber a diferença no sabor? Quantos acertos vão convencer o pesquisador dessa capacidade? Veja o quanto essa decisão é subjetiva. Definir esse ponto de corte, significa decidir a partir de que ponto poderemos considerar que o resultado não foi devido apenas à sorte ou ao acaso, mas sim a uma real diferença de sabor entre os dois tipos de amostras. O resultado obtido (acertar as 4 xícaras) tem 1.4% de probabilidade de ter ocorrido por acaso. O que fazer com esse resultado é a questão. Acreditamos na capacidade dela distinguir ou acreditamos que foi um mero acaso?
Esse limite, esse ponto subjetivo, a partir do qual aceitamos uma hipótese e rejeitamos a outra é denominado na literatura científica de nível de significância. Tem sido uma prática tradicional da ciência aceitar que um resultado que corresponda a aproximadamente 1 chance em 20 possa ser considerado significativo, ou seja, podemos considerar que não deve ter ocorrido por acaso. Em termos percentuais isso significa dizer que se a probabilidade de um evento ocorrer foi menor que 5%, quando nos depararmos com essa ocorrência, podemos acreditar que não deve ter ocorrido por acaso. Usando esse ponto de corte, passamos a acreditar que a Sra. Muriel realmente consegue distinguir as xícaras.
it is a convenient convention to take twice the standard error as the limit of significance; this is roughly equivalent to the corresponding limit P = ·05
Ronald Fisher, Statistical Methods for Research Workers, 5ed. 1934. p.113
…it is convenient to take this point (p=0.05) as a limit in judging whether a deviation is to be considered significant or not.
Ronald Fisher, Statistical Methods for Research Workers, 5ed. 1934. p.43
Entrentanto, não podemos deixar de ter em conta que existe ainda uma possibilidade dela ter acertado meramente por acaso. Esse é o papel do nível de significância, determinar previamente o ponto de corte a partir do qual o pesquisador irá considerar que o resultado não foi por acaso.
A probabilidade de encontrarmos um resultado positivo (de que há diferenças ou de que o medicamento faz efeito) e esse resultado na verdade ser falso é denotado por alpha ($\alpha$). A probabilidade de encontrarmos um resultado falso negativo (rejeitarmos a hipótese nula quando ela é verdadeira) é denotada por beta ($\beta$).
Essa medida denotada por alpha ($\alpha$) é chamada de nível de significância do teste. Mas afinal de contas o que significa isso?
Erros tipo I e tipo II
Um ponto que precisa ser enfatizado é que o resultado de um teste de hipóteses, sendo meramente probabilístico, pode ser errado. Nenhum pesquisador tem acesso à verdade absoluta, mas apenas aos resultados de seus testes. Portanto, toda pesquisa pode ter um resultado que não representa a verdade. Essa situação é tão comum estima-se que cerca de metade dos resultados da literatura científica médica são falsos (Ioannidis, 2005).
Existem duas maneiras pelas quais os resultados de uma pesquisa podem ser falso: Uma pesquisa pode rejeitar a hipótese nula quando na verdade ela é a verdadeira. Ou então, por outro lado, uma pesquisa pode não conseguir rejeitar a hipótese nula quando na verdade ela é falsa. Resumindo podemos errar de duas formas:
- rejeitar uma hipótese nula que é verdadeira (um falso positivo).
- não rejeitar uma hipótese nula que é falsa (um falso negativo).
Esses dois tipos de resultados errados recebem nomes especiais na literatura científica:
- Erro tipo I (falso positivo): rejeitar uma hipótese nula que é verdadeira
- Erro tipo II (falso negativo): falhar em rejeitar uma hipótese nula que é falsa.
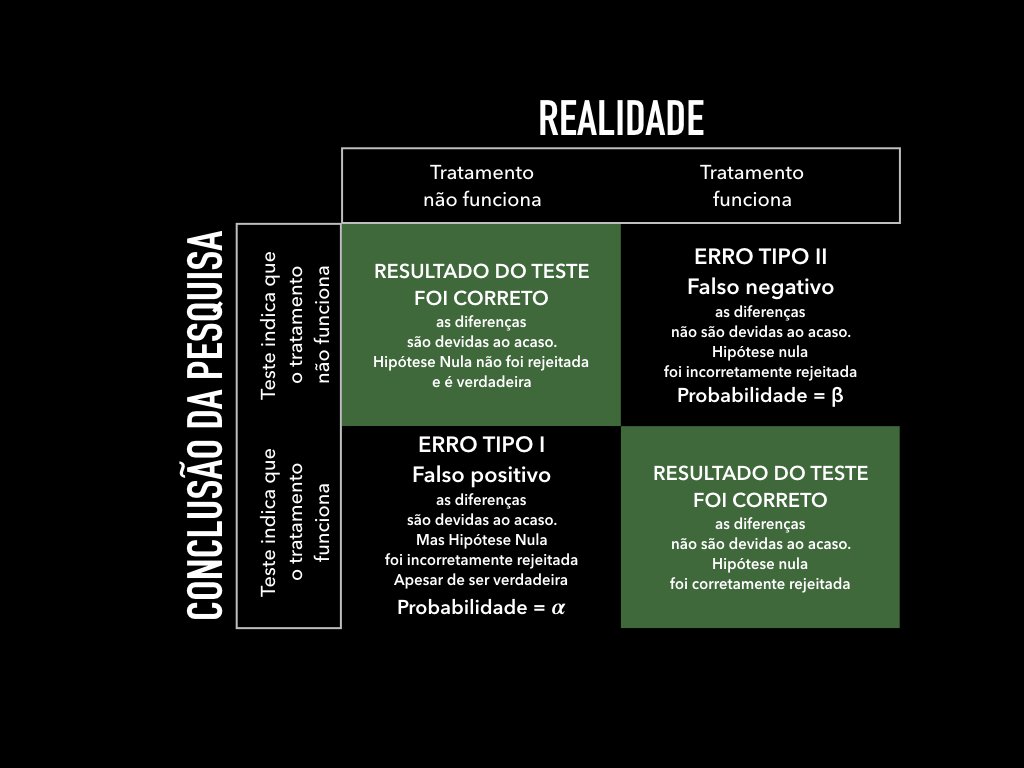
Teste unicaudal ou bicaudal
Antes de iniciarmos os procedimentos do teste propriamente dito precisamos definir mais uma questão acerca das hipóteses nula e alternativa: a direção do teste.
Às vezes uma pesquisa pretende demonstrar que um determinado medicamento reduz algo como, por exemplo, um medicamento que reduz a pressão arterial. Outras vezes pretende demonstrar que um medicamento aumenta algo como, por exemplo, um medicamento para aumentar a concentração nos estudos. No primeiro exemplo poderíamos fazer um teste para saber se o medicamento reduz a pressão arterial. No segundo caso, poderíamos fazer um teste para saber se o medicamento aumenta a concentração nos estudos. Nesses dois exemplos é feito apenas em uma direção, sendo então denominado unicaudal.
Entretanto, como frequentemente não podemos ter certeza dos efeitos do medicamento ou do agente em estudo, temos de ter em mente sempre a possibilidade de haver um efeito oposto ao que esperávamos acontecer. Pode ser que um determinado medicamento que supostamente aumente a concentração tenha na verdade o efeito contrário. Por isso mesmo considera-se que um testes estatísticos mais robusto sejam aqueles nos quais são consideradas essas duas possibilidades, nesse caso o teste é denominado bicaudal. Nesse tipo de teste é avaliado se o medicamento (ou agente em estudo) produz algum efeito, seja aumentando ou seja diminuindo alguma coisa. Esse teste que leve em conta a possibilidade desses dois desfechos é chamado de teste bicaudal.
p-values
Nas seções anteriores vimos que um pesquisador tem de definir o nível de significância de sua pesquisa e que esse nível de significância tem sido estabelecido habitualmente em 5% (0.05). Sendo esse o ponto de corte, o ponto que define o limite para decisão de rejeitar ou não a hipótese nula. Ou seja, habitualmente a hipótese nula é rejeitada se os dados encontrados na pesquisa têm uma probabilidade menor que 5% (0.05) de terem ocorrido por acaso.
Para podermos tomar a decisão de rejeitar ou não a hipótese nula precisamos de dois itens:
- O nível de significância, usualmente convencionado como sendo 5% (0.05) e indicado nos artigos científicos simplesmente por: ($\alpha = 0.05$).
- O cálculo da probabilidade de encontrarmos, meramente por acaso, dados iguais ou mais extremos que os que foram encontrados na pesquisa. Esse resultado, o valor da probabilidade, é o chamado valor de p (p-value) e denotado na literatura científica apenas por $p$.
Conclusão
Levando em conta o resultado encontrado no exemplo das de Fisher, o resultado poderia ser simplesmente escrito da seguinte maneira:
$\alpha = 0.05$
$p = 0.0143$
Como o valor de p foi menor que 0.05, rejeitamos a hipótese nula e aceitamos a evidência de que realmente há diferença no sabor do chá dependendo a ordem em que os ingredientes são colocados (chá e leite) e que essa diferença pode ser percebida pela Sra. Muriel.
Referências
- Ronald Fisher. The Design of Experiments. Hafner Publishing Company: New York, 1971.
- David Salsburg. The Lady Tasting Tea. How Statistics Revolutionized Science in the Twentieth Century. Holt Paperbacks: New York, 2001.
- John P. A. Ioannidis Why most published research findings are false. PLoS Med, v. 2, n. 8, p. e124, 2005.
p-values
1 library(ggplot2)
Introdução
Q: Why do so many colleges and grad schools teach p = 0.05?
A: Because that’s still what the scientific community and journal editors use.
Q: Why do so many people still use p = 0.05?
A: Because that’s what they were taught in college or grad school.
George Cobb, 2014
Como vimos no capítulo anterior, uma pesquisa científica visa produzir evidências a favor de uma de suas duas hipóteses: a hipótese nula ou a hipótese alternativa. Vimos também que o resultado de uma pesquisa pode ser falso de duas formas, falso positivo (erro tipo I) ou falso negativo (erro tipo II) e que, portando, nunca representa uma verdade absoluta, devendo sempre ser interpretado de forma probabilística. A medida de probabilidade usada para essa avaliação é o que se chama de valor de $p$, ou $p-value$.
Essa medida, o $p-value$, é calculada a partir dos resultados da pesquisa, ou seja, só pode ser calculada depois de coletados os dados. O mais adequado e intuitivo nesse momento seria nos perguntarmos tendo em vista esses dados, qual a chance da minha hipótese alternativa ser verdadeira?. Entretanto, a forma como a estatística lida com essa questão está bem longe de ser simples assim.
O $p-value$ não representa a probabilidade da hipótese alternativa ser verdadeira ou falsa e também não representa a probabilidade da hipótese nula ser verdadeira ou falsa. Muito pelo contrário, para o cálculo do p-value, a hipótese nula é dada como verdadeira. Ou seja, é a partir dessa premissa, que a hipótese nula seja verdadeira, é que o $p-value$ pode ser calculado.
O $p-value$ é a probabilidade de encontrarmos, apenas por acaso, o resultado que foi encontrado na pesquisa, ou resultados mais extremos. Ou seja, a probabilidade expressa pelo valor de $p$ não se refere às hipóteses, mas aos dados. O valor de $p$ representa a probabilidade de encontrarmos esses dados, ou dados mais extremos, apenas por acaso. É importante lembrar que afirmar que os resultados da pesquisa estão sendo influenciados apenas pelo acaso é o mesmo que dizer que a hipótese nula é verdadeira. A definição formal do valor de $p$ é usualmente descrita nesses termos:
A probabilidade do resultado encontrado, ou resultados mais extremos, terem sido observados, se a hipótese nula for verdadeira.
Origens e confusões
O $p-value$ foi proposto por Ronald Fisher por volta da década de 1920 para ser usado como uma medida da discrepância entre os dados observados e a hipótese nula, sendo apenas uma parte de um processo de análises dos resultados (GOODMAN, 1999). Para Fisher, um valor de p < 0.05 significava apenas que a experiência merecia ser repetida novamente e que, se numa série desses experimentos subsequentes o valor de $p$ se mantivesse sempre abaixo de 0.05, isso sim seria um indício de que os resultados não se deviam apenas ao acaso. Ou seja, a função original do valor de $p$ era apenas indicar que o resultado era digno de atenção e não prova de nenhum resultado (GOODMAN, 2008).
Entretanto, o $p-value$ passou a ser uma das mais frequentes e mais mal interpretadas dentre as medidas estatísticas nas pesquisas científicas da área da saúde. Goodman (2008) lista frequentes erros de interpretação do valor de $p$ que merecem ser repetidos aqui:
- Se $p=0.05$, a hipótese nula tem 5% de chance de ser verdadeira
- Uma $p > 0.05$ significa que não há diferença entre os grupos
- Um resultado estatisticamente significativo é também clinicamente significativo
- Estudos com valores de $p$ idênticos tem a mesma força de evidência sobre a hipótese nula
- Um valor de $p = 0.05$ significa que a chance de encontrar por acaso exatamente os dados da pesquisa é de 5%.
- $p = 0.05$ e $p \le 0.05$ tem o mesmo significado
- $p-values$ devem ser escritos com sinal de $<$ ou $>$
- $p=0.05$ significa que se você rejeitar a hipótese nula, a probabilidade de erro tipo I é de apenas 5%.
- Uma conclusão científica ou decisão de tratamento deve ser fundamentada num valor de $p$ significativo
Interpretação gráfica do valor de p
Uma probabilidade é calculada a partir de uma curva de distribuição, como a área abaixo a curva, à esquerda ou à direita de um determinado ponto. O $p-value$ não é exceção. É calculado como a área abaixo de uma curva de distribuição, mais extrema que o ponto médio dos dados observados na pesquisa.
Precisamos então responder a seguinte pergunta: Qual a distribuição deve ser usada para calcular o valor de $p$.
A definição do valor de $p$ é a probabilidade de encontrarmos os dados da pesquisa, ou dados mais extremos, supondo que a hipótese nula seja verdadeira. Ou seja, o valor de $p$ é calculado levando em conta como os dados estariam distribuídos caso a hipótese nula fosse verdadeira. Isso significa que o valor de $p$ é calculado a partir da distribuição nula.
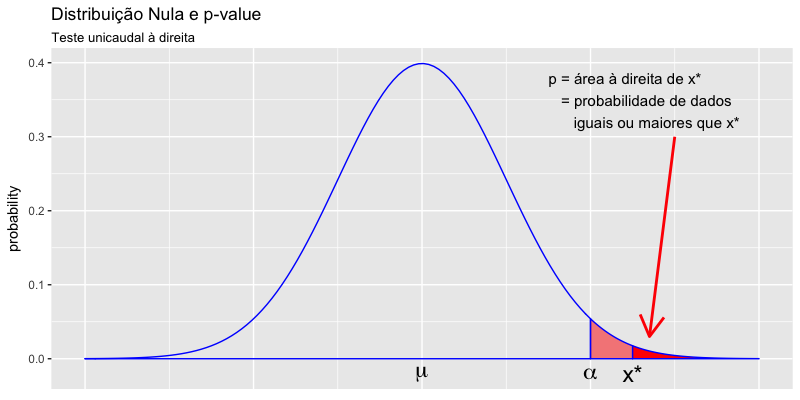
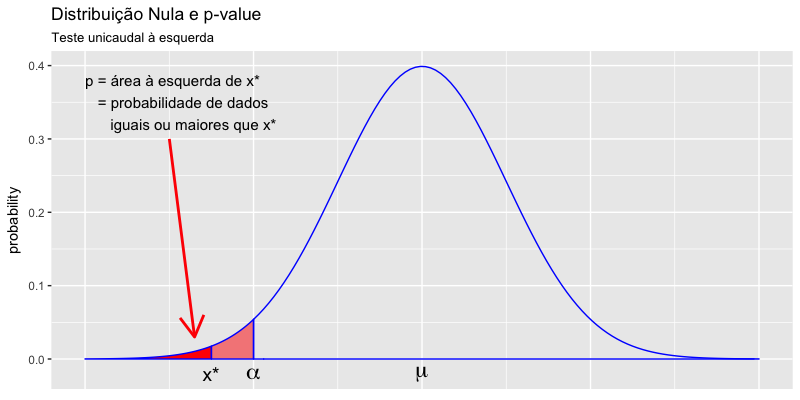
Referências
Ronald L. Wasserstein & Nicole A. Lazar (2016) The ASA’s Statement on p-Values: Context, Process, and Purpose, The American Statistician, 70:2, 129-133, DOI: 10.1080/00031305.2016.1154108
Goodman S. A dirty dozen: twelve p-value misconceptions. Semin Hematol. 2008
Jul;45(3):135-40. doi: 10.1053/j.seminhematol.2008.04.003. Review. Erratum in:
Semin Hematol. 2011 Oct;48(4):302.
Goodman SN. Toward evidence-based medical statistics. 1: The P value fallacy.
Ann Intern Med. 1999 Jun 15;130(12):995-1004.
Notes
Distribuição nula
1Ronald Fisher. The Design of Experiments. Hafner Publishing Company: New York, 1971. ↩
