Read Functional Programming for Mortals

Functional Programming for Mortals

Sam Halliday

About This Book
Copyleft Notice
Thanks
Practicalities
1. Introduction
- 1.1 Abstracting over Execution
- 1.2 Pure Functional Programming
2. For Comprehensions
3. Application Design
4. Data and Functionality
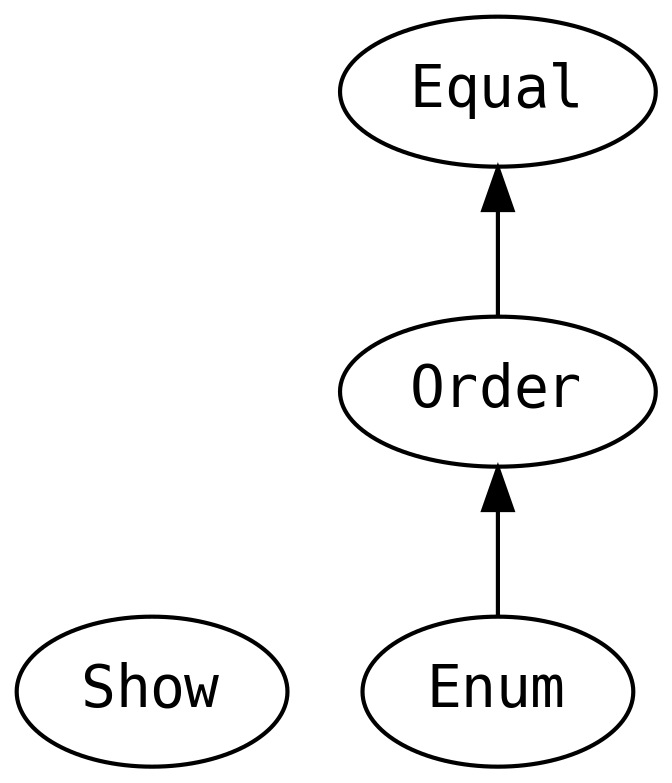
5. Scalaz Typeclasses
6. Scalaz Data Types
7. Advanced Monads
8. Typeclass Derivation
9. Wiring up the Application
Typeclass Cheatsheet
Haskell
Third Party Licenses
- Scala License
- Scalaz License

“Love is wise; hatred is foolish. In this world, which is getting more and more closely interconnected, we have to learn to tolerate each other, we have to learn to put up with the fact that some people say things that we don’t like. We can only live together in that way. But if we are to live together, and not die together, we must learn a kind of charity and a kind of tolerance, which is absolutely vital to the continuation of human life on this planet.”

― Bertrand Russell

About This Book

This book is for the typical Scala developer, probably with a Java background, who is both sceptical and curious about the Functional Programming (FP) paradigm. This book justifies every concept with practical examples, including writing a web application.

This book uses Scalaz 7.2, the most popular, stable, principled and comprehensive Functional Programming framework for Scala.

This book is designed to be read from cover to cover, in the order presented, with a rest between chapters. Earlier chapters encourage coding styles that we will later discredit: similar to how we learn Newton’s theory of gravity as children, and progress to Riemann / Einstein / Maxwell if we become students of physics.

A computer is not necessary to follow along, but studying the Scalaz source code is encouraged. Some of the more complex code snippets are available with the book’s source code and those who want practical exercises are encouraged to (re-)implement Scalaz (and the example application) using the partial descriptions presented in this book.

We also recommend The Red Book as further reading. It teaches how to write an FP library in Scala from first principles.

Copyleft Notice

This book is Libre and follows the philosophy of Free Software: you can use this book as you like, the source is available you can redistribute this book and you can distribute your own version. That means you can print it, photocopy it, e-mail it, upload it to websites, change it, translate it, charge for it, remix it, delete bits, and draw all over it.

This book is Copyleft: if you change the book and distribute your own version, you must also pass these freedoms to its recipients.

This book uses the Creative Commons Attribution ShareAlike 4.0 International (CC BY-SA 4.0) license.

All original code snippets in this book are separately CC0 licensed, you may use them without restriction. Excerpts from Scalaz and related libraries maintain their license, reproduced in full in the appendix.

The example application drone-dynamic-agents is distributed under the terms of the GPLv3: only the snippets in this book are available without restriction.

Thanks

Diego Esteban Alonso Blas, Raúl Raja Martínez and Peter Neyens of 47 degrees, Rúnar Bjarnason, Tony Morris, John de Goes and Edward Kmett for their help explaining the principles of FP. Kenji Yoshida and Jason Zaugg for being the main authors of Scalaz, and Paul Chiusano / Miles Sabin for fixing a critical bug in the Scala compiler (SI-2712).

Thanks to the readers who gave feedback on early drafts of this text.

Some material was particularly helpful for my own understanding of the concepts that are in this book. Thanks to Juan Manuel Serrano for All Roads Lead to Lambda, Pere Villega for On Free Monads, Dick Wall and Josh Suereth for For: What is it Good For?, Erik Bakker for Options in Futures, how to unsuck them, Noel Markham for ADTs for the Win!, Sukant Hajra for Classy Monad Transformers, Luka Jacobowitz for Optimizing Tagless Final, Vincent Marquez for Index your State, Gabriel Gonzalez for The Continuation Monad, and Yi Lin Wei / Zainab Ali for their tutorials at Hack The Tower meetups.

The helpul souls who patiently explained things to me: Merlin Göttlinger, Edmund Noble, Fabio Labella, Adelbert Chang, Michael Pilquist, Paul Snively, Daniel Spiewak, Stephen Compall, Brian McKenna, Ryan Delucchi, Pedro Rodriguez, Emily Pillmore, Aaron Vargo, Tomas Mikula, Jean-Baptiste Giraudeau, Itamar Ravid, Ross A. Baker, Alexander Konovalov, Harrison Houghton, Alexandre Archambault, Christopher Davenport, Jose Cardona, Isaac Elliott.

Practicalities

To set up a project that uses the libraries presented in this book, use a recent version of Scala with FP-specific features enabled (e.g. in build.sbt):

  scalaVersion in ThisBuild := "2.12.6"
  scalacOptions in ThisBuild ++= Seq(
    "-language:_",
    "-Ypartial-unification",
    "-Xfatal-warnings"
  )
  
  libraryDependencies ++= Seq(
    "com.github.mpilquist" %% "simulacrum"     % "0.13.0",
    "org.scalaz"           %% "scalaz-core"    % "7.2.26"
  )
  
  addCompilerPlugin("org.spire-math" %% "kind-projector" % "0.9.7")
  addCompilerPlugin("org.scalamacros" % "paradise" % "2.1.1" cross CrossVersion.full)

In order to keep our snippets short, we will omit the import section. Unless told otherwise, assume that all snippets have the following imports:

  import scalaz._, Scalaz._
  import simulacrum._

1. Introduction

It is human instinct to be sceptical of a new paradigm. To put some perspective on how far we have come, and the shifts we have already accepted on the JVM, let’s start with a quick recap of the last 20 years.

Java 1.2 introduced the Collections API, allowing us to write methods that abstracted over mutable collections. It was useful for writing general purpose algorithms and was the bedrock of our codebases.

But there was a problem, we had to perform runtime casting:

  public String first(Collection collection) {
    return (String)(collection.get(0));
  }

In response, developers defined domain objects in their business logic that were effectively CollectionOfThings, and the Collection API became implementation detail.

In 2005, Java 5 introduced generics, allowing us to define Collection<Thing>, abstracting over the container and its elements. Generics changed how we wrote Java.

The author of the Java generics compiler, Martin Odersky, then created Scala with a stronger type system, immutable data and multiple inheritance. This brought about a fusion of object oriented (OOP) and functional programming (FP).

For most developers, FP means using immutable data as much as possible, but mutable state is still a necessary evil that must be isolated and managed, e.g. with Akka actors or synchronized classes. This style of FP results in simpler programs that are easier to parallelise and distribute, an improvement over Java. But it is only scratching the surface of the benefits of FP, as we will discover in this book.

Scala also brings Future, making it easy to write asynchronous applications. But when a Future makes it into a return type, everything needs to be rewritten to accomodate it, including the tests, which are now subject to arbitrary timeouts.

We have a problem similar to Java 1.0: there is no way of abstracting over execution, much as we had no way of abstracting over collections.

1.1 Abstracting over Execution

Say we want to interact with the user over the command line interface. We can read what the user types and we can write a message to them.

  trait TerminalSync {
    def read(): String
    def write(t: String): Unit
  }
  
  trait TerminalAsync {
    def read(): Future[String]
    def write(t: String): Future[Unit]
  }

How do we write generic code that does something as simple as echo the user’s input synchronously or asynchronously depending on our runtime implementation?

We could write a synchronous version and wrap it with Future but now we have to worry about which thread pool we should be using for the work, or we could Await.result on the Future and introduce thread blocking. In either case, it is a lot of boilerplate and we are fundamentally dealing with different APIs that are not unified.

We can solve the problem, like Java 1.2, with a common parent using the higher kinded types (HKT) Scala language feature.

Higher Kinded Types allow us to use a type constructor in our type parameters, which looks like C[_]. This is a way of saying that whatever C is, it must take a type parameter. For example:

  trait Foo[C[_]] {
    def create(i: Int): C[Int]
  }

List is a type constructor because it takes a type (e.g. Int) and constructs a type (List[Int]). We can implement Foo using List:

  object FooList extends Foo[List] {
    def create(i: Int): List[Int] = List(i)
  }

We can implement Foo for anything with a type parameter hole, e.g. Either[String, _]. Unfortunately it is a bit clunky and we have to create a type alias to trick the compiler into accepting it:

  type EitherString[T] = Either[String, T]

Type aliases don’t define new types, they just use substitution and don’t provide extra type safety. The compiler substitutes EitherString[T] with Either[String, T] everywhere. This technique can be used to trick the compiler into accepting types with one hole when it would otherwise think there are two, like when we implement Foo with EitherString:

  object FooEitherString extends Foo[EitherString] {
    def create(i: Int): Either[String, Int] = Right(i)
  }

Alternatively, the kind projector plugin allows us to avoid the type alias and use ? syntax to tell the compiler where the type hole is:

  object FooEitherString extends Foo[Either[String, ?]] {
    def create(i: Int): Either[String, Int] = Right(i)
  }

Finally, there is this one weird trick we can use when we want to ignore the type constructor. Define a type alias to be equal to its parameter:

  type Id[T] = T

Before proceeding, understand that Id[Int] is the same thing as Int, by substituting Int into T. Because Id is a valid type constructor we can use Id in an implementation of Foo

  object FooId extends Foo[Id] {
    def create(i: Int): Int = i
  }

We want to define Terminal for a type constructor C[_]. By defining Now to construct to its type parameter (like Id), we can implement a common interface for synchronous and asynchronous terminals:

  trait Terminal[C[_]] {
    def read: C[String]
    def write(t: String): C[Unit]
  }
  
  type Now[X] = X
  
  object TerminalSync extends Terminal[Now] {
    def read: String = ???
    def write(t: String): Unit = ???
  }
  
  object TerminalAsync extends Terminal[Future] {
    def read: Future[String] = ???
    def write(t: String): Future[Unit] = ???
  }

We can think of C as a Context because we say “in the context of executing Now” or “in the Future”.

But we know nothing about C and we cannot do anything with a C[String]. What we need is a kind of execution environment that lets us call a method returning C[T] and then be able to do something with the T, including calling another method on Terminal. We also need a way of wrapping a value as a C[_]. This signature works well:

  trait Execution[C[_]] {
    def chain[A, B](c: C[A])(f: A => C[B]): C[B]
    def create[B](b: B): C[B]
  }

letting us write:

  def echo[C[_]](t: Terminal[C], e: Execution[C]): C[String] =
    e.chain(t.read) { in: String =>
      e.chain(t.write(in)) { _: Unit =>
        e.create(in)
      }
    }

We can now share the echo implementation between synchronous and asynchronous codepaths. We can write a mock implementation of Terminal[Now] and use it in our tests without any timeouts.

Implementations of Execution[Now] and Execution[Future] are reusable by generic methods like echo.

But the code for echo is horrible!

The implicit class Scala language feature gives C some methods. We will call these methods flatMap and map for reasons that will become clearer in a moment. Each method takes an implicit Execution[C], but this is nothing more than the flatMap and map that we’re used to on Seq, Option and Future

  object Execution {
    implicit class Ops[A, C[_]](c: C[A]) {
      def flatMap[B](f: A => C[B])(implicit e: Execution[C]): C[B] =
            e.chain(c)(f)
      def map[B](f: A => B)(implicit e: Execution[C]): C[B] =
            e.chain(c)(f andThen e.create)
    }
  }
  
  def echo[C[_]](implicit t: Terminal[C], e: Execution[C]): C[String] =
    t.read.flatMap { in: String =>
      t.write(in).map { _: Unit =>
        in
      }
    }

We can now reveal why we used flatMap as the method name: it lets us use a for comprehension, which is just syntax sugar over nested flatMap and map.

  def echo[C[_]](implicit t: Terminal[C], e: Execution[C]): C[String] =
    for {
      in <- t.read
       _ <- t.write(in)
    } yield in

Our Execution has the same signature as a trait in Scalaz called Monad, except chain is bind and create is pure. We say that C is monadic when there is an implicit Monad[C] available. In addition, Scalaz has the Id type alias.

The takeaway is: if we write methods that operate on monadic types, then we can write sequential code that abstracts over its execution context. Here, we have shown an abstraction over synchronous and asynchronous execution but it can also be for the purpose of more rigorous error handling (where C[_] is Either[Error, _]), managing access to volatile state, performing I/O, or auditing of the session.

1.2 Pure Functional Programming

Functional Programming is the act of writing programs with pure functions. Pure functions have three properties:

Total: return a value for every possible input
Deterministic: return the same value for the same input
Inculpable: no (direct) interaction with the world or program state.

Together, these properties give us an unprecedented ability to reason about our code. For example, input validation is easier to isolate with totality, caching is possible when functions are deterministic, and interacting with the world is easier to control, and test, when functions are inculpable.

The kinds of things that break these properties are side effects: directly accessing or changing mutable state (e.g. maintaining a var in a class or using a legacy API that is impure), communicating with external resources (e.g. files or network lookup), or throwing and catching exceptions.

We write pure functions by avoiding exceptions, and interacting with the world only through a safe F[_] execution context.

In the previous section, we abstracted over execution and defined echo[Id] and echo[Future]. We might reasonably expect that calling any echo will not perform any side effects, because it is pure. However, if we use Future or Id as the execution context, our application will start listening to stdin:

  val futureEcho: Future[String] = echo[Future]

We have broken purity and are no longer writing FP code: futureEcho is the result of running echo once. Future conflates the definition of a program with interpreting it (running it). As a result, applications built with Future are difficult to reason about.

We can define a simple safe F[_] execution context

  final class IO[A](val interpret: () => A) {
    def map[B](f: A => B): IO[B] = IO(f(interpret()))
    def flatMap[B](f: A => IO[B]): IO[B] = IO(f(interpret()).interpret())
  }
  object IO {
    def apply[A](a: =>A): IO[A] = new IO(() => a)
  }

which lazily evaluates a thunk. IO is just a data structure that references (potentially) impure code, it isn’t actually running anything. We can implement Terminal[IO]

  object TerminalIO extends Terminal[IO] {
    def read: IO[String]           = IO { io.StdIn.readLine }
    def write(t: String): IO[Unit] = IO { println(t) }
  }

and call echo[IO] to get back a value

  val delayed: IO[String] = echo[IO]

This val delayed can be reused, it is just the definition of the work to be done. We can map the String and compose additional programs, much as we would map over a Future. IO keeps us honest that we are depending on some interaction with the world, but does not prevent us from accessing the output of that interaction.

The impure code inside the IO is only evaluated when we .interpret() the value, which is an impure action

  delayed.interpret()

An application composed of IO programs is only interpreted once, in the main method, which is also called the end of the world.

In this book, we expand on the concepts introduced in this chapter and show how to write maintainable, pure functions, that achieve our business’s objectives.

2. For Comprehensions

Scala’s for comprehension is the ideal FP abstraction for sequential programs that interact with the world. Since we will be using it a lot, we’re going to relearn the principles of for and how Scalaz can help us to write cleaner code.

This chapter doesn’t try to write pure programs and the techniques are applicable to non-FP codebases.

2.1 Syntax Sugar

Scala’s for is just a simple rewrite rule, also called syntax sugar, that doesn’t have any contextual information.

To see what a for comprehension is doing, we use the show and reify feature in the REPL to print out what code looks like after type inference.

  scala> import scala.reflect.runtime.universe._
  scala> val a, b, c = Option(1)
  scala> show { reify {
           for { i <- a ; j <- b ; k <- c } yield (i + j + k)
         } }
  
  res:
  $read.a.flatMap(
    ((i) => $read.b.flatMap(
      ((j) => $read.c.map(
        ((k) => i.$plus(j).$plus(k)))))))

There is a lot of noise due to additional sugarings (e.g. + is rewritten $plus, etc). We will skip the show and reify for brevity when the REPL line is reify>, and manually clean up the generated code so that it doesn’t become a distraction.

  reify> for { i <- a ; j <- b ; k <- c } yield (i + j + k)
  
  a.flatMap {
    i => b.flatMap {
      j => c.map {
        k => i + j + k }}}

The rule of thumb is that every <- (called a generator) is a nested flatMap call, with the final generator a map containing the yield body.

2.1.1 Assignment

We can assign values inline like ij = i + j (a val keyword is not needed).

  reify> for {
           i <- a
           j <- b
           ij = i + j
           k <- c
         } yield (ij + k)
  
  a.flatMap {
    i => b.map { j => (j, i + j) }.flatMap {
      case (j, ij) => c.map {
        k => ij + k }}}

A map over the b introduces the ij which is flat-mapped along with the j, then the final map for the code in the yield.

Unfortunately we cannot assign before any generators. It has been requested as a language feature but has not been implemented: https://github.com/scala/bug/issues/907

  scala> for {
           initial = getDefault
           i <- a
         } yield initial + i
  <console>:1: error: '<-' expected but '=' found.

We can workaround the limitation by defining a val outside the for

  scala> val initial = getDefault
  scala> for { i <- a } yield initial + i

or create an Option out of the initial assignment

  scala> for {
           initial <- Option(getDefault)
           i <- a
         } yield initial + i

val doesn’t have to assign to a single value, it can be anything that works as a case in a pattern match.

  scala> val (first, second) = ("hello", "world")
  first: String = hello
  second: String = world
  
  scala> val list: List[Int] = ...
  scala> val head :: tail = list
  head: Int = 1
  tail: List[Int] = List(2, 3)

The same is true for assignment in for comprehensions

  scala> val maybe = Option(("hello", "world"))
  scala> for {
           entry <- maybe
           (first, _) = entry
         } yield first
  res: Some(hello)

But be careful not to miss any cases or there will be a runtime exception (a totality failure).

  scala> val a :: tail = list
  caught scala.MatchError: List()

2.1.2 Filter

It is possible to put if statements after a generator to filter values by a predicate

  reify> for {
           i  <- a
           j  <- b
           if i > j
           k  <- c
         } yield (i + j + k)
  
  a.flatMap {
    i => b.withFilter {
      j => i > j }.flatMap {
        j => c.map {
          k => i + j + k }}}

Older versions of Scala used filter, but Traversable.filter creates new collections for every predicate, so withFilter was introduced as the more performant alternative. We can accidentally trigger a withFilter by providing type information, interpreted as a pattern match.

  reify> for { i: Int <- a } yield i
  
  a.withFilter {
    case i: Int => true
    case _      => false
  }.map { case i: Int => i }

Like assignment, a generator can use a pattern match on the left hand side. But unlike assignment (which throws MatchError on failure), generators are filtered and will not fail at runtime. However, there is an inefficient double application of the pattern.

The compiler plugin better-monadic-for produces alternative, better, desugarings than the Scala compiler. This example is interpreted as:

  reify> for { i: Int <- a } yield i
  
  a.map { (i: Int) => i}

instead of inefficient double matching (in the best case) and silent filtering at runtime (in the worst case). Highly recommended.

2.1.3 For Each

Finally, if there is no yield, the compiler will use foreach instead of flatMap, which is only useful for side-effects.

  reify> for { i <- a ; j <- b } println(s"$i $j")
  
  a.foreach { i => b.foreach { j => println(s"$i $j") } }

2.1.4 Summary

The full set of methods supported by for comprehensions do not share a common super type; each generated snippet is independently compiled. If there were a trait, it would roughly look like:

  trait ForComprehensible[C[_]] {
    def map[A, B](f: A => B): C[B]
    def flatMap[A, B](f: A => C[B]): C[B]
    def withFilter[A](p: A => Boolean): C[A]
    def foreach[A](f: A => Unit): Unit
  }

If the context (C[_]) of a for comprehension doesn’t provide its own map and flatMap, all is not lost. If an implicit scalaz.Bind[T] is available for T, it will provide map and flatMap.

It often surprises developers when inline Future calculations in a for comprehension do not run in parallel:

  import scala.concurrent._
  import ExecutionContext.Implicits.global
  
  for {
    i <- Future { expensiveCalc() }
    j <- Future { anotherExpensiveCalc() }
  } yield (i + j)

This is because the flatMap spawning anotherExpensiveCalc is strictly after expensiveCalc. To ensure that two Future calculations begin in parallel, start them outside the for comprehension.

  val a = Future { expensiveCalc() }
  val b = Future { anotherExpensiveCalc() }
  for { i <- a ; j <- b } yield (i + j)

for comprehensions are fundamentally for defining sequential programs. We will show a far superior way of defining parallel computations in a later chapter. Spoiler: don’t use Future.

2.2 Unhappy path

So far we’ve only looked at the rewrite rules, not what is happening in map and flatMap. Consider what happens when the for context decides that it cannot proceed any further.

In the Option example, the yield is only called when i,j,k are all defined.

  for {
    i <- a
    j <- b
    k <- c
  } yield (i + j + k)

If any of a,b,c are None, the comprehension short-circuits with None but it doesn’t tell us what went wrong.

There are many functions in the wild that take Option parameters but actually require all parameters to exist. An alternative to throwing a runtime exception is to use a for comprehension, giving us totality (a return value for every input):

  def namedThings(
    someName  : Option[String],
    someNumber: Option[Int]
  ): Option[String] = for {
    name   <- someName
    number <- someNumber
  } yield s"$number ${name}s"

but this is verbose, clunky and bad style. If a function requires every input then it should make its requirement explicit, pushing the responsibility of dealing with optional parameters to its caller.

  def namedThings(name: String, num: Int) = s"$num ${name}s"

If we use Either, then a Left will cause the for comprehension to short circuit with extra information, much better than Option for error reporting:

  scala> val a = Right(1)
  scala> val b = Right(2)
  scala> val c: Either[String, Int] = Left("sorry, no c")
  scala> for { i <- a ; j <- b ; k <- c } yield (i + j + k)
  
  Left(sorry, no c)

And lastly, let’s see what happens with a Future that fails:

  scala> import scala.concurrent._
  scala> import ExecutionContext.Implicits.global
  scala> for {
           i <- Future.failed[Int](new Throwable)
           j <- Future { println("hello") ; 1 }
         } yield (i + j)
  scala> Await.result(f, duration.Duration.Inf)
  caught java.lang.Throwable

The Future that prints to the terminal is never called because, like Option and Either, the for comprehension short circuits.

Short circuiting for the unhappy path is a common and important theme. for comprehensions cannot express resource cleanup: there is no way to try / finally. This is good, in FP it puts a clear ownership of responsibility for unexpected error recovery and resource cleanup onto the context (which is usually a Monad as we will see later), not the business logic.

2.3 Gymnastics

Although it is easy to rewrite simple sequential code as a for comprehension, sometimes we will want to do something that appears to require mental summersaults. This section collects some practical examples and how to deal with them.

2.3.1 Fallback Logic

Say we are calling out to a method that returns an Option. If it is not successful we want to fallback to another method (and so on and so on), like when we’re using a cache:

  def getFromRedis(s: String): Option[String]
  def getFromSql(s: String): Option[String]
  
  getFromRedis(key) orElse getFromSql(key)

If we have to do this for an asynchronous version of the same API

  def getFromRedis(s: String): Future[Option[String]]
  def getFromSql(s: String): Future[Option[String]]

then we have to be careful not to do extra work because

  for {
    cache <- getFromRedis(key)
    sql   <- getFromSql(key)
  } yield cache orElse sql

will run both queries. We can pattern match on the first result but the type is wrong

  for {
    cache <- getFromRedis(key)
    res   <- cache match {
               case Some(_) => cache !!! wrong type !!!
               case None    => getFromSql(key)
             }
  } yield res

We need to create a Future from the cache

  for {
    cache <- getFromRedis(key)
    res   <- cache match {
               case Some(_) => Future.successful(cache)
               case None    => getFromSql(key)
             }
  } yield res

Future.successful creates a new Future, much like an Option or List constructor.

2.3.2 Early Exit

Say we have some condition that should exit early with a successful value.

If we want to exit early with an error, it is standard practice in OOP to throw an exception

  def getA: Int = ...
  
  val a = getA
  require(a > 0, s"$a must be positive")
  a * 10

which can be rewritten async

  def getA: Future[Int] = ...
  def error(msg: String): Future[Nothing] =
    Future.failed(new RuntimeException(msg))
  
  for {
    a <- getA
    b <- if (a <= 0) error(s"$a must be positive")
         else Future.successful(a)
  } yield b * 10

But if we want to exit early with a successful return value, the simple synchronous code:

  def getB: Int = ...
  
  val a = getA
  if (a <= 0) 0
  else a * getB

translates into a nested for comprehension when our dependencies are asynchronous:

  def getB: Future[Int] = ...
  
  for {
    a <- getA
    c <- if (a <= 0) Future.successful(0)
         else for { b <- getB } yield a * b
  } yield c

If there is an implicit Monad[T] for T[_] (i.e. T is monadic) then Scalaz lets us create a T[A] from a value a: A by calling a.pure[T].

Scalaz provides Monad[Future], and .pure[Future] calls Future.successful. Besides pure being slightly shorter to type, it is a general concept that works beyond Future, and is therefore recommended.

  for {
    a <- getA
    c <- if (a <= 0) 0.pure[Future]
         else for { b <- getB } yield a * b
  } yield c

2.4 Incomprehensible

The context we’re comprehending over must stay the same: we cannot mix contexts.

  scala> def option: Option[Int] = ...
  scala> def future: Future[Int] = ...
  scala> for {
           a <- option
           b <- future
         } yield a * b
  <console>:23: error: type mismatch;
   found   : Future[Int]
   required: Option[?]
           b <- future
                ^

Nothing can help us mix arbitrary contexts in a for comprehension because the meaning is not well defined.

But when we have nested contexts the intention is usually obvious yet the compiler still doesn’t accept our code.

  scala> def getA: Future[Option[Int]] = ...
  scala> def getB: Future[Option[Int]] = ...
  scala> for {
           a <- getA
           b <- getB
         } yield a * b
                   ^
  <console>:30: error: value * is not a member of Option[Int]

Here we want for to take care of the outer context and let us write our code on the inner Option. Hiding the outer context is exactly what a monad transformer does, and Scalaz provides implementations for Option and Either named OptionT and EitherT respectively.

The outer context can be anything that normally works in a for comprehension, but it needs to stay the same throughout.

We create an OptionT from each method call. This changes the context of the for from Future[Option[_]] to OptionT[Future, _].

  scala> val result = for {
           a <- OptionT(getA)
           b <- OptionT(getB)
         } yield a * b
  result: OptionT[Future, Int] = OptionT(Future(<not completed>))

.run returns us to the original context

  scala> result.run
  res: Future[Option[Int]] = Future(<not completed>)

The monad transformer also allows us to mix Future[Option[_]] calls with methods that just return plain Future via .liftM[OptionT] (provided by scalaz):

  scala> def getC: Future[Int] = ...
  scala> val result = for {
           a <- OptionT(getA)
           b <- OptionT(getB)
           c <- getC.liftM[OptionT]
         } yield a * b / c
  result: OptionT[Future, Int] = OptionT(Future(<not completed>))

and we can mix with methods that return plain Option by wrapping them in Future.successful (.pure[Future]) followed by OptionT

  scala> def getD: Option[Int] = ...
  scala> val result = for {
           a <- OptionT(getA)
           b <- OptionT(getB)
           c <- getC.liftM[OptionT]
           d <- OptionT(getD.pure[Future])
         } yield (a * b) / (c * d)
  result: OptionT[Future, Int] = OptionT(Future(<not completed>))

It is messy again, but it is better than writing nested flatMap and map by hand. We can clean it up with a DSL that handles all the required conversions into OptionT[Future, _]

  def liftFutureOption[A](f: Future[Option[A]]) = OptionT(f)
  def liftFuture[A](f: Future[A]) = f.liftM[OptionT]
  def liftOption[A](o: Option[A]) = OptionT(o.pure[Future])
  def lift[A](a: A)               = liftOption(Option(a))

combined with the |> operator, which applies the function on the right to the value on the left, to visually separate the logic from the transformers

  scala> val result = for {
           a <- getA       |> liftFutureOption
           b <- getB       |> liftFutureOption
           c <- getC       |> liftFuture
           d <- getD       |> liftOption
           e <- 10         |> lift
         } yield e * (a * b) / (c * d)
  result: OptionT[Future, Int] = OptionT(Future(<not completed>))

This approach also works for Either (and others) as the inner context, but their lifting methods are more complex and require parameters. Scalaz provides monad transformers for a lot of its own types, so it is worth checking if one is available.

3. Application Design

In this chapter we will write the business logic and tests for a purely functional server application. The source code for this application is included under the example directory along with the book’s source, however it is recommended not to read the source code until the final chapter as there will be significant refactors as we learn more about FP.

3.1 Specification

Our application will manage a just-in-time build farm on a shoestring budget. It will listen to a Drone Continuous Integration server, and spawn worker agents using Google Container Engine (GKE) to meet the demand of the work queue.

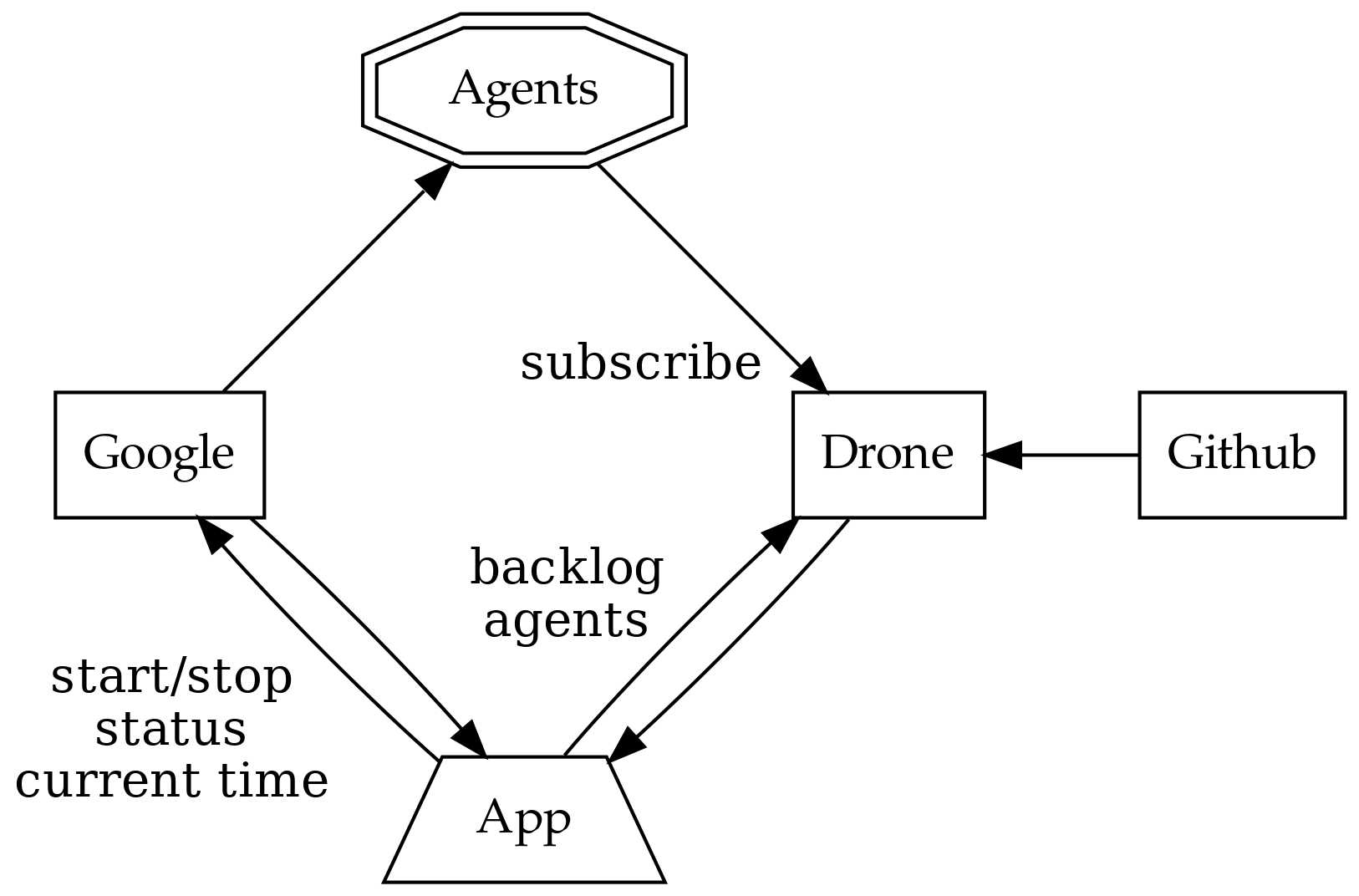
Drone receives work when a contributor submits a github pull request to a managed project. Drone assigns the work to its agents, each processing one job at a time.

The goal of our app is to ensure that there are enough agents to complete the work, with a cap on the number of agents, whilst minimising the total cost. Our app needs to know the number of items in the backlog and the number of available agents.

Google can spawn nodes, each can host multiple drone agents. When an agent starts up, it registers itself with drone and drone takes care of the lifecycle (including keep-alive calls to detect removed agents).

GKE charges a fee per minute of uptime, rounded up to the nearest hour for each node. One does not simply spawn a new node for each job in the work queue, we must re-use nodes and retain them until their 58th minute to get the most value for money.

Our app needs to be able to start and stop nodes, as well as check their status (e.g. uptimes, list of inactive nodes) and to know what time GKE believes it to be.

In addition, there is no API to talk directly to an agent so we do not know if any individual agent is performing any work for the drone server. If we accidentally stop an agent whilst it is performing work, it is inconvenient and requires a human to restart the job.

Contributors can manually add agents to the farm, so counting agents and nodes is not equivalent. We don’t need to supply any nodes if there are agents available.

The failure mode should always be to take the least costly option.

Both Drone and GKE have a JSON over REST API with OAuth 2.0 authentication.

3.2 Interfaces / Algebras

We will now codify the architecture diagram from the previous section. Firstly, we need to define a simple data type to capture a millisecond timestamp because such a simple thing does not exist in either the Java or Scala standard libraries:

  import scala.concurrent.duration._
  
  final case class Epoch(millis: Long) extends AnyVal {
    def +(d: FiniteDuration): Epoch = Epoch(millis + d.toMillis)
    def -(e: Epoch): FiniteDuration = (millis - e.millis).millis
  }

In FP, an algebra takes the place of an interface in Java, or the set of valid messages for an Actor in Akka. This is the layer where we define all side-effecting interactions of our system.

There is tight iteration between writing the business logic and the algebra: it is a good level of abstraction to design a system.

  trait Drone[F[_]] {
    def getBacklog: F[Int]
    def getAgents: F[Int]
  }
  
  final case class MachineNode(id: String)
  trait Machines[F[_]] {
    def getTime: F[Epoch]
    def getManaged: F[NonEmptyList[MachineNode]]
    def getAlive: F[Map[MachineNode, Epoch]]
    def start(node: MachineNode): F[MachineNode]
    def stop(node: MachineNode): F[MachineNode]
  }

We’ve used NonEmptyList, easily created by calling .toNel on the stdlib’s List (returning an Option[NonEmptyList]), otherwise everything should be familiar.

3.3 Business Logic

Now we write the business logic that defines the application’s behaviour, considering only the happy path.

We need a WorldView class to hold a snapshot of our knowledge of the world. If we were designing this application in Akka, WorldView would probably be a var in a stateful Actor.

WorldView aggregates the return values of all the methods in the algebras, and adds a pending field to track unfulfilled requests.

  final case class WorldView(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    pending: Map[MachineNode, Epoch],
    time: Epoch
  )

Now we are ready to write our business logic, but we need to indicate that we depend on Drone and Machines.

We can write the interface for the business logic

  trait DynAgents[F[_]] {
    def initial: F[WorldView]
    def update(old: WorldView): F[WorldView]
    def act(world: WorldView): F[WorldView]
  }

and implement it with a module. A module depends only on other modules, algebras and pure functions, and can be abstracted over F. If an implementation of an algebraic interface is tied to a specific type, e.g. IO, it is called an interpreter.

  final class DynAgentsModule[F[_]: Monad](D: Drone[F], M: Machines[F])
    extends DynAgents[F] {

The Monad context bound means that F is monadic, allowing us to use map, pure and, of course, flatMap via for comprehensions.

We have access to the algebra of Drone and Machines as D and M, respectively. Using a single capital letter name is a common naming convention for monad and algebra implementations.

Our business logic will run in an infinite loop (pseudocode)

  state = initial()
  while True:
    state = update(state)
    state = act(state)

3.3.1 initial

In initial we call all external services and aggregate their results into a WorldView. We default the pending field to an empty Map.

  def initial: F[WorldView] = for {
    db <- D.getBacklog
    da <- D.getAgents
    mm <- M.getManaged
    ma <- M.getAlive
    mt <- M.getTime
  } yield WorldView(db, da, mm, ma, Map.empty, mt)

Recall from Chapter 1 that flatMap (i.e. when we use the <- generator) allows us to operate on a value that is computed at runtime. When we return an F[_] we are returning another program to be interpreted at runtime, that we can then flatMap. This is how we safely chain together sequential side-effecting code, whilst being able to provide a pure implementation for tests. FP could be described as Extreme Mocking.

3.3.2 update

update should call initial to refresh our world view, preserving known pending actions.

If a node has changed state, we remove it from pending and if a pending action is taking longer than 10 minutes to do anything, we assume that it failed and forget that we asked to do it.

  def update(old: WorldView): F[WorldView] = for {
    snap <- initial
    changed = symdiff(old.alive.keySet, snap.alive.keySet)
    pending = (old.pending -- changed).filterNot {
      case (_, started) => (snap.time - started) >= 10.minutes
    }
    update = snap.copy(pending = pending)
  } yield update
  
  private def symdiff[T](a: Set[T], b: Set[T]): Set[T] =
    (a union b) -- (a intersect b)

Concrete functions like .symdiff don’t need test interpreters, they have explicit inputs and outputs, so we could move all pure code into standalone methods on a stateless object, testable in isolation. We’re happy testing only the public methods, preferring that our business logic is easy to read.

3.3.3 act

The act method is slightly more complex, so we will split it into two parts for clarity: detection of when an action needs to be taken, followed by taking action. This simplification means that we can only perform one action per invocation, but that is reasonable because we can control the invocations and may choose to re-run act until no further action is taken.

We write the scenario detectors as extractors for WorldView, which is nothing more than an expressive way of writing if / else conditions.

We need to add agents to the farm if there is a backlog of work, we have no agents, we have no nodes alive, and there are no pending actions. We return a candidate node that we would like to start:

  private object NeedsAgent {
    def unapply(world: WorldView): Option[MachineNode] = world match {
      case WorldView(backlog, 0, managed, alive, pending, _)
           if backlog > 0 && alive.isEmpty && pending.isEmpty
             => Option(managed.head)
      case _ => None
    }
  }

If there is no backlog, we should stop all nodes that have become stale (they are not doing any work). However, since Google charge per hour we only shut down machines in their 58th minute to get the most out of our money. We return the non-empty list of nodes to stop.

As a financial safety net, all nodes should have a maximum lifetime of 5 hours.

  private object Stale {
    def unapply(world: WorldView): Option[NonEmptyList[MachineNode]] = world match {
      case WorldView(backlog, _, _, alive, pending, time) if alive.nonEmpty =>
        (alive -- pending.keys).collect {
          case (n, started) if backlog == 0 && (time - started).toMinutes % 60 >= 58 => n
          case (n, started) if (time - started) >= 5.hours => n
        }.toList.toNel
  
      case _ => None
    }
  }

Now that we have detected the scenarios that can occur, we can write the act method. When we schedule a node to be started or stopped, we add it to pending noting the time that we scheduled the action.

  def act(world: WorldView): F[WorldView] = world match {
    case NeedsAgent(node) =>
      for {
        _ <- M.start(node)
        update = world.copy(pending = Map(node -> world.time))
      } yield update
  
    case Stale(nodes) =>
      nodes.foldLeftM(world) { (world, n) =>
        for {
          _ <- M.stop(n)
          update = world.copy(pending = world.pending + (n -> world.time))
        } yield update
      }
  
    case _ => world.pure[F]
  }

Because NeedsAgent and Stale do not cover all possible situations, we need a catch-all case _ to do nothing. Recall from Chapter 2 that .pure creates the for’s (monadic) context from a value.

foldLeftM is like foldLeft, but each iteration of the fold may return a monadic value. In our case, each iteration of the fold returns F[WorldView]. The M is for Monadic. We will find more of these lifted methods that behave as one would expect, taking monadic values in place of values.

3.4 Unit Tests

The FP approach to writing applications is a designer’s dream: delegate writing the implementations of algebras to team members while focusing on making business logic meet the requirements.

Our application is highly dependent on timing and third party webservices. If this was a traditional OOP application, we’d create mocks for all the method calls, or test actors for the outgoing mailboxes. FP mocking is equivalent to providing an alternative implementation of dependency algebras. The algebras already isolate the parts of the system that need to be mocked, i.e. interpreted differently in the unit tests.

We will start with some test data

  object Data {
    val node1   = MachineNode("1243d1af-828f-4ba3-9fc0-a19d86852b5a")
    val node2   = MachineNode("550c4943-229e-47b0-b6be-3d686c5f013f")
    val managed = NonEmptyList(node1, node2)
  
    val time1: Epoch = epoch"2017-03-03T18:07:00Z"
    val time2: Epoch = epoch"2017-03-03T18:59:00Z" // +52 mins
    val time3: Epoch = epoch"2017-03-03T19:06:00Z" // +59 mins
    val time4: Epoch = epoch"2017-03-03T23:07:00Z" // +5 hours
  
    val needsAgents = WorldView(5, 0, managed, Map.empty, Map.empty, time1)
  }
  import Data._

The epoch string interpolator is written with Jon Pretty’s contextual library, giving us compiletime safety around string constructors of a type:

  import java.time.Instant
  object EpochInterpolator extends Verifier[Epoch] {
    def check(s: String): Either[(Int, String), Epoch] =
      try Right(Epoch(Instant.parse(s).toEpochMilli))
      catch { case _ => Left((0, "not in ISO-8601 format")) }
  }
  implicit class EpochMillisStringContext(sc: StringContext) {
    val epoch = Prefix(EpochInterpolator, sc)
  }

We implement algebras by extending Drone and Machines with a specific monadic context, Id being the simplest.

Our “mock” implementations simply play back a fixed WorldView. We’ve isolated the state of our system, so we can use var to store the state:

  class Mutable(state: WorldView) {
    var started, stopped: Int = 0
  
    private val D: Drone[Id] = new Drone[Id] {
      def getBacklog: Int = state.backlog
      def getAgents: Int = state.agents
    }
  
    private val M: Machines[Id] = new Machines[Id] {
      def getAlive: Map[MachineNode, Epoch] = state.alive
      def getManaged: NonEmptyList[MachineNode] = state.managed
      def getTime: Epoch = state.time
      def start(node: MachineNode): MachineNode = { started += 1 ; node }
      def stop(node: MachineNode): MachineNode = { stopped += 1 ; node }
    }
  
    val program = new DynAgentsModule[Id](D, M)
  }

When we write a unit test (here using FlatSpec from Scalatest), we create an instance of Mutable and then import all of its members.

Our implicit drone and machines both use the Id execution context and therefore interpreting this program with them returns an Id[WorldView] that we can assert on.

In this trivial case we just check that the initial method returns the same value that we use in the static implementations:

  "Business Logic" should "generate an initial world view" in {
    val mutable = new Mutable(needsAgents)
    import mutable._
  
    program.initial shouldBe needsAgents
  }

We can create more advanced tests of the update and act methods, helping us flush out bugs and refine the requirements:

  it should "remove changed nodes from pending" in {
    val world = WorldView(0, 0, managed, Map(node1 -> time3), Map.empty, time3)
    val mutable = new Mutable(world)
    import mutable._
  
    val old = world.copy(alive = Map.empty,
                         pending = Map(node1 -> time2),
                         time = time2)
    program.update(old) shouldBe world
  }
  
  it should "request agents when needed" in {
    val mutable = new Mutable(needsAgents)
    import mutable._
  
    val expected = needsAgents.copy(
      pending = Map(node1 -> time1)
    )
  
    program.act(needsAgents) shouldBe expected
  
    mutable.stopped shouldBe 0
    mutable.started shouldBe 1
  }

It would be boring to go through the full test suite. The following tests are easy to implement using the same approach:

not request agents when pending
don’t shut down agents if nodes are too young
shut down agents when there is no backlog and nodes will shortly incur new costs
not shut down agents if there are pending actions
shut down agents when there is no backlog if they are too old
shut down agents, even if they are potentially doing work, if they are too old
ignore unresponsive pending actions during update

All of these tests are synchronous and isolated to the test runner’s thread (which could be running tests in parallel). If we’d designed our test suite in Akka, our tests would be subject to arbitrary timeouts and failures would be hidden in logfiles.

The productivity boost of simple tests for business logic cannot be overstated. Consider that 90% of an application developer’s time interacting with the customer is in refining, updating and fixing these business rules. Everything else is implementation detail.

3.5 Parallel

The application that we have designed runs each of its algebraic methods sequentially. But there are some obvious places where work can be performed in parallel.

3.5.1 initial

In our definition of initial we could ask for all the information we need at the same time instead of one query at a time.

As opposed to flatMap for sequential operations, Scalaz uses Apply syntax for parallel operations:

  ^^^^(D.getBacklog, D.getAgents, M.getManaged, M.getAlive, M.getTime)

which can also use infix notation:

  (D.getBacklog |@| D.getAgents |@| M.getManaged |@| M.getAlive |@| M.getTime)

If each of the parallel operations returns a value in the same monadic context, we can apply a function to the results when they all return. Rewriting initial to take advantage of this:

  def initial: F[WorldView] =
    ^^^^(D.getBacklog, D.getAgents, M.getManaged, M.getAlive, M.getTime) {
      case (db, da, mm, ma, mt) => WorldView(db, da, mm, ma, Map.empty, mt)
    }

3.5.2 act

In the current logic for act, we are stopping each node sequentially, waiting for the result, and then proceeding. But we could stop all the nodes in parallel and then update our view of the world.

A disadvantage of doing it this way is that any failures will cause us to short-circuit before updating the pending field. But that is a reasonable tradeoff since our update will gracefully handle the case where a node is shut down unexpectedly.

We need a method that operates on NonEmptyList that allows us to map each element into an F[MachineNode], returning an F[NonEmptyList[MachineNode]]. The method is called traverse, and when we flatMap over it we get a NonEmptyList[MachineNode] that we can deal with in a simple way:

  for {
    stopped <- nodes.traverse(M.stop)
    updates = stopped.map(_ -> world.time).toList.toMap
    update = world.copy(pending = world.pending ++ updates)
  } yield update

Arguably, this is easier to understand than the sequential version.

3.6 Summary

algebras define the interface between systems.
modules are implementations of an algebra in terms of other algebras.
interpreters are concrete implementations of an algebra for a fixed F[_].
Test interpreters can replace the side-effecting parts of the system, giving a high amount of test coverage.

4. Data and Functionality

From OOP we are used to thinking about data and functionality together: class hierarchies carry methods, and traits can demand that data fields exist. Runtime polymorphism of an object is in terms of “is a” relationships, requiring classes to inherit from common interfaces. This can get messy as a codebase grows. Simple data types become obscured by hundreds of lines of methods, trait mixins suffer from initialisation order errors, and testing / mocking of highly coupled components becomes a chore.

FP takes a different approach, defining data and functionality separately. In this chapter, we will cover the basics of data types and the advantages of constraining ourselves to a subset of the Scala language. We will also discover typeclasses as a way to achieve compiletime polymorphism: thinking about functionality of a data structure in terms of “has a” rather than “is a” relationships.

4.1 Data

The fundamental building blocks of data types are

final case class also known as products
sealed abstract class also known as coproducts
case object and Int, Double, String (etc) values

with no methods or fields other than the constructor parameters. We prefer abstract class to trait in order to get better binary compatibility and to discourage trait mixing.

The collective name for products, coproducts and values is Algebraic Data Type (ADT).

We compose data types from the AND and XOR (exclusive OR) Boolean algebra: a product contains every type that it is composed of, but a coproduct can be only one. For example

product: ABC = a AND b AND c
coproduct: XYZ = x XOR y XOR z

written in Scala

  // values
  case object A
  type B = String
  type C = Int
  
  // product
  final case class ABC(a: A.type, b: B, c: C)
  
  // coproduct
  sealed abstract class XYZ
  case object X extends XYZ
  case object Y extends XYZ
  final case class Z(b: B) extends XYZ

4.1.1 Recursive ADTs

When an ADT refers to itself, we call it a Recursive Algebraic Data Type.

scalaz.IList, a safe alternative to the stdlib List, is recursive because ICons contains a reference to IList.:

  sealed abstract class IList[A]
  final case class INil[A]() extends IList[A]
  final case class ICons[A](head: A, tail: IList[A]) extends IList[A]

4.1.2 Functions on ADTs

ADTs can contain pure functions

  final case class UserConfiguration(accepts: Int => Boolean)

But ADTs that contain functions come with some caveats as they don’t translate perfectly onto the JVM. For example, legacy Serializable, hashCode, equals and toString do not behave as one might reasonably expect.

Unfortunately, Serializable is used by popular frameworks, despite far superior alternatives. A common pitfall is forgetting that Serializable may attempt to serialise the entire closure of a function, which can crash production servers. A similar caveat applies to legacy Java classes such as Throwable, which can carry references to arbitrary objects.

We will explore alternatives to the legacy methods when we discuss the Scalaz library in the next chapter, at the cost of losing interoperability with some legacy Java and Scala code.

4.1.3 Exhaustivity

It is important that we use sealed abstract class, not just abstract class, when defining a data type. Sealing a class means that all subtypes must be defined in the same file, allowing the compiler to know about them in pattern match exhaustivity checks and in macros that eliminate boilerplate. e.g.

  scala> sealed abstract class Foo
         final case class Bar(flag: Boolean) extends Foo
         final case object Baz extends Foo
  
  scala> def thing(foo: Foo) = foo match {
           case Bar(_) => true
         }
  <console>:14: error: match may not be exhaustive.
  It would fail on the following input: Baz
         def thing(foo: Foo) = foo match {
                               ^

This shows the developer what they have broken when they add a new product to the codebase. We’re using -Xfatal-warnings, otherwise this is just a warning.

However, the compiler will not perform exhaustivity checking if the class is not sealed or if there are guards, e.g.

  scala> def thing(foo: Foo) = foo match {
           case Bar(flag) if flag => true
         }
  
  scala> thing(Baz)
  scala.MatchError: Baz (of class Baz$)
    at .thing(<console>:15)

To remain safe, don’t use guards on sealed types.

The -Xstrict-patmat-analysis flag has been proposed as a language improvement to perform additional pattern matcher checks.

4.1.4 Alternative Products and Coproducts

Another form of product is a tuple, which is like an unlabelled final case class.

(A.type, B, C) is equivalent to ABC in the above example but it is best to use final case class when part of an ADT because the lack of names is awkward to deal with, and case class has much better performance for primitive values.

Another form of coproduct is when we nest Either types. e.g.

  Either[X.type, Either[Y.type, Z]]

equivalent to the XYZ sealed abstract class. A cleaner syntax to define nested Either types is to create an alias type ending with a colon, allowing infix notation with association from the right:

  type |:[L,R] = Either[L, R]
  
  X.type |: Y.type |: Z

This is useful to create anonymous coproducts when we cannot put all the implementations into the same source file.

  type Accepted = String |: Long |: Boolean

Yet another alternative coproduct is to create a custom sealed abstract class with final case class definitions that simply wrap the desired type:

  sealed abstract class Accepted
  final case class AcceptedString(value: String) extends Accepted
  final case class AcceptedLong(value: Long) extends Accepted
  final case class AcceptedBoolean(value: Boolean) extends Accepted

Pattern matching on these forms of coproduct can be tedious, which is why Union Types are being explored in the Dotty next-generation Scala compiler. Macros such as totalitarian and iotaz exist as alternative ways of encoding anonymous coproducts.

4.1.5 Convey Information

Besides being a container for necessary business information, data types can be used to encode constraints. For example,

  final case class NonEmptyList[A](head: A, tail: IList[A])

can never be empty. This makes scalaz.NonEmptyList a useful data type despite containing the same information as IList.

Product types often contain types that are far more general than is allowed. In traditional OOP this would be handled with input validation through assertions:

  final case class Person(name: String, age: Int) {
    require(name.nonEmpty && age > 0) // breaks Totality, don't do this!
  }

Instead, we can use the Either data type to provide Right[Person] for valid instances and protect invalid instances from propagating. Note that the constructor is private:

  final case class Person private(name: String, age: Int)
  object Person {
    def apply(name: String, age: Int): Either[String, Person] = {
      if (name.nonEmpty && age > 0) Right(new Person(name, age))
      else Left(s"bad input: $name, $age")
    }
  }
  
  def welcome(person: Person): String =
    s"${person.name} you look wonderful at ${person.age}!"
  
  for {
    person <- Person("", -1)
  } yield welcome(person)

4.1.5.1 Refined Data Types

A clean way to restrict the values of a general type is with the refined library, providing a suite of restrictions to the contents of data. To install refined, add the following to build.sbt

  libraryDependencies += "eu.timepit" %% "refined-scalaz" % "0.9.2"

and the following imports

  import eu.timepit.refined
  import refined.api.Refined

Refined allows us to define Person using adhoc refined types to capture requirements exactly, written A Refined B.

  import refined.numeric.Positive
  import refined.collection.NonEmpty
  
  final case class Person(
    name: String Refined NonEmpty,
    age: Int Refined Positive
  )

The underlying value can be obtained with .value. We can construct a value at runtime using .refineV, returning an Either

  scala> import refined.refineV
  scala> refineV[NonEmpty]("")
  Left(Predicate isEmpty() did not fail.)
  
  scala> refineV[NonEmpty]("Sam")
  Right(Sam)

If we add the following import

  import refined.auto._

we can construct valid values at compiletime and get an error if the provided value does not meet the requirements

  scala> val sam: String Refined NonEmpty = "Sam"
  Sam
  
  scala> val empty: String Refined NonEmpty = ""
  <console>:21: error: Predicate isEmpty() did not fail.

More complex requirements can be captured, for example we can use the built-in rule MaxSize with the following imports

  import refined.W
  import refined.boolean.And
  import refined.collection.MaxSize

capturing the requirement that the String must be both non-empty and have a maximum size of 10 characters:

  type Name = NonEmpty And MaxSize[W.`10`.T]
  
  final case class Person(
    name: String Refined Name,
    age: Int Refined Positive
  )

It is easy to define custom requirements that are not covered by the refined library. For example in drone-dynamaic-agents we will need a way of ensuring that a String contains application/x-www-form-urlencoded content. We can create a Refined rule using the Java regular expression library:

  sealed abstract class UrlEncoded
  object UrlEncoded {
    private[this] val valid: Pattern =
      Pattern.compile("\\A(\\p{Alnum}++|[-.*_+=&]++|%\\p{XDigit}{2})*\\z")
  
    implicit def urlValidate: Validate.Plain[String, UrlEncoded] =
      Validate.fromPredicate(
        s => valid.matcher(s).find(),
        identity,
        new UrlEncoded {}
      )
  }

By not providing any functionality, ADTs can have a minimal set of dependencies. This makes them easy to publish and share with other developers. By using a simple data modelling language, it makes it possible to interact with cross-discipline teams, such as DBAs, UI developers and business analysts, using the actual code instead of a hand written document as the source of truth.

Furthermore, tooling can be more easily written to produce or consume schemas from other programming languages and wire protocols.

4.1.7 Counting Complexity

The complexity of a data type is the count of values that can exist. A good data type has the least amount of complexity it needs to hold the information it conveys, and no more.

Values have a built-in complexity:

Unit has one value (why it is called “unit”)
Boolean has two values
Int has 4,294,967,295 values
String has effectively infinite values

To find the complexity of a product, we multiply the complexity of each part.

(Boolean, Boolean) has 4 values (2*2)
(Boolean, Boolean, Boolean) has 8 values (2*2*2)

To find the complexity of a coproduct, we add the complexity of each part.

(Boolean |: Boolean) has 4 values (2+2)
(Boolean |: Boolean |: Boolean) has 6 values (2+2+2)

To find the complexity of a ADT with a type parameter, multiply each part by the complexity of the type parameter:

Option[Boolean] has 3 values, Some[Boolean] and None (2+1)

In FP, functions are total and must return an value for every input, no Exception. Minimising the complexity of inputs and outputs is the best way to achieve totality. As a rule of thumb, it is a sign of a badly designed function when the complexity of a function’s return value is larger than the product of its inputs: it is a source of entropy.

The complexity of a total function is the number of possible functions that can satisfy the type signature: the output to the power of the input.

Unit => Boolean has complexity 2
Boolean => Boolean has complexity 4
Option[Boolean] => Option[Boolean] has complexity 27
Boolean => Int is a mere quintillion going on a sextillion.
Int => Boolean is so big that if all implementations were assigned a unique number, each would require 4 gigabytes to represent.

In reality, Int => Boolean will be something simple like isOdd, isEven or a sparse BitSet. This function, when used in an ADT, could be better replaced with a coproduct labelling the limited set of functions that are relevant.

When our complexity is “infinity in, infinity out” we should introduce restrictive data types and validation closer to the point of input with Refined from the previous section.

The ability to count the complexity of a type signature has one other practical application: we can find simpler type signatures with High School algebra! To go from a type signature to its algebra of complexity, simply replace

Either[A, B] with a + b
(A, B) with a * b
A => B with b ^ a

do some rearranging, and convert back. For example, say we’ve designed a framework based on callbacks and we’ve managed to work ourselves into the situation where we have created this type signature:

  (A => C) => ((B => C) => C)

We can convert and rearrange

  (c ^ (c ^ b)) ^ (c ^ a)
  = c ^ ((c ^ b) * (c ^ a))
  = c ^ (c ^ (a + b))

then convert back to types and get

  (Either[A, B] => C) => C

which is much simpler: we only need to ask the users of our framework to provide a Either[A, B] => C.

The same line of reasoning can be used to prove that

  A => B => C

is equivalent to

  (A, B) => C

also known as Currying.

4.1.8 Prefer Coproduct over Product

An archetypal modelling problem that comes up a lot is when there are mutually exclusive configuration parameters a, b and c. The product (a: Boolean, b: Boolean, c: Boolean) has complexity 8 whereas the coproduct

  sealed abstract class Config
  object Config {
    case object A extends Config
    case object B extends Config
    case object C extends Config
  }

has a complexity of 3. It is better to model these configuration parameters as a coproduct rather than allowing 5 invalid states to exist.

The complexity of a data type also has implications on testing. It is practically impossible to test every possible input to a function, but it is easy to test a sample of values with the Scalacheck property testing framework. If a random sample of a data type has a low probability of being valid, it is a sign that the data is modelled incorrectly.

4.1.9 Optimisations

A big advantage of using a simplified subset of the Scala language to represent data types is that tooling can optimise the JVM bytecode representation.

For example, we could pack Boolean and Option fields into an Array[Byte], cache values, memoise hashCode, optimise equals, use @switch statements when pattern matching, and much more.

These optimisations are not applicable to OOP class hierarchies that may be managing state, throwing exceptions, or providing adhoc method implementations.

4.2 Functionality

Pure functions are typically defined as methods on an object.

  package object math {
    def sin(x: Double): Double = java.lang.Math.sin(x)
    ...
  }
  
  math.sin(1.0)

However, it can be clunky to use object methods since it reads inside-out, not left to right. In addition, a function on an object steals the namespace. If we were to define sin(t: T) somewhere else we get ambiguous reference errors. This is the same problem as Java’s static methods vs class methods.

With the implicit class language feature (also known as extension methodology or syntax), and a little boilerplate, we can get the familiar style:

  scala> implicit class DoubleOps(x: Double) {
           def sin: Double = math.sin(x)
         }
  
  scala> (1.0).sin
  res: Double = 0.8414709848078965

Often it is best to just skip the object definition and go straight for an implicit class, keeping boilerplate to a minimum:

  implicit class DoubleOps(x: Double) {
    def sin: Double = java.lang.Math.sin(x)
  }

implicit class is syntax sugar for an implicit conversion:

  implicit def DoubleOps(x: Double): DoubleOps = new DoubleOps(x)
  class DoubleOps(x: Double) {
    def sin: Double = java.lang.Math.sin(x)
  }

Which unfortunately has a runtime cost: each time the extension method is called, an intermediate DoubleOps will be constructed and then thrown away. This can contribute to GC pressure in hotspots.

There is a slightly more verbose form of implicit class that avoids the allocation and is therefore preferred:

  implicit final class DoubleOps(private val x: Double) extends AnyVal {
    def sin: Double = java.lang.Math.sin(x)
  }

4.2.1 Polymorphic Functions

The more common kind of function is a polymorphic function, which lives in a typeclass. A typeclass is a trait that:

holds no state
has a type parameter
has at least one abstract method (primitive combinators)
may contain generalised methods (derived combinators)
may extend other typeclasses

There can only be one implementation of a typeclass for any given type parameter, a property known as typeclass coherence. Typeclasses look superficially similar to algebraic interfaces from the previous chapter, but algebras do not have to be coherent.

Typeclasses are used in the Scala stdlib. We will explore a simplified version of scala.math.Numeric to demonstrate the principle:

  trait Ordering[T] {
    def compare(x: T, y: T): Int
  
    def lt(x: T, y: T): Boolean = compare(x, y) < 0
    def gt(x: T, y: T): Boolean = compare(x, y) > 0
  }
  
  trait Numeric[T] extends Ordering[T] {
    def plus(x: T, y: T): T
    def times(x: T, y: T): T
    def negate(x: T): T
    def zero: T
  
    def abs(x: T): T = if (lt(x, zero)) negate(x) else x
  }

We can see all the key features of a typeclass in action:

there is no state
Ordering and Numeric have type parameter T
Ordering has abstract compare and Numeric has abstract plus, times, negate and zero
Ordering defines generalised lt and gt based on compare, Numeric defines abs in terms of lt, negate and zero.
Numeric extends Ordering

We can now write functions for types that “have a” Numeric typeclass:

  def signOfTheTimes[T](t: T)(implicit N: Numeric[T]): T = {
    import N._
    times(negate(abs(t)), t)
  }

We are no longer dependent on the OOP hierarchy of our input types, i.e. we don’t demand that our input “is a” Numeric, which is vitally important if we want to support a third party class that we cannot redefine.

Another advantage of typeclasses is that the association of functionality to data is at compiletime, as opposed to OOP runtime dynamic dispatch.

For example, whereas the List class can only have one implementation of a method, a typeclass method allows us to have a different implementation depending on the List contents and therefore offload work to compiletime instead of leaving it to runtime.

4.2.2 Syntax

The syntax for writing signOfTheTimes is clunky, there are some things we can do to clean it up.

Downstream users will prefer to see our method use context bounds, since the signature reads cleanly as “takes a T that has a Numeric”

  def signOfTheTimes[T: Numeric](t: T): T = ...

but now we have to use implicitly[Numeric[T]] everywhere. By defining boilerplate on the companion of the typeclass

  object Numeric {
    def apply[T](implicit numeric: Numeric[T]): Numeric[T] = numeric
  }

we can obtain the implicit with less noise

  def signOfTheTimes[T: Numeric](t: T): T = {
    val N = Numeric[T]
    import N._
    times(negate(abs(t)), t)
  }

But it is still worse for us as the implementors. We have the syntactic problem of inside-out static methods vs class methods. We deal with this by introducing ops on the typeclass companion:

  object Numeric {
    def apply[T](implicit numeric: Numeric[T]): Numeric[T] = numeric
  
    object ops {
      implicit class NumericOps[T](t: T)(implicit N: Numeric[T]) {
        def +(o: T): T = N.plus(t, o)
        def *(o: T): T = N.times(t, o)
        def unary_-: T = N.negate(t)
        def abs: T = N.abs(t)
  
        // duplicated from Ordering.ops
        def <(o: T): T = N.lt(t, o)
        def >(o: T): T = N.gt(t, o)
      }
    }
  }

Note that -x is expanded into x.unary_- by the compiler’s syntax sugar, which is why we define unary_- as an extension method. We can now write the much cleaner:

  import Numeric.ops._
  def signOfTheTimes[T: Numeric](t: T): T = -(t.abs) * t

The good news is that we never need to write this boilerplate because Simulacrum provides a @typeclass macro annotation that automatically generates the apply and ops. It even allows us to define alternative (usually symbolic) names for common methods. In full:

  import simulacrum._
  
  @typeclass trait Ordering[T] {
    def compare(x: T, y: T): Int
    @op("<") def lt(x: T, y: T): Boolean = compare(x, y) < 0
    @op(">") def gt(x: T, y: T): Boolean = compare(x, y) > 0
  }
  
  @typeclass trait Numeric[T] extends Ordering[T] {
    @op("+") def plus(x: T, y: T): T
    @op("*") def times(x: T, y: T): T
    @op("unary_-") def negate(x: T): T
    def zero: T
    def abs(x: T): T = if (lt(x, zero)) negate(x) else x
  }
  
  import Numeric.ops._
  def signOfTheTimes[T: Numeric](t: T): T = -(t.abs) * t

When there is a custom symbolic @op, it can be pronounced like its method name. e.g. < is pronounced “less than”, not “left angle bracket”.

4.2.3 Instances

Instances of Numeric (which are also instances of Ordering) are defined as an implicit val that extends the typeclass, and can provide optimised implementations for the generalised methods:

  implicit val NumericDouble: Numeric[Double] = new Numeric[Double] {
    def plus(x: Double, y: Double): Double = x + y
    def times(x: Double, y: Double): Double = x * y
    def negate(x: Double): Double = -x
    def zero: Double = 0.0
    def compare(x: Double, y: Double): Int = java.lang.Double.compare(x, y)
  
    // optimised
    override def lt(x: Double, y: Double): Boolean = x < y
    override def gt(x: Double, y: Double): Boolean = x > y
    override def abs(x: Double): Double = java.lang.Math.abs(x)
  }

Although we are using +, *, unary_-, < and > here, which are the ops (and could be an infinite loop!), these methods exist already on Double. Class methods are always used in preference to extension methods. Indeed, the Scala compiler performs special handling of primitives and converts these method calls into raw dadd, dmul, dcmpl and dcmpg bytecode instructions, respectively.

We can also implement Numeric for Java’s BigDecimal class (avoid scala.BigDecimal, it is fundamentally broken)

  import java.math.{ BigDecimal => BD }
  
  implicit val NumericBD: Numeric[BD] = new Numeric[BD] {
    def plus(x: BD, y: BD): BD = x.add(y)
    def times(x: BD, y: BD): BD = x.multiply(y)
    def negate(x: BD): BD = x.negate
    def zero: BD = BD.ZERO
    def compare(x: BD, y: BD): Int = x.compareTo(y)
  }

We could create our own data structure for complex numbers:

  final case class Complex[T](r: T, i: T)

And derive a Numeric[Complex[T]] if Numeric[T] exists. Since these instances depend on the type parameter, it is a def, not a val.

  implicit def numericComplex[T: Numeric]: Numeric[Complex[T]] =
    new Numeric[Complex[T]] {
      type CT = Complex[T]
      def plus(x: CT, y: CT): CT = Complex(x.r + y.r, x.i + y.i)
      def times(x: CT, y: CT): CT =
        Complex(x.r * y.r + (-x.i * y.i), x.r * y.i + x.i * y.r)
      def negate(x: CT): CT = Complex(-x.r, -x.i)
      def zero: CT = Complex(Numeric[T].zero, Numeric[T].zero)
      def compare(x: CT, y: CT): Int = {
        val real = (Numeric[T].compare(x.r, y.r))
        if (real != 0) real
        else Numeric[T].compare(x.i, y.i)
      }
    }

The observant reader may notice that abs is not at all what a mathematician would expect. The correct return value for abs should be T, not Complex[T].

scala.math.Numeric tries to do too much and does not generalise beyond real numbers. This is a good lesson that smaller, well defined, typeclasses are often better than a monolithic collection of overly specific features.

4.2.4 Implicit Resolution

We’ve discussed implicits a lot: this section is to clarify what implicits are and how they work.

Implicit parameters are when a method requests that a unique instance of a particular type is in the implicit scope of the caller, with special syntax for typeclass instances. Implicit parameters are a clean way to thread configuration through an application.

In this example, foo requires that typeclass instances of Numeric and Typeable are available for A, as well as an implicit Handler object that takes two type parameters

  def foo[A: Numeric: Typeable](implicit A: Handler[String, A]) = ...

Implicit conversion is when an implicit def exists. One such use of implicit conversions is to enable extension methodology. When the compiler is resolving a call to a method, it first checks if the method exists on the type, then its ancestors (Java-like rules). If it fails to find a match, it will search the implicit scope for conversions to other types, then search for methods on those types.

Another use for implicit conversions is typeclass derivation. In the previous section we wrote an implicit def that derived a Numeric[Complex[T]] if a Numeric[T] is in the implicit scope. It is possible to chain together many implicit def (including recursively) which is the basis of typeful programming, allowing for computations to be performed at compiletime rather than runtime.

The glue that combines implicit parameters (receivers) with implicit conversion (providers) is implicit resolution.

First, the normal variable scope is searched for implicits, in order:

local scope, including scoped imports (e.g. the block or method)
outer scope, including scoped imports (e.g. members in the class)
ancestors (e.g. members in the super class)
the current package object
ancestor package objects (when using nested packages)
the file’s imports

If that fails to find a match, the special scope is searched, which looks for implicit instances inside a type’s companion, its package object, outer objects (if nested), and then repeated for ancestors. This is performed, in order, for the:

given parameter type
expected parameter type
type parameter (if there is one)

If two matching implicits are found in the same phase of implicit resolution, an ambiguous implicit error is raised.

Implicits are often defined on a trait, which is then extended by an object. This is to try and control the priority of an implicit relative to another more specific one, to avoid ambiguous implicits.

The Scala Language Specification is rather vague for corner cases, and the compiler implementation is the de facto standard. There are some rules of thumb that we will use throughout this book, e.g. prefer implicit val over implicit object despite the temptation of less typing. It is a quirk of implicit resolution that implicit object on companion objects are not treated the same as implicit val.

Implicit resolution falls short when there is a hierarchy of typeclasses, like Ordering and Numeric. If we write a function that takes an implicit Ordering, and we call it for a primitive type which has an instance of Numeric defined on the Numeric companion, the compiler will fail to find it.

Implicit resolution is particularly hit-or-miss if type aliases are used where the shape of the implicit parameters are changed. For example an implicit parameter using an alias such as type Values[A] = List[Option[A]] will probably fail to find implicits defined as raw List[Option[A]] because the shape is changed from a thing of things of A to a thing of A.

4.3 Modelling OAuth2

We will finish this chapter with a practical example of data modelling and typeclass derivation, combined with algebra / module design from the previous chapter.

In our drone-dynamic-agents application, we must communicate with Drone and Google Cloud using JSON over REST. Both services use OAuth2 for authentication. There are many ways to interpret OAuth2, but we will focus on the version that works for Google Cloud (the Drone version is even simpler).

4.3.1 Description

Every Google Cloud application needs to have an OAuth 2.0 Client Key set up at

  https://console.developers.google.com/apis/credentials?project={PROJECT_ID}

Obtaining a Client ID and a Client secret.

The application can then obtain a one time code by making the user perform an Authorization Request in their browser (yes, really, in their browser). We need to make this page open in the browser:

  https://accounts.google.com/o/oauth2/v2/auth?\
    redirect_uri={CALLBACK_URI}&\
    prompt=consent&\
    response_type=code&\
    scope={SCOPE}&\
    access_type=offline&\
    client_id={CLIENT_ID}

The code is delivered to the {CALLBACK_URI} in a GET request. To capture it in our application, we need to have a web server listening on localhost.

Once we have the code, we can perform an Access Token Request:

  POST /oauth2/v4/token HTTP/1.1
  Host: www.googleapis.com
  Content-length: {CONTENT_LENGTH}
  content-type: application/x-www-form-urlencoded
  user-agent: google-oauth-playground
  code={CODE}&\
    redirect_uri={CALLBACK_URI}&\
    client_id={CLIENT_ID}&\
    client_secret={CLIENT_SECRET}&\
    scope={SCOPE}&\
    grant_type=authorization_code

which gives a JSON response payload

  {
    "access_token": "BEARER_TOKEN",
    "token_type": "Bearer",
    "expires_in": 3600,
    "refresh_token": "REFRESH_TOKEN"
  }

Bearer tokens typically expire after an hour, and can be refreshed by sending an HTTP request with any valid refresh token:

  POST /oauth2/v4/token HTTP/1.1
  Host: www.googleapis.com
  Content-length: {CONTENT_LENGTH}
  content-type: application/x-www-form-urlencoded
  user-agent: google-oauth-playground
  client_secret={CLIENT_SECRET}&
    grant_type=refresh_token&
    refresh_token={REFRESH_TOKEN}&
    client_id={CLIENT_ID}

responding with

  {
    "access_token": "BEARER_TOKEN",
    "token_type": "Bearer",
    "expires_in": 3600
  }

All userland requests to the server should include the header

  Authorization: Bearer BEARER_TOKEN

after substituting the actual BEARER_TOKEN.

Google expires all but the most recent 50 bearer tokens, so the expiry times are just guidance. The refresh tokens persist between sessions and can be expired manually by the user. We can therefore have a one-time setup application to obtain the refresh token and then include the refresh token as configuration for the user’s install of the headless server.

Drone doesn’t implement the /auth endpoint, or the refresh, and simply provides a BEARER_TOKEN through their user interface.

4.3.2 Data

The first step is to model the data needed for OAuth2. We create an ADT with fields having exactly the same name as required by the OAuth2 server. We will use String and Long for brevity, but we could use refined types if they leak into our business models.

  import refined.api.Refined
  import refined.string.Url
  
  final case class AuthRequest(
    redirect_uri: String Refined Url,
    scope: String,
    client_id: String,
    prompt: String = "consent",
    response_type: String = "code",
    access_type: String = "offline"
  )
  final case class AccessRequest(
    code: String,
    redirect_uri: String Refined Url,
    client_id: String,
    client_secret: String,
    scope: String = "",
    grant_type: String = "authorization_code"
  )
  final case class AccessResponse(
    access_token: String,
    token_type: String,
    expires_in: Long,
    refresh_token: String
  )
  final case class RefreshRequest(
    client_secret: String,
    refresh_token: String,
    client_id: String,
    grant_type: String = "refresh_token"
  )
  final case class RefreshResponse(
    access_token: String,
    token_type: String,
    expires_in: Long
  )

4.3.3 Functionality

We need to marshal the data classes we defined in the previous section into JSON, URLs and POST-encoded forms. Since this requires polymorphism, we will need typeclasses.

jsonformat is a simple JSON library that we will study in more detail in a later chapter, as it has been written with principled FP and ease of readability as its primary design objectives. It consists of a JSON AST and encoder / decoder typeclasses:

  package jsonformat
  
  sealed abstract class JsValue
  final case object JsNull                                    extends JsValue
  final case class JsObject(fields: IList[(String, JsValue)]) extends JsValue
  final case class JsArray(elements: IList[JsValue])          extends JsValue
  final case class JsBoolean(value: Boolean)                  extends JsValue
  final case class JsString(value: String)                    extends JsValue
  final case class JsDouble(value: Double)                    extends JsValue
  final case class JsInteger(value: Long)                     extends JsValue
  
  @typeclass trait JsEncoder[A] {
    def toJson(obj: A): JsValue
  }
  
  @typeclass trait JsDecoder[A] {
    def fromJson(json: JsValue): String \/ A
  }

We need instances of JsDecoder[AccessResponse] and JsDecoder[RefreshResponse]. We can do this by making use of a helper function:

  implicit class JsValueOps(j: JsValue) {
    def getAs[A: JsDecoder](key: String): String \/ A = ...
  }

We put the instances on the companions of our data types, so that they are always in the implicit scope:

  import jsonformat._, JsDecoder.ops._
  
  object AccessResponse {
    implicit val json: JsDecoder[AccessResponse] = j =>
      for {
        acc <- j.getAs[String]("access_token")
        tpe <- j.getAs[String]("token_type")
        exp <- j.getAs[Long]("expires_in")
        ref <- j.getAs[String]("refresh_token")
      } yield AccessResponse(acc, tpe, exp, ref)
  }
  
  object RefreshResponse {
    implicit val json: JsDecoder[RefreshResponse] = j =>
      for {
        acc <- j.getAs[String]("access_token")
        tpe <- j.getAs[String]("token_type")
        exp <- j.getAs[Long]("expires_in")
      } yield RefreshResponse(acc, tpe, exp)
  }

We can then parse a string into an AccessResponse or a RefreshResponse

  scala> import jsonformat._, JsDecoder.ops._
  scala> val json = JsParser("""
                       {
                         "access_token": "BEARER_TOKEN",
                         "token_type": "Bearer",
                         "expires_in": 3600,
                         "refresh_token": "REFRESH_TOKEN"
                       }
                       """)
  
  scala> json.map(_.as[AccessResponse])
  AccessResponse(BEARER_TOKEN,Bearer,3600,REFRESH_TOKEN)

We need to write our own typeclasses for URL and POST encoding. The following is a reasonable design:

  // URL query key=value pairs, in un-encoded form.
  final case class UrlQuery(params: List[(String, String)])
  
  @typeclass trait UrlQueryWriter[A] {
    def toUrlQuery(a: A): UrlQuery
  }
  
  @typeclass trait UrlEncodedWriter[A] {
    def toUrlEncoded(a: A): String Refined UrlEncoded
  }

We need to provide typeclass instances for basic types:

  import java.net.URLEncoder
  
  object UrlEncodedWriter {
    implicit val encoded: UrlEncodedWriter[String Refined UrlEncoded] = identity
  
    implicit val string: UrlEncodedWriter[String] =
      (s => Refined.unsafeApply(URLEncoder.encode(s, "UTF-8")))
  
    implicit val url: UrlEncodedWriter[String Refined Url] =
      (s => s.value.toUrlEncoded)
  
    implicit val long: UrlEncodedWriter[Long] =
      (s => Refined.unsafeApply(s.toString))
  
    implicit def ilist[K: UrlEncodedWriter, V: UrlEncodedWriter]
      : UrlEncodedWriter[IList[(K, V)]] = { m =>
      val raw = m.map {
        case (k, v) => k.toUrlEncoded.value + "=" + v.toUrlEncoded.value
      }.intercalate("&")
      Refined.unsafeApply(raw) // by deduction
    }
  
  }

We use Refined.unsafeApply when we can logically deduce that the contents of the string are already url encoded, bypassing any further checks.

ilist is an example of simple typeclass derivation, much as we derived Numeric[Complex] from the underlying numeric representation. The .intercalate method is like .mkString but more general.

UrlEncodedWriter is making use of the Single Abstract Method (SAM types) Scala language feature. The full form of the above is

  implicit val string: UrlEncodedWriter[String] =
    new UrlEncodedWriter[String] {
      override def toUrlEncoded(s: String): String = ...
    }

When the Scala compiler expects a class (which has a single abstract method) but receives a lambda, it fills in the boilerplate automatically.

Prior to SAM types, a common pattern was to define a method named instance on the typeclass companion

  def instance[T](f: T => String): UrlEncodedWriter[T] =
    new UrlEncodedWriter[T] {
      override def toUrlEncoded(t: T): String = f(t)
    }

allowing for

  implicit val string: UrlEncodedWriter[String] = instance { s => ... }

This pattern is still used in code that must support older versions of Scala, or for typeclasses instances that need to provide more than one method.

Note that there are a lot of bugs around SAM types, as they do not interact with all the language features. Revert to the non-SAM variant if there are any strange compiler crashes.

In a dedicated chapter on Typeclass Derivation we will calculate instances of UrlQueryWriter automatically, as well as clean up what we have already written, but for now we will write the boilerplate for the types we wish to convert:

  import UrlEncodedWriter.ops._
  object AuthRequest {
    implicit val query: UrlQueryWriter[AuthRequest] = { a =>
      UrlQuery(List(
        ("redirect_uri"  -> a.redirect_uri.value),
        ("scope"         -> a.scope),
        ("client_id"     -> a.client_id),
        ("prompt"        -> a.prompt),
        ("response_type" -> a.response_type),
        ("access_type"   -> a.access_type))
    }
  }
  object AccessRequest {
    implicit val encoded: UrlEncodedWriter[AccessRequest] = { a =>
      IList(
        "code"          -> a.code.toUrlEncoded,
        "redirect_uri"  -> a.redirect_uri.toUrlEncoded,
        "client_id"     -> a.client_id.toUrlEncoded,
        "client_secret" -> a.client_secret.toUrlEncoded,
        "scope"         -> a.scope.toUrlEncoded,
        "grant_type"    -> a.grant_type.toUrlEncoded
      ).toUrlEncoded
    }
  }
  object RefreshRequest {
    implicit val encoded: UrlEncodedWriter[RefreshRequest] = { r =>
      IList(
        "client_secret" -> r.client_secret.toUrlEncoded,
        "refresh_token" -> r.refresh_token.toUrlEncoded,
        "client_id"     -> r.client_id.toUrlEncoded,
        "grant_type"    -> r.grant_type.toUrlEncoded
      ).toUrlEncoded
    }
  }

4.3.4 Module

That concludes the data and functionality modelling required to implement OAuth2. Recall from the previous chapter that we define components that need to interact with the world as algebras, and we define business logic in a module, so it can be thoroughly tested.

We define our dependency algebras, and use context bounds to show that our responses must have a JsDecoder and our POST payload must have a UrlEncodedWriter:

  trait JsonClient[F[_]] {
    def get[A: JsDecoder](
      uri: String Refined Url,
      headers: IList[(String, String)]
    ): F[A]
  
    def post[P: UrlEncodedWriter, A: JsDecoder](
      uri: String Refined Url,
      payload: P,
      headers: IList[(String, String] = IList.empty
    ): F[A]
  }

Note that we only define the happy path in the JsonClient API. We will get around to error handling in a later chapter.

Obtaining a CodeToken from the Google OAuth2 server involves

starting an HTTP server on the local machine, and obtaining its port number.
making the user open a web page in their browser, which allows them to log in with their Google credentials and authorise the application, with a redirect back to the local machine.
capturing the code, informing the user of next steps, and closing the HTTP server.

We can model this with three methods on a UserInteraction algebra.

  final case class CodeToken(token: String, redirect_uri: String Refined Url)
  
  trait UserInteraction[F[_]] {
    def start: F[String Refined Url]
    def open(uri: String Refined Url): F[Unit]
    def stop: F[CodeToken]
  }

It almost sounds easy when put like that.

We also need an algebra to abstract over the local system time

  trait LocalClock[F[_]] {
    def now: F[Epoch]
  }

And introduce data types that we will use in the refresh logic

  final case class ServerConfig(
    auth: String Refined Url,
    access: String Refined Url,
    refresh: String Refined Url,
    scope: String,
    clientId: String,
    clientSecret: String
  )
  final case class RefreshToken(token: String)
  final case class BearerToken(token: String, expires: Epoch)

Now we can write an OAuth2 client module:

  import http.encoding.UrlQueryWriter.ops._
  
  class OAuth2Client[F[_]: Monad](
    config: ServerConfig
  )(
    user: UserInteraction[F],
    client: JsonClient[F],
    clock: LocalClock[F]
  ) {
    def authenticate: F[CodeToken] =
      for {
        callback <- user.start
        params   = AuthRequest(callback, config.scope, config.clientId)
        _        <- user.open(params.toUrlQuery.forUrl(config.auth))
        code     <- user.stop
      } yield code
  
    def access(code: CodeToken): F[(RefreshToken, BearerToken)] =
      for {
        request <- AccessRequest(code.token,
                                 code.redirect_uri,
                                 config.clientId,
                                 config.clientSecret).pure[F]
        msg     <- client.post[AccessRequest, AccessResponse](
                     config.access, request)
        time    <- clock.now
        expires = time + msg.expires_in.seconds
        refresh = RefreshToken(msg.refresh_token)
        bearer  = BearerToken(msg.access_token, expires)
      } yield (refresh, bearer)
  
    def bearer(refresh: RefreshToken): F[BearerToken] =
      for {
        request <- RefreshRequest(config.clientSecret,
                                  refresh.token,
                                  config.clientId).pure[F]
        msg     <- client.post[RefreshRequest, RefreshResponse](
                     config.refresh, request)
        time    <- clock.now
        expires = time + msg.expires_in.seconds
        bearer  = BearerToken(msg.access_token, expires)
      } yield bearer
  }

4.4 Summary

algebraic data types (ADTs) are defined as products (final case class) and coproducts (sealed abstract class).
Refined types enforce constraints on values.
concrete functions can be defined in an implicit class to maintain left-to-right flow.
polymorphic functions are defined in typeclasses. Functionality is provided via “has a” context bounds, rather than “is a” class hierarchies.
typeclass instances are implementations of a typeclass.
@simulacrum.typeclass generates .ops on the companion, providing convenient syntax for typeclass functions.
typeclass derivation is compiletime composition of typeclass instances.

5. Scalaz Typeclasses

In this chapter we will tour most of the typeclasses in scalaz-core. We don’t use everything in drone-dynamic-agents so we will give standalone examples when appropriate.

There has been criticism of the naming in Scalaz, and functional programming in general. Most names follow the conventions introduced in the Haskell programming language, based on Category Theory. Feel free to set up type aliases if verbs based on the primary functionality are easier to remember when learning (e.g. Mappable, Pureable, FlatMappable).

Before we introduce the typeclass hierarchy, we will peek at the four most important methods from a control flow perspective: the methods we will use the most in typical FP applications:

Typeclass	Method	From	Given	To
`Functor`	`map`	`F[A]`	`A => B`	`F[B]`
`Applicative`	`pure`	`A`		`F[A]`
`Monad`	`flatMap`	`F[A]`	`A => F[B]`	`F[B]`
`Traverse`	`sequence`	`F[G[A]]`		`G[F[A]]`

We know that operations which return a F[_] can be run sequentially in a for comprehension by .flatMap, defined on its Monad[F]. The context F[_] can be thought of as a container for an intentional effect with A as the output: flatMap allows us to generate new effects F[B] at runtime based on the results of evaluating previous effects.

Of course, not all type constructors F[_] are effectful, even if they have a Monad[F]. Often they are data structures. By using the least specific abstraction, we can reuse code for List, Either, Future and more.

If we only need to transform the output from an F[_], that is just map, introduced by Functor. In Chapter 3, we ran effects in parallel by creating a product and mapping over them. In Functional Programming, parallelisable computations are considered less powerful than sequential ones.

In between Monad and Functor is Applicative, defining pure that lets us lift a value into an effect, or create a data structure from a single value.

.sequence is useful for rearranging type constructors. If we have an F[G[_]] but need a G[F[_]], e.g. List[Future[Int]] but need a Future[List[Int]], that is .sequence.

5.1 Agenda

This chapter is longer than usual and jam-packed with information: it is perfectly reasonable to attack it over several sittings. Remembering everything would require super-human powers, so treat this chapter as a way of knowing where to look for more information.

Notably absent are typeclasses that extend Monad. They get their own chapter later.

Scalaz uses code generation, not simulacrum. However, for brevity, we present code snippets with @typeclass. Equivalent syntax is available when we import scalaz._, Scalaz._ and is available under the scalaz.syntax package in the scalaz source code.

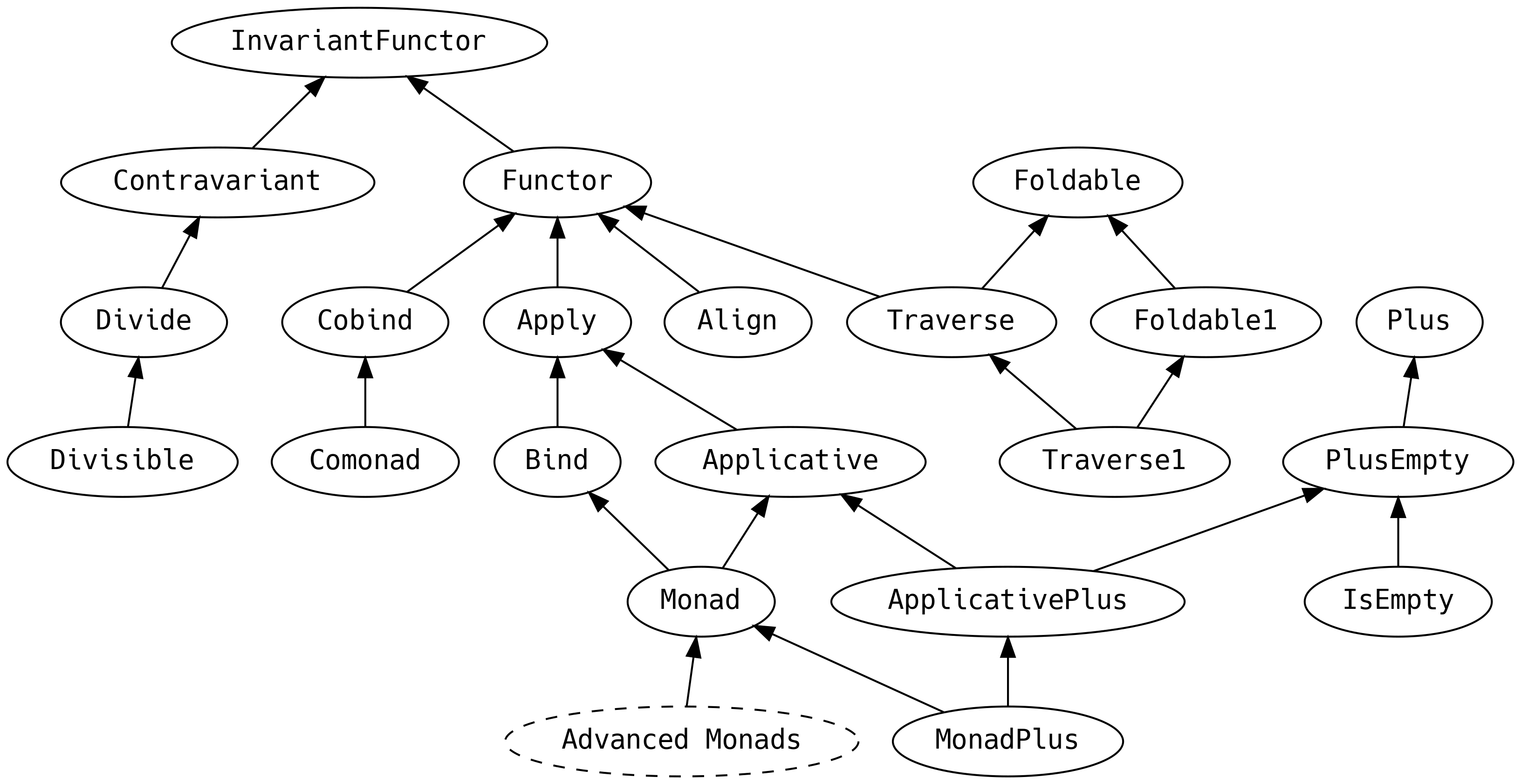
5.2 Appendable Things

  @typeclass trait Semigroup[A] {
    @op("|+|") def append(x: A, y: =>A): A
  
    def multiply1(value: F, n: Int): F = ...
  }
  
  @typeclass trait Monoid[A] extends Semigroup[A] {
    def zero: A
  
    def multiply(value: F, n: Int): F =
      if (n <= 0) zero else multiply1(value, n - 1)
  }
  
  @typeclass trait Band[A] extends Semigroup[A]

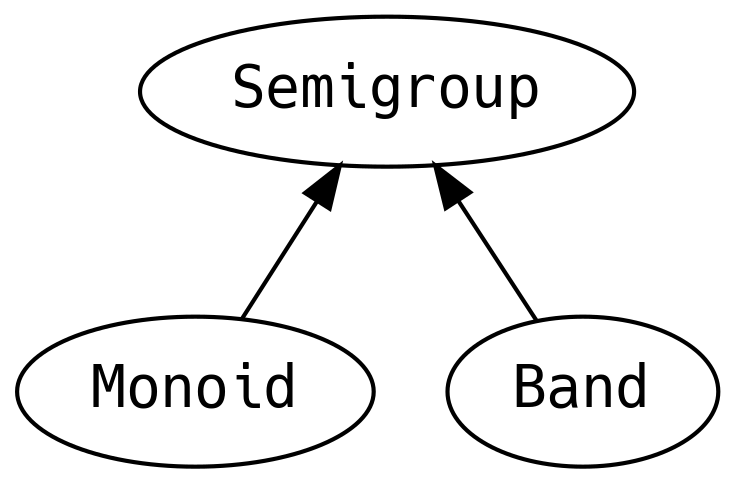
A Semigroup can be defined for a type if two values can be combined. The operation must be associative, meaning that the order of nested operations should not matter, i.e.

  (a |+| b) |+| c == a |+| (b |+| c)
  
  (1 |+| 2) |+| 3 == 1 |+| (2 |+| 3)

A Monoid is a Semigroup with a zero element (also called empty or identity). Combining zero with any other a should give a.

  a |+| zero == a
  
  a |+| 0 == a

This is probably bringing back memories of Numeric from Chapter 4. There are implementations of Monoid for all the primitive numbers, but the concept of appendable things is useful beyond numbers.

  scala> "hello" |+| " " |+| "world!"
  res: String = "hello world!"
  
  scala> List(1, 2) |+| List(3, 4)
  res: List[Int] = List(1, 2, 3, 4)

Band has the law that the append operation of the same two elements is idempotent, i.e. gives the same value. Examples are anything that can only be one value, such as Unit, least upper bounds, or a Set. Band provides no further methods yet users can make use of the guarantees for performance optimisation.

As a realistic example for Monoid, consider a trading system that has a large database of reusable trade templates. Populating the default values for a new trade involves selecting and combining multiple templates, with a “last rule wins” merge policy if two templates provide a value for the same field. The “selecting” work is already done for us by another system, it is our job to combine the templates in order.

We will create a simple template schema to demonstrate the principle, but keep in mind that a realistic system would have a more complicated ADT.

  sealed abstract class Currency
  case object EUR extends Currency
  case object USD extends Currency
  
  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: Option[Currency],
    otc: Option[Boolean]
  )

If we write a method that takes templates: List[TradeTemplate], we only need to call

  val zero = Monoid[TradeTemplate].zero
  templates.foldLeft(zero)(_ |+| _)

and our job is done!

But to get zero or call |+| we must have an instance of Monoid[TradeTemplate]. Although we will generically derive this in a later chapter, for now we will create an instance on the companion:

  object TradeTemplate {
    implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
      (a, b) => TradeTemplate(a.payments |+| b.payments,
                              a.ccy |+| b.ccy,
                              a.otc |+| b.otc),
      TradeTemplate(Nil, None, None)
    )
  }

However, this doesn’t do what we want because Monoid[Option[A]] will append its contents, e.g.

  scala> Option(2) |+| None
  res: Option[Int] = Some(2)
  scala> Option(2) |+| Option(1)
  res: Option[Int] = Some(3)

whereas we want “last rule wins”. We can override the default Monoid[Option[A]] with our own:

  implicit def lastWins[A]: Monoid[Option[A]] = Monoid.instance(
    {
      case (None, None)   => None
      case (only, None)   => only
      case (None, only)   => only
      case (_   , winner) => winner
    },
    None
  )

Now everything compiles, let’s try it out…

  scala> import java.time.{LocalDate => LD}
  scala> val templates = List(
           TradeTemplate(Nil,                     None,      None),
           TradeTemplate(Nil,                     Some(EUR), None),
           TradeTemplate(List(LD.of(2017, 8, 5)), Some(USD), None),
           TradeTemplate(List(LD.of(2017, 9, 5)), None,      Some(true)),
           TradeTemplate(Nil,                     None,      Some(false))
         )
  
  scala> templates.foldLeft(zero)(_ |+| _)
  res: TradeTemplate = TradeTemplate(
                         List(2017-08-05,2017-09-05),
                         Some(USD),
                         Some(false))

All we needed to do was implement one piece of business logic and Monoid took care of everything else for us!

Note that the list of payments are concatenated. This is because the default Monoid[List] uses concatenation of elements and happens to be the desired behaviour. If the business requirement was different, it would be a simple case of providing a custom Monoid[List[LocalDate]]. Recall from Chapter 4 that with compiletime polymorphism we can have a different implementation of append depending on the E in List[E], not just the base runtime class List.

5.3 Objecty Things

In the chapter on Data and Functionality we said that the JVM’s notion of equality breaks down for many things that we can put into an ADT. The problem is that the JVM was designed for Java, and equals is defined on java.lang.Object whether it makes sense or not. There is no way to remove equals and no way to guarantee that it is implemented.

However, in FP we prefer typeclasses for polymorphic functionality and even the concept of equality is captured at compiletime.

  @typeclass trait Equal[F]  {
    @op("===") def equal(a1: F, a2: F): Boolean
    @op("/==") def notEqual(a1: F, a2: F): Boolean = !equal(a1, a2)
  }

Indeed === (triple equals) is more typesafe than == (double equals) because it can only be compiled when the types are the same on both sides of the comparison. This catches a lot of bugs.

equal has the same implementation requirements as Object.equals

commutative f1 === f2 implies f2 === f1
reflexive f === f
transitive f1 === f2 && f2 === f3 implies f1 === f3

By throwing away the universal concept of Object.equals we don’t take equality for granted when we construct an ADT, stopping us at compiletime from expecting equality when there is none.

Continuing the trend of replacing old Java concepts, rather than data being a java.lang.Comparable, they now have an Order according to:

  @typeclass trait Order[F] extends Equal[F] {
    @op("?|?") def order(x: F, y: F): Ordering
  
    override  def equal(x: F, y: F): Boolean = order(x, y) == Ordering.EQ
    @op("<" ) def lt(x: F, y: F): Boolean = ...
    @op("<=") def lte(x: F, y: F): Boolean = ...
    @op(">" ) def gt(x: F, y: F): Boolean = ...
    @op(">=") def gte(x: F, y: F): Boolean = ...
  
    def max(x: F, y: F): F = ...
    def min(x: F, y: F): F = ...
    def sort(x: F, y: F): (F, F) = ...
  }
  
  sealed abstract class Ordering
  object Ordering {
    case object LT extends Ordering
    case object EQ extends Ordering
    case object GT extends Ordering
  }

Order implements .equal in terms of the new primitive .order. When a typeclass implements a parent’s primitive combinator with a derived combinator, an implied law of substitution for the typeclass is added. If an instance of Order were to override .equal for performance reasons, it must behave identically the same as the original.

Things that have an order may also be discrete, allowing us to walk successors and predecessors:

  @typeclass trait Enum[F] extends Order[F] {
    def succ(a: F): F
    def pred(a: F): F
    def min: Option[F]
    def max: Option[F]
  
    @op("-+-") def succn(n: Int, a: F): F = ...
    @op("---") def predn(n: Int, a: F): F = ...
  
    @op("|->" ) def fromToL(from: F, to: F): List[F] = ...
    @op("|-->") def fromStepToL(from: F, step: Int, to: F): List[F] = ...
    @op("|=>" ) def fromTo(from: F, to: F): EphemeralStream[F] = ...
    @op("|==>") def fromStepTo(from: F, step: Int, to: F): EphemeralStream[F] = ...
  }

  scala> 10 |--> (2, 20)
  res: List[Int] = List(10, 12, 14, 16, 18, 20)
  
  scala> 'm' |-> 'u'
  res: List[Char] = List(m, n, o, p, q, r, s, t, u)

We will discuss EphemeralStream in the next chapter, for now we just need to know that it is a potentially infinite data structure that avoids the memory retention problems in the stdlib Stream.

Similarly to Object.equals, the concept of .toString on every class does not make sense in Java. We would like to enforce stringyness at compiletime and this is exactly what Show achieves:

  trait Show[F] {
    def show(f: F): Cord = ...
    def shows(f: F): String = ...
  }

We will explore Cord in more detail in the chapter on data types, we need only know that it is an efficient data structure for storing and manipulating String.

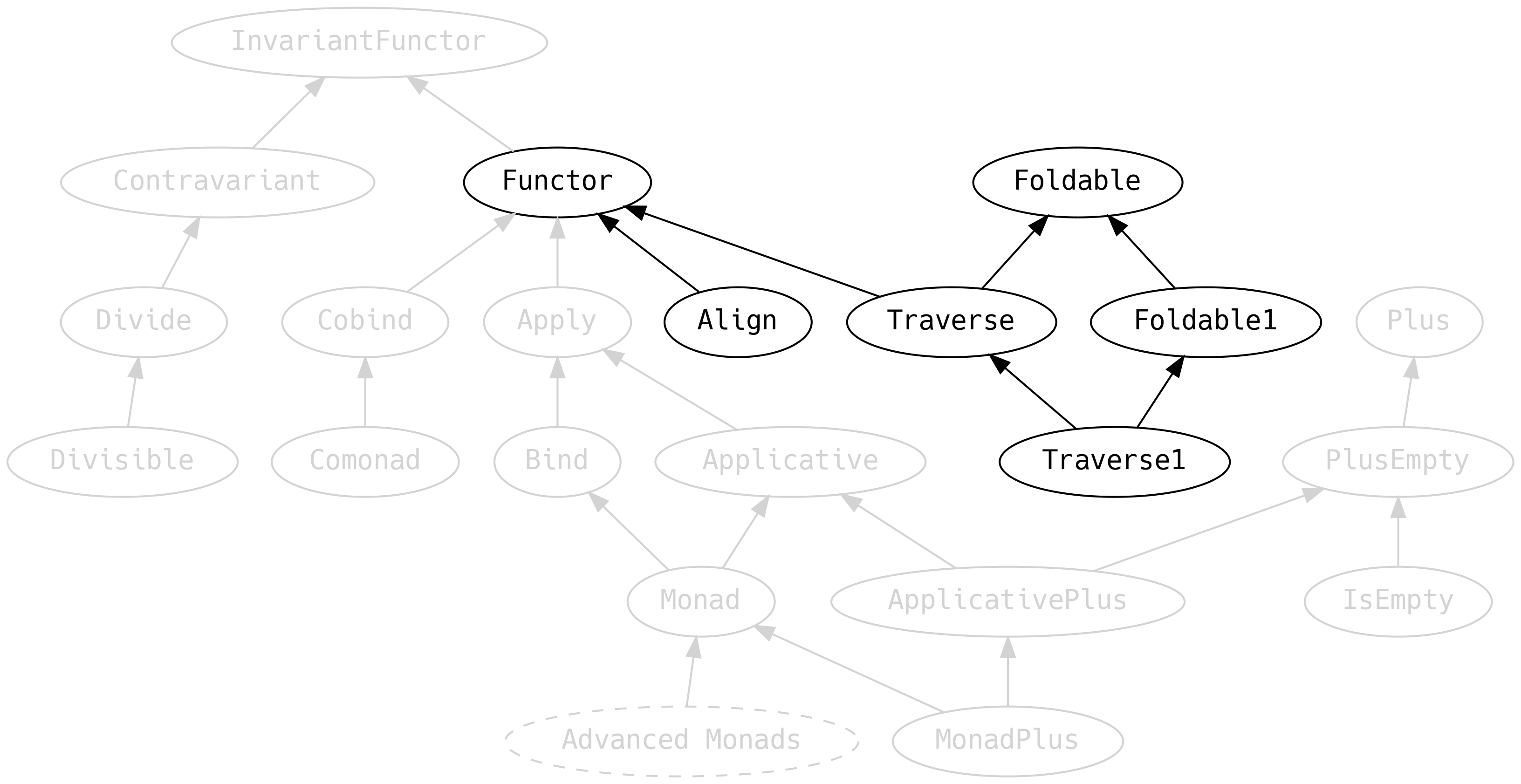
5.4 Mappable Things

We’re focusing on things that can be mapped over, or traversed, in some sense:

5.4.1 Functor

  @typeclass trait Functor[F[_]] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
  
    def void[A](fa: F[A]): F[Unit] = map(fa)(_ => ())
    def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)] = map(fa)(a => (a, f(a)))
  
    def fpair[A](fa: F[A]): F[(A, A)] = map(fa)(a => (a, a))
    def strengthL[A, B](a: A, f: F[B]): F[(A, B)] = map(f)(b => (a, b))
    def strengthR[A, B](f: F[A], b: B): F[(A, B)] = map(f)(a => (a, b))
  
    def lift[A, B](f: A => B): F[A] => F[B] = map(_)(f)
    def mapply[A, B](a: A)(f: F[A => B]): F[B] = map(f)((ff: A => B) => ff(a))
  }

The only abstract method is map, and it must compose, i.e. mapping with f and then again with g is the same as mapping once with the composition of f and g:

  fa.map(f).map(g) == fa.map(f.andThen(g))

The map should also perform a no-op if the provided function is identity (i.e. x => x)

  fa.map(identity) == fa
  
  fa.map(x => x) == fa

Functor defines some convenience methods around map that can be optimised by specific instances. The documentation has been intentionally omitted in the above definitions to encourage guessing what a method does before looking at the implementation. Please spend a moment studying only the type signature of the following before reading further:

  def void[A](fa: F[A]): F[Unit]
  def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)]
  
  def fpair[A](fa: F[A]): F[(A, A)]
  def strengthL[A, B](a: A, f: F[B]): F[(A, B)]
  def strengthR[A, B](f: F[A], b: B): F[(A, B)]
  
  // harder
  def lift[A, B](f: A => B): F[A] => F[B]
  def mapply[A, B](a: A)(f: F[A => B]): F[B]

void takes an instance of the F[A] and always returns an F[Unit], it forgets all the values whilst preserving the structure.
fproduct takes the same input as map but returns F[(A, B)], i.e. it tuples the contents with the result of applying the function. This is useful when we wish to retain the input.
fpair twins all the elements of A into a tuple F[(A, A)]
strengthL pairs the contents of an F[B] with a constant A on the left.
strengthR pairs the contents of an F[A] with a constant B on the right.
lift takes a function A => B and returns a F[A] => F[B]. In other words, it takes a function over the contents of an F[A] and returns a function that operates on the F[A] directly.
mapply is a mind bender. Say we have an F[_] of functions A => B and a value A, then we can get an F[B]. It has a similar signature to pure but requires the caller to provide the F[A => B].

fpair, strengthL and strengthR look pretty useless, but they are useful when we wish to retain some information that would otherwise be lost to scope.

Functor has some special syntax:

  implicit class FunctorOps[F[_]: Functor, A](self: F[A]) {
    def as[B](b: =>B): F[B] = Functor[F].map(self)(_ => b)
    def >|[B](b: =>B): F[B] = as(b)
  }

.as and >| are a way of replacing the output with a constant.

In our example application, as a nasty hack (which we didn’t even admit to until now), we defined start and stop to return their input:

  def start(node: MachineNode): F[MachineNode]
  def stop (node: MachineNode): F[MachineNode]

This allowed us to write terse business logic such as

  for {
    _      <- m.start(node)
    update = world.copy(pending = Map(node -> world.time))
  } yield update

and

  for {
    stopped <- nodes.traverse(m.stop)
    updates = stopped.map(_ -> world.time).toList.toMap
    update  = world.copy(pending = world.pending ++ updates)
  } yield update

But this hack pushes unnecessary complexity into the implementations. It is better if we let our algebras return F[Unit] and use as:

  m.start(node) as world.copy(pending = Map(node -> world.time))

and

  for {
    stopped <- nodes.traverse(a => m.stop(a) as a)
    updates = stopped.map(_ -> world.time).toList.toMap
    update  = world.copy(pending = world.pending ++ updates)
  } yield update

5.4.2 Foldable

Technically, Foldable is for data structures that can be walked to produce a summary value. However, this undersells the fact that it is a one-typeclass army that can provide most of what we would expect to see in a Collections API.

There are so many methods we are going to have to split them out, beginning with the abstract methods:

  @typeclass trait Foldable[F[_]] {
    def foldMap[A, B: Monoid](fa: F[A])(f: A => B): B
    def foldRight[A, B](fa: F[A], z: =>B)(f: (A, =>B) => B): B
    def foldLeft[A, B](fa: F[A], z: B)(f: (B, A) => B): B = ...

An instance of Foldable need only implement foldMap and foldRight to get all of the functionality in this typeclass, although methods are typically optimised for specific data structures.

.foldMap has a marketing buzzword name: MapReduce. Given an F[A], a function from A to B, and a way to combine B (provided by the Monoid, along with a zero B), we can produce a summary value of type B. There is no enforced operation order, allowing for parallel computation.

foldRight does not require its parameters to have a Monoid, meaning that it needs a starting value z and a way to combine each element of the data structure with the summary value. The order for traversing the elements is from right to left and therefore it cannot be parallelised.

foldRight is conceptually the same as the foldRight in the Scala stdlib. However, there is a problem with the stdlib foldRight signature, solved in Scalaz: very large data structures can stack overflow. List.foldRight cheats by implementing foldRight as a reversed foldLeft

  override def foldRight[B](z: B)(op: (A, B) => B): B =
    reverse.foldLeft(z)((right, left) => op(left, right))

but the concept of reversing is not universal and this workaround cannot be used for all data structures. Say we want to find a small number in a Stream, with an early exit:

  scala> def isSmall(i: Int): Boolean = i < 10
  scala> (1 until 100000).toStream.foldRight(false) {
           (el, acc) => isSmall(el) || acc
         }
  java.lang.StackOverflowError
    at scala.collection.Iterator.toStream(Iterator.scala:1403)
    ...

Scalaz solves the problem by taking a byname parameter for the aggregate value

  scala> (1 |=> 100000).foldRight(false)(el => acc => isSmall(el) || acc )
  res: Boolean = true

which means that the acc is not evaluated unless it is needed.

It is worth baring in mind that not all operations are stack safe in foldRight. If we were to require evaluation of all elements, we can also get a StackOverflowError with Scalaz’s EphemeralStream

  scala> (1L |=> 100000L).foldRight(0L)(el => acc => el |+| acc )
  java.lang.StackOverflowError
    at scalaz.Foldable.$anonfun$foldr$1(Foldable.scala:100)
    ...

foldLeft traverses elements from left to right. foldLeft can be implemented in terms of foldMap, but most instances choose to implement it because it is such a basic operation. Since it is usually implemented with tail recursion, there are no byname parameters.

The only law for Foldable is that foldLeft and foldRight should each be consistent with foldMap for monoidal operations. e.g. appending an element to a list for foldLeft and prepending an element to a list for foldRight. However, foldLeft and foldRight do not need to be consistent with each other: in fact they often produce the reverse of each other.

The simplest thing to do with foldMap is to use the identity function, giving fold (the natural sum of the monoidal elements), with left/right variants to allow choosing based on performance criteria:

  def fold[A: Monoid](t: F[A]): A = ...
  def sumr[A: Monoid](fa: F[A]): A = ...
  def suml[A: Monoid](fa: F[A]): A = ...

Recall that when we learnt about Monoid, we wrote this:

  scala> templates.foldLeft(Monoid[TradeTemplate].zero)(_ |+| _)

We now know this is silly and we should have written:

  scala> templates.toIList.fold
  res: TradeTemplate = TradeTemplate(
                         List(2017-08-05,2017-09-05),
                         Some(USD),
                         Some(false))

.fold doesn’t work on stdlib List because it already has a method called fold that does it is own thing in its own special way.

The strangely named intercalate inserts a specific A between each element before performing the fold

  def intercalate[A: Monoid](fa: F[A], a: A): A = ...

which is a generalised version of the stdlib’s mkString:

  scala> List("foo", "bar").intercalate(",")
  res: String = "foo,bar"

The foldLeft provides the means to obtain any element by traversal index, including a bunch of other related methods:

  def index[A](fa: F[A], i: Int): Option[A] = ...
  def indexOr[A](fa: F[A], default: =>A, i: Int): A = ...
  def length[A](fa: F[A]): Int = ...
  def count[A](fa: F[A]): Int = length(fa)
  def empty[A](fa: F[A]): Boolean = ...
  def element[A: Equal](fa: F[A], a: A): Boolean = ...

Scalaz is a pure library of only total functions. Whereas List(0) can throw an exception, Foldable.index returns an Option[A] with the convenient .indexOr returning an A when a default value is provided. .element is similar to the stdlib .contains but uses Equal rather than ill-defined JVM equality.

These methods really sound like a collections API. And, of course, anything with a Foldable can be converted into a List

  def toList[A](fa: F[A]): List[A] = ...

There are also conversions to other stdlib and Scalaz data types such as .toSet, .toVector, .toStream, .to[T <: TraversableLike], .toIList and so on.

There are useful predicate checks

  def filterLength[A](fa: F[A])(f: A => Boolean): Int = ...
  def all[A](fa: F[A])(p: A => Boolean): Boolean = ...
  def any[A](fa: F[A])(p: A => Boolean): Boolean = ...

filterLength is a way of counting how many elements are true for a predicate, all and any return true if all (or any) element meets the predicate, and may exit early.

We can split an F[A] into parts that result in the same B with splitBy

  def splitBy[A, B: Equal](fa: F[A])(f: A => B): IList[(B, Nel[A])] = ...
  def splitByRelation[A](fa: F[A])(r: (A, A) => Boolean): IList[Nel[A]] = ...
  def splitWith[A](fa: F[A])(p: A => Boolean): List[Nel[A]] = ...
  def selectSplit[A](fa: F[A])(p: A => Boolean): List[Nel[A]] = ...
  
  def findLeft[A](fa: F[A])(f: A => Boolean): Option[A] = ...
  def findRight[A](fa: F[A])(f: A => Boolean): Option[A] = ...

for example

  scala> IList("foo", "bar", "bar", "faz", "gaz", "baz").splitBy(_.charAt(0))
  res = [(f, [foo]), (b, [bar, bar]), (f, [faz]), (g, [gaz]), (b, [baz])]

noting that there are two values indexed by 'b'.

splitByRelation avoids the need for an Equal but we must provide the comparison operator.

splitWith splits the elements into groups that alternatively satisfy and don’t satisfy the predicate. selectSplit selects groups of elements that satisfy the predicate, discarding others. This is one of those rare occasions when two methods share the same type signature but have different meanings.

findLeft and findRight are for extracting the first element (from the left, or right, respectively) that matches a predicate.

Making further use of Equal and Order, we have the distinct methods which return groupings.

  def distinct[A: Order](fa: F[A]): IList[A] = ...
  def distinctE[A: Equal](fa: F[A]): IList[A] = ...
  def distinctBy[A, B: Equal](fa: F[A])(f: A => B): IList[A] =

distinct is implemented more efficiently than distinctE because it can make use of ordering and therefore use a quicksort-esque algorithm that is much faster than the stdlib’s naive List.distinct. Data structures (such as sets) can implement distinct in their Foldable without doing any work.

distinctBy allows grouping by the result of applying a function to the elements. For example, grouping names by their first letter.

We can make further use of Order by extracting the minimum or maximum element (or both extrema) including variations using the Of or By pattern to first map to another type or to use a different type to do the order comparison.

  def maximum[A: Order](fa: F[A]): Option[A] = ...
  def maximumOf[A, B: Order](fa: F[A])(f: A => B): Option[B] = ...
  def maximumBy[A, B: Order](fa: F[A])(f: A => B): Option[A] = ...
  
  def minimum[A: Order](fa: F[A]): Option[A] = ...
  def minimumOf[A, B: Order](fa: F[A])(f: A => B): Option[B] = ...
  def minimumBy[A, B: Order](fa: F[A])(f: A => B): Option[A] = ...
  
  def extrema[A: Order](fa: F[A]): Option[(A, A)] = ...
  def extremaOf[A, B: Order](fa: F[A])(f: A => B): Option[(B, B)] = ...
  def extremaBy[A, B: Order](fa: F[A])(f: A => B): Option[(A, A)] =

For example we can ask which String is maximum By length, or what is the maximum length Of the elements.

  scala> List("foo", "fazz").maximumBy(_.length)
  res: Option[String] = Some(fazz)
  
  scala> List("foo", "fazz").maximumOf(_.length)
  res: Option[Int] = Some(4)

This concludes the key features of Foldable. The takeaway is that anything we’d expect to find in a collection library is probably on Foldable and if it isn’t already, it probably should be.

We will conclude with some variations of the methods we’ve already seen. First there are methods that take a Semigroup instead of a Monoid:

  def fold1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  def foldMap1Opt[A, B: Semigroup](fa: F[A])(f: A => B): Option[B] = ...
  def sumr1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  def suml1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  ...

returning Option to account for empty data structures (recall that Semigroup does not have a zero).

The typeclass Foldable1 contains a lot more Semigroup variants of the Monoid methods shown here (all suffixed 1) and makes sense for data structures which are never empty, without requiring a Monoid on the elements.

Importantly, there are variants that take monadic return values. We already used foldLeftM when we first wrote the business logic of our application, now we know that it is from Foldable:

  def foldLeftM[G[_]: Monad, A, B](fa: F[A], z: B)(f: (B, A) => G[B]): G[B] = ...
  def foldRightM[G[_]: Monad, A, B](fa: F[A], z: =>B)(f: (A, =>B) => G[B]): G[B] = ...
  def foldMapM[G[_]: Monad, A, B: Monoid](fa: F[A])(f: A => G[B]): G[B] = ...
  def findMapM[M[_]: Monad, A, B](fa: F[A])(f: A => M[Option[B]]): M[Option[B]] = ...
  def allM[G[_]: Monad, A](fa: F[A])(p: A => G[Boolean]): G[Boolean] = ...
  def anyM[G[_]: Monad, A](fa: F[A])(p: A => G[Boolean]): G[Boolean] = ...
  ...

5.4.3 Traverse

Traverse is what happens when we cross a Functor with a Foldable

  trait Traverse[F[_]] extends Functor[F] with Foldable[F] {
    def traverse[G[_]: Applicative, A, B](fa: F[A])(f: A => G[B]): G[F[B]]
    def sequence[G[_]: Applicative, A](fga: F[G[A]]): G[F[A]] = ...
  
    def reverse[A](fa: F[A]): F[A] = ...
  
    def zipL[A, B](fa: F[A], fb: F[B]): F[(A, Option[B])] = ...
    def zipR[A, B](fa: F[A], fb: F[B]): F[(Option[A], B)] = ...
    def indexed[A](fa: F[A]): F[(Int, A)] = ...
    def zipWithL[A, B, C](fa: F[A], fb: F[B])(f: (A, Option[B]) => C): F[C] = ...
    def zipWithR[A, B, C](fa: F[A], fb: F[B])(f: (Option[A], B) => C): F[C] = ...
  
    def mapAccumL[S, A, B](fa: F[A], z: S)(f: (S, A) => (S, B)): (S, F[B]) = ...
    def mapAccumR[S, A, B](fa: F[A], z: S)(f: (S, A) => (S, B)): (S, F[B]) = ...
  }

At the beginning of the chapter we showed the importance of traverse and sequence for swapping around type constructors to fit a requirement (e.g. List[Future[_]] to Future[List[_]]).

In Foldable we weren’t able to assume that reverse was a universal concept, but now we can reverse a thing.

We can also zip together two things that have a Traverse, getting back None when one side runs out of elements, using zipL or zipR to decide which side to truncate when the lengths don’t match. A special case of zip is to add an index to every entry with indexed.

zipWithL and zipWithR allow combining the two sides of a zip into a new type, and then returning just an F[C].

mapAccumL and mapAccumR are regular map combined with an accumulator. If we find our old Java ways make us want to reach for a var, and refer to it from a map, we should be using mapAccumL.

For example, let’s say we have a list of words and we want to blank out words we’ve already seen. The filtering algorithm is not allowed to process the list of words a second time so it can be scaled to an infinite stream:

  scala> val freedom =
  """We campaign for these freedoms because everyone deserves them.
     With these freedoms, the users (both individually and collectively)
     control the program and what it does for them."""
     .split("\\s+")
     .toList
  
  scala> def clean(s: String): String = s.toLowerCase.replaceAll("[,.()]+", "")
  
  scala> freedom
         .mapAccumL(Set.empty[String]) { (seen, word) =>
           val cleaned = clean(word)
           (seen + cleaned, if (seen(cleaned)) "_" else word)
         }
         ._2
         .intercalate(" ")
  
  res: String =
  """We campaign for these freedoms because everyone deserves them.
     With _ _ the users (both individually and collectively)
     control _ program _ what it does _ _"""

Finally Traverse1, like Foldable1, provides variants of these methods for data structures that cannot be empty, accepting the weaker Semigroup instead of a Monoid, and an Apply instead of an Applicative. Recall that Semigroup does not have to provide an .empty, and Apply does not have to provide a .point.

5.4.4 Align

Align is about merging and padding anything with a Functor. Before looking at Align, meet the \&/ data type (spoken as These, or hurray!).

  sealed abstract class \&/[+A, +B]
  final case class This[A](aa: A) extends (A \&/ Nothing)
  final case class That[B](bb: B) extends (Nothing \&/ B)
  final case class Both[A, B](aa: A, bb: B) extends (A \&/ B)

i.e. it is a data encoding of inclusive logical OR. A or B or both A and B.

  @typeclass trait Align[F[_]] extends Functor[F] {
    def alignWith[A, B, C](f: A \&/ B => C): (F[A], F[B]) => F[C]
    def align[A, B](a: F[A], b: F[B]): F[A \&/ B] = ...
  
    def merge[A: Semigroup](a1: F[A], a2: F[A]): F[A] = ...
  
    def pad[A, B]: (F[A], F[B]) => F[(Option[A], Option[B])] = ...
    def padWith[A, B, C](f: (Option[A], Option[B]) => C): (F[A], F[B]) => F[C] = ...

alignWith takes a function from either an A or a B (or both) to a C and returns a lifted function from a tuple of F[A] and F[B] to an F[C]. align constructs a \&/ out of two F[_].

merge allows us to combine two F[A] when A has a Semigroup. For example, the implementation of Semigroup[Map[K, V]] defers to Semigroup[V], combining two entries results in combining their values, having the consequence that Map[K, List[A]] behaves like a multimap:

  scala> Map("foo" -> List(1)) merge Map("foo" -> List(1), "bar" -> List(2))
  res = Map(foo -> List(1, 1), bar -> List(2))

and a Map[K, Int] simply tally their contents when merging:

  scala> Map("foo" -> 1) merge Map("foo" -> 1, "bar" -> 2)
  res = Map(foo -> 2, bar -> 2)

.pad and .padWith are for partially merging two data structures that might be missing values on one side. For example if we wanted to aggregate independent votes and retain the knowledge of where the votes came from

  scala> Map("foo" -> 1) pad Map("foo" -> 1, "bar" -> 2)
  res = Map(foo -> (Some(1),Some(1)), bar -> (None,Some(2)))
  
  scala> Map("foo" -> 1, "bar" -> 2) pad Map("foo" -> 1)
  res = Map(foo -> (Some(1),Some(1)), bar -> (Some(2),None))

There are convenient variants of align that make use of the structure of \&/

  ...
    def alignSwap[A, B](a: F[A], b: F[B]): F[B \&/ A] = ...
    def alignA[A, B](a: F[A], b: F[B]): F[Option[A]] = ...
    def alignB[A, B](a: F[A], b: F[B]): F[Option[B]] = ...
    def alignThis[A, B](a: F[A], b: F[B]): F[Option[A]] = ...
    def alignThat[A, B](a: F[A], b: F[B]): F[Option[B]] = ...
    def alignBoth[A, B](a: F[A], b: F[B]): F[Option[(A, B)]] = ...
  }

which should make sense from their type signatures. Examples:

  scala> List(1,2,3) alignSwap List(4,5)
  res = List(Both(4,1), Both(5,2), That(3))
  
  scala> List(1,2,3) alignA List(4,5)
  res = List(Some(1), Some(2), Some(3))
  
  scala> List(1,2,3) alignB List(4,5)
  res = List(Some(4), Some(5), None)
  
  scala> List(1,2,3) alignThis List(4,5)
  res = List(None, None, Some(3))
  
  scala> List(1,2,3) alignThat List(4,5)
  res = List(None, None, None)
  
  scala> List(1,2,3) alignBoth List(4,5)
  res = List(Some((1,4)), Some((2,5)), None)

Note that the A and B variants use inclusive OR, whereas the This and That variants are exclusive, returning None if there is a value in both sides, or no value on either side.

5.5 Variance

We must return to Functor for a moment and discuss an ancestor that we previously ignored:

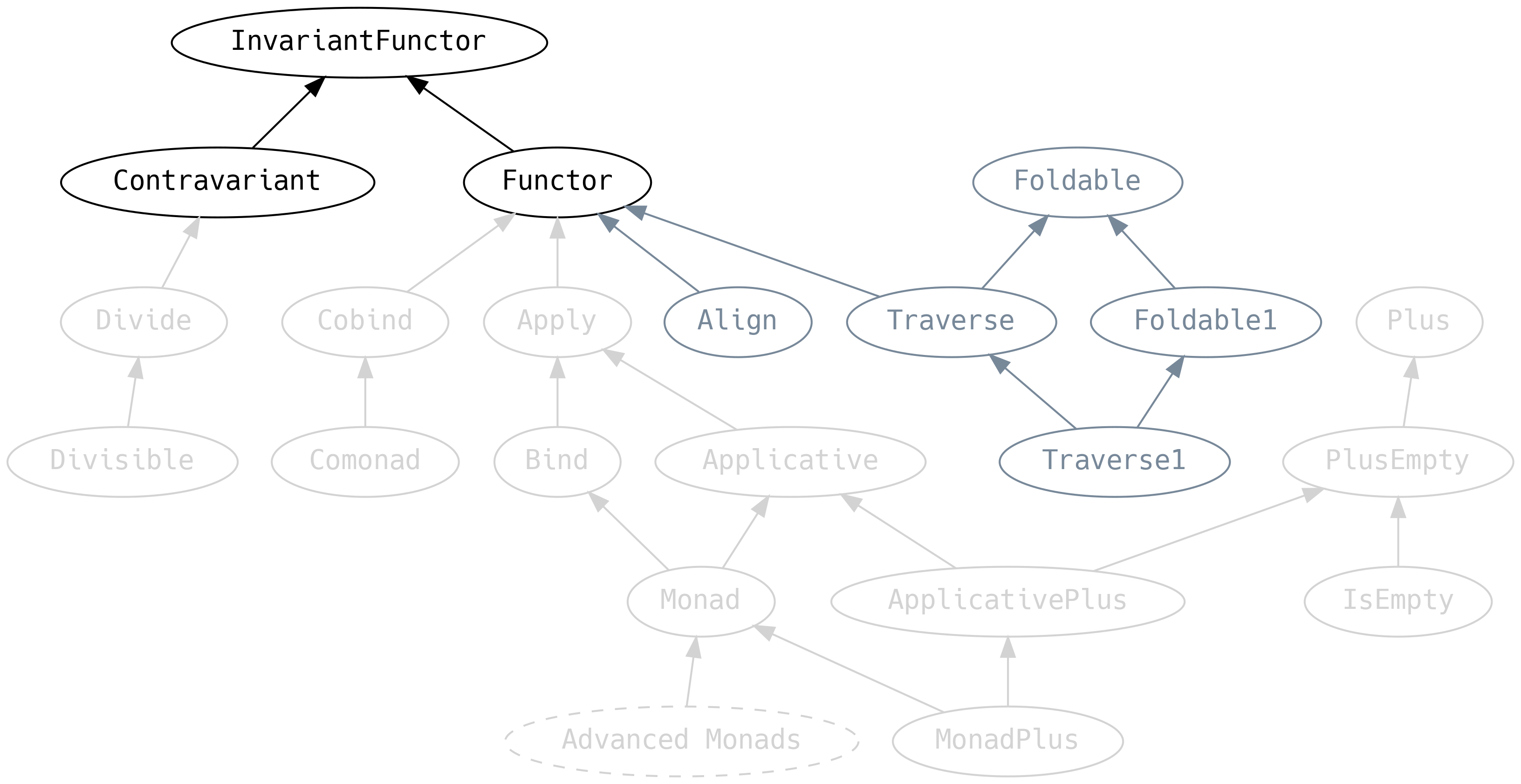
InvariantFunctor, also known as the exponential functor, has a method xmap which says that given a function from A to B, and a function from B to A, then we can convert F[A] to F[B].

Functor is a short name for what should be covariant functor. But since Functor is so popular it gets the nickname. Likewise Contravariant should really be contravariant functor.

Functor implements xmap with map and ignores the function from B to A. Contravariant, on the other hand, implements xmap with contramap and ignores the function from A to B:

  @typeclass trait InvariantFunctor[F[_]] {
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B]
    ...
  }
  
  @typeclass trait Functor[F[_]] extends InvariantFunctor[F] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = map(fa)(f)
    ...
  }
  
  @typeclass trait Contravariant[F[_]] extends InvariantFunctor[F] {
    def contramap[A, B](fa: F[A])(f: B => A): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = contramap(fa)(g)
    ...
  }

It is important to note that, although related at a theoretical level, the words covariant, contravariant and invariant do not directly refer to Scala type variance (i.e. + and - prefixes that may be written in type signatures). Invariance here means that it is possible to map the contents of a structure F[A] into F[B]. Using identity we can see that A can be safely downcast (or upcast) into B depending on the variance of the functor.

.map may be understand by its contract “if you give me an F of A and a way to turn an A into a B, then I can give you an F of B”.

Likewise, .contramap reads as “if you give me an F of A and a way to turn a B into a A, then I can give you an F of B”.

We will consider an example: in our application we introduce domain specific types Alpha, Beta, Gamma, etc, to ensure that we don’t mix up numbers in a financial calculation:

  final case class Alpha(value: Double)

but now we’re faced with the problem that we don’t have any typeclasses for these new types. If we use the values in JSON documents, we have to write instances of JsEncoder and JsDecoder.

However, JsEncoder has a Contravariant and JsDecoder has a Functor, so we can derive instances. Filling in the contract:

“if you give me a JsDecoder for a Double, and a way to go from a Double to an Alpha, then I can give you a JsDecoder for an Alpha”.
“if you give me a JsEncoder for a Double, and a way to go from an Alpha to a Double, then I can give you a JsEncoder for an Alpha”.

  object Alpha {
    implicit val decoder: JsDecoder[Alpha] = JsDecoder[Double].map(Alpha(_))
    implicit val encoder: JsEncoder[Alpha] = JsEncoder[Double].contramap(_.value)
  }

Methods on a typeclass can have their type parameters in contravariant position (method parameters) or in covariant position (return type). If a typeclass has a combination of covariant and contravariant positions, it might have an invariant functor. For example, Semigroup and Monoid have an InvariantFunctor, but not a Functor or a Contravariant.

5.6 Apply and Bind

Consider this the warm-up act to Applicative and Monad

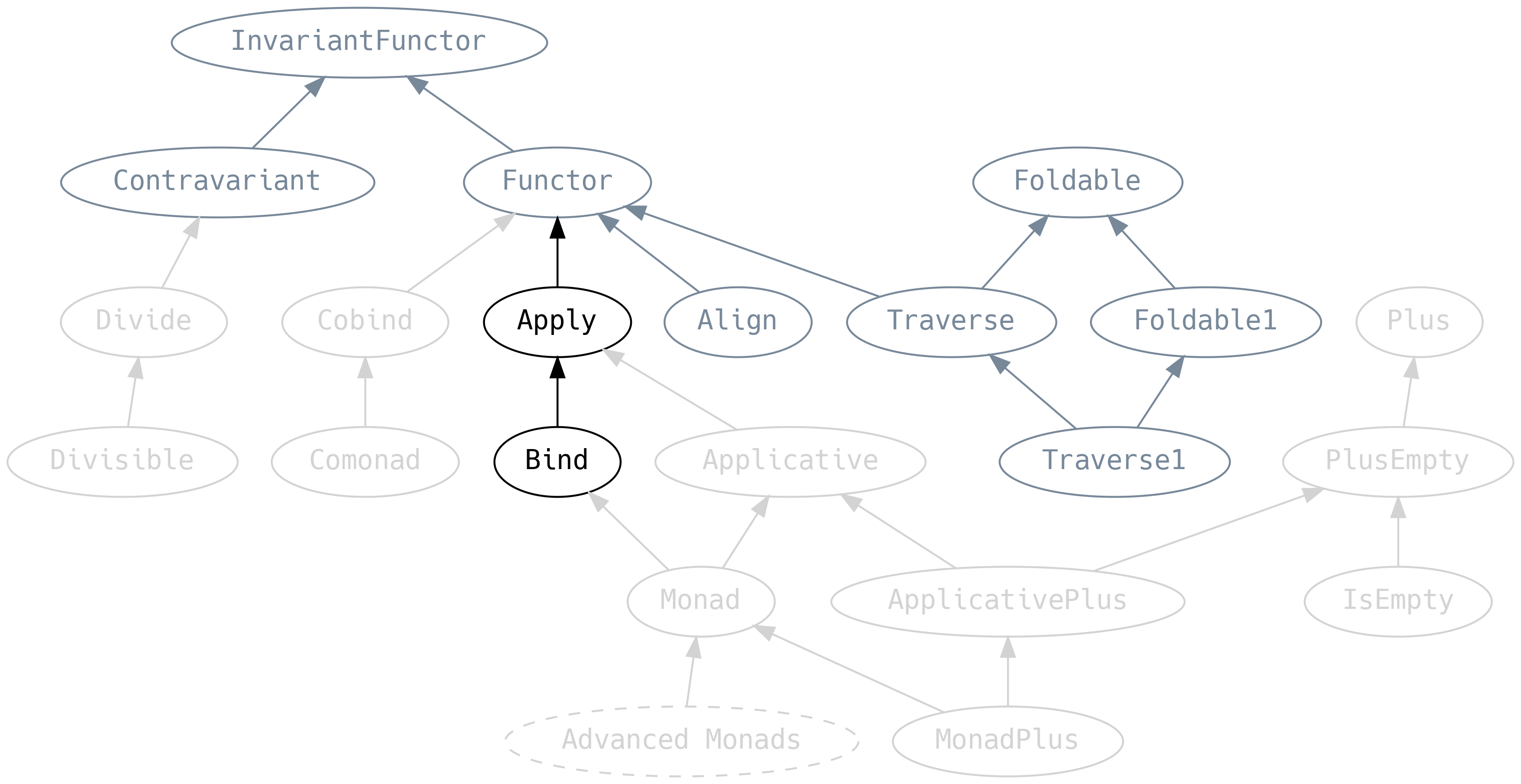
5.6.1 Apply

Apply extends Functor by adding a method named ap which is similar to map in that it applies a function to values. However, with ap, the function is in the same context as the values.

  @typeclass trait Apply[F[_]] extends Functor[F] {
    @op("<*>") def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B]
    ...

It is worth taking a moment to consider what that means for a simple data structure like Option[A], having the following implementation of .ap

  implicit def option[A]: Apply[Option[A]] = new Apply[Option[A]] {
    override def ap[A, B](fa: =>Option[A])(f: =>Option[A => B]) = f match {
      case Some(ff) => fa.map(ff)
      case None    => None
    }
    ...
  }

To implement .ap, we must first extract the function ff: A => B from f: Option[A => B], then we can map over fa. The extraction of the function from the context is the important power that Apply brings, allowing multiple function to be combined inside the context.

Returning to Apply, we find .applyX boilerplate that allows us to combine parallel functions and then map over their combined output:

  @typeclass trait Apply[F[_]] extends Functor[F] {
    ...
    def apply2[A,B,C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] = ...
    def apply3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
    ...
    def apply12[...]

Read .apply2 as a contract promising: “if you give me an F of A and an F of B, with a way of combining A and B into a C, then I can give you an F of C”. There are many uses for this contract and the two most important are:

constructing some typeclasses for a product type C from its constituents A and B
performing effects in parallel, like the drone and google algebras we created in Chapter 3, and then combining their results.

Indeed, Apply is so useful that it has special syntax:

  implicit class ApplyOps[F[_]: Apply, A](self: F[A]) {
    def *>[B](fb: F[B]): F[B] = Apply[F].apply2(self,fb)((_,b) => b)
    def <*[B](fb: F[B]): F[A] = Apply[F].apply2(self,fb)((a,_) => a)
    def |@|[B](fb: F[B]): ApplicativeBuilder[F, A, B] = ...
  }
  
  class ApplicativeBuilder[F[_]: Apply, A, B](a: F[A], b: F[B]) {
    def tupled: F[(A, B)] = Apply[F].apply2(a, b)(Tuple2(_))
    def |@|[C](cc: F[C]): ApplicativeBuilder3[C] = ...
  
    sealed abstract class ApplicativeBuilder3[C](c: F[C]) {
      ..ApplicativeBuilder4
        ...
          ..ApplicativeBuilder12
  }

which is exactly what we used in Chapter 3:

  (d.getBacklog |@| d.getAgents |@| m.getManaged |@| m.getAlive |@| m.getTime)

The syntax <* and *> (left bird and right bird) offer a convenient way to ignore the output from one of two parallel effects.

Unfortunately, although the |@| syntax is clear, there is a problem in that a new ApplicativeBuilder object is allocated for each additional effect. If the work is I/O-bound, the memory allocation cost is insignificant. However, when performing CPU-bound work, use the alternative lifting with arity syntax, which does not produce any intermediate objects:

  def ^[F[_]: Apply,A,B,C](fa: =>F[A],fb: =>F[B])(f: (A,B) =>C): F[C] = ...
  def ^^[F[_]: Apply,A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
  ...
  def ^^^^^^[F[_]: Apply, ...]

used like

  ^^^^(d.getBacklog, d.getAgents, m.getManaged, m.getAlive, m.getTime)

or directly call applyX

  Apply[F].apply5(d.getBacklog, d.getAgents, m.getManaged, m.getAlive, m.getTime)

Despite being more commonly used with effects, Apply works just as well with data structures. Consider rewriting

  for {
    foo <- data.foo: Option[String]
    bar <- data.bar: Option[Int]
  } yield foo + bar.shows

  (data.foo |@| data.bar)(_ + _.shows)

If we only want the combined output as a tuple, methods exist to do just that:

  @op("tuple") def tuple2[A,B](fa: =>F[A],fb: =>F[B]): F[(A,B)] = ...
  def tuple3[A,B,C](fa: =>F[A],fb: =>F[B],fc: =>F[C]): F[(A,B,C)] = ...
  ...
  def tuple12[...]

  (data.foo tuple data.bar) : Option[(String, Int)]

There are also the generalised versions of ap for more than two parameters:

  def ap2[A,B,C](fa: =>F[A],fb: =>F[B])(f: F[(A,B) => C]): F[C] = ...
  def ap3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: F[(A,B,C) => D]): F[D] = ...
  ...
  def ap12[...]

along with .lift methods that take normal functions and lift them into the F[_] context, the generalisation of Functor.lift

  def lift2[A,B,C](f: (A,B) => C): (F[A],F[B]) => F[C] = ...
  def lift3[A,B,C,D](f: (A,B,C) => D): (F[A],F[B],F[C]) => F[D] = ...
  ...
  def lift12[...]

and .apF, a partially applied syntax for ap

  def apF[A,B](f: =>F[A => B]): F[A] => F[B] = ...

Finally .forever

  def forever[A, B](fa: F[A]): F[B] = ...

repeating an effect without stopping. The instance of Apply must be stack safe or we will get StackOverflowError.

5.6.2 Bind

Bind introduces .bind, synonymous with .flatMap, which allows functions over the result of an effect to return a new effect, or for functions over the values of a data structure to return new data structures that are then joined.

  @typeclass trait Bind[F[_]] extends Apply[F] {
  
    @op(">>=") def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
    def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B] = bind(fa)(f)
  
    override def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B] =
      bind(f)(x => map(fa)(x))
    override def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] =
      bind(fa)(a => map(fb)(b => f(a, b)))
  
    def join[A](ffa: F[F[A]]): F[A] = bind(ffa)(identity)
  
    def mproduct[A, B](fa: F[A])(f: A => F[B]): F[(A, B)] = ...
    def ifM[B](value: F[Boolean], t: =>F[B], f: =>F[B]): F[B] = ...
  
  }

The .join may be familiar to users of .flatten in the stdlib, it takes a nested context and squashes it into one.

Derived combinators are introduced for .ap and .apply2 that require consistency with .bind. We will see later that this law has consequences for parallelisation strategies.

mproduct is like Functor.fproduct and pairs the function’s input with its output, inside the F.

ifM is a way to construct a conditional data structure or effect:

  scala> List(true, false, true).ifM(List(0), List(1, 1))
  res: List[Int] = List(0, 1, 1, 0)

ifM and ap are optimised to cache and reuse code branches, compare to the longer form

  scala> List(true, false, true).flatMap { b => if (b) List(0) else List(1, 1) }

which produces a fresh List(0) or List(1, 1) every time the branch is invoked.

Bind also has some special syntax

  implicit class BindOps[F[_]: Bind, A] (self: F[A]) {
    def >>[B](b: =>F[B]): F[B] = Bind[F].bind(self)(_ => b)
    def >>![B](f: A => F[B]): F[A] = Bind[F].bind(self)(a => f(a).map(_ => a))
  }

>> is when we wish to discard the input to bind and >>! is when we want to run an effect but discard its output.

5.7 Applicative and Monad

From a functionality point of view, Applicative is Apply with a pure method, and Monad extends Applicative with Bind.

  @typeclass trait Applicative[F[_]] extends Apply[F] {
    def point[A](a: =>A): F[A]
    def pure[A](a: =>A): F[A] = point(a)
  }
  
  @typeclass trait Monad[F[_]] extends Applicative[F] with Bind[F]

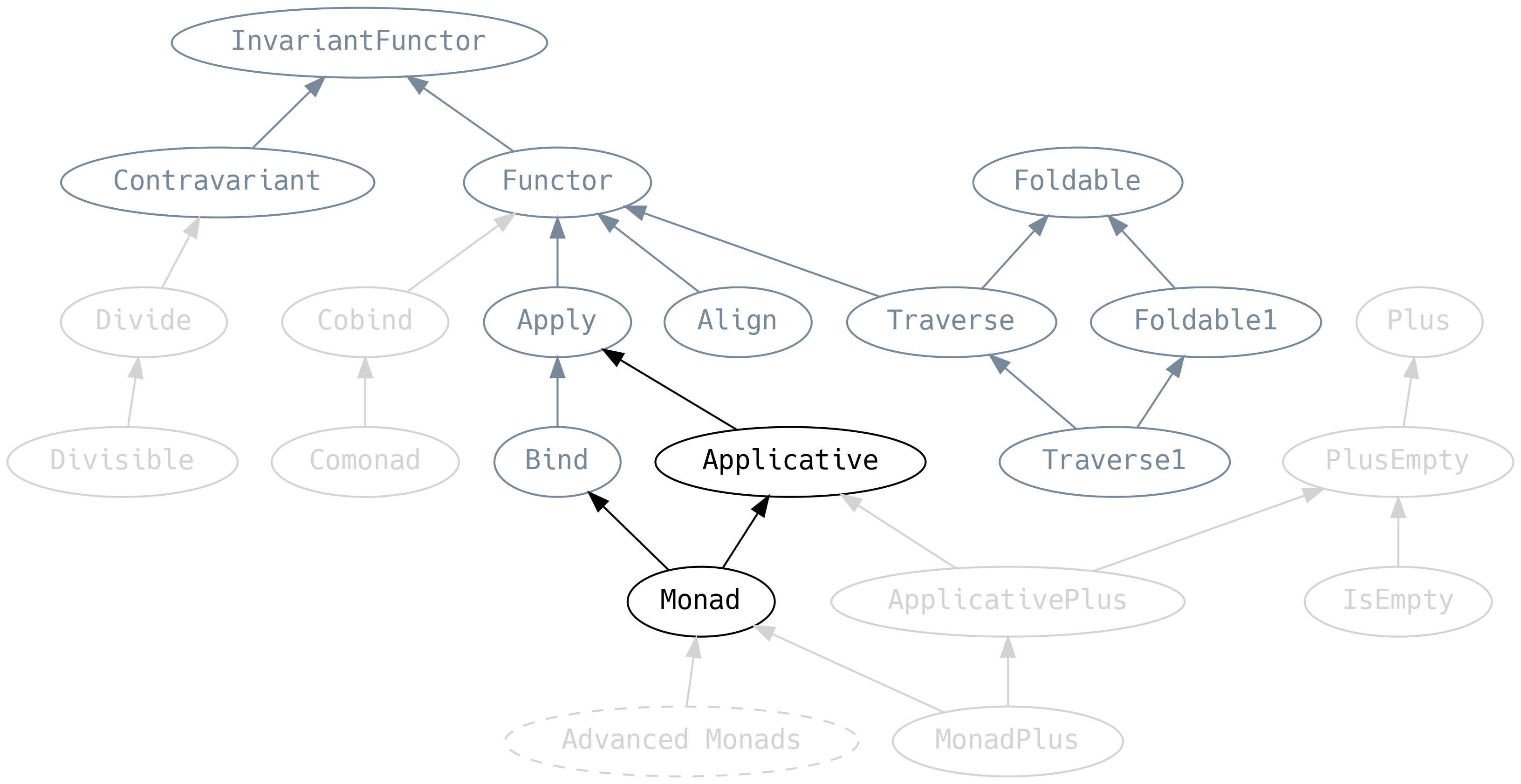
In many ways, Applicative and Monad are the culmination of everything we’ve seen in this chapter. .pure (or .point as it is more commonly known for data structures) allows us to create effects or data structures from values.

Instances of Applicative must meet some laws, effectively asserting that all the methods are consistent:

Identity: fa <*> pure(identity) === fa, (where fa is an F[A]) i.e. applying pure(identity) does nothing.
Homomorphism: pure(a) <*> pure(ab) === pure(ab(a)) (where ab is an A => B), i.e. applying a pure function to a pure value is the same as applying the function to the value and then using pure on the result.
Interchange: pure(a) <*> fab === fab <*> pure(f => f(a)), (where fab is an F[A => B]), i.e. pure is a left and right identity
Mappy: map(fa)(f) === fa <*> pure(f)

Monad adds additional laws:

Left Identity: pure(a).bind(f) === f(a)
Right Identity: a.bind(pure(_)) === a
Associativity: fa.bind(f).bind(g) === fa.bind(a => f(a).bind(g)) where fa is an F[A], f is an A => F[B] and g is a B => F[C].

Associativity says that chained bind calls must agree with nested bind. However, it does not mean that we can rearrange the order, which would be commutativity. For example, recalling that flatMap is an alias to bind, we cannot rearrange

  for {
    _ <- machine.start(node1)
    _ <- machine.stop(node1)
  } yield true

  for {
    _ <- machine.stop(node1)
    _ <- machine.start(node1)
  } yield true

start and stop are non-commutative, because the intended effect of starting then stopping a node is different to stopping then starting it!

But start is commutative with itself, and stop is commutative with itself, so we can rewrite

  for {
    _ <- machine.start(node1)
    _ <- machine.start(node2)
  } yield true

  for {
    _ <- machine.start(node2)
    _ <- machine.start(node1)
  } yield true

which are equivalent for our algebra, but not in general. We’re making a lot of assumptions about the Google Container API here, but this is a reasonable choice to make.

A practical consequence is that a Monad must be commutative if its applyX methods can be allowed to run in parallel. We cheated in Chapter 3 when we ran these effects in parallel

  (d.getBacklog |@| d.getAgents |@| m.getManaged |@| m.getAlive |@| m.getTime)

because we know that they are commutative among themselves. When it comes to interpreting our application, later in the book, we will have to provide evidence that these effects are in fact commutative, or an asynchronous implementation may choose to sequence the operations to be on the safe side.

The subtleties of how we deal with (re)-ordering of effects, and what those effects are, deserves a dedicated chapter on Advanced Monads.

5.8 Divide and Conquer

Divide is the Contravariant analogue of Apply

  @typeclass trait Divide[F[_]] extends Contravariant[F] {
    def divide[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C] = divide2(fa, fb)(f)
  
    def divide1[A1, Z](a1: F[A1])(f: Z => A1): F[Z] = ...
    def divide2[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C] = ...
    ...
    def divide22[...] = ...

divide says that if we can break a C into an A and a B, and we’re given an F[A] and an F[B], then we can get an F[C]. Hence, divide and conquer.

This is a great way to generate contravariant typeclass instances for product types by breaking the products into their parts. Scalaz has an instance of Divide[Equal], let’s construct an Equal for a new product type Foo

  scala> case class Foo(s: String, i: Int)
  scala> implicit val fooEqual: Equal[Foo] =
           Divide[Equal].divide2(Equal[String], Equal[Int]) {
             (foo: Foo) => (foo.s, foo.i)
           }
  scala> Foo("foo", 1) === Foo("bar", 1)
  res: Boolean = false

Mirroring Apply, Divide also has terse syntax for tuples. A softer divide so that we may reign approach to world domination:

  ...
    def tuple2[A1, A2](a1: F[A1], a2: F[A2]): F[(A1, A2)] = ...
    ...
    def tuple22[...] = ...
  }

Generally, if encoder typeclasses can provide an instance of Divide, rather than stopping at Contravariant, it makes it possible to derive instances for any case class. Similarly, decoder typeclasses can provide an Apply instance. We will explore this in a dedicated chapter on Typeclass Derivation.

Divisible is the Contravariant analogue of Applicative and introduces .conquer, the equivalent of .pure

  @typeclass trait Divisible[F[_]] extends Divide[F] {
    def conquer[A]: F[A]
  }

.conquer allows creating trivial implementations where the type parameter is ignored. Such values are called universally quantified. For example, the Divisible[Equal].conquer[INil[String]] returns an implementation of Equal for an empty list of String which is always true.

5.9 Plus

Plus is Semigroup but for type constructors, and PlusEmpty is the equivalent of Monoid (they even have the same laws) whereas IsEmpty is novel and allows us to query if an F[A] is empty:

  @typeclass trait Plus[F[_]] {
    @op("<+>") def plus[A](a: F[A], b: =>F[A]): F[A]
  }
  @typeclass trait PlusEmpty[F[_]] extends Plus[F] {
    def empty[A]: F[A]
  }
  @typeclass trait IsEmpty[F[_]] extends PlusEmpty[F] {
    def isEmpty[A](fa: F[A]): Boolean
  }

Although it may look on the surface as if <+> behaves like |+|

  scala> List(2,3) |+| List(7)
  res = List(2, 3, 7)
  
  scala> List(2,3) <+> List(7)
  res = List(2, 3, 7)

it is best to think of it as operating only at the F[_] level, never looking into the contents. Plus has the convention that it should ignore failures and “pick the first winner”. <+> can therefore be used as a mechanism for early exit (losing information) and failure-handling via fallbacks:

  scala> Option(1) |+| Option(2)
  res = Some(3)
  
  scala> Option(1) <+> Option(2)
  res = Some(1)
  
  scala> Option.empty[Int] <+> Option(1)
  res = Some(1)

For example, if we have a NonEmptyList[Option[Int]] and we want to ignore None values (failures) and pick the first winner (Some), we can call <+> from Foldable1.foldRight1:

  scala> NonEmptyList(None, None, Some(1), Some(2), None)
         .foldRight1(_ <+> _)
  res: Option[Int] = Some(1)

In fact, now that we know about Plus, we realise that we didn’t need to break typeclass coherence (when we defined a locally scoped Monoid[Option[A]]) in the section on Appendable Things. Our objective was to “pick the last winner”, which is the same as “pick the winner” if the arguments are swapped. Note the use of the TIE Interceptor for ccy and otc with arguments swapped.

  implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
    (a, b) => TradeTemplate(a.payments |+| b.payments,
                            b.ccy <+> a.ccy,
                            b.otc <+> a.otc),
    TradeTemplate(Nil, None, None)
  )

Applicative and Monad have specialised versions of PlusEmpty

  @typeclass trait ApplicativePlus[F[_]] extends Applicative[F] with PlusEmpty[F]
  
  @typeclass trait MonadPlus[F[_]] extends Monad[F] with ApplicativePlus[F] {
    def unite[T[_]: Foldable, A](ts: F[T[A]]): F[A] = ...
  
    def withFilter[A](fa: F[A])(f: A => Boolean): F[A] = ...
  }

.unite lets us fold a data structure using the outer container’s PlusEmpty[F].monoid rather than the inner content’s Monoid. For List[Either[String, Int]] this means Left[String] values are converted into .empty, then everything is concatenated. A convenient way to discard errors:

  scala> List(Right(1), Left("boo"), Right(2)).unite
  res: List[Int] = List(1, 2)
  
  scala> val boo: Either[String, Int] = Left("boo")
         boo.foldMap(a => a.pure[List])
  res: List[String] = List()
  
  scala> val n: Either[String, Int] = Right(1)
         n.foldMap(a => a.pure[List])
  res: List[Int] = List(1)

withFilter allows us to make use of for comprehension language support as discussed in Chapter 2. It is fair to say that the Scala language has built-in language support for MonadPlus, not just Monad!

Returning to Foldable for a moment, we can reveal some methods that we did not discuss earlier

  @typeclass trait Foldable[F[_]] {
    ...
    def msuml[G[_]: PlusEmpty, A](fa: F[G[A]]): G[A] = ...
    def collapse[X[_]: ApplicativePlus, A](x: F[A]): X[A] = ...
    ...
  }

msuml does a fold using the Monoid from the PlusEmpty[G] and collapse does a foldRight using the PlusEmpty of the target type:

  scala> IList(Option(1), Option.empty[Int], Option(2)).fold
  res: Option[Int] = Some(3) // uses Monoid[Option[Int]]
  
  scala> IList(Option(1), Option.empty[Int], Option(2)).msuml
  res: Option[Int] = Some(1) // uses PlusEmpty[Option].monoid
  
  scala> IList(1, 2).collapse[Option]
  res: Option[Int] = Some(1)

5.10 Lone Wolves

Some of the typeclasses in Scalaz are stand-alone and not part of the larger hierarchy.

5.10.1 Zippy

  @typeclass trait Zip[F[_]]  {
    def zip[A, B](a: =>F[A], b: =>F[B]): F[(A, B)]
  
    def zipWith[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C)
                        (implicit F: Functor[F]): F[C] = ...
  
    def ap(implicit F: Functor[F]): Apply[F] = ...
  
    @op("<*|*>") def apzip[A, B](f: =>F[A] => F[B], a: =>F[A]): F[(A, B)] = ...
  
  }

The core method is zip which is a less powerful version of Divide.tuple2, and if a Functor[F] is provided then zipWith can behave like Apply.apply2. Indeed, an Apply[F] can be created from a Zip[F] and a Functor[F] by calling ap.

apzip takes an F[A] and a lifted function from F[A] => F[B], producing an F[(A, B)] similar to Functor.fproduct.

  @typeclass trait Unzip[F[_]]  {
    @op("unfzip") def unzip[A, B](a: F[(A, B)]): (F[A], F[B])
  
    def firsts[A, B](a: F[(A, B)]): F[A] = ...
    def seconds[A, B](a: F[(A, B)]): F[B] = ...
  
    def unzip3[A, B, C](x: F[(A, (B, C))]): (F[A], F[B], F[C]) = ...
    ...
    def unzip7[A ... H](x: F[(A, (B, ... H))]): ...
  }

The core method is unzip with firsts and seconds allowing for selecting either the first or second element of a tuple in the F. Importantly, unzip is the opposite of zip.

The methods unzip3 to unzip7 are repeated applications of unzip to save on boilerplate. For example, if handed a bunch of nested tuples, the Unzip[Id] is a handy way to flatten them:

  scala> Unzip[Id].unzip7((1, (2, (3, (4, (5, (6, 7)))))))
  res = (1,2,3,4,5,6,7)

In a nutshell, Zip and Unzip are less powerful versions of Divide and Apply, providing useful features without requiring the F to make too many promises.

5.10.2 Optional

Optional is a generalisation of data structures that can optionally contain a value, like Option and Either.

Recall that \/ (disjunction) is Scalaz’s improvement of scala.Either. We will also see Maybe, Scalaz’s improvement of scala.Option

  sealed abstract class Maybe[A]
  final case class Empty[A]()    extends Maybe[A]
  final case class Just[A](a: A) extends Maybe[A]

  @typeclass trait Optional[F[_]] {
    def pextract[B, A](fa: F[A]): F[B] \/ A
  
    def getOrElse[A](fa: F[A])(default: =>A): A = ...
    def orElse[A](fa: F[A])(alt: =>F[A]): F[A] = ...
  
    def isDefined[A](fa: F[A]): Boolean = ...
    def nonEmpty[A](fa: F[A]): Boolean = ...
    def isEmpty[A](fa: F[A]): Boolean = ...
  
    def toOption[A](fa: F[A]): Option[A] = ...
    def toMaybe[A](fa: F[A]): Maybe[A] = ...
  }

These are methods that should be familiar, except perhaps pextract, which is a way of letting the F[_] return some implementation specific F[B] or the value. For example, Optional[Option].pextract returns Option[Nothing] \/ A, i.e. None \/ A.

Scalaz gives a ternary operator to things that have an Optional

  implicit class OptionalOps[F[_]: Optional, A](fa: F[A]) {
    def ?[X](some: =>X): Conditional[X] = new Conditional[X](some)
    final class Conditional[X](some: =>X) {
      def |(none: =>X): X = if (Optional[F].isDefined(fa)) some else none
    }
  }

for example

  scala> val knock_knock: Option[String] = ...
         knock_knock ? "who's there?" | "<tumbleweed>"

5.11 Co-things

A co-thing typically has some opposite type signature to whatever thing does, but is not necessarily its inverse. To highlight the relationship between thing and co-thing, we will include the type signature of thing wherever we can.

5.11.1 Cobind

  @typeclass trait Cobind[F[_]] extends Functor[F] {
    def cobind[A, B](fa: F[A])(f: F[A] => B): F[B]
  //def   bind[A, B](fa: F[A])(f: A => F[B]): F[B]
  
    def cojoin[A](fa: F[A]): F[F[A]] = ...
  //def   join[A](ffa: F[F[A]]): F[A] = ...
  }

cobind (also known as coflatmap) takes an F[A] => B that acts on an F[A] rather than its elements. But this is not necessarily the full fa, it can be a substructure that has been created by .coflatten.

Compelling use-cases for Cobind are rare, although when shown in the Functor permutation table (for F[_], A and B) it is difficult to argue why any method should be less important than the others:

method	parameter
`map`	`A => B`
`contramap`	`B => A`
`xmap`	`(A => B, B => A)`
`ap`	`F[A => B]`
`bind`	`A => F[B]`
`cobind`	`F[A] => B`

5.11.2 Comonad

  @typeclass trait Comonad[F[_]] extends Cobind[F] {
    def copoint[A](p: F[A]): A
  //def   point[A](a: =>A): F[A]
  }

.copoint (also .copure) unwraps an element from its context. The Id type alias that we encountered in Chapter 1 has an instance of Comonad, so we can reach into an Id and extract the value it contains. Similarly, Name has a Comonad with .value effectively being the Value strategy.

Another example of a Comonad is the NonEmptyList, where .copoint returns the .head element and .cobind operates on all the tails of the list.

Effects do not typically have an instance of Comonad since it would break referential transparency to interpret an IO[A] into an A.

Comonad allows navigation over elements of a data structure and eventually returning to one view of that data. Consider a neighbourhood (Hood for short) of a list, containing all the elements to the left (.lefts) of an element .focus, and all the elements to its right (.rights).

  final case class Hood[A](lefts: IList[A], focus: A, rights: IList[A])

The lefts and rights should each be ordered with the nearest to the focus at the head, such that we can recover the original IList via .toIList

  object Hood {
    implicit class Ops[A](hood: Hood[A]) {
      def toIList: IList[A] = hood.lefts.reverse ::: hood.focus :: hood.rights

We can write methods that let us move the focus one to the left (.previous) and one to the right (.next)

  ...
      def previous: Maybe[Hood[A]] = hood.lefts match {
        case INil() => Empty()
        case ICons(head, tail) =>
          Just(Hood(tail, head, hood.focus :: hood.rights))
      }
      def next: Maybe[Hood[A]] = hood.rights match {
        case INil() => Empty()
        case ICons(head, tail) =>
          Just(Hood(hood.focus :: hood.lefts, head, tail))
      }

.more repeatedly applies an optional function to Hood such that we calculate all the views that Hood can take on the list

  ...
      def more(f: Hood[A] => Maybe[Hood[A]]): IList[Hood[A]] =
        f(hood) match {
          case Empty() => INil()
          case Just(r) => ICons(r, r.more(f))
        }
      def positions: Hood[Hood[A]] = {
        val left  = hood.more(_.previous)
        val right = hood.more(_.next)
        Hood(left, hood, right)
      }
    }

We can now implement Comonad[Hood]

  ...
    implicit val comonad: Comonad[Hood] = new Comonad[Hood] {
      def map[A, B](fa: Hood[A])(f: A => B): Hood[B] =
        Hood(fa.lefts.map(f), f(fa.focus), fa.rights.map(f))
      def cobind[A, B](fa: Hood[A])(f: Hood[A] => B): Hood[B] =
        fa.positions.map(f)
      def copoint[A](fa: Hood[A]): A = fa.focus
    }
  }

.cojoin gives us a Hood[Hood[IList]] containing all the possible neighbourhoods in our initial IList

  scala> val middle = Hood(IList(4, 3, 2, 1), 5, IList(6, 7, 8, 9))
  scala> middle.cojoin
  res = Hood(
          [Hood([3,2,1],4,[5,6,7,8,9]),
           Hood([2,1],3,[4,5,6,7,8,9]),
           Hood([1],2,[3,4,5,6,7,8,9]),
           Hood([],1,[2,3,4,5,6,7,8,9])],
          Hood([4,3,2,1],5,[6,7,8,9]),
          [Hood([5,4,3,2,1],6,[7,8,9]),
           Hood([6,5,4,3,2,1],7,[8,9]),
           Hood([7,6,5,4,3,2,1],8,[9]),
           Hood([8,7,6,5,4,3,2,1],9,[])])

Indeed, .cojoin is just positions! We can override it with a more direct (and performant) implementation

  override def cojoin[A](fa: Hood[A]): Hood[Hood[A]] = fa.positions

Comonad generalises the concept of Hood to arbitrary data structures. Hood is an example of a zipper (unrelated to Zip). Scalaz comes with a Zipper data type for streams (i.e. infinite 1D data structures), which we will discuss in the next chapter.

One application of a zipper is for cellular automata, which compute the value of each cell in the next generation by performing a computation based on the neighbourhood of that cell.

5.11.3 Cozip

  @typeclass trait Cozip[F[_]] {
    def cozip[A, B](x: F[A \/ B]): F[A] \/ F[B]
  //def   zip[A, B](a: =>F[A], b: =>F[B]): F[(A, B)]
  //def unzip[A, B](a: F[(A, B)]): (F[A], F[B])
  
    def cozip3[A, B, C](x: F[A \/ (B \/ C)]): F[A] \/ (F[B] \/ F[C]) = ...
    ...
    def cozip7[A ... H](x: F[(A \/ (... H))]): F[A] \/ (... F[H]) = ...
  }

Although named cozip, it is perhaps more appropriate to talk about its symmetry with unzip. Whereas unzip splits F[_] of tuples (products) into tuples of F[_], cozip splits F[_] of disjunctions (coproducts) into disjunctions of F[_].

5.12 Bi-things

Sometimes we may find ourselves with a thing that has two type holes and we want to map over both sides. For example we might be tracking failures in the left of an Either and we want to do something with the failure messages.

The Functor / Foldable / Traverse typeclasses have bizarro relatives that allow us to map both ways.

  @typeclass trait Bifunctor[F[_, _]] {
    def bimap[A, B, C, D](fab: F[A, B])(f: A => C, g: B => D): F[C, D]
  
    @op("<-:") def leftMap[A, B, C](fab: F[A, B])(f: A => C): F[C, B] = ...
    @op(":->") def rightMap[A, B, D](fab: F[A, B])(g: B => D): F[A, D] = ...
    @op("<:>") def umap[A, B](faa: F[A, A])(f: A => B): F[B, B] = ...
  }
  
  @typeclass trait Bifoldable[F[_, _]] {
    def bifoldMap[A, B, M: Monoid](fa: F[A, B])(f: A => M)(g: B => M): M
  
    def bifoldRight[A,B,C](fa: F[A, B], z: =>C)(f: (A, =>C) => C)(g: (B, =>C) => C): C
    def bifoldLeft[A,B,C](fa: F[A, B], z: C)(f: (C, A) => C)(g: (C, B) => C): C = ...
  
    def bifoldMap1[A, B, M: Semigroup](fa: F[A,B])(f: A => M)(g: B => M): Option[M] = ...
  }
  
  @typeclass trait Bitraverse[F[_, _]] extends Bifunctor[F] with Bifoldable[F] {
    def bitraverse[G[_]: Applicative, A, B, C, D](fab: F[A, B])
                                                 (f: A => G[C])
                                                 (g: B => G[D]): G[F[C, D]]
  
    def bisequence[G[_]: Applicative, A, B](x: F[G[A], G[B]]): G[F[A, B]] = ...
  }

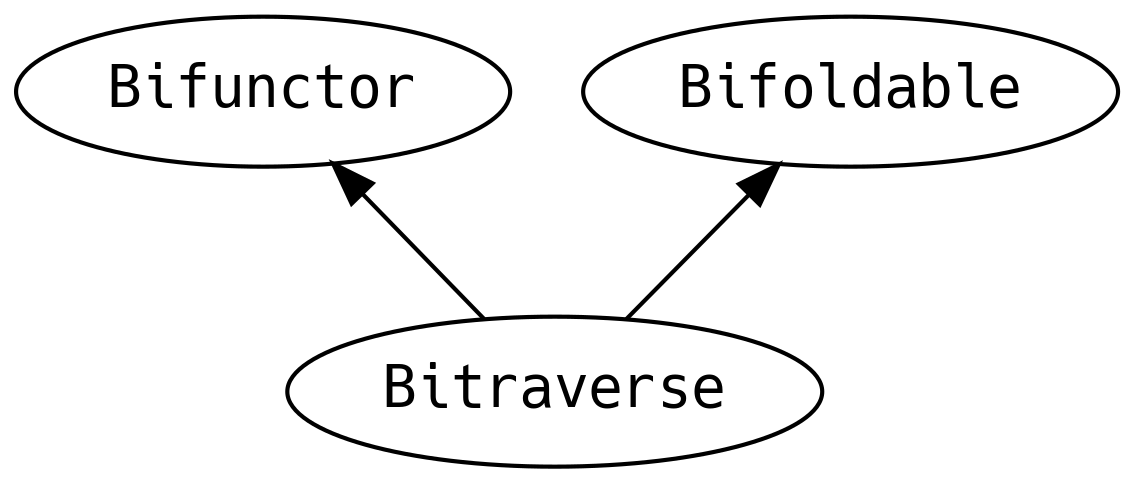
Although the type signatures are verbose, these are nothing more than the core methods of Functor, Foldable and Bitraverse taking two functions instead of one, often requiring both functions to return the same type so that their results can be combined with a Monoid or Semigroup.

  scala> val a: Either[String, Int] = Left("fail")
         val b: Either[String, Int] = Right(13)
  
  scala> b.bimap(_.toUpperCase, _ * 2)
  res: Either[String, Int] = Right(26)
  
  scala> a.bimap(_.toUpperCase, _ * 2)
  res: Either[String, Int] = Left(FAIL)
  
  scala> b :-> (_ * 2)
  res: Either[String,Int] = Right(26)
  
  scala> a :-> (_ * 2)
  res: Either[String, Int] = Left(fail)
  
  scala> { s: String => s.length } <-: a
  res: Either[Int, Int] = Left(4)
  
  scala> a.bifoldMap(_.length)(identity)
  res: Int = 4
  
  scala> b.bitraverse(s => Future(s.length), i => Future(i))
  res: Future[Either[Int, Int]] = Future(<not completed>)

In addition, we can revisit MonadPlus (recall it is Monad with the ability to filterWith and unite) and see that it can separate Bifoldable contents of a Monad

  @typeclass trait MonadPlus[F[_]] {
    ...
    def separate[G[_, _]: Bifoldable, A, B](value: F[G[A, B]]): (F[A], F[B]) = ...
    ...
  }

This is very useful if we have a collection of bi-things and we want to reorganise them into a collection of A and a collection of B

  scala> val list: List[Either[Int, String]] =
           List(Right("hello"), Left(1), Left(2), Right("world"))
  
  scala> list.separate
  res: (List[Int], List[String]) = (List(1, 2), List(hello, world))

5.13 Summary

That was a lot of material! We have just explored a standard library of polymorphic functionality. But to put it into perspective: there are more traits in the Scala stdlib Collections API than typeclasses in Scalaz.

It is normal for an FP application to only touch a small percentage of the typeclass hierarchy, with most functionality coming from domain-specific algebras and typeclasses. Even if the domain-specific typeclasses are just specialised clones of something in Scalaz, it is OK to refactor it later.

To help, we have included a cheat-sheet of the typeclasses and their primary methods in the Appendix, inspired by Adam Rosien’s Scalaz Cheatsheet.

To help further, Valentin Kasas explains how to combine N things:

6. Scalaz Data Types

Who doesn’t love a good data structure? The answer is nobody, because data structures are awesome.

In this chapter we will explore the collection-like data types in Scalaz, as well as data types that augment the Scala language with useful semantics and additional type safety.

The primary reason we care about having lots of collections at our disposal is performance. A vector and a list can do the same things, but their performance characteristics are different: a vector has constant lookup cost whereas a list must be traversed.

All of the collections presented here are persistent: if we add or remove an element we can still use the old version. Structural sharing is essential to the performance of persistent data structures, otherwise the entire collection is rebuilt with every operation.

Unlike the Java and Scala collections, there is no hierarchy to the data types in Scalaz: these collections are much simpler to understand. Polymorphic functionality is provided by optimised instances of the typeclasses we studied in the previous chapter. This makes it a lot easier to swap implementations for performance reasons, and to provide our own.

6.1 Type Variance

Many of Scalaz’s data types are invariant in their type parameters. For example, IList[A] is not a subtype of IList[B] when A <: B.

6.1.1 Covariance

The problem with covariant type parameters, such as class List[+A], is that List[A] is a subtype of List[Any] and it is easy to accidentally lose type information.

  scala> List("hello") ++ List(' ') ++ List("world!")
  res: List[Any] = List(hello,  , world!)

Note that the second list is a List[Char] and the compiler has unhelpfully inferred the Least Upper Bound (LUB) to be Any. Compare to IList, which requires explicit .widen[Any] to permit the heinous crime:

  scala> IList("hello") ++ IList(' ') ++ IList("world!")
  <console>:35: error: type mismatch;
   found   : Char(' ')
   required: String
  
  scala> IList("hello").widen[Any]
           ++ IList(' ').widen[Any]
           ++ IList("world!").widen[Any]
  res: IList[Any] = [hello, ,world!]

Similarly, when the compiler infers a type with Product with Serializable it is a strong indicator that accidental widening has occurred due to covariance.

Unfortunately we must be careful when constructing invariant data types because LUB calculations are performed on the parameters:

  scala> IList("hello", ' ', "world")
  res: IList[Any] = [hello, ,world]

Another similar problem arises from Scala’s Nothing type, which is a subtype of all other types, including sealed ADTs, final classes, primitives and null.

There are no values of type Nothing: functions that take a Nothing as a parameter cannot be run and functions that return Nothing will never return. Nothing was introduced as a mechanism to enable covariant type parameters, but a consequence is that we can write un-runnable code, by accident. Scalaz says we do not need covariant type parameters which means that we are limiting ourselves to writing practical code that can be run.

6.1.2 Contrarivariance

On the other hand, contravariant type parameters, such as trait Thing[-A], can expose devastating bugs in the compiler. Consider Paul Phillips’ (ex-scalac team) demonstration of what he calls contrarivariance:

  scala> :paste
         trait Thing[-A]
         def f(x: Thing[ Seq[Int]]): Byte   = 1
         def f(x: Thing[List[Int]]): Short  = 2
  
  scala> f(new Thing[ Seq[Int]] { })
         f(new Thing[List[Int]] { })
  
  res = 1
  res = 2

As expected, the compiler is finding the most specific argument in each call to f. However, implicit resolution gives unexpected results:

  scala> :paste
         implicit val t1: Thing[ Seq[Int]] =
           new Thing[ Seq[Int]] { override def toString = "1" }
         implicit val t2: Thing[List[Int]] =
           new Thing[List[Int]] { override def toString = "2" }
  
  scala> implicitly[Thing[ Seq[Int]]]
         implicitly[Thing[List[Int]]]
  
  res = 1
  res = 1

Implicit resolution flips its definition of “most specific” for contravariant types, rendering them useless for typeclasses or anything that requires polymorphic functionality. The behaviour is fixed in Dotty.

6.1.3 Limitations of subtyping

scala.Option has a method .flatten which will convert Option[Option[B]] into an Option[B]. However, Scala’s type system is unable to let us write the required type signature. Consider the following that appears correct, but has a subtle bug:

  sealed abstract class Option[+A] {
    def flatten[B, A <: Option[B]]: Option[B] = ...
  }

The A introduced on .flatten is shadowing the A introduced on the class. It is equivalent to writing

  sealed abstract class Option[+A] {
    def flatten[B, C <: Option[B]]: Option[B] = ...
  }

which is not the constraint we want.

To workaround this limitation, Scala defines infix classes <:< and =:= along with implicit evidence that always creates a witness

  sealed abstract class <:<[-From, +To] extends (From => To)
  implicit def conforms[A]: A <:< A = new <:<[A, A] { def apply(x: A): A = x }
  
  sealed abstract class =:=[ From,  To] extends (From => To)
  implicit def tpEquals[A]: A =:= A = new =:=[A, A] { def apply(x: A): A = x }

=:= can be used to require that two type parameters are exactly the same and <:< is used to describe subtype relationships, letting us implement .flatten as

  sealed abstract class Option[+A] {
    def flatten[B](implicit ev: A <:< Option[B]): Option[B] = this match {
      case None        => None
      case Some(value) => ev(value)
    }
  }
  final case class Some[+A](value: A) extends Option[A]
  case object None                    extends Option[Nothing]

Scalaz improves on <:< and =:= with Liskov (aliased to <~<) and Leibniz (===).

  sealed abstract class Liskov[-A, +B] {
    def apply(a: A): B = ...
    def subst[F[-_]](p: F[B]): F[A]
  
    def andThen[C](that: Liskov[B, C]): Liskov[A, C] = ...
    def onF[X](fa: X => A): X => B = ...
    ...
  }
  object Liskov {
    type <~<[-A, +B] = Liskov[A, B]
    type >~>[+B, -A] = Liskov[A, B]
  
    implicit def refl[A]: (A <~< A) = ...
    implicit def isa[A, B >: A]: A <~< B = ...
  
    implicit def witness[A, B](lt: A <~< B): A => B = ...
    ...
  }
  
  // type signatures have been simplified
  sealed abstract class Leibniz[A, B] {
    def apply(a: A): B = ...
    def subst[F[_]](p: F[A]): F[B]
  
    def flip: Leibniz[B, A] = ...
    def andThen[C](that: Leibniz[B, C]): Leibniz[A, C] = ...
    def onF[X](fa: X => A): X => B = ...
    ...
  }
  object Leibniz {
    type ===[A, B] = Leibniz[A, B]
  
    implicit def refl[A]: Leibniz[A, A] = ...
  
    implicit def subst[A, B](a: A)(implicit f: A === B): B = ...
    implicit def witness[A, B](f: A === B): A => B = ...
    ...
  }

Other than generally useful methods and implicit conversions, the Scalaz <~< and === evidence is more principled than in the stdlib.

6.2 Evaluation

Java is a strict evaluation language: all the parameters to a method must be evaluated to a value before the method is called. Scala introduces the notion of by-name parameters on methods with a: =>A syntax. These parameters are wrapped up as a zero argument function which is called every time the a is referenced. We seen by-name a lot in the typeclasses.

Scala also has by-need evaluation of values, with the lazy keyword: the computation is evaluated at most once to produce the value. Unfortunately, Scala does not support by-need evaluation of method parameters.

Scalaz formalises the three evaluation strategies with an ADT

  sealed abstract class Name[A] {
    def value: A
  }
  object Name {
    def apply[A](a: =>A) = new Name[A] { def value = a }
    ...
  }
  
  sealed abstract class Need[A] extends Name[A]
  object Need {
    def apply[A](a: =>A): Need[A] = new Need[A] {
      private lazy val value0: A = a
      def value = value0
    }
    ...
  }
  
  final case class Value[A](value: A) extends Need[A]

The weakest form of evaluation is Name, giving no computational guarantees. Next is Need, guaranteeing at most once evaluation, whereas Value is pre-computed and therefore exactly once evaluation.

If we wanted to be super-pedantic we could go back to all the typeclasses and make their methods take Name, Need or Value parameters. Instead we can assume that normal parameters can always be wrapped in a Value, and by-name parameters can be wrapped with Name.

When we write pure programs, we are free to replace any Name with Need or Value, and vice versa, with no change to the correctness of the program. This is the essence of referential transparency: the ability to replace a computation by its value, or a value by its computation.

In functional programming we almost always want Value or Need (also known as strict and lazy): there is little value in Name. Because there is no language level support for lazy method parameters, methods typically ask for a by-name parameter and then convert it into a Need internally, getting a boost to performance.

Name provides instances of the following typeclasses

Monad
Comonad
Traverse1
Align
Zip / Unzip / Cozip

6.3 Memoisation

Scalaz has the capability to memoise functions, formalised by Memo, which doesn’t make any guarantees about evaluation because of the diversity of implementations:

  sealed abstract class Memo[K, V] {
    def apply(z: K => V): K => V
  }
  object Memo {
    def memo[K, V](f: (K => V) => K => V): Memo[K, V]
  
    def nilMemo[K, V]: Memo[K, V] = memo[K, V](identity)
  
    def arrayMemo[V >: Null : ClassTag](n: Int): Memo[Int, V] = ...
    def doubleArrayMemo(n: Int, sentinel: Double = 0.0): Memo[Int, Double] = ...
  
    def immutableHashMapMemo[K, V]: Memo[K, V] = ...
    def immutableTreeMapMemo[K: scala.Ordering, V]: Memo[K, V] = ...
  }

memo allows us to create custom implementations of Memo, nilMemo doesn’t memoise, evaluating the function normally. The remaining implementations intercept calls to the function and cache results backed by stdlib collection implementations.

To use Memo we simply wrap a function with a Memo implementation and then call the memoised function:

  scala> def foo(n: Int): String = {
           println("running")
           if (n > 10) "wibble" else "wobble"
         }
  
  scala> val mem = Memo.arrayMemo[String](100)
         val mfoo = mem(foo)
  
  scala> mfoo(1)
  running // evaluated
  res: String = wobble
  
  scala> mfoo(1)
  res: String = wobble // memoised

If the function takes more than one parameter, we must tupled the method, with the memoised version taking a tuple.

  scala> def bar(n: Int, m: Int): String = "hello"
         val mem = Memo.immutableHashMapMemo[(Int, Int), String]
         val mbar = mem((bar _).tupled)
  
  scala> mbar((1, 2))
  res: String = "hello"

Memo is typically treated as a special construct and the usual rule about purity is relaxed for implementations. To be pure only requires that our implementations of Memo are referential transparent in the evaluation of K => V. We may use mutable data and perform I/O in the implementation of Memo, e.g. with an LRU or distributed cache, without having to declare an effect in the type signature. Other functional programming languages have automatic memoisation managed by their runtime environment and Memo is our way of extending the JVM to have similar support, unfortunately only on an opt-in basis.

6.4 Tagging

In the section introducing Monoid we built a Monoid[TradeTemplate] and realised that Scalaz does not do what we wanted with Monoid[Option[A]]. This is not an oversight of Scalaz: often we find that a data type can implement a fundamental typeclass in multiple valid ways and that the default implementation doesn’t do what we want, or simply isn’t defined.

Basic examples are Monoid[Boolean] (conjunction && vs disjunction ||) and Monoid[Int] (multiplication vs addition).

To implement Monoid[TradeTemplate] we found ourselves either breaking typeclass coherency, or using a different typeclass.

scalaz.Tag is designed to address the multiple typeclass implementation problem without breaking typeclass coherency.

The definition is quite contorted, but the syntax to use it is very clean. This is how we trick the compiler into allowing us to define an infix type A @@ T that is erased to A at runtime:

  type @@[A, T] = Tag.k.@@[A, T]
  
  object Tag {
    @inline val k: TagKind = IdTagKind
    @inline def apply[A, T](a: A): A @@ T = k(a)
    ...
  
    final class TagOf[T] private[Tag]() { ... }
    def of[T]: TagOf[T] = new TagOf[T]
  }
  sealed abstract class TagKind {
    type @@[A, T]
    def apply[A, T](a: A): A @@ T
    ...
  }
  private[scalaz] object IdTagKind extends TagKind {
    type @@[A, T] = A
    @inline override def apply[A, T](a: A): A = a
    ...
  }

Some useful tags are provided in the Tags object

  object Tags {
    sealed trait First
    val First = Tag.of[First]
  
    sealed trait Last
    val Last = Tag.of[Last]
  
    sealed trait Multiplication
    val Multiplication = Tag.of[Multiplication]
  
    sealed trait Disjunction
    val Disjunction = Tag.of[Disjunction]
  
    sealed trait Conjunction
    val Conjunction = Tag.of[Conjunction]
  
    ...
  }

First / Last are used to select Monoid instances that pick the first or last non-zero operand. Multiplication is for numeric multiplication instead of addition. Disjunction / Conjunction are to select && or ||, respectively.

In our TradeTemplate, instead of using Option[Currency] we can use Option[Currency] @@ Tags.Last. Indeed this is so common that we can use the built-in alias, LastOption

  type LastOption[A] = Option[A] @@ Tags.Last

letting us write a much cleaner Monoid[TradeTemplate]

  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: LastOption[Currency],
    otc: LastOption[Boolean]
  )
  object TradeTemplate {
    implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
      (a, b) =>
        TradeTemplate(a.payments |+| b.payments,
                      a.ccy |+| b.ccy,
                      a.otc |+| b.otc),
        TradeTemplate(Nil, Tag(None), Tag(None))
    )
  }

To create a raw value of type LastOption, we apply Tag to an Option. Here we are calling Tag(None).

In the chapter on typeclass derivation, we will go one step further and automatically derive the monoid.

It is tempting to use Tag to markup data types for some form of validation (e.g. String @@ PersonName), but this should be avoided because there are no checks on the content of the runtime value. Tag should only be used for typeclass selection purposes. Prefer the Refined library, introduced in Chapter 4, to constrain values.

6.5 Natural Transformations

A function from one type to another is written as A => B in Scala, which is syntax sugar for a Function1[A, B]. Scalaz provides similar syntax sugar F ~> G for functions over type constructors F[_] to G[_].

These F ~> G are called natural transformations and are universally quantified because they don’t care about the contents of F[_].

  type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]
  trait NaturalTransformation[-F[_], +G[_]] {
    def apply[A](fa: F[A]): G[A]
  
    def compose[E[_]](f: E ~> F): E ~> G = ...
    def andThen[H[_]](f: G ~> H): F ~> H = ...
  }

An example of a natural transformation is a function that converts an IList into a List

  scala> val convert = new (IList ~> List) {
           def apply[A](fa: IList[A]): List[A] = fa.toList
         }
  
  scala> convert(IList(1, 2, 3))
  res: List[Int] = List(1, 2, 3)

Or, more concisely, making use of kind-projector’s syntax sugar:

  scala> val convert = λ[IList ~> List](_.toList)
  
  scala> val convert = Lambda[IList ~> List](_.toList)

However, in day-to-day development, it is far more likely that we will use a natural transformation to map between algebras. For example, in drone-dynamic-agents we may want to implement our Google Container Engine Machines algebra with an off-the-shelf algebra, BigMachines. Instead of changing all our business logic and tests to use this new BigMachines interface, we may be able to write a transformation from Machines ~> BigMachines. We will return to this idea in the chapter on Advanced Monads.

6.6 `Isomorphism`

Sometimes we have two types that are really the same thing, causing compatibility problems because the compiler doesn’t know what we know. This typically happens when we use third party code that is the same as something we already have.

This is when Isomorphism can help us out. An isomorphism defines a formal “is equivalent to” relationship between two types. There are three variants, to account for types of different shapes:

  object Isomorphism {
    trait Iso[Arr[_, _], A, B] {
      def to: Arr[A, B]
      def from: Arr[B, A]
    }
    type IsoSet[A, B] = Iso[Function1, A, B]
    type <=>[A, B] = IsoSet[A, B]
    object IsoSet {
      def apply[A, B](to: A => B, from: B => A): A <=> B = ...
    }
  
    trait Iso2[Arr[_[_], _[_]], F[_], G[_]] {
      def to: Arr[F, G]
      def from: Arr[G, F]
    }
    type IsoFunctor[F[_], G[_]] = Iso2[NaturalTransformation, F, G]
    type <~>[F[_], G[_]] = IsoFunctor[F, G]
    object IsoFunctor {
      def apply[F[_], G[_]](to: F ~> G, from: G ~> F): F <~> G = ...
    }
  
    trait Iso3[Arr[_[_, _], _[_, _]], F[_, _], G[_, _]] {
      def to: Arr[F, G]
      def from: Arr[G, F]
    }
    type IsoBifunctor[F[_, _], G[_, _]] = Iso3[~~>, F, G]
    type <~~>[F[_, _], G[_, _]] = IsoBifunctor[F, G]
  
    ...
  }

The type aliases IsoSet, IsoFunctor and IsoBifunctor cover the common cases: a regular function, natural transformation and binatural. Convenience functions allow us to generate instances from existing functions or natural transformations. However, it is often easier to use one of the abstract Template classes to define an isomorphism. For example:

  val listIListIso: List <~> IList =
    new IsoFunctorTemplate[List, IList] {
      def to[A](fa: List[A]) = fromList(fa)
      def from[A](fa: IList[A]) = fa.toList
    }

If we introduce an isomorphism, we can generate many of the standard typeclasses. For example

  trait IsomorphismSemigroup[F, G] extends Semigroup[F] {
    implicit def G: Semigroup[G]
    def iso: F <=> G
    def append(f1: F, f2: =>F): F = iso.from(G.append(iso.to(f1), iso.to(f2)))
  }

allows us to derive a Semigroup[F] for a type F if we have an F <=> G and a Semigroup[G]. Almost all the typeclasses in the hierarchy provide an isomorphic variant. If we find ourselves copying and pasting a typeclass implementation, it is worth considering if Isomorphism is the better solution.

6.7 Containers

6.7.1 Maybe

We have already encountered Scalaz’s improvement over scala.Option, called Maybe. It is an improvement because it is invariant and does not have any unsafe methods like Option.get, which can throw an exception.

It is typically used to represent when a thing may be present or not without giving any extra context as to why it may be missing.

  sealed abstract class Maybe[A] { ... }
  object Maybe {
    final case class Empty[A]()    extends Maybe[A]
    final case class Just[A](a: A) extends Maybe[A]
  
    def empty[A]: Maybe[A] = Empty()
    def just[A](a: A): Maybe[A] = Just(a)
  
    def fromOption[A](oa: Option[A]): Maybe[A] = ...
    def fromNullable[A](a: A): Maybe[A] = if (null == a) empty else just(a)
    ...
  }

The .empty and .just companion methods are preferred to creating raw Empty or Just instances because they return a Maybe, helping with type inference. This pattern is often referred to as returning a sum type, which is when we have multiple implementations of a sealed trait but never use a specific subtype in a method signature.

A convenient implicit class allows us to call .just on any value and receive a Maybe

  implicit class MaybeOps[A](self: A) {
    def just: Maybe[A] = Maybe.just(self)
  }

Maybe has a typeclass instance for all the things

Align
Traverse
MonadPlus / IsEmpty
Cobind
Cozip / Zip / Unzip
Optional

and delegate instances depending on A

Monoid / Band
Equal / Order / Show

In addition to the above, Maybe has functionality that is not supported by a polymorphic typeclass.

  sealed abstract class Maybe[A] {
    def cata[B](f: A => B, b: =>B): B = this match {
      case Just(a) => f(a)
      case Empty() => b
    }
  
    def |(a: =>A): A = cata(identity, a)
    def toLeft[B](b: =>B): A \/ B = cata(\/.left, \/-(b))
    def toRight[B](b: =>B): B \/ A = cata(\/.right, -\/(b))
    def <\/[B](b: =>B): A \/ B = toLeft(b)
    def \/>[B](b: =>B): B \/ A = toRight(b)
  
    def orZero(implicit A: Monoid[A]): A = getOrElse(A.zero)
    def orEmpty[F[_]: Applicative: PlusEmpty]: F[A] =
      cata(Applicative[F].point(_), PlusEmpty[F].empty)
    ...
  }

.cata is a terser alternative to .map(f).getOrElse(b) and has the simpler form | if the map is identity (i.e. just .getOrElse).

.toLeft and .toRight, and their symbolic aliases, create a disjunction (explained in the next section) by taking a fallback for the Empty case.

.orZero takes a Monoid to define the default value.

.orEmpty uses an ApplicativePlus to create a single element or empty container, not forgetting that we already get support for stdlib collections from the Foldable instance’s .to method.

  scala> 1.just.orZero
  res: Int = 1
  
  scala> Maybe.empty[Int].orZero
  res: Int = 0
  
  scala> Maybe.empty[Int].orEmpty[IList]
  res: IList[Int] = []
  
  scala> 1.just.orEmpty[IList]
  res: IList[Int] = [1]
  
  scala> 1.just.to[List] // from Foldable
  res: List[Int] = List(1)

Methods are defined in OOP style on Maybe, contrary to our Chapter 4 lesson to use an object or implicit class. This is a common theme in Scalaz and the reason is largely historical:

text editors failed to find extension methods, but this now works seamlessly in IntelliJ, ENSIME and ScalaIDE.
there are corner cases where the compiler would fail to infer the types and not be able to find the extension method.
the stdlib defines some implicit class instances that add methods to all values, with conflicting method names. + is the most prominent example, turning everything into a concatenated String.

The same is true for functionality that is provided by typeclass instances, such as these methods which are otherwise provided by Optional

  sealed abstract class Maybe[A] {
    def getOrElse(a: =>A): A = ...
    ...
  }

However, recent versions of Scala have addressed many bugs and we are now less likely to encounter problems.

6.7.2 Either

Scalaz’s improvement over scala.Either is symbolic, but it is common to speak about it as either or Disjunction

  sealed abstract class \/[+A, +B] { ... }
  final case class -\/[+A](a: A) extends (A \/ Nothing)
  final case class \/-[+B](b: B) extends (Nothing \/ B)
  
  type Disjunction[+A, +B] = \/[A, B]
  
  object \/ {
    def left [A, B]: A => A \/ B = -\/(_)
    def right[A, B]: B => A \/ B = \/-(_)
  
    def fromEither[A, B](e: Either[A, B]): A \/ B = ...
    ...
  }

with corresponding syntax

  implicit class EitherOps[A](val self: A) {
    final def left [B]: (A \/ B) = -\/(self)
    final def right[B]: (B \/ A) = \/-(self)
  }

allowing for easy construction of values. Note that the extension method takes the type of the other side. So if we wish to create a String \/ Int and we have an Int, we must pass String when calling .right

  scala> 1.right[String]
  res: String \/ Int = \/-(1)
  
  scala> "hello".left[Int]
  res: String \/ Int = -\/(hello)

The symbolic nature of \/ makes it read well in type signatures when shown infix. Note that symbolic types in Scala associate from the left and nested \/ must have parentheses, e.g. (A \/ (B \/ (C \/ D)).

\/ has right-biased (i.e. flatMap applies to \/-) typeclass instances for:

Monad / MonadError
Traverse / Bitraverse
Plus
Optional
Cozip

and depending on the contents

Equal / Order
Semigroup / Monoid / Band

In addition, there are custom methods

  sealed abstract class \/[+A, +B] { self =>
    def fold[X](l: A => X, r: B => X): X = self match {
      case -\/(a) => l(a)
      case \/-(b) => r(b)
    }
  
    def swap: (B \/ A) = self match {
      case -\/(a) => \/-(a)
      case \/-(b) => -\/(b)
    }
  
    def |[BB >: B](x: =>BB): BB = getOrElse(x) // Optional[_]
    def |||[C, BB >: B](x: =>C \/ BB): C \/ BB = orElse(x) // Optional[_]
  
    def +++[AA >: A: Semigroup, BB >: B: Semigroup](x: =>AA \/ BB): AA \/ BB = ...
  
    def toEither: Either[A, B] = ...
  
    final class SwitchingDisjunction[X](right: =>X) {
      def <<?:(left: =>X): X = ...
    }
    def :?>>[X](right: =>X) = new SwitchingDisjunction[X](right)
    ...
  }

.fold is similar to Maybe.cata and requires that both the left and right sides are mapped to the same type.

.swap swaps a left into a right and a right into a left.

The | alias to getOrElse appears similarly to Maybe. We also get ||| as an alias to orElse.

+++ is for combining disjunctions with lefts taking preference over right:

right(v1) +++ right(v2) gives right(v1 |+| v2)
right(v1) +++ left (v2) gives left (v2)
left (v1) +++ right(v2) gives left (v1)
left (v1) +++ left (v2) gives left (v1 |+| v2)

.toEither is provided for backwards compatibility with the Scala stdlib.

The combination of :?>> and <<?: allow for a convenient syntax to ignore the contents of an \/, but pick a default based on its type

  scala> 1 <<?: foo :?>> 2
  res: Int = 2 // foo is a \/-
  
  scala> 1 <<?: foo.swap :?>> 2
  res: Int = 1

6.7.3 Validation

At first sight, Validation (aliased with \?/, happy Elvis) appears to be a clone of Disjunction:

  sealed abstract class Validation[+E, +A] { ... }
  final case class Success[A](a: A) extends Validation[Nothing, A]
  final case class Failure[E](e: E) extends Validation[E, Nothing]
  
  type ValidationNel[E, +X] = Validation[NonEmptyList[E], X]
  
  object Validation {
    type \?/[+E, +A] = Validation[E, A]
  
    def success[E, A]: A => Validation[E, A] = Success(_)
    def failure[E, A]: E => Validation[E, A] = Failure(_)
    def failureNel[E, A](e: E): ValidationNel[E, A] = Failure(NonEmptyList(e))
  
    def lift[E, A](a: A)(f: A => Boolean, fail: E): Validation[E, A] = ...
    def liftNel[E, A](a: A)(f: A => Boolean, fail: E): ValidationNel[E, A] = ...
    def fromEither[E, A](e: Either[E, A]): Validation[E, A] = ...
    ...
  }

With convenient syntax

  implicit class ValidationOps[A](self: A) {
    def success[X]: Validation[X, A] = Validation.success[X, A](self)
    def successNel[X]: ValidationNel[X, A] = success
    def failure[X]: Validation[A, X] = Validation.failure[A, X](self)
    def failureNel[X]: ValidationNel[A, X] = Validation.failureNel[A, X](self)
  }

However, the data structure itself is not the complete story. Validation intentionally does not have an instance of any Monad, restricting itself to success-biased versions of:

Applicative
Traverse / Bitraverse
Cozip
Plus
Optional

and depending on the contents

Equal / Order
Show
Semigroup / Monoid

The big advantage of restricting to Applicative is that Validation is explicitly for situations where we wish to report all failures, whereas Disjunction is used to stop at the first failure. To accommodate failure accumulation, a popular form of Validation is ValidationNel, having a NonEmptyList[E] in the failure position.

Consider performing input validation of data provided by a user using Disjunction and flatMap:

  scala> :paste
         final case class Credentials(user: Username, name: Fullname)
         final case class Username(value: String) extends AnyVal
         final case class Fullname(value: String) extends AnyVal
  
         def username(in: String): String \/ Username =
           if (in.isEmpty) "empty username".left
           else if (in.contains(" ")) "username contains spaces".left
           else Username(in).right
  
         def realname(in: String): String \/ Fullname =
           if (in.isEmpty) "empty real name".left
           else Fullname(in).right
  
  scala> for {
           u <- username("sam halliday")
           r <- realname("")
         } yield Credentials(u, r)
  res = -\/(username contains spaces)

If we use |@| syntax

  scala> (username("sam halliday") |@| realname("")) (Credentials.apply)
  res = -\/(username contains spaces)

we still get back the first failure. This is because Disjunction is a Monad, its .applyX methods must be consistent with .flatMap and not assume that any operations can be performed out of order. Compare to:

  scala> :paste
         def username(in: String): ValidationNel[String, Username] =
           if (in.isEmpty) "empty username".failureNel
           else if (in.contains(" ")) "username contains spaces".failureNel
           else Username(in).success
  
         def realname(in: String): ValidationNel[String, Fullname] =
           if (in.isEmpty) "empty real name".failureNel
           else Fullname(in).success
  
  scala> (username("sam halliday") |@| realname("")) (Credentials.apply)
  res = Failure(NonEmpty[username contains spaces,empty real name])

This time, we get back all the failures!

Validation has many of the same methods as Disjunction, such as .fold, .swap and +++, plus some extra:

  sealed abstract class Validation[+E, +A] {
    def append[F >: E: Semigroup, B >: A: Semigroup](x: F \?/ B]): F \?/ B = ...
  
    def disjunction: (E \/ A) = ...
    ...
  }

.append (aliased by +|+) has the same type signature as +++ but prefers the success case

failure(v1) +|+ failure(v2) gives failure(v1 |+| v2)
failure(v1) +|+ success(v2) gives success(v2)
success(v1) +|+ failure(v2) gives success(v1)
success(v1) +|+ success(v2) gives success(v1 |+| v2)

.disjunction converts a Validated[A, B] into an A \/ B. Disjunction has the mirror .validation and .validationNel to convert into Validation, allowing for easy conversion between sequential and parallel failure accumulation.

\/ and Validation are the more performant FP equivalent of a checked exception for input validation, avoiding both a stacktrace and requiring the caller to deal with the failure resulting in more robust systems.

6.7.4 These

We encountered These, a data encoding of inclusive logical OR, when we learnt about Align.

  sealed abstract class \&/[+A, +B] { ... }
  object \&/ {
    type These[A, B] = A \&/ B
  
    final case class This[A](aa: A) extends (A \&/ Nothing)
    final case class That[B](bb: B) extends (Nothing \&/ B)
    final case class Both[A, B](aa: A, bb: B) extends (A \&/ B)
  
    def apply[A, B](a: A, b: B): These[A, B] = Both(a, b)
  }

with convenient construction syntax

  implicit class TheseOps[A](self: A) {
    final def wrapThis[B]: A \&/ B = \&/.This(self)
    final def wrapThat[B]: B \&/ A = \&/.That(self)
  }
  implicit class ThesePairOps[A, B](self: (A, B)) {
    final def both: A \&/ B = \&/.Both(self._1, self._2)
  }

These has typeclass instances for

Monad
Bitraverse
Traverse
Cobind

and depending on contents

Semigroup / Monoid / Band
Equal / Order
Show

These (\&/) has many of the methods we have come to expect of Disjunction (\/) and Validation (\?/)

  sealed abstract class \&/[+A, +B] {
    def fold[X](s: A => X, t: B => X, q: (A, B) => X): X = ...
    def swap: (B \&/ A) = ...
  
    def append[X >: A: Semigroup, Y >: B: Semigroup](o: =>(X \&/ Y)): X \&/ Y = ...
  
    def &&&[X >: A: Semigroup, C](t: X \&/ C): X \&/ (B, C) = ...
    ...
  }

.append has 9 possible arrangements and data is never thrown away because cases of This and That can always be converted into a Both.

.flatMap is right-biased (Both and That), taking a Semigroup of the left content (This) to combine rather than break early. &&& is a convenient way of binding over two of these, creating a tuple on the right and dropping data if it is not present in each of these.

Although it is tempting to use \&/ in return types, overuse is an anti-pattern. The main reason to use \&/ is to combine or split potentially infinite streams of data in finite memory. Convenient functions exist on the companion to deal with EphemeralStream (aliased here to fit in a single line) or anything with a MonadPlus

  type EStream[A] = EphemeralStream[A]
  
  object \&/ {
    def concatThisStream[A, B](x: EStream[A \&/ B]): EStream[A] = ...
    def concatThis[F[_]: MonadPlus, A, B](x: F[A \&/ B]): F[A] = ...
  
    def concatThatStream[A, B](x: EStream[A \&/ B]): EStream[B] = ...
    def concatThat[F[_]: MonadPlus, A, B](x: F[A \&/ B]): F[B] = ...
  
    def unalignStream[A, B](x: EStream[A \&/ B]): (EStream[A], EStream[B]) = ...
    def unalign[F[_]: MonadPlus, A, B](x: F[A \&/ B]): (F[A], F[B]) = ...
  
    def merge[A: Semigroup](t: A \&/ A): A = ...
    ...
  }

6.7.5 Higher Kinded Either

The Coproduct data type (not to be confused with the more general concept of a coproduct in an ADT) wraps Disjunction for type constructors:

  final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A]) { ... }
  object Coproduct {
    def leftc[F[_], G[_], A](x: F[A]): Coproduct[F, G, A] = Coproduct(-\/(x))
    def rightc[F[_], G[_], A](x: G[A]): Coproduct[F, G, A] = Coproduct(\/-(x))
    ...
  }

Typeclass instances simply delegate to those of the F[_] and G[_].

The most popular use case for Coproduct is when we want to create an anonymous coproduct of multiple ADTs.

6.7.6 Not So Eager

Built-in Scala tuples, and basic data types like Maybe and Disjunction are eagerly-evaluated value types.

For convenience, by-name alternatives to Name are provided, having the expected typeclass instances:

  sealed abstract class LazyTuple2[A, B] {
    def _1: A
    def _2: B
  }
  ...
  sealed abstract class LazyTuple4[A, B, C, D] {
    def _1: A
    def _2: B
    def _3: C
    def _4: D
  }
  
  sealed abstract class LazyOption[+A] { ... }
  private final case class LazySome[A](a: () => A) extends LazyOption[A]
  private case object LazyNone extends LazyOption[Nothing]
  
  sealed abstract class LazyEither[+A, +B] { ... }
  private case class LazyLeft[A, B](a: () => A) extends LazyEither[A, B]
  private case class LazyRight[A, B](b: () => B) extends LazyEither[A, B]

The astute reader will note that Lazy* is a misnomer, and these data types should perhaps be: ByNameTupleX, ByNameOption and ByNameEither.

6.7.7 Const

Const, for constant, is a wrapper for a value of type A, along with a spare type parameter B.

  final case class Const[A, B](getConst: A)

Const provides an instance of Applicative[Const[A, ?]] if there is a Monoid[A] available:

  implicit def applicative[A: Monoid]: Applicative[Const[A, ?]] =
    new Applicative[Const[A, ?]] {
      def point[B](b: =>B): Const[A, B] =
        Const(Monoid[A].zero)
      def ap[B, C](fa: =>Const[A, B])(fbc: =>Const[A, B => C]): Const[A, C] =
        Const(fbc.getConst |+| fa.getConst)
    }

The most important thing about this Applicative is that it ignores the B parameters, continuing on without failing and only combining the constant values that it encounters.

Going back to our example application drone-dynamic-agents, we should first refactor our logic.scala file to use Applicative instead of Monad. We wrote logic.scala before we learnt about Applicative and now we know better:

  final class DynAgentsModule[F[_]: Applicative](D: Drone[F], M: Machines[F])
    extends DynAgents[F] {
    ...
    def act(world: WorldView): F[WorldView] = world match {
      case NeedsAgent(node) =>
        M.start(node) >| world.copy(pending = Map(node -> world.time))
  
      case Stale(nodes) =>
        nodes.traverse { node =>
          M.stop(node) >| node
        }.map { stopped =>
          val updates = stopped.strengthR(world.time).toList.toMap
          world.copy(pending = world.pending ++ updates)
        }
  
      case _ => world.pure[F]
    }
    ...
  }

Since our business logic only requires an Applicative, we can write mock implementations with F[a] as Const[String, a]. In each case, we return the name of the function that is called:

  object ConstImpl {
    type F[a] = Const[String, a]
  
    private val D = new Drone[F] {
      def getBacklog: F[Int] = Const("backlog")
      def getAgents: F[Int]  = Const("agents")
    }
  
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]     = Const("alive")
      def getManaged: F[NonEmptyList[MachineNode]] = Const("managed")
      def getTime: F[Epoch]                        = Const("time")
      def start(node: MachineNode): F[Unit]        = Const("start")
      def stop(node: MachineNode): F[Unit]         = Const("stop")
    }
  
    val program = new DynAgentsModule[F](D, M)
  }

With this interpretation of our program, we can assert on the methods that are called:

  it should "call the expected methods" in {
    import ConstImpl._
  
    val alive    = Map(node1 -> time1, node2 -> time1)
    val world    = WorldView(1, 1, managed, alive, Map.empty, time4)
  
    program.act(world).getConst shouldBe "stopstop"
  }

Alternatively, we could have counted total method calls by using Const[Int, ?] or an IMap[String, Int].

With this test, we’ve gone beyond traditional Mock testing with a Const test that asserts on what is called without having to provide implementations. This is useful if our specification demands that we make certain calls for certain input, e.g. for accounting purposes. Furthermore, we’ve achieved this with compiletime safety.

Taking this line of thinking a little further, say we want to monitor (in production) the nodes that we are stopping in act. We can create implementations of Drone and Machines with Const, calling it from our wrapped version of act

  final class Monitored[U[_]: Functor](program: DynAgents[U]) {
    type F[a] = Const[Set[MachineNode], a]
    private val D = new Drone[F] {
      def getBacklog: F[Int] = Const(Set.empty)
      def getAgents: F[Int]  = Const(Set.empty)
    }
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]     = Const(Set.empty)
      def getManaged: F[NonEmptyList[MachineNode]] = Const(Set.empty)
      def getTime: F[Epoch]                        = Const(Set.empty)
      def start(node: MachineNode): F[Unit]        = Const(Set.empty)
      def stop(node: MachineNode): F[Unit]         = Const(Set(node))
    }
    val monitor = new DynAgentsModule[F](D, M)
  
    def act(world: WorldView): U[(WorldView, Set[MachineNode])] = {
      val stopped = monitor.act(world).getConst
      program.act(world).strengthR(stopped)
    }
  }

We can do this because monitor is pure and running it produces no side effects.

This runs the program with ConstImpl, extracting all the calls to Machines.stop, then returning it alongside the WorldView. We can unit test this:

  it should "monitor stopped nodes" in {
    val underlying = new Mutable(needsAgents).program
  
    val alive = Map(node1 -> time1, node2 -> time1)
    val world = WorldView(1, 1, managed, alive, Map.empty, time4)
    val expected = world.copy(pending = Map(node1 -> time4, node2 -> time4))
  
    val monitored = new Monitored(underlying)
    monitored.act(world) shouldBe (expected -> Set(node1, node2))
  }

We have used Const to do something that looks like Aspect Oriented Programming, once popular in Java. We built on top of our business logic to support a monitoring concern, without having to complicate the business logic.

It gets even better. We can run ConstImpl in production to gather what we want to stop, and then provide an optimised implementation of act that can make use of implementation-specific batched calls.

The silent hero of this story is Applicative. Const lets us show off what is possible. If we need to change our program to require a Monad, we can no longer use Const and must write full mocks to be able to assert on what is called under certain inputs. The Rule of Least Power demands that we use Applicative instead of Monad wherever we can.

6.8 Collections

Unlike the stdlib Collections API, the Scalaz approach describes collection behaviours in the typeclass hierarchy, e.g. Foldable, Traverse, Monoid. What remains to be studied are the implementations in terms of data structures, which have different performance characteristics and niche methods.

This section goes into the implementation details for each data type. It is not essential to remember everything presented here: the goal is to gain a high level understanding of how each data structure works.

Because all the collection data types provide more or less the same list of typeclass instances, we shall avoid repeating the list, which is often some variation of:

Monoid
Traverse / Foldable
MonadPlus / IsEmpty
Cobind / Comonad
Zip / Unzip
Align
Equal / Order
Show

Data structures that are provably non-empty are able to provide

Traverse1 / Foldable1

and provide Semigroup instead of Monoid, Plus instead of IsEmpty.

6.8.1 Lists

We have used IList[A] and NonEmptyList[A] so many times by now that they should be familiar. They codify a classic linked list data structure:

  sealed abstract class IList[A] {
    def ::(a: A): IList[A] = ...
    def :::(as: IList[A]): IList[A] = ...
    def toList: List[A] = ...
    def toNel: Option[NonEmptyList[A]] = ...
    ...
  }
  final case class INil[A]() extends IList[A]
  final case class ICons[A](head: A, tail: IList[A]) extends IList[A]
  
  final case class NonEmptyList[A](head: A, tail: IList[A]) {
    def <::(b: A): NonEmptyList[A] = nel(b, head :: tail)
    def <:::(bs: IList[A]): NonEmptyList[A] = ...
    ...
  }

The source code for Scalaz 7.3 reveals that INil is implemented as

  sealed abstract case class INil[A] private() extends IList[A]
  object INil {
    private[this] val value: INil[Nothing] = new INil[Nothing]{}
    def apply[A](): IList[A] = value.asInstanceOf[IList[A]]
  }

which exploits JVM implementation details to avoid an object allocation when creating an INil.

This optimisation is manually applied to all zero-parameter classes. Indeed, Scalaz is full of many optimisations of this nature: debated and accepted only when presented with evidence of a significant performance boost and no risk of a semantic change.

The main advantage of IList over stdlib List is that there are no unsafe methods, like .head which throws an exception on an empty list.

In addition, IList is a lot simpler, having no hierarchy and a much smaller bytecode footprint. Furthermore, the stdlib List has a terrifying implementation that uses var to workaround performance problems in the stdlib collection design:

  package scala.collection.immutable
  
  sealed abstract class List[+A]
    extends AbstractSeq[A]
    with LinearSeq[A]
    with GenericTraversableTemplate[A, List]
    with LinearSeqOptimized[A, List[A]] { ... }
  case object Nil extends List[Nothing] { ... }
  final case class ::[B](
    override val head: B,
    private[scala] var tl: List[B]
  ) extends List[B] { ... }

List creation requires careful, and slow, Thread synchronisation to ensure safe publishing. IList requires no such hacks and can therefore outperform List.

6.8.2 `EphemeralStream`

The stdlib Stream is a lazy version of List, but is riddled with memory leaks and unsafe methods. EphemeralStream does not keep references to computed values, helping to alleviate the memory retention problem, and removing unsafe methods in the same spirit as IList.

  sealed abstract class EphemeralStream[A] {
    def headOption: Option[A]
    def tailOption: Option[EphemeralStream[A]]
    ...
  }
  // private implementations
  object EphemeralStream extends EphemeralStreamInstances {
    type EStream[A] = EphemeralStream[A]
  
    def emptyEphemeralStream[A]: EStream[A] = ...
    def cons[A](a: =>A, as: =>EStream[A]): EStream[A] = ...
    def unfold[A, B](start: =>B)(f: B => Option[(A, B)]): EStream[A] = ...
    def iterate[A](start: A)(f: A => A): EStream[A] = ...
  
    implicit class ConsWrap[A](e: =>EStream[A]) {
      def ##::(h: A): EStream[A] = cons(h, e)
    }
    object ##:: {
      def unapply[A](xs: EStream[A]): Option[(A, EStream[A])] =
        if (xs.isEmpty) None
        else Some((xs.head(), xs.tail()))
    }
    ...
  }

.cons, .unfold and .iterate are mechanisms for creating streams, and the convenient syntax ##:: puts a new element at the head of a by-name EStream reference. .unfold is for creating a finite (but possibly infinite) stream by repeatedly applying a function f to get the next value and input for the following f. .iterate creates an infinite stream by repeating a function f on the previous element.

EStream may appear in pattern matches with the symbol ##::, matching the syntax for .cons.

Although EStream addresses the value memory retention problem, it is still possible to suffer from slow memory leaks if a live reference points to the head of an infinite stream. Problems of this nature, as well as the need to compose effectful streams, are why fs2 exists.

6.8.3 `CorecursiveList`

Corecursion is when we start from a base state and produce subsequent steps deterministically, like the EphemeralStream.unfold method that we just studied:

  def unfold[A, B](b: =>B)(f: B => Option[(A, B)]): EStream[A] = ...

Contrast to recursion, which breaks data into a base state and then terminates.

A CorecursiveList is a data encoding of EphemeralStream.unfold, offering an alternative to EStream that may perform better in some circumstances:

  sealed abstract class CorecursiveList[A] {
    type S
    def init: S
    def step: S => Maybe[(S, A)]
  }
  
  object CorecursiveList {
    private final case class CorecursiveListImpl[S0, A](
      init: S0,
      step: S0 => Maybe[(S0, A)]
    ) extends CorecursiveList[A] { type S = S0 }
  
    def apply[S, A](init: S)(step: S => Maybe[(S, A)]): CorecursiveList[A] =
      CorecursiveListImpl(init, step)
  
    ...
  }

Corecursion is useful when implementing Comonad.cojoin, like our Hood example. CorecursiveList is a good way to codify non-linear recurrence equations like those used in biology population models, control systems, macro economics, and investment banking models.

6.8.4 `ImmutableArray`

A simple wrapper around mutable stdlib Array, with primitive specialisations:

  sealed abstract class ImmutableArray[+A] {
    def ++[B >: A: ClassTag](o: ImmutableArray[B]): ImmutableArray[B]
    ...
  }
  object ImmutableArray {
    final class StringArray(s: String) extends ImmutableArray[Char] { ... }
    sealed class ImmutableArray1[+A](as: Array[A]) extends ImmutableArray[A] { ... }
    final class ofRef[A <: AnyRef](as: Array[A]) extends ImmutableArray1[A](as)
    ...
    final class ofLong(as: Array[Long]) extends ImmutableArray1[Long](as)
  
    def fromArray[A](x: Array[A]): ImmutableArray[A] = ...
    def fromString(str: String): ImmutableArray[Char] = ...
    ...
  }

Array is unrivalled in terms of read performance and heap size. However, there is zero structural sharing when creating new arrays, therefore arrays are typically used only when their contents are not expected to change, or as a way of safely wrapping raw data from a legacy system.

6.8.5 `Dequeue`

A Dequeue (pronounced like a “deck” of cards) is a linked list that allows items to be put onto or retrieved from the front (cons) or the back (snoc) in constant time. Removing an element from either end is constant time on average.

  sealed abstract class Dequeue[A] {
    def frontMaybe: Maybe[A]
    def backMaybe: Maybe[A]
  
    def ++(o: Dequeue[A]): Dequeue[A] = ...
    def +:(a: A): Dequeue[A] = cons(a)
    def :+(a: A): Dequeue[A] = snoc(a)
    def cons(a: A): Dequeue[A] = ...
    def snoc(a: A): Dequeue[A] = ...
    def uncons: Maybe[(A, Dequeue[A])] = ...
    def unsnoc: Maybe[(A, Dequeue[A])] = ...
    ...
  }
  private final case class SingletonDequeue[A](single: A) extends Dequeue[A] { ... }
  private final case class FullDequeue[A](
    front: NonEmptyList[A],
    fsize: Int,
    back: NonEmptyList[A],
    backSize: Int) extends Dequeue[A] { ... }
  private final case object EmptyDequeue extends Dequeue[Nothing] { ... }
  
  object Dequeue {
    def empty[A]: Dequeue[A] = EmptyDequeue()
    def apply[A](as: A*): Dequeue[A] = ...
    def fromFoldable[F[_]: Foldable, A](fa: F[A]): Dequeue[A] = ...
    ...
  }

The way it works is that there are two lists, one for the front data and another for the back. Consider an instance holding symbols a0, a1, a2, a3, a4, a5, a6

  FullDequeue(
    NonEmptyList('a0, IList('a1, 'a2, 'a3)), 4,
    NonEmptyList('a6, IList('a5, 'a4)), 3)

which can be visualised as

Note that the list holding the back is in reverse order.

Reading the snoc (final element) is a simple lookup into back.head. Adding an element to the end of the Dequeue means adding a new element to the head of the back, and recreating the FullDequeue wrapper (which will increase backSize by one). Almost all of the original structure is shared. Compare to adding a new element to the end of an IList, which would involve recreating the entire structure.

The frontSize and backSize are used to re-balance the front and back so that they are always approximately the same size. Re-balancing means that some operations can be slower than others (e.g. when the entire structure must be rebuilt) but because it happens only occasionally, we can take the average of the cost and say that it is constant.

6.8.6 `DList`

Linked lists have poor performance characteristics when large lists are appended together. Consider the work that goes into evaluating the following:

  ((as ::: bs) ::: (cs ::: ds)) ::: (es ::: (fs ::: gs))

This creates six intermediate lists, traversing and rebuilding every list three times (except for gs which is shared between all stages).

The DList (for difference list) is a more efficient solution for this scenario. Instead of performing the calculations at each stage, it is represented as a function IList[A] => IList[A]

  final case class DList[A](f: IList[A] => IList[A]) {
    def toIList: IList[A] = f(IList.empty)
    def ++(as: DList[A]): DList[A] = DList(xs => f(as.f(xs)))
    ...
  }
  object DList {
    def fromIList[A](as: IList[A]): DList[A] = DList(xs => as ::: xs)
  }

The equivalent calculation is (the symbols created via DList.fromIList)

  (((a ++ b) ++ (c ++ d)) ++ (e ++ (f ++ g))).toIList

which breaks the work into right-associative (i.e. fast) appends

  (as ::: (bs ::: (cs ::: (ds ::: (es ::: (fs ::: gs))))))

utilising the fast constructor on IList.

As always, there is no free lunch. There is a memory allocation overhead that can slow down code that naturally results in right-associative appends. The largest speedup is when IList operations are left-associative, e.g.

  ((((((as ::: bs) ::: cs) ::: ds) ::: es) ::: fs) ::: gs)

Difference lists suffer from bad marketing. If they were called a ListBuilderFactory they’d probably be in the standard library.

6.8.7 `ISet`

Tree structures are excellent for storing ordered data, with every binary node holding elements that are less than in one branch, and greater than in the other. However, naive implementations of a tree structure can become unbalanced depending on the insertion order. It is possible to maintain a perfectly balanced tree, but it is incredibly inefficient as every insertion effectively rebuilds the entire tree.

ISet is an implementation of a tree of bounded balance, meaning that it is approximately balanced, using the size of each branch to balance a node.

  sealed abstract class ISet[A] {
    val size: Int = this match {
      case Tip()        => 0
      case Bin(_, l, r) => 1 + l.size + r.size
    }
    ...
  }
  object ISet {
    private final case class Tip[A]() extends ISet[A]
    private final case class Bin[A](a: A, l: ISet[A], r: ISet[A]) extends ISet[A]
  
    def empty[A]: ISet[A] = Tip()
    def singleton[A](x: A): ISet[A] = Bin(x, Tip(), Tip())
    def fromFoldable[F[_]: Foldable, A: Order](xs: F[A]): ISet[A] =
      xs.foldLeft(empty[A])((a, b) => a insert b)
    ...
  }

ISet requires A to have an Order. The Order[A] instance must remain the same between calls or internal assumptions will be invalid, leading to data corruption: i.e. we are assuming typeclass coherence such that Order[A] is unique for any A.

The ISet ADT unfortunately permits invalid trees. We strive to write ADTs that fully describe what is and isn’t valid through type restrictions, but sometimes there are situations where it can only be achieved by the inspired touch of an immortal. Instead, Tip / Bin are private, to stop users from accidentally constructing invalid trees. .insert is the only way to build an ISet, therefore defining what constitutes a valid tree.

  sealed abstract class ISet[A] {
    ...
    def contains(x: A)(implicit o: Order[A]): Boolean = ...
    def union(other: ISet[A])(implicit o: Order[A]): ISet[A] = ...
    def delete(x: A)(implicit o: Order[A]): ISet[A] = ...
  
    def insert(x: A)(implicit o: Order[A]): ISet[A] = this match {
      case Tip() => ISet.singleton(x)
      case self @ Bin(y, l, r) => o.order(x, y) match {
        case LT => balanceL(y, l.insert(x), r)
        case GT => balanceR(y, l, r.insert(x))
        case EQ => self
      }
    }
    ...
  }

The internal methods .balanceL and .balanceR are mirrors of each other, so we only study .balanceL, which is called when the value we are inserting is less than the current node. It is also called by the .delete method.

  def balanceL[A](y: A, left: ISet[A], right: ISet[A]): ISet[A] = (left, right) match {
  ...

Balancing requires us to classify the scenarios that can occur. We will go through each possible scenario, visualising the (y, left, right) on the left side of the page, with the balanced structure on the right, also known as the rotated tree.

filled circles visualise a Tip
three columns visualise the left | value | right fields of Bin
diamonds visualise any ISet

The first scenario is the trivial case, which is when both the left and right are Tip. In fact we will never encounter this scenario from .insert, but we hit it in .delete

  case (Tip(), Tip()) => singleton(y)

The second case is when left is a Bin containing only Tip, we don’t need to balance anything, we just create the obvious connection:

  case (Bin(lx, Tip(), Tip()), Tip()) => Bin(y, left, Tip())

The third case is when it starts to get interesting: left is a Bin containing a Bin in its right

  case (Bin(lx, Tip(), Bin(lrx, _, _)), Tip()) =>
    Bin(lrx, singleton(lx), singleton(y))

But what happened to the two diamonds sitting below lrx? Didn’t we just lose information? No, we didn’t lose information, because we can reason (based on size balancing) that they are always Tip! There is no rule in any of the following scenarios (or in .balanceR) that can produce a tree of the shape where the diamonds are Bin.

The fourth case is the opposite of the third case.

  case (Bin(lx, ll, Tip()), Tip()) => Bin(lx, ll, singleton(y))

The fifth case is when we have full trees on both sides of the left and we must use their relative sizes to decide on how to re-balance.

  case (Bin(lx, ll, lr), Tip()) if (2*ll.size > lr.size) =>
    Bin(lx, ll, Bin(y, lr, Tip()))
  case (Bin(lx, ll, Bin(lrx, lrl, lrr)), Tip()) =>
    Bin(lrx, Bin(lx, ll, lrl), Bin(y, lrr, Tip()))

For the first branch, 2*ll.size > lr.size

and for the second branch 2*ll.size <= lr.size

The sixth scenario introduces a tree on the right. When the left is empty we create the obvious connection. This scenario never arises from .insert because the left is always non-empty:

  case (Tip(), r) => Bin(y, Tip(), r)

The final scenario is when we have non-empty trees on both sides. Unless the left is three times or more the size of the right, we can do the simple thing and create a new Bin

  case _ if l.size <= 3 * r.size => Bin(y, l, r)

However, should the left be more than three times the size of the right, we must balance based on the relative sizes of ll and lr, like in scenario five.

  case (Bin(lx, ll, lr), r) if (2*ll.size > lr.size) =>
    Bin(lx, ll, Bin(y, lr, r))
  case (Bin(lx, ll, Bin(lrx, lrl, lrr)), r) =>
    Bin(lrx, Bin(lx, ll, lrl), Bin(y, lrr, r))

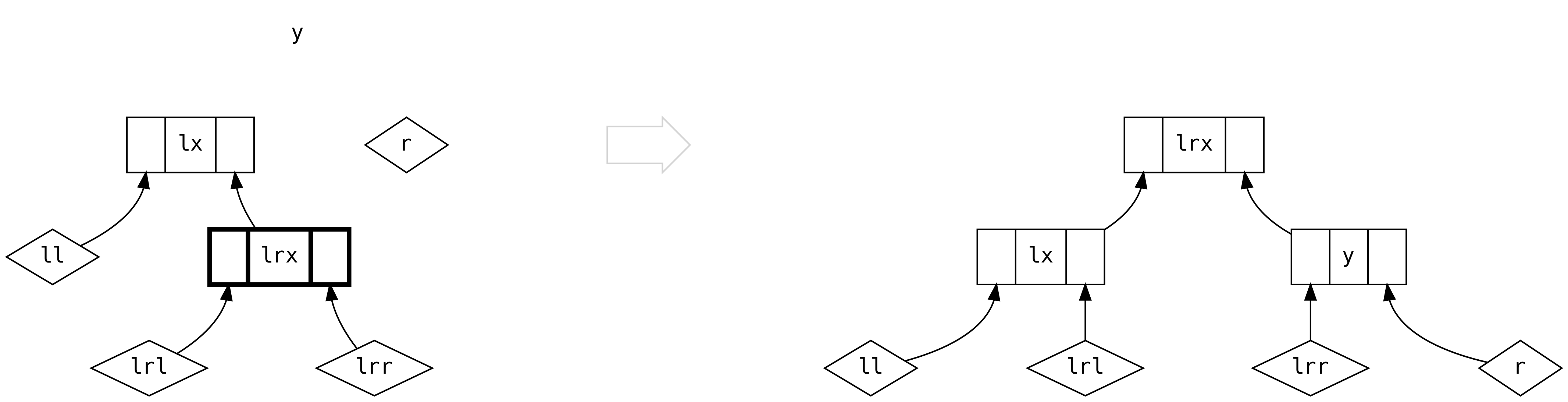
This concludes our study of the .insert method and how the ISet is constructed. It should be of no surprise that Foldable is implemented in terms of depth-first search along the left or right, as appropriate. Methods such as .minimum and .maximum are optimal because the data structure already encodes the ordering.

It is worth noting that some typeclass methods cannot be implemented as efficiently as we would like. Consider the signature of Foldable.element

  @typeclass trait Foldable[F[_]] {
    ...
    def element[A: Equal](fa: F[A], a: A): Boolean
    ...
  }

The obvious implementation for .element is to defer to (almost) binary-search ISet.contains. However, it is not possible because .element provides Equal whereas .contains requires Order.

ISet is unable to provide a Functor for the same reason. In practice this turns out to be a sensible constraint: performing a .map would involve rebuilding the entire structure. It is sensible to convert to some other datatype, such as IList, perform the .map, and convert back. A consequence is that it is not possible to have Traverse[ISet] or Applicative[ISet].

6.8.8 `IMap`

  sealed abstract class ==>>[A, B] {
    val size: Int = this match {
      case Tip()           => 0
      case Bin(_, _, l, r) => 1 + l.size + r.size
    }
  }
  object ==>> {
    type IMap[A, B] = A ==>> B
  
    private final case class Tip[A, B]() extends (A ==>> B)
    private final case class Bin[A, B](
      key: A,
      value: B,
      left: A ==>> B,
      right: A ==>> B
    ) extends ==>>[A, B]
  
    def apply[A: Order, B](x: (A, B)*): A ==>> B = ...
  
    def empty[A, B]: A ==>> B = Tip[A, B]()
    def singleton[A, B](k: A, x: B): A ==>> B = Bin(k, x, Tip(), Tip())
    def fromFoldable[F[_]: Foldable, A: Order, B](fa: F[(A, B)]): A ==>> B = ...
    ...
  }

This is very familiar! Indeed, IMap (an alias to the lightspeed operator ==>>) is another size-balanced tree, but with an extra value: B field in each binary branch, allowing it to store key/value pairs. Only the key type A needs an Order and a suite of convenient methods are provided to allow easy entry updating

  sealed abstract class ==>>[A, B] {
    ...
    def adjust(k: A, f: B => B)(implicit o: Order[A]): A ==>> B = ...
    def adjustWithKey(k: A, f: (A, B) => B)(implicit o: Order[A]): A ==>> B = ...
    ...
  }

6.8.9 `StrictTree` and `Tree`

Both StrictTree and Tree are implementations of a Rose Tree, a tree structure with an unbounded number of branches in every node (unfortunately built from standard library collections for legacy reasons):

  case class StrictTree[A](
    rootLabel: A,
    subForest: Vector[StrictTree[A]]
  )

Tree is a by-need version of StrictTree with convenient constructors

  class Tree[A](
    rootc: Need[A],
    forestc: Need[Stream[Tree[A]]]
  ) {
    def rootLabel = rootc.value
    def subForest = forestc.value
  }
  object Tree {
    object Node {
      def apply[A](root: =>A, forest: =>Stream[Tree[A]]): Tree[A] = ...
    }
    object Leaf {
      def apply[A](root: =>A): Tree[A] = ...
    }
  }

The user of a Rose Tree is expected to manually balance it, which makes it suitable for cases where it is useful to encode domain knowledge of a hierarchy into the data structure. For example, in artificial intelligence, a Rose Tree can be used in clustering algorithms to organise data into a hierarchy of increasingly similar things. It is possible to represent XML documents with a Rose Tree.

When working with hierarchical data, consider using a Rose Tree instead of rolling a custom data structure.

6.8.10 `FingerTree`

Finger trees are generalised sequences with amortised constant cost lookup and logarithmic concatenation. A is the type of data, ignore V for now:

  sealed abstract class FingerTree[V, A] {
    def +:(a: A): FingerTree[V, A] = ...
    def :+(a: =>A): FingerTree[V, A] = ...
    def <++>(right: =>FingerTree[V, A]): FingerTree[V, A] = ...
    ...
  }
  object FingerTree {
    private class Empty[V, A]() extends FingerTree[V, A]
    private class Single[V, A](v: V, a: =>A) extends FingerTree[V, A]
    private class Deep[V, A](
      v: V,
      left: Finger[V, A],
      spine: =>FingerTree[V, Node[V, A]],
      right: Finger[V, A]
    ) extends FingerTree[V, A]
  
    sealed abstract class Finger[V, A]
    final case class One[V, A](v: V, a1: A) extends Finger[V, A]
    final case class Two[V, A](v: V, a1: A, a2: A) extends Finger[V, A]
    final case class Three[V, A](v: V, a1: A, a2: A, a3: A) extends Finger[V, A]
    final case class Four[V, A](v: V, a1: A, a2: A, a3: A, a4: A) extends Finger[V, A]
  
    sealed abstract class Node[V, A]
    private class Node2[V, A](v: V, a1: =>A, a2: =>A) extends Node[V, A]
    private class Node3[V, A](v: V, a1: =>A, a2: =>A, a3: =>A) extends Node[V, A]
    ...
  }

Visualising FingerTree as dots, Finger as boxes and Node as boxes within boxes:

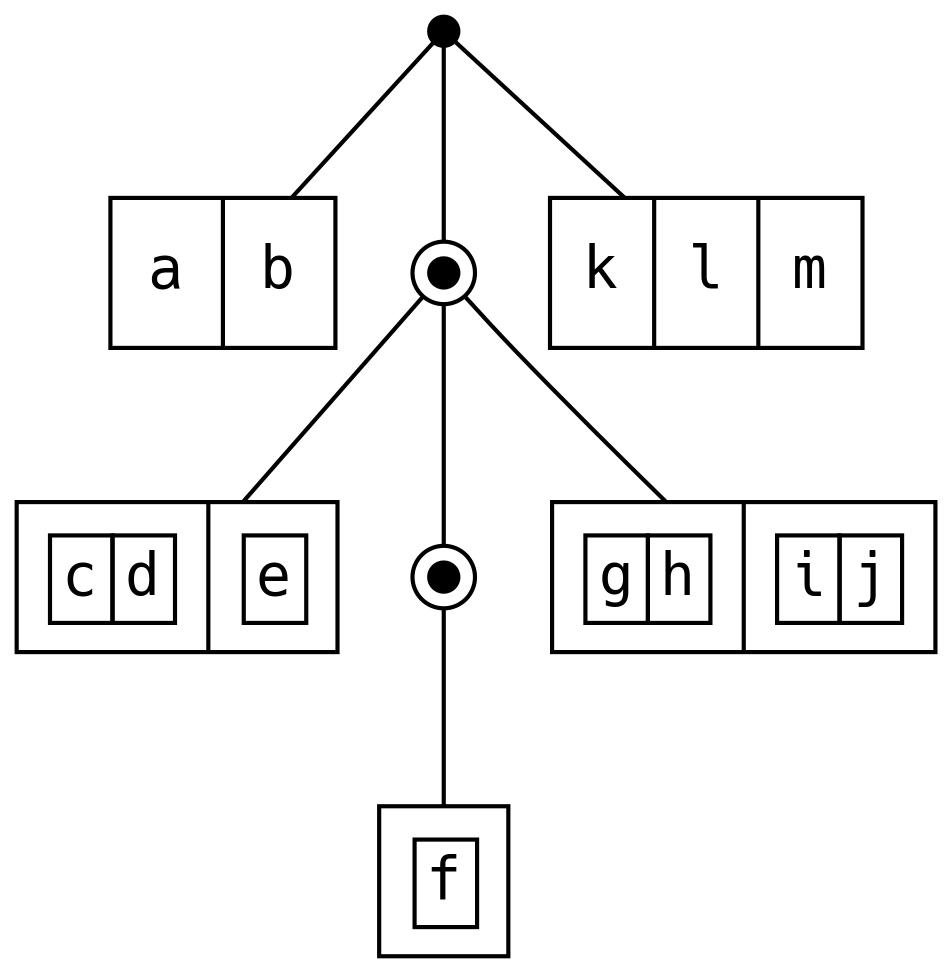
Adding elements to the front of a FingerTree with +: is efficient because Deep simply adds the new element to its left finger. If the finger is a Four, we rebuild the spine to take 3 of the elements as a Node3. Adding to the end, :+, is the same but in reverse.

Appending |+| (also <++>) is more efficient than adding one element at a time because the case of two Deep trees can retain the outer branches, rebuilding the spine based on the 16 possible combinations of the two Finger values in the middle.

In the above we skipped over V. Not shown in the ADT description is an implicit measurer: Reducer[A, V] on every element of the ADT.

Reducer is an extension of Monoid that allows for single elements to be added to an M

  class Reducer[C, M: Monoid] {
    def unit(c: C): M
  
    def snoc(m: M, c: C): M = append(m, unit(c))
    def cons(c: C, m: M): M = append(unit(c), m)
  }

For example, Reducer[A, IList[A]] can provide an efficient .cons

  implicit def reducer[A]: Reducer[A, IList[A]] = new Reducer[A, IList[A]] {
    override def unit(a: A): IList[A] = IList.single(a)
    override def cons(a: A, as: IList[A]): IList[A] = a :: as
  }

6.8.10.1 `IndSeq`

If we use Int as V, we can get an indexed sequence, where the measure is size, allowing us to perform index-based lookup by comparing the desired index with the size at each branch in the structure:

  final class IndSeq[A](val self: FingerTree[Int, A])
  object IndSeq {
    private implicit def sizer[A]: Reducer[A, Int] = _ => 1
    def apply[A](as: A*): IndSeq[A] = ...
  }

Another use of FingerTree is as an ordered sequence, where the measure stores the largest value contained by each branch:

6.8.10.2 `OrdSeq`

  final class OrdSeq[A: Order](val self: FingerTree[LastOption[A], A]) {
    def partition(a: A): (OrdSeq[A], OrdSeq[A]) = ...
    def insert(a: A): OrdSeq[A] = ...
    def ++(xs: OrdSeq[A]): OrdSeq[A] = ...
  }
  object OrdSeq {
    private implicit def keyer[A]: Reducer[A, LastOption[A]] = a => Tag(Some(a))
    def apply[A: Order](as: A*): OrdSeq[A] = ...
  }

OrdSeq has no typeclass instances so it is only useful for incrementally building up an ordered sequence, with duplicates. We can access the underlying FingerTree when needed.

6.8.10.3 `Cord`

The most common use of FingerTree is as an intermediate holder for String representations in Show. Building a single String can be thousands of times faster than the default case class implementation of nested .toString, which builds a String for every layer in the ADT.

  final case class Cord(self: FingerTree[Int, String]) {
    override def toString: String = {
      val sb = new java.lang.StringBuilder(self.measure)
      self.foreach(sb.append) // locally scoped side effect
      sb.toString
    }
    ...
  }

For example, the Cord[String] instance returns a Three with the string in the middle and quotes on either side

  implicit val show: Show[String] = s => Cord(FingerTree.Three("\"", s, "\""))

Therefore a String renders as it is written in source code

  scala> val s = "foo"
         s.toString
  res: String = foo
  
  scala> s.show
  res: Cord = "foo"

6.8.11 `Heap` Priority Queue

A priority queue is a data structure that allows fast insertion of ordered elements, allowing duplicates, with fast access to the minimum value (highest priority). The structure is not required to store the non-minimal elements in order. A naive implementation of a priority queue could be

  final case class Vip[A] private (val peek: Maybe[A], xs: IList[A]) {
    def push(a: A)(implicit O: Order[A]): Vip[A] = peek match {
      case Maybe.Just(min) if a < min => Vip(a.just, min :: xs)
      case _                          => Vip(peek, a :: xs)
    }
  
    def pop(implicit O: Order[A]): Maybe[(A, Vip[A])] = peek strengthR reorder
    private def reorder(implicit O: Order[A]): Vip[A] = xs.sorted match {
      case INil()           => Vip(Maybe.empty, IList.empty)
      case ICons(min, rest) => Vip(min.just, rest)
    }
  }
  object Vip {
    def fromList[A: Order](xs: IList[A]): Vip[A] = Vip(Maybe.empty, xs).reorder
  }

This push is a very fast O(1), but reorder (and therefore pop) relies on IList.sorted costing O(n log n).

Scalaz encodes a priority queue with a tree structure where every node has a value less than its children. Heap has fast push (insert), union, size, pop (uncons) and peek (minimumO) operations:

  sealed abstract class Heap[A] {
    def insert(a: A)(implicit O: Order[A]): Heap[A] = ...
    def +(a: A)(implicit O: Order[A]): Heap[A] = insert(a)
  
    def union(as: Heap[A])(implicit O: Order[A]): Heap[A] = ...
  
    def uncons(implicit O: Order[A]): Option[(A, Heap[A])] = minimumO strengthR deleteMin
    def minimumO: Option[A] = ...
    def deleteMin(implicit O: Order[A]): Heap[A] = ...
  
    ...
  }
  object Heap {
    def fromData[F[_]: Foldable, A: Order](as: F[A]): Heap[A] = ...
  
    private final case class Ranked[A](rank: Int, value: A)
  
    private final case class Empty[A]() extends Heap[A]
    private final case class NonEmpty[A](
      size: Int,
      tree: Tree[Ranked[A]]
    ) extends Heap[A]
  
    ...
  }

Heap is implemented with a Rose Tree of Ranked values, where the rank is the depth of a subtree, allowing us to depth-balance the tree. We manually maintain the tree so the minimum value is at the top. An advantage of encoding the minimum value in the data structure is that minimumO (also known as peek) is a free lookup:

  def minimumO: Option[A] = this match {
    case Empty()                        => None
    case NonEmpty(_, Tree.Node(min, _)) => Some(min.value)
  }

When inserting a new entry, we compare to the current minimum and replace if the new entry is lower:

  def insert(a: A)(implicit O: Order[A]): Heap[A] = this match {
    case Empty() =>
      NonEmpty(1, Tree.Leaf(Ranked(0, a)))
    case NonEmpty(size, tree @ Tree.Node(min, _)) if a <= min.value =>
      NonEmpty(size + 1, Tree.Node(Ranked(0, a), Stream(tree)))
  ...

Insertions of non-minimal values result in an unordered structure in the branches of the minimum. When we encounter two or more subtrees of equal rank, we optimistically put the minimum to the front:

  ...
    case NonEmpty(size, Tree.Node(min,
           (t1 @ Tree.Node(Ranked(r1, x1), xs1)) #::
           (t2 @ Tree.Node(Ranked(r2, x2), xs2)) #:: ts)) if r1 == r2 =>
      lazy val t0 = Tree.Leaf(Ranked(0, a))
      val sub =
        if (x1 <= a && x1 <= x2)
          Tree.Node(Ranked(r1 + 1, x1), t0 #:: t2 #:: xs1)
        else if (x2 <= a && x2 <= x1)
          Tree.Node(Ranked(r2 + 1, x2), t0 #:: t1 #:: xs2)
        else
          Tree.Node(Ranked(r1 + 1, a), t1 #:: t2 #:: Stream())
  
      NonEmpty(size + 1, Tree.Node(Ranked(0, min.value), sub #:: ts))
  
    case NonEmpty(size,  Tree.Node(min, rest)) =>
      val t0 = Tree.Leaf(Ranked(0, a))
      NonEmpty(size + 1, Tree.Node(Ranked(0, min.value), t0 #:: rest))
  }

Avoiding a full ordering of the tree makes insert very fast, O(1), such that producers adding to the queue are not penalised. However, the consumer pays the cost when calling uncons, with deleteMin costing O(log n) because it must search for the minimum value, and remove it from the tree by rebuilding. That Is fast when compared to the naive implementation.

The union operation also delays ordering allowing it to be O(1).

If the Order[Foo] does not correctly capture the priority we want for the Heap[Foo], we can use Tag and provide a custom Order[Foo @@ Custom] for a Heap[Foo @@ Custom].

6.8.12 `Diev` (Discrete Intervals)

We can efficiently encode the (unordered) integer values 6, 9, 2, 13, 8, 14, 10, 7, 5 as inclusive intervals [2, 2], [5, 10], [13, 14]. Diev is an efficient encoding of intervals for elements A that have an Enum[A], getting more efficient as the contents become denser.

  sealed abstract class Diev[A] {
    def +(interval: (A, A)): Diev[A]
    def +(value: A): Diev[A]
    def ++(other: Diev[A]): Diev[A]
  
    def -(interval: (A, A)): Diev[A]
    def -(value: A): Diev[A]
    def --(other: Diev[A]): Diev[A]
  
    def intervals: Vector[(A, A)]
    def contains(value: A): Boolean
    def contains(interval: (A, A)): Boolean
    ...
  }
  object Diev {
    private final case class DieVector[A: Enum](
      intervals: Vector[(A, A)]
    ) extends Diev[A]
  
    def empty[A: Enum]: Diev[A] = ...
    def fromValuesSeq[A: Enum](values: Seq[A]): Diev[A] = ...
    def fromIntervalsSeq[A: Enum](intervals: Seq[(A, A)]): Diev[A] = ...
  }

When updating the Diev, adjacent intervals are merged (and then ordered) such that there is a unique representation for a given set of values.

  scala> Diev.fromValuesSeq(List(6, 9, 2, 13, 8, 14, 10, 7, 5))
  res: Diev[Int] = ((2,2)(5,10)(13,14))
  
  scala> Diev.fromValuesSeq(List(6, 9, 2, 13, 8, 14, 10, 7, 5).reverse)
  res: Diev[Int] = ((2,2)(5,10)(13,14))

A great usecase for Diev is for storing time periods. For example, in our TradeTemplate from the previous chapter

  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: Option[Currency],
    otc: Option[Boolean]
  )

if we find that the payments are very dense, we may wish to swap to a Diev representation for performance reasons, without any change in our business logic because we used Monoid, not any List specific methods. We would, however, have to provide an Enum[LocalDate], which is an otherwise useful thing to have.

6.8.13 `OneAnd`

Recall that Foldable is the Scalaz equivalent of a collections API and Foldable1 is for non-empty collections. So far we have only seen NonEmptyList to provide a Foldable1. The simple data structure OneAnd wraps any other collection to turn it into a Foldable1:

  final case class OneAnd[F[_], A](head: A, tail: F[A])

NonEmptyList[A] could be an alias to OneAnd[IList, A]. Similarly, we can create non-empty Stream, DList and Tree structures. However it may break ordering and uniqueness characteristics of the underlying structure: a OneAnd[ISet, A] is not a non-empty ISet, it is an ISet with a guaranteed first element that may also be in the ISet.

6.9 Summary

In this chapter we have skimmed over the data types that Scalaz has to offer.

It is not necessary to remember everything from this chapter: think of each section as having planted the kernel of an idea.

The world of functional data structures is an active area of research. Academic publications appear regularly with new approaches to old problems. Implementing a functional data structure from the literature is a good contribution to the Scalaz ecosystem.

7. Advanced Monads

You have to know things like Advanced Monads in order to be an advanced functional programmer.

However, we are developers yearning for a simple life, and our idea of “advanced” is modest. To put it into context: scala.concurrent.Future is more complicated and nuanced than any Monad in this chapter.

In this chapter we will study some of the most important implementations of Monad.

7.1 Always in motion is the `Future`

The biggest problem with Future is that it eagerly schedules work during construction. As we discovered in the introduction, Future conflates the definition of a program with interpreting it (i.e. running it).

Future is also bad from a performance perspective: every time .flatMap is called, a closure is submitted to an Executor, resulting in unnecessary thread scheduling and context switching. It is not unusual to see 50% of our CPU power dealing with thread scheduling, instead of doing the work. So much so that parallelising work with Future can often make it slower.

Combined, eager evaluation and executor submission means that it is impossible to know when a job started, when it finished, or the sub-tasks that were spawned to calculate the final result. It should not surprise us that performance monitoring “solutions” for Future based frameworks are a solid earner for the modern day snake oil merchant.

Furthermore, Future.flatMap requires an ExecutionContext to be in implicit scope: users are forced to think about business logic and execution semantics at the same time.

7.2 Effects and Side Effects

If we cannot call side-effecting methods in our business logic, or in Future (or Id, or Either, or Const, etc), when can we write them? The answer is: in a Monad that delays execution until it is interpreted at the application’s entrypoint. We can now refer to I/O and mutation as an effect on the world, captured by the type system, as opposed to having a hidden side-effect.

The simplest implementation of such a Monad is IO, formalising the version we wrote in the introduction:

  final class IO[A](val interpret: () => A)
  object IO {
    def apply[A](a: =>A): IO[A] = new IO(() => a)
  
    implicit val monad: Monad[IO] = new Monad[IO] {
      def point[A](a: =>A): IO[A] = IO(a)
      def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] = IO(f(fa.interpret()).interpret())
    }
  }

The .interpret method is only called once, in the entrypoint of an application:

  def main(args: Array[String]): Unit = program.interpret()

However, there are two big problems with this simple IO:

it can stack overflow
it doesn’t support parallel computations

Both of these problems will be overcome in this chapter. However, no matter how complicated the internal implementation of a Monad, the principles described here remain true: we’re modularising the definition of a program and its execution, such that we can capture effects in type signatures, allowing us to reason about them, and reuse more code.

7.3 Stack Safety

On the JVM, every method call adds an entry to the call stack of the Thread, like adding to the front of a List. When the method completes, the method at the head is thrown away. The maximum length of the call stack is determined by the -Xss flag when starting up java. Tail recursive methods are detected by the Scala compiler and do not add an entry. If we hit the limit, by calling too many chained methods, we get a StackOverflowError.

Unfortunately, every nested call to our IO’s .flatMap adds another method call to the stack. The easiest way to see this is to repeat an action forever, and see if it survives for longer than a few seconds. We can use .forever, from Apply (a parent of Monad):

  scala> val hello = IO { println("hello") }
  scala> Apply[IO].forever(hello).interpret()
  
  hello
  hello
  hello
  ...
  hello
  java.lang.StackOverflowError
      at java.io.FileOutputStream.write(FileOutputStream.java:326)
      at ...
      at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
      at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
      at ...

Scalaz has a typeclass that Monad instances can implement if they are stack safe: BindRec requires a constant stack space for recursive bind:

  @typeclass trait BindRec[F[_]] extends Bind[F] {
    def tailrecM[A, B](f: A => F[A \/ B])(a: A): F[B]
  
    override def forever[A, B](fa: F[A]): F[B] = ...
  }

We don’t need BindRec for all programs, but it is essential for a general purpose Monad implementation.

The way to achieve stack safety is to convert method calls into references to an ADT, the Free monad:

  sealed abstract class Free[S[_], A]
  object Free {
    private final case class Return[S[_], A](a: A)     extends Free[S, A]
    private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
    private final case class Gosub[S[_], A0, B](
      a: Free[S, A0],
      f: A0 => Free[S, B]
    ) extends Free[S, B] { type A = A0 }
    ...
  }

The Free ADT is a natural data type representation of the Monad interface:

Return represents .point
Gosub represents .bind / .flatMap

When an ADT mirrors the arguments of related functions, it is called a Church encoding.

Free is named because it can be generated for free for any S[_]. For example, we could set S to be the Drone or Machines algebras from Chapter 3 and generate a data structure representation of our program. We will return to why this is useful at the end of this chapter.

7.3.1 `Trampoline`

Free is more general than we need for now. Setting the algebra S[_] to () => ?, a deferred calculation or thunk, we get Trampoline and can implement a stack safe Monad

  object Free {
    type Trampoline[A] = Free[() => ?, A]
    implicit val trampoline: Monad[Trampoline] with BindRec[Trampoline] =
      new Monad[Trampoline] with BindRec[Trampoline] {
        def point[A](a: =>A): Trampoline[A] = Return(a)
        def bind[A, B](fa: Trampoline[A])(f: A => Trampoline[B]): Trampoline[B] =
          Gosub(fa, f)
  
        def tailrecM[A, B](f: A => Trampoline[A \/ B])(a: A): Trampoline[B] =
          bind(f(a)) {
            case -\/(a) => tailrecM(f)(a)
            case \/-(b) => point(b)
          }
      }
    ...
  }

The BindRec implementation, .tailrecM, runs .bind until we get a B. Although this is not technically a @tailrec implementation, it uses constant stack space because each call returns a heap object, with delayed recursion.

Convenient functions are provided to create a Trampoline eagerly (.done) or by-name (.delay). We can also create a Trampoline from a by-name Trampoline (.suspend):

  object Trampoline {
    def done[A](a: A): Trampoline[A]                  = Return(a)
    def delay[A](a: =>A): Trampoline[A]               = suspend(done(a))
    def suspend[A](a: =>Trampoline[A]): Trampoline[A] = unit >> a
  
    private val unit: Trampoline[Unit] = Suspend(() => done(()))
  }

When we see Trampoline[A] in a codebase we can always mentally substitute it with A, because it is simply adding stack safety to the pure computation. We get the A by interpreting Free, provided by .run.

It is instructive, although not necessary, to understand how Free.run is implemented: .resume evaluates a single layer of the Free, and go runs it to completion.

In the following Trampoline[A] is used as a synonym for Free[() => ?, A] to make the code easier to read.

  sealed abstract class Trampoline[A] {
    def run: A = go(f => f())
  
    def go(f: () => Trampoline[A] => Trampoline[A]): A = {
      @tailrec def go2(t: Trampoline[A]): A = t.resume match {
        case -\/(s) => go2(f(s))
        case \/-(r) => r
      }
      go2(this)
    }
  
    @tailrec def resume: () => Trampoline[A] \/ A = this match {
      case Return(a) => \/-(a)
      case Suspend(t) => -\/(t.map(Return(_)))
      case Gosub(Return(a), f) => f(a).resume
      case Gosub(Suspend(t), f) => -\/(t.map(f))
      case Gosub(Gosub(a, g), f) => a >>= (z => g(z) >>= f).resume
    }
    ...
  }

The case that is most likely to cause confusion is when we have nested Gosub: apply the inner function g then pass it to the outer one f, it is just function composition.

7.3.2 Example: Stack Safe `DList`

In the previous chapter we described the data type DList as

  final case class DList[A](f: IList[A] => IList[A]) {
    def toIList: IList[A] = f(IList.empty)
    def ++(as: DList[A]): DList[A] = DList(xs => f(as.f(xs)))
    ...
  }

However, the actual implementation looks more like:

  final case class DList[A](f: IList[A] => Trampoline[IList[A]]) {
    def toIList: IList[A] = f(IList.empty).run
    def ++(as: =>DList[A]): DList[A] = DList(xs => suspend(as.f(xs) >>= f))
    ...
  }

Instead of applying nested calls to f we use a suspended Trampoline. We interpret the trampoline with .run only when needed, e.g. in toIList. The changes are minimal, but we now have a stack safe DList that can rearrange the concatenation of a large number lists without blowing the stack!

7.3.3 Stack Safe `IO`

Similarly, our IO can be made stack safe thanks to Trampoline:

  final class IO[A](val tramp: Trampoline[A]) {
    def unsafePerformIO(): A = tramp.run
  }
  object IO {
    def apply[A](a: =>A): IO[A] = new IO(Trampoline.delay(a))
  
    implicit val Monad: Monad[IO] with BindRec[IO] =
      new Monad[IO] with BindRec[IO] {
        def point[A](a: =>A): IO[A] = IO(a)
        def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] =
          new IO(fa.tramp >>= (a => f(a).tramp))
        def tailrecM[A, B](f: A => IO[A \/ B])(a: A): IO[B] = ...
      }
  }

The interpreter, .unsafePerformIO(), has an intentionally scary name to discourage using it except in the entrypoint of the application.

This time, we don’t get a stack overflow error:

  scala> val hello = IO { println("hello") }
  scala> Apply[IO].forever(hello).unsafePerformIO()
  
  hello
  hello
  hello
  ...
  hello

Using a Trampoline typically introduces a performance regression vs a regular reference. It is Free in the sense of freely generated, not free as in beer.

7.4 Monad Transformer Library

Monad transformers are data structures that wrap an underlying value and provide a monadic effect.

For example, in Chapter 2 we used OptionT to let us use F[Option[A]] in a for comprehension as if it was just a F[A]. This gave our program the effect of an optional value. Alternatively, we can get the effect of optionality if we have a MonadPlus.

This subset of data types and extensions to Monad are often referred to as the Monad Transformer Library (MTL), summarised below. In this section, we will explain each of the transformers, why they are useful, and how they work.

Effect	Underlying	Transformer	Typeclass
optionality	`F[Maybe[A]]`	`MaybeT`	`MonadPlus`
errors	`F[E \/ A]`	`EitherT`	`MonadError`
a runtime value	`A => F[B]`	`ReaderT`	`MonadReader`
journal / multitask	`F[(W, A)]`	`WriterT`	`MonadTell`
evolving state	`S => F[(S, A)]`	`StateT`	`MonadState`
keep calm & carry on	`F[E \&/ A]`	`TheseT`
control flow	`(A => F[B]) => F[B]`	`ContT`

7.4.1 `MonadTrans`

Each transformer has the general shape T[F[_], A], providing at least an instance of Monad and Hoist (and therefore MonadTrans):

  @typeclass trait MonadTrans[T[_[_], _]] {
    def liftM[F[_]: Monad, A](a: F[A]): T[F, A]
  }
  
  @typeclass trait Hoist[F[_[_], _]] extends MonadTrans[F] {
    def hoist[M[_]: Monad, N[_]](f: M ~> N): F[M, ?] ~> F[N, ?]
  }

.liftM lets us create a monad transformer if we have an F[A]. For example, we can create an OptionT[IO, String] by calling .liftM[OptionT] on an IO[String].

.hoist is the same idea, but for natural transformations.

Generally, there are three ways to create a monad transformer:

from the underlying, using the transformer’s constructor
from a single value A, using .pure from the Monad syntax
from an F[A], using .liftM from the MonadTrans syntax

Due to the way that type inference works in Scala, this often means that a complex type parameter must be explicitly written. As a workaround, transformers provide convenient constructors on their companion that are easier to use.

7.4.2 `MaybeT`

OptionT, MaybeT and LazyOptionT have similar implementations, providing optionality through Option, Maybe and LazyOption, respectively. We will focus on MaybeT to avoid repetition.

  final case class MaybeT[F[_], A](run: F[Maybe[A]])
  object MaybeT {
    def just[F[_]: Applicative, A](v: =>A): MaybeT[F, A] =
      MaybeT(Maybe.just(v).pure[F])
    def empty[F[_]: Applicative, A]: MaybeT[F, A] =
      MaybeT(Maybe.empty.pure[F])
    ...
  }

providing a MonadPlus

  implicit def monad[F[_]: Monad] = new MonadPlus[MaybeT[F, ?]] {
    def point[A](a: =>A): MaybeT[F, A] = MaybeT.just(a)
    def bind[A, B](fa: MaybeT[F, A])(f: A => MaybeT[F, B]): MaybeT[F, B] =
      MaybeT(fa.run >>= (_.cata(f(_).run, Maybe.empty.pure[F])))
  
    def empty[A]: MaybeT[F, A] = MaybeT.empty
    def plus[A](a: MaybeT[F, A], b: =>MaybeT[F, A]): MaybeT[F, A] = a orElse b
  }

This monad looks fiddly, but it is just delegating everything to the Monad[F] and then re-wrapping with a MaybeT. It is plumbing.

With this monad we can write logic that handles optionality in the F[_] context, rather than carrying around Option or Maybe.

For example, say we are interfacing with a social media website to count the number of stars a user has, and we start with a String that may or may not correspond to a user. We have this algebra:

  trait Twitter[F[_]] {
    def getUser(name: String): F[Maybe[User]]
    def getStars(user: User): F[Int]
  }
  def T[F[_]](implicit t: Twitter[F]): Twitter[F] = t

We need to call getUser followed by getStars. If we use Monad as our context, our function is difficult because we have to handle the Empty case:

  def stars[F[_]: Monad: Twitter](name: String): F[Maybe[Int]] = for {
    maybeUser  <- T.getUser(name)
    maybeStars <- maybeUser.traverse(T.getStars)
  } yield maybeStars

However, if we have a MonadPlus as our context, we can suck Maybe into the F[_] with .orEmpty, and forget about it:

  def stars[F[_]: MonadPlus: Twitter](name: String): F[Int] = for {
    user  <- T.getUser(name) >>= (_.orEmpty[F])
    stars <- T.getStars(user)
  } yield stars

However adding a MonadPlus requirement can cause problems downstream if the context does not have one. The solution is to either change the context of the program to MaybeT[F, ?] (lifting the Monad[F] into a MonadPlus), or to explicitly use MaybeT in the return type, at the cost of slightly more code:

  def stars[F[_]: Monad: Twitter](name: String): MaybeT[F, Int] = for {
    user  <- MaybeT(T.getUser(name))
    stars <- T.getStars(user).liftM[MaybeT]
  } yield stars

The decision to require a more powerful Monad vs returning a transformer is something that each team can decide for themselves based on the interpreters that they plan on using for their program.

7.4.3 `EitherT`

An optional value is a special case of a value that may be an error, but we don’t know anything about the error. EitherT (and the lazy variant LazyEitherT) allows us to use any type we want as the error value, providing contextual information about what went wrong.

EitherT is a wrapper around an F[A \/ B]

  final case class EitherT[F[_], A, B](run: F[A \/ B])
  object EitherT {
    def either[F[_]: Applicative, A, B](d: A \/ B): EitherT[F, A, B] = ...
    def leftT[F[_]: Functor, A, B](fa: F[A]): EitherT[F, A, B] = ...
    def rightT[F[_]: Functor, A, B](fb: F[B]): EitherT[F, A, B] = ...
    def pureLeft[F[_]: Applicative, A, B](a: A): EitherT[F, A, B] = ...
    def pure[F[_]: Applicative, A, B](b: B): EitherT[F, A, B] = ...
    ...
  }

The Monad is a MonadError

  @typeclass trait MonadError[F[_], E] extends Monad[F] {
    def raiseError[A](e: E): F[A]
    def handleError[A](fa: F[A])(f: E => F[A]): F[A]
  }

.raiseError and .handleError are self-descriptive: the equivalent of throw and catch an exception, respectively.

MonadError has some addition syntax for dealing with common problems:

  implicit final class MonadErrorOps[F[_], E, A](self: F[A])(implicit val F: MonadError[F, E])\
 {
    def attempt: F[E \/ A] = ...
    def recover(f: E => A): F[A] = ...
    def emap[B](f: A => E \/ B): F[B] = ...
  }

.attempt brings errors into the value, which is useful for exposing errors in subsystems as first class values.

.recover is for turning an error into a value for all cases, as opposed to .handleError which takes an F[A] and therefore allows partial recovery.

.emap, either map, is to apply transformations that can fail.

The MonadError for EitherT is:

  implicit def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
    def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
    def bind[A, B](fa: EitherT[F, E, A])
                  (f: A => EitherT[F, E, B]): EitherT[F, E, B] =
      EitherT(fa.run >>= (_.fold(_.left[B].pure[F], b => f(b).run)))
    def point[A](a: =>A): EitherT[F, E, A] = EitherT.pure(a)
  
    def raiseError[A](e: E): EitherT[F, E, A] = EitherT.pureLeft(e)
    def handleError[A](fa: EitherT[F, E, A])
                      (f: E => EitherT[F, E, A]): EitherT[F, E, A] =
      EitherT(fa.run >>= {
        case -\/(e) => f(e).run
        case right => right.pure[F]
      })
  }

It should be of no surprise that we can rewrite the MonadPlus example with MonadError, inserting informative error messages:

  def stars[F[_]: Twitter](name: String)
                          (implicit F: MonadError[F, String]): F[Int] = for {
    user  <- T.getUser(name) >>= (_.orError(s"user '$name' not found")(F))
    stars <- T.getStars(user)
  } yield stars

where .orError is a convenience method on Maybe

  sealed abstract class Maybe[A] {
    ...
    def orError[F[_], E](e: E)(implicit F: MonadError[F, E]): F[A] =
      cata(F.point(_), F.raiseError(e))
  }

The version using EitherT directly looks like

  def stars[F[_]: Monad: Twitter](name: String): EitherT[F, String, Int] = for {
    user <- EitherT(T.getUser(name).map(_ \/> s"user '$name' not found"))
    stars <- EitherT.rightT(T.getStars(user))
  } yield stars

The simplest instance of MonadError is for \/, perfect for testing business logic that requires a MonadError. For example,

  final class MockTwitter extends Twitter[String \/ ?] {
    def getUser(name: String): String \/ Maybe[User] =
      if (name.contains(" ")) Maybe.empty.right
      else if (name === "wobble") "connection error".left
      else User(name).just.right
  
    def getStars(user: User): String \/ Int =
      if (user.name.startsWith("w")) 10.right
      else "stars have been replaced by hearts".left
  }

Our unit tests for .stars might cover these cases:

  scala> stars("wibble")
  \/-(10)
  
  scala> stars("wobble")
  -\/(connection error)
  
  scala> stars("i'm a fish")
  -\/(user 'i'm a fish' not found)
  
  scala> stars("fommil")
  -\/(stars have been replaced by hearts)

As we’ve now seen several times, we can focus on testing the pure business logic without distraction.

Finally, if we return to our JsonClient algebra from Chapter 4.3

  trait JsonClient[F[_]] {
    def get[A: JsDecoder](
      uri: String Refined Url,
      headers: IList[(String, String)]
    ): F[A]
    ...
  }

recall that we only coded the happy path into the API. If our interpreter for this algebra only works for an F having a MonadError we get to define the kinds of errors as a tangential concern. Indeed, we can have two layers of error if we define the interpreter for a EitherT[IO, JsonClient.Error, ?]

  object JsonClient {
    sealed abstract class Error
    final case class ServerError(status: Int)       extends Error
    final case class DecodingError(message: String) extends Error
  }

which cover I/O (network) problems, server status problems, and issues with our modelling of the server’s JSON payloads.

7.4.3.1 Choosing an error type

The community is undecided on the best strategy for the error type E in MonadError.

One school of thought says that we should pick something general, like a String. The other school says that an application should have an ADT of errors, allowing different errors to be reported or handled differently. An unprincipled gang prefers using Throwable for maximum JVM compatibility.

There are two problems with an ADT of errors on the application level:

it is very awkward to create a new error. One file becomes a monolithic repository of errors, aggregating the ADTs of individual subsystems.
no matter how granular the errors are, the resolution is often the same: log it and try it again, or give up. We don’t need an ADT for this.

An error ADT is of value if every entry allows a different kind of recovery to be performed.

A compromise between an error ADT and a String is an intermediary format. JSON is a good choice as it can be understood by most logging and monitoring frameworks.

A problem with not having a stacktrace is that it can be hard to localise which piece of code was the source of an error. With sourcecode by Li Haoyi, we can include contextual information as metadata in our errors:

  final case class Meta(fqn: String, file: String, line: Int)
  object Meta {
    implicit def gen(implicit fqn: sourcecode.FullName,
                              file: sourcecode.File,
                              line: sourcecode.Line): Meta =
      new Meta(fqn.value, file.value, line.value)
  }
  
  final case class Err(msg: String)(implicit val meta: Meta)

Although Err is referentially transparent, the implicit construction of a Meta does not appear to be referentially transparent from a natural reading: two calls to Meta.gen (invoked implicitly when creating an Err) will produce different values because the location in the source code impacts the returned value:

  scala> println(Err("hello world").meta)
  Meta(com.acme,<console>,10)
  
  scala> println(Err("hello world").meta)
  Meta(com.acme,<console>,11)

To understand this, we have to appreciate that sourcecode.* methods are macros that are generating source code for us. If we were to write the above explicitly it is clear what is happening:

  scala> println(Err("hello world")(Meta("com.acme", "<console>", 10)).meta)
  Meta(com.acme,<console>,10)
  
  scala> println(Err("hello world")(Meta("com.acme", "<console>", 11)).meta)
  Meta(com.acme,<console>,11)

Yes, we’ve made a deal with the macro devil, but we could also write the Meta manually and have it go out of date quicker than our documentation.

7.4.4 `ReaderT`

The reader monad wraps A => F[B] allowing a program F[B] to depend on a runtime value A. For those familiar with dependency injection, the reader monad is the FP equivalent of Spring or Guice’s @Inject, without the XML and reflection.

ReaderT is just an alias to another more generally useful data type named after the mathematician Heinrich Kleisli.

  type ReaderT[F[_], A, B] = Kleisli[F, A, B]
  
  final case class Kleisli[F[_], A, B](run: A => F[B]) {
    def dimap[C, D](f: C => A, g: B => D)(implicit F: Functor[F]): Kleisli[F, C, D] =
      Kleisli(c => run(f(c)).map(g))
  
    def >=>[C](k: Kleisli[F, B, C])(implicit F: Bind[F]): Kleisli[F, A, C] = ...
    def >==>[C](k: B => F[C])(implicit F: Bind[F]): Kleisli[F, A, C] = this >=> Kleisli(k)
    ...
  }
  object Kleisli {
    implicit def kleisliFn[F[_], A, B](k: Kleisli[F, A, B]): A => F[B] = k.run
    ...
  }

An implicit conversion on the companion allows us to use a Kleisli in place of a function, so we can provide it as the parameter to a monad’s .bind, or >>=.

The most common use for ReaderT is to provide environment information to a program. In drone-dynamic-agents we need access to the user’s OAuth 2.0 Refresh Token to be able to contact Google. The obvious thing is to load the RefreshTokens from disk on startup, and make every method take a RefreshToken parameter. In fact, this is such a common requirement that Martin Odersky has proposed implicit functions.

A better solution is for our program to have an algebra that provides the configuration when needed, e.g.

  trait ConfigReader[F[_]] {
    def token: F[RefreshToken]
  }

We have reinvented MonadReader, the typeclass associated to ReaderT, where .ask is the same as our .token, and S is RefreshToken:

  @typeclass trait MonadReader[F[_], S] extends Monad[F] {
    def ask: F[S]
  
    def local[A](f: S => S)(fa: F[A]): F[A]
  }

with the implementation

  implicit def monad[F[_]: Monad, R] = new MonadReader[Kleisli[F, R, ?], R] {
    def point[A](a: =>A): Kleisli[F, R, A] = Kleisli(_ => F.point(a))
    def bind[A, B](fa: Kleisli[F, R, A])(f: A => Kleisli[F, R, B]) =
      Kleisli(a => Monad[F].bind(fa.run(a))(f))
  
    def ask: Kleisli[F, R, R] = Kleisli(_.pure[F])
    def local[A](f: R => R)(fa: Kleisli[F, R, A]): Kleisli[F, R, A] =
      Kleisli(f andThen fa.run)
  }

A law of MonadReader is that the S cannot change between invocations, i.e. ask >> ask === ask. For our usecase, this is to say that the configuration is read once. If we decide later that we want to reload configuration every time we need it, e.g. allowing us to change the token without restarting the application, we can reintroduce ConfigReader which has no such law.

In our OAuth 2.0 implementation we could first move the Monad evidence onto the methods:

  def bearer(refresh: RefreshToken)(implicit F: Monad[F]): F[BearerToken] =
    for { ...

and then refactor the refresh parameter to be part of the Monad

  def bearer(implicit F: MonadReader[F, RefreshToken]): F[BearerToken] =
    for {
      refresh <- F.ask

Any parameter can be moved into the MonadReader. This is of most value to immediate callers when they simply want to thread through this information from above. With ReaderT, we can reserve implicit parameter blocks entirely for the use of typeclasses, reducing the mental burden of using Scala.

The other method in MonadReader is .local

  def local[A](f: S => S)(fa: F[A]): F[A]

We can change S and run a program fa within that local context, returning to the original S. A use case for .local is to generate a “stack trace” that makes sense to our domain. giving us nested logging! Leaning on the Meta data structure from the previous section, we define a function to checkpoint:

  def traced[A](fa: F[A])(implicit F: MonadReader[F, IList[Meta]]): F[A] =
    F.local(Meta.gen :: _)(fa)

and we can use it to wrap functions that operate in this context.

  def foo: F[Foo] = traced(getBar) >>= barToFoo

automatically passing through anything that is not explicitly traced. A compiler plugin or macro could do the opposite, opting everything in by default.

If we access .ask we can see the breadcrumb trail of exactly how we were called, without the distraction of bytecode implementation details. A referentially transparent stacktrace!

A defensive programmer may wish to truncate the IList[Meta] at a certain length to avoid the equivalent of a stack overflow. Indeed, a more appropriate data structure is Dequeue.

.local can also be used to keep track of contextual information that is directly relevant to the task at hand, like the number of spaces that must indent a line when pretty printing a human readable file format, bumping it by two spaces when we enter a nested structure.

Finally, if we cannot request a MonadReader because our application does not provide one, we can always return a ReaderT

  def bearer(implicit F: Monad[F]): ReaderT[F, RefreshToken, BearerToken] =
    ReaderT( token => for {
    ...

If a caller receives a ReaderT, and they have the token parameter to hand, they can call access.run(token) and get back an F[BearerToken].

Admittedly, since we don’t have many callers, we should just revert to a regular function parameter. MonadReader is of most use when:

we may wish to refactor the code later to reload config
the value is not needed by intermediate callers
or, we want to locally scope some variable

Dotty can keep its implicit functions… we already have ReaderT and MonadReader.

7.4.5 `WriterT`

The opposite to reading is writing. The WriterT monad transformer is typically for writing to a journal.

  final case class WriterT[F[_], W, A](run: F[(W, A)])
  object WriterT {
    def put[F[_]: Functor, W, A](value: F[A])(w: W): WriterT[F, W, A] = ...
    def putWith[F[_]: Functor, W, A](value: F[A])(w: A => W): WriterT[F, W, A] = ...
    ...
  }

The wrapped type is F[(W, A)] with the journal accumulated in W.

There is not just one associated monad, but two! MonadTell and MonadListen

  @typeclass trait MonadTell[F[_], W] extends Monad[F] {
    def writer[A](w: W, v: A): F[A]
    def tell(w: W): F[Unit] = ...
  
    def :++>[A](fa: F[A])(w: =>W): F[A] = ...
    def :++>>[A](fa: F[A])(f: A => W): F[A] = ...
  }
  
  @typeclass trait MonadListen[F[_], W] extends MonadTell[F, W] {
    def listen[A](fa: F[A]): F[(A, W)]
  
    def written[A](fa: F[A]): F[W] = ...
  }

MonadTell is for writing to the journal and MonadListen is to recover it. The WriterT implementation is

  implicit def monad[F[_]: Monad, W: Monoid] = new MonadListen[WriterT[F, W, ?], W] {
    def point[A](a: =>A) = WriterT((Monoid[W].zero, a).point)
    def bind[A, B](fa: WriterT[F, W, A])(f: A => WriterT[F, W, B]) = WriterT(
      fa.run >>= { case (wa, a) => f(a).run.map { case (wb, b) => (wa |+| wb, b) } })
  
    def writer[A](w: W, v: A) = WriterT((w -> v).point)
    def listen[A](fa: WriterT[F, W, A]) = WriterT(
      fa.run.map { case (w, a) => (w, (a, w)) })
  }

The most obvious example is to use MonadTell for logging, or audit reporting. Reusing Meta from our error reporting we could imagine creating a log structure like

  sealed trait Log
  final case class Debug(msg: String)(implicit m: Meta)   extends Log
  final case class Info(msg: String)(implicit m: Meta)    extends Log
  final case class Warning(msg: String)(implicit m: Meta) extends Log

and use Dequeue[Log] as our journal type. We could change our OAuth2 authenticate method to

  def debug(msg: String)(implicit m: Meta): Dequeue[Log] = Dequeue(Debug(msg))
  
  def authenticate: F[CodeToken] =
    for {
      callback <- user.start :++> debug("started the webserver")
      params   = AuthRequest(callback, config.scope, config.clientId)
      url      = config.auth.withQuery(params.toUrlQuery)
      _        <- user.open(url) :++> debug(s"user visiting $url")
      code     <- user.stop :++> debug("stopped the webserver")
    } yield code

We could even combine this with the ReaderT traces and get structured logs.

The caller can recover the logs with .written and do something with them.

However, there is a strong argument that logging deserves its own algebra. The log level is often needed at the point of creation for performance reasons and writing out the logs is typically managed at the application level rather than something each component needs to be concerned about.

The W in WriterT has a Monoid, allowing us to journal any kind of monoidic calculation as a secondary value along with our primary program. For example, counting the number of times we do something, building up an explanation of a calculation, or building up a TradeTemplate for a new trade while we price it.

A popular specialisation of WriterT is when the monad is Id, meaning the underlying run value is just a simple tuple (W, A).

  type Writer[W, A] = WriterT[Id, W, A]
  object WriterT {
    def writer[W, A](v: (W, A)): Writer[W, A] = WriterT[Id, W, A](v)
    def tell[W](w: W): Writer[W, Unit] = WriterT((w, ()))
    ...
  }
  final implicit class WriterOps[A](self: A) {
    def set[W](w: W): Writer[W, A] = WriterT(w -> self)
    def tell: Writer[A, Unit] = WriterT.tell(self)
  }

which allows us to let any value carry around a secondary monoidal calculation, without needing a context F[_].

In a nutshell, WriterT / MonadTell is how to multi-task in FP.

7.4.6 `StateT`

StateT lets us .put, .get and .modify a value that is handled by the monadic context. It is the FP replacement of var.

If we were to write an impure method that has access to some mutable state, held in a var, it might have the signature () => F[A] and return a different value on every call, breaking referential transparency. With pure FP the function takes the state as input and returns the updated state as output, which is why the underlying type of StateT is S => F[(S, A)].

The associated monad is MonadState

  @typeclass trait MonadState[F[_], S] extends Monad[F] {
    def put(s: S): F[Unit]
    def get: F[S]
  
    def modify(f: S => S): F[Unit] = get >>= (s => put(f(s)))
    ...
  }

StateT is implemented slightly differently than the monad transformers we have studied so far. Instead of being a case class it is an ADT with two members:

  sealed abstract class StateT[F[_], S, A]
  object StateT {
    def apply[F[_], S, A](f: S => F[(S, A)]): StateT[F, S, A] = Point(f)
  
    private final case class Point[F[_], S, A](
      run: S => F[(S, A)]
    ) extends StateT[F, S, A]
    private final case class FlatMap[F[_], S, A, B](
      a: StateT[F, S, A],
      f: (S, A) => StateT[F, S, B]
    ) extends StateT[F, S, B]
    ...
  }

which are a specialised form of Trampoline, giving us stack safety when we want to recover the underlying data structure, .run:

  sealed abstract class StateT[F[_], S, A] {
    def run(initial: S)(implicit F: Monad[F]): F[(S, A)] = this match {
      case Point(f) => f(initial)
      case FlatMap(Point(f), g) =>
        f(initial) >>= { case (s, x) => g(s, x).run(s) }
      case FlatMap(FlatMap(f, g), h) =>
        FlatMap(f, (s, x) => FlatMap(g(s, x), h)).run(initial)
    }
    ...
  }

StateT can straightforwardly implement MonadState with its ADT:

  implicit def monad[F[_]: Applicative, S] = new MonadState[StateT[F, S, ?], S] {
    def point[A](a: =>A) = Point(s => (s, a).point[F])
    def bind[A, B](fa: StateT[F, S, A])(f: A => StateT[F, S, B]) =
      FlatMap(fa, (_, a: A) => f(a))
  
    def get       = Point(s => (s, s).point[F])
    def put(s: S) = Point(_ => (s, ()).point[F])
  }

With .pure mirrored on the companion as .stateT:

  object StateT {
    def stateT[F[_]: Applicative, S, A](a: A): StateT[F, S, A] = ...
    ...
  }

and MonadTrans.liftM providing the F[A] => StateT[F, S, A] constructor as usual.

A common variant of StateT is when F = Id, giving the underlying type signature S => (S, A). Scalaz provides a type alias and convenience functions for interacting with the State monad transformer directly, and mirroring MonadState:

  type State[a] = StateT[Id, a]
  object State {
    def apply[S, A](f: S => (S, A)): State[S, A] = StateT[Id, S, A](f)
    def state[S, A](a: A): State[S, A] = State((_, a))
  
    def get[S]: State[S, S] = State(s => (s, s))
    def put[S](s: S): State[S, Unit] = State(_ => (s, ()))
    def modify[S](f: S => S): State[S, Unit] = ...
    ...
  }

For an example we can return to the business logic tests of drone-dynamic-agents. Recall from Chapter 3 that we created Mutable as test interpreters for our application and we stored the number of started and stoped nodes in var.

  class Mutable(state: WorldView) {
    var started, stopped: Int = 0
  
    implicit val drone: Drone[Id] = new Drone[Id] { ... }
    implicit val machines: Machines[Id] = new Machines[Id] { ... }
    val program = new DynAgentsModule[Id]
  }

We now know that we can write a much better test simulator with State. We will take the opportunity to upgrade the accuracy of the simulation at the same time. Recall that a core domain object is our application’s view of the world:

  final case class WorldView(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    pending: Map[MachineNode, Epoch],
    time: Epoch
  )

Since we’re writing a simulation of the world for our tests, we can create a data type that captures the ground truth of everything

  final case class World(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    started: Set[MachineNode],
    stopped: Set[MachineNode],
    time: Epoch
  )

The key difference being that the started and stopped nodes can be separated out. Our interpreter can be implemented in terms of State[World, a] and we can write our tests to assert on what both the World and WorldView looks like after the business logic has run.

The interpreters, which are mocking out contacting external Drone and Google services, may be implemented like this:

  import State.{ get, modify }
  object StateImpl {
    type F[a] = State[World, a]
  
    private val D = new Drone[F] {
      def getBacklog: F[Int] = get.map(_.backlog)
      def getAgents: F[Int]  = get.map(_.agents)
    }
  
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]   = get.map(_.alive)
      def getManaged: F[NonEmptyList[MachineNode]] = get.map(_.managed)
      def getTime: F[Epoch]                      = get.map(_.time)
  
      def start(node: MachineNode): F[Unit] =
        modify(w => w.copy(started = w.started + node))
      def stop(node: MachineNode): F[Unit] =
        modify(w => w.copy(stopped = w.stopped + node))
    }
  
    val program = new DynAgentsModule[F](D, M)
  }

and we can rewrite our tests to follow a convention where:

world1 is the state of the world before running the program
view1 is the application’s belief about the world
world2 is the state of the world after running the program
view2 is the application’s belief after running the program

For example,

  it should "request agents when needed" in {
    val world1          = World(5, 0, managed, Map(), Set(), Set(), time1)
    val view1           = WorldView(5, 0, managed, Map(), Map(), time1)
  
    val (world2, view2) = StateImpl.program.act(view1).run(world1)
  
    view2.shouldBe(view1.copy(pending = Map(node1 -> time1)))
    world2.stopped.shouldBe(world1.stopped)
    world2.started.shouldBe(Set(node1))
  }

We would be forgiven for looking back to our business logic loop

  state = initial()
  while True:
    state = update(state)
    state = act(state)

and use StateT to manage the state. However, our DynAgents business logic requires only Applicative and we would be violating the Rule of Least Power to require the more powerful MonadState. It is therefore entirely reasonable to handle the state manually by passing it in to update and act, and let whoever calls us use a StateT if they wish.

7.4.7 `IndexedStateT`

The code that we have studied thus far is not how Scalaz implements StateT. Instead, a type alias points to IndexedStateT

  type StateT[F[_], S, A] = IndexedStateT[F, S, S, A]

The implementation of IndexedStateT is much as we have studied, with an extra type parameter allowing the input state S1 and output state S2 to differ:

  sealed abstract class IndexedStateT[F[_], -S1, S2, A] {
    def run(initial: S1)(implicit F: Bind[F]): F[(S2, A)] = ...
    ...
  }
  object IndexedStateT {
    def apply[F[_], S1, S2, A](
      f: S1 => F[(S2, A)]
    ): IndexedStateT[F, S1, S2, A] = Wrap(f)
  
    private final case class Wrap[F[_], S1, S2, A](
      run: S1 => F[(S2, A)]
    ) extends IndexedStateT[F, S1, S2, A]
    private final case class FlatMap[F[_], S1, S2, S3, A, B](
      a: IndexedStateT[F, S1, S2, A],
      f: (S2, A) => IndexedStateT[F, S2, S3, B]
    ) extends IndexedStateT[F, S1, S3, B]
    ...
  }

IndexedStateT does not have a MonadState when S1 != S2, although it has a Monad.

The following example is adapted from Index your State by Vincent Marquez. Consider the scenario where we must design an algebraic interface for an Int to String lookup. This may have a networked implementation and the order of calls is essential. Our first attempt at the API may look something like:

  trait Cache[F[_]] {
    def read(k: Int): F[Maybe[String]]
  
    def lock: F[Unit]
    def update(k: Int, v: String): F[Unit]
    def commit: F[Unit]
  }

with runtime errors if .update or .commit is called without a .lock. A more complex design may involve multiple traits and a custom DSL that nobody remembers how to use.

Instead, we can use IndexedStateT to require that the caller is in the correct state. First we define our possible states as an ADT

  sealed abstract class Status
  final case class Ready()                          extends Status
  final case class Locked(on: ISet[Int])            extends Status
  final case class Updated(values: Int ==>> String) extends Status

and then revisit our algebra

  trait Cache[M[_]] {
    type F[in, out, a] = IndexedStateT[M, in, out, a]
  
    def read(k: Int): F[Ready, Ready, Maybe[String]]
    def readLocked(k: Int): F[Locked, Locked, Maybe[String]]
    def readUncommitted(k: Int): F[Updated, Updated, Maybe[String]]
  
    def lock: F[Ready, Locked, Unit]
    def update(k: Int, v: String): F[Locked, Updated, Unit]
    def commit: F[Updated, Ready, Unit]
  }

which will give a compiletime error if we try to .update without a .lock

  for {
        a1 <- C.read(13)
        _  <- C.update(13, "wibble")
        _  <- C.commit
      } yield a1
  
  [error]  found   : IndexedStateT[M,Locked,Ready,Maybe[String]]
  [error]  required: IndexedStateT[M,Ready,?,?]
  [error]       _  <- C.update(13, "wibble")
  [error]          ^

but allowing us to construct functions that can be composed by explicitly including their state:

  def wibbleise[M[_]: Monad](C: Cache[M]): F[Ready, Ready, String] =
    for {
      _  <- C.lock
      a1 <- C.readLocked(13)
      a2 = a1.cata(_ + "'", "wibble")
      _  <- C.update(13, a2)
      _  <- C.commit
    } yield a2

We introduced code duplication in our API when we defined multiple .read operations

  def read(k: Int): F[Ready, Ready, Maybe[String]]
  def readLocked(k: Int): F[Locked, Locked, Maybe[String]]
  def readUncommitted(k: Int): F[Updated, Updated, Maybe[String]]

Instead of

  def read[S <: Status](k: Int): F[S, S, Maybe[String]]

The reason we didn’t do this is, because subtyping. This (broken) code would compile with the inferred type signature F[Nothing, Ready, Maybe[String]]

  for {
    a1 <- C.read(13)
    _  <- C.update(13, "wibble")
    _  <- C.commit
  } yield a1

Scala has a Nothing type which is the subtype of all other types. Thankfully, this code can not make it to runtime, as it would be impossible to call it, but it is a bad API since users need to remember to add type ascriptions.

Another approach would be to stop the compiler from inferring Nothing. Scalaz provides implicit evidence to assert that a type is not inferred as Nothing and we can use it instead:

  def read[S <: Status](k: Int)(implicit NN: NotNothing[S]): F[S, S, Maybe[String]]

The choice of which of the three alternative APIs to prefer is left to the personal taste of the API designer.

7.4.8 `IndexedReaderWriterStateT`

Those wanting to have a combination of ReaderT, WriterT and IndexedStateT will not be disappointed. The transformer IndexedReaderWriterStateT wraps (R, S1) => F[(W, A, S2)] with R having Reader semantics, W for monoidic writes, and the S parameters for indexed state updates.

  sealed abstract class IndexedReaderWriterStateT[F[_], -R, W, -S1, S2, A] {
    def run(r: R, s: S1)(implicit F: Monad[F]): F[(W, A, S2)] = ...
    ...
  }
  object IndexedReaderWriterStateT {
    def apply[F[_], R, W, S1, S2, A](f: (R, S1) => F[(W, A, S2)]) = ...
  }
  
  type ReaderWriterStateT[F[_], -R, W, S, A] = IndexedReaderWriterStateT[F, R, W, S, S, A]
  object ReaderWriterStateT {
    def apply[F[_], R, W, S, A](f: (R, S) => F[(W, A, S)]) = ...
  }

Abbreviations are provided because otherwise, let’s be honest, these types are so long they look like they are part of a J2EE API:

  type IRWST[F[_], -R, W, -S1, S2, A] = IndexedReaderWriterStateT[F, R, W, S1, S2, A]
  val IRWST = IndexedReaderWriterStateT
  type RWST[F[_], -R, W, S, A] = ReaderWriterStateT[F, R, W, S, A]
  val RWST = ReaderWriterStateT

IRWST is a more efficient implementation than a manually created transformer stack of ReaderT[WriterT[IndexedStateT[F, ...], ...], ...].

7.4.9 `TheseT`

TheseT allows errors to either abort the calculation or to be accumulated if there is some partial success. Hence keep calm and carry on.

The underlying data type is F[A \&/ B] with A being the error type, requiring a Semigroup to enable the accumulation of errors.

  final case class TheseT[F[_], A, B](run: F[A \&/ B])
  object TheseT {
    def `this`[F[_]: Functor, A, B](a: F[A]): TheseT[F, A, B] = ...
    def that[F[_]: Functor, A, B](b: F[B]): TheseT[F, A, B] = ...
    def both[F[_]: Functor, A, B](ab: F[(A, B)]): TheseT[F, A, B] = ...
  
    implicit def monad[F[_]: Monad, A: Semigroup] = new Monad[TheseT[F, A, ?]] {
      def bind[B, C](fa: TheseT[F, A, B])(f: B => TheseT[F, A, C]) =
        TheseT(fa.run >>= {
          case This(a) => a.wrapThis[C].point[F]
          case That(b) => f(b).run
          case Both(a, b) =>
            f(b).run.map {
              case This(a_)     => (a |+| a_).wrapThis[C]
              case That(c_)     => Both(a, c_)
              case Both(a_, c_) => Both(a |+| a_, c_)
            }
        })
  
      def point[B](b: =>B) = TheseT(b.wrapThat.point[F])
    }
  }

There is no special monad associated with TheseT, it is just a regular Monad. If we wish to abort a calculation we can return a This value, but we accumulate errors when we return a Both which also contains a successful part of the calculation.

TheseT can also be thought of from a different angle: A does not need to be an error. Similarly to WriterT, the A may be a secondary calculation that we are computing along with the primary calculation B. TheseT allows early exit when something special about A demands it, like when Charlie Bucket found the last golden ticket (A) he threw away his chocolate bar (B).

7.4.10 `ContT`

Continuation Passing Style (CPS) is a style of programming where functions never return, instead continuing to the next computation. CPS is popular in Javascript and Lisp as they allow non-blocking I/O via callbacks when data is available. A direct translation of the pattern into impure Scala looks like

  def foo[I, A](input: I)(next: A => Unit): Unit = next(doSomeStuff(input))

We can make this pure by introducing an F[_] context

  def foo[F[_], I, A](input: I)(next: A => F[Unit]): F[Unit]

and refactor to return a function for the provided input

  def foo[F[_], I, A](input: I): (A => F[Unit]) => F[Unit]

ContT is just a container for this signature, with a Monad instance

  final case class ContT[F[_], B, A](_run: (A => F[B]) => F[B]) {
    def run(f: A => F[B]): F[B] = _run(f)
  }
  object IndexedContT {
    implicit def monad[F[_], B] = new Monad[ContT[F, B, ?]] {
      def point[A](a: =>A) = ContT(_(a))
      def bind[A, C](fa: ContT[F, B, A])(f: A => ContT[F, B, C]) =
        ContT(c_fb => fa.run(a => f(a).run(c_fb)))
    }
  }

and convenient syntax to create a ContT from a monadic value:

  implicit class ContTOps[F[_]: Monad, A](self: F[A]) {
    def cps[B]: ContT[F, B, A] = ContT(a_fb => self >>= a_fb)
  }

However, the simple callback use of continuations brings nothing to pure functional programming because we already know how to sequence non-blocking, potentially distributed, computations: that is what Monad is for and we can do this with .bind or a Kleisli arrow. To see why continuations are useful we need to consider a more complex example under a rigid design constraint.

7.4.10.1 Control Flow

Say we have modularised our application into components that can perform I/O, with each component owned by a different development team:

  final case class A0()
  final case class A1()
  final case class A2()
  final case class A3()
  final case class A4()
  
  def bar0(a4: A4): IO[A0] = ...
  def bar2(a1: A1): IO[A2] = ...
  def bar3(a2: A2): IO[A3] = ...
  def bar4(a3: A3): IO[A4] = ...

Our goal is to produce an A0 given an A1. Whereas Javascript and Lisp would reach for continuations to solve this problem (because the I/O could block) we can just chain the functions

  def simple(a: A1): IO[A0] = bar2(a) >>= bar3 >>= bar4 >>= bar0

We can lift .simple into its continuation form by using the convenient .cps syntax and a little bit of extra boilerplate for each step:

  def foo1(a: A1): ContT[IO, A0, A2] = bar2(a).cps
  def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).cps
  def foo3(a: A3): ContT[IO, A0, A4] = bar4(a).cps
  
  def flow(a: A1): IO[A0]  = (foo1(a) >>= foo2 >>= foo3).run(bar0)

So what does this buy us? Firstly, it is worth noting that the control flow of this application is left to right

What if we are the authors of foo2 and we want to post-process the a0 that we receive from the right (downstream), i.e. we want to split our foo2 into foo2a and foo2b

Add the constraint that we cannot change the definition of flow or bar0. Perhaps it is not our code and is defined by the framework we are using.

It is not possible to process the output of a0 by modifying any of the remaining barX methods. However, with ContT we can modify foo2 to process the result of the next continuation:

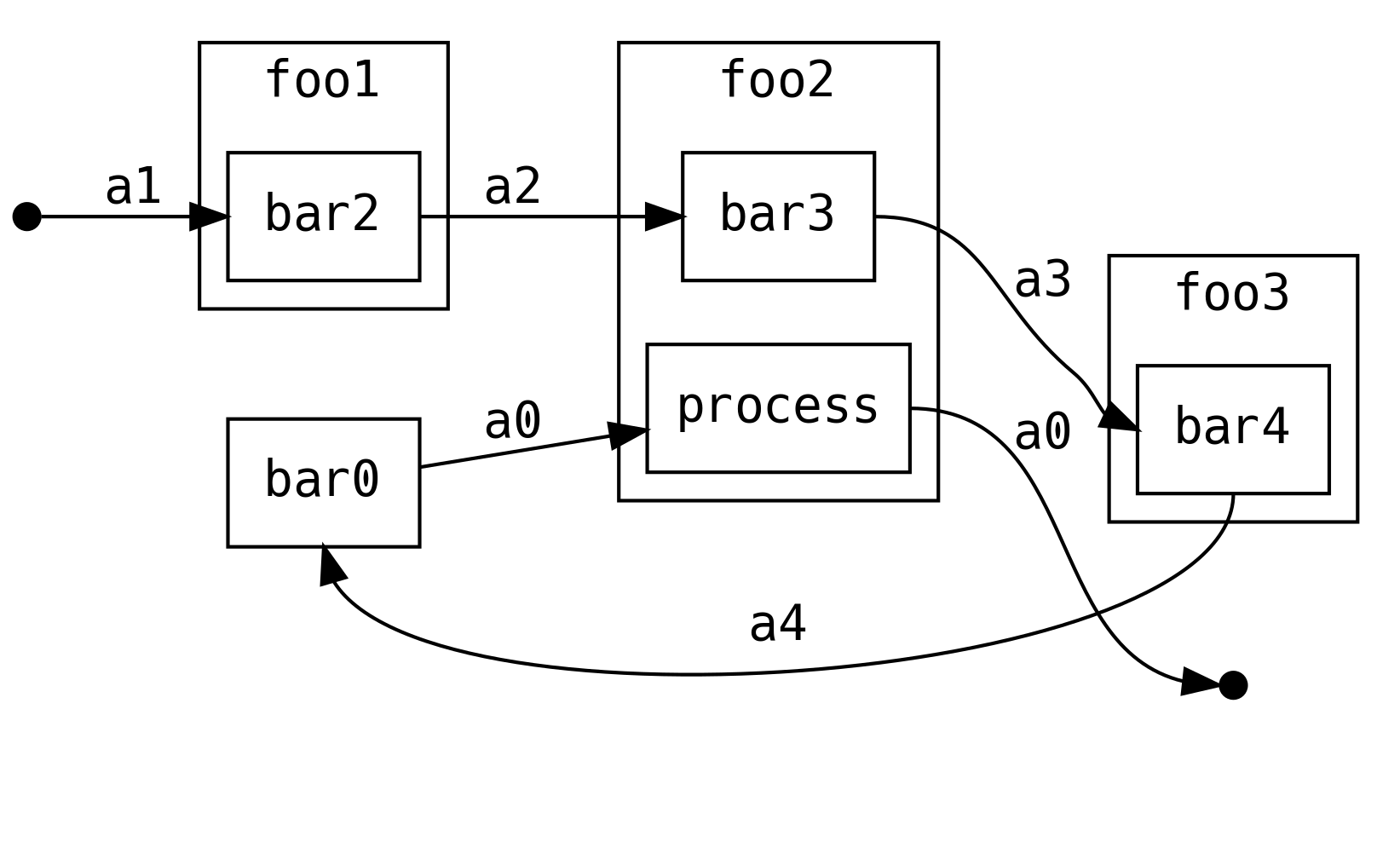
Which can be defined with

  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
    } yield process(a0)
  }

We are not limited to .map over the return value, we can .bind into another control flow turning the linear flow into a graph!

  def elsewhere: ContT[IO, A0, A4] = ???
  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
      a0_ <- if (check(a0)) a0.pure[IO]
             else elsewhere.run(bar0)
    } yield a0_
  }

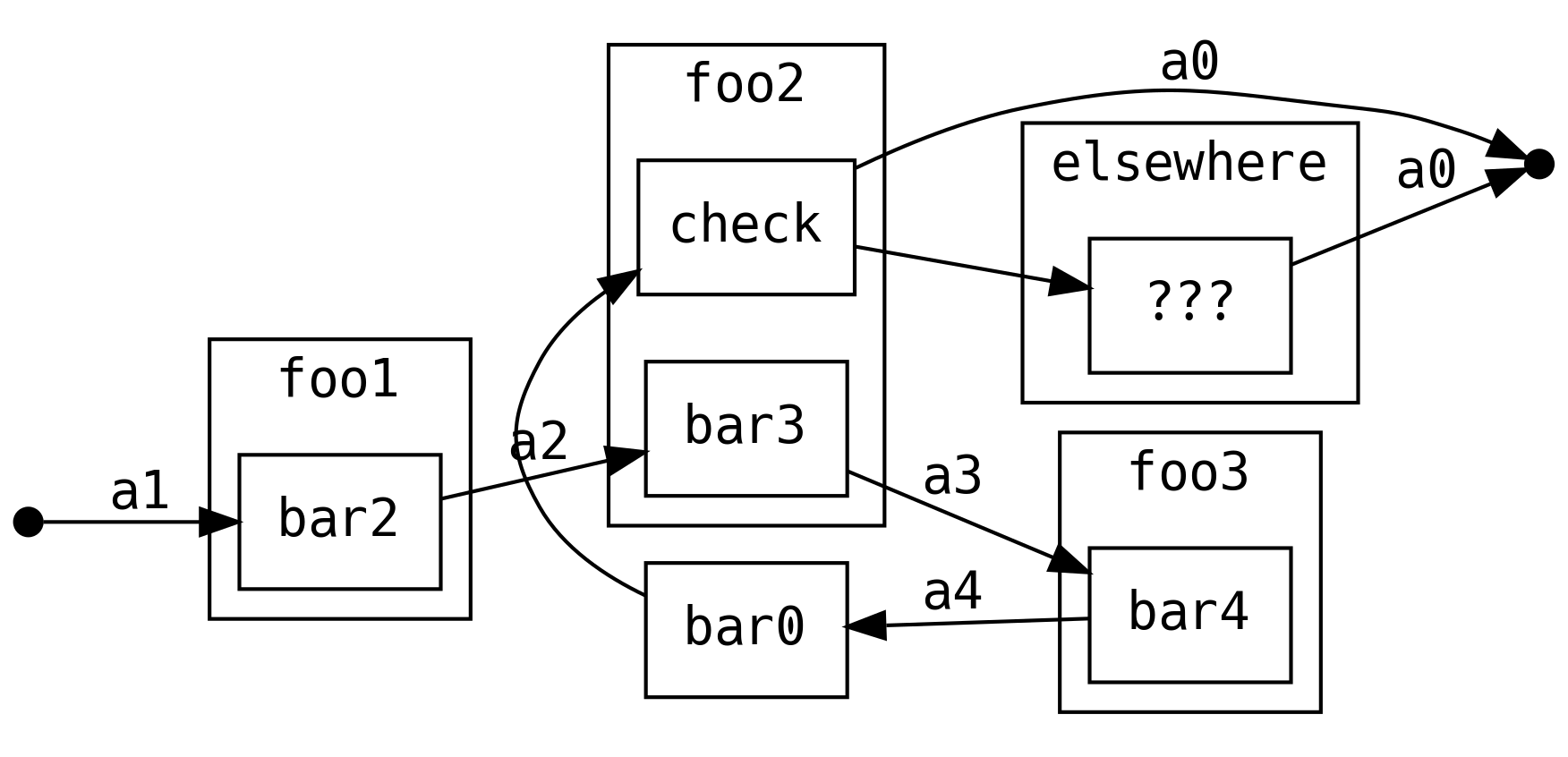
Or we can stay within the original flow and retry everything downstream

  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
      a0_ <- if (check(a0)) a0.pure[IO]
             else next(a3)
    } yield a0_
  }

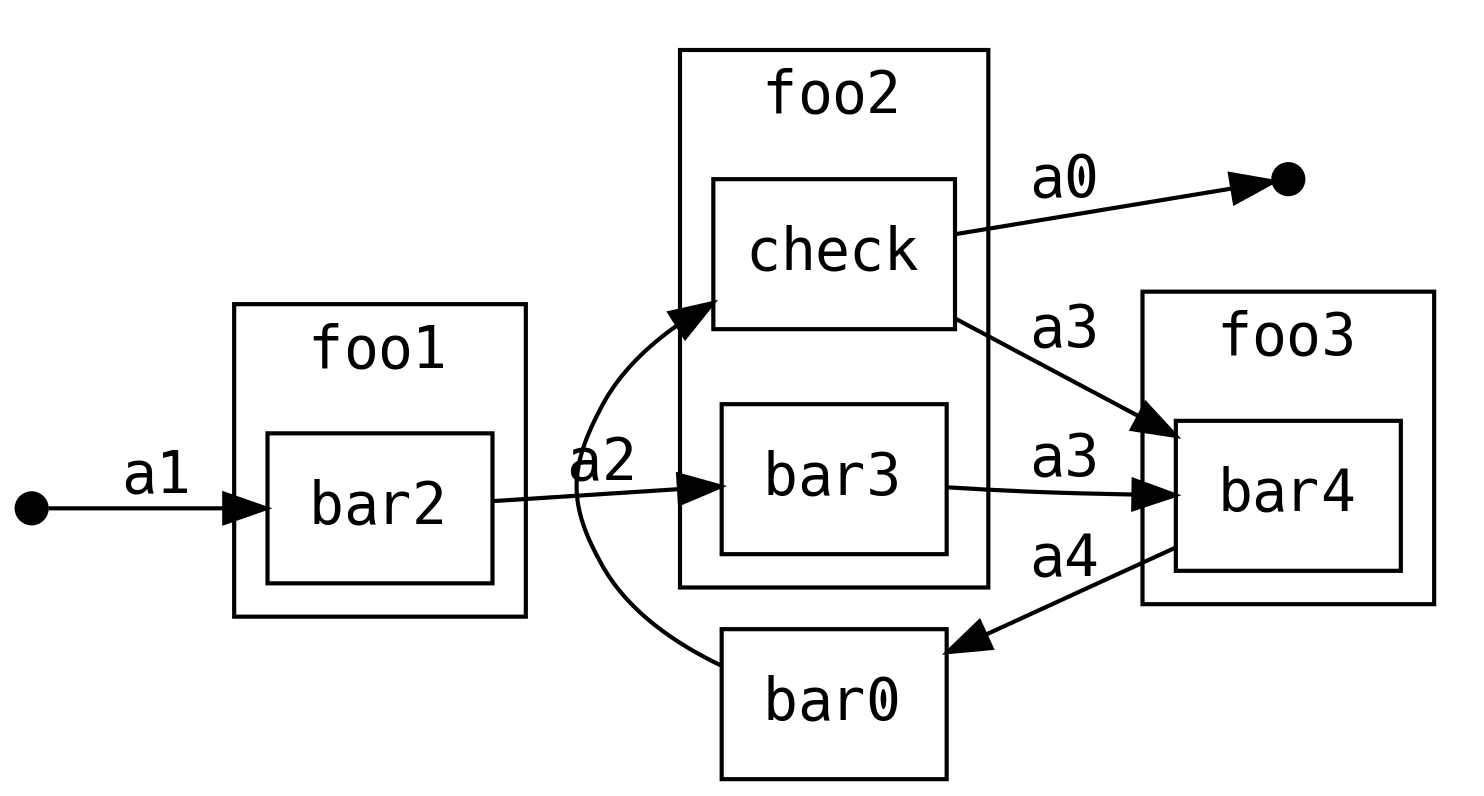
This is just one retry, not an infinite loop. For example, we might want downstream to reconfirm a potentially dangerous action.

Finally, we can perform actions that are specific to the context of the ContT, in this case IO which lets us do error handling and resource cleanup:

  def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).ensuring(cleanup).cps

7.4.10.2 When to Order Spaghetti

It is not an accident that these diagrams look like spaghetti, that is just what happens when we start messing with control flow. All the mechanisms we’ve discussed in this section are simple to implement directly if we can edit the definition of flow, therefore we do not typically need to use ContT.

However, if we are designing a framework, we should consider exposing the plugin system as ContT callbacks to allow our users more power over their control flow. Sometimes the customer just really wants the spaghetti.

For example, if the Scala compiler was written using CPS, it would allow for a principled approach to communication between compiler phases. A compiler plugin would be able to perform some action based on the inferred type of an expression, computed at a later stage in the compile. Similarly, continuations would be a good API for an extensible build tool or text editor.

A caveat with ContT is that it is not stack safe, so cannot be used for programs that run forever.

7.4.10.3 Great, kid. Don’t get `ContT`.

A more complex variant of ContT called IndexedContT wraps (A => F[B]) => F[C]. The new type parameter C allows the return type of the entire computation to be different to the return type between each component. But if B is not equal to C then there is no Monad.

Not missing an opportunity to generalise as much as possible, IndexedContT is actually implemented in terms of an even more general structure (note the extra s before the T)

  final case class IndexedContsT[W[_], F[_], C, B, A](_run: W[A => F[B]] => F[C])
  
  type IndexedContT[f[_], c, b, a] = IndexedContsT[Id, f, c, b, a]
  type ContT[f[_], b, a]           = IndexedContsT[Id, f, b, b, a]
  type ContsT[w[_], f[_], b, a]    = IndexedContsT[w, f, b, b, a]
  type Cont[b, a]                  = IndexedContsT[Id, Id, b, b, a]

where W[_] has a Comonad, and ContT is actually implemented as a type alias. Companion objects exist for these type aliases with convenient constructors.

Admittedly, five type parameters is perhaps a generalisation too far. But then again, over-generalisation is consistent with the sensibilities of continuations.

7.4.11 Transformer Stacks and Ambiguous Implicits

This concludes our tour of the monad transformers in Scalaz.

When multiple transformers are combined, we call this a transformer stack and although it is verbose, it is possible to read off the features by reading the transformers. For example if we construct an F[_] context which is a set of composed transformers, such as

  type Ctx[A] = StateT[EitherT[IO, E, ?], S, A]

we know that we are adding error handling with error type E (there is a MonadError[Ctx, E]) and we are managing state S (there is a MonadState[Ctx, S]).

But there are unfortunately practical drawbacks to using monad transformers and their companion Monad typeclasses:

Multiple implicit Monad parameters mean that the compiler cannot find the correct syntax to use for the context.
Monads do not compose in the general case, which means that the order of nesting of the transformers is important.
All the interpreters must be lifted into the common context. For example, we might have an implementation of some algebra that uses for IO and now we need to wrap it with StateT and EitherT even though they are unused inside the interpreter.
There is a performance cost associated to each layer. And some monad transformers are worse than others. StateT is particularly bad but even EitherT can cause memory allocation problems for high throughput applications.

We need to talk about workarounds.

7.4.11.1 No Syntax

Say we have an algebra

  trait Lookup[F[_]] {
    def look: F[Int]
  }

and some data types

  final case class Problem(bad: Int)
  final case class Table(last: Int)

that we want to use in our business logic

  def foo[F[_]](L: Lookup[F])(
    implicit
      E: MonadError[F, Problem],
      S: MonadState[F, Table]
  ): F[Int] = for {
    old <- S.get
    i   <- L.look
    _   <- if (i === old.last) E.raiseError(Problem(i))
           else ().pure[F]
  } yield i

The first problem we encounter is that this fails to compile

  [error] value flatMap is not a member of type parameter F[Table]
  [error]     old <- S.get
  [error]              ^

There are some tactical solutions to this problem. The most obvious is to make all the parameters explicit

  def foo1[F[_]: Monad](
    L: Lookup[F],
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = ...

and require only Monad to be passed implicitly via context bounds. However, this means that we must manually wire up the MonadError and MonadState when calling foo1 and when calling out to another method that requires an implicit.

A second solution is to leave the parameters implicit and use name shadowing to make all but one of the parameters explicit. This allows upstream to use implicit resolution when calling us but we still need to pass parameters explicitly if we call out.

  @inline final def shadow[A, B, C](a: A, b: B)(f: (A, B) => C): C = f(a, b)
  
  def foo2a[F[_]: Monad](L: Lookup[F])(
    implicit
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = shadow(E, S) { (E, S) => ...

or we could shadow just one Monad, leaving the other one to provide our syntax and to be available for when we call out to other methods

  @inline final def shadow[A, B](a: A)(f: A => B): B = f(a)
  ...
  
  def foo2b[F[_]](L: Lookup[F])(
    implicit
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = shadow(E) { E => ...

A third option, with a higher up-front cost, is to create a custom Monad typeclass that holds implicit references to the two Monad classes that we care about

  trait MonadErrorState[F[_], E, S] {
    implicit def E: MonadError[F, E]
    implicit def S: MonadState[F, S]
  }

and a derivation of the typeclass given a MonadError and MonadState

  object MonadErrorState {
    implicit def create[F[_], E, S](
      implicit
        E0: MonadError[F, E],
        S0: MonadState[F, S]
    ) = new MonadErrorState[F, E, S] {
      def E: MonadError[F, E] = E0
      def S: MonadState[F, S] = S0
    }
  }

Now if we want access to S or E we get them via F.S or F.E

  def foo3a[F[_]: Monad](L: Lookup[F])(
    implicit F: MonadErrorState[F, Problem, Table]
  ): F[Int] =
    for {
      old <- F.S.get
      i   <- L.look
      _ <- if (i === old.last) F.E.raiseError(Problem(i))
      else ().pure[F]
    } yield i

Like the second solution, we can choose one of the Monad instances to be implicit within the block, achieved by importing it

  def foo3b[F[_]](L: Lookup[F])(
    implicit F: MonadErrorState[F, Problem, Table]
  ): F[Int] = {
    import F.E
    ...
  }

7.4.11.2 Composing Transformers

An EitherT[StateT[...], ...] has a MonadError but does not have a MonadState, whereas StateT[EitherT[...], ...] can provide both.

The workaround is to study the implicit derivations on the companion of the transformers and to make sure that the outer most transformer provides everything we need.

A rule of thumb is that more complex transformers go on the outside, with this chapter presenting transformers in increasing order of complex.

7.4.11.3 Lifting Interpreters

Continuing the same example, let’s say our Lookup algebra has an IO interpreter

  object LookupRandom extends Lookup[IO] {
    def look: IO[Int] = IO { util.Random.nextInt }
  }

but we want our context to be

  type Ctx[A] = StateT[EitherT[IO, Problem, ?], Table, A]

to give us a MonadError and a MonadState. This means we need to wrap LookupRandom to operate over Ctx.

Firstly, we want to make use of the .liftM syntax on Monad, which uses MonadTrans to lift from our starting F[A] into G[F, A]

  final class MonadOps[F[_]: Monad, A](fa: F[A]) {
    def liftM[G[_[_], _]: MonadTrans]: G[F, A] = ...
    ...
  }

It is important to realise that the type parameters to .liftM have two type holes, one of shape _[_] and another of shape _. If we create type aliases of this shape

  type Ctx0[F[_], A] = StateT[EitherT[F, Problem, ?], Table, A]
  type Ctx1[F[_], A] = EitherT[F, Problem, A]
  type Ctx2[F[_], A] = StateT[F, Table, A]

We can abstract over MonadTrans to lift a Lookup[F] to any Lookup[G[F, ?]] where G is a Monad Transformer:

  def liftM[F[_]: Monad, G[_[_], _]: MonadTrans](f: Lookup[F]) =
    new Lookup[G[F, ?]] {
      def look: G[F, Int] = f.look.liftM[G]
    }

Allowing us to wrap once for EitherT, and then again for StateT

  val wrap1 = Lookup.liftM[IO, Ctx1](LookupRandom)
  val wrap2: Lookup[Ctx] = Lookup.liftM[EitherT[IO, Problem, ?], Ctx2](wrap1)

Another way to achieve this, in a single step, is to use MonadIO which enables lifting an IO into a transformer stack:

  @typeclass trait MonadIO[F[_]] extends Monad[F] {
    def liftIO[A](ioa: IO[A]): F[A]
  }

with MonadIO instances for all the common combinations of transformers.

The boilerplate overhead to lift an IO interpreter to anything with a MonadIO instance is therefore two lines of code (for the interpreter definition), plus one line per element of the algebra, and a final line to call it:

  def liftIO[F[_]: MonadIO](io: Lookup[IO]) = new Lookup[F] {
    def look: F[Int] = io.look.liftIO[F]
  }
  
  val L: Lookup[Ctx] = Lookup.liftIO(LookupRandom)

7.4.11.4 Performance

The biggest problem with Monad Transformers is their performance overhead. EitherT has a reasonably low overhead, with every .flatMap call generating a handful of objects, but this can impact high throughput applications where every object allocation matters. Other transformers, such as StateT, effectively add a trampoline, and ContT keeps the entire call-chain retained in memory.

If performance becomes a problem, the solution is to not use Monad Transformers. At least not the transformer data structures. A big advantage of the Monad typeclasses, like MonadState is that we can create an optimised F[_] for our application that provides the typeclasses naturally. We will learn how to create an optimal F[_] over the next two chapters, when we deep dive into two structures which we have already seen: Free and IO.

7.5 A Free Lunch

Our industry craves safe high-level languages, trading developer efficiency and reliability for reduced runtime performance.

The Just In Time (JIT) compiler on the JVM performs so well that simple functions can have comparable performance to their C or C++ equivalents, ignoring the cost of garbage collection. However, the JIT only performs low level optimisations: branch prediction, inlining methods, unrolling loops, and so on.

The JIT does not perform optimisations of our business logic, for example batching network calls or parallelising independent tasks. The developer is responsible for writing the business logic and optimisations at the same time, reducing readability and making it harder to maintain. It would be good if optimisation was a tangential concern.

If instead, we have a data structure that describes our business logic in terms of high level concepts, not machine instructions, we can perform high level optimisation. Data structures of this nature are typically called Free structures and can be generated for free for the members of the algebraic interfaces of our program. For example, a Free Applicative can be generated that allows us to batch or de-duplicate expensive network I/O.

In this section we will learn how to create free structures, and how they can be used.

7.5.1 `Free` (`Monad`)

Fundamentally, a monad describes a sequential program where every step depends on the previous one. We are therefore limited to modifications that only know about things that we’ve already run and the next thing we are going to run.

As a refresher, Free is the data structure representation of a Monad and is defined by three members

  sealed abstract class Free[S[_], A] {
    def mapSuspension[T[_]](f: S ~> T): Free[T, A] = ...
    def foldMap[M[_]: Monad](f: S ~> M): M[A] = ...
    ...
  }
  object Free {
    implicit def monad[S[_], A]: Monad[Free[S, A]] = ...
  
    private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
    private final case class Return[S[_], A](a: A)     extends Free[S, A]
    private final case class Gosub[S[_], A0, B](
      a: Free[S, A0],
      f: A0 => Free[S, B]
    ) extends Free[S, B] { type A = A0 }
  
    def liftF[S[_], A](value: S[A]): Free[S, A] = Suspend(value)
    ...
  }

Suspend represents a program that has not yet been interpreted
Return is .pure
Gosub is .bind

A Free[S, A] can be freely generated for any algebra S. To make this explicit, consider our application’s Machines algebra

  trait Machines[F[_]] {
    def getTime: F[Epoch]
    def getManaged: F[NonEmptyList[MachineNode]]
    def getAlive: F[Map[MachineNode, Epoch]]
    def start(node: MachineNode): F[Unit]
    def stop(node: MachineNode): F[Unit]
  }

We define a freely generated Free for Machines by creating an ADT with a data type for each element of the algebra. Each data type has the same input parameters as its corresponding element, is parameterised over the return type, and has the same name:

  object Machines {
    sealed abstract class Ast[A]
    final case class GetTime()                extends Ast[Epoch]
    final case class GetManaged()             extends Ast[NonEmptyList[MachineNode]]
    final case class GetAlive()               extends Ast[Map[MachineNode, Epoch]]
    final case class Start(node: MachineNode) extends Ast[Unit]
    final case class Stop(node: MachineNode)  extends Ast[Unit]
    ...

The ADT defines an Abstract Syntax Tree (AST) because each member is representing a computation in a program.

We then define .liftF, an implementation of Machines, with Free[Ast, ?] as the context. Every method simply delegates to Free.liftT to create a Suspend

  ...
    def liftF = new Machines[Free[Ast, ?]] {
      def getTime = Free.liftF(GetTime())
      def getManaged = Free.liftF(GetManaged())
      def getAlive = Free.liftF(GetAlive())
      def start(node: MachineNode) = Free.liftF(Start(node))
      def stop(node: MachineNode) = Free.liftF(Stop(node))
    }
  }

When we construct our program, parameterised over a Free, we run it by providing an interpreter (a natural transformation Ast ~> M) to the .foldMap method. For example, if we could provide an interpreter that maps to IO we can construct an IO[Unit] program via the free AST

  def program[F[_]: Monad](M: Machines[F]): F[Unit] = ...
  
  val interpreter: Machines.Ast ~> IO = ...
  
  val app: IO[Unit] = program[Free[Machines.Ast, ?]](Machines.liftF)
                        .foldMap(interpreter)

For completeness, an interpreter that delegates to a direct implementation is easy to write. This might be useful if the rest of the application is using Free as the context and we already have an IO implementation that we want to use:

  def interpreter[F[_]](f: Machines[F]): Ast ~> F = λ[Ast ~> F] {
    case GetTime()    => f.getTime
    case GetManaged() => f.getManaged
    case GetAlive()   => f.getAlive
    case Start(node)  => f.start(node)
    case Stop(node)   => f.stop(node)
  }

But our business logic needs more than just Machines, we also need access to the Drone algebra, recall defined as

  trait Drone[F[_]] {
    def getBacklog: F[Int]
    def getAgents: F[Int]
  }
  object Drone {
    sealed abstract class Ast[A]
    ...
    def liftF = ...
    def interpreter = ...
  }

What we want is for our AST to be a combination of the Machines and Drone ASTs. We studied Coproduct in Chapter 6, a higher kinded disjunction:

  final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A])

We can use the context Free[Coproduct[Machines.Ast, Drone.Ast, ?], ?].

We could manually create the coproduct but we would be swimming in boilerplate, and we’d have to do it all again if we wanted to add a third algebra.

The scalaz.Inject typeclass helps:

  type :<:[F[_], G[_]] = Inject[F, G]
  sealed abstract class Inject[F[_], G[_]] {
    def inj[A](fa: F[A]): G[A]
    def prj[A](ga: G[A]): Option[F[A]]
  }
  object Inject {
    implicit def left[F[_], G[_]]: F :<: Coproduct[F, G, ?]] = ...
    ...
  }

The implicit derivations generate Inject instances when we need them, letting us rewrite our liftF to work for any combination of ASTs:

  def liftF[F[_]](implicit I: Ast :<: F) = new Machines[Free[F, ?]] {
    def getTime                  = Free.liftF(I.inj(GetTime()))
    def getManaged               = Free.liftF(I.inj(GetManaged()))
    def getAlive                 = Free.liftF(I.inj(GetAlive()))
    def start(node: MachineNode) = Free.liftF(I.inj(Start(node)))
    def stop(node: MachineNode)  = Free.liftF(I.inj(Stop(node)))
  }

It is nice that F :<: G reads as if our Ast is a member of the complete F instruction set: this syntax is intentional.

Putting it all together, lets say we have a program that we wrote abstracting over Monad

  def program[F[_]: Monad](M: Machines[F], D: Drone[F]): F[Unit] = ...

and we have some existing implementations of Machines and Drone, we can create interpreters from them:

  val MachinesIO: Machines[IO] = ...
  val DroneIO: Drone[IO]       = ...
  
  val M: Machines.Ast ~> IO = Machines.interpreter(MachinesIO)
  val D: Drone.Ast ~> IO    = Drone.interpreter(DroneIO)

and combine them into the larger instruction set using a convenience method from the NaturalTransformation companion

  object NaturalTransformation {
    def or[F[_], G[_], H[_]](fg: F ~> G, hg: H ~> G): Coproduct[F, H, ?] ~> G = ...
    ...
  }
  
  type Ast[a] = Coproduct[Machines.Ast, Drone.Ast, a]
  
  val interpreter: Ast ~> IO = NaturalTransformation.or(M, D)

Then use it to produce an IO

  val app: IO[Unit] = program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
                        .foldMap(interpreter)

But we’ve gone in circles! We could have used IO as the context for our program in the first place and avoided Free. So why did we put ourselves through all this pain? Here are some examples of where Free might be useful.

7.5.1.1 Testing: Mocks and Stubs

It might sound hypocritical to propose that Free can be used to reduce boilerplate, given how much code we have written. However, there is a tipping point where the Ast pays for itself when we have many tests that require stub implementations.

If the .Ast and .liftF is defined for an algebra, we can create partial interpreters

  val M: Machines.Ast ~> Id = stub[Map[MachineNode, Epoch]] {
    case Machines.GetAlive() => Map.empty
  }
  val D: Drone.Ast ~> Id = stub[Int] {
    case Drone.GetBacklog() => 1
  }

which can be used to test our program

  program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
    .foldMap(or(M, D))
    .shouldBe(1)

By using partial functions, and not total functions, we are exposing ourselves to runtime errors. Many teams are happy to accept this risk in their unit tests since the test would fail if there is a programmer error.

Arguably we could also achieve the same thing with implementations of our algebras that implement every method with ???, overriding what we need on a case by case basis.

The library smock is more powerful, but for the purposes of this short example we can define stub ourselves using a type inference trick that can be found all over the Scalaz source code. The reason for Stub being a separate class is so that we only need to provide the A type parameter, with F and G inferred from the left hand side of the expression:

  object Mocker {
    final class Stub[A] {
      def apply[F[_], G[_]](pf: PartialFunction[F[A], G[A]]): F ~> G = new (F ~> G) {
        def apply[α](fa: F[α]) = pf.asInstanceOf[PartialFunction[F[α], G[α]]](fa)
      }
    }
    def stub[A]: Stub[A] = new Stub[A]
  }

7.5.1.2 Monitoring

It is typical for server applications to be monitored by runtime agents that manipulate bytecode to insert profilers and extract various kinds of usage or performance information.

If our application’s context is Free, we do not need to resort to bytecode manipulation, we can instead implement a side-effecting monitor as an interpreter that we have complete control over.

For example, consider using this Ast ~> Ast “agent”

  val Monitor = λ[Demo.Ast ~> Demo.Ast](
    _.run match {
      case \/-(m @ Drone.GetBacklog()) =>
        JmxAbstractFactoryBeanSingletonProviderUtilImpl.count("backlog")
        Coproduct.rightc(m)
      case other =>
        Coproduct(other)
    }
  )

which records method invocations: we would use a vendor-specific routine in real code. We could also watch for specific messages of interest and log them as a debugging aid.

We can attach Monitor to our production Free application with

  .mapSuspension(Monitor).foldMap(interpreter)

or combine the natural transformations and run with a single

  .foldMap(Monitor.andThen(interpreter))

7.5.1.3 Monkey Patching

As engineers, we are used to requests for bizarre workarounds to be added to the core logic of the application. We might want to codify such corner cases as exceptions to the rule and handle them tangentially to our core logic.

For example, suppose we get a memo from accounting telling us

URGENT: Bob is using node #c0ffee to run the year end. DO NOT STOP THIS MACHINE!1!

There is no possibility to discuss why Bob shouldn’t be using our machines for his super-important accounts, so we have to hack our business logic and put out a release to production as soon as possible.

Our monkey patch can map into a Free structure, allowing us to return a pre-canned result (Free.pure) instead of scheduling the instruction. We special case the instruction in a custom natural transformation with its return value:

  val monkey = λ[Machines.Ast ~> Free[Machines.Ast, ?]] {
    case Machines.Stop(MachineNode("#c0ffee")) => Free.pure(())
    case other                                 => Free.liftF(other)
  }

eyeball that it works, push it to prod, and set an alarm for next week to remind us to remove it, and revoke Bob’s access to our servers.

Our unit test could use State as the target context, so we can keep track of all the nodes we stopped:

  type S = Set[MachineNode]
  val M: Machines.Ast ~> State[S, ?] = Mocker.stub[Unit] {
    case Machines.Stop(node) => State.modify[S](_ + node)
  }
  
  Machines
    .liftF[Machines.Ast]
    .stop(MachineNode("#c0ffee"))
    .foldMap(monkey)
    .foldMap(M)
    .exec(Set.empty)
    .shouldBe(Set.empty)

along with a test that “normal” nodes are not affected.

An advantage of using Free to avoid stopping the #c0ffee nodes is that we can be sure to catch all the usages instead of having to go through the business logic and look for all usages of .stop. If our application context is just an IO we could, of course, implement this logic in the Machines[IO] implementation but an advantage of using Free is that we don’t need to touch the existing code and can instead isolate and test this (temporary) behaviour, without being tied to the IO implementations.

7.5.2 `FreeAp` (`Applicative`)

Despite this chapter being called Advanced Monads, the takeaway is: we shouldn’t use monads unless we really really have to. In this section, we will see why FreeAp (free applicative) is preferable to Free monads.

FreeAp is defined as the data structure representation of the ap and pure methods from the Applicative typeclass:

  sealed abstract class FreeAp[S[_], A] {
    def hoist[G[_]](f: S ~> G): FreeAp[G,A] = ...
    def foldMap[G[_]: Applicative](f: S ~> G): G[A] = ...
    def monadic: Free[S, A] = ...
    def analyze[M:Monoid](f: F ~> λ[α => M]): M = ...
    ...
  }
  object FreeAp {
    implicit def applicative[S[_], A]: Applicative[FreeAp[S, A]] = ...
  
    private final case class Pure[S[_], A](a: A) extends FreeAp[S, A]
    private final case class Ap[S[_], A, B](
      value: () => S[B],
      function: () => FreeAp[S, B => A]
    ) extends FreeAp[S, A]
  
    def pure[S[_], A](a: A): FreeAp[S, A] = Pure(a)
    def lift[S[_], A](x: =>S[A]): FreeAp[S, A] = ...
    ...
  }

The methods .hoist and .foldMap are like their Free analogues .mapSuspension and .foldMap.

As a convenience, we can generate a Free[S, A] from our FreeAp[S, A] with .monadic. This is especially useful to optimise smaller Applicative subsystems yet use them as part of a larger Free program.

Like Free, we must create a FreeAp for our ASTs, more boilerplate…

  def liftA[F[_]](implicit I: Ast :<: F) = new Machines[FreeAp[F, ?]] {
    def getTime = FreeAp.lift(I.inj(GetTime()))
    ...
  }

7.5.2.1 Batching Network Calls

We opened this chapter with grand claims about performance. Time to deliver.

Philip Stark’s Humanised version of Peter Norvig’s Latency Numbers serve as motivation for why we should focus on reducing network calls to optimise an application:

Computer	Human Timescale	Human Analogy
L1 cache reference	0.5 secs	One heart beat
Branch mispredict	5 secs	Yawn
L2 cache reference	7 secs	Long yawn
Mutex lock/unlock	25 secs	Making a cup of tea
Main memory reference	100 secs	Brushing your teeth
Compress 1K bytes with Zippy	50 min	Scala compiler CI pipeline
Send 2K bytes over 1Gbps network	5.5 hr	Train London to Edinburgh
SSD random read	1.7 days	Weekend
Read 1MB sequentially from memory	2.9 days	Long weekend
Round trip within same datacenter	5.8 days	Long US Vacation
Read 1MB sequentially from SSD	11.6 days	Short EU Holiday
Disk seek	16.5 weeks	Term of university
Read 1MB sequentially from disk	7.8 months	Fully paid maternity in Norway
Send packet CA->Netherlands->CA	4.8 years	Government’s term

Although Free and FreeAp incur a memory allocation overhead, the equivalent of 100 seconds in the humanised chart, every time we can turn two sequential network calls into one batch call, we save nearly 5 years.

When we are in a Applicative context, we can safely optimise our application without breaking any of the expectations of the original program, and without cluttering the business logic.

Luckily, our main business logic only requires an Applicative, recall

  final class DynAgentsModule[F[_]: Applicative](D: Drone[F], M: Machines[F])
      extends DynAgents[F] {
    def act(world: WorldView): F[WorldView] = ...
    ...
  }

To begin, we create the lift boilerplate for a new Batch algebra

  trait Batch[F[_]] {
    def start(nodes: NonEmptyList[MachineNode]): F[Unit]
  }
  object Batch {
    sealed abstract class Ast[A]
    final case class Start(nodes: NonEmptyList[MachineNode]) extends Ast[Unit]
  
    def liftA[F[_]](implicit I: Ast :<: F) = new Batch[FreeAp[F, ?]] {
      def start(nodes: NonEmptyList[MachineNode]) = FreeAp.lift(I.inj(Start(nodes)))
    }
  }

and then we will create an instance of DynAgentsModule with FreeAp as the context

  type Orig[a] = Coproduct[Machines.Ast, Drone.Ast, a]
  
  val world: WorldView = ...
  val program = new DynAgentsModule(Drone.liftA[Orig], Machines.liftA[Orig])
  val freeap  = program.act(world)

In Chapter 6, we studied the Const data type, which allows us to analyse a program. It should not be surprising that FreeAp.analyze is implemented in terms of Const:

  sealed abstract class FreeAp[S[_], A] {
    ...
    def analyze[M: Monoid](f: S ~> λ[α => M]): M =
      foldMap(λ[S ~> Const[M, ?]](x => Const(f(x)))).getConst
  }

We provide a natural transformation to record all node starts and .analyze our program to get all the nodes that need to be started:

  val gather = λ[Orig ~> λ[α => IList[MachineNode]]] {
    case Coproduct(-\/(Machines.Start(node))) => IList.single(node)
    case _                                    => IList.empty
  }
  val gathered: IList[MachineNode] = freeap.analyze(gather)

The next step is to extend the instruction set from Orig to Extended, which includes the Batch.Ast and write a FreeAp program that starts all our gathered nodes in a single network call

  type Extended[a] = Coproduct[Batch.Ast, Orig, a]
  def batch(nodes: IList[MachineNode]): FreeAp[Extended, Unit] =
    nodes.toNel match {
      case None        => FreeAp.pure(())
      case Some(nodes) => FreeAp.lift(Coproduct.leftc(Batch.Start(nodes)))
    }

We also need to remove all the calls to Machines.Start, which we can do with a natural transformation

  val nostart = λ[Orig ~> FreeAp[Extended, ?]] {
    case Coproduct(-\/(Machines.Start(_))) => FreeAp.pure(())
    case other                             => FreeAp.lift(Coproduct.rightc(other))
  }

Now we have two programs, and need to combine them. Recall the *> syntax from Apply

  val patched = batch(gathered) *> freeap.foldMap(nostart)

Putting it all together under a single method:

  def optimise[A](orig: FreeAp[Orig, A]): FreeAp[Extended, A] =
    (batch(orig.analyze(gather)) *> orig.foldMap(nostart))

That Is it! We .optimise every time we call act in our main loop, which is just a matter of plumbing.

7.5.3 `Coyoneda` (`Functor`)

Named after mathematician Nobuo Yoneda, we can freely generate a Functor data structure for any algebra S[_]

  sealed abstract class Coyoneda[F[_], A] {
    def run(implicit F: Functor[F]): F[A] = ...
    def trans[G[_]](f: F ~> G): Coyoneda[G, A] = ...
    ...
  }
  object Coyoneda {
    implicit def functor[F[_], A]: Functor[Coyoneda[F, A]] = ...
  
    private final case class Map[F[_], A, B](fa: F[A], f: A => B) extends Coyoneda[F, A]
    def apply[F[_], A, B](sa: F[A])(f: A => B) = Map[F, A, B](sa, f)
    def lift[F[_], A](sa: F[A]) = Map[F, A, A](sa, identity)
    ...
  }

and there is also a contravariant version

  sealed abstract class ContravariantCoyoneda[F[_], A] {
    def run(implicit F: Contravariant[F]): F[A] = ...
    def trans[G[_]](f: F ~> G): ContravariantCoyoneda[G, A] = ...
    ...
  }
  object ContravariantCoyoneda {
    implicit def contravariant[F[_], A]: Contravariant[ContravariantCoyoneda[F, A]] = ...
  
    private final case class Contramap[F[_], A, B](fa: F[A], f: B => A)
      extends ContravariantCoyoneda[F, A]
    def apply[F[_], A, B](sa: F[A])(f: B => A) = Contramap[F, A, B](sa, f)
    def lift[F[_], A](sa: F[A]) = Contramap[F, A, A](sa, identity)
    ...
  }

The API is somewhat simpler than Free and FreeAp, allowing a natural transformation with .trans and a .run (taking an actual Functor or Contravariant, respectively) to escape the free structure.

Coyo and cocoyo can be a useful utility if we want to .map or .contramap over a type, and we know that we can convert into a data type that has a Functor but we don’t want to commit to the final data structure too early. For example, we create a Coyoneda[ISet, ?] (recall ISet does not have a Functor) to use methods that require a Functor, then convert into IList later on.

If we want to optimise a program with coyo or cocoyo we have to provide the expected boilerplate for each algebra:

  def liftCoyo[F[_]](implicit I: Ast :<: F) = new Machines[Coyoneda[F, ?]] {
    def getTime = Coyoneda.lift(I.inj(GetTime()))
    ...
  }
  def liftCocoyo[F[_]](implicit I: Ast :<: F) = new Machines[ContravariantCoyoneda[F, ?]] {
    def getTime = ContravariantCoyoneda.lift(I.inj(GetTime()))
    ...
  }

An optimisation we get by using Coyoneda is map fusion (and contramap fusion), which allows us to rewrite

  xs.map(a).map(b).map(c)

into

  xs.map(x => c(b(a(x))))

avoiding intermediate representations. For example, if xs is a List of a thousand elements, we save two thousand object allocations because we only map over the data structure once.

However it is arguably a lot easier to just make this kind of change in the original function by hand, or to wait for the scalaz-plugin project to be released and automatically perform these sorts of optimisations.

7.5.4 Extensible Effects

Programs are just data: free structures help to make this explicit and give us the ability to rearrange and optimise that data.

Free is more special than it appears: it can sequence arbitrary algebras and typeclasses.

For example, a free structure for MonadState is available. The Ast and .liftF are more complicated than usual because we have to account for the S type parameter on MonadState, and the inheritance from Monad:

  object MonadState {
    sealed abstract class Ast[S, A]
    final case class Get[S]()     extends Ast[S, S]
    final case class Put[S](s: S) extends Ast[S, Unit]
  
    def liftF[F[_], S](implicit I: Ast[S, ?] :<: F) =
      new MonadState[Free[F, ?], S] with BindRec[Free[F, ?]] {
        def get       = Free.liftF(I.inj(Get[S]()))
        def put(s: S) = Free.liftF(I.inj(Put[S](s)))
  
        val delegate         = Free.freeMonad[F]
        def point[A](a: =>A) = delegate.point(a)
        ...
      }
    ...
  }

This gives us the opportunity to use optimised interpreters. For example, we could store the S in an atomic field instead of building up a nested StateT trampoline.

We can create an Ast and .liftF for almost any algebra or typeclass! The only restriction is that the F[_] does not appear as a parameter to any of the instructions, i.e. it must be possible for the algebra to have an instance of Functor. This unfortunately rules out MonadError and Monoid.

The reason why free encodings do not work for all algebras and typeclasses is quite subtle.

Consider what happens if we create an Ast for MonadError, with F[_] in contravariant position, i.e. as a parameter.

  object MonadError {
    sealed abstract class Ast[F[_], E, A]
    final case class RaiseError[F[_], E, A](e: E) extends Ast[F, E, A]
    final case class HandleError[F[_], E, A](fa: F[A], f: E => F[A]) extends Ast[F, E, A]
  
    def liftF[F[_], E](implicit I: Ast[F, E, ?] :<: F): MonadError[F, E] = ...
    ...
  }

When we come to interpret a program that uses MonadError.Ast we must construct the coproduct of instructions. Say we extend a Drone program:

  type Ast[a] = Coproduct[MonadError.Ast[Ast, String, ?], Drone.Ast, a]

This fails to compile because Ast refers to itself!

Algebras that are not entirely made of covariant functor signatures, i.e. F[_] in return position, are impossible to interpret because the resulting type of the program is self-referential. Indeed the name algebra that we have been using has its roots in F-Algebras, where the F is for Functor.

Thanks to Edmund Noble for initiating this discussion.

As the AST of a free program grows, performance degrades because the interpreter must match over instruction sets with an O(n) cost. An alternative to scalaz.Coproduct is iotaz’s encoding, which uses an optimised data structure to perform O(1) dynamic dispatch (using integers that are assigned to each coproduct at compiletime).

For historical reasons a free AST for an algebra or typeclass is called Initial Encoding, and a direct implementation (e.g. with IO) is called Finally Tagless. Although we have explored interesting ideas with Free, it is generally accepted that finally tagless is superior. But to use finally tagless style, we need a high performance effect type that provides all the monad typeclasses we’ve covered in this chapter. We also still need to be able to run our Applicative code in parallel. This is exactly what we will cover next.

7.6 `Parallel`

There are two effectful operations that we almost always want to run in parallel:

.map over a collection of effects, returning a single effect. This is achieved by .traverse, which delegates to the effect’s .apply2.
running a fixed number of effects with the scream operator |@|, and combining their output, again delegating to .apply2.

However, in practice, neither of these operations execute in parallel by default. The reason is that if our F[_] is implemented by a Monad, then the derived combinator laws for .apply2 must be satisfied, which say

  @typeclass trait Bind[F[_]] extends Apply[F] {
    ...
    override def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] =
      bind(fa)(a => map(fb)(b => f(a, b)))
    ...
  }

In other words, Monad is explicitly forbidden from running effects in parallel.

However, if we have an F[_] that is not monadic, then it may implement .apply2 in parallel. We can use the @@ (tag) mechanism to create an instance of Applicative for F[_] @@ Parallel, which is conveniently assigned to the type alias Applicative.Par

  object Applicative {
    type Par[F[_]] = Applicative[λ[α => F[α] @@ Tags.Parallel]]
    ...
  }

Monadic programs can then request an implicit Par in addition to their Monad

  def foo[F[_]: Monad: Applicative.Par]: F[Unit] = ...

Scalaz’s Traverse syntax supports parallelism:

  implicit class TraverseSyntax[F[_], A](self: F[A]) {
    ...
    def parTraverse[G[_], B](f: A => G[B])(
      implicit F: Traverse[F], G: Applicative.Par[G]
    ): G[F[B]] = Tag.unwrap(F.traverse(self)(a => Tag(f(a))))
  }

If the implicit Applicative.Par[IO] is in scope, we can choose between sequential and parallel traversal:

  val input: IList[String] = ...
  def network(in: String): IO[Int] = ...
  
  input.traverse(network): IO[IList[Int]] // one at a time
  input.parTraverse(network): IO[IList[Int]] // all in parallel

Similarly, we can call .parApply or .parTupled after using scream operators

  val fa: IO[String] = ...
  val fb: IO[String] = ...
  val fc: IO[String] = ...
  
  (fa |@| fb).parTupled: IO[(String, String)]
  
  (fa |@| fb |@| fc).parApply { case (a, b, c) => a + b + c }: IO[String]

It is worth noting that when we have Applicative programs, such as

  def foo[F[_]: Applicative]: F[Unit] = ...

we can use F[A] @@ Parallel as our program’s context and get parallelism as the default on .traverse and |@|. Converting between the raw and @@ Parallel versions of F[_] must be handled manually in the glue code, which can be painful. Therefore it is often easier to simply request both forms of Applicative

  def foo[F[_]: Applicative: Applicative.Par]: F[Unit] = ...

7.6.1 Breaking the Law

We can take a more daring approach to parallelism: opt-out of the law that .apply2 must be sequential for Monad. This is highly controversial, but works well for the majority of real world applications. We must first audit our codebase (including third party dependencies) to ensure that nothing is making use of the .apply2 implied law.

We wrap IO

  final class MyIO[A](val io: IO[A]) extends AnyVal

and provide our own implementation of Monad which runs .apply2 in parallel by delegating to a @@ Parallel instance

  object MyIO {
    implicit val monad: Monad[MyIO] = new Monad[MyIO] {
      override def apply2[A, B, C](fa: MyIO[A], fb: MyIO[B])(f: (A, B) => C): MyIO[C] =
        Applicative[IO.Par].apply2(fa.io, fb.io)(f)
      ...
    }
  }

We can now use MyIO as our application’s context instead of IO, and get parallelism by default.

Wrapping an existing type and providing custom typeclass instances is known as newtyping.

@@ and newtyping are complementary: @@ allows us to request specific typeclass variants on our domain model, whereas newtyping allow us to define the instances on the implementation. Same thing, different insertion points.

The @newtype macro by Cary Robbins has an optimised runtime representation (more efficient than extends AnyVal), that makes it easy to delegate typeclasses that we do not wish to customise. For example, we can customise Monad but delegate the Plus:

  @newtype class MyIO[A](io: IO[A])
  object MyIO {
    implicit val monad: Monad[MyIO] = ...
    implicit val plus: Plus[MyIO] = derived
  }

For completeness: a naive and inefficient implementation of Applicative.Par for our toy IO could use Future:

  object IO {
    ...
    type Par[a] = IO[a] @@ Parallel
    implicit val ParApplicative = new Applicative[Par] {
      override def apply2[A, B, C](fa: =>Par[A], fb: =>Par[B])(f: (A, B) => C): Par[C] =
        Tag(
          IO {
            val forked = Future { Tag.unwrap(fa).interpret() }
            val b      = Tag.unwrap(fb).interpret()
            val a      = Await.result(forked, Duration.Inf)
            f(a, b)
          }
        )
  }

and due to a bug in the Scala compiler that treats all @@ instances as orphans, we must explicitly import the implicit:

  import IO.ParApplicative

In the final section of this chapter we will see how Scalaz’s IO is actually implemented.

7.7 `IO`

Scalaz’s IO is the fastest asynchronous programming construct in the Scala ecosystem: up to 50 times faster than Future. IO is a free data structure specialised for use as a general effect monad.

  sealed abstract class IO[E, A] { ... }
  object IO {
    private final class FlatMap         ... extends IO[E, A]
    private final class Point           ... extends IO[E, A]
    private final class Strict          ... extends IO[E, A]
    private final class SyncEffect      ... extends IO[E, A]
    private final class Fail            ... extends IO[E, A]
    private final class AsyncEffect     ... extends IO[E, A]
    ...
  }

IO has two type parameters: it has a Bifunctor allowing the error type to be an application specific ADT. But because we are on the JVM, and must interact with legacy libraries, a convenient type alias is provided that uses exceptions for the error type:

  type Task[A] = IO[Throwable, A]

scalaz.ioeffect.IO is a high performance IO by John de Goes. It has a separate lifecycle to the core Scalaz library and must be manually added to our build.sbt with

  libraryDependencies += "org.scalaz" %% "scalaz-ioeffect" % "2.10.1"

Do not use the deprecated scalaz-effect and scalaz-concurrency packages.

Prefer the scalaz.ioeffect variants of all typeclasses and data types.

7.7.1 Creating

There are multiple ways to create an IO that cover a variety of eager, lazy, safe and unsafe code blocks:

  object IO {
    // eager evaluation of an existing value
    def now[E, A](a: A): IO[E, A] = ...
    // lazy evaluation of a pure calculation
    def point[E, A](a: =>A): IO[E, A] = ...
    // lazy evaluation of a side-effecting, yet Total, code block
    def sync[E, A](effect: =>A): IO[E, A] = ...
    // lazy evaluation of a side-effecting code block that may fail
    def syncThrowable[A](effect: =>A): IO[Throwable, A] = ...
  
    // create a failed IO
    def fail[E, A](error: E): IO[E, A] = ...
    // asynchronously sleeps for a specific period of time
    def sleep[E](duration: Duration): IO[E, Unit] = ...
    ...
  }

with convenient Task constructors:

  object Task {
    def apply[A](effect: =>A): Task[A] = IO.syncThrowable(effect)
    def now[A](effect: A): Task[A] = IO.now(effect)
    def fail[A](error: Throwable): Task[A] = IO.fail(error)
    def fromFuture[E, A](io: Task[Future[A]])(ec: ExecutionContext): Task[A] = ...
  }

The most common constructors, by far, when dealing with legacy code are Task.apply and Task.fromFuture:

  val fa: Task[Future[String]] = Task { ... impure code here ... }
  
  Task.fromFuture(fa)(ExecutionContext.global): Task[String]

We cannot pass around raw Future, because it eagerly evaluates, so must always be constructed inside a safe block.

Note that the ExecutionContext is not implicit, contrary to the convention. Recall that in Scalaz we reserve the implicit keyword for typeclass derivation, to simplify the language: ExecutionContext is configuration that must be provided explicitly.

7.7.2 Running

The IO interpreter is called RTS, for runtime system. Its implementation is beyond the scope of this book. We will instead focus on the features that IO provides.

IO is just a data structure, and is interpreted at the end of the world by extending SafeApp and implementing .run

  trait SafeApp extends RTS {
  
    sealed trait ExitStatus
    object ExitStatus {
      case class ExitNow(code: Int)                         extends ExitStatus
      case class ExitWhenDone(code: Int, timeout: Duration) extends ExitStatus
      case object DoNotExit                                 extends ExitStatus
    }
  
    def run(args: List[String]): IO[Void, ExitStatus]
  
    final def main(args0: Array[String]): Unit = ... calls run ...
  }

If we are integrating with a legacy system and are not in control of the entry point of our application, we can extend the RTS and gain access to unsafe methods to evaluate the IO at the entry point to our principled FP code.

7.7.3 Features

IO provides typeclass instances for Bifunctor, MonadError[E, ?], BindRec, Plus, MonadPlus (if E forms a Monoid), and an Applicative[IO.Par[E, ?]].

In addition to the functionality from the typeclasses, there are implementation specific methods:

  sealed abstract class IO[E, A] {
    // retries an action N times, until success
    def retryN(n: Int): IO[E, A] = ...
    // ... with exponential backoff
    def retryBackoff(n: Int, factor: Double, duration: Duration): IO[E, A] = ...
  
    // repeats an action with a pause between invocations, until it fails
    def repeat[B](interval: Duration): IO[E, B] = ...
  
    // cancel the action if it does not complete within the timeframe
    def timeout(duration: Duration): IO[E, Maybe[A]] = ...
  
    // runs `release` on success or failure.
    // Note that IO[Void, Unit] cannot fail.
    def bracket[B](release: A => IO[Void, Unit])(use: A => IO[E, B]): IO[E, B] = ...
    // alternative syntax for bracket
    def ensuring(finalizer: IO[Void, Unit]): IO[E, A] =
    // ignore failure and success, e.g. to ignore the result of a cleanup action
    def ignore: IO[Void, Unit] = ...
  
    // runs two effects in parallel
    def par[B](that: IO[E, B]): IO[E, (A, B)] = ...
    ...

It is possible for an IO to be in a terminated state, which represents work that is intended to be discarded (it is neither an error nor a success). The utilities related to termination are:

  ...
    // terminate whatever actions are running with the given throwable.
    // bracket / ensuring is honoured.
    def terminate[E, A](t: Throwable): IO[E, A] = ...
  
    // runs two effects in parallel, return the winner and terminate the loser
    def race(that: IO[E, A]): IO[E, A] = ...
  
    // ignores terminations
    def uninterruptibly: IO[E, A] = ...
  ...

7.7.4 `Fiber`

An IO may spawn fibers, a lightweight abstraction over a JVM Thread. We can .fork an IO, and .supervise any incomplete fibers to ensure that they are terminated when the IO action completes

  ...
    def fork[E2]: IO[E2, Fiber[E, A]] = ...
    def supervised(error: Throwable): IO[E, A] = ...
  ...

When we have a Fiber we can .join back into the IO, or interrupt the underlying work.

  trait Fiber[E, A] {
    def join: IO[E, A]
    def interrupt[E2](t: Throwable): IO[E2, Unit]
  }

We can use fibers to achieve a form of optimistic concurrency control. Consider the case where we have data that we need to analyse, but we also need to validate it. We can optimistically begin the analysis and cancel the work if the validation fails, which is performed in parallel.

  final class BadData(data: Data) extends Throwable with NoStackTrace
  
  for {
    fiber1   <- analysis(data).fork
    fiber2   <- validate(data).fork
    valid    <- fiber2.join
    _        <- if (!valid) fiber1.interrupt(BadData(data))
                else IO.unit
    result   <- fiber1.join
  } yield result

Another usecase for fibers is when we need to perform a fire and forget action. For example, low priority logging over a network.

7.7.5 `Promise`

A promise represents an asynchronous variable that can be set exactly once (with complete or error). An unbounded number of listeners can get the variable.

  final class Promise[E, A] private (ref: AtomicReference[State[E, A]]) {
    def complete[E2](a: A): IO[E2, Boolean] = ...
    def error[E2](e: E): IO[E2, Boolean] = ...
    def get: IO[E, A] = ...
  
    // interrupts all listeners
    def interrupt[E2](t: Throwable): IO[E2, Boolean] = ...
  }
  object Promise {
    def make[E, A]: IO[E, Promise[E, A]] = ...
  }

Promise is not something that we typically use in application code. It is a building block for high level concurrency frameworks.

7.7.6 `IORef`

IORef is the IO equivalent of an atomic mutable variable.

We can read the variable and we have a variety of ways to write or update it.

  final class IORef[A] private (ref: AtomicReference[A]) {
    def read[E]: IO[E, A] = ...
  
    // write with immediate consistency guarantees
    def write[E](a: A): IO[E, Unit] = ...
    // write with eventual consistency guarantees
    def writeLater[E](a: A): IO[E, Unit] = ...
    // return true if an immediate write succeeded, false if not (and abort)
    def tryWrite[E](a: A): IO[E, Boolean] = ...
  
    // atomic primitives for updating the value
    def compareAndSet[E](prev: A, next: A): IO[E, Boolean] = ...
    def modify[E](f: A => A): IO[E, A] = ...
    def modifyFold[E, B](f: A => (B, A)): IO[E, B] = ...
  }
  object IORef {
    def apply[E, A](a: A): IO[E, IORef[A]] = ...
  }

IORef is another building block and can be used to provide a high performance MonadState. For example, create a newtype specialised to Task

  final class StateTask[A](val io: Task[A]) extends AnyVal
  object StateTask {
    def create[S](initial: S): Task[MonadState[StateTask, S]] =
      for {
        ref <- IORef(initial)
      } yield
        new MonadState[StateTask, S] {
          override def get       = new StateTask(ref.read)
          override def put(s: S) = new StateTask(ref.write(s))
          ...
        }
  }

We can make use of this optimised MonadState implementation in a SafeApp, where our .program depends on optimised MTL typeclasses:

  object FastState extends SafeApp {
    def program[F[_]](implicit F: MonadState[F, Int]): F[ExitStatus] = ...
  
    def run(@unused args: List[String]): IO[Void, ExitStatus] =
      for {
        stateMonad <- StateTask.create(10)
        output     <- program(stateMonad).io
      } yield output
  }

A more realistic application would take a variety of algebras and typeclasses as input.

7.7.6.1 `MonadIO`

The MonadIO that we previously studied was simplified to hide the E parameter. The actual typeclass is

  trait MonadIO[M[_], E] {
    def liftIO[A](io: IO[E, A])(implicit M: Monad[M]): M[A]
  }

with a minor change to the boilerplate on the companion of our algebra, accounting for the extra E:

  trait Lookup[F[_]] {
    def look: F[Int]
  }
  object Lookup {
    def liftIO[F[_]: Monad, E](io: Lookup[IO[E, ?]])(implicit M: MonadIO[F, E]) =
      new Lookup[F] {
        def look: F[Int] = M.liftIO(io.look)
      }
    ...
  }

7.8 Summary

The Future is broke, don’t go there.
Manage stack safety with a Trampoline.
The Monad Transformer Library (MTL) abstracts over common effects with typeclasses.
Monad Transformers provide default implementations of the MTL.
Free data structures let us analyse, optimise and easily test our programs.
IO gives us the ability to implement algebras as effects on the world.
IO can perform effects in parallel and is a high performance backbone for any application.

8. Typeclass Derivation

Typeclasses provide polymorphic functionality to our applications. But to use a typeclass we need instances for our business domain objects.

The creation of a typeclass instance from existing instances is known as typeclass derivation and is the topic of this chapter.

There are four approaches to typeclass derivation:

Manual instances for every domain object. This is infeasible for real world applications as it results in hundreds of lines of boilerplate for every line of a case class. It is useful only for educational purposes and adhoc performance optimisations.
Abstract over the typeclass by an existing Scalaz typeclass. This is the approach of scalaz-deriving, producing automated tests and derivations for products and coproducts
Macros. However, writing a macro for each typeclass requires an advanced and experienced developer. Fortunately, Jon Pretty’s Magnolia library abstracts over hand-rolled macros with a simple API, centralising the complex interaction with the compiler.
Write a generic program using the Shapeless library. The implicit mechanism is a language within the Scala language and can be used to write programs at the type level.

In this chapter we will study increasingly complex typeclasses and their derivations. We will begin with scalaz-deriving as the most principled mechanism, repeating some lessons from Chapter 5 “Scalaz Typeclasses”, then Magnolia (the easiest to use), finishing with Shapeless (the most powerful) for typeclasses with complex derivation logic.

8.1 Running Examples

This chapter will show how to define derivations for five specific typeclasses. Each example exhibits a feature that can be generalised:

  @typeclass trait Equal[A]  {
    // type parameter is in contravariant (parameter) position
    @op("===") def equal(a1: A, a2: A): Boolean
  }
  
  // for requesting default values of a type when testing
  @typeclass trait Default[A] {
    // type parameter is in covariant (return) position
    def default: String \/ A
  }
  
  @typeclass trait Semigroup[A] {
    // type parameter is in both covariant and contravariant position (invariant)
    @op("|+|") def append(x: A, y: =>A): A
  }
  
  @typeclass trait JsEncoder[T] {
    // type parameter is in contravariant position and needs access to field names
    def toJson(t: T): JsValue
  }
  
  @typeclass trait JsDecoder[T] {
    // type parameter is in covariant position and needs access to field names
    def fromJson(j: JsValue): String \/ T
  }

There is a school of thought that says serialisation formats, such as JSON and XML, should not have typeclass encoders and decoders, because it can lead to typeclass decoherence (i.e. more than one encoder or decoder may exist for the same type). The alternative is to use algebras and avoid using the implicit language feature entirely.

Although it is possible to apply the techniques in this chapter to either typeclass or algebra derivation, the latter involves a lot more boilerplate. We therefore consciously choose to restrict our study to encoders and decoders that are coherent. As we will see later in this chapter, use-site automatic derivation with Magnolia and Shapeless, combined with limitations of the Scala compiler’s implicit search, commonly leads to typeclass decoherence.

8.2 `scalaz-deriving`

The scalaz-deriving library is an extension to Scalaz and can be added to a project’s build.sbt with

  val derivingVersion = "1.0.0"
  libraryDependencies += "org.scalaz" %% "scalaz-deriving" % derivingVersion

providing new typeclasses, shown below in relation to core Scalaz typeclasses:

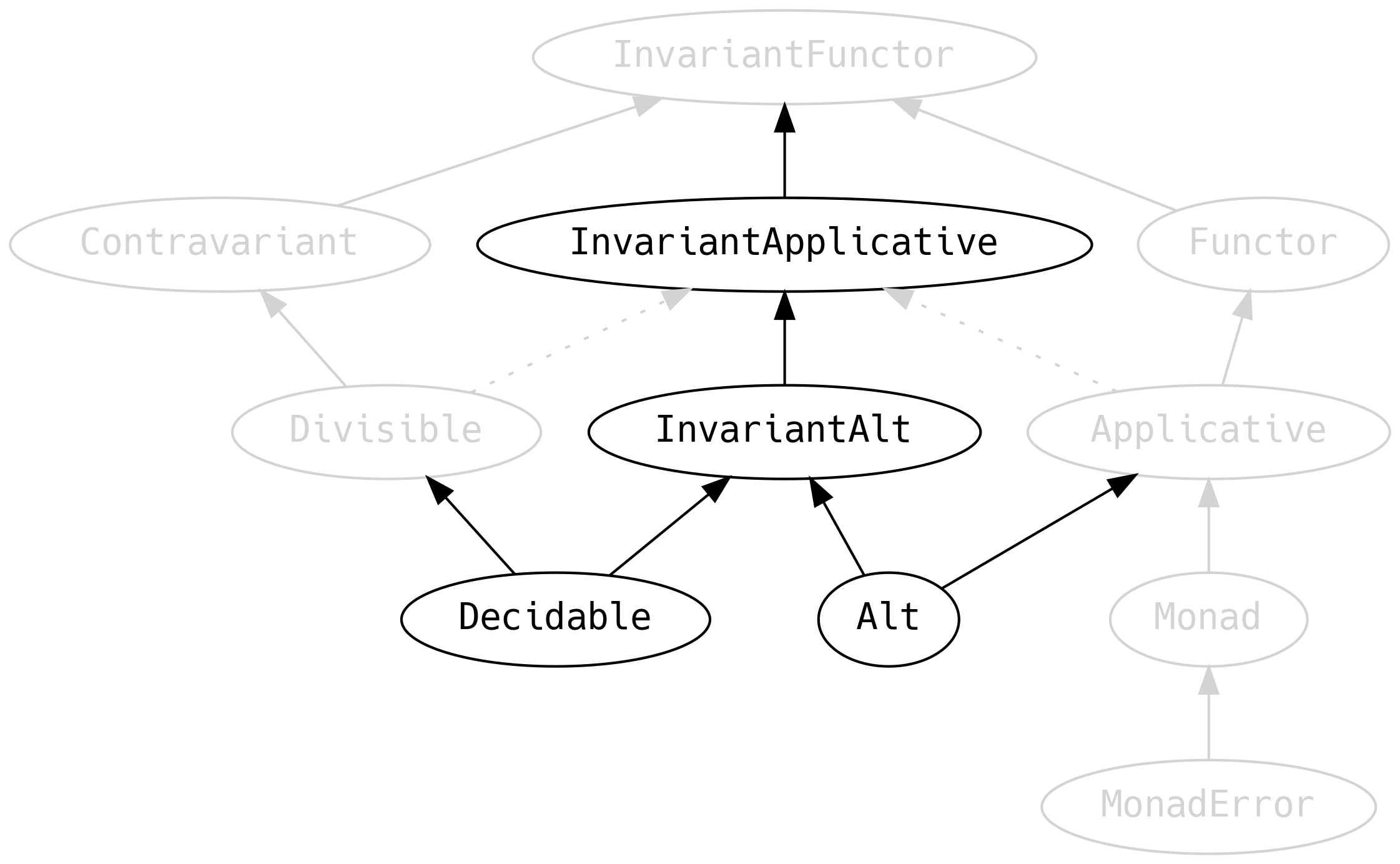
A recorded presentation of this chapter is available at https://www.youtube.com/watch?v=JmOFKdpuF9g

Before we proceed, here is a quick recap of the core Scalaz typeclasses:

  @typeclass trait InvariantFunctor[F[_]] {
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B]
  }
  
  @typeclass trait Contravariant[F[_]] extends InvariantFunctor[F] {
    def contramap[A, B](fa: F[A])(f: B => A): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = contramap(fa)(g)
  }
  
  @typeclass trait Divisible[F[_]] extends Contravariant[F] {
    def conquer[A]: F[A]
    def divide2[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C]
    ...
    def divide22[...] = ...
  }
  
  @typeclass trait Functor[F[_]] extends InvariantFunctor[F] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = map(fa)(f)
  }
  
  @typeclass trait Applicative[F[_]] extends Functor[F] {
    def point[A](a: =>A): F[A]
    def apply2[A,B,C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] = ...
    ...
    def apply12[...]
  }
  
  @typeclass trait Monad[F[_]] extends Functor[F] {
    @op(">>=") def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
  }
  @typeclass trait MonadError[F[_], E] extends Monad[F] {
    def raiseError[A](e: E): F[A]
    def emap[A, B](fa: F[A])(f: A => E \/ B): F[B] = ...
    ...
  }

8.2.1 Don’t Repeat Yourself

The simplest way to derive a typeclass is to reuse one that already exists.

The Equal typeclass has an instance of Contravariant[Equal], providing .contramap:

  object Equal {
    implicit val contravariant = new Contravariant[Equal] {
      def contramap[A, B](fa: Equal[A])(f: B => A): Equal[B] =
        (b1, b2) => fa.equal(f(b1), f(b2))
    }
    ...
  }

As users of Equal, we can use .contramap for our single parameter data types. Recall that typeclass instances go on the data type companions to be in their implicit scope:

  final case class Foo(s: String)
  object Foo {
    implicit val equal: Equal[Foo] = Equal[String].contramap(_.s)
  }
  
  scala> Foo("hello") === Foo("world")
  false

However, not all typeclasses can have an instance of Contravariant. In particular, typeclasses with type parameters in covariant position may have a Functor instead:

  object Default {
    def instance[A](d: =>String \/ A) = new Default[A] { def default = d }
    implicit val string: Default[String] = instance("".right)
  
    implicit val functor: Functor[Default] = new Functor[Default] {
      def map[A, B](fa: Default[A])(f: A => B): Default[B] = instance(fa.default.map(f))
    }
    ...
  }

We can now derive a Default[Foo]

  object Foo {
    implicit val default: Default[Foo] = Default[String].map(Foo(_))
    ...
  }

If a typeclass has parameters in both covariant and contravariant position, as is the case with Semigroup, it may provide an InvariantFunctor

  object Semigroup {
    implicit val invariant = new InvariantFunctor[Semigroup] {
      def xmap[A, B](ma: Semigroup[A], f: A => B, g: B => A) = new Semigroup[B] {
        def append(x: B, y: =>B): B = f(ma.append(g(x), g(y)))
      }
    }
    ...
  }

and we can call .xmap

  object Foo {
    implicit val semigroup: Semigroup[Foo] = Semigroup[String].xmap(Foo(_), _.s)
    ...
  }

Generally, it is simpler to just use .xmap instead of .map or .contramap:

  final case class Foo(s: String)
  object Foo {
    implicit val equal: Equal[Foo]         = Equal[String].xmap(Foo(_), _.s)
    implicit val default: Default[Foo]     = Default[String].xmap(Foo(_), _.s)
    implicit val semigroup: Semigroup[Foo] = Semigroup[String].xmap(Foo(_), _.s)
  }

The @xderiving annotation automatically inserts .xmap boilerplate. Add the following to build.sbt

  addCompilerPlugin("org.scalaz" %% "deriving-plugin" % derivingVersion)
  libraryDependencies += "org.scalaz" %% "deriving-macro" % derivingVersion % "provided"

and use it as

  @xderiving(Equal, Default, Semigroup)
  final case class Foo(s: String)

8.2.2 `MonadError`

Typically things that write from a polymorphic value have a Contravariant, and things that read into a polymorphic value have a Functor. However, it is very much expected that reading can fail. For example, if we have a default String it does not mean that we can simply derive a default String Refined NonEmpty from it

  import eu.timepit.refined.refineV
  import eu.timepit.refined.api._
  import eu.timepit.refined.collection._
  
  implicit val nes: Default[String Refined NonEmpty] =
    Default[String].map(refineV[NonEmpty](_))

fails to compile with

  [error] default.scala:41:32: polymorphic expression cannot be instantiated to expected type;
  [error]  found   : Either[String, String Refined NonEmpty]
  [error]  required: String Refined NonEmpty
  [error]     Default[String].map(refineV[NonEmpty](_))
  [error]                                          ^

Recall from Chapter 4.1 that refineV returns an Either, as the compiler has reminded us.

As the typeclass author of Default, we can do better than Functor and provide a MonadError[Default, String]:

  implicit val monad = new MonadError[Default, String] {
    def point[A](a: =>A): Default[A] =
      instance(a.right)
    def bind[A, B](fa: Default[A])(f: A => Default[B]): Default[B] =
      instance((fa >>= f).default)
    def handleError[A](fa: Default[A])(f: String => Default[A]): Default[A] =
      instance(fa.default.handleError(e => f(e).default))
    def raiseError[A](e: String): Default[A] =
      instance(e.left)
  }

Now we have access to .emap syntax and can derive our refined type

  implicit val nes: Default[String Refined NonEmpty] =
    Default[String].emap(refineV[NonEmpty](_).disjunction)

In fact, we can provide a derivation rule for all refined types

  implicit def refined[A: Default, P](
    implicit V: Validate[A, P]
  ): Default[A Refined P] = Default[A].emap(refineV[P](_).disjunction)

where Validate is from the refined library and is required by refineV.

The refined-scalaz extension to refined provides support for automatically deriving all typeclasses for refined types with the following import

  import eu.timepit.refined.scalaz._

if there is a Contravariant or MonadError[?, String] in the implicit scope.

However, due to limitations of the Scala compiler it rarely works in practice and we must write implicit def refined derivations for each typeclass.

Similarly we can use .emap to derive an Int decoder from a Long, with protection around the non-total .toInt stdlib method.

  implicit val long: Default[Long] = instance(0L.right)
  implicit val int: Default[Int] = Default[Long].emap {
    case n if (Int.MinValue <= n && n <= Int.MaxValue) => n.toInt.right
    case big => s"$big does not fit into 32 bits".left
  }

As authors of the Default typeclass, we might want to reconsider our API design so that it can never fail, e.g. with the following type signature

  @typeclass trait Default[A] {
    def default: A
  }

We would not be able to define a MonadError, forcing us to provide instances that always succeed. This will result in more boilerplate but gains compiletime safety. However, we will continue with String \/ A as the return type as it is a more general example.

8.2.3 `.fromIso`

All of the typeclasses in Scalaz have a method on their companion with a signature similar to the following:

  object Equal {
    def fromIso[F, G: Equal](D: F <=> G): Equal[F] = ...
    ...
  }
  
  object Monad {
    def fromIso[F[_], G[_]: Monad](D: F <~> G): Monad[F] = ...
    ...
  }

These mean that if we have a type F, and a way to convert it into a G that has an instance, we can call Equal.fromIso to obtain an instance for F.

For example, as typeclass users, if we have a data type Bar we can define an isomorphism to (String, Int)

  import Isomorphism._
  
  final case class Bar(s: String, i: Int)
  object Bar {
    val iso: Bar <=> (String, Int) = IsoSet(b => (b.s, b.i), t => Bar(t._1, t._2))
  }

and then derive Equal[Bar] because there is already an Equal for all tuples:

  object Bar {
    ...
    implicit val equal: Equal[Bar] = Equal.fromIso(iso)
  }

The .fromIso mechanism can also assist us as typeclass authors. Consider Default which has a core type signature of the form Unit => F[A]. Our default method is in fact isomorphic to Kleisli[F, Unit, A], the ReaderT monad transformer.

Since Kleisli already provides a MonadError (if F has one), we can derive MonadError[Default, String] by creating an isomorphism between Default and Kleisli:

  private type Sig[a] = Unit => String \/ a
  private val iso = Kleisli.iso(
    λ[Sig ~> Default](s => instance(s(()))),
    λ[Default ~> Sig](d => _ => d.default)
  )
  implicit val monad: MonadError[Default, String] = MonadError.fromIso(iso)

giving us the .map, .xmap and .emap that we’ve been making use of so far, effectively for free.

8.2.4 `Divisible` and `Applicative`

To derive the Equal for our case class with two parameters, we reused the instance that Scalaz provides for tuples. But where did the tuple instance come from?

A more specific typeclass than Contravariant is Divisible. Equal has an instance:

  implicit val divisible = new Divisible[Equal] {
    ...
    def divide[A1, A2, Z](a1: =>Equal[A1], a2: =>Equal[A2])(
      f: Z => (A1, A2)
    ): Equal[Z] = { (z1, z2) =>
      val (s1, s2) = f(z1)
      val (t1, t2) = f(z2)
      a1.equal(s1, t1) && a2.equal(s2, t2)
    }
    def conquer[A]: Equal[A] = (_, _) => true
  }

When implementing Divisible the compiler will require us to provide .contramap, which we can do directly with an optimised implementation or with this derived combinator:

  override def contramap[A, B](fa: F[A])(f: B => A): F[B] =
    divide2(conquer[Unit], fa)(c => ((), f(c)))

This has been added to Divisible in Scalaz 7.3.

And from divide2, Divisible is able to build up derivations all the way to divide22. We can call these methods directly for our data types:

  final case class Bar(s: String, i: Int)
  object Bar {
    implicit val equal: Equal[Bar] =
      Divisible[Equal].divide2(Equal[String], Equal[Int])(b => (b.s, b.i))
  }

The equivalent for type parameters in covariant position is Applicative:

  object Bar {
    ...
    implicit val default: Default[Bar] =
      Applicative[Default].apply2(Default[String], Default[Int])(Bar(_, _))
  }

But we must be careful that we do not break the typeclass laws when we implement Divisible or Applicative. In particular, it is easy to break the law of composition which says that the following two codepaths must yield exactly the same output

divide2(divide2(a1, a2)(dupe), a3)(dupe)
divide2(a1, divide2(a2, a3)(dupe))(dupe)
for any dupe: A => (A, A)

with similar laws for Applicative.

Consider JsEncoder and a proposed instance of Divisible

  new Divisible[JsEncoder] {
    ...
    def divide[A, B, C](fa: JsEncoder[A], fb: JsEncoder[B])(
      f: C => (A, B)
    ): JsEncoder[C] = { c =>
      val (a, b) = f(c)
      JsArray(IList(fa.toJson(a), fb.toJson(b)))
    }
  
    def conquer[A]: JsEncoder[A] = _ => JsNull
  }

On one side of the composition laws, for a String input, we get

  JsArray([JsArray([JsString(hello),JsString(hello)]),JsString(hello)])

and on the other

  JsArray([JsString(hello),JsArray([JsString(hello),JsString(hello)])])

which are different. We could experiment with variations of the divide implementation, but it will never satisfy the laws for all inputs.

We therefore cannot provide a Divisible[JsEncoder] because it would break the mathematical laws and invalidates all the assumptions that users of Divisible rely upon.

To aid in testing laws, Scalaz typeclasses contain the codified versions of their laws on the typeclass itself. We can write an automated test, asserting that the law fails, to remind us of this fact:

  val D: Divisible[JsEncoder] = ...
  val S: JsEncoder[String] = JsEncoder[String]
  val E: Equal[JsEncoder[String]] = (p1, p2) => p1.toJson("hello") === p2.toJson("hello")
  assert(!D.divideLaw.composition(S, S, S)(E))

On the other hand, a similar JsDecoder test meets the Applicative composition laws

  final case class Comp(a: String, b: Int)
  object Comp {
    implicit val equal: Equal[Comp] = ...
    implicit val decoder: JsDecoder[Comp] = ...
  }
  
  def composeTest(j: JsValue) = {
    val A: Applicative[JsDecoder] = Applicative[JsDecoder]
    val fa: JsDecoder[Comp] = JsDecoder[Comp]
    val fab: JsDecoder[Comp => (String, Int)] = A.point(c => (c.a, c.b))
    val fbc: JsDecoder[((String, Int)) => (Int, String)] = A.point(_.swap)
    val E: Equal[JsDecoder[(Int, String)]] = (p1, p2) => p1.fromJson(j) === p2.fromJson(j)
    assert(A.applyLaw.composition(fbc, fab, fa)(E))
  }

for some test data

  composeTest(JsObject(IList("a" -> JsString("hello"), "b" -> JsInteger(1))))
  composeTest(JsNull)
  composeTest(JsObject(IList("a" -> JsString("hello"))))
  composeTest(JsObject(IList("b" -> JsInteger(1))))

Now we are reasonably confident that our derived MonadError is lawful.

However, just because we have a test that passes for a small set of data does not prove that the laws are satisfied. We must also reason through the implementation to convince ourselves that it should satisfy the laws, and try to propose corner cases where it could fail.

One way of generating a wide variety of test data is to use the scalacheck library, which provides an Arbitrary typeclass that integrates with most testing frameworks to repeat a test with randomly generated data.

The jsonformat library provides an Arbitrary[JsValue] (everybody should provide an Arbitrary for their ADTs!) allowing us to make use of Scalatest’s forAll feature:

  forAll(SizeRange(10))((j: JsValue) => composeTest(j))

This test gives us even more confidence that our typeclass meets the Applicative composition laws. By checking all the laws on Divisible and MonadError we also get a lot of smoke tests for free.

8.2.5 `Decidable` and `Alt`

Where Divisible and Applicative give us typeclass derivation for products (built from tuples), Decidable and Alt give us the coproducts (built from nested disjunctions):

  @typeclass trait Alt[F[_]] extends Applicative[F] with InvariantAlt[F] {
    def alt[A](a1: =>F[A], a2: =>F[A]): F[A]
  
    def altly1[Z, A1](a1: =>F[A1])(f: A1 => Z): F[Z] = ...
    def altly2[Z, A1, A2](a1: =>F[A1], a2: =>F[A2])(f: A1 \/ A2 => Z): F[Z] = ...
    def altly3 ...
    def altly4 ...
    ...
  }
  
  @typeclass trait Decidable[F[_]] extends Divisible[F] with InvariantAlt[F] {
    def choose1[Z, A1](a1: =>F[A1])(f: Z => A1): F[Z] = ...
    def choose2[Z, A1, A2](a1: =>F[A1], a2: =>F[A2])(f: Z => A1 \/ A2): F[Z] = ...
    def choose3 ...
    def choose4 ...
    ...
  }

The four core typeclasses have symmetric signatures:

Typeclass	method	given	signature	returns
`Applicative`	`apply2`	`F[A1], F[A2]`	`(A1, A2) => Z`	`F[Z]`
`Alt`	`altly2`	`F[A1], F[A2]`	`(A1 \/ A2) => Z`	`F[Z]`
`Divisible`	`divide2`	`F[A1], F[A2]`	`Z => (A1, A2)`	`F[Z]`
`Decidable`	`choose2`	`F[A1], F[A2]`	`Z => (A1 \/ A2)`	`F[Z]`

supporting covariant products; covariant coproducts; contravariant products; contravariant coproducts.

We can write a Decidable[Equal], letting us derive Equal for any ADT!

  implicit val decidable = new Decidable[Equal] {
    ...
    def choose2[Z, A1, A2](a1: =>Equal[A1], a2: =>Equal[A2])(
      f: Z => A1 \/ A2
    ): Equal[Z] = { (z1, z2) =>
      (f(z1), f(z2)) match {
        case (-\/(s), -\/(t)) => a1.equal(s, t)
        case (\/-(s), \/-(t)) => a2.equal(s, t)
        case _ => false
      }
    }
  }

For an ADT

  sealed abstract class Darth { def widen: Darth = this }
  final case class Vader(s: String, i: Int)  extends Darth
  final case class JarJar(i: Int, s: String) extends Darth

where the products (Vader and JarJar) have an Equal

  object Vader {
    private val g: Vader => (String, Int) = d => (d.s, d.i)
    implicit val equal: Equal[Vader] = Divisible[Equal].divide2(Equal[String], Equal[Int])(g)
  }
  object JarJar {
    private val g: JarJar => (Int, String) = d => (d.i, d.s)
    implicit val equal: Equal[JarJar] = Divisible[Equal].divide2(Equal[Int], Equal[String])(g)
  }

we can derive the equal for the whole ADT

  object Darth {
    private def g(t: Darth): Vader \/ JarJar = t match {
      case p @ Vader(_, _)  => -\/(p)
      case p @ JarJar(_, _) => \/-(p)
    }
    implicit val equal: Equal[Darth] = Decidable[Equal].choose2(Equal[Vader], Equal[JarJar])(g)
  }
  
  scala> Vader("hello", 1).widen === JarJar(1, "hello).widen
  false

Typeclasses that have an Applicative can be eligible for an Alt. If we want to use our Kleisli.iso trick, we have to extend IsomorphismMonadError and mix in Alt. Upgrade our MonadError[Default, String] to have an Alt[Default]:

  private type K[a] = Kleisli[String \/ ?, Unit, a]
  implicit val monad = new IsomorphismMonadError[Default, K, String] with Alt[Default] {
    override val G = MonadError[K, String]
    override val iso = ...
  
    def alt[A](a1: =>Default[A], a2: =>Default[A]): Default[A] = instance(a1.default)
  }

The primitive of Alt is alt, much as the primitive of Applicative is ap, but it often makes more sense to use altly2 and apply2 as the primitives with the following overrides:

  override def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B] =
    apply2(fa, f)((a, abc) => abc(a))
  
  override def alt[A](a1: =>F[A], a2: =>F[A]): F[A] = altly2(a1, a2) {
    case -\/(a) => a
    case \/-(a) => a
  }

Just don’t forget to implement apply2 and altly2 or there will be an infinite loop at runtime.

Letting us derive our Default[Darth]

  object Darth {
    ...
    private def f(e: Vader \/ JarJar): Darth = e.merge
    implicit val default: Default[Darth] =
      Alt[Default].altly2(Default[Vader], Default[JarJar])(f)
  }
  object Vader {
    ...
    private val f: (String, Int) => Vader = Vader(_, _)
    implicit val default: Default[Vader] =
      Alt[Default].apply2(Default[String], Default[Int])(f)
  }
  object JarJar {
    ...
    private val f: (Int, String) => JarJar = JarJar(_, _)
    implicit val default: Default[JarJar] =
      Alt[Default].apply2(Default[Int], Default[String])(f)
  }
  
  scala> Default[Darth].default
  \/-(Vader())

Returning to the scalaz-deriving typeclasses, the invariant parents of Alt and Decidable are:

  @typeclass trait InvariantApplicative[F[_]] extends InvariantFunctor[F] {
    def xproduct0[Z](f: =>Z): F[Z]
    def xproduct1[Z, A1](a1: =>F[A1])(f: A1 => Z, g: Z => A1): F[Z] = ...
    def xproduct2 ...
    def xproduct3 ...
    def xproduct4 ...
  }
  
  @typeclass trait InvariantAlt[F[_]] extends InvariantApplicative[F] {
    def xcoproduct1[Z, A1](a1: =>F[A1])(f: A1 => Z, g: Z => A1): F[Z] = ...
    def xcoproduct2 ...
    def xcoproduct3 ...
    def xcoproduct4 ...
  }

supporting typeclasses with an InvariantFunctor like Monoid and Semigroup.

8.2.6 Arbitrary Arity and `@deriving`

There are two problems with InvariantApplicative and InvariantAlt:

they only support products of four fields and coproducts of four entries.
there is a lot of boilerplate on the data type companions.

In this section we solve both problems with additional typeclasses introduced by scalaz-deriving

Effectively, our four central typeclasses Applicative, Divisible, Alt and Decidable all get extended to arbitrary arity using the iotaz library, hence the z postfix.

The iotaz library has three main types:

TList which describes arbitrary length chains of types
Prod[A <: TList] for products
Cop[A <: TList] for coproducts

By way of example, a TList representation of Darth from the previous section is

  import iotaz._, TList._
  
  type DarthT  = Vader  :: JarJar :: TNil
  type VaderT  = String :: Int    :: TNil
  type JarJarT = Int    :: String :: TNil

which can be instantiated:

  val vader: Prod[VaderT]    = Prod("hello", 1)
  val jarjar: Prod[JarJarT]  = Prod(1, "hello")
  
  val VaderI = Cop.Inject[Vader, Cop[DarthT]]
  val darth: Cop[DarthT] = VaderI.inj(Vader("hello", 1))

To be able to use the scalaz-deriving API, we need an Isomorphism between our ADTs and the iotaz generic representation. It is a lot of boilerplate, we will get to that in a moment:

  object Darth {
    private type Repr   = Vader :: JarJar :: TNil
    private val VaderI  = Cop.Inject[Vader, Cop[Repr]]
    private val JarJarI = Cop.Inject[JarJar, Cop[Repr]]
    private val iso     = IsoSet(
      {
        case d: Vader  => VaderI.inj(d)
        case d: JarJar => JarJarI.inj(d)
      }, {
        case VaderI(d)  => d
        case JarJarI(d) => d
      }
    )
    ...
  }
  
  object Vader {
    private type Repr = String :: Int :: TNil
    private val iso   = IsoSet(
      d => Prod(d.s, d.i),
      p => Vader(p.head, p.tail.head)
    )
    ...
  }
  
  object JarJar {
    private type Repr = Int :: String :: TNil
    private val iso   = IsoSet(
      d => Prod(d.i, d.s),
      p => JarJar(p.head, p.tail.head)
    )
    ...
  }

With that out of the way we can call the Deriving API for Equal, possible because scalaz-deriving provides an optimised instance of Deriving[Equal]

  object Darth {
    ...
    implicit val equal: Equal[Darth] = Deriving[Equal].xcoproductz(
      Prod(Need(Equal[Vader]), Need(Equal[JarJar])))(iso.to, iso.from)
  }
  object Vader {
    ...
    implicit val equal: Equal[Vader] = Deriving[Equal].xproductz(
      Prod(Need(Equal[String]), Need(Equal[Int])))(iso.to, iso.from)
  }
  object JarJar {
    ...
    implicit val equal: Equal[JarJar] = Deriving[Equal].xproductz(
      Prod(Need(Equal[Int]), Need(Equal[String])))(iso.to, iso.from)
  }

To be able to do the same for our Default typeclass, we need to provide an instance of Deriving[Default]. This is just a case of wrapping our existing Alt with a helper:

  object Default {
    ...
    implicit val deriving: Deriving[Default] = ExtendedInvariantAlt(monad)
  }

and then calling it from the companions

  object Darth {
    ...
    implicit val default: Default[Darth] = Deriving[Default].xcoproductz(
      Prod(Need(Default[Vader]), Need(Default[JarJar])))(iso.to, iso.from)
  }
  object Vader {
    ...
    implicit val default: Default[Vader] = Deriving[Default].xproductz(
      Prod(Need(Default[String]), Need(Default[Int])))(iso.to, iso.from)
  }
  object JarJar {
    ...
    implicit val default: Default[JarJar] = Deriving[Default].xproductz(
      Prod(Need(Default[Int]), Need(Default[String])))(iso.to, iso.from)
  }

We have solved the problem of arbitrary arity, but we have introduced even more boilerplate.

The punchline is that the @deriving annotation, which comes from deriving-plugin, generates all this boilerplate automatically and only needs to be applied at the top level of an ADT:

  @deriving(Equal, Default)
  sealed abstract class Darth { def widen: Darth = this }
  final case class Vader(s: String, i: Int)  extends Darth
  final case class JarJar(i: Int, s: String) extends Darth

Also included in scalaz-deriving are instances for Order, Semigroup and Monoid. Instances of Show and Arbitrary are available by installing the scalaz-deriving-magnolia and scalaz-deriving-scalacheck extras.

You’re welcome!

8.2.7 Examples

We finish our study of scalaz-deriving with fully worked implementations of all the example typeclasses. Before we do that we need to know about a new data type: /~\, aka the snake in the road, for containing two higher kinded structures that share the same type parameter:

  sealed abstract class /~\[A[_], B[_]] {
    type T
    def a: A[T]
    def b: B[T]
  }
  object /~\ {
    type APair[A[_], B[_]]  = A /~\ B
    def unapply[A[_], B[_]](p: A /~\ B): Some[(A[p.T], B[p.T])] = ...
    def apply[A[_], B[_], Z](az: =>A[Z], bz: =>B[Z]): A /~\ B = ...
  }

We typically use this in the context of Id /~\ TC where TC is our typeclass, meaning that we have a value, and an instance of a typeclass for that value, without knowing anything about the value.

In addition, all the methods on the Deriving API have implicit evidence of the form A PairedWith FA, allowing the iotaz library to be able to perform .zip, .traverse, and other operations on Prod and Cop. We can ignore these parameters, as we don’t use them directly.

8.2.7.1 `Equal`

As with Default we could define a regular fixed-arity Decidable and wrap it with ExtendedInvariantAlt (the simplest approach), but we choose to implement Decidablez directly for the performance benefit. We make two additional optimisations:

perform instance equality .eq before applying the Equal.equal, allowing for shortcut equality between identical values.
Foldable.all allowing early exit when any comparison is false. e.g. if the first fields don’t match, we don’t even request the Equal for remaining values.

  new Decidablez[Equal] {
    @inline private final def quick(a: Any, b: Any): Boolean =
      a.asInstanceOf[AnyRef].eq(b.asInstanceOf[AnyRef])
  
    def dividez[Z, A <: TList, FA <: TList](tcs: Prod[FA])(g: Z => Prod[A])(
      implicit ev: A PairedWith FA
    ): Equal[Z] = (z1, z2) => (g(z1), g(z2)).zip(tcs).all {
      case (a1, a2) /~\ fa => quick(a1, a2) || fa.value.equal(a1, a2)
    }
  
    def choosez[Z, A <: TList, FA <: TList](tcs: Prod[FA])(g: Z => Cop[A])(
      implicit ev: A PairedWith FA
    ): Equal[Z] = (z1, z2) => (g(z1), g(z2)).zip(tcs) match {
      case -\/(_)               => false
      case \/-((a1, a2) /~\ fa) => quick(a1, a2) || fa.value.equal(a1, a2)
    }
  }

8.2.7.2 `Default`

Unfortunately, the iotaz API for .traverse (and its analogy, .coptraverse) requires us to define natural transformations, which have a clunky syntax, even with the kind-projector plugin.

  private type K[a] = Kleisli[String \/ ?, Unit, a]
  new IsomorphismMonadError[Default, K, String] with Altz[Default] {
    type Sig[a] = Unit => String \/ a
    override val G = MonadError[K, String]
    override val iso = Kleisli.iso(
      λ[Sig ~> Default](s => instance(s(()))),
      λ[Default ~> Sig](d => _ => d.default)
    )
  
    val extract = λ[NameF ~> (String \/ ?)](a => a.value.default)
    def applyz[Z, A <: TList, FA <: TList](tcs: Prod[FA])(f: Prod[A] => Z)(
      implicit ev: A PairedWith FA
    ): Default[Z] = instance(tcs.traverse(extract).map(f))
  
    val always = λ[NameF ~> Maybe](a => a.value.default.toMaybe)
    def altlyz[Z, A <: TList, FA <: TList](tcs: Prod[FA])(f: Cop[A] => Z)(
      implicit ev: A PairedWith FA
    ): Default[Z] = instance {
      tcs.coptraverse[A, NameF, Id](always).map(f).headMaybe \/> "not found"
    }
  }

8.2.7.3 `Semigroup`

It is not possible to define a Semigroup for general coproducts, however it is possible to define one for general products. We can use the arbitrary arity InvariantApplicative:

  new InvariantApplicativez[Semigroup] {
    type L[a] = ((a, a), NameF[a])
    val appender = λ[L ~> Id] { case ((a1, a2), fa) => fa.value.append(a1, a2) }
  
    def xproductz[Z, A <: TList, FA <: TList](tcs: Prod[FA])
                                             (f: Prod[A] => Z, g: Z => Prod[A])
                                             (implicit ev: A PairedWith FA) =
      new Semigroup[Z] {
        def append(z1: Z, z2: =>Z): Z = f(tcs.ziptraverse2(g(z1), g(z2), appender))
      }
  }

8.2.7.4 `JsEncoder` and `JsDecoder`

scalaz-deriving does not provide access to field names so it is not possible to write a JSON encoder or decoder.

8.3 Magnolia

The Magnolia macro library provides a clean API for writing typeclass derivations. It is installed with the following build.sbt entry

  libraryDependencies += "com.propensive" %% "magnolia" % "0.10.1"

A typeclass author implements the following members:

  import magnolia._
  
  object MyDerivation {
    type Typeclass[A]
  
    def combine[A](ctx: CaseClass[Typeclass, A]): Typeclass[A]
    def dispatch[A](ctx: SealedTrait[Typeclass, A]): Typeclass[A]
  
    def gen[A]: Typeclass[A] = macro Magnolia.gen[A]
  }

The Magnolia API is:

  class CaseClass[TC[_], A] {
    def typeName: TypeName
    def construct[B](f: Param[TC, A] => B): A
    def constructMonadic[F[_]: Monadic, B](f: Param[TC, A] => F[B]): F[A]
    def parameters: Seq[Param[TC, A]]
    def annotations: Seq[Any]
  }
  
  class SealedTrait[TC[_], A] {
    def typeName: TypeName
    def subtypes: Seq[Subtype[TC, A]]
    def dispatch[B](value: A)(handle: Subtype[TC, A] => B): B
    def annotations: Seq[Any]
  }

with helpers

  final case class TypeName(short: String, full: String)
  
  class Param[TC[_], A] {
    type PType
    def label: String
    def index: Int
    def typeclass: TC[PType]
    def dereference(param: A): PType
    def default: Option[PType]
    def annotations: Seq[Any]
  }
  
  class Subtype[TC[_], A] {
    type SType <: A
    def typeName: TypeName
    def index: Int
    def typeclass: TC[SType]
    def cast(a: A): SType
    def annotations: Seq[Any]
  }

The Monadic typeclass, used in constructMonadic, is automatically generated if our data type has a .map and .flatMap method when we import mercator._

It does not make sense to use Magnolia for typeclasses that can be abstracted by Divisible, Decidable, Applicative or Alt, since those abstractions provide a lot of extra structure and tests for free. However, Magnolia offers features that scalaz-deriving cannot provide: access to field names, type names, annotations and default values.

8.3.1 Example: JSON

We have some design choices to make with regards to JSON serialisation:

Should we include fields with null values?
Should decoding treat missing vs null differently?
How do we encode the name of a coproduct?
How do we deal with coproducts that are not JsObject?

We choose sensible defaults

do not include fields if the value is a JsNull.
handle missing fields the same as null values.
use a special field "type" to disambiguate coproducts using the type name.
put primitive values into a special field "xvalue".

and let the users attach an annotation to coproducts and product fields to customise their formats:

  sealed class json extends Annotation
  object json {
    final case class nulls()          extends json
    final case class field(f: String) extends json
    final case class hint(f: String)  extends json
  }

For example

  @json.field("TYPE")
  sealed abstract class Cost
  final case class Time(s: String) extends Cost
  final case class Money(@json.field("integer") i: Int) extends Cost

Start with a JsEncoder that handles only our sensible defaults:

  object JsMagnoliaEncoder {
    type Typeclass[A] = JsEncoder[A]
  
    def combine[A](ctx: CaseClass[JsEncoder, A]): JsEncoder[A] = { a =>
      val empty = IList.empty[(String, JsValue)]
      val fields = ctx.parameters.foldRight(empty) { (p, acc) =>
        p.typeclass.toJson(p.dereference(a)) match {
          case JsNull => acc
          case value  => (p.label -> value) :: acc
        }
      }
      JsObject(fields)
    }
  
    def dispatch[A](ctx: SealedTrait[JsEncoder, A]): JsEncoder[A] = a =>
      ctx.dispatch(a) { sub =>
        val hint = "type" -> JsString(sub.typeName.short)
        sub.typeclass.toJson(sub.cast(a)) match {
          case JsObject(fields) => JsObject(hint :: fields)
          case other            => JsObject(IList(hint, "xvalue" -> other))
        }
      }
  
    def gen[A]: JsEncoder[A] = macro Magnolia.gen[A]
  }

We can see how the Magnolia API makes it easy to access field names and typeclasses for each parameter.

Now add support for annotations to handle user preferences. To avoid looking up the annotations on every encoding, we will cache them in an array. Although field access to an array is non-total, we are guaranteed that the indices will always align. Performance is usually the victim in the trade-off between specialisation and generalisation.

  object JsMagnoliaEncoder {
    type Typeclass[A] = JsEncoder[A]
  
    def combine[A](ctx: CaseClass[JsEncoder, A]): JsEncoder[A] =
      new JsEncoder[A] {
        private val anns = ctx.parameters.map { p =>
          val nulls = p.annotations.collectFirst {
            case json.nulls() => true
          }.getOrElse(false)
          val field = p.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse(p.label)
          (nulls, field)
        }.toArray
  
        def toJson(a: A): JsValue = {
          val empty = IList.empty[(String, JsValue)]
          val fields = ctx.parameters.foldRight(empty) { (p, acc) =>
            val (nulls, field) = anns(p.index)
            p.typeclass.toJson(p.dereference(a)) match {
              case JsNull if !nulls => acc
              case value            => (field -> value) :: acc
            }
          }
          JsObject(fields)
        }
      }
  
    def dispatch[A](ctx: SealedTrait[JsEncoder, A]): JsEncoder[A] =
      new JsEncoder[A] {
        private val field = ctx.annotations.collectFirst {
          case json.field(name) => name
        }.getOrElse("type")
        private val anns = ctx.subtypes.map { s =>
          val hint = s.annotations.collectFirst {
            case json.hint(name) => field -> JsString(name)
          }.getOrElse(field -> JsString(s.typeName.short))
          val xvalue = s.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse("xvalue")
          (hint, xvalue)
        }.toArray
  
        def toJson(a: A): JsValue = ctx.dispatch(a) { sub =>
          val (hint, xvalue) = anns(sub.index)
          sub.typeclass.toJson(sub.cast(a)) match {
            case JsObject(fields) => JsObject(hint :: fields)
            case other            => JsObject(hint :: (xvalue -> other) :: IList.empty)
          }
        }
      }
  
    def gen[A]: JsEncoder[A] = macro Magnolia.gen[A]
  }

For the decoder we use .constructMonadic which has a type signature similar to .traverse

  object JsMagnoliaDecoder {
    type Typeclass[A] = JsDecoder[A]
  
    def combine[A](ctx: CaseClass[JsDecoder, A]): JsDecoder[A] = {
      case obj @ JsObject(_) =>
        ctx.constructMonadic(
          p => p.typeclass.fromJson(obj.get(p.label).getOrElse(JsNull))
        )
      case other => fail("JsObject", other)
    }
  
    def dispatch[A](ctx: SealedTrait[JsDecoder, A]): JsDecoder[A] = {
      case obj @ JsObject(_) =>
        obj.get("type") match {
          case \/-(JsString(hint)) =>
            ctx.subtypes.find(_.typeName.short == hint) match {
              case None => fail(s"a valid '$hint'", obj)
              case Some(sub) =>
                val value = obj.get("xvalue").getOrElse(obj)
                sub.typeclass.fromJson(value)
            }
          case _ => fail("JsObject with type", obj)
        }
      case other => fail("JsObject", other)
    }
  
    def gen[A]: JsDecoder[A] = macro Magnolia.gen[A]
  }

Again, adding support for user preferences and default field values, along with some optimisations:

  object JsMagnoliaDecoder {
    type Typeclass[A] = JsDecoder[A]
  
    def combine[A](ctx: CaseClass[JsDecoder, A]): JsDecoder[A] =
      new JsDecoder[A] {
        private val nulls = ctx.parameters.map { p =>
          p.annotations.collectFirst {
            case json.nulls() => true
          }.getOrElse(false)
        }.toArray
  
        private val fieldnames = ctx.parameters.map { p =>
          p.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse(p.label)
        }.toArray
  
        def fromJson(j: JsValue): String \/ A = j match {
          case obj @ JsObject(_) =>
            import mercator._
            val lookup = obj.fields.toMap
            ctx.constructMonadic { p =>
              val field = fieldnames(p.index)
              lookup
                .get(field)
                .into {
                  case Maybe.Just(value) => p.typeclass.fromJson(value)
                  case _ =>
                    p.default match {
                      case Some(default) => \/-(default)
                      case None if nulls(p.index) =>
                        s"missing field '$field'".left
                      case None => p.typeclass.fromJson(JsNull)
                    }
                }
            }
          case other => fail("JsObject", other)
        }
      }
  
    def dispatch[A](ctx: SealedTrait[JsDecoder, A]): JsDecoder[A] =
      new JsDecoder[A] {
        private val subtype = ctx.subtypes.map { s =>
          s.annotations.collectFirst {
            case json.hint(name) => name
          }.getOrElse(s.typeName.short) -> s
        }.toMap
        private val typehint = ctx.annotations.collectFirst {
          case json.field(name) => name
        }.getOrElse("type")
        private val xvalues = ctx.subtypes.map { sub =>
          sub.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse("xvalue")
        }.toArray
  
        def fromJson(j: JsValue): String \/ A = j match {
          case obj @ JsObject(_) =>
            obj.get(typehint) match {
              case \/-(JsString(h)) =>
                subtype.get(h) match {
                  case None => fail(s"a valid '$h'", obj)
                  case Some(sub) =>
                    val xvalue = xvalues(sub.index)
                    val value  = obj.get(xvalue).getOrElse(obj)
                    sub.typeclass.fromJson(value)
                }
              case _ => fail(s"JsObject with '$typehint' field", obj)
            }
          case other => fail("JsObject", other)
        }
      }
  
    def gen[A]: JsDecoder[A] = macro Magnolia.gen[A]
  }

We call the JsMagnoliaEncoder.gen or JsMagnoliaDecoder.gen method from the companion of our data types. For example, the Google Maps API

  final case class Value(text: String, value: Int)
  final case class Elements(distance: Value, duration: Value, status: String)
  final case class Rows(elements: List[Elements])
  final case class DistanceMatrix(
    destination_addresses: List[String],
    origin_addresses: List[String],
    rows: List[Rows],
    status: String
  )
  
  object Value {
    implicit val encoder: JsEncoder[Value] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[Value] = JsMagnoliaDecoder.gen
  }
  object Elements {
    implicit val encoder: JsEncoder[Elements] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[Elements] = JsMagnoliaDecoder.gen
  }
  object Rows {
    implicit val encoder: JsEncoder[Rows] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[Rows] = JsMagnoliaDecoder.gen
  }
  object DistanceMatrix {
    implicit val encoder: JsEncoder[DistanceMatrix] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[DistanceMatrix] = JsMagnoliaDecoder.gen
  }

Thankfully, the @deriving annotation supports Magnolia! If the typeclass author provides a file deriving.conf with their jar, containing this text

  jsonformat.JsEncoder=jsonformat.JsMagnoliaEncoder.gen
  jsonformat.JsDecoder=jsonformat.JsMagnoliaDecoder.gen

the deriving-macro will call the user-provided method:

  @deriving(JsEncoder, JsDecoder)
  final case class Value(text: String, value: Int)
  @deriving(JsEncoder, JsDecoder)
  final case class Elements(distance: Value, duration: Value, status: String)
  @deriving(JsEncoder, JsDecoder)
  final case class Rows(elements: List[Elements])
  @deriving(JsEncoder, JsDecoder)
  final case class DistanceMatrix(
    destination_addresses: List[String],
    origin_addresses: List[String],
    rows: List[Rows],
    status: String
  )

8.3.2 Fully Automatic Derivation

Generating implicit instances on the companion of the data type is historically known as semi-auto derivation, in contrast to full-auto which is when the .gen is made implicit

  object JsMagnoliaEncoder {
    ...
    implicit def gen[A]: JsEncoder[A] = macro Magnolia.gen[A]
  }
  object JsMagnoliaDecoder {
    ...
    implicit def gen[A]: JsDecoder[A] = macro Magnolia.gen[A]
  }

Users can import these methods into their scope and get magical derivation at the point of use

  scala> final case class Value(text: String, value: Int)
  scala> import JsMagnoliaEncoder.gen
  scala> Value("hello", 1).toJson
  res = JsObject([("text","hello"),("value",1)])

This may sound tempting, as it involves the least amount of typing, but there are two caveats:

the macro is invoked at every use site, i.e. every time we call .toJson. This slows down compilation and also produces more objects at runtime, which will impact runtime performance.
unexpected things may be derived.

The first caveat is self evident, but unexpected derivations manifests as subtle bugs. Consider what would happen for

  @deriving(JsEncoder)
  final case class Foo(s: Option[String])

if we forgot to provide an implicit derivation for Option. We might expect a Foo(Some("hello")) to look like

  {
    "s":"hello"
  }

But it would instead be

  {
    "s": {
      "type":"Some",
      "get":"hello"
    }
  }

because Magnolia derived an Option encoder for us.

This is confusing, we would rather have the compiler tell us if we forgot something. Full auto is therefore not recommended.

8.4 Shapeless

The Shapeless library is notoriously the most complicated library in Scala. The reason why it has such a reputation is because it takes the implicit language feature to the extreme: creating a kind of generic programming language at the level of the types.

This is not an entirely foreign concept: in Scalaz we try to limit our use of the implicit language feature to typeclasses, but we sometimes ask the compiler to provide us with evidence relating types. For example Liskov or Leibniz relationship (<~< and ===), and to Inject a free algebra into a scalaz.Coproduct of algebras.

To install Shapeless, add the following to build.sbt

  libraryDependencies += "com.chuusai" %% "shapeless" % "2.3.3"

At the core of Shapeless are the HList and Coproduct data types

  package shapeless
  
  sealed trait HList
  final case class ::[+H, +T <: HList](head: H, tail: T) extends HList
  sealed trait NNil extends HList
  case object HNil extends HNil {
    def ::[H](h: H): H :: HNil = ::(h, this)
  }
  
  sealed trait Coproduct
  sealed trait :+:[+H, +T <: Coproduct] extends Coproduct
  final case class Inl[+H, +T <: Coproduct](head: H) extends :+:[H, T]
  final case class Inr[+H, +T <: Coproduct](tail: T) extends :+:[H, T]
  sealed trait CNil extends Coproduct // no implementations

which are generic representations of products and coproducts, respectively. The sealed trait HNil is for convenience so we never need to type HNil.type.

Shapeless has a clone of the IsoSet datatype, called Generic, which allows us to move between an ADT and its generic representation:

  trait Generic[T] {
    type Repr
    def to(t: T): Repr
    def from(r: Repr): T
  }
  object Generic {
    type Aux[T, R] = Generic[T] { type Repr = R }
    def apply[T](implicit G: Generic[T]): Aux[T, G.Repr] = G
    implicit def materialize[T, R]: Aux[T, R] = macro ...
  }

Many of the types in Shapeless have a type member (Repr) and an .Aux type alias on their companion that makes the second type visible. This allows us to request the Generic[Foo] for a type Foo without having to provide the generic representation, which is generated by a macro.

  scala> import shapeless._
  scala> final case class Foo(a: String, b: Long)
         Generic[Foo].to(Foo("hello", 13L))
  res: String :: Long :: HNil = hello :: 13 :: HNil
  
  scala> Generic[Foo].from("hello" :: 13L :: HNil)
  res: Foo = Foo(hello,13)
  
  scala> sealed abstract class Bar
         case object Irish extends Bar
         case object English extends Bar
  
  scala> Generic[Bar].to(Irish)
  res: English.type :+: Irish.type :+: CNil.type = Inl(Irish)
  
  scala> Generic[Bar].from(Inl(Irish))
  res: Bar = Irish

There is a complementary LabelledGeneric that includes the field names

  scala> import shapeless._, labelled._
  scala> final case class Foo(a: String, b: Long)
  
  scala> LabelledGeneric[Foo].to(Foo("hello", 13L))
  res: String with KeyTag[Symbol with Tagged[String("a")], String] ::
       Long   with KeyTag[Symbol with Tagged[String("b")],   Long] ::
       HNil =
       hello :: 13 :: HNil
  
  scala> sealed abstract class Bar
         case object Irish extends Bar
         case object English extends Bar
  
  scala> LabelledGeneric[Bar].to(Irish)
  res: Irish.type   with KeyTag[Symbol with Tagged[String("Irish")],     Irish.type] :+:
       English.type with KeyTag[Symbol with Tagged[String("English")], English.type] :+:
       CNil.type =
       Inl(Irish)

Note that the value of a LabelledGeneric representation is the same as the Generic representation: field names only exist in the type and are erased at runtime.

We never need to type KeyTag manually, we use the type alias:

  type FieldType[K, +V] = V with KeyTag[K, V]

If we want to access the field name from a FieldType[K, A], we ask for implicit evidence Witness.Aux[K], which allows us to access the value of K at runtime.

Superficially, this is all we need to know about Shapeless to be able to derive a typeclass. However, things get increasingly complex, so we will proceed with increasingly complex examples.

8.4.1 Example: Equal

A typical pattern to follow is to extend the typeclass that we wish to derive, and put the Shapeless code on its companion. This gives us an implicit scope that the compiler can search without requiring complex imports

  trait DerivedEqual[A] extends Equal[A]
  object DerivedEqual {
    ...
  }

The entry point to a Shapeless derivation is a method, gen, requiring two type parameters: the A that we are deriving and the R for its generic representation. We then ask for the Generic.Aux[A, R], relating A to R, and an instance of the Derived typeclass for the R. We begin with this signature and simple implementation:

  import shapeless._
  
  object DerivedEqual {
    def gen[A, R: DerivedEqual](implicit G: Generic.Aux[A, R]): Equal[A] =
      (a1, a2) => Equal[R].equal(G.to(a1), G.to(a2))
  }

We’ve reduced the problem to providing an implicit Equal[R] for an R that is the Generic representation of A. First consider products, where R <: HList. This is the signature we want to implement:

  implicit def hcons[H: Equal, T <: HList: DerivedEqual]: DerivedEqual[H :: T]

because if we can implement it for a head and a tail, the compiler will be able to recurse on this method until it reaches the end of the list. Where we will need to provide an instance for the empty HNil

  implicit def hnil: DerivedEqual[HNil]

We implement these methods

  implicit def hcons[H: Equal, T <: HList: DerivedEqual]: DerivedEqual[H :: T] =
    (h1, h2) => Equal[H].equal(h1.head, h2.head) && Equal[T].equal(h1.tail, h2.tail)
  
  implicit val hnil: DerivedEqual[HNil] = (_, _) => true

and for coproducts we want to implement these signatures

  implicit def ccons[H: Equal, T <: Coproduct: DerivedEqual]: DerivedEqual[H :+: T]
  implicit def cnil: DerivedEqual[CNil]

Scalaz and Shapeless share many type names, when mixing them we often need to exclude certain elements from the import, e.g.

  import scalaz.{ Coproduct => _, :+: => _, _ }, Scalaz._
  import shapeless._

.cnil will never be called for a typeclass like Equal with type parameters only in contravariant position, but the compiler doesn’t know that so we have to provide a stub:

  implicit val cnil: DerivedEqual[CNil] = (_, _) => sys.error("impossible")

For the coproduct case we can only compare two things if they align, which is when they are both Inl or Inr

  implicit def ccons[H: Equal, T <: Coproduct: DerivedEqual]: DerivedEqual[H :+: T] = {
    case (Inl(c1), Inl(c2)) => Equal[H].equal(c1, c2)
    case (Inr(c1), Inr(c2)) => Equal[T].equal(c1, c2)
    case _                  => false
  }

It is noteworthy that our methods align with the concept of conquer (hnil), divide2 (hlist) and alt2 (coproduct)! However, we don’t get any of the advantages of implementing Decidable, as now we must start from scratch when writing tests for this code.

So let’s test this thing with a simple ADT

  sealed abstract class Foo
  final case class Bar(s: String)          extends Foo
  final case class Faz(b: Boolean, i: Int) extends Foo
  final case object Baz                    extends Foo

We need to provide instances on the companions:

  object Foo {
    implicit val equal: Equal[Foo] = DerivedEqual.gen
  }
  object Bar {
    implicit val equal: Equal[Bar] = DerivedEqual.gen
  }
  object Faz {
    implicit val equal: Equal[Faz] = DerivedEqual.gen
  }
  final case object Baz extends Foo {
    implicit val equal: Equal[Baz.type] = DerivedEqual.gen
  }

But it doesn’t compile

  [error] shapeless.scala:41:38: ambiguous implicit values:
  [error]  both value hnil in object DerivedEqual of type => DerivedEqual[HNil]
  [error]  and value cnil in object DerivedEqual of type => DerivedEqual[CNil]
  [error]  match expected type DerivedEqual[R]
  [error]     : Equal[Baz.type] = DerivedEqual.gen
  [error]                                      ^

Welcome to Shapeless compilation errors!

The problem, which is not at all evident from the error, is that the compiler is unable to work out what R is, and gets caught thinking it is something else. We need to provide the explicit type parameters when calling gen, e.g.

  implicit val equal: Equal[Baz.type] = DerivedEqual.gen[Baz.type, HNil]

or we can use the Generic macro to help us and let the compiler infer the generic representation

  final case object Baz extends Foo {
    implicit val generic                = Generic[Baz.type]
    implicit val equal: Equal[Baz.type] = DerivedEqual.gen[Baz.type, generic.Repr]
  }
  ...

The reason why this fixes the problem is because the type signature

  def gen[A, R: DerivedEqual](implicit G: Generic.Aux[A, R]): Equal[A]

desugars into

  def gen[A, R](implicit R: DerivedEqual[R], G: Generic.Aux[A, R]): Equal[A]

The Scala compiler solves type constraints left to right, so it finds many different solutions to DerivedEqual[R] before constraining it with the Generic.Aux[A, R]. Another way to solve this is to not use context bounds.

With this in mind, we no longer need the implicit val generic or the explicit type parameters on the call to .gen. We can wire up @deriving by adding an entry in deriving.conf (assuming we want to override the scalaz-deriving implementation)

  scalaz.Equal=fommil.DerivedEqual.gen

and write

  @deriving(Equal) sealed abstract class Foo
  @deriving(Equal) final case class Bar(s: String)          extends Foo
  @deriving(Equal) final case class Faz(b: Boolean, i: Int) extends Foo
  @deriving(Equal) final case object Baz

But replacing the scalaz-deriving version means that compile times get slower. This is because the compiler is solving N implicit searches for each product of N fields or coproduct of N products, whereas scalaz-deriving and Magnolia do not.

Note that when using scalaz-deriving or Magnolia we can put the @deriving on just the top member of an ADT, but for Shapeless we must add it to all entries.

However, this implementation still has a bug: it fails for recursive types at runtime, e.g.

  @deriving(Equal) sealed trait ATree
  @deriving(Equal) final case class Leaf(value: String)               extends ATree
  @deriving(Equal) final case class Branch(left: ATree, right: ATree) extends ATree

  scala> val leaf1: Leaf    = Leaf("hello")
         val leaf2: Leaf    = Leaf("goodbye")
         val branch: Branch = Branch(leaf1, leaf2)
         val tree1: ATree   = Branch(leaf1, branch)
         val tree2: ATree   = Branch(leaf2, branch)
  
  scala> assert(tree1 /== tree2)
  [error] java.lang.NullPointerException
  [error] at DerivedEqual$.shapes$DerivedEqual$$$anonfun$hcons$1(shapeless.scala:16)
          ...

The reason why this happens is because Equal[Tree] depends on the Equal[Branch], which depends on the Equal[Tree]. Recursion and BANG! It must be loaded lazily, not eagerly.

Both scalaz-deriving and Magnolia deal with lazy automatically, but in Shapeless it is the responsibility of the typeclass author.

The macro types Cached, Strict and Lazy modify the compiler’s type inference behaviour allowing us to achieve the laziness we require. The pattern to follow is to use Cached[Strict[_]] on the entry point and Lazy[_] around the H instances.

It is best to depart from context bounds and SAM types entirely at this point:

  sealed trait DerivedEqual[A] extends Equal[A]
  object DerivedEqual {
    def gen[A, R](
      implicit G: Generic.Aux[A, R],
      R: Cached[Strict[DerivedEqual[R]]]
    ): Equal[A] = new Equal[A] {
      def equal(a1: A, a2: A) =
        quick(a1, a2) || R.value.value.equal(G.to(a1), G.to(a2))
    }
  
    implicit def hcons[H, T <: HList](
      implicit H: Lazy[Equal[H]],
      T: DerivedEqual[T]
    ): DerivedEqual[H :: T] = new DerivedEqual[H :: T] {
      def equal(ht1: H :: T, ht2: H :: T) =
        (quick(ht1.head, ht2.head) || H.value.equal(ht1.head, ht2.head)) &&
          T.equal(ht1.tail, ht2.tail)
    }
  
    implicit val hnil: DerivedEqual[HNil] = new DerivedEqual[HNil] {
      def equal(@unused h1: HNil, @unused h2: HNil) = true
    }
  
    implicit def ccons[H, T <: Coproduct](
      implicit H: Lazy[Equal[H]],
      T: DerivedEqual[T]
    ): DerivedEqual[H :+: T] = new DerivedEqual[H :+: T] {
      def equal(ht1: H :+: T, ht2: H :+: T) = (ht1, ht2) match {
        case (Inl(c1), Inl(c2)) => quick(c1, c2) || H.value.equal(c1, c2)
        case (Inr(c1), Inr(c2)) => T.equal(c1, c2)
        case _                  => false
      }
    }
  
    implicit val cnil: DerivedEqual[CNil] = new DerivedEqual[CNil] {
      def equal(@unused c1: CNil, @unused c2: CNil) = sys.error("impossible")
    }
  
    @inline private final def quick(a: Any, b: Any): Boolean =
      a.asInstanceOf[AnyRef].eq(b.asInstanceOf[AnyRef])
  }

While we were at it, we optimised using the quick shortcut from scalaz-deriving.

We can now call

  assert(tree1 /== tree2)

without a runtime exception.

8.4.2 Example: `Default`

There are no new snares in the implementation of a typeclass with a type parameter in covariant position. Here we create HList and Coproduct values, and must provide a value for the CNil case as it corresponds to the case where no coproduct is able to provide a value.

  sealed trait DerivedDefault[A] extends Default[A]
  object DerivedDefault {
    def gen[A, R](
      implicit G: Generic.Aux[A, R],
      R: Cached[Strict[DerivedDefault[R]]]
    ): Default[A] = new Default[A] {
      def default = R.value.value.default.map(G.from)
    }
  
    implicit def hcons[H, T <: HList](
      implicit H: Lazy[Default[H]],
      T: DerivedDefault[T]
    ): DerivedDefault[H :: T] = new DerivedDefault[H :: T] {
      def default =
        for {
          head <- H.value.default
          tail <- T.default
        } yield head :: tail
    }
  
    implicit val hnil: DerivedDefault[HNil] = new DerivedDefault[HNil] {
      def default = HNil.right
    }
  
    implicit def ccons[H, T <: Coproduct](
      implicit H: Lazy[Default[H]],
      T: DerivedDefault[T]
    ): DerivedDefault[H :+: T] = new DerivedDefault[H :+: T] {
      def default = H.value.default.map(Inl(_)).orElse(T.default.map(Inr(_)))
    }
  
    implicit val cnil: DerivedDefault[CNil] = new DerivedDefault[CNil] {
      def default = "not a valid coproduct".left
    }
  }

Much as we could draw an analogy between Equal and Decidable, we can see the relationship to Alt in .point (hnil), .apply2 (.hcons) and .altly2 (.ccons).

There is little to be learned from an example like Semigroup, so we will skip to encoders and decoders.

8.4.3 Example: `JsEncoder`

To be able to reproduce our Magnolia JSON encoder, we must be able to access:

field names and class names
annotations for user preferences
default values on a case class

We will begin by creating an encoder that handles only the sensible defaults.

To get field names, we use LabelledGeneric instead of Generic, and when defining the type of the head element, use FieldType[K, H] instead of just H. A Witness.Aux[K] provides the value of the field name at runtime.

All of our methods are going to return JsObject, so rather than returning a JsValue we can specialise and create DerivedJsEncoder that has a different type signature to JsEncoder.

  import shapeless._, labelled._
  
  sealed trait DerivedJsEncoder[R] {
    def toJsFields(r: R): IList[(String, JsValue)]
  }
  object DerivedJsEncoder {
    def gen[A, R](
      implicit G: LabelledGeneric.Aux[A, R],
      R: Cached[Strict[DerivedJsEncoder[R]]]
    ): JsEncoder[A] = new JsEncoder[A] {
      def toJson(a: A) = JsObject(R.value.value.toJsFields(G.to(a)))
    }
  
    implicit def hcons[K <: Symbol, H, T <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[T]
    ): DerivedJsEncoder[FieldType[K, H] :: T] =
      new DerivedJsEncoder[A, FieldType[K, H] :: T] {
        private val field = K.value.name
        def toJsFields(ht: FieldType[K, H] :: T) =
          ht match {
            case head :: tail =>
              val rest = T.toJsFields(tail)
              H.value.toJson(head) match {
                case JsNull => rest
                case value  => (field -> value) :: rest
              }
          }
      }
  
    implicit val hnil: DerivedJsEncoder[HNil] =
      new DerivedJsEncoder[HNil] {
        def toJsFields(h: HNil) = IList.empty
      }
  
    implicit def ccons[K <: Symbol, H, T <: Coproduct](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[T]
    ): DerivedJsEncoder[FieldType[K, H] :+: T] =
      new DerivedJsEncoder[FieldType[K, H] :+: T] {
        private val hint = ("type" -> JsString(K.value.name))
        def toJsFields(ht: FieldType[K, H] :+: T) = ht match {
          case Inl(head) =>
            H.value.toJson(head) match {
              case JsObject(fields) => hint :: fields
              case v                => IList.single("xvalue" -> v)
            }
  
          case Inr(tail) => T.toJsFields(tail)
        }
      }
  
    implicit val cnil: DerivedJsEncoder[CNil] =
      new DerivedJsEncoder[CNil] {
        def toJsFields(c: CNil) = sys.error("impossible")
      }
  
  }

A pattern has emerged in many Shapeless derivation libraries that introduce “hints” with a default implicit

  trait ProductHint[A] {
    def nulls(field: String): Boolean
    def fieldname(field: String): String
  }
  object ProductHint {
    implicit def default[A]: ProductHint[A] = new ProductHint[A] {
      def nulls(field: String)     = false
      def fieldname(field: String) = field
    }
  }

Users are supposed to provide a custom instance of ProductHint on their companions or package objects. This is a terrible idea that relies on fragile implicit ordering and is a source of typeclass decoherence: if we derive a JsEncoder[Foo], we will get a different result depending on which ProductHint[Foo] is in scope. It is best avoided.

Shapeless selects codepaths at compiletime based on the presence of annotations, which can lead to more optimised code, at the expense of code repetition. This means that the number of annotations we are dealing with, and their subtypes, must be manageable or we can find ourselves writing 10x the amount of code. We change our three annotations into one containing all the customisation parameters:

  case class json(
    nulls: Boolean,
    field: Option[String],
    hint: Option[String]
  ) extends Annotation

All users of the annotation must provide all three values since default values and convenience methods are not available to annotation constructors. We can write custom extractors so we don’t have to change our Magnolia code

  object json {
    object nulls {
      def unapply(j: json): Boolean = j.nulls
    }
    object field {
      def unapply(j: json): Option[String] = j.field
    }
    object hint {
      def unapply(j: json): Option[String] = j.hint
    }
  }

We can request Annotation[json, A] for a case class or sealed trait to get access to the annotation, but we must write an hcons and a ccons dealing with both cases because the evidence will not be generated if the annotation is not present. We therefore have to introduce a lower priority implicit scope and put the “no annotation” evidence there.

We can also request Annotations.Aux[json, A, J] evidence to obtain an HList of the json annotation for type A. Again, we must provide hcons and ccons dealing with the case where there is and is not an annotation.

To support this one annotation, we must write four times as much code as before!

Lets start by rewriting the JsEncoder, only handling user code that doesn’t have any annotations. Now any code that uses the @json will fail to compile, which is a good safety net.

We must add an A and J type to the DerivedJsEncoder and thread through the annotations on its .toJsObject method. Our .hcons and .ccons evidence now provides instances for DerivedJsEncoder with a None.type annotation and we move them to a lower priority so that we can deal with Annotation[json, A] in the higher priority.

Note that the evidence for J is listed before R. This is important, since the compiler must first fix the type of J before it can solve for R.

  sealed trait DerivedJsEncoder[A, R, J <: HList] {
    def toJsFields(r: R, anns: J): IList[(String, JsValue)]
  }
  object DerivedJsEncoder extends DerivedJsEncoder1 {
    def gen[A, R, J <: HList](
      implicit
      G: LabelledGeneric.Aux[A, R],
      J: Annotations.Aux[json, A, J],
      R: Cached[Strict[DerivedJsEncoder[A, R, J]]]
    ): JsEncoder[A] = new JsEncoder[A] {
      def toJson(a: A) = JsObject(R.value.value.toJsFields(G.to(a), J()))
    }
  
    implicit def hnil[A]: DerivedJsEncoder[A, HNil, HNil] =
      new DerivedJsEncoder[A, HNil, HNil] {
        def toJsFields(h: HNil, a: HNil) = IList.empty
      }
  
    implicit def cnil[A]: DerivedJsEncoder[A, CNil, HNil] =
      new DerivedJsEncoder[A, CNil, HNil] {
        def toJsFields(c: CNil, a: HNil) = sys.error("impossible")
      }
  }
  private[jsonformat] trait DerivedJsEncoder1 {
    implicit def hcons[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, None.type :: J] =
      new DerivedJsEncoder[A, FieldType[K, H] :: T, None.type :: J] {
        private val field = K.value.name
        def toJsFields(ht: FieldType[K, H] :: T, anns: None.type :: J) =
          ht match {
            case head :: tail =>
              val rest = T.toJsFields(tail, anns.tail)
              H.value.toJson(head) match {
                case JsNull => rest
                case value  => (field -> value) :: rest
              }
          }
      }
  
    implicit def ccons[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J] =
      new DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J] {
        private val hint = ("type" -> JsString(K.value.name))
        def toJsFields(ht: FieldType[K, H] :+: T, anns: None.type :: J) =
          ht match {
            case Inl(head) =>
              H.value.toJson(head) match {
                case JsObject(fields) => hint :: fields
                case v                => IList.single("xvalue" -> v)
              }
            case Inr(tail) => T.toJsFields(tail, anns.tail)
          }
      }
  }

Now we can add the type signatures for the six new methods, covering all the possibilities of where the annotation can be. Note that we only support one annotation in each position. If the user provides multiple annotations, anything after the first will be silently ignored.

We’re now running out of names for things, so we will arbitrarily call it Annotated when there is an annotation on the A, and Custom when there is an annotation on a field:

  object DerivedJsEncoder extends DerivedJsEncoder1 {
    ...
    implicit def hconsAnnotated[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, None.type :: J]
  
    implicit def cconsAnnotated[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J]
  
    implicit def hconsAnnotatedCustom[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, Some[json] :: J]
  
    implicit def cconsAnnotatedCustom[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J]
  }
  private[jsonformat] trait DerivedJsEncoder1 {
    ...
    implicit def hconsCustom[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, Some[json] :: J] = ???
  
    implicit def cconsCustom[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J]
  }

We don’t actually need .hconsAnnotated or .hconsAnnotatedCustom for anything, since an annotation on a case class does not mean anything to the encoding of that product, it is only used in .cconsAnnotated*. We can therefore delete two methods.

.cconsAnnotated and .cconsAnnotatedCustom can be defined as

  new DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J] {
    private val hint = A().field.getOrElse("type") -> JsString(K.value.name)
    def toJsFields(ht: FieldType[K, H] :+: T, anns: None.type :: J) = ht match {
      case Inl(head) =>
        H.value.toJson(head) match {
          case JsObject(fields) => hint :: fields
          case v                => IList.single("xvalue" -> v)
        }
      case Inr(tail) => T.toJsFields(tail, anns.tail)
    }
  }

and

  new DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J] {
    private val hintfield = A().field.getOrElse("type")
    def toJsFields(ht: FieldType[K, H] :+: T, anns: Some[json] :: J) = ht match {
      case Inl(head) =>
        val ann = anns.head.get
        H.value.toJson(head) match {
          case JsObject(fields) =>
            val hint = (hintfield -> JsString(ann.hint.getOrElse(K.value.name)))
            hint :: fields
          case v =>
            val xvalue = ann.field.getOrElse("xvalue")
            IList.single(xvalue -> v)
        }
      case Inr(tail) => T.toJsFields(tail, anns.tail)
    }
  }

The use of .head and .get may be concerned but recall that the types here are :: and Some meaning that these methods are total and safe to use.

.hconsCustom and .cconsCustom are written

  new DerivedJsEncoder[A, FieldType[K, H] :: T, Some[json] :: J] {
    def toJsFields(ht: FieldType[K, H] :: T, anns: Some[json] :: J) = ht match {
      case head :: tail =>
        val ann  = anns.head.get
        val next = T.toJsFields(tail, anns.tail)
        H.value.toJson(head) match {
          case JsNull if !ann.nulls => next
          case value =>
            val field = ann.field.getOrElse(K.value.name)
            (field -> value) :: next
        }
    }
  }

and

  new DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J] {
    def toJsFields(ht: FieldType[K, H] :+: T, anns: Some[json] :: J) = ht match {
      case Inl(head) =>
        val ann = anns.head.get
        H.value.toJson(head) match {
          case JsObject(fields) =>
            val hint = ("type" -> JsString(ann.hint.getOrElse(K.value.name)))
            hint :: fields
          case v =>
            val xvalue = ann.field.getOrElse("xvalue")
            IList.single(xvalue -> v)
        }
      case Inr(tail) => T.toJsFields(tail, anns.tail)
    }
  }

Obviously, there is a lot of boilerplate, but looking closely one can see that each method is implemented as efficiently as possible with the information it has available: codepaths are selected at compiletime rather than runtime.

The performance obsessed may be able to refactor this code so all annotation information is available in advance, rather than injected via the .toJsFields method, with another layer of indirection. For absolute performance, we could also treat each customisation as a separate annotation, but that would multiply the amount of code we’ve written yet again, with additional cost to compilation time on downstream users. Such optimisations are beyond the scope of this book, but they are possible and people do them: the ability to shift work from runtime to compiletime is one of the most appealing things about generic programming.

One more caveat that we need to be aware of: LabelledGeneric is not compatible with scalaz.@@, but there is a workaround. Say we want to effectively ignore tags so we add the following derivation rules to the companions of our encoder and decoder

  object JsEncoder {
    ...
    implicit def tagged[A: JsEncoder, Z]: JsEncoder[A @@ Z] =
      JsEncoder[A].contramap(Tag.unwrap)
  }
  object JsDecoder {
    ...
    implicit def tagged[A: JsDecoder, Z]: JsDecoder[A @@ Z] =
      JsDecoder[A].map(Tag(_))
  }

We would then expect to be able to derive a JsDecoder for something like our TradeTemplate from Chapter 5

  final case class TradeTemplate(
    otc: Option[Boolean] @@ Tags.Last
  )
  object TradeTemplate {
    implicit val encoder: JsEncoder[TradeTemplate] = DerivedJsEncoder.gen
  }

But we instead get a compiler error

  [error] could not find implicit value for parameter G: LabelledGeneric.Aux[A,R]
  [error]   implicit val encoder: JsEncoder[TradeTemplate] = DerivedJsEncoder.gen
  [error]                                                                     ^

The error message is as helpful as always. The workaround is to introduce evidence for H @@ Z on the lower priority implicit scope, and then just call the code that the compiler should have found in the first place:

  object DerivedJsEncoder extends DerivedJsEncoder1 with DerivedJsEncoder2 {
    ...
  }
  private[jsonformat] trait DerivedJsEncoder2 {
    this: DerivedJsEncoder.type =>
  
    // WORKAROUND https://github.com/milessabin/shapeless/issues/309
    implicit def hconsTagged[A, K <: Symbol, H, Z, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H @@ Z]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H @@ Z] :: T, None.type :: J] = hcons(K, H, T)
  
    implicit def hconsCustomTagged[A, K <: Symbol, H, Z, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H @@ Z]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H @@ Z] :: T, Some[json] :: J] = hconsCustom(K, H, T)
  }

Thankfully, we only need to consider products, since coproducts cannot be tagged.

8.4.4 `JsDecoder`

The decoding side is much as we can expect based on previous examples. We can construct an instance of a FieldType[K, H] with the helper field[K](h: H). Supporting only the sensible defaults means we write:

  sealed trait DerivedJsDecoder[A] {
    def fromJsObject(j: JsObject): String \/ A
  }
  object DerivedJsDecoder {
    def gen[A, R](
      implicit G: LabelledGeneric.Aux[A, R],
      R: Cached[Strict[DerivedJsDecoder[R]]]
    ): JsDecoder[A] = new JsDecoder[A] {
      def fromJson(j: JsValue) = j match {
        case o @ JsObject(_) => R.value.value.fromJsObject(o).map(G.from)
        case other           => fail("JsObject", other)
      }
    }
  
    implicit def hcons[K <: Symbol, H, T <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H]],
      T: DerivedJsDecoder[T]
    ): DerivedJsDecoder[FieldType[K, H] :: T] =
      new DerivedJsDecoder[FieldType[K, H] :: T] {
        private val fieldname = K.value.name
        def fromJsObject(j: JsObject) = {
          val value = j.get(fieldname).getOrElse(JsNull)
          for {
            head  <- H.value.fromJson(value)
            tail  <- T.fromJsObject(j)
          } yield field[K](head) :: tail
        }
      }
  
    implicit val hnil: DerivedJsDecoder[HNil] = new DerivedJsDecoder[HNil] {
      private val nil               = HNil.right[String]
      def fromJsObject(j: JsObject) = nil
    }
  
    implicit def ccons[K <: Symbol, H, T <: Coproduct](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H]],
      T: DerivedJsDecoder[T]
    ): DerivedJsDecoder[FieldType[K, H] :+: T] =
      new DerivedJsDecoder[FieldType[K, H] :+: T] {
        private val hint = ("type" -> JsString(K.value.name))
        def fromJsObject(j: JsObject) =
          if (j.fields.element(hint)) {
            j.get("xvalue")
              .into {
                case \/-(xvalue) => H.value.fromJson(xvalue)
                case -\/(_)      => H.value.fromJson(j)
              }
              .map(h => Inl(field[K](h)))
          } else
            T.fromJsObject(j).map(Inr(_))
      }
  
    implicit val cnil: DerivedJsDecoder[CNil] = new DerivedJsDecoder[CNil] {
      def fromJsObject(j: JsObject) = fail(s"JsObject with 'type' field", j)
    }
  }

Adding user preferences via annotations follows the same route as DerivedJsEncoder and is mechanical, so left as an exercise to the reader.

One final thing is missing: case class default values. We can request evidence but a big problem is that we can no longer use the same derivation mechanism for products and coproducts: the evidence is never created for coproducts.

The solution is quite drastic. We must split our DerivedJsDecoder into DerivedCoproductJsDecoder and DerivedProductJsDecoder. We will focus our attention on the DerivedProductJsDecoder, and while we are at it we will use a Map for faster field lookup:

  sealed trait DerivedProductJsDecoder[A, R, J <: HList, D <: HList] {
    private[jsonformat] def fromJsObject(
      j: Map[String, JsValue],
      anns: J,
      defaults: D
    ): String \/ R
  }

We can request evidence of default values with Default.Aux[A, D] and duplicate all the methods to deal with the case where we do and do not have a default value. However, Shapeless is merciful (for once) and provides Default.AsOptions.Aux[A, D] letting us handle defaults at runtime.

  object DerivedProductJsDecoder {
    def gen[A, R, J <: HList, D <: HList](
      implicit G: LabelledGeneric.Aux[A, R],
      J: Annotations.Aux[json, A, J],
      D: Default.AsOptions.Aux[A, D],
      R: Cached[Strict[DerivedProductJsDecoder[A, R, J, D]]]
    ): JsDecoder[A] = new JsDecoder[A] {
      def fromJson(j: JsValue) = j match {
        case o @ JsObject(_) =>
          R.value.value.fromJsObject(o.fields.toMap, J(), D()).map(G.from)
        case other => fail("JsObject", other)
      }
    }
    ...
  }

We must move the .hcons and .hnil methods onto the companion of the new sealed typeclass, which can handle default values

  object DerivedProductJsDecoder {
    ...
      implicit def hnil[A]: DerivedProductJsDecoder[A, HNil, HNil, HNil] =
      new DerivedProductJsDecoder[A, HNil, HNil, HNil] {
        private val nil = HNil.right[String]
        def fromJsObject(j: StringyMap[JsValue], a: HNil, defaults: HNil) = nil
      }
  
    implicit def hcons[A, K <: Symbol, H, T <: HList, J <: HList, D <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H]],
      T: DerivedProductJsDecoder[A, T, J, D]
    ): DerivedProductJsDecoder[A, FieldType[K, H] :: T, None.type :: J, Option[H] :: D] =
      new DerivedProductJsDecoder[A, FieldType[K, H] :: T, None.type :: J, Option[H] :: D] {
        private val fieldname = K.value.name
        def fromJsObject(
          j: StringyMap[JsValue],
          anns: None.type :: J,
          defaults: Option[H] :: D
        ) =
          for {
            head <- j.get(fieldname) match {
                     case Maybe.Just(v) => H.value.fromJson(v)
                     case _ =>
                       defaults.head match {
                         case Some(default) => \/-(default)
                         case None          => H.value.fromJson(JsNull)
                       }
                   }
            tail <- T.fromJsObject(j, anns.tail, defaults.tail)
          } yield field[K](head) :: tail
      }
    ...
  }

We can no longer use @deriving for products and coproducts: there can only be one entry in the deriving.conf file.

Oh, and don’t forget to add @@ support

  object DerivedProductJsDecoder extends DerivedProductJsDecoder1 {
    ...
  }
  private[jsonformat] trait DerivedProductJsDecoder2 {
    this: DerivedProductJsDecoder.type =>
  
    implicit def hconsTagged[
      A, K <: Symbol, H, Z, T <: HList, J <: HList, D <: HList
    ](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H @@ Z]],
      T: DerivedProductJsDecoder[A, T, J, D]
    ): DerivedProductJsDecoder[
      A,
      FieldType[K, H @@ Z] :: T,
      None.type :: J,
      Option[H @@ Z] :: D
    ] = hcons(K, H, T)
  
    implicit def hconsCustomTagged[
      A, K <: Symbol, H, Z, T <: HList, J <: HList, D <: HList
    ](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H @@ Z]],
      T: DerivedProductJsDecoder[A, T, J, D]
    ): DerivedProductJsDecoder[
      A,
      FieldType[K, H @@ Z] :: T,
      Some[json] :: J,
      Option[H @@ Z] :: D
    ] = hconsCustomTagged(K, H, T)
  }

8.4.5 Complicated Derivations

Shapeless allows for a lot more kinds of derivations than are possible with scalaz-deriving or Magnolia. As an example of an encoder / decoder that are not possible with Magnolia, consider this XML model from xmlformat

  @deriving(Equal, Show, Arbitrary)
  sealed abstract class XNode
  
  @deriving(Equal, Show, Arbitrary)
  final case class XTag(
    name: String,
    attrs: IList[XAttr],
    children: IList[XTag],
    body: Maybe[XString]
  )
  
  @deriving(Equal, Show, Arbitrary)
  final case class XAttr(name: String, value: XString)
  
  @deriving(Show)
  @xderiving(Equal, Monoid, Arbitrary)
  final case class XChildren(tree: IList[XTag]) extends XNode
  
  @deriving(Show)
  @xderiving(Equal, Semigroup, Arbitrary)
  final case class XString(text: String) extends XNode

Given the nature of XML it makes sense to have separate encoder / decoder pairs for XChildren and XString content. We could provide a derivation for the XChildren with Shapeless but we want to special case fields based on the kind of typeclass they have, as well as Option fields. We could even require that fields are annotated with their encoded name. In addition, when decoding we wish to have different strategies for handling XML element bodies, which can be multipart, depending on if our type has a Semigroup, Monoid or neither.

8.4.6 Example: `UrlQueryWriter`

Along similar lines as xmlformat, our drone-dynamic-agents application could benefit from a typeclass derivation of the UrlQueryWriter typeclass, which is built out of UrlEncodedWriter instances for each field entry. It does not support coproducts:

  @typeclass trait UrlQueryWriter[A] {
    def toUrlQuery(a: A): UrlQuery
  }
  trait DerivedUrlQueryWriter[T] extends UrlQueryWriter[T]
  object DerivedUrlQueryWriter {
    def gen[T, Repr](
      implicit
      G: LabelledGeneric.Aux[T, Repr],
      CR: Cached[Strict[DerivedUrlQueryWriter[Repr]]]
    ): UrlQueryWriter[T] = { t =>
      CR.value.value.toUrlQuery(G.to(t))
    }
  
    implicit val hnil: DerivedUrlQueryWriter[HNil] = { _ =>
      UrlQuery(IList.empty)
    }
    implicit def hcons[Key <: Symbol, A, Remaining <: HList](
      implicit Key: Witness.Aux[Key],
      LV: Lazy[UrlEncodedWriter[A]],
      DR: DerivedUrlQueryWriter[Remaining]
    ): DerivedUrlQueryWriter[FieldType[Key, A] :: Remaining] = {
      case head :: tail =>
        val first =
          Key.value.name -> URLDecoder.decode(LV.value.toUrlEncoded(head).value, "UTF-8")
        val rest = DR.toUrlQuery(tail)
        UrlQuery(first :: rest.params)
    }
  }

It is reasonable to ask if these 30 lines are actually an improvement over the 8 lines for the 2 manual instances our application needs: a decision to be taken on a case by case basis.

For completeness, the UrlEncodedWriter derivation can be written with Magnolia

  object UrlEncodedWriterMagnolia {
    type Typeclass[a] = UrlEncodedWriter[a]
    def combine[A](ctx: CaseClass[UrlEncodedWriter, A]) = a =>
      Refined.unsafeApply(ctx.parameters.map { p =>
        p.label + "=" + p.typeclass.toUrlEncoded(p.dereference(a))
      }.toList.intercalate("&"))
    def gen[A]: UrlEncodedWriter[A] = macro Magnolia.gen[A]
  }

8.4.7 The Dark Side of Derivation

“Beware fully automatic derivation. Anger, fear, aggression; the dark side of the derivation are they. Easily they flow, quick to join you in a fight. If once you start down the dark path, forever will it dominate your compiler, consume you it will.”

― an ancient Shapeless master

In addition to all the warnings about fully automatic derivation that were mentioned for Magnolia, Shapeless is much worse. Not only is fully automatic Shapeless derivation the most common cause of slow compiles, it is also a painful source of typeclass coherence bugs.

Fully automatic derivation is when the def gen are implicit such that a call will recurse for all entries in the ADT. Because of the way that implicit scopes work, an imported implicit def will have a higher priority than custom instances on companions, creating a source of typeclass decoherence. For example, consider this code if our .gen were implicit

  import DerivedJsEncoder._
  
  @xderiving(JsEncoder)
  final case class Foo(s: String)
  final case class Bar(foo: Foo)

We might expect the full-auto encoded form of Bar("hello") to look like

  {
    "foo":"hello"
  }

because we have used xderiving for Foo. But it can instead be

  {
    "foo": {
      "s":"hello"
    }
  }

Worse yet is when implicit methods are added to the companion of the typeclass, meaning that the typeclass is always derived at the point of use and users are unable opt out.

Fundamentally, when writing generic programs, implicits can be ignored by the compiler depending on scope, meaning that we lose the compiletime safety that was our motivation for programming at the type level in the first place!

Everything is much simpler in the light side, where implicit is only used for coherent, globally unique, typeclasses. Fear of boilerplate is the path to the dark side. Fear leads to anger. Anger leads to hate. Hate leads to suffering.

8.5 Performance

There is no silver bullet when it comes to typeclass derivation. An axis to consider is performance: both at compiletime and runtime.

8.5.0.1 Compile Times

When it comes to compilation times, Shapeless is the outlier. It is not uncommon to see a small project expand from a one second compile to a one minute compile. To investigate compilation issues, we can profile our applications with the scalac-profiling plugin

  addCompilerPlugin("ch.epfl.scala" %% "scalac-profiling" % "1.0.0")
  scalacOptions ++= Seq("-Ystatistics:typer", "-P:scalac-profiling:no-profiledb")

It produces output that can generate a flame graph.

For a typical Shapeless derivation, we get a lively chart

almost the entire compile time is spent in implicit resolution. Note that this also includes compiling the scalaz-deriving, Magnolia and manual instances, but the Shapeless computations dominate.

And this is when it works. If there is a problem with a shapeless derivation, the compiler can get stuck in an infinite loop and must be killed.

8.5.0.2 Runtime Performance

If we move to runtime performance, the answer is always it depends.

Assuming that the derivation logic has been written in an efficient way, it is only possible to know which is faster through experimentation.

The jsonformat library uses the Java Microbenchmark Harness (JMH) on models that map to GeoJSON, Google Maps, and Twitter, contributed by Andriy Plokhotnyuk. There are three tests per model:

encoding the ADT to a JsValue
a successful decoding of the same JsValue back into an ADT
a failure decoding of a JsValue with a data error

applied to the following implementations:

Magnolia
Shapeless
manually written

with the equivalent optimisations in each. The results are in operations per second (higher is better), on a powerful desktop computer, using a single thread:

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*encode*
  Benchmark                                 Mode  Cnt       Score      Error  Units
  
  GeoJSONBenchmarks.encodeMagnolia         thrpt    5   70527.223 ±  546.991  ops/s
  GeoJSONBenchmarks.encodeShapeless        thrpt    5   65925.215 ±  309.623  ops/s
  GeoJSONBenchmarks.encodeManual           thrpt    5   96435.691 ±  334.652  ops/s
  
  GoogleMapsAPIBenchmarks.encodeMagnolia   thrpt    5   73107.747 ±  439.803  ops/s
  GoogleMapsAPIBenchmarks.encodeShapeless  thrpt    5   53867.845 ±  510.888  ops/s
  GoogleMapsAPIBenchmarks.encodeManual     thrpt    5  127608.402 ± 1584.038  ops/s
  
  TwitterAPIBenchmarks.encodeMagnolia      thrpt    5  133425.164 ± 1281.331  ops/s
  TwitterAPIBenchmarks.encodeShapeless     thrpt    5   84233.065 ±  352.611  ops/s
  TwitterAPIBenchmarks.encodeManual        thrpt    5  281606.574 ± 1975.873  ops/s

We see that the manual implementations are in the lead, followed by Magnolia, with Shapeless from 30% to 70% the performance of the manual instances. Now for decoding

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*decode.*Success
  Benchmark                                        Mode  Cnt       Score      Error  Units
  
  GeoJSONBenchmarks.decodeMagnoliaSuccess         thrpt    5   40850.270 ±  201.457  ops/s
  GeoJSONBenchmarks.decodeShapelessSuccess        thrpt    5   41173.199 ±  373.048  ops/s
  GeoJSONBenchmarks.decodeManualSuccess           thrpt    5  110961.246 ±  468.384  ops/s
  
  GoogleMapsAPIBenchmarks.decodeMagnoliaSuccess   thrpt    5   44577.796 ±  457.861  ops/s
  GoogleMapsAPIBenchmarks.decodeShapelessSuccess  thrpt    5   31649.792 ±  861.169  ops/s
  GoogleMapsAPIBenchmarks.decodeManualSuccess     thrpt    5   56250.913 ±  394.105  ops/s
  
  TwitterAPIBenchmarks.decodeMagnoliaSuccess      thrpt    5   55868.832 ± 1106.543  ops/s
  TwitterAPIBenchmarks.decodeShapelessSuccess     thrpt    5   47711.161 ±  356.911  ops/s
  TwitterAPIBenchmarks.decodeManualSuccess        thrpt    5   71962.394 ±  465.752  ops/s

This is a tighter race for second place, with Shapeless and Magnolia keeping pace. Finally, decoding from a JsValue that contains invalid data (in an intentionally awkward position)

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*decode.*Error
  Benchmark                                      Mode  Cnt        Score       Error  Units
  
  GeoJSONBenchmarks.decodeMagnoliaError         thrpt    5   981094.831 ± 11051.370  ops/s
  GeoJSONBenchmarks.decodeShapelessError        thrpt    5   816704.635 ±  9781.467  ops/s
  GeoJSONBenchmarks.decodeManualError           thrpt    5   586733.762 ±  6389.296  ops/s
  
  GoogleMapsAPIBenchmarks.decodeMagnoliaError   thrpt    5  1288888.446 ± 11091.080  ops/s
  GoogleMapsAPIBenchmarks.decodeShapelessError  thrpt    5  1010145.363 ±  9448.110  ops/s
  GoogleMapsAPIBenchmarks.decodeManualError     thrpt    5  1417662.720 ±  1197.283  ops/s
  
  TwitterAPIBenchmarks.decodeMagnoliaError      thrpt    5   128704.299 ±   832.122  ops/s
  TwitterAPIBenchmarks.decodeShapelessError     thrpt    5   109715.865 ±   826.488  ops/s
  TwitterAPIBenchmarks.decodeManualError        thrpt    5   148814.730 ±  1105.316  ops/s

Just when we thought we were seeing a pattern, both Magnolia and Shapeless win the race when decoding invalid GeoJSON data, but manual instances win the Google Maps and Twitter challenges.

We want to include scalaz-deriving in the comparison, so we compare an equivalent implementation of Equal, tested on two values that contain the same contents (True) and two values that contain slightly different contents (False)

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*equal*
  Benchmark                                     Mode  Cnt        Score       Error  Units
  
  GeoJSONBenchmarks.equalScalazTrue            thrpt    5   276851.493 ±  1776.428  ops/s
  GeoJSONBenchmarks.equalMagnoliaTrue          thrpt    5    93106.945 ±  1051.062  ops/s
  GeoJSONBenchmarks.equalShapelessTrue         thrpt    5   266633.522 ±  4972.167  ops/s
  GeoJSONBenchmarks.equalManualTrue            thrpt    5   599219.169 ±  8331.308  ops/s
  
  GoogleMapsAPIBenchmarks.equalScalazTrue      thrpt    5    35442.577 ±   281.597  ops/s
  GoogleMapsAPIBenchmarks.equalMagnoliaTrue    thrpt    5    91016.557 ±   688.308  ops/s
  GoogleMapsAPIBenchmarks.equalShapelessTrue   thrpt    5   107245.505 ±   468.427  ops/s
  GoogleMapsAPIBenchmarks.equalManualTrue      thrpt    5   302247.760 ±  1927.858  ops/s
  
  TwitterAPIBenchmarks.equalScalazTrue         thrpt    5    99066.013 ±  1125.422  ops/s
  TwitterAPIBenchmarks.equalMagnoliaTrue       thrpt    5   236289.706 ±  3182.664  ops/s
  TwitterAPIBenchmarks.equalShapelessTrue      thrpt    5   251578.931 ±  2430.738  ops/s
  TwitterAPIBenchmarks.equalManualTrue         thrpt    5   865845.158 ±  6339.379  ops/s

As expected, the manual instances are far ahead of the crowd, with Shapeless mostly leading the automatic derivations. scalaz-deriving makes a great effort for GeoJSON but falls far behind in both the Google Maps and Twitter tests. The False tests are more of the same:

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*equal*
  Benchmark                                     Mode  Cnt        Score       Error  Units
  
  GeoJSONBenchmarks.equalScalazFalse           thrpt    5    89552.875 ±   821.791  ops/s
  GeoJSONBenchmarks.equalMagnoliaFalse         thrpt    5    86044.021 ±  7790.350  ops/s
  GeoJSONBenchmarks.equalShapelessFalse        thrpt    5   262979.062 ±  3310.750  ops/s
  GeoJSONBenchmarks.equalManualFalse           thrpt    5   599989.203 ± 23727.672  ops/s
  
  GoogleMapsAPIBenchmarks.equalScalazFalse     thrpt    5    35970.818 ±   288.609  ops/s
  GoogleMapsAPIBenchmarks.equalMagnoliaFalse   thrpt    5    82381.975 ±   625.407  ops/s
  GoogleMapsAPIBenchmarks.equalShapelessFalse  thrpt    5   110721.122 ±   579.331  ops/s
  GoogleMapsAPIBenchmarks.equalManualFalse     thrpt    5   303588.815 ±  2562.747  ops/s
  
  TwitterAPIBenchmarks.equalScalazFalse        thrpt    5   193930.568 ±  1176.421  ops/s
  TwitterAPIBenchmarks.equalMagnoliaFalse      thrpt    5   429764.654 ± 11944.057  ops/s
  TwitterAPIBenchmarks.equalShapelessFalse     thrpt    5   494510.588 ±  1455.647  ops/s
  TwitterAPIBenchmarks.equalManualFalse        thrpt    5  1631964.531 ± 13110.291  ops/s

The runtime performance of scalaz-deriving, Magnolia and Shapeless is usually good enough. We should be realistic: we are not writing applications that need to be able to encode more than 130,000 values to JSON, per second, on a single core, on the JVM. If that is a problem, look into C++.

It is unlikely that derived instances will be an application’s bottleneck. Even if it is, there is the manually written escape hatch, which is more powerful and therefore more dangerous: it is easy to introduce typos, bugs, and even performance regressions by accident when writing a manual instance.

In conclusion: hokey derivations and ancient macros are no match for a good hand written instance at your side, kid.

8.6 Summary

When deciding on a technology to use for typeclass derivation, this feature chart may help:

Feature	Scalaz	Magnolia	Shapeless	Manual
`@deriving`	yes	yes	yes
Laws	yes
Fast compiles	yes	yes		yes
Field names		yes	yes
Annotations		yes	partially
Default values		yes	with caveats
Complicated			painfully so
Performance				hold my beer

Prefer scalaz-deriving if possible, using Magnolia for encoders / decoders or if performance is a larger concern, escalating to Shapeless for complicated derivations only if compilation times are not a concern.

Manual instances are always an escape hatch for special cases and to achieve the ultimate performance. Avoid introducing typo bugs with manual instances by using a code generation tool.

9. Wiring up the Application

To finish, we will apply what we have learnt to wire up the example application, and implement an HTTP client and server using the http4s pure FP library.

The source code to the drone-dynamic-agents application is available along with the book’s source code at https://github.com/fommil/fpmortals under the examples folder. It is not necessary to be at a computer to read this chapter, but many readers may prefer to explore the codebase in addition to this text.

Some parts of the application have been left unimplemented, as an exercise to the reader. See the README for further instructions.

9.1 Overview

Our main application only requires an implementation of the DynAgents algebra.

  trait DynAgents[F[_]] {
    def initial: F[WorldView]
    def update(old: WorldView): F[WorldView]
    def act(world: WorldView): F[WorldView]
  }

We have an implementation already, DynAgentsModule, which requires implementations of the Drone and Machines algebras, which require a JsonClient, LocalClock and OAuth2 algebras, etc, etc, etc.

It is helpful to get a complete picture of all the algebras, modules and interpreters of the application. This is the layout of the source code:

  ├── dda
  │   ├── algebra.scala
  │   ├── DynAgents.scala
  │   ├── main.scala
  │   └── interpreters
  │       ├── DroneModule.scala
  │       └── GoogleMachinesModule.scala
  ├── http
  │   ├── JsonClient.scala
  │   ├── OAuth2JsonClient.scala
  │   ├── encoding
  │   │   ├── UrlEncoded.scala
  │   │   ├── UrlEncodedWriter.scala
  │   │   ├── UrlQuery.scala
  │   │   └── UrlQueryWriter.scala
  │   ├── oauth2
  │   │   ├── Access.scala
  │   │   ├── Auth.scala
  │   │   ├── Refresh.scala
  │   │   └── interpreters
  │   │       └── BlazeUserInteraction.scala
  │   └── interpreters
  │       └── BlazeJsonClient.scala
  ├── os
  │   └── Browser.scala
  └── time
      ├── Epoch.scala
      ├── LocalClock.scala
      └── Sleep.scala

The signatures of all the algebras can be summarised as

  trait Sleep[F[_]] {
    def sleep(time: FiniteDuration): F[Unit]
  }
  
  trait LocalClock[F[_]] {
    def now: F[Epoch]
  }
  
  trait JsonClient[F[_]] {
    def get[A: JsDecoder](
      uri: String Refined Url,
      headers: IList[(String, String)]
    ): F[A]
  
    def post[P: UrlEncodedWriter, A: JsDecoder](
      uri: String Refined Url,
      payload: P,
      headers: IList[(String, String)]
    ): F[A]
  }
  
  trait Auth[F[_]] {
    def authenticate: F[CodeToken]
  }
  trait Access[F[_]] {
    def access(code: CodeToken): F[(RefreshToken, BearerToken)]
  }
  trait Refresh[F[_]] {
    def bearer(refresh: RefreshToken): F[BearerToken]
  }
  trait OAuth2JsonClient[F[_]] {
    // same methods as JsonClient, but doing OAuth2 transparently
  }
  
  trait UserInteraction[F[_]] {
    def start: F[String Refined Url]
    def open(uri: String Refined Url): F[Unit]
    def stop: F[CodeToken]
  }
  
  trait Drone[F[_]] {
    def getBacklog: F[Int]
    def getAgents: F[Int]
  }
  
  trait Machines[F[_]] {
    def getTime: F[Epoch]
    def getManaged: F[NonEmptyList[MachineNode]]
    def getAlive: F[MachineNode ==>> Epoch]
    def start(node: MachineNode): F[Unit]
    def stop(node: MachineNode): F[Unit]
  }

Note that some signatures from previous chapters have been refactored to use Scalaz data types, now that we know why they are superior to the stdlib.

The data types are:

  @xderiving(Order, Arbitrary)
  final case class Epoch(millis: Long) extends AnyVal
  
  @deriving(Order, Show)
  final case class MachineNode(id: String)
  
  @deriving(Equal, Show)
  final case class CodeToken(token: String, redirect_uri: String Refined Url)
  
  @xderiving(Equal, Show, ConfigReader)
  final case class RefreshToken(token: String) extends AnyVal
  
  @deriving(Equal, Show, ConfigReader)
  final case class BearerToken(token: String, expires: Epoch)
  
  @deriving(ConfigReader)
  final case class OAuth2Config(token: RefreshToken, server: ServerConfig)
  
  @deriving(ConfigReader)
  final case class AppConfig(drone: BearerToken, machines: OAuth2Config)
  
  @xderiving(UrlEncodedWriter)
  final case class UrlQuery(params: IList[(String, String)]) extends AnyVal

and the typeclasses are

  @typeclass trait UrlEncodedWriter[A] {
    def toUrlEncoded(a: A): String Refined UrlEncoded
  }
  @typeclass trait UrlQueryWriter[A] {
    def toUrlQuery(a: A): UrlQuery
  }

We derive useful typeclasses using scalaz-deriving and Magnolia. The ConfigReader typeclass is from the pureconfig library and is used to read runtime configuration from HOCON property files.

And without going into the detail of how to implement the algebras, we need to know the dependency graph of our DynAgentsModule.

  final class DynAgentsModule[F[_]: Applicative](
    D: Drone[F],
    M: Machines[F]
  ) extends DynAgents[F] { ... }
  
  final class DroneModule[F[_]](
    H: OAuth2JsonClient[F]
  ) extends Drone[F] { ... }
  
  final class GoogleMachinesModule[F[_]](
    H: OAuth2JsonClient[F]
  ) extends Machines[F] { ... }

There are two modules implementing OAuth2JsonClient, one that will use the OAuth2 Refresh algebra (for Google) and another that reuses a non-expiring BearerToken (for Drone).

  final class OAuth2JsonClientModule[F[_]](
    token: RefreshToken
  )(
    H: JsonClient[F],
    T: LocalClock[F],
    A: Refresh[F]
  )(
    implicit F: MonadState[F, BearerToken]
  ) extends OAuth2JsonClient[F] { ... }
  
  final class BearerJsonClientModule[F[_]: Monad](
    bearer: BearerToken
  )(
    H: JsonClient[F]
  ) extends OAuth2JsonClient[F] { ... }

So far we have seen requirements for F to have an Applicative[F], Monad[F] and MonadState[F, BearerToken]. All of these requirements can be satisfied by using StateT[Task, BearerToken, ?] as our application’s context.

However, some of our algebras only have one interpreter, using Task

  final class LocalClockTask extends LocalClock[Task] { ... }
  final class SleepTask extends Sleep[Task] { ... }

But recall that our algebras can provide a liftM on their companion, see Chapter 7.4 on the Monad Transformer Library, allowing us to lift a LocalClock[Task] into our desired StateT[Task, BearerToken, ?] context, and everything is consistent.

Unfortunately, that is not the end of the story. Things get more complicated when we go to the next layer. Our JsonClient has an interpreter using a different context

  final class BlazeJsonClient[F[_]](H: Client[Task])(
    implicit
    F: MonadError[F, JsonClient.Error],
    I: MonadIO[F, Throwable]
  ) extends JsonClient[F] { ... }
  object BlazeJsonClient {
    def apply[F[_]](
      implicit
      F: MonadError[F, JsonClient.Error],
      I: MonadIO[F, Throwable]
    ): Task[JsonClient[F]] = ...
  }

Note that the BlazeJsonClient constructor returns a Task[JsonClient[F]], not a JsonClient[F]. This is because the act of creating the client is effectful: mutable connection pools are created and managed internally by http4s.

OAuth2JsonClientModule requires a MonadState and BlazeJsonClient requires MonadError and MonadIO. Our application’s context will now likely be the combination of both:

  StateT[EitherT[Task, JsonClient.Error, ?], BearerToken, ?]

A monad stack. Monad stacks automatically provide appropriate instances of MonadState and MonadError when nested, so we don’t need to think about it. If we had hard-coded the implementation in the interpreter, and returned an EitherT[Task, Error, ?] from BlazeJsonClient, it would make it a lot harder to instantiate.

We must not forget that we need to provide a RefreshToken for GoogleMachinesModule. We could ask the user to do all the legwork, but we are nice and provide a separate one-shot application that uses the Auth and Access algebras. The AuthModule and AccessModule implementations bring in additional dependencies, but thankfully no change to the application’s F[_] context.

  final class AuthModule[F[_]: Monad](
    config: ServerConfig
  )(
    I: UserInteraction[F]
  ) extends Auth[F] { ... }
  
  final class AccessModule[F[_]: Monad](
    config: ServerConfig
  )(
    H: JsonClient[F],
    T: LocalClock[F]
  ) extends Access[F] { ... }
  
  final class BlazeUserInteraction private (
    pserver: Promise[Void, Server[Task]],
    ptoken: Promise[Void, String]
  ) extends UserInteraction[Task] { ... }
  object BlazeUserInteraction {
    def apply(): Task[BlazeUserInteraction] = ...
  }

The interpreter for UserInteraction is the most complex part of our codebase: it starts an HTTP server, sends the user to visit a webpage in their browser, captures a callback in the server, and then returns the result while safely shutting down the web server.

Rather than using a StateT to manage this state, we use a Promise primitive (from ioeffect). We should always use Promise (or IORef) instead of a StateT when we are writing an IO interpreter since it allows us to contain the abstraction. If we were to use a StateT, not only would it have a performance impact on the entire application, but it would also leak internal state management to the main application, which would become responsible for providing the initial value. We also couldn’t use StateT in this scenario because we need “wait for” semantics that are only provided by Promise.

9.2 `Main`

The ugliest part of FP is making sure that monads are all aligned and this tends to happen in the Main entrypoint.

Our main loop is

  state = initial()
  while True:
    state = update(state)
    state = act(state)

and the good news is that the actual code will look like

  for {
    old     <- F.get
    updated <- A.update(old)
    changed <- A.act(updated)
    _       <- F.put(changed)
    _       <- S.sleep(10.seconds)
  } yield ()

where F holds the state of the world in a MonadState[F, WorldView]. We can put this into a method called .step and repeat it forever by calling .step[F].forever[Unit].

There are two approaches we can take, and we will explore both. The first, and simplest, is to construct one monad stack that all algebras are compatible with. Everything gets a .liftM added to it to lift it into the larger stack.

The code we want to write for the one-shot authentication mode is

  def auth(name: String): Task[Unit] = {
    for {
      config    <- readConfig[ServerConfig](name + ".server")
      ui        <- BlazeUserInteraction()
      auth      = new AuthModule(config)(ui)
      codetoken <- auth.authenticate
      client    <- BlazeJsonClient
      clock     = new LocalClockTask
      access    = new AccessModule(config)(client, clock)
      token     <- access.access(codetoken)
      _         <- putStrLn(s"got token: $token")
    } yield ()
  }.run

where .readConfig and .putStrLn are library calls. We can think of them as Task interpreters of algebras that read the application’s runtime configuration and print a string to the screen.

But this code does not compile, for two reasons. Firstly, we need to consider what our monad stack is going to be. The BlazeJsonClient constructor returns a Task but the JsonClient methods require a MonadError[..., JsonClient.Error]. This can be provided by EitherT. We can therefore construct the common monad stack for the entire for comprehension as

  type H[a] = EitherT[Task, JsonClient.Error, a]

Unfortunately this means we must .liftM everything that returns a Task, which adds quite a lot of boilerplate. Unfortunately, the .liftM method does not take a type of shape H[_], it takes a type of shape H[_[_], _], so we need to create a type alias to help out the compiler:

  type HT[f[_], a] = EitherT[f, JsonClient.Error, a]
  type H[a]        = HT[Task, a]

we can now call .liftM[HT] when we receive a Task

  for {
    config    <- readConfig[ServerConfig](name + ".server").liftM[HT]
    ui        <- BlazeUserInteraction().liftM[HT]
    auth      = new AuthModule(config)(ui)
    codetoken <- auth.authenticate.liftM[HT]
    client    <- BlazeJsonClient[H].liftM[HT]
    clock     = new LocalClockTask
    access    = new AccessModule(config)(client, clock)
    token     <- access.access(codetoken)
    _         <- putStrLn(s"got token: $token").liftM[HT]
  } yield ()

But this still doesn’t compile, because clock is a LocalClock[Task] and AccessModule requires a LocalClock[H]. We simply add the necessary .liftM boilerplate to the companion of LocalClock and can then lift the entire algebra

  clock     = LocalClock.liftM[Task, HT](new LocalClockTask)

and now everything compiles!

The second approach to wiring up an application is more complex, but necessary when there are conflicts in the monad stack, such as we need in our main loop. If we perform an analysis we find that the following are needed:

MonadError[F, JsonClient.Error] for uses of the JsonClient
MonadState[F, BearerToken] for uses of the OAuth2JsonClient
MonadState[F, WorldView] for our main loop

Unfortunately, the two MonadState requirements are in conflict. We could construct a data type that captures all the state of the program, but that is a leaky abstraction. Instead, we nest our for comprehensions and provide state where it is needed.

We now need to think about three layers, which we will call F, G, H

  type HT[f[_], a] = EitherT[f, JsonClient.Error, a]
  type GT[f[_], a] = StateT[f, BearerToken, a]
  type FT[f[_], a] = StateT[f, WorldView, a]
  
  type H[a]        = HT[Task, a]
  type G[a]        = GT[H, a]
  type F[a]        = FT[G, a]

Now some bad news about .liftM… it only works for one layer at a time. If we have a Task[A] and we want an F[A], we have to go through each step and type ta.liftM[HT].liftM[GT].liftM[FT]. Likewise, when lifting algebras we have to call liftM multiple times. To get a Sleep[F], we have to type

  val S: Sleep[F] = {
    import Sleep.liftM
    liftM(liftM(liftM(new SleepTask)))
  }

and to get a LocalClock[G] we do two lifts

  val T: LocalClock[G] = {
    import LocalClock.liftM
    liftM(liftM(new LocalClockTask))
  }

The main application then becomes

  def agents(bearer: BearerToken): Task[Unit] = {
    ...
    for {
      config <- readConfig[AppConfig]
      blaze  <- BlazeJsonClient[G]
      _ <- {
        val bearerClient = new BearerJsonClientModule(bearer)(blaze)
        val drone        = new DroneModule(bearerClient)
        val refresh      = new RefreshModule(config.machines.server)(blaze, T)
        val oauthClient =
          new OAuth2JsonClientModule(config.machines.token)(blaze, T, refresh)
        val machines = new GoogleMachinesModule(oauthClient)
        val agents   = new DynAgentsModule(drone, machines)
        for {
          start <- agents.initial
          _ <- {
            val fagents = DynAgents.liftM[G, FT](agents)
            step(fagents, S).forever[Unit]
          }.run(start)
        } yield ()
      }.eval(bearer).run
    } yield ()
  }

where the outer loop is using Task, the middle loop is using G, and the inner loop is using F.

The calls to .run(start) and .eval(bearer) are where we provide the initial state for the StateT parts of our application. The .run is to reveal the EitherT error.

We can call these two application entry points from our SafeApp

  object Main extends SafeApp {
    def run(args: List[String]): IO[Void, ExitStatus] = {
      if (args.contains("--machines")) auth("machines")
      else agents(BearerToken("<invalid>", Epoch(0)))
    }.attempt[Void].map {
      case \/-(_)   => ExitStatus.ExitNow(0)
      case -\/(err) => ExitStatus.ExitNow(1)
    }
  }

and then run it!

  > runMain fommil.dda.Main --machines
  [info] Running (fork) fommil.dda.Main --machines
  ...
  [info] Service bound to address /127.0.0.1:46687
  ...
  [info] Created new window in existing browser session.
  ...
  [info] Headers(Host: localhost:46687, Connection: keep-alive, User-Agent: Mozilla/5.0 ...)
  ...
  [info] POST https://www.googleapis.com/oauth2/v4/token
  ...
  [info] got token: "<elided>"

Yay!

9.3 Blaze

We implement the HTTP client and server with the third party library http4s. The interpreters for their client and server algebras are called Blaze.

We need the following dependencies

  val http4sVersion = "0.18.16"
  libraryDependencies ++= Seq(
    "org.http4s"            %% "http4s-dsl"          % http4sVersion,
    "org.http4s"            %% "http4s-blaze-server" % http4sVersion,
    "org.http4s"            %% "http4s-blaze-client" % http4sVersion
  )

9.3.1 `BlazeJsonClient`

We will need some imports

  import org.http4s
  import org.http4s.{ EntityEncoder, MediaType }
  import org.http4s.headers.`Content-Type`
  import org.http4s.client.Client
  import org.http4s.client.blaze.{ BlazeClientConfig, Http1Client }

The Client module can be summarised as

  final class Client[F[_]](
    val shutdown: F[Unit]
  )(implicit F: MonadError[F, Throwable]) {
    def fetch[A](req: Request[F])(f: Response[F] => F[A]): F[A] = ...
    ...
  }

where Request and Response are data types:

  final case class Request[F[_]](
    method: Method
    uri: Uri,
    headers: Headers,
    body: EntityBody[F]
  ) {
    def withBody[A](a: A)
                   (implicit F: Monad[F], A: EntityEncoder[F, A]): F[Request[F]] = ...
    ...
  }
  
  final case class Response[F[_]](
    status: Status,
    headers: Headers,
    body: EntityBody[F]
  )

made of

  final case class Headers(headers: List[Header])
  final case class Header(name: String, value: String)
  
  final case class Uri( ... )
  object Uri {
    // not total, only use if `s` is guaranteed to be a URL
    def unsafeFromString(s: String): Uri = ...
    ...
  }
  
  final case class Status(code: Int) {
    def isSuccess: Boolean = ...
    ...
  }
  
  type EntityBody[F[_]] = fs2.Stream[F, Byte]

The EntityBody type is an alias to Stream from the fs2 library. The Stream data type can be thought of as an effectful, lazy, pull-based stream of data. It is implemented as a Free monad with exception catching and interruption. Stream takes two type parameters: an effect type and a content type, and has an efficient internal representation for batching the data. For example, although we are using Stream[F, Byte], it is actually wrapping the raw Array[Byte] that arrives over the network.

We need to convert our header and URL representations into the versions required by http4s:

  def convert(headers: IList[(String, String)]): http4s.Headers =
    http4s.Headers(
      headers.foldRight(List[http4s.Header]()) {
        case ((key, value), acc) => http4s.Header(key, value) :: acc
      }
    )
  
  def convert(uri: String Refined Url): http4s.Uri =
    http4s.Uri.unsafeFromString(uri.value) // we already validated our String

Both our .get and .post methods require a conversion from the http4s Response type into an A. We can factor this out into a single function, .handler

  import JsonClient.Error
  
  final class BlazeJsonClient[F[_]] private (H: Client[Task])(
    implicit
    F: MonadError[F, Error],
    I: MonadIO[F, Throwable]
  ) extends JsonClient[F] {
    ...
    def handler[A: JsDecoder](resp: http4s.Response[Task]): Task[Error \/ A] = {
      if (!resp.status.isSuccess)
        Task.now(JsonClient.ServerError(resp.status.code).left)
      else
        for {
          text <- resp.body.through(fs2.text.utf8Decode).compile.foldMonoid
          res = JsParser(text)
            .flatMap(_.as[A])
            .leftMap(JsonClient.DecodingError(_))
        } yield res
    }
  }

The .through(fs2.text.utf8Decode) is to convert a Stream[Task, Byte] into a Stream[Task, String], with .compile.foldMonoid interpreting it with our Task and combining all the parts using the Monoid[String], giving us a Task[String].

We then parse the string as JSON and use the JsDecoder[A] to create the required output.

This is our implementation of .get

  def get[A: JsDecoder](
    uri: String Refined Url,
    headers: IList[(String, String)]
  ): F[A] =
    I.liftIO(
        H.fetch(
          http4s.Request[Task](
            uri = convert(uri),
            headers = convert(headers)
          )
        )(handler[A])
      )
      .emap(identity)

.get is all plumbing: we convert our input types into the http4s.Request, then call .fetch on the Client with our handler. This gives us back a Task[Error \/ A], but we need to return a F[A]. Therefore we use the MonadIO.liftIO to create a F[Error \/ A] and then .emap to push the error into the F.

Unfortunately, if we try to compile this code it will fail. The error will look something like

  [error] BlazeJsonClient.scala:95:64: could not find implicit value for parameter
  [error]  F: cats.effect.Sync[scalaz.ioeffect.Task]

Basically, something about a missing cat.

The reason for this failure is that http4s is using a different core FP library, not Scalaz. Thankfully, scalaz-ioeffect provides a compatibility layer and the shims project provides seamless (until it isn’t) implicit conversions. We can get our code to compile with these dependencies:

  libraryDependencies ++= Seq(
    "com.codecommit" %% "shims"                % "1.4.0",
    "org.scalaz"     %% "scalaz-ioeffect-cats" % "2.10.1"
  )

and these imports

  import shims._
  import scalaz.ioeffect.catz._

The implementation of .post is similar but we must also provide an instance of

  EntityEncoder[Task, String Refined UrlEncoded]

Thankfully, the EntityEncoder typeclass provides conveniences to let us derive one from the existing String encoder

  implicit val encoder: EntityEncoder[Task, String Refined UrlEncoded] =
    EntityEncoder[Task, String]
      .contramap[String Refined UrlEncoded](_.value)
      .withContentType(
        `Content-Type`(MediaType.`application/x-www-form-urlencoded`)
      )

The only difference between .get and .post is the way we construct our http4s.Request

  http4s.Request[Task](
    method = http4s.Method.POST,
    uri = convert(uri),
    headers = convert(headers)
  )
  .withBody(payload.toUrlEncoded)

and the final piece is the constructor, which is a case of calling Http1Client with a configuration object

  object BlazeJsonClient {
    def apply[F[_]](
      implicit
      F: MonadError[F, JsonClient.Error],
      I: MonadIO[F, Throwable]
    ): Task[JsonClient[F]] =
      Http1Client(BlazeClientConfig.defaultConfig).map(new BlazeJsonClient(_))
  }

9.3.2 `BlazeUserInteraction`

We need to spin up an HTTP server, which is a lot easier than it sounds. First, the imports

  import org.http4s._
  import org.http4s.dsl._
  import org.http4s.server.Server
  import org.http4s.server.blaze._

We need to create a dsl for our effect type, which we then import

  private val dsl = new Http4sDsl[Task] {}
  import dsl._

Now we can use the http4s dsl to create HTTP endpoints. Rather than describe everything that can be done, we will simply implement the endpoint which is similar to any of other HTTP DSLs

  private object Code extends QueryParamDecoderMatcher[String]("code")
  private val service: HttpService[Task] = HttpService[Task] {
    case GET -> Root :? Code(code) => ...
  }

The return type of each pattern match is a Task[Response[Task]]. In our implementation we want to take the code and put it into the ptoken promise:

  final class BlazeUserInteraction private (
    pserver: Promise[Throwable, Server[Task]],
    ptoken: Promise[Throwable, String]
  ) extends UserInteraction[Task] {
    ...
    private val service: HttpService[Task] = HttpService[Task] {
      case GET -> Root :? Code(code) =>
        ptoken.complete(code) >> Ok(
          "That seems to have worked, go back to the console."
        )
    }
    ...
  }

but the definition of our services routes is not enough, we need to launch a server, which we do with BlazeBuilder

  private val launch: Task[Server[Task]] =
    BlazeBuilder[Task].bindHttp(0, "localhost").mountService(service, "/").start

Binding to port 0 makes the operating system assign an ephemeral port. We can discover which port it is actually running on by querying the server.address field.

Our implementation of the .start and .stop methods is now straightforward

  def start: Task[String Refined Url] =
    for {
      server  <- launch
      updated <- pserver.complete(server)
      _ <- if (updated) Task.unit
           else server.shutdown *> fail("server was already running")
    } yield mkUrl(server)
  
  def stop: Task[CodeToken] =
    for {
      server <- pserver.get
      token  <- ptoken.get
      _      <- IO.sleep(1.second) *> server.shutdown
    } yield CodeToken(token, mkUrl(server))
  
  private def mkUrl(s: Server[Task]): String Refined Url = {
    val port = s.address.getPort
    Refined.unsafeApply(s"http://localhost:${port}/")
  }
  private def fail[A](s: String): String =
    Task.fail(new IOException(s) with NoStackTrace)

The 1.second sleep is necessary to avoid shutting down the server before the response is sent back to the browser. IO doesn’t mess around when it comes to concurrency performance!

Finally, to create a BlazeUserInteraction, we just need the two uninitialised promises

  object BlazeUserInteraction {
    def apply(): Task[BlazeUserInteraction] = {
      for {
        p1 <- Promise.make[Void, Server[Task]].widenError[Throwable]
        p2 <- Promise.make[Void, String].widenError[Throwable]
      } yield new BlazeUserInteraction(p1, p2)
    }
  }

We could use IO[Void, ?] instead, but since the rest of our application is using Task (i.e. IO[Throwable, ?]), we .widenError to avoid introducing any boilerplate that would distract us.

9.4 Thank You

And that is it! Congratulations on reaching the end.

If you learnt something from this book, then please tell your friends. This book does not have a marketing department, so word of mouth is the only way that readers find out about it.

Get involved with Scalaz by joining the gitter chat room. From there you can ask for advice, help newcomers (you’re an expert now), and contribute to the next release.

Typeclass Cheatsheet

Typeclass	Method	From	Given	To
`InvariantFunctor`	`xmap`	`F[A]`	`A => B, B => A`	`F[B]`
`Contravariant`	`contramap`	`F[A]`	`B => A`	`F[B]`
`Functor`	`map`	`F[A]`	`A => B`	`F[B]`
`Apply`	`ap` / `<*>`	`F[A]`	`F[A => B]`	`F[B]`
	`apply2`	`F[A], F[B]`	`(A, B) => C`	`F[C]`
`Alt`	`altly2`	`F[A], F[B]`	`(A \/ B) => C`	`F[C]`
`Divide`	`divide2`	`F[A], F[B]`	`C => (A, B)`	`F[C]`
`Decidable`	`choose2`	`F[A], F[B]`	`C => (A \/ B)`	`F[C]`
`Bind`	`bind` / `>>=`	`F[A]`	`A => F[B]`	`F[B]`
	`join`	`F[F[A]]`		`F[A]`
`Cobind`	`cobind`	`F[A]`	`F[A] => B`	`F[B]`
	`cojoin`	`F[A]`		`F[F[A]]`
`Applicative`	`point`	`A`		`F[A]`
`Divisible`	`conquer`			`F[A]`
`Comonad`	`copoint`	`F[A]`		`A`
`Semigroup`	`append`	`A, A`		`A`
`Plus`	`plus` / `<+>`	`F[A], F[A]`		`F[A]`
`MonadPlus`	`withFilter`	`F[A]`	`A => Boolean`	`F[A]`
`Align`	`align`	`F[A], F[B]`		`F[A \&/ B]`
	`merge`	`F[A], F[A]`		`F[A]`
`Zip`	`zip`	`F[A], F[B]`		`F[(A, B)]`
`Unzip`	`unzip`	`F[(A, B)]`		`(F[A], F[B])`
`Cozip`	`cozip`	`F[A \/ B]`		`F[A] \/ F[B]`
`Foldable`	`foldMap`	`F[A]`	`A => B`	`B`
	`foldMapM`	`F[A]`	`A => G[B]`	`G[B]`
`Traverse`	`traverse`	`F[A]`	`A => G[B]`	`G[F[B]]`
	`sequence`	`F[G[A]]`		`G[F[A]]`
`Equal`	`equal` / `===`	`A, A`		`Boolean`
`Show`	`shows`	`A`		`String`
`Bifunctor`	`bimap`	`F[A, B]`	`A => C, B => D`	`F[C, D]`
	`leftMap`	`F[A, B]`	`A => C`	`F[C, B]`
	`rightMap`	`F[A, B]`	`B => C`	`F[A, C]`
`Bifoldable`	`bifoldMap`	`F[A, B]`	`A => C, B => C`	`C`
(with `MonadPlus`)	`separate`	`F[G[A, B]]`		`(F[A], F[B])`
`Bitraverse`	`bitraverse`	`F[A, B]`	`A => G[C], B => G[D]`	`G[F[C, D]]`
	`bisequence`	`F[G[A], G[B]]`		`G[F[A, B]]`

Haskell

Scalaz documentation often cites libraries or papers written in the Haskell programming language. In this short chapter, we will learn enough Haskell to be able to understand the source material, and to attend Haskell talks at functional programming conferences.

Data

Haskell has a very clean syntax for ADTs. This is a linked list structure:

  data List a = Nil | Cons a (List a)

List is a type constructor, a is the type parameter, | separates the data constructors, which are: Nil the empty list and a Cons cell. Cons takes two parameters, which are separated by whitespace: no commas and no parameter brackets.

There is no subtyping in Haskell, so there is no such thing as the Nil type or the Cons type: both construct a List.

Roughly translated to Scala:

  sealed abstract class List[A]
  object Nil {
    def apply[A]: List[A] = ...
    def unapply[A](as: List[A]): Option[Unit] = ...
  }
  object Cons {
    def apply[A](head: A, tail: List[A]): List[A] = ...
    def unapply[A](as: List[A]): Option[(A, List[A])] = ...
  }

i.e. the type constructor is like sealed abstract class, and each data constructor is .apply / .unapply. Note that Scala does not perform exhaustive pattern matches on this encoding, which is why Scalaz does not use it.

We can use infix, a nicer definition might use the symbol :. instead of Cons

  data List t = Nil | t :. List t
  infixr 5 :.

where we specify a fixity, which can be infix, infixl or infixr for no, left, and right associativity, respectively. A number from 0 (loose) to 9 (tight) specifies precedence. We can now create a list of integers by typing

  1 :. 2 :. Nil

Haskell already comes with a linked list, which is so fundamental to functional programming that it gets language-level square bracket syntax [a]

  data [] a = [] | a : [a]
  infixr 5 :

and a convenient multi-argument value constructor: [1, 2, 3] instead of 1 : 2 : 3 : [].

Ultimately our ADTs need to hold primitive values. The most common primitive data types are:

Char a unicode character
Text for blocks of unicode text
Int a machine dependent, fixed precision signed integer
Word an unsigned Int, and fixed size Word8 / Word16 / Word32 / Word64
Float / Double IEEE single and double precision numbers
Integer / Natural arbitrary precision signed / non-negative integers
(,) tuples, from 0 (also known as unit) to 62 fields
IO the inspiration for Scalaz’s IO, implemented in the runtime.

with honorary mentions for

  data Bool       = True | False
  data Maybe a    = Nothing | Just a
  data Either a b = Left a  | Right b
  data Ordering   = LT | EQ | GT

Like Scala, Haskell has type aliases: an alias or its expanded form can be used interchangeably. For legacy reasons, String is defined as a linked list of Char

  type String = [Char]

which is very inefficient and we always want to use Text instead.

Finally we can define field names on ADTs using record syntax, which means we contain the data constructors in curly brackets and use double colon type annotations to indicate the types

  -- raw ADT
  data Resource = Human Int String
  data Company  = Company String [Resource]
  
  -- with record syntax
  data Resource = Human
                  { serial    :: Int
                  , humanName :: String
                  }
  data Company  = Company
                  { companyName :: String
                  , employees   :: [Resource]
                  }

Note that the Human data constructor and Resource type do not have the same name. Record syntax generates the equivalent of a field accessor and a copy method.

  -- construct
  adam = Human 0 Adam
  -- field access
  serial adam
  -- copy
  eve = adam { humanName = "Eve" }

A more efficient alternative to single field data definitions is to use a newtype, which has no runtime overhead:

  newtype Alpha = Alpha { underlying :: Double }

equivalent to extends AnyVal but without the caveats.

A limitation of Haskell’s record syntax is that a field name cannot be used in different data types. However, we can workaround this by enabling a LANGUAGE extension, allowing us to use name in both Human and Company:

  {-# LANGUAGE DuplicateRecordFields #-}
  
  data Resource = Human
                  { serial :: Int
                  , name   :: String
                  }
  data Company  = Company
                  { name      :: String
                  , employees :: [Resource]
                  }

There are a lot of language extensions and it is not uncommon to have 20 or more in a small project. Haskell is extremely conservative and new language features are opt-in for a long period of time before they can be accepted into the language standard.

Functions

Although not necessary, it is good practice to explicitly write the type signature of a function: its name followed by its type. For example foldl specialised for a linked list

  foldl :: (b -> a -> b) -> b -> [a] -> b

All functions are curried in Haskell, each parameter is separated by a -> and the final type is the return type. This is equivalent to the following Scala signature:

  def foldLeft[A, B](f: (B, A) => B)(b: B)(as: List[A]): B

Some observations:

there is no keyword
there is no need to declare the types that are introduced
there is no need to name the parameters

which makes for terse code.

Infix functions are defined in parentheses and need a fixity definition:

  (++) :: [a] -> [a] -> [a]
  infixr 5 ++

Regular functions can be called in infix position by surrounding their name with backticks. The following are equivalent:

  a `foo` b
  foo a b

An infix function can be called like a regular function if we keep it surrounded by brackets, and can be curried on either the left or the right, often giving different semantics:

  invert = (1.0 /)
  half   = (/ 2.0)

Functions are typically written with the most general parameter first, to enable maximum reuse of the curried forms.

The definition of a function may use pattern matching, with one line per case. This is where we may name the parameters, using the data constructors to extract parameters much like a Scala case clause:

  fmap :: (a -> b) -> Maybe a -> Maybe b
  fmap f (Just a) = Just (f a)
  fmap _ Nothing  = Nothing

Underscores are a placeholder for ignored parameters and function names can be in infix position:

  (<+>) :: Maybe a -> Maybe a -> Maybe a
  Just a <+> _      = Just a
  Empty  <+> Just a = Just a
  Empty  <+> Empty  = Empty

We can define anonymous lambda functions with a backslash, which looks like the Greek letter λ. The following are equivalent:

  (*)
  (\a1 -> \a2 -> a1 * a2)
  (\a1 a2     -> a1 * a2)

Pattern matched Haskell functions are just syntax sugar for nested lambda functions. Consider a simple function that creates a tuple when given three inputs:

  tuple :: a -> b -> c -> (a, b, c)

The implementation

  tuple a b c = (a, b, c)

desugars into

  tuple = \a -> \b -> \c -> (a, b, c)

In the body of a function we can create local value bindings with let or where clauses. The following are equivalent definitions of map for a linked list (an apostrophe is a valid identifier name):

  map :: (a -> b) -> [a] -> [b]
  
  -- explicit
  map f as = foldr map' [] as
             where map' a bs = f a : bs
  
  -- terser, making use of currying
  map f    = foldr map' []
             where map' a = (f a :)
  
  -- let binding
  map f    = let map' a = (f a :)
             in foldr map' []
  
  -- actual implementation
  map _ []       = []
  map f (x : xs) = f x : map f xs

if / then / else are keywords for conditional statements:

  filter :: (a -> Bool) -> [a] -> [a]
  filter _ [] = []
  filter f (head : tail) = if f head
                           then head : filter f tail
                           else filter f tail

An alternative style is to use case guards

  filter f (head : tail) | f head    = head : filter f tail
                         | otherwise = filter f tail

Pattern matching on any term is with case ... of

  unfoldr :: (a -> Maybe (b, a)) -> a -> [b]
  unfoldr f b = case f b of
                  Just (b', a') -> b' : unfoldr f a'
                  Nothing       -> []

Guards can be used within matches. For example, say we want to special case zeros:

  unfoldrInt :: (a -> Maybe (Int, a)) -> a -> [Int]
  unfoldrInt f b = case f b of
                     Just (i, a') | i == 0    -> unfoldrInt f a'
                                  | otherwise -> i : unfoldrInt f a'
                     Nothing                  -> []

Finally, two functions that are worth noting are ($) and (.)

  -- application operator
  ($) :: (a -> b) -> a -> b
  infixr 0
  
  -- function composition
  (.) :: (b -> c) -> (a -> b) -> a -> c
  infixr 9

Both of these functions are stylistic alternatives to nested parentheses.

The following are equivalent:

  Just (f a)
  Just $ f a

as are

  putStrLn (show (1 + 1))
  putStrLn $ show $ 1 + 1

There is a tendency to prefer function composition with . instead of multiple $

  (putStrLn . show) $ 1 + 1

Typeclasses

To define a typeclass we use the class keyword, followed by the name of the typeclass, its type parameter, then the required members in a where clause.

If there are dependencies between typeclasses, i.e. Applicative requires a Functor to exist, we call this a constraint and use => notation:

  class Functor f where
    (<$>) :: (a -> b) -> f a -> f b
    infixl 4 <$>
  
  class Functor f => Applicative f where
    pure  :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b
    infixl 4 <*>
  
  class Applicative f => Monad f where
    (=<<) :: (a -> f b) -> f a -> f b
    infixr 1 =<<

We provide an implementation of a typeclass with the instance keyword. If we wish to repeat the type signature on instance functions, useful for clarity, we must enable the InstanceSigs language extension.

  {-# LANGUAGE InstanceSigs #-}
  
  data List a = Nil | a :. List a
  
  -- defined elsewhere
  (++) :: List a -> List a -> List a
  map :: (a -> b) -> List a -> List b
  flatMap :: (a -> List b) -> List a -> List b
  foldLeft :: (b -> a -> b) -> b -> List a -> b
  
  instance Functor List where
    (<$>) :: (a -> b) -> List a -> List b
    f <$> as = map f as
  
  instance Applicative List where
    pure a = a :. Nil
  
    Nil <*> _  = Nil
    fs  <*> as = foldLeft (++) Nil $ (<$> as) <$> fs
  
  instance Monad List where
    f =<< list = flatMap f list

If we have a typeclass constraint in a function, we use the same => notation. For example we can define something similar to Scalaz’s Apply.apply2

  apply2 :: Applicative f => (a -> b -> c) -> f a -> f b -> f c
  apply2 f fa fb = f <$> fa <*> fb

Since we have introduced Monad, it is a good time to introduce do notation, which was the inspiration for Scala’s for comprehensions:

  do
    a <- f
    b <- g
    c <- h
    pure (a, b, c)

desugars to

  f >>= \a ->
    g >>= \b ->
      h >>= \c ->
        pure (a, b, c)

where >>= is =<< with parameters flipped

  (>>=) :: Monad f => f a -> (a -> f b) -> f b
  (>>=) = flip (=<<)
  infixl 1 >>=
  
  -- from the stdlib
  flip :: (a -> b -> c) -> b -> a -> c

Unlike Scala, we do not need to bind unit values, or provide a yield if we are returning (). For example

  for {
    _ <- putStr("hello")
    _ <- putStr(" world")
  } yield ()

translates to

  do putStr "hello"
     putStr " world"

Non-monadic values can be bound with the let keyword:

  nameReturn :: IO String
  nameReturn = do putStr "What is your first name? "
                  first <- getLine
                  putStr "And your last name? "
                  last  <- getLine
                  let full = first ++ " " ++ last
                  putStrLn ("Pleased to meet you, " ++ full ++ "!")
                  pure full

Finally, Haskell has typeclass derivation with the deriving keyword, the inspiration for @scalaz.deriving. Defining the derivation rules is an advanced topic, but it is easy to derive a typeclass for an ADT:

  data List a = Nil | a :. List a
                deriving (Eq, Ord)

Records of Functions

In Scala, typeclasses and algebras are both defined as a trait interface. Typeclasses are injected by the implicit feature and algebras are passed as explicit parameters. There is no language-level support in Haskell for algebras: they are just data!

Consider Console from the introduction. We can rewrite it into Haskell:

  data Console m = Console
                    { println :: Text -> m ()
                    , readln  :: m Text
                    }

with business logic using a Monad constraint

  echo :: (Monad m) => Console m -> m ()
  echo c = do line <- readln c
              println c line

A production implementation of Console would likely have type Console IO. The Scalaz liftIO function is inspired by a Haskell function of the same name and can lift Console IO into any Advanced Monad stack.

Two additional language extensions make the business logic even cleaner. For example, RecordWildCards allows us to import all the fields of a data type by using {..}:

  echo :: (Monad m) => Console m -> m ()
  echo Console{..} = do line <- readln
                        println line

NamedFieldPuns requires each imported field to be listed explicitly, which is more boilerplate but makes the code easier to read:

  echo :: (Monad m) => Console m -> m ()
  echo Console{readln, println} = do line <- readln
                                     println line

Whereas in Scala this encoding may be called Finally Tagless, in Haskell it is known as MTL style with records of functions. Without going into details, some Scala developers didn’t understand a research paper about the performance benefits of Generalised ADTs in Haskell.

An alternative to MTL style are Extensible Effects, also known as Free Monad style.

Modules

Haskell source code is arranged into hierarchical modules with the restriction that all contents of a module must live in a single file. The top of a file declares the module name

  module Silly.Tree where

A convention is to use directories on disk to organise the code, so this file would go into Silly/Tree.hs.

By default all symbols in the file are exported but we can choose to export specific members, for example the Tree type and data constructors, and a fringe function, omitting sapling:

  module Silly.Tree (Tree(..), fringe) where
  
  data Tree a = Leaf a | Branch (Tree a) (Tree a)
  
  fringe :: Tree a -> [a]
  fringe (Leaf x)            = [x]
  fringe (Branch left right) = fringe left ++ fringe right
  
  sapling :: Tree String
  sapling = Leaf ""

Interestingly, we can export symbols that are imported into the module, allowing library authors to package up their entire API into a single module, regardless of how it is implemented.

In a different file we can import all the exported members from Silly.Tree

  import Silly.Tree

which is roughly equivalent to Scala’s import silly.tree._ syntax. If we want to restrict the symbols that we import we can provide an explicit list in parentheses after the import

  import Silly.Tree (Tree, fringe)

Here we only import the Tree type constructor (not the data constructors) and the fringe function. If we want to import all the data constructors (and pattern matchers) we can use Tree(..). If we only want to import the Branch constructor we can list it explicitly:

  import Silly.Tree (Tree(Branch), fringe)

If we have a name collision on a symbol we can use a qualified import, with an optional list of symbols to import

  import qualified Silly.Tree (fringe)

and now to call the fringe function we have to type Silly.Tree.fringe instead of just fringe. We can change the name of the module when importing it

  import qualified Silly.Tree as T

The fringe function is now accessed by T.fringe.

Alternatively, rather than select what we want to import, we can choose what not to import

  import Silly.Tree hiding (fringe)

By default the Prelude module is implicitly imported but if we add an explicit import from the Prelude module, only our version is used. We can use this technique to hide unsafe legacy functions

  import Prelude hiding ((!!), head)

or use a custom prelude and disable the default prelude with the NoImplicitPrelude language extension.

Evaluation

Haskell compiles to native code, there is no virtual machine, but there is a garbage collector. A fundamental aspect of the runtime is that all parameters are lazily evaluated by default. Haskell treats all terms as a promise to provide a value when needed, called a thunk. Thunks get reduced only as much as necessary to proceed, no more.

A huge advantage of lazy evaluation is that it is much harder to trigger a stack overflow! A disadvantage is that there is an overhead compared to strict evaluation, which is why Haskell allows us to opt in to strict evaluation on a per parameter basis.

Haskell is also nuanced about what strict evaluation means: a term is said to be in weak head normal-form (WHNF) if the outermost code blocks cannot be reduced further, and normal form if the term is fully evaluated. Scala’s default evaluation strategy roughly corresponds to normal form.

For example, these terms are normal form:

  42
  (2, "foo")
  \x -> x + 1

whereas these are not in normal form (they can be reduced further):

  1 + 2            -- reduces to 3
  (\x -> x + 1) 2  -- reduces to 3
  "foo" ++ "bar"   -- reduces to "foobar"
  (1 + 1, "foo")   -- reduces to (2, "foo")

The following terms are in WHNF because the outer code cannot be reduced further (even though the inner parts can be):

  (1 + 1, "foo")
  \x -> 2 + 2
  'f' : ("oo" ++ "bar")

and the following are not in WHNF

  1 + 1              -- reduces to 2
  (\x y -> x + y) 2  -- reduces to \y -> 2 + y
  "foo" ++ "bar"     -- reduces to "foobar"

The default evaluation strategy is to perform no reductions when passing a term as a parameter. Language level support allows us to request WHNF for any term with ($!)

  -- evaluates `a` to WHNF, then calls the function with that value
  ($!) :: (a -> b) -> a -> b
  infixr 0

We can use an exclamation mark ! on data parameters

  data StrictList t = StrictNil | !t :. !(StrictList t)
  
  data Employee = Employee
                    { name :: !Text
                    , age :: !Int
                    }

The StrictData language extension enables strict parameters for all data in the module.

Another extension, BangPatterns, allows ! to be used on the arguments of functions. The Strict language extension makes all functions and data parameters in the module strict by default.

Going to the extreme we can use ($!!) and the NFData typeclass for normal form evaluation:

  class NFData a where
    rnf :: a -> ()
  
  ($!!) :: (NFData a) => (a -> b) -> a -> b

which is subject to the availability of an NFData instance.

The cost of strictness is that Haskell behaves like any other strict language and may perform unnecessary work. Opting in to strictness must therefore be done with great care, and only for measured performance improvements. If in doubt, be lazy and stick with the defaults.

Next Steps

Haskell is a faster, safer and simpler language than Scala and has proven itself in industry. Consider taking the data61 course on functional programming, and ask questions in the #qfpl chat room on freenode.net.

Some additional learning materials are:

Programming in Haskell to learn Haskell from first principles.
Parallel and Concurrent Programming in Haskell and What I Wish I Knew When Learning Haskell for intermediate wisdom.
Glasgow Haskell Compiler User Guide and HaskellWiki for the cold hard facts.
Eta, i.e. Haskell for the JVM.

If you enjoy using Haskell and understand the value that it would bring to your business, then tell your managers! That way, the small percentage of managers who commission Haskell projects will be able to attract functional programming talent from the many teams who do not, and everybody will be happy.

Third Party Licenses

Some of the source code in this book has been copied from free / libre software projects. The license of those projects require that the following texts are distributed with the source that is presented in this book.

Scala License

  Copyright (c) 2002-2017 EPFL
  Copyright (c) 2011-2017 Lightbend, Inc.
  
  All rights reserved.
  
  Redistribution and use in source and binary forms, with or without modification,
  are permitted provided that the following conditions are met:
  
    * Redistributions of source code must retain the above copyright notice,
      this list of conditions and the following disclaimer.
    * Redistributions in binary form must reproduce the above copyright notice,
      this list of conditions and the following disclaimer in the documentation
      and/or other materials provided with the distribution.
    * Neither the name of the EPFL nor the names of its contributors
      may be used to endorse or promote products derived from this software
      without specific prior written permission.
  
  THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS
  "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT
  LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR
  A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR
  CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL,
  EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO,
  PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR
  PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF
  LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING
  NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS
  SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.

Scalaz License

  Copyright (c) 2009-2014 Tony Morris, Runar Bjarnason, Tom Adams,
                          Kristian Domagala, Brad Clow, Ricky Clarkson,
                          Paul Chiusano, Trygve Laugstøl, Nick Partridge,
                          Jason Zaugg
  All rights reserved.
  
  Redistribution and use in source and binary forms, with or without
  modification, are permitted provided that the following conditions
  are met:
  
  1. Redistributions of source code must retain the above copyright
     notice, this list of conditions and the following disclaimer.
  2. Redistributions in binary form must reproduce the above copyright
     notice, this list of conditions and the following disclaimer in the
     documentation and/or other materials provided with the distribution.
  3. Neither the name of the copyright holder nor the names of
     its contributors may be used to endorse or promote products derived from
     this software without specific prior written permission.
  
  THIS SOFTWARE IS PROVIDED BY THE AUTHOR ``AS IS'' AND ANY EXPRESS OR
  IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES
  OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED.
  IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY DIRECT, INDIRECT,
  INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT
  NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE,
  DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY
  THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT
  (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF
  THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.