Leanpub: Publish Early, Publish Often

8. Typeclass Derivation

Typeclasses provide polymorphic functionality to our applications. But to use a typeclass we need instances for our business domain objects.

The creation of a typeclass instance from existing instances is known as typeclass derivation and is the topic of this chapter.

There are four approaches to typeclass derivation:

Manual instances for every domain object. This is infeasible for real world applications as it results in hundreds of lines of boilerplate for every line of a case class. It is useful only for educational purposes and adhoc performance optimisations.
Abstract over the typeclass by an existing scalaz typeclass. This is the approach of scalaz-deriving, producing automated tests and derivations for products and coproducts
Macros. However, writing a macro for each typeclass requires an advanced and experienced developer. Fortunately, Jon Pretty’s Magnolia library abstracts over hand-rolled macros with a simple API, centralising the complex interaction with the compiler.
Write a generic program using the Shapeless library. The implicit mechanism is a language within the Scala language and can be used to write programs at the type level.

In this chapter we will study increasingly complex typeclasses and their derivations. We will begin with scalaz-deriving as the most principled mechanism, repeating some lessons from Chapter 5 “Scalaz Typeclasses”, then Magnolia (the easiest to use), finishing with Shapeless (the most powerful) for typeclasses with complex derivation logic.

8.1 Running Examples

This chapter will show how to define derivations for five specific typeclasses. Each example exhibits a feature that can be generalised:

  @typeclass trait Equal[A]  {
    // type parameter is in contravariant (parameter) position
    @op("===") def equal(a1: A, a2: A): Boolean
  }
  
  // for requesting default values of a type when testing
  @typeclass trait Default[A] {
    // type parameter is in covariant (return) position
    def default: String \/ A
  }
  
  @typeclass trait Semigroup[A] {
    // type parameter is in both covariant and contravariant position (invariant)
    @op("|+|") def append(x: A, y: =>A): A
  }
  
  @typeclass trait JsEncoder[T] {
    // type parameter is in contravariant position and needs access to field names
    def toJson(t: T): JsValue
  }
  
  @typeclass trait JsDecoder[T] {
    // type parameter is in covariant position and needs access to field names
    def fromJson(j: JsValue): String \/ T
  }

There is a school of thought that says serialisation formats, such as JSON and XML, should not have typeclass encoders and decoders, because it can lead to typeclass decoherence (i.e. more than one encoder or decoder may exist for the same type). The alternative is to use algebras and avoid using the implicit language feature entirely.

Although it is possible to apply the techniques in this chapter to either typeclass or algebra derivation, the latter involves a lot more boilerplate. We therefore consciously choose to restrict our study to encoders and decoders that are coherent. As we will see later in this chapter, use-site automatic derivation with Magnolia and Shapeless, combined with limitations of the scala compiler’s implicit search, commonly leads to typeclass decoherence.

8.2 `scalaz-deriving`

The scalaz-deriving library is an extension to Scalaz and can be added to a project’s build.sbt with

  val derivingVersion = "1.0.0-RC8"
  libraryDependencies += "com.fommil" %% "scalaz-deriving" % derivingVersion

providing new typeclasses, shown below in relation to core scalaz typeclasses:

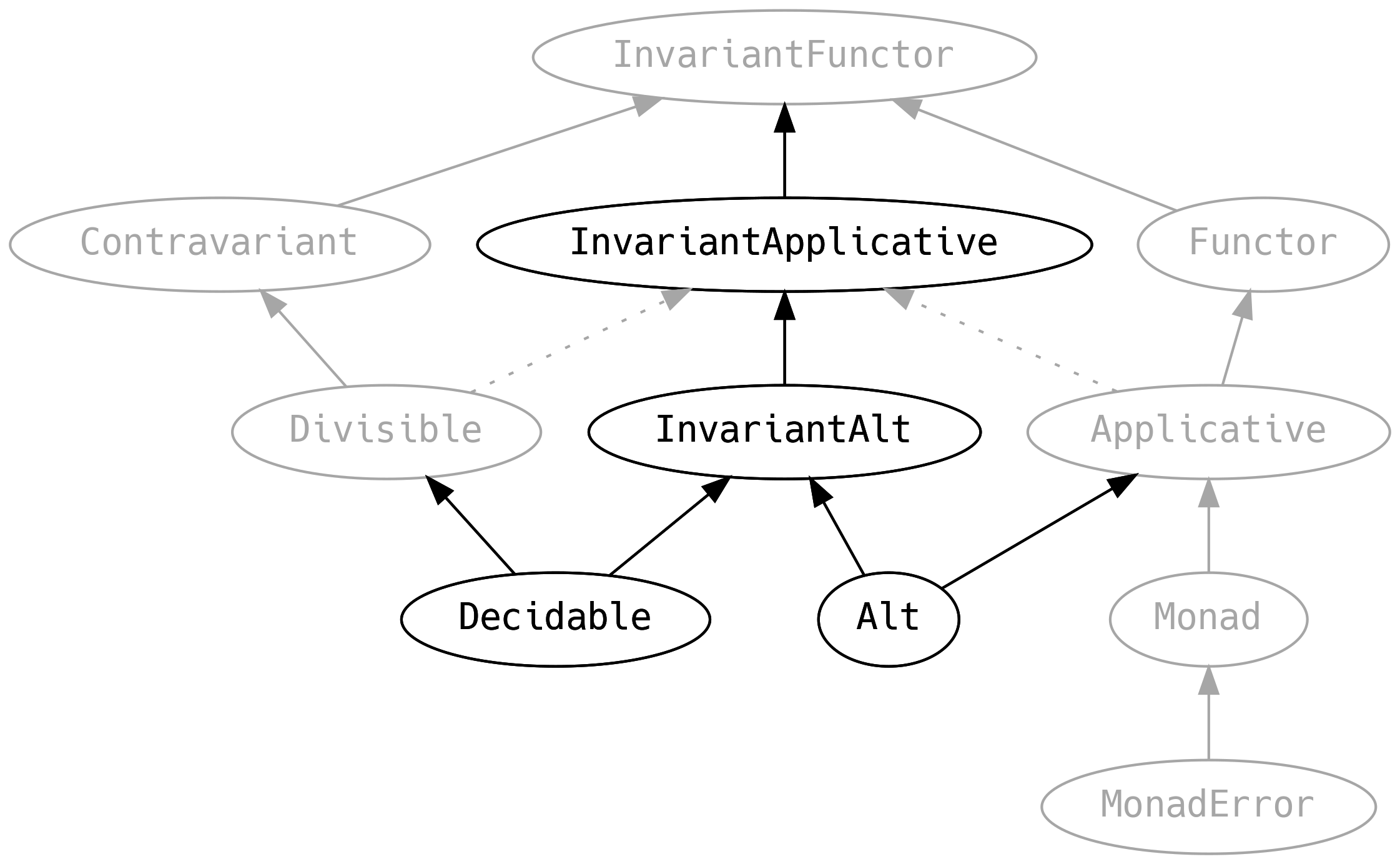
Before we proceed, here is a quick recap of the core scalaz typeclasses:

  @typeclass trait InvariantFunctor[F[_]] {
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B]
  }
  
  @typeclass trait Contravariant[F[_]] extends InvariantFunctor[F] {
    def contramap[A, B](fa: F[A])(f: B => A): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = contramap(fa)(g)
  }
  
  @typeclass trait Divisible[F[_]] extends Contravariant[F] {
    def conquer[A]: F[A]
    def divide2[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C]
    ...
    def divide22[...] = ...
  }
  
  @typeclass trait Functor[F[_]] extends InvariantFunctor[F] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = map(fa)(f)
  }
  
  @typeclass trait Applicative[F[_]] extends Functor[F] {
    def point[A](a: =>A): F[A]
    def apply2[A,B,C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] = ...
    def apply3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
    ...
    def apply12[...]
  }
  
  @typeclass trait Monad[F[_]] extends Functor[F] {
    @op(">>=") def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
  }
  @typeclass trait MonadError[F[_], E] extends Monad[F] {
    def raiseError[A](e: E): F[A]
    def handleError[A](fa: F[A])(f: E => F[A]): F[A]
    def emap[A, B](fa: F[A])(f: A => S \/ B): F[B] = ...
  }

8.2.1 Don’t Repeat Yourself

The simplest way to derive a typeclass is to reuse one that already exists.

The Equal typeclass has an instance of Contravariant[Equal], providing .contramap:

  object Equal {
    implicit val contravariant = new Contravariant[Equal] {
      def contramap[A, B](fa: Equal[A])(f: B => A): Equal[B] =
        (b1, b2) => fa.equal(f(b1), f(b2))
    }
    ...
  }

As users of Equal, we can use .contramap for our single parameter data types. Recall that typeclass instances go on the data type companions to be in their implicit scope:

  final case class Foo(s: String)
  object Foo {
    implicit val equal: Equal[Foo] = Equal[String].contramap(_.s)
  }
  
  scala> Foo("hello") === Foo("world")
  false

However, not all typeclasses can have an instance of Contravariant. In particular, typeclasses with type parameters in covariant position may have a Functor instead:

  object Default {
    def instance[A](d: =>String \/ A) = new Default[A] { def default = d }
    implicit val string: Default[String] = instance("".right)
  
    implicit val functor: Functor[Default] = new Functor[Default] {
      def map[A, B](fa: Default[A])(f: A => B): Default[B] = instance(fa.default.map(f))
    }
    ...
  }

We can now derive a Default[Foo]

  object Foo {
    implicit val default: Default[Foo] = Default[String].map(Foo(_))
    ...
  }

If a typeclass has parameters in both covariant and contravariant position, as is the case with Semigroup, it may provide an InvariantFunctor

  object Semigroup {
    implicit val invariant = new InvariantFunctor[Semigroup] {
      def xmap[A, B](ma: Semigroup[A], f: A => B, g: B => A) = new Semigroup[B] {
        def append(x: B, y: =>B): B = f(ma.append(g(x), g(y)))
      }
    }
    ...
  }

and we can call .xmap

  object Foo {
    implicit val semigroup: Semigroup[Foo] = Semigroup[String].xmap(Foo(_), _.s)
    ...
  }

Generally, it is simpler to just use .xmap instead of .map or .contramap:

  final case class Foo(s: String)
  object Foo {
    implicit val equal: Equal[Foo]         = Equal[String].xmap(Foo(_), _.s)
    implicit val default: Default[Foo]     = Default[String].xmap(Foo(_), _.s)
    implicit val semigroup: Semigroup[Foo] = Semigroup[String].xmap(Foo(_), _.s)
  }

The @xderiving annotation automatically inserts .xmap boilerplate. Add the following to build.sbt

  addCompilerPlugin("com.fommil" %% "deriving-plugin" % derivingVersion)
  libraryDependencies += "com.fommil" %% "deriving-macro" % derivingVersion % "provided"

and use it as

  @xderiving(Equal, Default, Semigroup)
  final case class Foo(s: String)

8.2.2 `MonadError`

Typically things that write from a polymorphic value have a Contravariant, and things that read into a polymorphic value have a Functor. However, it is very much expected that reading can fail. For example, if we have a default String it does not mean that we can simply derive a default String Refined NonEmpty from it

  import eu.timepit.refined.refineV
  import eu.timepit.refined.api._
  import eu.timepit.refined.collection._
  
  implicit val nes: Default[String Refined NonEmpty] =
    Default[String].map(refineV[NonEmpty](_))

fails to compile with

  [error] default.scala:41:32: polymorphic expression cannot be instantiated to expected type;
  [error]  found   : Either[String, String Refined NonEmpty]
  [error]  required: String Refined NonEmpty
  [error]     Default[String].map(refineV[NonEmpty](_))
  [error]                                          ^

Recall from Chapter 4.1 that refineV returns an Either, as the compiler has reminded us.

As the typeclass author of Default, we can do better than Functor and provide a MonadError[Default, String]:

  implicit val monad = new MonadError[Default, String] {
    def point[A](a: =>A): Default[A] =
      instance(a.right)
    def bind[A, B](fa: Default[A])(f: A => Default[B]): Default[B] =
      instance((fa >>= f).default)
    def handleError[A](fa: Default[A])(f: String => Default[A]): Default[A] =
      instance(fa.default.handleError(e => f(e).default))
    def raiseError[A](e: String): Default[A] =
      instance(e.left)
  }

Now we have access to .emap syntax and can derive our refined type

  implicit val nes: Default[String Refined NonEmpty] =
    Default[String].emap(refineV[NonEmpty](_).disjunction)

In fact, we can provide a derivation rule for all refined types

  implicit def refined[A: Default, P](
    implicit V: Validate[A, P]
  ): Default[A Refined P] = Default[A].emap(refineV[P](_).disjunction)

where Validate is from the refined library and is required by refineV.

The refined-scalaz extension to refined provides support for automatically deriving all typeclasses for refined types with the following import

  import eu.timepit.refined.scalaz._

if there is a Contravariant or MonadError[?, String] in the implicit scope.

However, due to limitations of the scala compiler it rarely works in practice and we must write implicit def refined derivations for each typeclass.

Similarly we can use .emap to derive an Int decoder from a Long, with protection around the non-total .toInt stdlib method.

  implicit val long: Default[Long] = instance(0L.right)
  implicit val int: Default[Int] = Default[Long].emap {
    case n if (Int.MinValue <= n && n <= Int.MaxValue) => n.toInt.right
    case big => s"$big does not fit into 32 bits".left
  }

As authors of the Default typeclass, we might want to reconsider our API design so that it can never fail, e.g. with the following type signature

  @typeclass trait Default[A] {
    def default: A
  }

We would not be able to define a MonadError, forcing us to provide instances that always succeed. This will result in more boilerplate but trades runtime failure detection for compiletime safety. However, we will continue with String \/ A as the return type as it is by far the more common use case.

8.2.3 `.fromIso`

All of the typeclasses in scalaz have a method on their companion with a signature similar to the following:

  object Equal {
    def fromIso[F, G: Equal](D: F <=> G): Equal[F] = ...
    ...
  }
  
  object Monad {
    def fromIso[F[_], G[_]: Monad](D: F <~> G): Monad[F] = ...
    ...
  }

These mean that if we have a type F, and a way to convert it into a G that has an instance, we can call Equal.fromIso to obtain an instance for F.

For example, as typeclass users, if we have a data type Bar we can define an isomorphism to (String, Int)

  import Isomorphism._
  
  final case class Bar(s: String, i: Int)
  object Bar {
    val iso: Bar <=> (String, Int) = IsoSet(b => (b.s, b.i), t => Bar(t._1, t._2))
  }

and then derive Equal[Bar] because there is already an Equal for all tuples:

  object Bar {
    ...
    implicit val equal: Equal[Bar] = Equal.fromIso(iso)
  }

The .fromIso mechanism can also assist us as typeclass authors. Consider Default which has a core type signature of the form Unit => F[A]. Our default method is in fact isomorphic to Kleisli[F, Unit, A], the ReaderT monad transformer.

Since Kleisli already provides a MonadError (if F has one), we can derive MonadError[Default, String] by creating an isomorphism between Default and Kleisli:

  private type Sig[a] = Unit => String \/ a
  private val iso = Kleisli.iso(
    λ[Sig ~> Default](s => instance(s(()))),
    λ[Default ~> Sig](d => _ => d.default)
  )
  implicit val monad: MonadError[Default, String] = MonadError.fromIso(iso)

giving us the .map, .xmap and .emap that we’ve been making use of so far, effectively for free.

8.2.4 `Divisible` and `Applicative`

To derive the Equal for our case class with two parameters, we reused the instance that scalaz provides for tuples. But where did the tuple instance come from?

A more specific typeclass than Contravariant is Divisible, and Equal provides an instance:

  implicit val divisible = new Divisible[Equal] {
    ...
    def divide[A1, A2, Z](a1: =>Equal[A1], a2: =>Equal[A2])(
      f: Z => (A1, A2)
    ): Equal[Z] = { (z1, z2) =>
      val (s1, s2) = f(z1)
      val (t1, t2) = f(z2)
      a1.equal(s1, t1) && a2.equal(s2, t2)
    }
    def conquer[A]: Equal[A] = (_, _) => true
  }

When implementing Divisible the compiler will require us to implement contramap, which we can do with the following derived combinator:

  override def contramap[A, B](fa: F[A])(f: B => A): F[B] =
    divide2(conquer[Unit], fa)(c => ((), f(c)))

This has been added to Divisible in scalaz 7.3.

And from divide2, Divisible is able to build up derivations all the way to divide22. We can call these methods directly for our data types:

  final case class Bar(s: String, i: Int)
  object Bar {
    implicit val equal: Equal[Bar] =
      Divisible[Equal].divide2(Equal[String], Equal[Int])(b => (b.s, b.i))
  }

The equivalent for type parameters in covariant position is Applicative:

  object Bar {
    ...
    implicit val default: Default[Bar] =
      Applicative[Default].apply2(Default[String], Default[Int])(Bar(_, _))
  }

But we must be careful that we do not break the typeclass laws when we implement Divisible or Applicative. In particular, it is easy to break the law of composition which says that the following two codepaths must yield exactly the same output

divide2(divide2(a1, a2)(dupe), a3)(dupe)
divide2(a1, divide2(a2, a3)(dupe))(dupe)
for any dupe: A => (A, A)

with similar laws for Applicative.

Consider JsEncoder and a proposed instance of Divisible

  new Divisible[JsEncoder] {
    ...
    def divide[A, B, C](fa: JsEncoder[A], fb: JsEncoder[B])(
      f: C => (A, B)
    ): JsEncoder[C] = { c =>
      val (a, b) = f(c)
      JsArray(IList(fa.toJson(a), fb.toJson(b)))
    }
  
    def conquer[A]: JsEncoder[A] = _ => JsNull
  }

On one side of the composition laws, for a String input, we get

  JsArray([JsArray([JsString(hello),JsString(hello)]),JsString(hello)])

and on the other

  JsArray([JsString(hello),JsArray([JsString(hello),JsString(hello)])])

which are different. We could experiment with variations of the divide implementation, but it will never satisfy the laws for all inputs.

We therefore cannot provide a Divisible[JsEncoder], even though we can write one down, because it breaks the mathematical laws and invalidates all the assumptions that users of Divisible rely upon.

To aid in testing laws, scalaz typeclasses contain the codified versions of their laws on the typeclass itself. We can write an automated test, asserting that the law fails, to remind us of this fact:

  val D: Divisible[JsEncoder] = ...
  val S: JsEncoder[String] = JsEncoder[String]
  val E: Equal[JsEncoder[String]] = (p1, p2) => p1.toJson("hello") === p2.toJson("hello")
  assert(!D.divideLaw.composition(S, S, S)(E))

On the other hand, a similar JsDecoder test meets the Applicative composition laws

  final case class Comp(a: String, b: Int)
  object Comp {
    implicit val equal: Equal[Comp] = ...
    implicit val decoder: JsDecoder[Comp] = ...
  }
  
  def composeTest(j: JsValue) = {
    val A: Applicative[JsDecoder] = Applicative[JsDecoder]
    val fa: JsDecoder[Comp] = JsDecoder[Comp]
    val fab: JsDecoder[Comp => (String, Int)] = A.point(c => (c.a, c.b))
    val fbc: JsDecoder[((String, Int)) => (Int, String)] = A.point(_.swap)
    val E: Equal[JsDecoder[(Int, String)]] = (p1, p2) => p1.fromJson(j) === p2.fromJson(j)
    assert(A.applyLaw.composition(fbc, fab, fa)(E))
  }

for some test data

  composeTest(JsObject(IList("a" -> JsString("hello"), "b" -> JsInteger(1))))
  composeTest(JsNull)
  composeTest(JsObject(IList("a" -> JsString("hello"))))
  composeTest(JsObject(IList("b" -> JsInteger(1))))

Now we are reasonably confident that our derived MonadError is lawful.

However, just because we have a test that passes for a small set of data does not prove that the laws are satisfied. We must also reason through the implementation to convince ourselves that it should satisfy the laws, and try to propose corner cases where it could fail.

One way of generating a wide variety of test data is to use the scalacheck library, which provides an Arbitrary typeclass that integrates with most testing frameworks to repeat a test with randomly generated data.

The jsonformat library provides an Arbitrary[JsValue] (everybody should provide an Arbitrary for their ADTs!) allowing us to make use of scalatest’s forAll feature:

  forAll(SizeRange(10))((j: JsValue) => composeTest(j))

This test gives us even more confidence that our typeclass meets the Applicative composition laws. By checking all the laws on Divisible and MonadError we also get a lot of smoke tests for free.

8.2.5 `Decidable` and `Alt`

Where Divisible and Applicative give us typeclass derivation for products (built from tuples), Decidable and Alt give us the coproducts (built from nested disjunctions):

  @typeclass trait Alt[F[_]] extends Applicative[F] with InvariantAlt[F] {
    def alt[A](a1: =>F[A], a2: =>F[A]): F[A]
  
    def altly1[Z, A1](a1: =>F[A1])(f: A1 => Z): F[Z] = ...
    def altly2[Z, A1, A2](a1: =>F[A1], a2: =>F[A2])(f: A1 \/ A2 => Z): F[Z] = ...
    def altly3 ...
    def altly4 ...
    ...
  }
  
  trait Decidable[F[_]] extends Divisible[F] with InvariantAlt[F] {
    def choose1[Z, A1](a1: =>F[A1])(f: Z => A1): F[Z] = ...
    def choose2[Z, A1, A2](a1: =>F[A1], a2: =>F[A2])(f: Z => A1 \/ A2): F[Z] = ...
    def choose3 ...
    def choose4 ...
    ...
  }

The four core typeclasses have symmetric signatures:

Typeclass	method	given	signature	returns
`Applicative`	`apply2`	`F[A1], F[A2]`	`(A1, A2) => Z`	`F[Z]`
`Alt`	`altly2`	`F[A1], F[A2]`	`(A1 \/ A2) => Z`	`F[Z]`
`Divisible`	`divide2`	`F[A1], F[A2]`	`Z => (A1, A2)`	`F[Z]`
`Decidable`	`choose2`	`F[A1], F[A2]`	`Z => (A1 \/ A2)`	`F[Z]`

supporting covariant products; covariant coproducts; contravariant products; contravariant coproducts.

We can write a Decidable[Equal], letting us derive Equal for any ADT!

  implicit val decidable = new Decidable[Equal] {
    ...
    def choose2[Z, A1, A2](a1: =>Equal[A1], a2: =>Equal[A2])(
      f: Z => A1 \/ A2
    ): Equal[Z] = { (z1, z2) =>
      (f(z1), f(z2)) match {
        case (-\/(s), -\/(t)) => a1.equal(s, t)
        case (\/-(s), \/-(t)) => a2.equal(s, t)
        case _ => false
      }
    }
  }

For an ADT

  sealed abstract class Darth { def widen: Darth = this }
  final case class Vader(s: String, i: Int)  extends Darth
  final case class JarJar(i: Int, s: String) extends Darth

where the products (Vader and JarJar) have an Equal

  object Vader {
    private val g: Vader => (String, Int) = d => (d.s, d.i)
    implicit val equal: Equal[Vader] = Divisible[Equal].divide2(Equal[String], Equal[Int])(g)
  }
  object JarJar {
    private val g: JarJar => (Int, String) = d => (d.i, d.s)
    implicit val equal: Equal[JarJar] = Divisible[Equal].divide2(Equal[Int], Equal[String])(g)
  }

we can derive the equal for the whole ADT

  object Darth {
    private def g(t: Darth): Vader \/ JarJar = t match {
      case p @ Vader(_, _)  => -\/(p)
      case p @ JarJar(_, _) => \/-(p)
    }
    implicit val equal: Equal[Darth] = Decidable[Equal].choose2(Equal[Vader], Equal[JarJar])(g)
  }
  
  scala> Vader("hello").widen === JarJar(1).widen
  false

Typeclasses that have an Applicative can be eligible for an Alt. If we want to use our Kleisli.iso trick, we have to extend IsomorphismMonadError and mix in Alt. Let’s upgrade our MonadError[Default, String] to have an Alt[Default]:

  private type K[a] = Kleisli[String \/ ?, Unit, a]
  implicit val monad = new IsomorphismMonadError[Default, K, String] with Alt[Default] {
    override val G = MonadError[K, String]
    override val iso = ...
  
    def alt[A](a1: =>Default[A], a2: =>Default[A]): Default[A] = instance(a1.default)
  }

The primitive of Alt is alt, much as the primitive of Applicative is ap, but it often makes more sense to use altly2 and apply2 as the primitives with the following overrides:

  override def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B] =
    apply2(fa, f)((a, abc) => abc(a))
  
  override def alt[A](a1: =>F[A], a2: =>F[A]): F[A] = altly2(a1, a2) {
    case -\/(a) => a
    case \/-(a) => a
  }

Just don’t forget to implement apply2 and altly2 or there will be an infinite loop at runtime.

Letting us derive our Default[Darth]

  object Darth {
    ...
    private def f(e: Vader \/ JarJar): Darth = e.merge
    implicit val default: Default[Darth] =
      Alt[Default].altly2(Default[Vader], Default[JarJar])(f)
  }
  object Vader {
    ...
    private val f: (String, Int) => Vader = Vader(_, _)
    implicit val default: Default[Vader] =
      Alt[Default].apply2(Default[String], Default[Int])(f)
  }
  object JarJar {
    ...
    private val f: (Int, String) => JarJar = JarJar(_, _)
    implicit val default: Default[JarJar] =
      Alt[Default].apply2(Default[Int], Default[String])(f)
  }
  
  scala> Default[Darth].default
  \/-(Vader())

Returning to the scalaz-deriving typeclasses, the invariant parents of Alt and Decidable are:

  @typeclass trait InvariantApplicative[F[_]] extends InvariantFunctor[F] {
    def xproduct0[Z](f: =>Z): F[Z]
    def xproduct1[Z, A1](a1: =>F[A1])(f: A1 => Z, g: Z => A1): F[Z] = ...
    def xproduct2 ...
    def xproduct3 ...
    def xproduct4 ...
  }
  
  @typeclass trait InvariantAlt[F[_]] extends InvariantApplicative[F] {
    def xcoproduct1[Z, A1](a1: =>F[A1])(f: A1 => Z, g: Z => A1): F[Z] = ...
    def xcoproduct2 ...
    def xcoproduct3 ...
    def xcoproduct4 ...
  }

Letting us write consistent boilerplate for all derivations:

  object Darth {
    ...
    implicit val equal: Equal[Darth] =
      InvariantAlt[Equal].xcoproduct2(Equal[Vader], Equal[JarJar])(f, g)
    implicit val default: Default[Darth] =
      InvariantAlt[Default].xcoproduct2(Default[Vader], Default[JarJar])(f, g)
  }
  object Vader {
    ...
    implicit val equal: Equal[Vader] =
      InvariantApplicative[Equal].xproduct2(Equal[String], Equal[Int])(f, g)
    implicit val default: Default[Vader] =
      InvariantApplicative[Default].xproduct2(Default[String], Default[Int])(f, g)
  }
  object JarJar {
    ...
    implicit val equal: Equal[JarJar] =
      InvariantApplicative[Equal].xproduct2(Equal[Int], Equal[String])(f, g)
    implicit val default: Default[JarJar] =
      InvariantApplicative[Default].xproduct2(Default[Int], Default[String])(f, g)
  }

This boilerplate also works when we have a typeclass like Semigroup that can only provide an InvariantApplicative, not an Applicative.

8.2.6 Arbitrary Arity and `@deriving`

There are two problems with InvariantApplicative and InvariantAlt:

they only support products of four fields and coproducts of four entries.
there is a lot of boilerplate on the data type companions.

In this section we solve both problems with additional typeclasses introduced by scalaz-deriving

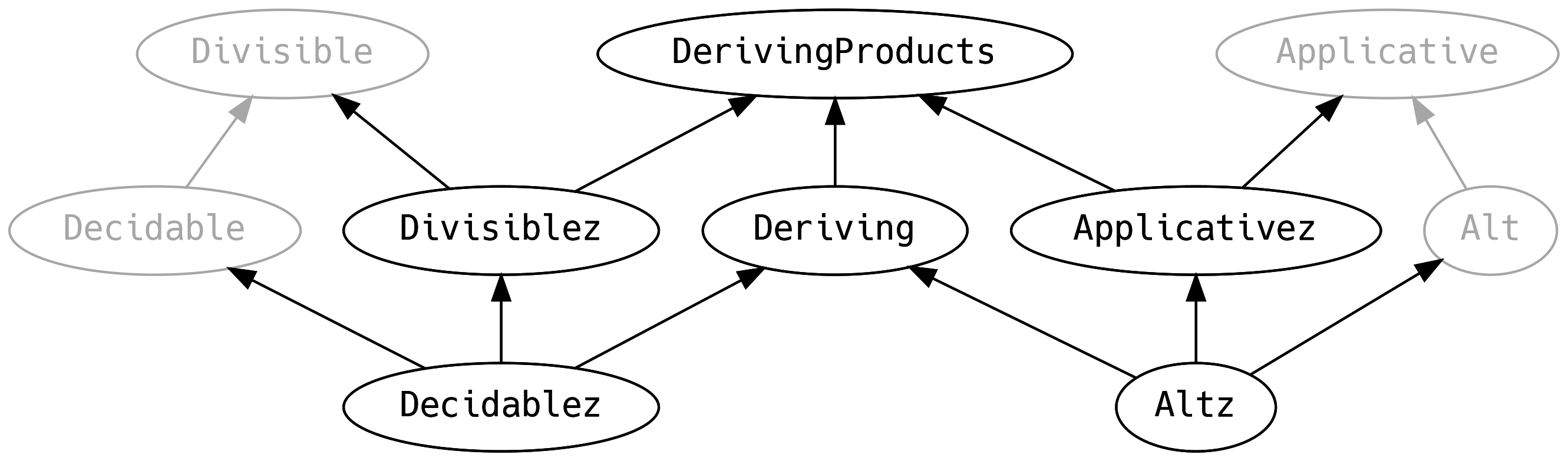
Effectively, our four central typeclasses Applicative, Divisible, Alt and Decidable all get extended to arbitrary arity using the iotaz library, hence the z postfix.

The iotaz library has three main types:

TList which describes arbitrary length chains of types
Prod[A <: TList] for products
Cop[A <: TList] for coproducts

By way of example, a TList representation of Darth from the previous section is

  import iotaz._, TList._
  
  type DarthT  = Vader  :: JarJar :: TNil
  type VaderT  = String :: Int    :: TNil
  type JarJarT = Int    :: String :: TNil

which can be instantiated:

  val vader: Prod[VaderT]    = Prod("hello", 1)
  val jarjar: Prod[JarJarT]  = Prod(1, "hello")
  
  val VaderI = Cop.Inject[Vader, Cop[DarthT]]
  val darth: Cop[DarthT] = VaderI.inj(Vader("hello", 1))

To be able to use the scalaz-deriving API, we need an Isomorphism between our ADTs and the iotaz generic representation. It’s a lot of boilerplate, but it pays off:

  object Darth {
    private type Repr   = Vader :: JarJar :: TNil
    private val VaderI  = Cop.Inject[Vader, Cop[Repr]]
    private val JarJarI = Cop.Inject[JarJar, Cop[Repr]]
    private val iso     = IsoSet(
      {
        case d: Vader  => VaderI.inj(d)
        case d: JarJar => JarJarI.inj(d)
      }, {
        case VaderI(d)  => d
        case JarJarI(d) => d
      }
    )
    ...
  }
  
  object Vader {
    private type Repr = String :: Int :: TNil
    private val iso   = IsoSet(
      d => Prod(d.s, d.i),
      p => Vader(p.head, p.tail.head)
    )
    ...
  }
  
  object JarJar {
    private type Repr = Int :: String :: TNil
    private val iso   = IsoSet(
      d => Prod(d.i, d.s),
      p => JarJar(p.head, p.tail.head)
    )
    ...
  }

With that out of the way we can call the Deriving API for Equal, possible because scalaz-deriving provides an optimised instance of Deriving[Equal]

  object Darth {
    ...
    implicit val equal: Equal[Darth] = Deriving[Equal].xcoproductz(
      Prod(Need(Equal[Vader]), Need(Equal[JarJar])))(iso.to, iso.from)
  }
  object Vader {
    ...
    implicit val equal: Equal[Vader] = Deriving[Equal].xproductz(
      Prod(Need(Equal[String]), Need(Equal[Int])))(iso.to, iso.from)
  }
  object JarJar {
    ...
    implicit val equal: Equal[JarJar] = Deriving[Equal].xproductz(
      Prod(Need(Equal[Int]), Need(Equal[String])))(iso.to, iso.from)
  }

To be able to do the same for our Default typeclass, we need to provide an instance of Deriving[Default]. This is just a case of wrapping our existing Alt with a helper:

  object Default {
    ...
    implicit val deriving: Deriving[Default] = ExtendedInvariantAlt(monad)
  }

and then calling it from the companions

  object Darth {
    ...
    implicit val default: Default[Darth] = Deriving[Default].xcoproductz(
      Prod(Need(Default[Vader]), Need(Default[JarJar])))(iso.to, iso.from)
  }
  object Vader {
    ...
    implicit val default: Default[Vader] = Deriving[Default].xproductz(
      Prod(Need(Default[String]), Need(Default[Int])))(iso.to, iso.from)
  }
  object JarJar {
    ...
    implicit val default: Default[JarJar] = Deriving[Default].xproductz(
      Prod(Need(Default[Int]), Need(Default[String])))(iso.to, iso.from)
  }

We have solved the problem of arbitrary arity, but we have introduced even more boilerplate.

The punchline is that the @deriving annotation, which comes from deriving-plugin, generates all this boilerplate automatically and only needs to be applied at the top level of an ADT:

  @deriving(Equal, Default)
  sealed abstract class Darth { def widen: Darth = this }
  final case class Vader(s: String, i: Int)  extends Darth
  final case class JarJar(i: Int, s: String) extends Darth

Also included in scalaz-deriving are instances for Order, Semigroup and Monoid. Instances of Show and Arbitrary are available by installing the scalaz-deriving-magnolia and scalaz-deriving-scalacheck extras.

You’re welcome!

8.2.7 Examples

We finish our study of scalaz-deriving with fully worked implementations of all the example typeclasses. Before we do that we need to know about a new data type: /~\, aka the snake in the road, for containing two higher kinded structures that share the same type parameter:

  sealed abstract class /~\[A[_], B[_]] {
    type T
    def a: A[T]
    def b: B[T]
  }
  object /~\ {
    type APair[A[_], B[_]]  = A /~\ B
    @inline final def unapply[A[_], B[_]](p: A /~\ B): Some[(A[p.T], B[p.T])] = ...
    @inline final def apply[A[_], B[_], Z](az: =>A[Z], bz: =>B[Z]): A /~\ B = ...
  }

We typically use this in the context of Id /~\ TC where TC is our typeclass, meaning that we have a value, and an instance of a typeclass for that value, without knowing anything about the value.

In addition, all the methods on the Deriving API have implicit evidence of the form A PairedWith FA, allowing the iotaz library to be able to perform .zip, .traverse, and other operations on Prod and Cop. We can ignore these parameters, as we don’t use them directly.

8.2.7.1 `Equal`

As with Default we could define a regular fixed-arity Decidable and wrap it with ExtendedInvariantAlt (the simplest approach), but we choose to implement Decidablez directly for the performance benefit. We make two additional optimisations:

perform instance equality .eq before applying the Equal.equal, allowing for shortcut equality between identical values.
Foldable.all allowing early exit when any comparison is false. e.g. if the first fields don’t match, we don’t even request the Equal for remaining values.

  new Decidablez[Equal] {
    @inline private final def quick(a: Any, b: Any): Boolean =
      a.asInstanceOf[AnyRef].eq(b.asInstanceOf[AnyRef])
  
    def dividez[Z, A <: TList, FA <: TList](tcs: Prod[FA])(g: Z => Prod[A])(
      implicit ev: A PairedWith FA
    ): Equal[Z] = (z1, z2) =>
      (g(z1), g(z2)).zip(tcs).all {
        case (a1, a2) /~\ fa => (quick(a1, a2) || fa.value.equal(a1, a2))
      }
  
    def choosez[Z, A <: TList, FA <: TList](tcs: Prod[FA])(g: Z => Cop[A])(
      implicit ev: A PairedWith FA
    ): Equal[Z] = (z1, z2) =>
      (g(z1), g(z2)).zip(tcs) match {
        case -\/(_)               => false
        case \/-((a1, a2) /~\ fa) => quick(a1, a2) || fa.value.equal(a1, a2)
      }
  }

8.2.7.2 `Default`

We’ve already seen how to define an Alt and lift it to a Deriving with the ExtendedInvariantAlt helper. However, for completeness, say we wish to define an Altz directly.

Unfortunately, the iotaz API for .traverse (and its analogy, .coptraverse) requires us to define natural transformations, which have a clunky syntax, even with the kind-projector plugin.

  private type K[a] = Kleisli[String \/ ?, Unit, a]
  new IsomorphismMonadError[Default, K, String] with Altz[Default] {
    type Sig[a] = Unit => String \/ a
    override val G = MonadError[K, String]
    override val iso = Kleisli.iso(
      λ[Sig ~> Default](s => instance(s(()))),
      λ[Default ~> Sig](d => _ => d.default)
    )
  
    val extract = λ[NameF ~> (String \/ ?)](a => a.value.default)
    def applyz[Z, A <: TList, FA <: TList](tcs: Prod[FA])(f: Prod[A] => Z)(
      implicit ev: A PairedWith FA
    ): Default[Z] = instance(tcs.traverse(extract).map(f))
  
    val always = λ[NameF ~> Maybe](a => a.value.default.toMaybe)
    def altlyz[Z, A <: TList, FA <: TList](tcs: Prod[FA])(f: Cop[A] => Z)(
      implicit ev: A PairedWith FA
    ): Default[Z] = instance {
      tcs.coptraverse[A, NameF, Id](always).map(f).headMaybe \/> "not found"
    }
  }

8.2.7.3 `Semigroup`

It is not possible to define a Semigroup for general coproducts, however it is possible to define one for general products. We can use the arbitrary arity InvariantApplicative:

  new InvariantApplicativez[Semigroup] {
    type L[a] = ((a, a), NameF[a])
    val appender = λ[L ~> Id] { case ((a1, a2), fa) => fa.value.append(a1, a2) }
  
    override def xproductz[Z, A <: TList, FA <: TList](
      tcs: Prod[FA]
    )(
      f: Prod[A] => Z,
      g: Z => Prod[A]
    )(
      implicit ev: A PairedWith FA
    ): Semigroup[Z] = new Semigroup[Z] {
      def append(z1: Z, z2: =>Z): Z = f(tcs.ziptraverse2(g(z1), g(z2), appender))
    }
  }

8.2.7.4 `JsEncoder` and `JsDecoder`

scalaz-deriving does not provide access to field names so it is not possible, which is why we will study Magnolia in the next section.

8.3 Magnolia

The Magnolia macro library provides a clean API for writing typeclass derivations. It is installed with the following build.sbt entry

  libraryDependencies += "com.propensive" %% "magnolia" % "0.10.0"

A typeclass author implements the following members:

  import magnolia._
  
  object MyDerivation {
    type Typeclass[A]
  
    def combine[A](ctx: CaseClass[Typeclass, A]): Typeclass[A]
    def dispatch[A](ctx: SealedTrait[Typeclass, A]): Typeclass[A]
  
    def gen[A]: Typeclass[A] = macro Magnolia.gen[A]
  }

The Magnolia objects are:

  class CaseClass[TC[_], A] {
    def typeName: TypeName
    def construct[B](f: Param[TC, A] => B): A
    def constructMonadic[F[_]: Monadic, B](f: Param[TC, A] => F[B]): F[A]
    def parameters: Seq[Param[TC, A]]
    def annotations: Seq[Any]
  }
  
  class SealedTrait[TC[_], A] {
    def typeName: TypeName
    def subtypes: Seq[Subtype[TC, A]]
    def dispatch[B](value: A)(handle: Subtype[TC, A] => B): B
    def annotations: Seq[Any]
  }

with helpers

  final case class TypeName(short: String, full: String)
  
  class Param[TC[_], A] {
    type PType
    def label: String
    def index: Int
    def typeclass: TC[PType]
    def dereference(param: A): PType
    def default: Option[PType]
    def annotations: Seq[Any]
  }
  
  class Subtype[TC[_], A] {
    type SType <: A
    def typeName: TypeName
    def index: Int
    def typeclass: TC[SType]
    def cast(a: A): SType
    def annotations: Seq[Any]
  }

The Monadic typeclass, used in constructMonadic, is automatically generated if our data type has a .map and .flatMap method when we import mercator._

It does not make sense to use Magnolia for typeclasses that can be abstracted by Divisible, Decidable, Applicative or Alt, since those abstractions provide a lot of extra structure and tests for free. However, Magnolia offers features that scalaz-deriving cannot provide: access to field names, type names, annotations and default values.

8.3.1 Example: JSON

We have some design choices to make with regards to JSON serialisation:

Should we include fields with null values?
Should decoding treat missing vs null differently?
How do we encode the name of a coproduct?
How do we deal with coproducts that are not JsObject?

We choose sensible defaults

do not include fields if the value is a JsNull.
handle missing fields the same as null values.
use a special field "type" to disambiguate coproducts using the type name.
put primitive values into a special field "xvalue".

and let the users attach an annotation to coproducts and product fields to customise their formats:

  sealed class json extends Annotation
  object json {
    final case class nulls()          extends json
    final case class field(f: String) extends json
    final case class hint(f: String)  extends json
  }

For example

  @json.field("TYPE")
  sealed abstract class Cost
  final case class Time(s: String) extends Cost
  final case class Money(@json.field("integer") i: Int) extends Cost

These user preferences also allow us to distinguish between null, missing and valid values without any further modifications to JsValue, JsEncoder or JsDecoder. For example, through this ADT

  sealed abstract class Possibly[A]
  object Possibly {
    final case class Missing[A]()   extends Possibly[A]
    final case class Found[A](a: A) extends Possibly[A]
  
    implicit def encoder[A: JsEncoder]: JsEncoder[Possibly] = JsEncoder[A].contramap(_.a)
    implicit def decoder[A: JsDecoder]: JsDecoder[Possibly] = JsDecoder[A].map(Found(_))
  }

we can say that we require null values, otherwise using a default, then check for null with Option:

  final case class(
    @json.nulls() s: Possibly[Option[String]] = Missing()
  )

Let’s start with a JsDecoder that handles only our “sensible defaults”:

  object JsMagnoliaEncoder {
    type Typeclass[A] = JsEncoder[A]
  
    def combine[A](ctx: CaseClass[JsEncoder, A]): JsEncoder[A] = { a =>
      val empty = IList.empty[(String, JsValue)]
      val fields = ctx.parameters.foldRight(right) { (p, acc) =>
        p.typeclass.toJson(p.dereference(a)) match {
          case JsNull => acc
          case value  => (p.label -> value) :: acc
        }
      }
      JsObject(fields)
    }
  
    def dispatch[A](ctx: SealedTrait[JsEncoder, A]): JsEncoder[A] = a =>
      ctx.dispatch(a) { sub =>
        val hint = "type" -> JsString(sub.typeName.short)
        sub.typeclass.toJson(sub.cast(a)) match {
          case JsObject(fields) => JsObject(hint :: fields)
          case other            => JsObject(IList(hint, "xvalue" -> other))
        }
      }
  
    def gen[A]: JsEncoder[A] = macro Magnolia.gen[A]
  }

We can see how the Magnolia API makes it easy to access field names and typeclasses for each parameter.

Now add support for annotations to handle user preferences. To avoid looking up the annotations on every encoding, we’ll cache them in an array. Although field access to an array is non-total, we are guaranteed that the indices will always align. Performance is usually the victim in the trade-off between specialisation and generalisation.

  object JsMagnoliaEncoder {
    type Typeclass[A] = JsEncoder[A]
  
    def combine[A](ctx: CaseClass[JsEncoder, A]): JsEncoder[A] =
      new JsEncoder[A] {
        private val anns = ctx.parameters.map { p =>
          val nulls = p.annotations.collectFirst {
            case json.nulls() => true
          }.getOrElse(false)
          val field = p.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse(p.label)
          (nulls, field)
        }.toArray
  
        def toJson(a: A): JsValue = {
          val empty = IList.empty[(String, JsValue)]
          val fields = ctx.parameters.foldRight(empty) { (p, acc) =>
            val (nulls, field) = anns(p.index)
            p.typeclass.toJson(p.dereference(a)) match {
              case JsNull if !nulls => acc
              case value            => (field -> value) :: acc
            }
          }
          JsObject(fields)
        }
      }
  
    def dispatch[A](ctx: SealedTrait[JsEncoder, A]): JsEncoder[A] =
      new JsEncoder[A] {
        private val field = ctx.annotations.collectFirst {
          case json.field(name) => name
        }.getOrElse("type")
        private val anns = ctx.subtypes.map { s =>
          val hint = s.annotations.collectFirst {
            case json.hint(name) => field -> JsString(name)
          }.getOrElse(field -> JsString(s.typeName.short))
          val xvalue = s.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse("xvalue")
          (hint, xvalue)
        }.toArray
  
        def toJson(a: A): JsValue = ctx.dispatch(a) { sub =>
          val (hint, xvalue) = anns(sub.index)
          sub.typeclass.toJson(sub.cast(a)) match {
            case JsObject(fields) => JsObject(hint :: fields)
            case other            => JsObject(hint :: (xvalue -> other) :: IList.empty)
          }
        }
      }
  
    def gen[A]: JsEncoder[A] = macro Magnolia.gen[A]
  }

For the decoder we use .constructMonadic which has a type signature similar to .traverse

  object JsMagnoliaDecoder {
    type Typeclass[A] = JsDecoder[A]
  
    def combine[A](ctx: CaseClass[JsDecoder, A]): JsDecoder[A] = {
      case obj @ JsObject(_) =>
        ctx.constructMonadic(
          p => p.typeclass.fromJson(obj.get(p.label).getOrElse(JsNull))
        )
      case other => fail("JsObject", other)
    }
  
    def dispatch[A](ctx: SealedTrait[JsDecoder, A]): JsDecoder[A] = {
      case obj @ JsObject(_) =>
        obj.get("type") match {
          case \/-(JsString(hint)) =>
            ctx.subtypes.find(_.typeName.short == hint) match {
              case None => fail(s"a valid '$hint'", obj)
              case Some(sub) =>
                val value = obj.get("xvalue").getOrElse(obj)
                sub.typeclass.fromJson(value)
            }
          case _ => fail("JsObject with type", obj)
        }
      case other => fail("JsObject", other)
    }
  
    def gen[A]: JsDecoder[A] = macro Magnolia.gen[A]
  }

Again, adding support for user preferences and default field values, along with some optimisations:

  object JsMagnoliaDecoder {
    type Typeclass[A] = JsDecoder[A]
  
    def combine[A](ctx: CaseClass[JsDecoder, A]): JsDecoder[A] =
      new JsDecoder[A] {
        private val nulls = ctx.parameters.map { p =>
          p.annotations.collectFirst {
            case json.nulls() => true
          }.getOrElse(false)
        }.toArray
  
        private val fieldnames = ctx.parameters.map { p =>
          p.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse(p.label)
        }.toArray
  
        def fromJson(j: JsValue): String \/ A = j match {
          case obj @ JsObject(_) =>
            import mercator._
            val lookup = obj.fields.toMap
            ctx.constructMonadic { p =>
              val field = fieldnames(p.index)
              lookup
                .get(field)
                .into {
                  case Maybe.Just(value) => p.typeclass.fromJson(value)
                  case _ =>
                    p.default match {
                      case Some(default) => \/-(default)
                      case None if nulls(p.index) =>
                        s"missing field '$field'".left
                      case None => p.typeclass.fromJson(JsNull)
                    }
                }
            }
          case other => fail("JsObject", other)
        }
      }
  
    def dispatch[A](ctx: SealedTrait[JsDecoder, A]): JsDecoder[A] =
      new JsDecoder[A] {
        private val subtype = ctx.subtypes.map { s =>
          s.annotations.collectFirst {
            case json.hint(name) => name
          }.getOrElse(s.typeName.short) -> s
        }.toMap
        private val typehint = ctx.annotations.collectFirst {
          case json.field(name) => name
        }.getOrElse("type")
        private val xvalues = ctx.subtypes.map { sub =>
          sub.annotations.collectFirst {
            case json.field(name) => name
          }.getOrElse("xvalue")
        }.toArray
  
        def fromJson(j: JsValue): String \/ A = j match {
          case obj @ JsObject(_) =>
            obj.get(typehint) match {
              case \/-(JsString(h)) =>
                subtype.get(h) match {
                  case None => fail(s"a valid '$h'", obj)
                  case Some(sub) =>
                    val xvalue = xvalues(sub.index)
                    val value  = obj.get(xvalue).getOrElse(obj)
                    sub.typeclass.fromJson(value)
                }
              case _ => fail(s"JsObject with '$typehint' field", obj)
            }
          case other => fail("JsObject", other)
        }
      }
  
    def gen[A]: JsDecoder[A] = macro Magnolia.gen[A]
  }

We call the JsMagnoliaEncoder.gen or JsMagnoliaDecoder.gen method from the companion of our data types. For example, the Google Maps API

  final case class Value(text: String, value: Int)
  final case class Elements(distance: Value, duration: Value, status: String)
  final case class Rows(elements: List[Elements])
  final case class DistanceMatrix(
    destination_addresses: List[String],
    origin_addresses: List[String],
    rows: List[Rows],
    status: String
  )
  
  object Value {
    implicit val encoder: JsEncoder[Value] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[Value] = JsMagnoliaDecoder.gen
  }
  object Elements {
    implicit val encoder: JsEncoder[Elements] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[Elements] = JsMagnoliaDecoder.gen
  }
  object Rows {
    implicit val encoder: JsEncoder[Rows] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[Rows] = JsMagnoliaDecoder.gen
  }
  object DistanceMatrix {
    implicit val encoder: JsEncoder[DistanceMatrix] = JsMagnoliaEncoder.gen
    implicit val decoder: JsDecoder[DistanceMatrix] = JsMagnoliaDecoder.gen
  }

Thankfully, the @deriving annotation supports Magnolia! If the typeclass author provides a file deriving.conf with their jar, containing this text

  jsonformat.JsEncoder=jsonformat.JsMagnoliaEncoder.gen
  jsonformat.JsDecoder=jsonformat.JsMagnoliaDecoder.gen

the deriving-macro will call the user-provided method:

  @deriving(JsEncoder, JsDecoder)
  final case class Value(text: String, value: Int)
  @deriving(JsEncoder, JsDecoder)
  final case class Elements(distance: Value, duration: Value, status: String)
  @deriving(JsEncoder, JsDecoder)
  final case class Rows(elements: List[Elements])
  @deriving(JsEncoder, JsDecoder)
  final case class DistanceMatrix(
    destination_addresses: List[String],
    origin_addresses: List[String],
    rows: List[Rows],
    status: String
  )

8.3.2 Fully Automatic Derivation

Generating implicit instances on the companion of the data type is historically known as semi-auto derivation, in contrast to full-auto which is when the .gen is made implicit

  object JsMagnoliaEncoder {
    ...
    implicit def gen[A]: JsEncoder[A] = macro Magnolia.gen[A]
  }
  object JsMagnoliaDecoder {
    ...
    implicit def gen[A]: JsDecoder[A] = macro Magnolia.gen[A]
  }

Users can import these methods into their scope and get magical derivation at the point of use

  scala> final case class Value(text: String, value: Int)
  scala> import JsMagnoliaEncoder.gen
  scala> Value("hello", 1).toJson
  res = JsObject([("text","hello"),("value",1)])

This may sound tempting, as it involves the least amount of typing, but there are two caveats:

the macro is invoked at every use site, i.e. every time we call .toJson. This slows down compilation and also produces more objects at runtime, which will impact runtime performance.
unexpected things may be derived.

The first caveat is self evident, but unexpected derivations manifests as subtle bugs. Consider what would happen for

  @deriving(JsEncoder)
  final case class Foo(s: Option[String])

if we forgot to provide an implicit derivation for Option. We might expect a Foo(Some("hello")) to look like

  {
    "s":"hello"
  }

But it would instead be

  {
    "s": {
      "type":"Some",
      "get":"hello"
    }
  }

because Magnolia derived an Option encoder for us.

This is confusing, we would rather have the compiler tell us if we forgot something. Full auto is therefore not recommended.

8.4 Shapeless

The Shapeless library is notoriously the most complicated library in Scala. The reason why it has such a reputation is because it takes the implicit language feature to the extreme: creating a kind of generic programming language at the level of the types.

This is not an entirely foreign concept: in Scalaz we try to limit our use of the implicit language feature to typeclasses, but we sometimes ask the compiler to provide us with evidence relating types. For example Liskov or Leibniz relationship (<~< and ===), and to Inject a free algebra into a scalaz.Coproduct of algebras.

To install Shapeless, add the following to build.sbt

  libraryDependencies += "com.chuusai" %% "shapeless" % "2.3.3"

At the core of Shapeless are the HList and Coproduct data types

  package shapeless
  
  sealed trait HList
  final case class ::[+H, +T <: HList](head: H, tail: T) extends HList
  sealed trait NNil extends HList
  case object HNil extends HNil {
    def ::[H](h: H): H :: HNil = ::(h, this)
  }
  
  sealed trait Coproduct
  sealed trait :+:[+H, +T <: Coproduct] extends Coproduct
  final case class Inl[+H, +T <: Coproduct](head: H) extends :+:[H, T]
  final case class Inr[+H, +T <: Coproduct](tail: T) extends :+:[H, T]
  sealed trait CNil extends Coproduct // no instances

which are generic representations of products and coproducts, respectively. The sealed trait HNil is for convenience so we never need to type HNil.type.

Shapeless has a clone of the IsoSet datatype, called Generic, which allows us to move between an ADT and its generic representation:

  trait Generic[T] {
    type Repr
    def to(t: T): Repr
    def from(r: Repr): T
  }
  object Generic {
    type Aux[T, R] = Generic[T] { type Repr = R }
    def apply[T](implicit G: Generic[T]): Aux[T, G.Repr] = G
    implicit def materialize[T, R]: Aux[T, R] = macro ...
  }

Many of the data types have a type member (Repr) and an .Aux type alias on their companion that makes the second type visible. This allows us to request the Generic[Foo] for a type Foo without having to provide the verbose type of the generic representation, instead generated by a .materialize macro:

  scala> import shapeless._
  scala> final case class Foo(a: String, b: Long)
         Generic[Foo].to(Foo("hello", 13L))
  res: String :: Long :: HNil = hello :: 13 :: HNil
  
  scala> Generic[Foo].from("hello" :: 13L :: HNil)
  res: Foo = Foo(hello,13)
  
  scala> sealed abstract class Bar
         case object Irish extends Bar
         case object English extends Bar
  
  scala> Generic[Bar].to(Irish)
  res: English.type :+: Irish.type :+: CNil.type = Inl(Irish)
  
  scala> Generic[Bar].from(Inl(Irish))
  res: Bar = Irish

There is a complementary LabelledGeneric that includes the field names

  scala> import shapeless._, labelled._
  scala> final case class Foo(a: String, b: Long)
  
  scala> LabelledGeneric[Foo].to(Foo("hello", 13L))
  res: String with KeyTag[Symbol with Tagged[String("a")], String] ::
       Long   with KeyTag[Symbol with Tagged[String("b")],   Long] ::
       HNil =
       hello :: 13 :: HNil
  
  scala> sealed abstract class Bar
         case object Irish extends Bar
         case object English extends Bar
  
  scala> LabelledGeneric[Bar].to(Irish)
  res: Irish.type   with KeyTag[Symbol with Tagged[String("Irish")],     Irish.type] :+:
       English.type with KeyTag[Symbol with Tagged[String("English")], English.type] :+:
       CNil.type =
       Inl(Irish)

Note that the value of a LabelledGeneric representation is the same as the Generic representation: field names only exist in the type and are erased at runtime.

We never need to type KeyTag manually, we use the type alias:

  type FieldType[K, +V] = V with KeyTag[K, V]

If we want to access the field name from a FieldType[K, A], we ask for implicit evidence Witness.Aux[K], which allows us to access the value of K at runtime.

Superficially, this is all we need to know about Shapeless to be able to derive a typeclass. However, things get increasingly complex, so we will proceed with increasingly complex examples.

8.4.1 Example: Equal

A typical pattern to follow is to extend the typeclass that we wish to derive, and put the Shapeless code on its companion. This gives us an implicit scope that the compiler can search with without requiring the user to provide complex imports

  trait DerivedEqual[A] extends Equal[A]
  object DerivedEqual {
    ...
  }

The entry point to a Shapeless derivation is a method, gen, requiring two type parameters: the A that we are deriving and the R for its generic representation. We then ask for the Generic.Aux[A, R], relating A to R, and an instance of the Derived typeclass for the R. We begin with this signature and simple implementation:

  import shapeless._
  
  object DerivedEqual {
    def gen[A, R: DerivedEqual](implicit G: Generic.Aux[A, R]): Equal[A] =
      (a1, a2) => Equal[R].equal(G.to(a1), G.to(a2))
  }

We’ve reduced the problem to providing an implicit Equal[R] for an arbitrary R that has an instance of a Generic. Let’s first consider products, where R <: HList. This is the signature we want to implement:

  implicit def hcons[H: Equal, T <: HList: DerivedEqual]: DerivedEqual[H :: T]

because if we can implement it for a head and a tail, the compiler will be able to recurse on this method until it reaches the end of the list. Where we will need to provide an instance for the empty HNil

  implicit def hnil: DerivedEqual[HNil]

Let’s look to implement these methods

  implicit def hcons[H: Equal, T <: HList: DerivedEqual]: DerivedEqual[H :: T] =
    (h1, h2) => Equal[H].equal(h1.head, h2.head) && Equal[T].equal(h1.tail, h2.tail)
  
  implicit val hnil: DerivedEqual[HNil] = (_, _) => true

and for coproducts we want to implement these signatures

  implicit def ccons[H: Equal, T <: Coproduct: DerivedEqual]: DerivedEqual[H :+: T]
  implicit def cnil: DerivedEqual[CNil]

Scalaz and Shapeless share many type names, when mixing them we often need to exclude certain elements from the import, e.g.

  import scalaz.{ Coproduct => _, :+: => _, _ }, Scalaz._
  import shapeless._

There is no instance for cnil so it can just throw an exception as it will never be called: it’s a leak in the type system

  implicit val cnil: DerivedEqual[CNil] = (_, _) => sys.error("impossible")

For the coproduct case we can only compare two things if they align, which is when they are both Inl or Inr

  implicit def ccons[H: Equal, T <: Coproduct: DerivedEqual]: DerivedEqual[H :+: T] = {
    case (Inl(c1), Inl(c2)) => Equal[H].equal(c1, c2)
    case (Inr(c1), Inr(c2)) => Equal[T].equal(c1, c2)
    case _                  => false
  }

It is noteworthy that our methods align with the concept of conquer (hnil), divide2 (hlist) and alt2 (coproduct)! However, we don’t get any of the advantages of implementing Decidable, as now we must start from scratch when writing tests for this code.

So let’s test this thing with a simple ADT

  sealed abstract class Foo
  final case class Bar(s: String)          extends Foo
  final case class Faz(b: Boolean, i: Int) extends Foo
  final case object Baz                    extends Foo

We need to provide instances on the companions:

  object Foo {
    implicit val equal: Equal[Foo] = DerivedEqual.gen
  }
  object Bar {
    implicit val equal: Equal[Bar] = DerivedEqual.gen
  }
  object Faz {
    implicit val equal: Equal[Faz] = DerivedEqual.gen
  }
  final case object Baz extends Foo {
    implicit val equal: Equal[Baz.type] = DerivedEqual.gen
  }

But it doesn’t compile

  [error] shapeless.scala:41:38: ambiguous implicit values:
  [error]  both value hnil in object DerivedEqual of type => DerivedEqual[HNil]
  [error]  and value cnil in object DerivedEqual of type => DerivedEqual[CNil]
  [error]  match expected type DerivedEqual[R]
  [error]     : Equal[Baz.type] = DerivedEqual.gen
  [error]                                      ^

Welcome to Shapeless compilation errors!

The problem, which is not at all evident in the error, is that the compiler is unable to work out what R is, and gets caught thinking it is something else. We need to provide the explicit type parameters when calling gen, e.g.

  implicit val equal: Equal[Baz.type] = DerivedEqual.gen[Baz.type, HNil]

or we can use the Generic macro to help us and let the compiler infer the generic representation

  object Foo {
    implicit val generic           = Generic[Foo]
    implicit val equal: Equal[Foo] = DerivedEqual.gen[Foo, generic.Repr]
  }
  object Bar {
    implicit val generic           = Generic[Bar]
    implicit val equal: Equal[Bar] = DerivedEqual.gen[Bar, generic.Repr]
  }
  object Faz {
    implicit val generic           = Generic[Faz]
    implicit val equal: Equal[Faz] = DerivedEqual.gen[Faz, generic.Repr]
  }
  final case object Baz extends Foo {
    implicit val generic                = Generic[Baz.type]
    implicit val equal: Equal[Baz.type] = DerivedEqual.gen[Baz.type, generic.Repr]
  }

The reason why this fixes the problem is because the type signature

  def gen[A, R: DerivedEqual](implicit G: Generic.Aux[A, R]): Equal[A]

desugars into

  def gen[A, R](implicit R: DerivedEqual[R], G: Generic.Aux[A, R]): Equal[A]

The Scala compiler solves type constraints left to right, so it finds many different solutions to DerivedEqual[R] before constraining it with the Generic.Aux[A, R]. Another way to solve this is to not use context bounds.

With this in mind, we no longer need the implicit val generic or the explicit type parameters on the call to .gen. We can wire up @deriving by adding an entry in deriving.conf (assuming we want to override the scalaz-deriving implementation)

  scalaz.Equal=fommil.DerivedEqual.gen

and write

  @deriving(Equal) sealed abstract class Foo
  @deriving(Equal) final case class Bar(s: String)          extends Foo
  @deriving(Equal) final case class Faz(b: Boolean, i: Int) extends Foo
  @deriving(Equal) final case object Baz

But replacing the scalaz-deriving version means that compile times get slower. This is because the compiler is solving N implicit searches for each product of N fields or coproduct of N products, whereas scalaz-deriving and Magnolia do not.

Note that when using scalaz-deriving or Magnolia we can put the @deriving on just the top member of an ADT, but for Shapeless we must add it to all entries.

However, this implementation still has a bug: it fails for recursive types at runtime, e.g.

  @deriving(Equal) sealed trait ATree
  @deriving(Equal) final case class Leaf(value: String)               extends ATree
  @deriving(Equal) final case class Branch(left: ATree, right: ATree) extends ATree

  scala> val leaf1: Leaf    = Leaf("hello")
         val leaf2: Leaf    = Leaf("goodbye")
         val branch: Branch = Branch(leaf1, leaf2)
         val tree1: ATree   = Branch(leaf1, branch)
         val tree2: ATree   = Branch(leaf2, branch)
  
  scala> assert(tree1 /== tree2)
  [error] java.lang.NullPointerException
  [error] at DerivedEqual$.shapes$DerivedEqual$$$anonfun$hcons$1(shapeless.scala:16)
          ...

The reason why this happens is because Equal[Tree] depends on the Equal[Branch], which depends on the Equal[Tree]. Recursion and BANG! It must be loaded lazily, not eagerly.

Both scalaz-deriving and Magnolia deal with lazy automatically, but in Shapeless it is the responsibility of the typeclass author.

The macro types Cached, Strict and Lazy modify the compiler’s type inference behaviour allowing us to achieve the laziness we require. The pattern to follow is to use Cached[Strict[_]] on the entry point and Lazy[_] around the H instances.

It is best to depart from context bounds and SAM types entirely at this point:

  sealed trait DerivedEqual[A] extends Equal[A]
  object DerivedEqual {
    def gen[A, R](
      implicit G: Generic.Aux[A, R],
      R: Cached[Strict[DerivedEqual[R]]]
    ): Equal[A] = new Equal[A] {
      def equal(a1: A, a2: A) =
        quick(a1, a2) || R.value.value.equal(G.to(a1), G.to(a2))
    }
  
    implicit def hcons[H, T <: HList](
      implicit H: Lazy[Equal[H]],
      T: DerivedEqual[T]
    ): DerivedEqual[H :: T] = new DerivedEqual[H :: T] {
      def equal(ht1: H :: T, ht2: H :: T) =
        (quick(ht1.head, ht2.head) || H.value.equal(ht1.head, ht2.head)) &&
          T.equal(ht1.tail, ht2.tail)
    }
  
    implicit val hnil: DerivedEqual[HNil] = new DerivedEqual[HNil] {
      def equal(@unused h1: HNil, @unused h2: HNil) = true
    }
  
    implicit def ccons[H, T <: Coproduct](
      implicit H: Lazy[Equal[H]],
      T: DerivedEqual[T]
    ): DerivedEqual[H :+: T] = new DerivedEqual[H :+: T] {
      def equal(ht1: H :+: T, ht2: H :+: T) = (ht1, ht2) match {
        case (Inl(c1), Inl(c2)) => quick(c1, c2) || H.value.equal(c1, c2)
        case (Inr(c1), Inr(c2)) => T.equal(c1, c2)
        case _                  => false
      }
    }
  
    implicit val cnil: DerivedEqual[CNil] = new DerivedEqual[CNil] {
      def equal(@unused c1: CNil, @unused c2: CNil) = sys.error("impossible")
    }
  
    @inline private final def quick(a: Any, b: Any): Boolean =
      a.asInstanceOf[AnyRef].eq(b.asInstanceOf[AnyRef])
  }

While we were at it, we optimised using the quick shortcut from scalaz-deriving.

We can now call

  assert(tree1 /== tree2)

without a runtime exception.

8.4.2 Example: `Default`

There are no new snares in the implementation of a typeclass with a type parameter in covariant position. Here we create HList and Coproduct values, and must provide a value for the CNil case as it corresponds to the case where no coproduct is able to provide a value.

  sealed trait DerivedDefault[A] extends Default[A]
  object DerivedDefault {
    def gen[A, R](
      implicit G: Generic.Aux[A, R],
      R: Cached[Strict[DerivedDefault[R]]]
    ): Default[A] = new Default[A] {
      def default = R.value.value.default.map(G.from)
    }
  
    implicit def hcons[H, T <: HList](
      implicit H: Lazy[Default[H]],
      T: DerivedDefault[T]
    ): DerivedDefault[H :: T] = new DerivedDefault[H :: T] {
      def default =
        for {
          head <- H.value.default
          tail <- T.default
        } yield head :: tail
    }
  
    implicit val hnil: DerivedDefault[HNil] = new DerivedDefault[HNil] {
      def default = HNil.right
    }
  
    implicit def ccons[H, T <: Coproduct](
      implicit H: Lazy[Default[H]],
      T: DerivedDefault[T]
    ): DerivedDefault[H :+: T] = new DerivedDefault[H :+: T] {
      def default = H.value.default.map(Inl(_)).orElse(T.default.map(Inr(_)))
    }
  
    implicit val cnil: DerivedDefault[CNil] = new DerivedDefault[CNil] {
      def default = "not a valid coproduct".left
    }
  }

Much as we could draw an analogy between Equal and Decidable, we can see the relationship to Alt in .point (hnil), .apply2 (.hcons) and .altly2 (.ccons).

There is little to be learned from an example like Semigroup, so we will skip to encoders and decoders.

8.4.3 Example: `JsEncoder`

To be able to reproduce our Magnolia JSON encoder, we must be able to access:

field names and class names
annotations for user preferences
default values on a case class

We’ll begin by creating an encoder that handles only the sensible defaults.

To get field names, we use LabelledGeneric instead of Generic, and when defining the type of the head element, use FieldType[K, H] instead of just H. Request a Witness.Aux[K] to be able to access the value of the field name K at runtime.

  import shapeless._, labelled._
  
  sealed trait DerivedJsEncoder[R] {
    def toJsFields(r: R): IList[(String, JsValue)]
  }
  object DerivedJsEncoder {
    def gen[A, R](
      implicit G: LabelledGeneric.Aux[A, R],
      R: Cached[Strict[DerivedJsEncoder[R]]]
    ): JsEncoder[A] = new JsEncoder[A] {
      def toJson(a: A) = JsObject(R.value.value.toJsFields(G.to(a)))
    }
  
    implicit def hcons[K <: Symbol, H, T <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[T]
    ): DerivedJsEncoder[FieldType[K, H] :: T] =
      new DerivedJsEncoder[A, FieldType[K, H] :: T] {
        private val field = K.value.name
        def toJsFields(ht: FieldType[K, H] :: T) =
          ht match {
            case head :: tail =>
              val rest = T.toJsFields(tail)
              H.value.toJson(head) match {
                case JsNull => rest
                case value  => (field -> value) :: rest
              }
          }
      }
  
    implicit val hnil: DerivedJsEncoder[HNil] =
      new DerivedJsEncoder[HNil] {
        def toJsFields(h: HNil) = IList.empty
      }
  
    implicit def ccons[K <: Symbol, H, T <: Coproduct](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[T]
    ): DerivedJsEncoder[FieldType[K, H] :+: T] =
      new DerivedJsEncoder[FieldType[K, H] :+: T] {
        private val hint = ("type" -> JsString(K.value.name))
        def toJsFields(ht: FieldType[K, H] :+: T) = ht match {
          case Inl(head) =>
            H.value.toJson(head) match {
              case JsObject(fields) => hint :: fields
              case v                => IList.single("xvalue" -> v)
            }
  
          case Inr(tail) => T.toJsFields(tail)
        }
      }
  
    implicit val cnil: DerivedJsEncoder[CNil] =
      new DerivedJsEncoder[CNil] {
        def toJsFields(c: CNil) = sys.error("impossible")
      }
  
  }

A pattern has emerged in many Shapeless derivation libraries that introduce “hints” with a default implicit

  trait ProductHint[A] {
    def nulls(field: String): Boolean
    def fieldname(field: String): String
  }
  object ProductHint {
    implicit def default[A]: ProductHint[A] = new ProductHint[A] {
      def nulls(field: String)     = false
      def fieldname(field: String) = field
    }
  }

Users are supposed to provide a custom instance of ProductHint on their companions or package objects.

This mechanism relies on fragile implicit ordering and is a source of typeclass decoherence: if we derive a JsEncoder[Foo], we will get a different result depending on which ProductHint[Foo] is in scope. It is best avoided.

Shapeless selects codepaths at compiletime based on the presence of annotations, which can lead to more optimised code, at the expense of code repetition. This means that the number of annotations we are dealing with, and their subtypes, must minimised or we can find ourselves writing 10x the amount of code. Let’s refactor our three annotations into one containing all the customisation parameters:

  case class json(
    nulls: Boolean,
    field: Option[String],
    hint: Option[String]
  ) extends Annotation

All users of the annotation must provide all three values since default values and convenience methods are not available to annotation constructors. We can write custom extractors so we don’t have to change our Magnolia code

  object json {
    object nulls {
      def unapply(j: json): Boolean = j.nulls
    }
    object field {
      def unapply(j: json): Option[String] = j.field
    }
    object hint {
      def unapply(j: json): Option[String] = j.hint
    }
  }

We can request Annotation[json, A] for a case class or sealed trait to get access to the annotation, but we must write an hcons and a ccons dealing with both cases because the evidence will not be generated if the annotation is not present. We therefore have to introduce a lower priority implicit scope and put the “no annotation” evidence there.

We can also request Annotations.Aux[json, A, J] evidence to obtain an HList of the json annotation for type A. Again, we must provide hcons and ccons dealing with the case where there is and is not an annotation.

To support this one annotation, we must write four times as much code as before!

Lets start by rewriting the JsEncoder, only handling user code that doesn’t have any annotations. Now any code that uses the @json will fail to compile, which is a good safety net.

We must add an A and J type to the DerivedJsEncoder and thread through the annotations on its .toJsObject method. Our .hcons and .ccons evidence now provides instances for DerivedJsEncoder with a None.type annotation and we move them to a lower priority so that we can deal with Annotation[json, A] in the higher priority.

Note that the evidence for J is listed before R. This is important, since the compiler must first fix the type of J before it can solve for R.

  sealed trait DerivedJsEncoder[A, R, J <: HList] {
    def toJsFields(r: R, anns: J): IList[(String, JsValue)]
  }
  object DerivedJsEncoder extends DerivedJsEncoder1 {
    def gen[A, R, J <: HList](
      implicit
      G: LabelledGeneric.Aux[A, R],
      J: Annotations.Aux[json, A, J],
      R: Cached[Strict[DerivedJsEncoder[A, R, J]]]
    ): JsEncoder[A] = new JsEncoder[A] {
      def toJson(a: A) = JsObject(R.value.value.toJsFields(G.to(a), J()))
    }
  
    implicit def hnil[A]: DerivedJsEncoder[A, HNil, HNil] =
      new DerivedJsEncoder[A, HNil, HNil] {
        def toJsFields(h: HNil, a: HNil) = IList.empty
      }
  
    implicit def cnil[A]: DerivedJsEncoder[A, CNil, HNil] =
      new DerivedJsEncoder[A, CNil, HNil] {
        def toJsFields(c: CNil, a: HNil) = sys.error("impossible")
      }
  }
  private[jsonformat] trait DerivedJsEncoder1 {
    implicit def hcons[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, None.type :: J] =
      new DerivedJsEncoder[A, FieldType[K, H] :: T, None.type :: J] {
        private val field = K.value.name
        def toJsFields(ht: FieldType[K, H] :: T, anns: None.type :: J) =
          ht match {
            case head :: tail =>
              val rest = T.toJsFields(tail, anns.tail)
              H.value.toJson(head) match {
                case JsNull => rest
                case value  => (field -> value) :: rest
              }
          }
      }
  
    implicit def ccons[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J] =
      new DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J] {
        private val hint = ("type" -> JsString(K.value.name))
        def toJsFields(ht: FieldType[K, H] :+: T, anns: None.type :: J) =
          ht match {
            case Inl(head) =>
              H.value.toJson(head) match {
                case JsObject(fields) => hint :: fields
                case v                => IList.single("xvalue" -> v)
              }
            case Inr(tail) => T.toJsFields(tail, anns.tail)
          }
      }
  }

Now we can add the type signatures for the six new methods, covering all the possibilities of where the annotation can be. Note that we only support one annotation in each position. If the user provides multiple annotations, anything after the first will be silently ignored.

We’re now running out of names for things, so we will arbitrarily call it Annotated when there is an annotation on the A, and Custom when there is an annotation on a field:

  object DerivedJsEncoder extends DerivedJsEncoder1 {
    ...
    implicit def hconsAnnotated[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, None.type :: J]
  
    implicit def cconsAnnotated[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J]
  
    implicit def hconsAnnotatedCustom[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, Some[json] :: J]
  
    implicit def cconsAnnotatedCustom[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      A: Annotation[json, A],
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J]
  }
  private[jsonformat] trait DerivedJsEncoder1 {
    ...
    implicit def hconsCustom[A, K <: Symbol, H, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :: T, Some[json] :: J] = ???
  
    implicit def cconsCustom[A, K <: Symbol, H, T <: Coproduct, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J]
  }

We don’t actually need .hconsAnnotated or .hconsAnnotatedCustom for anything, since an annotation on a case class does not mean anything to the encoding of that product, it is only used in .cconsAnnotated*. We can therefore delete two methods.

.cconsAnnotated and .cconsAnnotatedCustom can be defined as

  new DerivedJsEncoder[A, FieldType[K, H] :+: T, None.type :: J] {
    private val hint = A().field.getOrElse("type") -> JsString(K.value.name)
    def toJsFields(ht: FieldType[K, H] :+: T, anns: None.type :: J) = ht match {
      case Inl(head) =>
        H.value.toJson(head) match {
          case JsObject(fields) => hint :: fields
          case v                => IList.single("xvalue" -> v)
        }
      case Inr(tail) => T.toJsFields(tail, anns.tail)
    }
  }

and

  new DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J] {
    private val hintfield = A().field.getOrElse("type")
    def toJsFields(ht: FieldType[K, H] :+: T, anns: Some[json] :: J) = ht match {
      case Inl(head) =>
        val ann = anns.head.get
        H.value.toJson(head) match {
          case JsObject(fields) =>
            val hint = (hintfield -> JsString(ann.hint.getOrElse(K.value.name)))
            hint :: fields
          case v =>
            val xvalue = ann.field.getOrElse("xvalue")
            IList.single(xvalue -> v)
        }
      case Inr(tail) => T.toJsFields(tail, anns.tail)
    }
  }

The use of .head and .get may be concerned but recall that the types here are :: and Some meaning that these methods are total and safe to use.

.hconsCustom and .cconsCustom are written

  new DerivedJsEncoder[A, FieldType[K, H] :: T, Some[json] :: J] {
    def toJsFields(ht: FieldType[K, H] :: T, anns: Some[json] :: J) = ht match {
      case head :: tail =>
        val ann  = anns.head.get
        val next = T.toJsFields(tail, anns.tail)
        H.value.toJson(head) match {
          case JsNull if !ann.nulls => next
          case value =>
            val field = ann.field.getOrElse(K.value.name)
            (field -> value) :: next
        }
    }
  }

and

  new DerivedJsEncoder[A, FieldType[K, H] :+: T, Some[json] :: J] {
    def toJsFields(ht: FieldType[K, H] :+: T, anns: Some[json] :: J) = ht match {
      case Inl(head) =>
        val ann = anns.head.get
        H.value.toJson(head) match {
          case JsObject(fields) =>
            val hint = ("type" -> JsString(ann.hint.getOrElse(K.value.name)))
            hint :: fields
          case v =>
            val xvalue = ann.field.getOrElse("xvalue")
            IList.single(xvalue -> v)
        }
      case Inr(tail) => T.toJsFields(tail, anns.tail)
    }
  }

Obviously, there is a lot of boilerplate, but looking closely one can see that each method is implemented as efficiently as possible with the information it has available: codepaths are selected at compiletime rather than runtime.

The performance obsessed may be able to refactor this code so all annotation information is available in advance, rather than injected via the .toJsFields method, with another layer of indirection. For absolute performance, we could also treat each customisation as a separate annotation, but that would multiply the amount of code we’ve written yet again, with additional cost to compilation time on downstream users. Such optimisations are beyond the scope of this book, but they are possible and people do them: the ability to shift work from runtime to compiletime is one of the most appealing things about generic programming.

One more caveat that we need to be aware of: LabelledGeneric is not compatible with scalaz.@@, but there is a workaround. Say we want to effectively ignore tags so we add the following derivation rules to the companions of our encoder and decoder

  object JsEncoder {
    ...
    implicit def tagged[A: JsEncoder, Z]: JsEncoder[A @@ Z] = JsEncoder[A].contramap(Tag.unwra\
p)
  }
  object JsDecoder {
    ...
    implicit def tagged[A: JsDecoder, Z]: JsDecoder[A @@ Z] = JsDecoder[A].map(Tag(_))
  }

We would then expect to be able to derive a JsDecoder for something like our TradeTemplate from Chapter 5

  final case class TradeTemplate(
    otc: Option[Boolean] @@ Tags.Last
  )
  object TradeTemplate {
    implicit val encoder: JsEncoder[TradeTemplate] = DerivedJsEncoder.gen
  }

But we instead get a compiler error

  [error] could not find implicit value for parameter G: LabelledGeneric.Aux[A,R]
  [error]   implicit val encoder: JsEncoder[TradeTemplate] = DerivedJsEncoder.gen
  [error]                                                                     ^

The error message is as helpful as always. The workaround is to introduce evidence for H @@ Z on the lower priority implicit scope, and then just call the code that the compiler should have found in the first place:

  object DerivedJsEncoder extends DerivedJsEncoder1 with DerivedJsEncoder2 {
    ...
  }
  private[jsonformat] trait DerivedJsEncoder2 {
    this: DerivedJsEncoder.type =>
  
    // WORKAROUND https://github.com/milessabin/shapeless/issues/309
    implicit def hconsTagged[A, K <: Symbol, H, Z, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H @@ Z]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H @@ Z] :: T, None.type :: J] = hcons(K, H, T)
  
    implicit def hconsCustomTagged[A, K <: Symbol, H, Z, T <: HList, J <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsEncoder[H @@ Z]],
      T: DerivedJsEncoder[A, T, J]
    ): DerivedJsEncoder[A, FieldType[K, H @@ Z] :: T, Some[json] :: J] = hconsCustom(K, H, T)
  }

Thankfully, we only need to consider products, since coproducts cannot be tagged.

8.4.4 `JsDecoder`

The decoding side is much as we can expect based on previous examples. We can construct an instance of a FieldType[K, H] with the helper field[K](h: H). Supporting only the sensible defaults means we write:

  sealed trait DerivedJsDecoder[A] {
    def fromJsObject(j: JsObject): String \/ A
  }
  object DerivedJsDecoder {
    def gen[A, R](
      implicit G: LabelledGeneric.Aux[A, R],
      R: Cached[Strict[DerivedJsDecoder[R]]]
    ): JsDecoder[A] = new JsDecoder[A] {
      def fromJson(j: JsValue) = j match {
        case o @ JsObject(_) => R.value.value.fromJsObject(o).map(G.from)
        case other           => fail("JsObject", other)
      }
    }
  
    implicit def hcons[K <: Symbol, H, T <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H]],
      T: DerivedJsDecoder[T]
    ): DerivedJsDecoder[FieldType[K, H] :: T] =
      new DerivedJsDecoder[FieldType[K, H] :: T] {
        private val fieldname = K.value.name
        def fromJsObject(j: JsObject) = {
          val value = j.get(fieldname).getOrElse(JsNull)
          for {
            head  <- H.value.fromJson(value)
            tail  <- T.fromJsObject(j)
          } yield field[K](head) :: tail
        }
      }
  
    implicit val hnil: DerivedJsDecoder[HNil] = new DerivedJsDecoder[HNil] {
      private val nil               = HNil.right[String]
      def fromJsObject(j: JsObject) = nil
    }
  
    implicit def ccons[K <: Symbol, H, T <: Coproduct](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H]],
      T: DerivedJsDecoder[T]
    ): DerivedJsDecoder[FieldType[K, H] :+: T] =
      new DerivedJsDecoder[FieldType[K, H] :+: T] {
        private val hint = ("type" -> JsString(K.value.name))
        def fromJsObject(j: JsObject) =
          if (j.fields.element(hint)) {
            j.get("xvalue")
              .into {
                case \/-(xvalue) => H.value.fromJson(xvalue)
                case -\/(_)      => H.value.fromJson(j)
              }
              .map(h => Inl(field[K](h)))
          } else
            T.fromJsObject(j).map(Inr(_))
      }
  
    implicit val cnil: DerivedJsDecoder[CNil] = new DerivedJsDecoder[CNil] {
      def fromJsObject(j: JsObject) = fail(s"JsObject with 'type' field", j)
    }
  }

Adding user preferences via annotations follows the same route as DerivedJsEncoder and is mechanical, so left as an exercise to the reader.

One final thing is missing: case class default values. We can request evidence but a big problem is that we can no longer use the same derivation mechanism for products and coproducts: the evidence is never created for coproducts.

The solution is quite drastic. We must split our DerivedJsDecoder into DerivedCoproductJsDecoder and DerivedProductJsDecoder. We will focus our attention on the DerivedProductJsDecoder, and while we are at it we will use a Map for faster field lookup:

  sealed trait DerivedProductJsDecoder[A, R, J <: HList, D <: HList] {
    private[jsonformat] def fromJsObject(
      j: Map[String, JsValue],
      anns: J,
      defaults: D
    ): String \/ R
  }

We can request evidence of default values with Default.Aux[A, D] and duplicate all the methods to deal with the case where we do and do not have a default value. However, Shapeless is merciful (for once) and provides Default.AsOptions.Aux[A, D] letting us handle defaults at runtime.

  object DerivedProductJsDecoder {
    def gen[A, R, J <: HList, D <: HList](
      implicit G: LabelledGeneric.Aux[A, R],
      J: Annotations.Aux[json, A, J],
      D: Default.AsOptions.Aux[A, D],
      R: Cached[Strict[DerivedProductJsDecoder[A, R, J, D]]]
    ): JsDecoder[A] = new JsDecoder[A] {
      def fromJson(j: JsValue) = j match {
        case o @ JsObject(_) =>
          R.value.value.fromJsObject(o.fields.toMap, J(), D()).map(G.from)
        case other => fail("JsObject", other)
      }
    }
    ...
  }

We must move the .hcons and .hnil methods onto the companion of the new sealed typeclass, which can handle default values

  object DerivedProductJsDecoder {
    ...
      implicit def hnil[A]: DerivedProductJsDecoder[A, HNil, HNil, HNil] =
      new DerivedProductJsDecoder[A, HNil, HNil, HNil] {
        private val nil = HNil.right[String]
        def fromJsObject(j: StringyMap[JsValue], a: HNil, defaults: HNil) = nil
      }
  
    implicit def hcons[A, K <: Symbol, H, T <: HList, J <: HList, D <: HList](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H]],
      T: DerivedProductJsDecoder[A, T, J, D]
    ): DerivedProductJsDecoder[A, FieldType[K, H] :: T, None.type :: J, Option[H] :: D] =
      new DerivedProductJsDecoder[A, FieldType[K, H] :: T, None.type :: J, Option[H] :: D] {
        private val fieldname = K.value.name
        def fromJsObject(
          j: StringyMap[JsValue],
          anns: None.type :: J,
          defaults: Option[H] :: D
        ) =
          for {
            head <- j.get(fieldname) match {
                     case Maybe.Just(v) => H.value.fromJson(v)
                     case _ =>
                       defaults.head match {
                         case Some(default) => \/-(default)
                         case None          => H.value.fromJson(JsNull)
                       }
                   }
            tail <- T.fromJsObject(j, anns.tail, defaults.tail)
          } yield field[K](head) :: tail
      }
    ...
  }

We can’t use @deriving any more for products and coproducts. One possible hack is to make DerivedCoproductJsDecoder extend from JsDecoder, adding an entry in the deriving.conf for DerivedCoproductJsDecoder as well as one for JsDecoder (which points to DerivedProductJsDecoder), but this adds to the mental burden at the point of use, which is not ideal.

Oh, and don’t forget to add @@ support

  object DerivedProductJsDecoder extends DerivedProductJsDecoder1 {
    ...
  }
  private[jsonformat] trait DerivedProductJsDecoder2 {
    this: DerivedProductJsDecoder.type =>
  
    implicit def hconsTagged[
      A, K <: Symbol, H, Z, T <: HList, J <: HList, D <: HList
    ](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H @@ Z]],
      T: DerivedProductJsDecoder[A, T, J, D]
    ): DerivedProductJsDecoder[
      A,
      FieldType[K, H @@ Z] :: T,
      None.type :: J,
      Option[H @@ Z] :: D
    ] = hcons(K, H, T)
  
    implicit def hconsCustomTagged[
      A, K <: Symbol, H, Z, T <: HList, J <: HList, D <: HList
    ](
      implicit
      K: Witness.Aux[K],
      H: Lazy[JsDecoder[H @@ Z]],
      T: DerivedProductJsDecoder[A, T, J, D]
    ): DerivedProductJsDecoder[
      A,
      FieldType[K, H @@ Z] :: T,
      Some[json] :: J,
      Option[H @@ Z] :: D
    ] = hconsCustomTagged(K, H, T)
  }

8.4.5 Complicated Derivations

Shapeless allows for a lot more kinds of derivations than are possible with scalaz-deriving or Magnolia. As an example of an encoder / decoder than are not possible with Magnolia, consider this simple XML model from xmlformat

  @deriving(Equal, Show, Arbitrary)
  sealed abstract class XNode
  
  @deriving(Equal, Show, Arbitrary)
  final case class XTag(
    name: String,
    attrs: IList[XAttr],
    children: IList[XTag],
    body: Maybe[XString]
  )
  
  @deriving(Equal, Show, Arbitrary)
  final case class XAttr(name: String, value: XString)
  
  @deriving(Show)
  @xderiving(Equal, Monoid, Arbitrary)
  final case class XChildren(tree: IList[XTag]) extends XNode
  
  @deriving(Show)
  @xderiving(Equal, Semigroup, Arbitrary)
  final case class XString(text: String) extends XNode

Given the nature of XML it makes sense to have separate encoder / decoder pairs for XChildren and XString content. We could provide a derivation for the XChildren with Shapeless but we want to special case fields based on the kind of typeclass they have, as well as Option fields. We could even require that fields are annotated with their encoded name. In addition, when decoding we wish to have different strategies for handling XML element bodies, which can be multipart, depending on if our type has a Semigroup, Monoid or neither.

8.4.6 Example: `UrlQueryWriter`

Along similar lines as xmlformat, our drone-dynamic-agents application could benefit from a typeclass derivation of the UrlQueryWriter typeclass, which is built out of UrlEncodedWriter instances for each field entry. It does not support coproducts:

  @typeclass trait UrlQueryWriter[A] {
    def toUrlQuery(a: A): UrlQuery
  }
  trait DerivedUrlQueryWriter[T] extends UrlQueryWriter[T]
  object DerivedUrlQueryWriter {
    def gen[T, Repr](
      implicit
      G: LabelledGeneric.Aux[T, Repr],
      CR: Cached[Strict[DerivedUrlQueryWriter[Repr]]]
    ): UrlQueryWriter[T] = { t =>
      CR.value.value.toUrlQuery(G.to(t))
    }
  
    implicit val hnil: DerivedUrlQueryWriter[HNil] = { _ =>
      UrlQuery(IList.empty)
    }
    implicit def hcons[Key <: Symbol, A, Remaining <: HList](
      implicit Key: Witness.Aux[Key],
      LV: Lazy[UrlEncodedWriter[A]],
      DR: DerivedUrlQueryWriter[Remaining]
    ): DerivedUrlQueryWriter[FieldType[Key, A] :: Remaining] = {
      case head :: tail =>
        val first = Key.value.name -> URLDecoder.decode(LV.value.toUrlEncoded(head).value, "UT\
F-8")
        val rest = DR.toUrlQuery(tail)
        UrlQuery(first :: rest.params)
    }
  }

It is reasonable to ask if these 30 lines are an improvement over the 16 lines for the 3 manual instances our application needs.

8.4.7 The Dark Side of Derivation

“Beware fully automatic derivation. Anger, fear, aggression; the dark side of the derivation are they. Easily they flow, quick to join you in a fight. If once you start down the dark path, forever will it dominate your compiler, consume you it will.”

― an ancient Shapeless master

In addition to all the warnings about fully automatic derivation that were mentioned for Magnolia, Shapeless is much worse. Not only is fully automatic Shapeless derivation the most common cause of slow compiles, it is also a painful source of typeclass coherence bugs.

Fully automatic derivation is when the def gen are implicit such that a call will recurse for all entries in the ADT. Because of the way that implicit scopes work, an imported implicit def will have a higher priority than custom instances on companions, creating a source of typeclass decoherence. For example, consider this code if our .gen were implicit

  import DerivedJsEncoder._
  
  @xderiving(JsEncoder)
  final case class Foo(s: String)
  final case class Bar(foo: Foo)

We might expect the full-auto encoded form of Bar("hello") to look like

  {
    "foo":"hello"
  }

because we have used xderiving for Foo. But it can instead be

  {
    "foo": {
      "s":"hello"
    }
  }

Worse yet is when implicit methods are added to the companion of the typeclass, meaning that the typeclass is always derived at the point of use and users are unable opt out.

Fundamentally, when writing generic programs, implicits can be ignored by the compiler depending on scope, meaning that we lose the compiletime safety that was our motivation for programming at the type level in the first place!

Everything is much simpler in the light side, where implicit is only used for coherent, globally unique, typeclasses. Fear of boilerplate is the path to the dark side. Fear leads to anger. Anger leads to hate. Hate leads to suffering.

8.5 Performance

There is no silver bullet when it comes to typeclass derivation. An axis to consider is performance: both at compiletime and runtime.

8.5.0.1 Compile Times

When it comes to compilation times, Shapeless is the outlier. It is not uncommon to see a small project expand from a one second compile to a one minute compile. To investigate compilation issues, we can profile our applications with the scalac-profiling plugin

  addCompilerPlugin("ch.epfl.scala" %% "scalac-profiling" % "1.0.0")
  scalacOptions ++= Seq("-Ystatistics:typer", "-P:scalac-profiling:no-profiledb")

It produces output that can generate a flame graph.

For a typical Shapeless derivation, we get a lively chart

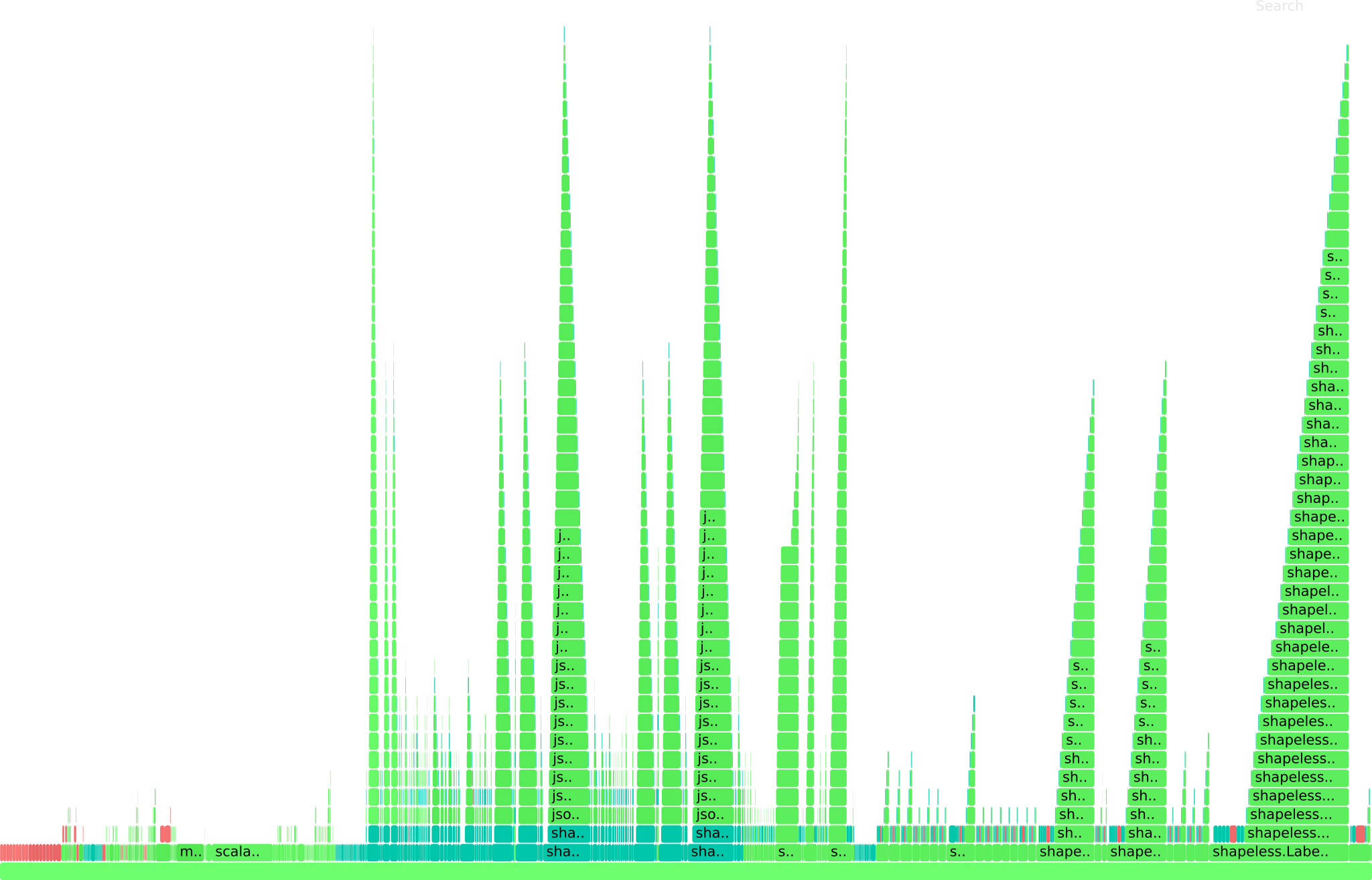
almost the entire compile time is spent in implicit resolution. Note that this also includes compiling the scalaz-deriving, Magnolia and manual instances, but the Shapeless computations dominate. Implicit resolution for scalaz-deriving, Magnolia and manual instances are simple: everything is on the data type companions.

And this is when it works. If there is a problem with a shapeless derivation, the compiler can get stuck in an infinite loop and must be killed.

8.5.0.2 Runtime Performance

If we move to runtime performance, the answer is always it depends.

Assuming that the derivation logic has been written in an efficient way, it is only possible to know which is faster through experimentation.

The jsonformat library uses the Java Microbenchmark Harness (JMH) on models that map to GeoJSON, Google Maps, and Twitter, contributed by Andriy Plokhotnyuk. There are three tests per model:

encoding the ADT to a JsValue
a successful decoding of the same JsValue back into an ADT
a failure decoding of a JsValue with a data error

applied to the following implementations:

Magnolia
Shapeless
manually written

with the equivalent optimisations in each. The results are in operations per second (higher is better), on a powerful desktop computer, using a single thread:

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*encode*
  Benchmark                                 Mode  Cnt       Score      Error  Units
  
  GeoJSONBenchmarks.encodeMagnolia         thrpt    5   70527.223 ±  546.991  ops/s
  GeoJSONBenchmarks.encodeShapeless        thrpt    5   65925.215 ±  309.623  ops/s
  GeoJSONBenchmarks.encodeManual           thrpt    5   96435.691 ±  334.652  ops/s
  
  GoogleMapsAPIBenchmarks.encodeMagnolia   thrpt    5   73107.747 ±  439.803  ops/s
  GoogleMapsAPIBenchmarks.encodeShapeless  thrpt    5   53867.845 ±  510.888  ops/s
  GoogleMapsAPIBenchmarks.encodeManual     thrpt    5  127608.402 ± 1584.038  ops/s
  
  TwitterAPIBenchmarks.encodeMagnolia      thrpt    5  133425.164 ± 1281.331  ops/s
  TwitterAPIBenchmarks.encodeShapeless     thrpt    5   84233.065 ±  352.611  ops/s
  TwitterAPIBenchmarks.encodeManual        thrpt    5  281606.574 ± 1975.873  ops/s

We see that the manual implementations are in the lead, followed by Magnolia, with Shapeless from 30% to 70% the performance of the manual instances. Now for decoding

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*decode.*Success
  Benchmark                                        Mode  Cnt       Score      Error  Units
  
  GeoJSONBenchmarks.decodeMagnoliaSuccess         thrpt    5   40850.270 ±  201.457  ops/s
  GeoJSONBenchmarks.decodeShapelessSuccess        thrpt    5   41173.199 ±  373.048  ops/s
  GeoJSONBenchmarks.decodeManualSuccess           thrpt    5  110961.246 ±  468.384  ops/s
  
  GoogleMapsAPIBenchmarks.decodeMagnoliaSuccess   thrpt    5   44577.796 ±  457.861  ops/s
  GoogleMapsAPIBenchmarks.decodeShapelessSuccess  thrpt    5   31649.792 ±  861.169  ops/s
  GoogleMapsAPIBenchmarks.decodeManualSuccess     thrpt    5   56250.913 ±  394.105  ops/s
  
  TwitterAPIBenchmarks.decodeMagnoliaSuccess      thrpt    5   55868.832 ± 1106.543  ops/s
  TwitterAPIBenchmarks.decodeShapelessSuccess     thrpt    5   47711.161 ±  356.911  ops/s
  TwitterAPIBenchmarks.decodeManualSuccess        thrpt    5   71962.394 ±  465.752  ops/s

This is a tighter race, with Shapeless keeping pace with Magnolia, by and large, and manual instances performing the best on the GeoJSON data. Finally, decoding from a JsValue that contains invalid data (in an intentionally awkward position)

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*decode.*Error
  Benchmark                                      Mode  Cnt        Score       Error  Units
  
  GeoJSONBenchmarks.decodeMagnoliaError         thrpt    5   981094.831 ± 11051.370  ops/s
  GeoJSONBenchmarks.decodeShapelessError        thrpt    5   816704.635 ±  9781.467  ops/s
  GeoJSONBenchmarks.decodeManualError           thrpt    5   586733.762 ±  6389.296  ops/s
  
  GoogleMapsAPIBenchmarks.decodeMagnoliaError   thrpt    5  1288888.446 ± 11091.080  ops/s
  GoogleMapsAPIBenchmarks.decodeShapelessError  thrpt    5  1010145.363 ±  9448.110  ops/s
  GoogleMapsAPIBenchmarks.decodeManualError     thrpt    5  1417662.720 ±  1197.283  ops/s
  
  TwitterAPIBenchmarks.decodeMagnoliaError      thrpt    5   128704.299 ±   832.122  ops/s
  TwitterAPIBenchmarks.decodeShapelessError     thrpt    5   109715.865 ±   826.488  ops/s
  TwitterAPIBenchmarks.decodeManualError        thrpt    5   148814.730 ±  1105.316  ops/s

Just when we thought we were seeing a pattern, both Magnolia and Shapeless win the race when decoding invalid GeoJSON data, but manual instances win the Google Maps and Twitter challenges.

We want to include scalaz-deriving in the comparison, so we compare an equivalent implementation of Equal, tested on two values that contain the same contents (True) and two values that contain slightly different contents (False)

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*equal*
  Benchmark                                     Mode  Cnt        Score       Error  Units
  
  GeoJSONBenchmarks.equalScalazTrue            thrpt    5   276851.493 ±  1776.428  ops/s
  GeoJSONBenchmarks.equalMagnoliaTrue          thrpt    5    93106.945 ±  1051.062  ops/s
  GeoJSONBenchmarks.equalShapelessTrue         thrpt    5   266633.522 ±  4972.167  ops/s
  GeoJSONBenchmarks.equalManualTrue            thrpt    5   599219.169 ±  8331.308  ops/s
  
  GoogleMapsAPIBenchmarks.equalScalazTrue      thrpt    5    35442.577 ±   281.597  ops/s
  GoogleMapsAPIBenchmarks.equalMagnoliaTrue    thrpt    5    91016.557 ±   688.308  ops/s
  GoogleMapsAPIBenchmarks.equalShapelessTrue   thrpt    5   107245.505 ±   468.427  ops/s
  GoogleMapsAPIBenchmarks.equalManualTrue      thrpt    5   302247.760 ±  1927.858  ops/s
  
  TwitterAPIBenchmarks.equalScalazTrue         thrpt    5    99066.013 ±  1125.422  ops/s
  TwitterAPIBenchmarks.equalMagnoliaTrue       thrpt    5   236289.706 ±  3182.664  ops/s
  TwitterAPIBenchmarks.equalShapelessTrue      thrpt    5   251578.931 ±  2430.738  ops/s
  TwitterAPIBenchmarks.equalManualTrue         thrpt    5   865845.158 ±  6339.379  ops/s

As expected, the manual instances are far ahead of the crowd, with Shapeless mostly leading the automatic derivations. scalaz-deriving makes a great effort for GeoJSON but falls far behind in both the Google Maps and Twitter tests. The False tests are more of the same:

  > jsonformat/jmh:run -i 5 -wi 5 -f1 -t1 -w1 -r1 .*equal*
  Benchmark                                     Mode  Cnt        Score       Error  Units
  
  GeoJSONBenchmarks.equalScalazFalse           thrpt    5    89552.875 ±   821.791  ops/s
  GeoJSONBenchmarks.equalMagnoliaFalse         thrpt    5    86044.021 ±  7790.350  ops/s
  GeoJSONBenchmarks.equalShapelessFalse        thrpt    5   262979.062 ±  3310.750  ops/s
  GeoJSONBenchmarks.equalManualFalse           thrpt    5   599989.203 ± 23727.672  ops/s
  
  GoogleMapsAPIBenchmarks.equalScalazFalse     thrpt    5    35970.818 ±   288.609  ops/s
  GoogleMapsAPIBenchmarks.equalMagnoliaFalse   thrpt    5    82381.975 ±   625.407  ops/s
  GoogleMapsAPIBenchmarks.equalShapelessFalse  thrpt    5   110721.122 ±   579.331  ops/s
  GoogleMapsAPIBenchmarks.equalManualFalse     thrpt    5   303588.815 ±  2562.747  ops/s
  
  TwitterAPIBenchmarks.equalScalazFalse        thrpt    5   193930.568 ±  1176.421  ops/s
  TwitterAPIBenchmarks.equalMagnoliaFalse      thrpt    5   429764.654 ± 11944.057  ops/s
  TwitterAPIBenchmarks.equalShapelessFalse     thrpt    5   494510.588 ±  1455.647  ops/s
  TwitterAPIBenchmarks.equalManualFalse        thrpt    5  1631964.531 ± 13110.291  ops/s

The runtime performance of scalaz-deriving, Magnolia and Shapeless is usually good enough. Let’s be honest: we are not writing applications that need to be able to encode more than 130,000 values to JSON, per second, on a single core, on the JVM. If that’s a problem, you might want to look into C++.

It is unlikely that derived instances will be an application’s bottleneck. Even if it is, there is the manually written escape hatch, which is more powerful and therefore more dangerous: it is easy to introduce typos, bugs, and even performance regressions by accident when writing a manual instance.

In conclusion: hokey derivations and ancient macros are no match for a good hand written instance at your side, kid.

8.6 Summary

When deciding on a technology to use for typeclass derivation, this feature chart may help:

Feature	Scalaz	Magnolia	Shapeless	Manual
`@deriving`	yes	yes	yes
Laws	yes
Fast compiles	yes	yes		yes
Field names		yes	yes
Annotations		yes	partially
Default values		yes	with caveats
Complicated			painfully so
Performance				hold my beer

Prefer scalaz-deriving if possible, using Magnolia for encoders / decoders or if performance is a larger concern, escalating to Shapeless for complicated derivations only if compilation times are not a concern.

Manual instances are always an escape hatch for special cases and to achieve the ultimate performance. Avoid introducing typo bugs with manual instances by using a code generation tool.

8. Typeclass Derivation

8.1 Running Examples

8.2 scalaz-deriving

8.2.1 Don’t Repeat Yourself

8.2.2 MonadError

8.2.3 .fromIso

8.2.4 Divisible and Applicative

8.2.5 Decidable and Alt

8.2.6 Arbitrary Arity and @deriving