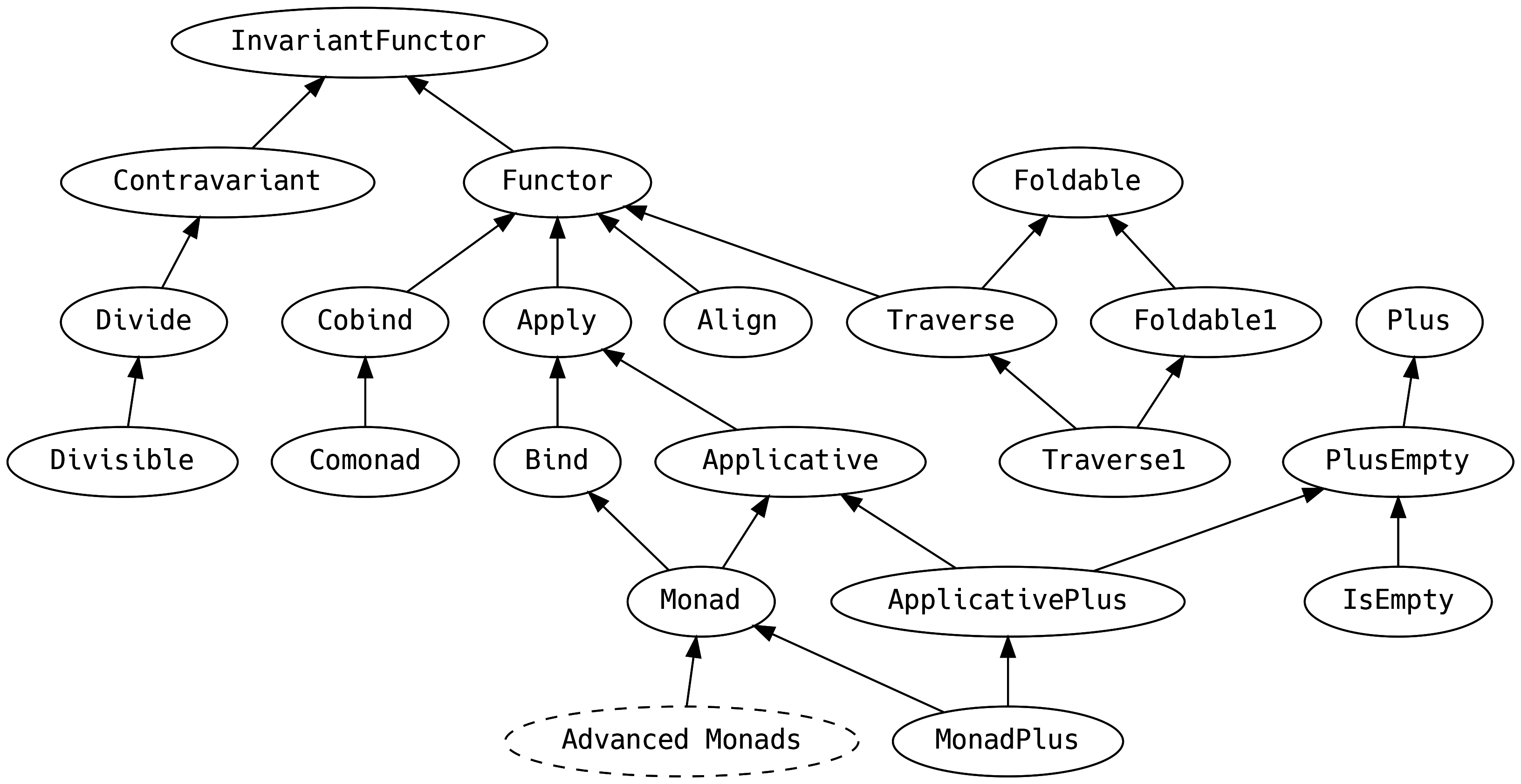
5. Scalaz Typeclasses

In this chapter we will tour most of the typeclasses in scalaz-core. We don’t use everything in drone-dynamic-agents so we will give standalone examples when appropriate.

There has been criticism of the naming in scalaz, and functional programming in general. Most names follow the conventions introduced in the Haskell programming language, based on Category Theory. Feel free to set up type aliases in your own codebase if you would prefer to use verbs based on the primary functionality of the typeclass (e.g. Mappable, Pureable, FlatMappable) until you are comfortable with the standard names.

Before we introduce the typeclass hierarchy, we will peek at the four most important methods from a control flow perspective: the methods we will use the most in typical FP applications:

We know that operations which return a F[_] can be run sequentially in a for comprehension by .flatMap, defined on its Monad[F]. The context F[_] can be thought of as a container for an intentional effect with A as the output: flatMap allows us to generate new effects F[B] at runtime based on the results of evaluating previous effects.

Of course, not all type constructors F[_] are effectful, even if they have a Monad[F]. Often they are data structures. By using the least specific abstraction, we can reuse code for List, Either, Future and more.

If we only need to transform the output from an F[_], that’s just map, introduced by Functor. In Chapter 3, we ran effects in parallel by creating a product and mapping over them. In Functional Programming, parallelisable computations are considered less powerful than sequential ones.

In between Monad and Functor is Applicative, defining pure that lets us lift a value into an effect, or create a data structure from a single value.

traverse is useful for rearranging type constructors. If you find yourself with an F[G[_]] but you really need a G[F[_]] then you need Traverse. For example, say you have a List[Future[Int]] but you need it to be a Future[List[Int]], just call .traverse(identity), or its simpler sibling .sequence.

5.1 Agenda

This chapter is longer than usual and jam-packed with information: it is perfectly reasonable to attack it over several sittings. You are not expected to remember everything (doing so would require super-human powers) so treat this chapter as a way of knowing where to look for more information.

Notably absent are typeclasses that extend Monad, which get their own chapter later.

Scalaz uses code generation, not simulacrum. However, for brevity, we present code snippets with @typeclass. Equivalent syntax is available when we import scalaz._, Scalaz._ and is available under the scalaz.syntax package in the scalaz source code.

5.2 Appendable Things

  @typeclass trait Semigroup[A] {
    @op("|+|") def append(x: A, y: =>A): A
  
    def multiply1(value: F, n: Int): F = ...
  }
  
  @typeclass trait Monoid[A] extends Semigroup[A] {
    def zero: A
  
    def multiply(value: F, n: Int): F =
      if (n <= 0) zero else multiply1(value, n - 1)
  }
  
  @typeclass trait Band[A] extends Semigroup[A]

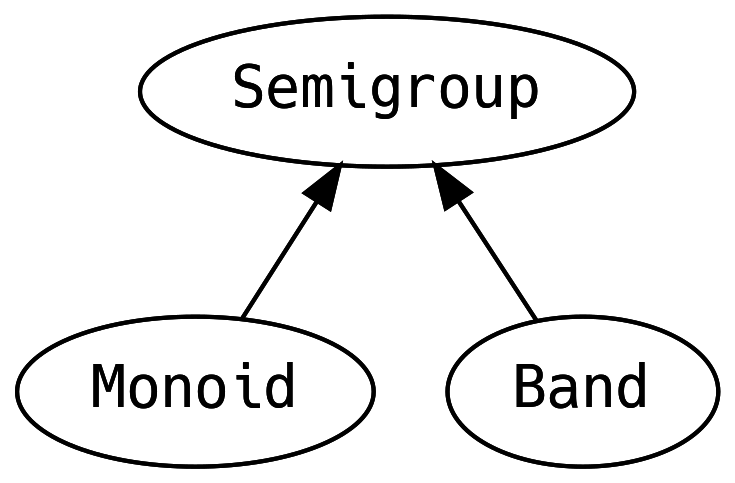
A Semigroup should exist for a type if two elements can be combined to produce another element of the same type. The operation must be associative, meaning that the order of nested operations should not matter, i.e.

  (a |+| b) |+| c == a |+| (b |+| c)
  
  (1 |+| 2) |+| 3 == 1 |+| (2 |+| 3)

A Monoid is a Semigroup with a zero element (also called empty or identity). Combining zero with any other a should give a.

  a |+| zero == a
  
  a |+| 0 == a

This is probably bringing back memories of Numeric from Chapter 4, which tried to do too much and was unusable beyond the most basic of number types. There are implementations of Monoid for all the primitive numbers, but the concept of appendable things is useful beyond numbers.

  scala> "hello" |+| " " |+| "world!"
  res: String = "hello world!"
  
  scala> List(1, 2) |+| List(3, 4)
  res: List[Int] = List(1, 2, 3, 4)

Band has the law that the append operation of the same two elements is idempotent, i.e. gives the same value. Examples are anything that can only be one value, such as Unit, least upper bounds, or a Set. Band provides no further methods yet users can make use of the guarantees for performance optimisation.

As a realistic example for Monoid, consider a trading system that has a large database of reusable trade templates. Creating the default values for a new trade involves selecting and combining templates with a “last rule wins” merge policy (e.g. if templates have a value for the same field).

We’ll create a simple template schema to demonstrate the principle, but keep in mind that a realistic system would have a more complicated ADT.

  sealed abstract class Currency
  case object EUR extends Currency
  case object USD extends Currency
  
  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: Option[Currency],
    otc: Option[Boolean]
  )

If we write a method that takes templates: List[TradeTemplate], we only need to call

  val zero = Monoid[TradeTemplate].zero
  templates.foldLeft(zero)(_ |+| _)

and our job is done!

But to get zero or call |+| we must have an instance of Monoid[TradeTemplate]. Although we will generically derive this in a later chapter, for now we’ll create an instance on the companion:

  object TradeTemplate {
    implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
      (a, b) => TradeTemplate(a.payments |+| b.payments,
                              a.ccy |+| b.ccy,
                              a.otc |+| b.otc),
      TradeTemplate(Nil, None, None)
    )
  }

However, this doesn’t do what we want because Monoid[Option[A]] will append its contents, e.g.

  scala> Option(2) |+| None
  res: Option[Int] = Some(2)
  scala> Option(2) |+| Option(1)
  res: Option[Int] = Some(3)

whereas we want “last rule wins”. We can override the default Monoid[Option[A]] with our own:

  implicit def lastWins[A]: Monoid[Option[A]] = Monoid.instance(
    {
      case (None, None)   => None
      case (only, None)   => only
      case (None, only)   => only
      case (_   , winner) => winner
    },
    None
  )

Now everything compiles, let’s try it out…

  scala> import java.time.{LocalDate => LD}
  scala> val templates = List(
           TradeTemplate(Nil,                     None,      None),
           TradeTemplate(Nil,                     Some(EUR), None),
           TradeTemplate(List(LD.of(2017, 8, 5)), Some(USD), None),
           TradeTemplate(List(LD.of(2017, 9, 5)), None,      Some(true)),
           TradeTemplate(Nil,                     None,      Some(false))
         )
  
  scala> templates.foldLeft(zero)(_ |+| _)
  res: TradeTemplate = TradeTemplate(
                         List(2017-08-05,2017-09-05),
                         Some(USD),
                         Some(false))

All we needed to do was implement one piece of business logic and Monoid took care of everything else for us!

Note that the list of payments are concatenated. This is because the default Monoid[List] uses concatenation of elements and happens to be the desired behaviour. If the business requirement was different, it would be a simple case of providing a custom Monoid[List[LocalDate]]. Recall from Chapter 4 that with compiletime polymorphism we can have a different implementation of append depending on the E in List[E], not just the base runtime class List.

5.3 Objecty Things

In the chapter on Data and Functionality we said that the JVM’s notion of equality breaks down for many things that we can put into an ADT. The problem is that the JVM was designed for Java, and equals is defined on java.lang.Object whether it makes sense or not. There is no way to remove equals and no way to guarantee that it is implemented.

However, in FP we prefer typeclasses for polymorphic functionality and even concepts as simple equality are captured at compiletime.

  @typeclass trait Equal[F]  {
    @op("===") def equal(a1: F, a2: F): Boolean
    @op("/==") def notEqual(a1: F, a2: F): Boolean = !equal(a1, a2)
  }

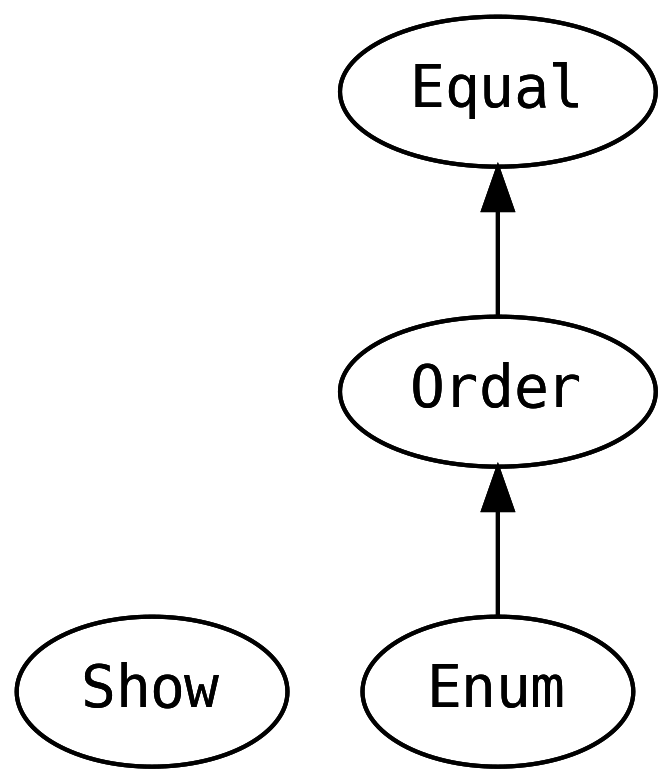
Indeed === (triple equals) is more typesafe than == (double equals) because it can only be compiled when the types are the same on both sides of the comparison. You’d be surprised how many bugs this catches.

equal has the same implementation requirements as Object.equals

• commutative f1 === f2 implies f2 === f1
• reflexive f === f
• transitive f1 === f2 && f2 === f3 implies f1 === f3

By throwing away the universal concept of Object.equals we don’t take equality for granted when we construct an ADT, stopping us at compiletime from expecting equality when there is none.

Continuing the trend of replacing old Java concepts, rather than data being a java.lang.Comparable, they now have an Order according to:

  @typeclass trait Order[F] extends Equal[F] {
    @op("?|?") def order(x: F, y: F): Ordering
  
    override  def equal(x: F, y: F): Boolean = order(x, y) == Ordering.EQ
    @op("<" ) def lt(x: F, y: F): Boolean = ...
    @op("<=") def lte(x: F, y: F): Boolean = ...
    @op(">" ) def gt(x: F, y: F): Boolean = ...
    @op(">=") def gte(x: F, y: F): Boolean = ...
  
    def max(x: F, y: F): F = ...
    def min(x: F, y: F): F = ...
    def sort(x: F, y: F): (F, F) = ...
  }
  
  sealed abstract class Ordering
  object Ordering {
    case object LT extends Ordering
    case object EQ extends Ordering
    case object GT extends Ordering
  }

Order implements .equal in terms of the new primitive .order. When a typeclass implements a parent’s primitive combinator with a derived combinator, an implied law of substitution for the typeclass is added. If an instance of Order were to override .equal for performance reasons, it must behave identically the same as the original.

Things that have an order may also be discrete, allowing us to walk successors and predecessors:

  @typeclass trait Enum[F] extends Order[F] {
    def succ(a: F): F
    def pred(a: F): F
    def min: Option[F]
    def max: Option[F]
  
    @op("-+-") def succn(n: Int, a: F): F = ...
    @op("---") def predn(n: Int, a: F): F = ...
  
    @op("|->" ) def fromToL(from: F, to: F): List[F] = ...
    @op("|-->") def fromStepToL(from: F, step: Int, to: F): List[F] = ...
    @op("|=>" ) def fromToL(from: F, to: F): EphemeralStream[F] = ...
    @op("|==>") def fromStepToL(from: F, step: Int, to: F): EphemeralStream[F] = ...
  }

  scala> 10 |--> (2, 20)
  res: List[Int] = List(10, 12, 14, 16, 18, 20)
  
  scala> 'm' |-> 'u'
  res: List[Char] = List(m, n, o, p, q, r, s, t, u)

We’ll discuss EphemeralStream in the next chapter, for now you just need to know that it is a potentially infinite data structure that avoids memory retention problems in the stdlib Stream.

Similarly to Object.equals, the concept of a .toString on every class does not make sense in Java. We would like to enforce stringyness at compiletime and this is exactly what Show achieves:

  trait Show[F] {
    def show(f: F): Cord = ...
    def shows(f: F): String = ...
  }

We’ll explore Cord in more detail in the chapter on data types, you need only know that it is an efficient data structure for storing and manipulating String.

Unfortunately, due to Scala’s default implicit conversions in Predef, and language level support for toString in interpolated strings, it can be incredibly hard to remember to use shows instead of toString.

5.4 Mappable Things

We’re focusing on things that can be mapped over, or traversed, in some sense:

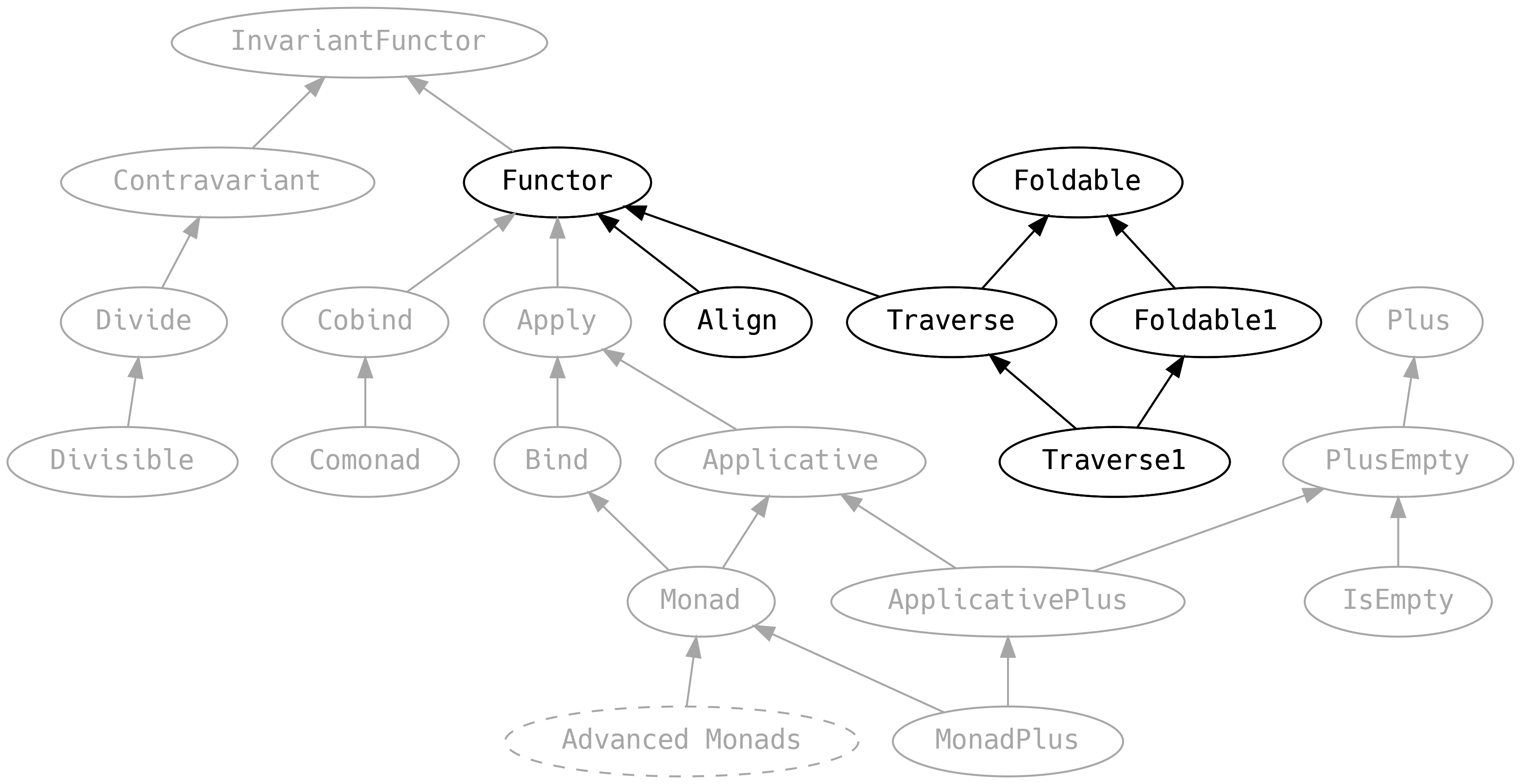
5.4.1 Functor

  @typeclass trait Functor[F[_]] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
  
    def void[A](fa: F[A]): F[Unit] = map(fa)(_ => ())
    def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)] = map(fa)(a => (a, f(a)))
  
    def fpair[A](fa: F[A]): F[(A, A)] = map(fa)(a => (a, a))
    def strengthL[A, B](a: A, f: F[B]): F[(A, B)] = map(f)(b => (a, b))
    def strengthR[A, B](f: F[A], b: B): F[(A, B)] = map(f)(a => (a, b))
  
    def lift[A, B](f: A => B): F[A] => F[B] = map(_)(f)
    def mapply[A, B](a: A)(f: F[A => B]): F[B] = map(f)((ff: A => B) => ff(a))
  }

The only abstract method is map, and it must compose, i.e. mapping with f and then again with g is the same as mapping once with the composition of f and g:

  fa.map(f).map(g) == fa.map(f.andThen(g))

The map should also perform a no-op if the provided function is identity (i.e. x => x)

  fa.map(identity) == fa
  
  fa.map(x => x) == fa

Functor defines some convenience methods around map that can be optimised by specific instances. The documentation has been intentionally omitted in the above definitions to encourage you to guess what a method does before looking at the implementation. Please spend a moment studying only the type signature of the following before reading further:

  def void[A](fa: F[A]): F[Unit]
  def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)]
  
  def fpair[A](fa: F[A]): F[(A, A)]
  def strengthL[A, B](a: A, f: F[B]): F[(A, B)]
  def strengthR[A, B](f: F[A], b: B): F[(A, B)]
  
  // harder
  def lift[A, B](f: A => B): F[A] => F[B]
  def mapply[A, B](a: A)(f: F[A => B]): F[B]

1. void takes an instance of the F[A] and always returns an F[Unit], it forgets all the values whilst preserving the structure.
2. fproduct takes the same input as map but returns F[(A, B)], i.e. it tuples the contents with the result of applying the function. This is useful when we wish to retain the input.
3. fpair twins all the elements of A into a tuple F[(A, A)]
4. strengthL pairs the contents of an F[B] with a constant A on the left.
5. strengthR pairs the contents of an F[A] with a constant B on the right.
6. lift takes a function A => B and returns a F[A] => F[B]. In other words, it takes a function over the contents of an F[A] and returns a function that operates on the F[A] directly.
7. mapply is a mind bender. Say you have an F[_] of functions A => B and a value A, then you can get an F[B]. It has a similar signature to pure but requires the caller to provide the F[A => B].

fpair, strengthL and strengthR look pretty useless, but they are useful when we wish to retain some information that would otherwise be lost to scope.

Functor has some special syntax:

  implicit class FunctorOps[F[_]: Functor, A](self: F[A]) {
    def as[B](b: =>B): F[B] = Functor[F].map(self)(_ => b)
    def >|[B](b: =>B): F[B] = as(b)
  }

as and >| are a way of replacing the output with a constant.

In our example application, as a nasty hack (which we didn’t even admit to until now), we defined start and stop to return their input:

  def start(node: MachineNode): F[MachineNode]
  def stop (node: MachineNode): F[MachineNode]

This allowed us to write terse business logic such as

  for {
    _      <- m.start(node)
    update = world.copy(pending = Map(node -> world.time))
  } yield update

and

  for {
    stopped <- nodes.traverse(m.stop)
    updates = stopped.map(_ -> world.time).toList.toMap
    update  = world.copy(pending = world.pending ++ updates)
  } yield update

But this hack pushes unnecessary complexity into the implementations. It is better if we let our algebras return F[Unit] and use as:

  m.start(node) as world.copy(pending = Map(node -> world.time))

and

  for {
    stopped <- nodes.traverse(a => m.stop(a) as a)
    updates = stopped.map(_ -> world.time).toList.toMap
    update  = world.copy(pending = world.pending ++ updates)
  } yield update

As a bonus, we are now using the less powerful Functor instead of Monad when starting a node.

5.4.2 Foldable

Technically, Foldable is for data structures that can be walked to produce a summary value. However, this undersells the fact that it is a one-typeclass army that can provide most of what you’d expect to see in a Collections API.

There are so many methods we are going to have to split them out, beginning with the abstract methods:

  @typeclass trait Foldable[F[_]] {
    def foldMap[A, B: Monoid](fa: F[A])(f: A => B): B
    def foldRight[A, B](fa: F[A], z: =>B)(f: (A, =>B) => B): B
    def foldLeft[A, B](fa: F[A], z: B)(f: (B, A) => B): B = ...

An instance of Foldable need only implement foldMap and foldRight to get all of the functionality in this typeclass, although methods are typically optimised for specific data structures.

You might recognise foldMap by its marketing buzzword name, MapReduce. Given an F[A], a function from A to B, and a way to combine B (provided by the Monoid, along with a zero B), we can produce a summary value of type B. There is no enforced operation order, allowing for parallel computation.

foldRight does not require its parameters to have a Monoid, meaning that it needs a starting value z and a way to combine each element of the data structure with the summary value. The order for traversing the elements is from right to left and therefore it cannot be parallelised.

foldLeft traverses elements from left to right. foldLeft can be implemented in terms of foldMap, but most instances choose to implement it because it is such a basic operation. Since it is usually implemented with tail recursion, there are no byname parameters.

The only law for Foldable is that foldLeft and foldRight should each be consistent with foldMap for monoidal operations. e.g. appending an element to a list for foldLeft and prepending an element to a list for foldRight. However, foldLeft and foldRight do not need to be consistent with each other: in fact they often produce the reverse of each other.

The simplest thing to do with foldMap is to use the identity function, giving fold (the natural sum of the monoidal elements), with left/right variants to allow choosing based on performance criteria:

  def fold[A: Monoid](t: F[A]): A = ...
  def sumr[A: Monoid](fa: F[A]): A = ...
  def suml[A: Monoid](fa: F[A]): A = ...

Recall that when we learnt about Monoid, we wrote this:

  scala> templates.foldLeft(Monoid[TradeTemplate].zero)(_ |+| _)

We now know this is silly and we should have written:

  scala> templates.toIList.fold
  res: TradeTemplate = TradeTemplate(
                         List(2017-08-05,2017-09-05),
                         Some(USD),
                         Some(false))

.fold doesn’t work on stdlib List because it already has a method called fold that does it is own thing in its own special way.

The strangely named intercalate inserts a specific A between each element before performing the fold

  def intercalate[A: Monoid](fa: F[A], a: A): A = ...

which is a generalised version of the stdlib’s mkString:

  scala> List("foo", "bar").intercalate(",")
  res: String = "foo,bar"

The foldLeft provides the means to obtain any element by traversal index, including a bunch of other related methods:

  def index[A](fa: F[A], i: Int): Option[A] = ...
  def indexOr[A](fa: F[A], default: =>A, i: Int): A = ...
  def length[A](fa: F[A]): Int = ...
  def count[A](fa: F[A]): Int = length(fa)
  def empty[A](fa: F[A]): Boolean = ...
  def element[A: Equal](fa: F[A], a: A): Boolean = ...

Scalaz is a pure library of only total functions, whereas the stdlib .apply returns A and can throw an exception, Foldable.index returns an Option[A] with the convenient .indexOr returning an A when a default value is provided. .element is similar to the stdlib .contains but uses Equal rather than ill-defined JVM equality.

These methods really sound like a collections API. And, of course, anything with a Foldable can be converted into a List

  def toList[A](fa: F[A]): List[A] = ...

There are also conversions to other stdlib and scalaz data types such as .toSet, .toVector, .toStream, .to[T <: TraversableLike], .toIList and so on.

There are useful predicate checks

  def filterLength[A](fa: F[A])(f: A => Boolean): Int = ...
  def all[A](fa: F[A])(p: A => Boolean): Boolean = ...
  def any[A](fa: F[A])(p: A => Boolean): Boolean = ...

filterLength is a way of counting how many elements are true for a predicate, all and any return true if all (or any) element meets the predicate, and may exit early.

We can split an F[A] into parts that result in the same B with splitBy

  def splitBy[A, B: Equal](fa: F[A])(f: A => B): IList[(B, Nel[A])] = ...
  def splitByRelation[A](fa: F[A])(r: (A, A) => Boolean): IList[Nel[A]] = ...
  def splitWith[A](fa: F[A])(p: A => Boolean): List[Nel[A]] = ...
  def selectSplit[A](fa: F[A])(p: A => Boolean): List[Nel[A]] = ...
  
  def findLeft[A](fa: F[A])(f: A => Boolean): Option[A] = ...
  def findRight[A](fa: F[A])(f: A => Boolean): Option[A] = ...

for example

  scala> IList("foo", "bar", "bar", "faz", "gaz", "baz").splitBy(_.charAt(0))
  res = [(f, [foo]), (b, [bar, bar]), (f, [faz]), (g, [gaz]), (b, [baz])]

noting that there are two parts indexed by f.

splitByRelation avoids the need for an Equal but we must provide the comparison operator.

splitWith splits the elements into groups that alternatively satisfy and don’t satisfy the predicate. selectSplit selects groups of elements that satisfy the predicate, discarding others. This is one of those rare occasions when two methods share the same type signature but have different meanings.

findLeft and findRight are for extracting the first element (from the left, or right, respectively) that matches a predicate.

Making further use of Equal and Order, we have the distinct methods which return groupings.

  def distinct[A: Order](fa: F[A]): IList[A] = ...
  def distinctE[A: Equal](fa: F[A]): IList[A] = ...
  def distinctBy[A, B: Equal](fa: F[A])(f: A => B): IList[A] =

distinct is implemented more efficiently than distinctE because it can make use of ordering and therefore use a quicksort-esque algorithm that is much faster than the stdlib’s naive List.distinct. Data structures (such as sets) can implement distinct in their Foldable without doing any work.

distinctBy allows grouping by the result of applying a function to the elements. For example, grouping names by their first letter.

We can make further use of Order by extracting the minimum or maximum element (or both extrema) including variations using the Of or By pattern to first map to another type or to use a different type to do the order comparison.

  def maximum[A: Order](fa: F[A]): Option[A] = ...
  def maximumOf[A, B: Order](fa: F[A])(f: A => B): Option[B] = ...
  def maximumBy[A, B: Order](fa: F[A])(f: A => B): Option[A] = ...
  
  def minimum[A: Order](fa: F[A]): Option[A] = ...
  def minimumOf[A, B: Order](fa: F[A])(f: A => B): Option[B] = ...
  def minimumBy[A, B: Order](fa: F[A])(f: A => B): Option[A] = ...
  
  def extrema[A: Order](fa: F[A]): Option[(A, A)] = ...
  def extremaOf[A, B: Order](fa: F[A])(f: A => B): Option[(B, B)] = ...
  def extremaBy[A, B: Order](fa: F[A])(f: A => B): Option[(A, A)] =

For example we can ask which String is maximum By length, or what is the maximum length Of the elements.

  scala> List("foo", "fazz").maximumBy(_.length)
  res: Option[String] = Some(fazz)
  
  scala> List("foo", "fazz").maximumOf(_.length)
  res: Option[Int] = Some(4)

This concludes the key features of Foldable. You are forgiven for already forgetting all the methods you’ve just seen: the key takeaway is that anything you’d expect to find in a collection library is probably on Foldable and if it isn’t already, it probably should be.

We’ll conclude with some variations of the methods we’ve already seen. First there are methods that take a Semigroup instead of a Monoid:

  def fold1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  def foldMap1Opt[A, B: Semigroup](fa: F[A])(f: A => B): Option[B] = ...
  def sumr1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  def suml1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  ...

returning Option to account for empty data structures (recall that Semigroup does not have a zero).

The typeclass Foldable1 contains a lot more Semigroup variants of the Monoid methods shown here (all suffixed 1) and makes sense for data structures which are never empty, without requiring a Monoid on the elements.

Very importantly, there are variants that take monadic return values. We already used foldLeftM when we first wrote the business logic of our application, now you know that Foldable is where it came from:

  def foldLeftM[G[_]: Monad, A, B](fa: F[A], z: B)(f: (B, A) => G[B]): G[B] = ...
  def foldRightM[G[_]: Monad, A, B](fa: F[A], z: =>B)(f: (A, =>B) => G[B]): G[B] = ...
  def foldMapM[G[_]: Monad, A, B: Monoid](fa: F[A])(f: A => G[B]): G[B] = ...
  def findMapM[M[_]: Monad, A, B](fa: F[A])(f: A => M[Option[B]]): M[Option[B]] = ...
  def allM[G[_]: Monad, A](fa: F[A])(p: A => G[Boolean]): G[Boolean] = ...
  def anyM[G[_]: Monad, A](fa: F[A])(p: A => G[Boolean]): G[Boolean] = ...
  ...

You may also see Curried versions, e.g.

  def foldl[A, B](fa: F[A], z: B)(f: B => A => B): B = ...
  def foldr[A, B](fa: F[A], z: =>B)(f: A => (=> B) => B): B = ...
  ...

5.4.3 Traverse

Traverse is what happens when you cross a Functor with a Foldable

  trait Traverse[F[_]] extends Functor[F] with Foldable[F] {
    def traverse[G[_]: Applicative, A, B](fa: F[A])(f: A => G[B]): G[F[B]]
    def sequence[G[_]: Applicative, A](fga: F[G[A]]): G[F[A]] = ...
  
    def reverse[A](fa: F[A]): F[A] = ...
  
    def zipL[A, B](fa: F[A], fb: F[B]): F[(A, Option[B])] = ...
    def zipR[A, B](fa: F[A], fb: F[B]): F[(Option[A], B)] = ...
    def indexed[A](fa: F[A]): F[(Int, A)] = ...
    def zipWithL[A, B, C](fa: F[A], fb: F[B])(f: (A, Option[B]) => C): F[C] = ...
    def zipWithR[A, B, C](fa: F[A], fb: F[B])(f: (Option[A], B) => C): F[C] = ...
  
    def mapAccumL[S, A, B](fa: F[A], z: S)(f: (S, A) => (S, B)): (S, F[B]) = ...
    def mapAccumR[S, A, B](fa: F[A], z: S)(f: (S, A) => (S, B)): (S, F[B]) = ...
  }

At the beginning of the chapter we showed the importance of traverse and sequence for swapping around type constructors to fit a requirement (e.g. List[Future[_]] to Future[List[_]]). You will use these methods more than you could possibly imagine.

In Foldable we weren’t able to assume that reverse was a universal concept, but now we can reverse a thing.

We can also zip together two things that have a Traverse, getting back None when one side runs out of elements, using zipL or zipR to decide which side to truncate when the lengths don’t match. A special case of zip is to add an index to every entry with indexed.

zipWithL and zipWithR allow combining the two sides of a zip into a new type, and then returning just an F[C].

mapAccumL and mapAccumR are regular map combined with an accumulator. If you find your old Java sins are making you want to reach for a var, and refer to it from a map, you want mapAccumL.

For example, let’s say we have a list of words and we want to blank out words we’ve already seen. The filtering algorithm is not allowed to process the list of words a second time so it can be scaled to an infinite stream:

  scala> val freedom =
  """We campaign for these freedoms because everyone deserves them.
     With these freedoms, the users (both individually and collectively)
     control the program and what it does for them."""
     .split("\\s+")
     .toList
  
  scala> def clean(s: String): String = s.toLowerCase.replaceAll("[,.()]+", "")
  
  scala> freedom
         .mapAccumL(Set.empty[String]) { (seen, word) =>
           val cleaned = clean(word)
           (seen + cleaned, if (seen(cleaned)) "_" else word)
         }
         ._2
         .intercalate(" ")
  
  res: String =
  """We campaign for these freedoms because everyone deserves them.
     With _ _ the users (both individually and collectively)
     control _ program _ what it does _ _"""

Finally Traverse1, like Foldable1, provides variants of these methods for data structures that cannot be empty, accepting the weaker Semigroup instead of a Monoid, and an Apply instead of an Applicative.

5.4.4 Align

Align is about merging and padding anything with a Functor. Before looking at Align, meet the \&/ data type (spoken as These, or hurray!).

  sealed abstract class \&/[+A, +B]
  final case class This[A](aa: A) extends (A \&/ Nothing)
  final case class That[B](bb: B) extends (Nothing \&/ B)
  final case class Both[A, B](aa: A, bb: B) extends (A \&/ B)

i.e. it is a data encoding of inclusive logical OR.

  @typeclass trait Align[F[_]] extends Functor[F] {
    def alignWith[A, B, C](f: A \&/ B => C): (F[A], F[B]) => F[C]
    def align[A, B](a: F[A], b: F[B]): F[A \&/ B] = ...
  
    def merge[A: Semigroup](a1: F[A], a2: F[A]): F[A] = ...
  
    def pad[A, B]: (F[A], F[B]) => F[(Option[A], Option[B])] = ...
    def padWith[A, B, C](f: (Option[A], Option[B]) => C): (F[A], F[B]) => F[C] = ...

Hopefully by this point you are becoming more capable of reading type signatures to understand the purpose of a method.

alignWith takes a function from either an A or a B (or both) to a C and returns a lifted function from a tuple of F[A] and F[B] to an F[C]. align constructs a \&/ out of two F[_].

merge allows us to combine two F[A] when A has a Semigroup. For example, the implementation of Semigroup[Map[K, V]] defers to Semigroup[V], combining two entries results in combining their values, having the consequence that Map[K, List[A]] behaves like a multimap:

  scala> Map("foo" -> List(1)) merge Map("foo" -> List(1), "bar" -> List(2))
  res = Map(foo -> List(1, 1), bar -> List(2))

and a Map[K, Int] simply tally their contents when merging:

  scala> Map("foo" -> 1) merge Map("foo" -> 1, "bar" -> 2)
  res = Map(foo -> 2, bar -> 2)

.pad and .padWith are for partially merging two data structures that might be missing values on one side. For example if we wanted to aggregate independent votes and retain the knowledge of where the votes came from

  scala> Map("foo" -> 1) pad Map("foo" -> 1, "bar" -> 2)
  res = Map(foo -> (Some(1),Some(1)), bar -> (None,Some(2)))
  
  scala> Map("foo" -> 1, "bar" -> 2) pad Map("foo" -> 1)
  res = Map(foo -> (Some(1),Some(1)), bar -> (Some(2),None))

There are convenient variants of align that make use of the structure of \&/

  ...
    def alignSwap[A, B](a: F[A], b: F[B]): F[B \&/ A] = ...
    def alignA[A, B](a: F[A], b: F[B]): F[Option[A]] = ...
    def alignB[A, B](a: F[A], b: F[B]): F[Option[B]] = ...
    def alignThis[A, B](a: F[A], b: F[B]): F[Option[A]] = ...
    def alignThat[A, B](a: F[A], b: F[B]): F[Option[B]] = ...
    def alignBoth[A, B](a: F[A], b: F[B]): F[Option[(A, B)]] = ...
  }

which should make sense from their type signatures. Examples:

  scala> List(1,2,3) alignSwap List(4,5)
  res = List(Both(4,1), Both(5,2), That(3))
  
  scala> List(1,2,3) alignA List(4,5)
  res = List(Some(1), Some(2), Some(3))
  
  scala> List(1,2,3) alignB List(4,5)
  res = List(Some(4), Some(5), None)
  
  scala> List(1,2,3) alignThis List(4,5)
  res = List(None, None, Some(3))
  
  scala> List(1,2,3) alignThat List(4,5)
  res = List(None, None, None)
  
  scala> List(1,2,3) alignBoth List(4,5)
  res = List(Some((1,4)), Some((2,5)), None)

Note that the A and B variants use inclusive OR, whereas the This and That variants are exclusive, returning None if there is a value in both sides, or no value on either side.

5.5 Variance

We must return to Functor for a moment and discuss an ancestor that we previously ignored:

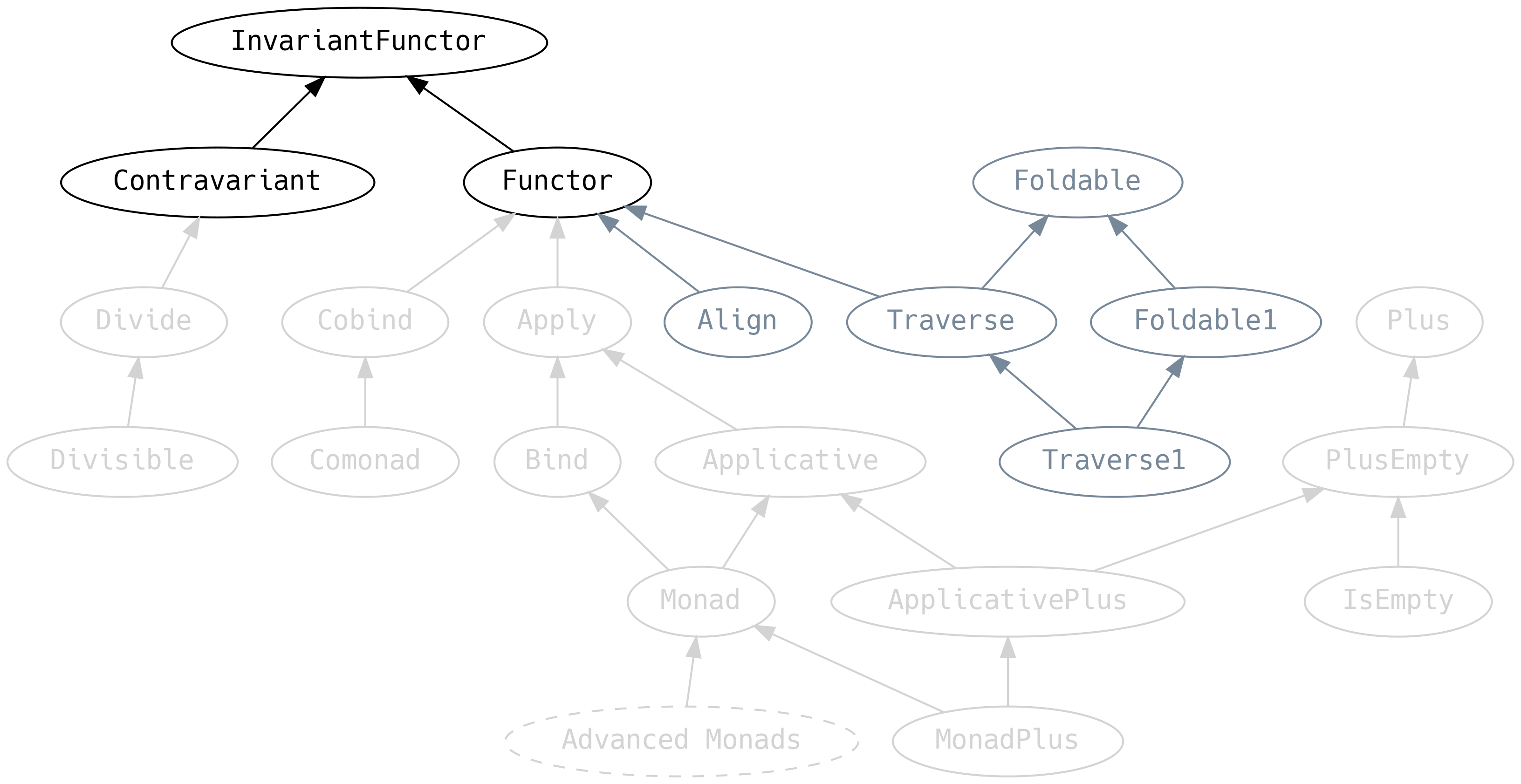
InvariantFunctor, also known as the exponential functor, has a method xmap which says that given a function from A to B, and a function from B to A, then we can convert F[A] to F[B].

Functor is a short name for what should be covariant functor. But since Functor is so popular it gets the nickname. Likewise Contravariant should really be contravariant functor.

Functor implements xmap with map and ignores the function from B to A. Contravariant, on the other hand, implements xmap with contramap and ignores the function from A to B:

  @typeclass trait InvariantFunctor[F[_]] {
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B]
    ...
  }
  
  @typeclass trait Functor[F[_]] extends InvariantFunctor[F] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = map(fa)(f)
    ...
  }
  
  @typeclass trait Contravariant[F[_]] extends InvariantFunctor[F] {
    def contramap[A, B](fa: F[A])(f: B => A): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = contramap(fa)(g)
    ...
  }

It is important to note that, although related at a theoretical level, the words covariant, contravariant and invariant do not directly refer to Scala type variance (i.e. + and - prefixes that may be written in type signatures). Invariance here means that it is possible to map the contents of a structure F[A] into F[B]. Using identity we can see that A can be safely downcast (or upcast) into B depending on the variance of the functor.

This sounds so hopelessly abstract that it needs a practical example immediately, before we can take it seriously. In Chapter 4 we used jsonformat to derive a JSON encoder for our data types and we gave a brief description of the JsEncoder typeclass. This is an expanded version:

  @typeclass trait JsEncoder[A] {
    def toJson(obj: A): JsValue
  }
  object JsEncoder {
    implicit val contravariant: Contravariant[JsEncoder] =
      new Contravariant[JsEncoder] {
        def contramap[A, B](fa: JsEncoder[A])(f: B => A): JsEncoder[B] =
          b => fa.toJson(f(b))
      }
    ...
  }

Now consider the case where we want to write an instance of an JsEncoder[B] in terms of another JsEncoder[A]: we have a data type Alpha that simply wraps a Double. This is exactly what contramap is for:

  final case class Alpha(value: Double)
  
  object Alpha {
    implicit val encoder: JsEncoder[Alpha] = JsEncoder[Double].contramap(_.value)
  }

On the other hand, a JsDecoder has a Functor:

  @typeclass trait JsDecoder[A] { self =>
    def fromJson(json: JsValue): String \/ A
  }
  object JsDecoder {
    implicit val functor: Functor[JsDecoder] = new Functor[JsDecoder] {
      def map[A, B](fa: JsDecoder[A])(f: A => B): JsDecoder[B] =
        j => fa.fromJson(j).map(f)
    }
    ...
  }

Methods on a typeclass can have their type parameters in contravariant position (method parameters) or in covariant position (return type). If a typeclass has a combination of covariant and contravariant positions, it might have an invariant functor.

5.5.1 Composition

Invariants can be composed via methods with intimidating type signatures. There are many permutations of compose on most typeclasses, we will not list them all.

  @typeclass trait Functor[F[_]] extends InvariantFunctor[F] {
    def compose[G[_]: Functor]: Functor[λ[α => F[G[α]]]] = ...
    def icompose[G[_]: Contravariant]: Contravariant[λ[α => F[G[α]]]] = ...
    ...
  }
  @typeclass trait Contravariant[F[_]] extends InvariantFunctor[F] {
    def compose[G[_]: Contravariant]: Functor[λ[α => F[G[α]]]] = ...
    def icompose[G[_]: Functor]: Contravariant[λ[α => F[G[α]]]] = ...
    ...
  }

The α => type syntax is a kind-projector type lambda that says if Functor[F] is composed with a type G[_] (that has a Functor[G]), we get a Functor[F[G[_]]] that operates on the A in F[G[A]].

An example of Functor.compose is where F[_] is List, G[_] is Option, and we want to be able to map over the Int inside a List[Option[Int]] without changing the two structures:

  scala> val lo = List(Some(1), None, Some(2))
  scala> Functor[List].compose[Option].map(lo)(_ + 1)
  res: List[Option[Int]] = List(Some(2), None, Some(3))

This lets us jump into nested effects and structures and apply a function at the layer we want.

5.6 Apply and Bind

Consider this the warm-up act to Applicative and Monad

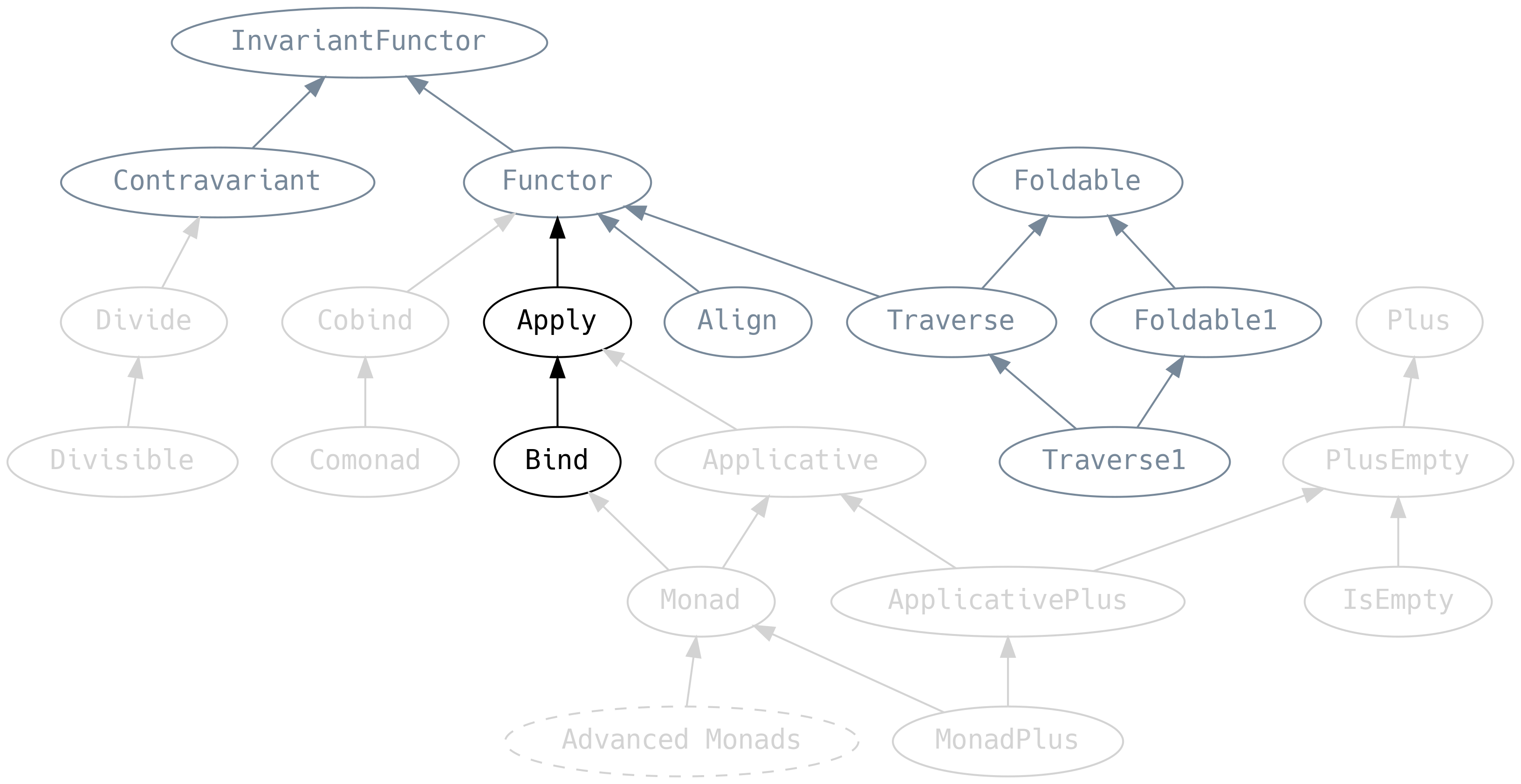
5.6.1 Apply

Apply extends Functor by adding a method named ap which is similar to map in that it applies a function to values. However, with ap, the function is in a similar context to the values.

  @typeclass trait Apply[F[_]] extends Functor[F] {
    @op("<*>") def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B]
    ...

It is worth taking a moment to consider what that means for a simple data structure like Option[A], having the following implementation of .ap

  implicit def option[A]: Apply[Option[A]] = new Apply[Option[A]] {
    override def ap[A, B](fa: =>Option[A])(f: =>Option[A => B]) = f match {
      case Some(ff) => fa.map(ff)
      case None    => None
    }
    ...
  }

To implement .ap, we must first extract the function ff: A => B from f: Option[A => B], then we can map over fa. The extraction of the function from the context is the important power that Apply brings, allowing multiple function to be combined inside the context.

Returning to Apply, we find .applyX boilerplate that allows us to combine parallel functions and then map over their combined output:

  @typeclass trait Apply[F[_]] extends Functor[F] {
    ...
    def apply2[A,B,C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] = ...
    def apply3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
    ...
    def apply12[...]

Read .apply2 as a contract promising: “if you give me an F of A and an F of B, with a way of combining A and B into a C, then I can give you an F of C”. There are many uses for this contract and the two most important are:

• constructing some typeclasses for a product type C from its constituents A and B
• performing effects in parallel, like the drone and google algebras we created in Chapter 3, and then combining their results.

Indeed, Apply is so useful that it has special syntax:

  implicit class ApplyOps[F[_]: Apply, A](self: F[A]) {
    def *>[B](fb: F[B]): F[B] = Apply[F].apply2(self,fb)((_,b) => b)
    def <*[B](fb: F[B]): F[A] = Apply[F].apply2(self,fb)((a,_) => a)
    def |@|[B](fb: F[B]): ApplicativeBuilder[F, A, B] = ...
  }
  
  class ApplicativeBuilder[F[_]: Apply, A, B](a: F[A], b: F[B]) {
    def tupled: F[(A, B)] = Apply[F].apply2(a, b)(Tuple2(_))
    def |@|[C](cc: F[C]): ApplicativeBuilder3[C] = ...
  
    sealed abstract class ApplicativeBuilder3[C](c: F[C]) {
      ..ApplicativeBuilder4
        ...
          ..ApplicativeBuilder12
  }

which is exactly what we used in Chapter 3:

  (d.getBacklog |@| d.getAgents |@| m.getManaged |@| m.getAlive |@| m.getTime)

The syntax <* and *> (left bird and right bird) offer a convenient way to ignore the output from one of two parallel effects.

Unfortunately, although the |@| syntax is clear, there is a problem in that a new ApplicativeBuilder object is allocated for each additional effect. If the work is I/O-bound, the memory allocation cost is insignificant. However, when performing CPU-bound work, use the alternative lifting with arity syntax, which does not produce any intermediate objects:

  def ^[F[_]: Apply,A,B,C](fa: =>F[A],fb: =>F[B])(f: (A,B) =>C): F[C] = ...
  def ^^[F[_]: Apply,A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
  ...
  def ^^^^^^[F[_]: Apply, ...]

used like

  ^^^^(d.getBacklog, d.getAgents, m.getManaged, m.getAlive, m.getTime)

or directly call applyX

  Apply[F].apply5(d.getBacklog, d.getAgents, m.getManaged, m.getAlive, m.getTime)

Despite being of most value for dealing with effects, Apply provides convenient syntax for dealing with data structures. Consider rewriting

  for {
    foo <- data.foo: Option[String]
    bar <- data.bar: Option[Int]
  } yield foo + bar.shows

as

  (data.foo |@| data.bar)(_ + _.shows) : Option[String]

If we only want the combined output as a tuple, methods exist to do just that:

  @op("tuple") def tuple2[A,B](fa: =>F[A],fb: =>F[B]): F[(A,B)] = ...
  def tuple3[A,B,C](fa: =>F[A],fb: =>F[B],fc: =>F[C]): F[(A,B,C)] = ...
  ...
  def tuple12[...]

  (data.foo tuple data.bar) : Option[(String, Int)]

There are also the generalised versions of ap for more than two parameters:

  def ap2[A,B,C](fa: =>F[A],fb: =>F[B])(f: F[(A,B) => C]): F[C] = ...
  def ap3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: F[(A,B,C) => D]): F[D] = ...
  ...
  def ap12[...]

along with lift methods that take normal functions and lift them into the F[_] context, the generalisation of Functor.lift

  def lift2[A,B,C](f: (A,B) => C): (F[A],F[B]) => F[C] = ...
  def lift3[A,B,C,D](f: (A,B,C) => D): (F[A],F[B],F[C]) => F[D] = ...
  ...
  def lift12[...]

and apF, a partially applied syntax for ap

  def apF[A,B](f: =>F[A => B]): F[A] => F[B] = ...

Finally forever

  def forever[A, B](fa: F[A]): F[B] = ...

repeating an effect without stopping. The instance of Apply must be stack safe or we’ll get StackOverflowError.

5.6.2 Bind

Bind introduces bind, synonymous with flatMap, which allows functions over the result of an effect to return a new effect, or for functions over the values of a data structure to return new data structures that are then joined.

  @typeclass trait Bind[F[_]] extends Apply[F] {
  
    @op(">>=") def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
    def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B] = bind(fa)(f)
  
    override def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B] =
      bind(f)(x => map(fa)(x))
    override def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] =
      bind(fa)(a => map(fb)(b => f(a, b)))
  
    def join[A](ffa: F[F[A]]): F[A] = bind(ffa)(identity)
  
    def mproduct[A, B](fa: F[A])(f: A => F[B]): F[(A, B)] = ...
    def ifM[B](value: F[Boolean], t: =>F[B], f: =>F[B]): F[B] = ...
  
  }

The .join may be familiar if you have ever used .flatten in the stdlib, it takes a nested context and squashes it into one.

Although not necessarily implemented as such, we can think of .bind as being a Functor.map followed by .join

  def bind[A, B](fa: F[A])(f: A => F[B]): F[B] = join(map(fa)(f))

Derived combinators are introduced for .ap and .apply2 that require consistency with .bind. We will see later that this law has consequences for parallelisation strategies.

mproduct is like Functor.fproduct and pairs the function’s input with its output, inside the F.

ifM is a way to construct a conditional data structure or effect:

  scala> List(true, false, true).ifM(List(0), List(1, 1))
  res: List[Int] = List(0, 1, 1, 0)

ifM and ap are optimised to cache and reuse code branches, compare to the longer form

  scala> List(true, false, true).flatMap { b => if (b) List(0) else List(1, 1) }

which produces a fresh List(0) or List(1, 1) every time the branch is invoked.

Bind also has some special syntax

  implicit class BindOps[F[_]: Bind, A] (self: F[A]) {
    def >>[B](b: =>F[B]): F[B] = Bind[F].bind(self)(_ => b)
    def >>![B](f: A => F[B]): F[A] = Bind[F].bind(self)(a => f(a).map(_ => a))
  }

>> is when we wish to discard the input to bind and >>! is when we want to run an effect but discard its output.

5.7 Applicative and Monad

From a functionality point of view, Applicative is Apply with a pure method, and Monad extends Applicative with Bind.

  @typeclass trait Applicative[F[_]] extends Apply[F] {
    def point[A](a: =>A): F[A]
    def pure[A](a: =>A): F[A] = point(a)
  }
  
  @typeclass trait Monad[F[_]] extends Applicative[F] with Bind[F]

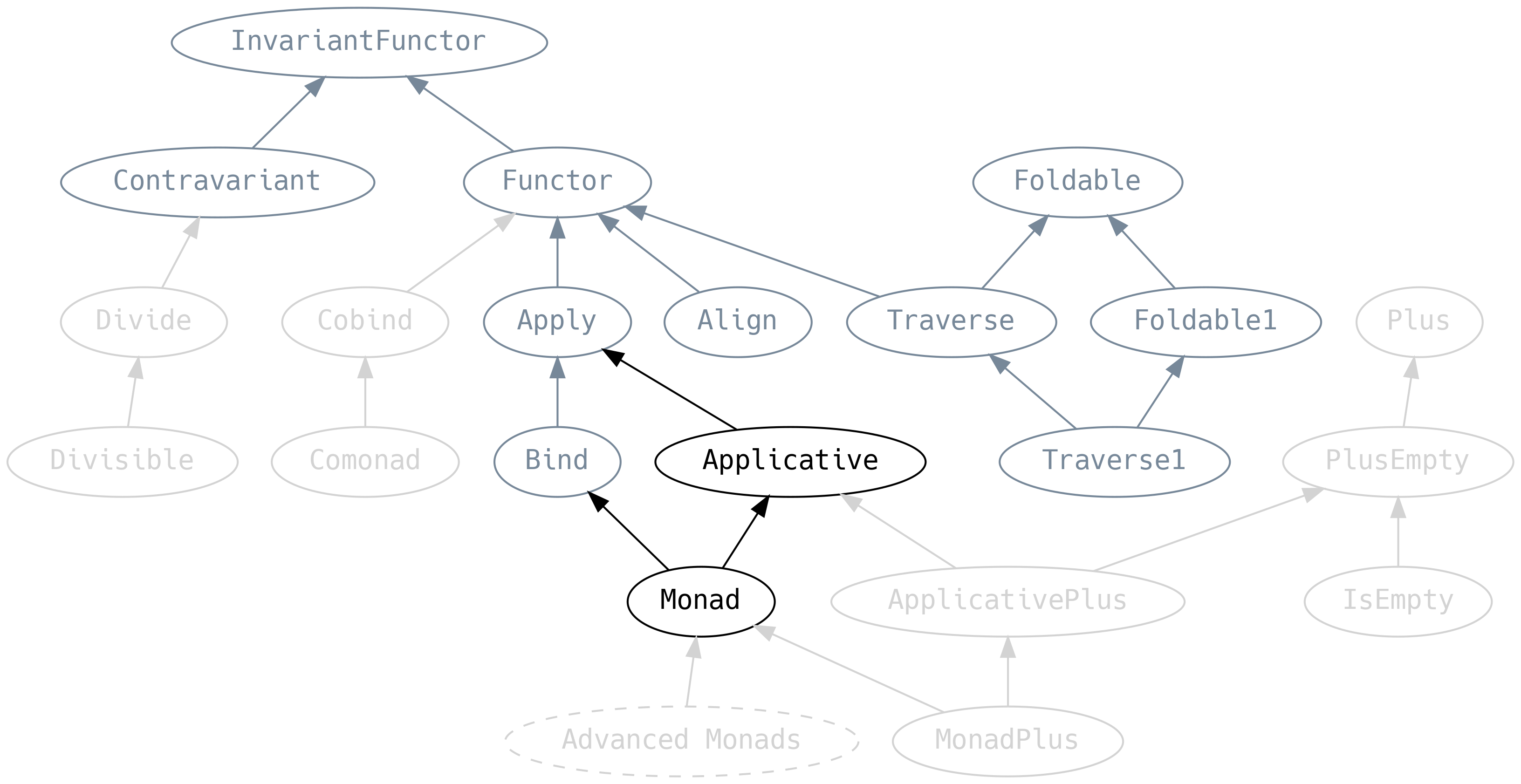
In many ways, Applicative and Monad are the culmination of everything we’ve seen in this chapter. .pure (or .point as it is more commonly known for data structures) allows us to create effects or data structures from values.

Instances of Applicative must meet some laws, effectively asserting that all the methods are consistent:

• Identity: fa <*> pure(identity) === fa, (where fa is an F[A]) i.e. applying pure(identity) does nothing.
• Homomorphism: pure(a) <*> pure(ab) === pure(ab(a)) (where ab is an A => B), i.e. applying a pure function to a pure value is the same as applying the function to the value and then using pure on the result.
• Interchange: pure(a) <*> fab === fab <*> pure(f => f(a)), (where fab is an F[A => B]), i.e. pure is a left and right identity
• Mappy: map(fa)(f) === fa <*> pure(f)

Monad adds additional laws:

• Left Identity: pure(a).bind(f) === f(a)
• Right Identity: a.bind(pure(_)) === a
• Associativity: fa.bind(f).bind(g) === fa.bind(a => f(a).bind(g)) where fa is an F[A], f is an A => F[B] and g is a B => F[C].

Associativity says that chained bind calls must agree with nested bind. However, it does not mean that we can rearrange the order, which would be commutativity. For example, recalling that flatMap is an alias to bind, we cannot rearrange

  for {
    _ <- machine.start(node1)
    _ <- machine.stop(node1)
  } yield true

as

  for {
    _ <- machine.stop(node1)
    _ <- machine.start(node1)
  } yield true

start and stop are non-commutative, because the intended effect of starting then stopping a node is different to stopping then starting it!

But start is commutative with itself, and stop is commutative with itself, so we can rewrite

  for {
    _ <- machine.start(node1)
    _ <- machine.start(node2)
  } yield true

as

  for {
    _ <- machine.start(node2)
    _ <- machine.start(node1)
  } yield true

which are equivalent. We’re making a lot of assumptions about the Google Container API here, but this is a reasonable choice to make.

A practical consequence is that a Monad must be commutative if its applyX methods can be allowed to run in parallel. We cheated in Chapter 3 when we ran these effects in parallel

  (d.getBacklog |@| d.getAgents |@| m.getManaged |@| m.getAlive |@| m.getTime)

because we know that they are commutative among themselves. When it comes to interpreting our application, later in the book, we will have to provide evidence that these effects are in fact commutative, or an asynchronous implementation may choose to sequence the operations to be on the safe side.

The subtleties of how we deal with (re)-ordering of effects, and what those effects are, deserves a dedicated chapter on Advanced Monads.

5.8 Divide and Conquer

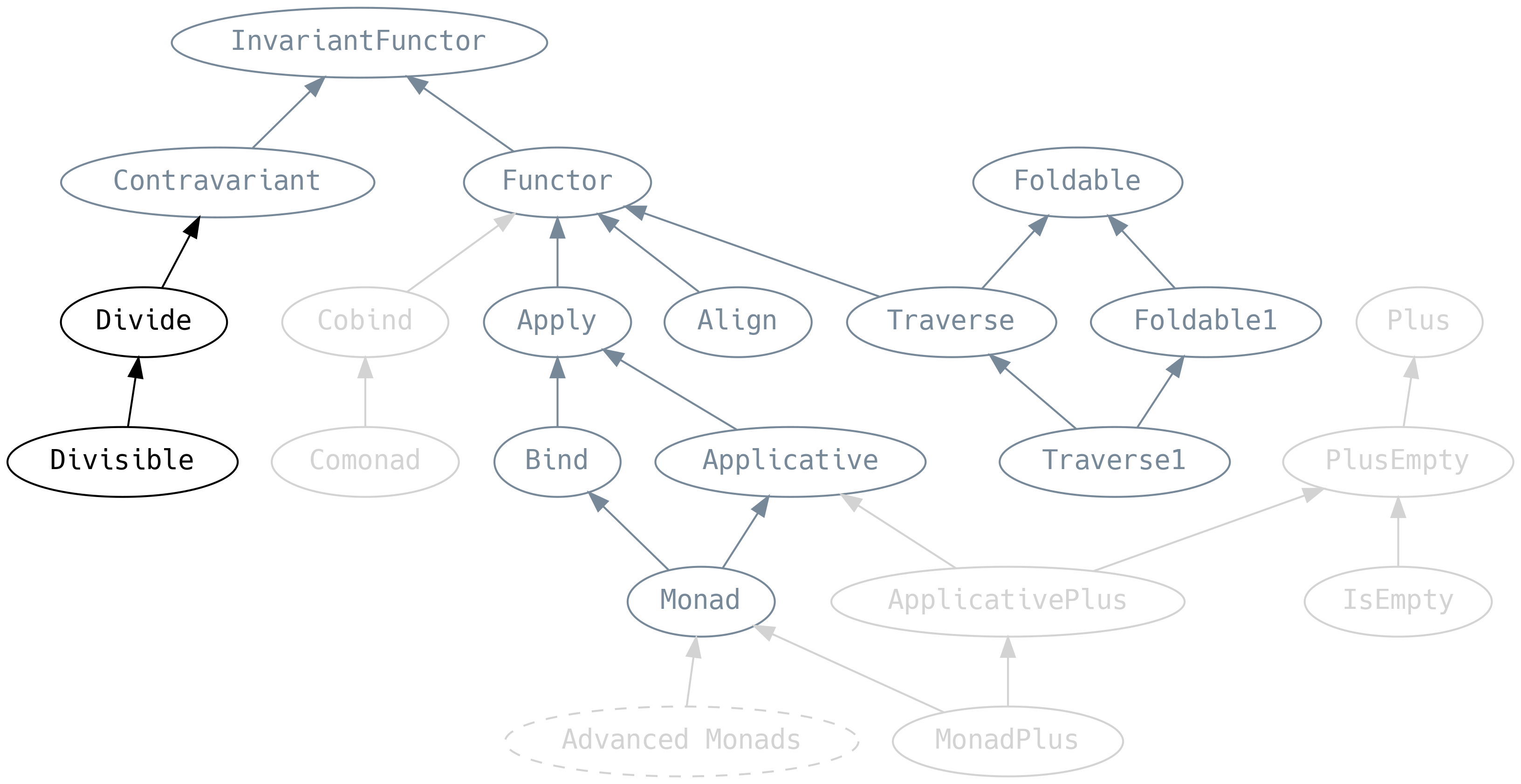
Divide is the Contravariant analogue of Apply

  @typeclass trait Divide[F[_]] extends Contravariant[F] {
    def divide[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C] = divide2(fa, fb)(f)
  
    def divide1[A1, Z](a1: F[A1])(f: Z => A1): F[Z] = ...
    def divide2[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C] = ...
    ...
    def divide22[...] = ...

divide says that if we can break a C into an A and a B, and we’re given an F[A] and an F[B], then we can get an F[C]. Hence, divide and conquer.

This is a great way to generate contravariant typeclass instances for product types by breaking the products into their parts. Scalaz has an instance of Divide[Equal], let’s construct an Equal for a new product type Foo

  scala> case class Foo(s: String, i: Int)
  scala> implicit val fooEqual: Equal[Foo] =
           Divide[Equal].divide2(Equal[String], Equal[Int]) {
             (foo: Foo) => (foo.s, foo.i)
           }
  scala> Foo("foo", 1) === Foo("bar", 1)
  res: Boolean = false

It is a good moment to look again at Apply

  @typeclass trait Apply[F[_]] extends Functor[F] {
    ...
    def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] = ...
    def apply3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
    ...
    def apply12[...]
    ...
  }

It is now easier to spot that applyX is how we can derive typeclasses for covariant typeclasses.

Mirroring Apply, Divide also has terse syntax for tuples. A softer divide so that you may reign approach to world domination:

  ...
    def tuple2[A1, A2](a1: F[A1], a2: F[A2]): F[(A1, A2)] = ...
    ...
    def tuple22[...] = ...
  
    def deriving2[A1: F, A2: F, Z](f: Z => (A1, A2)): F[Z] = ...
    ...
    def deriving22[...] = ...
  }

and deriving, which is even more convenient to use for typeclass derivation:

  implicit val fooEqual: Equal[Foo] = Divide[Equal].deriving2(f => (f.s, f.i))

Generally, if encoder typeclasses can provide an instance of Divide, rather than stopping at Contravariant, it makes it possible to derive instances for any case class. Similarly, decoder typeclasses can provide an Apply instance. We will explore this in a dedicated chapter on Typeclass Derivation.

Divisible is the Contravariant analogue of Applicative and introduces conquer, the equivalent of pure

  @typeclass trait Divisible[F[_]] extends Divide[F] {
    def conquer[A]: F[A]
  }

conquer allows creating fallback implementations that effectively ignore the type parameter. Such values are called universally quantified. For example, the Divisible[Equal].conquer[String] returns a trivial implementation of Equal that always returns true, which allows us to implement contramap in terms of divide

  override def contramap[A, B](fa: F[A])(f: B => A): F[B] =
    divide(conquer[Unit], fa)(c => ((), f(c)))

5.9 Plus

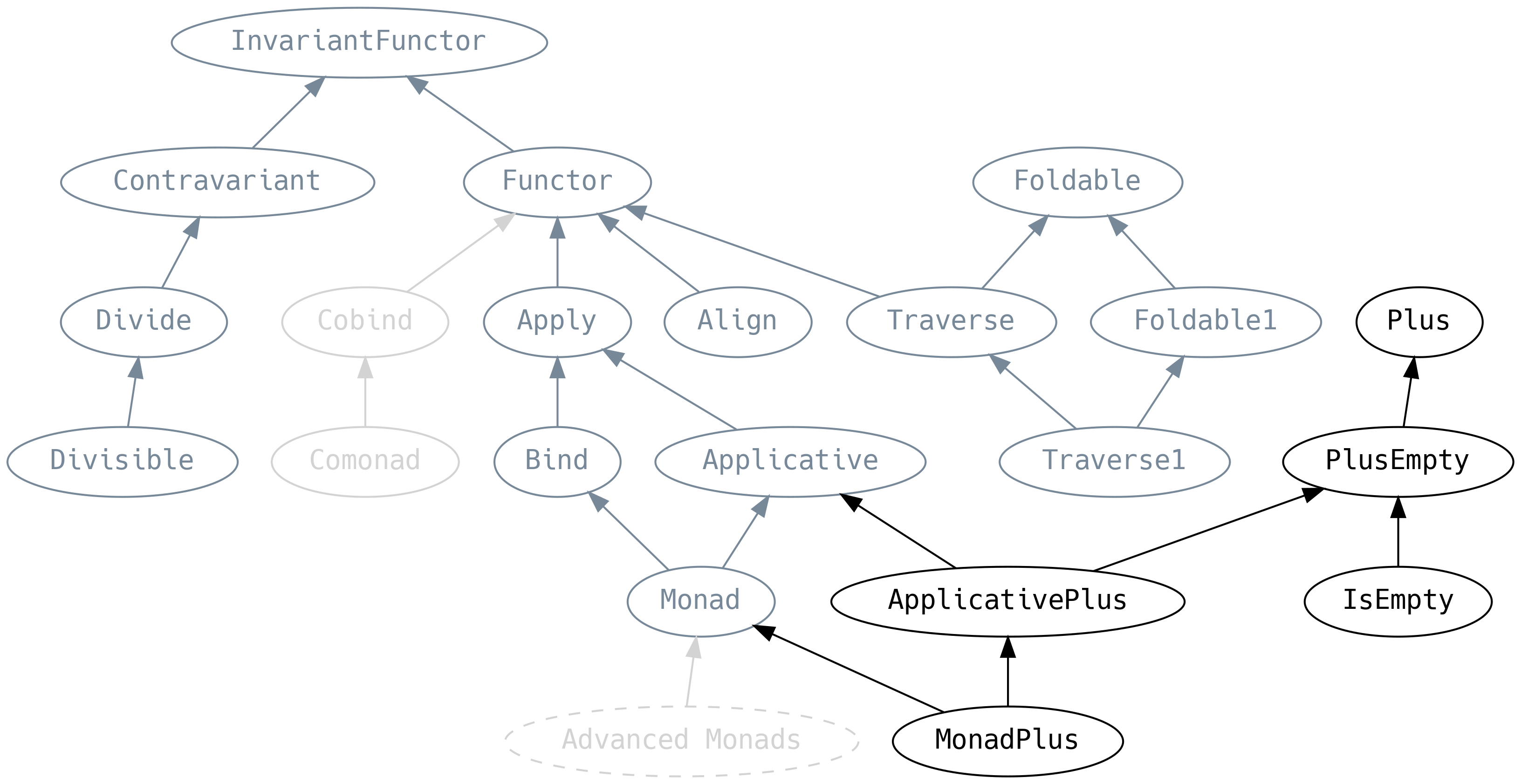
Plus is Semigroup but for type constructors, and PlusEmpty is the equivalent of Monoid (they even have the same laws) whereas IsEmpty is novel and allows us to query if an F[A] is empty:

  @typeclass trait Plus[F[_]] {
    @op("<+>") def plus[A](a: F[A], b: =>F[A]): F[A]
  }
  @typeclass trait PlusEmpty[F[_]] extends Plus[F] {
    def empty[A]: F[A]
  }
  @typeclass trait IsEmpty[F[_]] extends PlusEmpty[F] {
    def isEmpty[A](fa: F[A]): Boolean
  }

Although it may look on the surface as if <+> behaves like |+|

  scala> List(2,3) |+| List(7)
  res = List(2, 3, 7)
  
  scala> List(2,3) <+> List(7)
  res = List(2, 3, 7)

it is best to think of it as operating only at the F[_] level, never looking into the contents. Plus has the convention that it should ignore failures and “pick the first winner”. <+> can therefore be used as a mechanism for early exit (losing information) and failure-handling via fallbacks:

  scala> Option(1) |+| Option(2)
  res = Some(3)
  
  scala> Option(1) <+> Option(2)
  res = Some(1)
  
  scala> Option.empty[Int] <+> Option(1)
  res = Some(1)

For example, if we have a NonEmptyList[Option[Int]] and we want to ignore None values (failures) and pick the first winner (Some), we can call <+> from Foldable1.foldRight1:

  scala> NonEmptyList(None, None, Some(1), Some(2), None)
         .foldRight1(_ <+> _)
  res: Option[Int] = Some(1)

In fact, now that we know about Plus, we release that we didn’t need to break typeclass coherence (when we defined a locally scoped Monoid[Option[A]]) in the section on Appendable Things. Our objective was to “pick the last winner”, which is the same as “pick the winner” if the arguments are swapped. Note the use of the TIE Interceptor for ccy and otc and that b comes before a in

  implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
    (a, b) =>
      TradeTemplate(a.payments |+| b.payments,
                    b.ccy <+> a.ccy,
                    b.otc <+> a.otc),
    TradeTemplate(Nil, None, None)
  )

Applicative and Monad have specialised versions of PlusEmpty

  @typeclass trait ApplicativePlus[F[_]] extends Applicative[F] with PlusEmpty[F]
  
  @typeclass trait MonadPlus[F[_]] extends Monad[F] with ApplicativePlus[F] {
    def unite[T[_]: Foldable, A](ts: F[T[A]]): F[A] = ...
  
    def withFilter[A](fa: F[A])(f: A => Boolean): F[A] = ...
  }

ApplicativePlus is also known as Alternative.

unite looks a Foldable.fold on the contents of F[_] but is folding with the PlusEmpty[F].monoid (not the Monoid[A]). For example, uniting List[Either[_, _]] means Left becomes empty (Nil) and the contents of Right become single element List, which are then concatenated:

  scala> List(Right(1), Left("boo"), Right(2)).unite
  res: List[Int] = List(1, 2)
  
  scala> val boo: Either[String, Int] = Left("boo")
         boo.foldMap(a => a.pure[List])
  res: List[String] = List()
  
  scala> val n: Either[String, Int] = Right(1)
         n.foldMap(a => a.pure[List])
  res: List[Int] = List(1)

withFilter allows us to make use of for comprehension language support as discussed in Chapter 2. It is fair to say that the Scala language has built-in language support for MonadPlus, not just Monad!

Returning to Foldable for a moment, we can reveal some methods that we did not discuss earlier

  @typeclass trait Foldable[F[_]] {
    ...
    def msuml[G[_]: PlusEmpty, A](fa: F[G[A]]): G[A] = ...
    def collapse[X[_]: ApplicativePlus, A](x: F[A]): X[A] = ...
    ...
  }

msuml does a fold using the Monoid from the PlusEmpty[G] and collapse does a foldRight using the PlusEmpty of the target type:

  scala> IList(Option(1), Option.empty[Int], Option(2)).fold
  res: Option[Int] = Some(3) // uses Monoid[Option[Int]]
  
  scala> IList(Option(1), Option.empty[Int], Option(2)).msuml
  res: Option[Int] = Some(1) // uses PlusEmpty[Option].monoid
  
  scala> IList(1, 2).collapse[Option]
  res: Option[Int] = Some(1)

5.10 Lone Wolves

Some of the typeclasses in scalaz are stand-alone and not part of the larger hierarchy.

5.10.1 Zippy

  @typeclass trait Zip[F[_]]  {
    def zip[A, B](a: =>F[A], b: =>F[B]): F[(A, B)]
  
    def zipWith[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C)
                        (implicit F: Functor[F]): F[C] = ...
  
    def ap(implicit F: Functor[F]): Apply[F] = ...
  
    @op("<*|*>") def apzip[A, B](f: =>F[A] => F[B], a: =>F[A]): F[(A, B)] = ...
  
  }

The core method is zip which is a less powerful version of Divide.tuple2, and if a Functor[F] is provided then zipWith can behave like Apply.apply2. Indeed, an Apply[F] can be created from a Zip[F] and a Functor[F] by calling ap.

apzip takes an F[A] and a lifted function from F[A] => F[B], producing an F[(A, B)] similar to Functor.fproduct.

  @typeclass trait Unzip[F[_]]  {
    @op("unfzip") def unzip[A, B](a: F[(A, B)]): (F[A], F[B])
  
    def firsts[A, B](a: F[(A, B)]): F[A] = ...
    def seconds[A, B](a: F[(A, B)]): F[B] = ...
  
    def unzip3[A, B, C](x: F[(A, (B, C))]): (F[A], F[B], F[C]) = ...
    ...
    def unzip7[A ... H](x: F[(A, (B, ... H))]): ...
  }

The core method is unzip with firsts and seconds allowing for selecting either the first or second element of a tuple in the F. Importantly, unzip is the opposite of zip.

The methods unzip3 to unzip7 are repeated applications of unzip to save on boilerplate. For example, if handed a bunch of nested tuples, the Unzip[Id] is a handy way to flatten them:

  scala> Unzip[Id].unzip7((1, (2, (3, (4, (5, (6, 7)))))))
  res = (1,2,3,4,5,6,7)

In a nutshell, Zip and Unzip are less powerful versions of Divide and Apply, providing useful features without requiring the F to make too many promises.

5.10.2 Optional

Optional is a generalisation of data structures that can optionally contain a value, like Option and Either.

Recall that \/ (disjunction) is scalaz’s improvement of scala.Either. We will also see Maybe, scalaz’s improvement of scala.Option

  sealed abstract class Maybe[A]
  final case class Empty[A]()    extends Maybe[A]
  final case class Just[A](a: A) extends Maybe[A]

  @typeclass trait Optional[F[_]] {
    def pextract[B, A](fa: F[A]): F[B] \/ A
  
    def getOrElse[A](fa: F[A])(default: =>A): A = ...
    def orElse[A](fa: F[A])(alt: =>F[A]): F[A] = ...
  
    def isDefined[A](fa: F[A]): Boolean = ...
    def nonEmpty[A](fa: F[A]): Boolean = ...
    def isEmpty[A](fa: F[A]): Boolean = ...
  
    def toOption[A](fa: F[A]): Option[A] = ...
    def toMaybe[A](fa: F[A]): Maybe[A] = ...
  }

These are methods that should be familiar, except perhaps pextract, which is a way of letting the F[_] return some implementation specific F[B] or the value. For example, Optional[Option].pextract returns Option[Nothing] \/ A, i.e. None \/ A.

Scalaz gives a ternary operator to things that have an Optional

  implicit class OptionalOps[F[_]: Optional, A](fa: F[A]) {
    def ?[X](some: =>X): Conditional[X] = new Conditional[X](some)
    final class Conditional[X](some: =>X) {
      def |(none: =>X): X = if (Optional[F].isDefined(fa)) some else none
    }
  }

for example

  scala> val knock_knock: Option[String] = ...
         knock_knock ? "who's there?" | "<tumbleweed>"

Next time you write a function that takes an Option, consider rewriting it to take Optional instead: it’ll make it easier to migrate to data structures that have better error handling without any loss of functionality.

5.10.3 Catchable

Our grand plans to write total functions that return a value for every input may be in ruins when exceptions are the norm in the Java standard library, the Scala standard library, and the myriad of legacy systems that we must interact with.

scalaz does not magically handle exceptions automatically, but it does provide the mechanism to protect against bad legacy systems.

  @typeclass trait Catchable[F[_]] {
    def attempt[A](f: F[A]): F[Throwable \/ A]
    def fail[A](err: Throwable): F[A]
  }

attempt will catch any exceptions inside F[_] and make the JVM Throwable an explicit return type that can be mapped into an error reporting ADT, or left as an indicator to downstream callers that Here be Dragons.

fail permits callers to throw an exception in the F[_] context and, since this breaks purity, will be removed from scalaz. Exceptions that are raised via fail must be later handled by attempt since it is just as bad as calling legacy code that throws an exception.

It is worth noting that Catchable[Id] cannot be implemented. An Id[A] cannot exist in a state that may contain an exception. However, there are instances for both scala.concurrent.Future (asynchronous) and scala.Either (synchronous), allowing Catchable to abstract over the unhappy path. MonadError, as we will see in a later chapter, is a superior replacement.

5.11 Co-things

A co-thing typically has some opposite type signature to whatever thing does, but is not necessarily its inverse. To highlight the relationship between thing and co-thing, we will include the type signature of thing wherever we can.

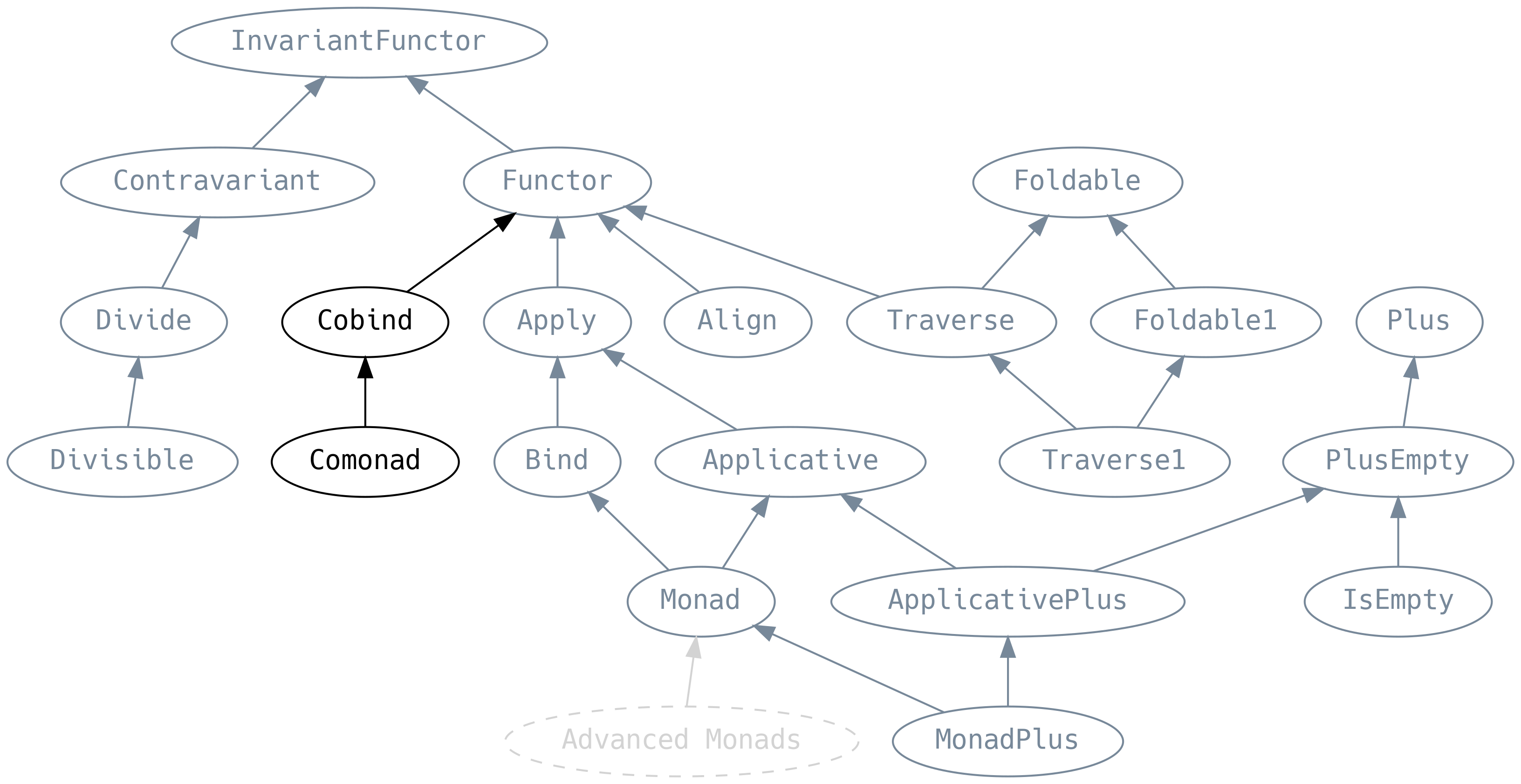
5.11.1 Cobind

  @typeclass trait Cobind[F[_]] extends Functor[F] {
    def cobind[A, B](fa: F[A])(f: F[A] => B): F[B]
  //def   bind[A, B](fa: F[A])(f: A => F[B]): F[B]
  
    def cojoin[A](fa: F[A]): F[F[A]] = ...
  //def   join[A](ffa: F[F[A]]): F[A] = ...
  }

cobind (also known as coflatmap) takes an F[A] => B that acts on an F[A] rather than its elements. But this is not necessarily the full fa, it is usually some substructure as defined by cojoin (also known as coflatten) which expands a data structure.

Compelling use-cases for Cobind are rare, although when shown in the Functor permutation table (for F[_], A and B) it is difficult to argue why any method should be less important than the others:

5.11.2 Comonad

  @typeclass trait Comonad[F[_]] extends Cobind[F] {
    def copoint[A](p: F[A]): A
  //def   point[A](a: =>A): F[A]
  }

copoint (also copure) unwraps an element from a context. When interpreting a pure program, we typically require a Comonad to run the interpreter inside the application’s def main entry point. For example, Comonad[Future].copoint will await the execution of a Future[Unit].

Far more interesting is the Comonad of a data structure. This is a way to construct a view of all elements alongside their neighbours. Consider a neighbourhood (Hood for short) for a list containing all the elements to the left of an element (lefts), the element itself (the focus), and all the elements to its right (rights).

  final case class Hood[A](lefts: IList[A], focus: A, rights: IList[A])

The lefts and rights should each be ordered with the nearest to the focus at the head, such that we can recover the original IList via .toList

  object Hood {
    implicit class Ops[A](hood: Hood[A]) {
      def toList: IList[A] = hood.lefts.reverse ::: hood.focus :: hood.rights

We can write methods that let us move the focus one to the left (previous) and one to the right (next)

  ...
      def previous: Maybe[Hood[A]] = hood.lefts match {
        case INil() => Empty()
        case ICons(head, tail) =>
          Just(Hood(tail, head, hood.focus :: hood.rights))
      }
      def next: Maybe[Hood[A]] = hood.rights match {
        case INil() => Empty()
        case ICons(head, tail) =>
          Just(Hood(hood.focus :: hood.lefts, head, tail))
      }

By introducing more to repeatedly apply an optional function to Hood we can calculate all the positions that Hood can take in the list

  ...
      def more(f: Hood[A] => Maybe[Hood[A]]): IList[Hood[A]] =
        f(hood) match {
          case Empty() => INil()
          case Just(r) => ICons(r, r.more(f))
        }
      def positions: Hood[Hood[A]] = {
        val left  = hood.more(_.previous)
        val right = hood.more(_.next)
        Hood(left, hood, right)
      }
    }

We can now implement Comonad[Hood]

  ...
    implicit val comonad: Comonad[Hood] = new Comonad[Hood] {
      def map[A, B](fa: Hood[A])(f: A => B): Hood[B] =
        Hood(fa.lefts.map(f), f(fa.focus), fa.rights.map(f))
      def cobind[A, B](fa: Hood[A])(f: Hood[A] => B): Hood[B] =
        fa.positions.map(f)
      def copoint[A](fa: Hood[A]): A = fa.focus
    }
  }

cojoin gives us a Hood[Hood[IList]] containing all the possible neighbourhoods in our initial IList

  scala> val middle = Hood(IList(4, 3, 2, 1), 5, IList(6, 7, 8, 9))
         println(middle.cojoin)
  
  res = Hood(
          [Hood([3,2,1],4,[5,6,7,8,9]),
           Hood([2,1],3,[4,5,6,7,8,9]),
           Hood([1],2,[3,4,5,6,7,8,9]),
           Hood([],1,[2,3,4,5,6,7,8,9])],
          Hood([4,3,2,1],5,[6,7,8,9]),
          [Hood([5,4,3,2,1],6,[7,8,9]),
           Hood([6,5,4,3,2,1],7,[8,9]),
           Hood([7,6,5,4,3,2,1],8,[9]),
           Hood([8,7,6,5,4,3,2,1],9,[])])

Indeed, cojoin is just positions! We can override it with a more direct (and performant) implementation

  override def cojoin[A](fa: Hood[A]): Hood[Hood[A]] = fa.positions

Comonad generalises the concept of Hood to arbitrary data structures. Hood is an example of a zipper (unrelated to Zip). Scalaz comes with a Zipper data type for streams (i.e. infinite 1D data structures), which we will discuss in the next chapter.

One application of a zipper is for cellular automata, which compute the value of each cell in the next generation by performing a computation based on the neighbourhood of that cell.

5.11.3 Cozip

  @typeclass trait Cozip[F[_]] {
    def cozip[A, B](x: F[A \/ B]): F[A] \/ F[B]
  //def   zip[A, B](a: =>F[A], b: =>F[B]): F[(A, B)]
  //def unzip[A, B](a: F[(A, B)]): (F[A], F[B])
  
    def cozip3[A, B, C](x: F[A \/ (B \/ C)]): F[A] \/ (F[B] \/ F[C]) = ...
    ...
    def cozip7[A ... H](x: F[(A \/ (... H))]): F[A] \/ (... F[H]) = ...
  }

Although named cozip, it is perhaps more appropriate to talk about its symmetry with unzip. Whereas unzip splits F[_] of tuples (products) into tuples of F[_], cozip splits F[_] of disjunctions (coproducts) into disjunctions of F[_].

5.12 Bi-things

Sometimes we may find ourselves with a thing that has two type holes and we want to map over both sides. For example we might be tracking failures in the left of an Either and we want to do something with the failure messages.

The Functor / Foldable / Traverse typeclasses have bizarro relatives that allow us to map both ways.

  @typeclass trait Bifunctor[F[_, _]] {
    def bimap[A, B, C, D](fab: F[A, B])(f: A => C, g: B => D): F[C, D]
  
    @op("<-:") def leftMap[A, B, C](fab: F[A, B])(f: A => C): F[C, B] = ...
    @op(":->") def rightMap[A, B, D](fab: F[A, B])(g: B => D): F[A, D] = ...
    @op("<:>") def umap[A, B](faa: F[A, A])(f: A => B): F[B, B] = ...
  }
  
  @typeclass trait Bifoldable[F[_, _]] {
    def bifoldMap[A, B, M: Monoid](fa: F[A, B])(f: A => M)(g: B => M): M
  
    def bifoldRight[A,B,C](fa: F[A, B], z: =>C)(f: (A, =>C) => C)(g: (B, =>C) => C): C
    def bifoldLeft[A,B,C](fa: F[A, B], z: C)(f: (C, A) => C)(g: (C, B) => C): C = ...
  
    def bifoldMap1[A, B, M: Semigroup](fa: F[A,B])(f: A => M)(g: B => M): Option[M] = ...
  }
  
  @typeclass trait Bitraverse[F[_, _]] extends Bifunctor[F] with Bifoldable[F] {
    def bitraverse[G[_]: Applicative, A, B, C, D](fab: F[A, B])
                                                 (f: A => G[C])
                                                 (g: B => G[D]): G[F[C, D]]
  
    def bisequence[G[_]: Applicative, A, B](x: F[G[A], G[B]]): G[F[A, B]] = ...
  }

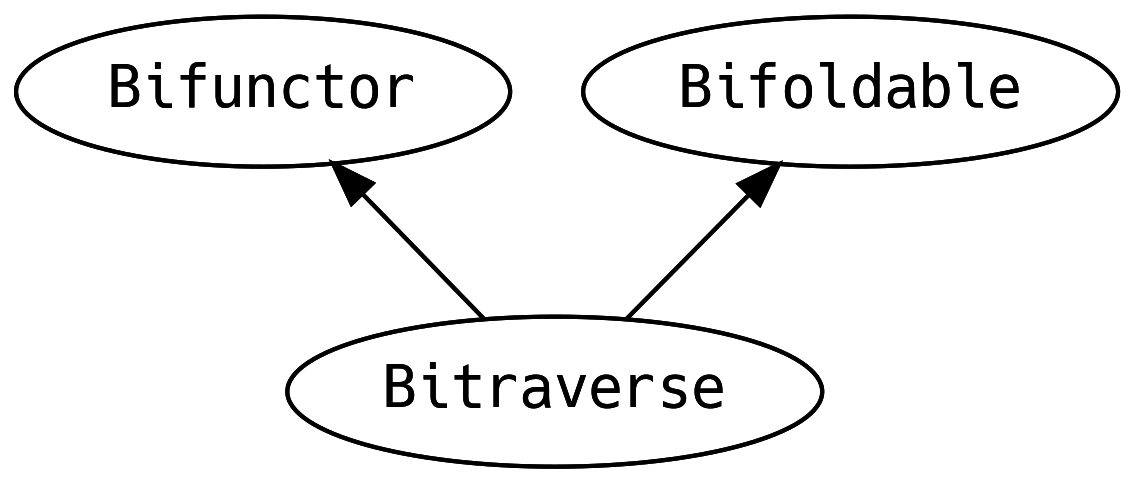
Although the type signatures are verbose, these are nothing more than the core methods of Functor, Foldable and Bitraverse taking two functions instead of one, often requiring both functions to return the same type so that their results can be combined with a Monoid or Semigroup.

  scala> val a: Either[String, Int] = Left("fail")
         val b: Either[String, Int] = Right(13)
  
  scala> b.bimap(_.toUpperCase, _ * 2)
  res: Either[String, Int] = Right(26)
  
  scala> a.bimap(_.toUpperCase, _ * 2)
  res: Either[String, Int] = Left(FAIL)
  
  scala> b :-> (_ * 2)
  res: Either[String,Int] = Right(26)
  
  scala> a :-> (_ * 2)
  res: Either[String, Int] = Left(fail)
  
  scala> { s: String => s.length } <-: a
  res: Either[Int, Int] = Left(4)
  
  scala> a.bifoldMap(_.length)(identity)
  res: Int = 4
  
  scala> b.bitraverse(s => Future(s.length), i => Future(i))
  res: Future[Either[Int, Int]] = Future(<not completed>)

In addition, we can revisit MonadPlus (recall it is Monad with the ability to filterWith and unite) and see that it can separate Bifoldable contents of a Monad

  @typeclass trait MonadPlus[F[_]] {
    ...
    def separate[G[_, _]: Bifoldable, A, B](value: F[G[A, B]]): (F[A], F[B]) = ...
    ...
  }

This is very useful if we have a collection of bi-things and we want to reorganise them into a collection of A and a collection of B

  scala> val list: List[Either[Int, String]] =
           List(Right("hello"), Left(1), Left(2), Right("world"))
  
  scala> list.separate
  res: (List[Int], List[String]) = (List(1, 2), List(hello, world))

5.13 Very Abstract Things

What remains of the typeclass hierarchy are things that allow us to meta-reason about functional programming and scalaz. We are not going to discuss these yet as they deserve a full chapter on Category Theory and are not needed in typical FP applications.

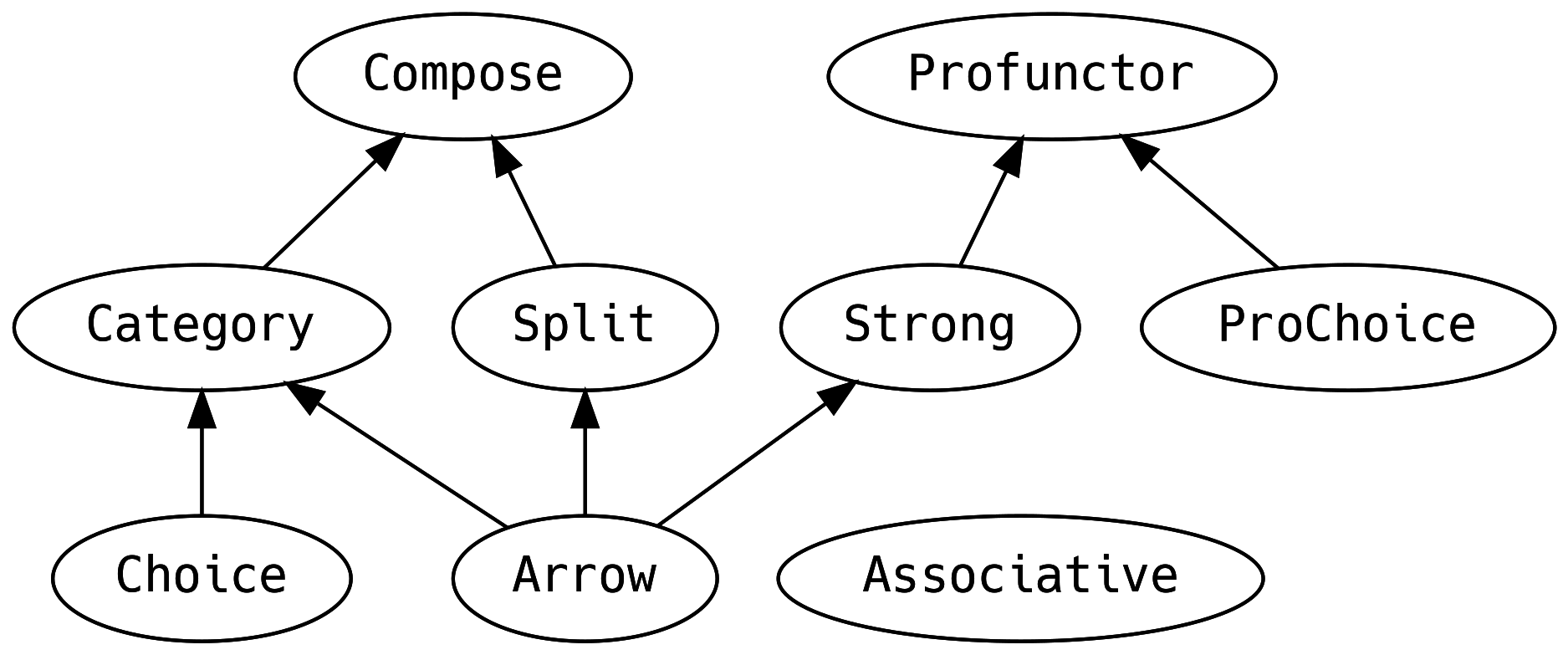
5.14 Summary

That was a lot of material! We have just explored a standard library of polymorphic functionality. But to put it into perspective: there are more traits in the Scala stdlib Collections API than typeclasses in scalaz.

It is normal for an FP application to only touch a small percentage of the typeclass hierarchy, with most functionality coming from domain-specific typeclasses. Even if the domain-specific typeclasses are just specialised clones of something in scalaz, it is better to write the code and later refactor it, than to over-abstract too early.

To help, we have included a cheat-sheet of the typeclasses and their primary methods in the Appendix, inspired by Adam Rosien’s Scalaz Cheatsheet. These cheat-sheets make an excellent replacement for the family portrait on your office desk.

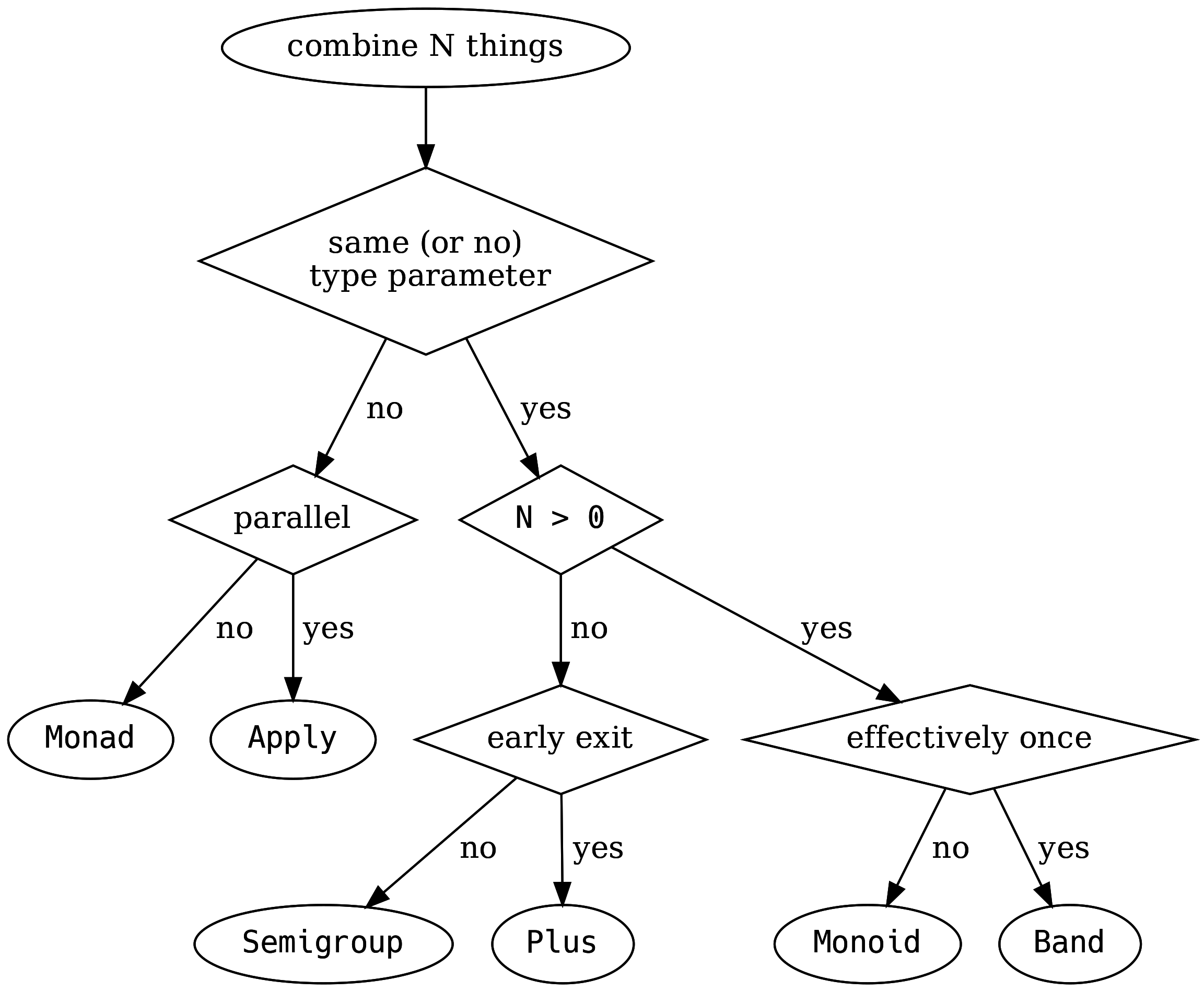
To help further, Valentin Kasas explains how to combine N things: