7. Advanced Monads

You have to know things like Advanced Monads in order to be an advanced functional programmer. However, we are developers yearning for a simple life, and our idea of “advanced” is modest. To put it into context: scala.concurrent.Future is more complicated and nuanced than any Monad in this chapter.

In this chapter we will study some of the most important implementations of Monad and explain why Future needlessly complicates an application: we will offer simpler and faster alternatives.

7.1 Always in motion is the Future

The biggest problem with Future is that it eagerly schedules work during construction. As we discovered in the introduction, Future conflates the definition of a program with interpreting it (i.e. running it).

Future is also bad from a performance perspective: every time .flatMap is called, a closure is submitted to an Executor, resulting in unnecessary thread scheduling and context switching. It is not unusual to see 50% of our CPU power dealing with thread scheduling, instead of doing the work. So much so that parallelising work with Future can often make it slower.

Combined, eager evaluation and executor submission means that it is impossible to know when a job started, when it finished, or the sub-tasks that were spawned to calculate the final result. It should not surprise us that performance monitoring “solutions” are a solid earner for the modern day snake oil merchant.

Furthermore, Future.flatMap requires an ExecutionContext to be in implicit scope: users are forced to think about business logic and execution semantics at the same time.

7.2 Effects and Side Effects

If we can’t call side-effecting methods in our business logic, or in Future (or Id, or Either, or Const, etc), when can we write them? The answer is: in a Monad that delays execution until it is interpreted at the application’s entrypoint. We can now refer to I/O and mutation as an effect on the world, captured by the type system, as opposed to having a hidden side-effect.

The simplest implementation of such a Monad is IO, formalising the version we wrote in the introduction:

  final class IO[A](val interpret: () => A)
  object IO {
    def apply[A](a: =>A): IO[A] = new IO(() => a)
  
    implicit val monad: Monad[IO] = new Monad[IO] {
      def point[A](a: =>A): IO[A] = IO(a)
      def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] = IO(f(fa.interpret()).interpret())
    }
  }

The .interpret method is only called once, in the entrypoint of an application:

  def main(args: Array[String]): Unit = program.interpret()

However, there are two big problems with this simple IO:

1. it can stack overflow
2. it doesn’t support parallel computations

Both of these problems will be overcome in this chapter. However, no matter how complicated the internal implementation of a Monad, the principles described here remain true: we’re modularising the definition of a program and its execution, such that we can capture effects in type signatures, allowing us to reason about them, and reuse more code.

7.3 Stack Safety

On the JVM, every method call adds an entry to the call stack of the Thread, like adding to the front of a List. When the method completes, the method at the head is thrown away. The maximum length of the call stack is determined by the -Xss flag when starting up java. Tail recursive methods are detected by the scala compiler and do not add an entry. If we hit the limit, by calling too many chained methods, we get a StackOverflowError.

Unfortunately, every nested call to our IO’s .flatMap adds another method call to the stack. The easiest way to see this is to repeat an action forever, and see if it survives for longer than a few seconds. We can use .forever, from Apply (a parent of Monad):

  scala> val hello = IO { println("hello") }
  scala> Apply[IO].forever(hello).interpret()
  
  hello
  hello
  hello
  ...
  hello
  java.lang.StackOverflowError
      at java.io.FileOutputStream.write(FileOutputStream.java:326)
      at ...
      at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
      at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
      at ...

Scalaz has a typeclass that Monad instances can implement if they are stack safe: BindRec requires a constant stack space for recursive bind:

  @typeclass trait BindRec[F[_]] extends Bind[F] {
    def tailrecM[A, B](f: A => F[A \/ B])(a: A): F[B]
  
    override def forever[A, B](fa: F[A]): F[B] = ...
  }

We don’t need BindRec for all programs, but it is essential for a general purpose Monad implementation.

The way to achieve stack safety is to convert method calls into references to an ADT, the Free monad:

  sealed abstract class Free[S[_], A]
  object Free {
    private final case class Return[S[_], A](a: A)     extends Free[S, A]
    private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
    private final case class Gosub[S[_], A0, B](
      a: Free[S, A0],
      f: A0 => Free[S, B]
    ) extends Free[S, B] { type A = A0 }
    ...
  }

The Free monad is named because it can be generated for free for any S[_]. For example, we could set S to be the Drone or Machines algebras from Chapter 3 and generate a data structure representation of our program. We’ll return to why this is useful at the end of this chapter.

7.3.1 Trampoline

Free is more general than we need for now. Setting the algebra S[_] to () => ?, a deferred calculation or thunk, we get Trampoline and can implement a stack safe Monad

  object Free {
    type Trampoline[A] = Free[() => ?, A]
    implicit val trampoline: Monad[Trampoline] with BindRec[Trampoline] =
      new Monad[Trampoline] with BindRec[Trampoline] {
        def point[A](a: =>A): Trampoline[A] = Return(a)
        def bind[A, B](fa: Trampoline[A])(f: A => Trampoline[B]): Trampoline[B] =
          Gosub(fa, f)
  
        def tailrecM[A, B](f: A => Trampoline[A \/ B])(a: A): Trampoline[B] =
          bind(f(a)) {
            case -\/(a) => tailrecM(f)(a)
            case \/-(b) => point(b)
          }
      }
    ...
  }

The Free ADT is a natural data type representation of the Monad interface:

1. Return represents .point
2. Gosub represents .bind / .flatMap

When an ADT mirrors the arguments of related functions, it is called a Church encoding.

The BindRec implementation, .tailrecM, runs .bind until we get a B. Although this is not technically a @tailrec implementation, it uses constant stack space because each call returns a heap object, with delayed recursion.

Convenient functions are provided to create a Trampoline eagerly (.done) or by-name (.delay). We can also create a Trampoline from a by-name Trampoline (.suspend):

  object Trampoline {
    def done[A](a: A): Trampoline[A]                  = Return(a)
    def delay[A](a: =>A): Trampoline[A]               = suspend(done(a))
    def suspend[A](a: =>Trampoline[A]): Trampoline[A] = unit >> a
  
    private val unit: Trampoline[Unit] = Suspend(() => done(()))
  }

When we see Trampoline[A] in a codebase we can always mentally substitute it with A, because it is simply adding stack safety to the pure computation. We get the A by interpreting Free, provided by .run.

7.3.2 Example: Stack Safe DList

In the previous chapter we described the data type DList as

  final case class DList[A](f: IList[A] => IList[A]) {
    def toIList: IList[A] = f(IList.empty)
    def ++(as: DList[A]): DList[A] = DList(xs => f(as.f(xs)))
    ...
  }

However, the actual implementation looks more like:

  final case class DList[A](f: IList[A] => Trampoline[IList[A]]) {
    def toIList: IList[A] = f(IList.empty).run
    def ++(as: =>DList[A]): DList[A] = DList(xs => suspend(as.f(xs) >>= f))
    ...
  }

Instead of applying nested calls to f we use a suspended Trampoline. We interpret the trampoline with .run only when needed, e.g. in toIList. The changes are minimal, but we now have a stack safe DList that can rearrange the concatenation of a large number lists without blowing the stack!

7.3.3 Stack Safe IO

Similarly, our IO can be made stack safe thanks to Trampoline:

  final class IO[A](val tramp: Trampoline[A]) {
    def unsafePerformIO(): A = tramp.run
  }
  object IO {
    def apply[A](a: =>A): IO[A] = new IO(Trampoline.delay(a))
  
    implicit val Monad: Monad[IO] with BindRec[IO] =
      new Monad[IO] with BindRec[IO] {
        def point[A](a: =>A): IO[A] = IO(a)
        def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] =
          new IO(fa.tramp >>= (a => f(a).tramp))
        def tailrecM[A, B](f: A => IO[A \/ B])(a: A): IO[B] = ...
      }
  }

The interpreter, .unsafePerformIO(), has an intentionally scary name to discourage using it except in the entrypoint of the application.

This time, we don’t get a stack overflow error:

  scala> val hello = IO { println("hello") }
  scala> Apply[IO].forever(hello).unsafePerformIO()
  
  hello
  hello
  hello
  ...
  hello

Using a Trampoline typically introduces a performance regression vs a regular reference. It is Free in the sense of freely generated, not free as in beer.

7.4 Monad Transformer Library

Monad transformers are data structures that wrap an underlying value and provide a monadic effect.

For example, in Chapter 2 we used OptionT to let us use F[Option[A]] in a for comprehension as if it was just a F[A]. This gave our program the effect of an optional value. Alternatively, we can get the effect of optionality if we have a MonadPlus.

This subset of data types and extensions to Monad are often referred to as the Monad Transformer Library (MTL), summarised below. In this section, we will explain each of the transformers, why they are useful, and how they work.

7.4.1 MonadTrans

Each transformer has the general shape T[F[_], A], providing at least an instance of Monad and Hoist (and therefore MonadTrans):

  @typeclass trait MonadTrans[T[_[_], _]] {
    def liftM[F[_]: Monad, A](a: F[A]): T[F, A]
  }
  
  @typeclass trait Hoist[F[_[_], _]] extends MonadTrans[F] {
    def hoist[M[_]: Monad, N[_]](f: M ~> N): F[M, ?] ~> F[N, ?]
  }

.liftM lets us create a monad transformer if we have an F[A]. For example, we can create an OptionT[IO, String] by calling .liftM[OptionT] on an IO[String].

.hoist is the same idea, but for natural transformations.

Generally, there are three ways to create a monad transformer:

• from the underlying, using the transformer’s constructor
• from a single value A, using .pure from the Monad syntax
• from an F[A], using .liftM from the MonadTrans syntax

Due to the way that type inference works in Scala, this often means that a complex type parameter must be explicitly written. As a workaround, transformers provide convenient constructors on their companion that are easier to use.

7.4.2 MaybeT

OptionT, MaybeT and LazyOptionT have similar implementations, providing optionality through Option, Maybe and LazyOption, respectively. We will focus on MaybeT to avoid repetition.

  final case class MaybeT[F[_], A](run: F[Maybe[A]])
  object MaybeT {
    def just[F[_]: Applicative, A](v: =>A): MaybeT[F, A] =
      MaybeT(Maybe.just(v).pure[F])
    def empty[F[_]: Applicative, A]: MaybeT[F, A] =
      MaybeT(Maybe.empty.pure[F])
    ...
  }

providing a MonadPlus

  implicit def monad[F[_]: Monad] = new MonadPlus[MaybeT[F, ?]] {
    def point[A](a: =>A): MaybeT[F, A] = MaybeT.just(a)
    def bind[A, B](fa: MaybeT[F, A])(f: A => MaybeT[F, B]): MaybeT[F, B] =
      MaybeT(fa.run >>= (_.cata(f(_).run, Maybe.empty.pure[F])))
  
    def empty[A]: MaybeT[F, A] = MaybeT.empty
  
    def plus[A](a: MaybeT[F, A], b: =>MaybeT[F, A]): MaybeT[F, A] = ...
  }

This monad looks fiddly, but it is just delegating everything to the Monad[F] and then re-wrapping with a MaybeT. It is plumbing.

With this monad we can write logic that handles optionality in the F[_] context, rather than carrying around Option or Maybe.

For example, say we are interfacing with a social media website to count the number of stars a user has, and we start with a String that may or may not correspond to a user. We have this algebra:

  trait Twitter[F[_]] {
    def getUser(name: String): F[Maybe[User]]
    def getStars(user: User): F[Int]
  }
  def T[F[_]](implicit t: Twitter[F]): Twitter[F] = t

We need to call getUser followed by getStars. If we use Monad as our context, our function is difficult because we have to handle the Empty case:

  def stars[F[_]: Monad: Twitter](name: String): F[Maybe[Int]] = for {
    maybeUser  <- T.getUser(name)
    maybeStars <- maybeUser.traverse(T.getStars)
  } yield maybeStars

However, if we have a MonadPlus as our context, we can suck Maybe into the F[_] with .orEmpty, and forget about it:

  def stars[F[_]: MonadPlus: Twitter](name: String): F[Int] = for {
    user  <- T.getUser(name) >>= (_.orEmpty[F])
    stars <- T.getStars(user)
  } yield stars

However adding a MonadPlus requirement can cause problems downstream if the context does not have one. The solution is to either change the context of the program to MaybeT[F, ?] (lifting the Monad[F] into a MonadPlus), or to explicitly use MaybeT in the return type, at the cost of slightly more code:

  def stars[F[_]: Monad: Twitter](name: String): MaybeT[F, Int] = for {
    user  <- MaybeT(T.getUser(name))
    stars <- T.getStars(user).liftM[MaybeT]
  } yield stars

The decision to require a more powerful Monad vs returning a transformer is something that each team can decide for themselves based on the interpreters that they plan on using for their program.

7.4.3 EitherT

An optional value is a special case of a value that may be an error, but we don’t know anything about the error. EitherT (and the lazy variant LazyEitherT) allows us to use any type we want as the error value, providing contextual information about what went wrong.

Where \/ and Validation is the FP equivalent of a checked exception, EitherT makes it convenient to both create and ignore errors until something can be done about it.

EitherT is a wrapper around an F[A \/ B]

  final case class EitherT[F[_], A, B](run: F[A \/ B])
  object EitherT {
    def either[F[_]: Applicative, A, B](d: A \/ B): EitherT[F, A, B] = ...
    def leftT[F[_]: Functor, A, B](fa: F[A]): EitherT[F, A, B] = ...
    def rightT[F[_]: Functor, A, B](fb: F[B]): EitherT[F, A, B] = ...
    def pureLeft[F[_]: Applicative, A, B](a: A): EitherT[F, A, B] = ...
    def pure[F[_]: Applicative, A, B](b: B): EitherT[F, A, B] = ...
    ...
  }

The Monad is a MonadError

  @typeclass trait MonadError[F[_], E] extends Monad[F] {
    def raiseError[A](e: E): F[A]
    def handleError[A](fa: F[A])(f: E => F[A]): F[A]
  
    def emap[A, B](fa: F[A])(f: A => S \/ B): F[B] =
      bind(fa)(a => f(a).fold(raiseError(_), pure(_)))
  }

.raiseError and .handleError are self-descriptive: the equivalent of throw and catch an exception, respectively.

.emap, either map, is for functions that could fail and is very useful for writing decoders in terms of existing ones, much as we used .contramap to define new encoders in terms of existing ones. For example, say we have an XML decoder like

  @typeclass trait XDecoder[A] {
    def fromXml(x: Xml): String \/ A
  }
  object XDecoder {
    implicit val monad: MonadError[String \/ ?, String] = ...
    implicit val string: XDecoder[String] = ...
  }

we can define a decoder for Char in terms of a String decoder

  implicit val char: XDecoder[Char] = XDecoder[String].emap { s =>
    if (s.length == 1) s(0).right
    else s"not a char: $s".left
  }

The MonadError for EitherT is:

  implicit def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
    def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
    def bind[A, B](fa: EitherT[F, E, A])
                  (f: A => EitherT[F, E, B]): EitherT[F, E, B] =
      EitherT(fa.run >>= (_.fold(_.left[B].pure[F], b => f(b).run)))
    def point[A](a: =>A): EitherT[F, E, A] = EitherT.pure(a)
  
    def raiseError[A](e: E): EitherT[F, E, A] = EitherT.pureLeft(e)
    def handleError[A](fa: EitherT[F, E, A])
                      (f: E => EitherT[F, E, A]): EitherT[F, E, A] =
      EitherT(fa.run >>= {
        case -\/(e) => f(e).run
        case right => right.pure[F]
      })
  }

It should be of no surprise that we can rewrite the MonadPlus example with MonadError, inserting informative error messages:

  def stars[F[_]: Twitter](name: String)
                          (implicit F: MonadError[F, String]): F[Int] = for {
    user  <- T.getUser(name) >>= (_.orError(s"user '$name' not found")(F))
    stars <- T.getStars(user)
  } yield stars

where .orError is a convenience method on Maybe

  sealed abstract class Maybe[A] {
    ...
    def orError[F[_], E](e: E)(implicit F: MonadError[F, E]): F[A] =
      cata(F.point(_), F.raiseError(e))
  }

The version using EitherT directly looks like

  def stars[F[_]: Monad: Twitter](name: String): EitherT[F, String, Int] = for {
    user <- EitherT(T.getUser(name).map(_ \/> s"user '$name' not found"))
    stars <- EitherT.rightT(T.getStars(user))
  } yield stars

The simplest instance of MonadError is for \/, perfect for testing business logic that requires a MonadError. For example,

  final class MockTwitter extends Twitter[String \/ ?] {
    def getUser(name: String): String \/ Maybe[User] =
      if (name.contains(" ")) Maybe.empty.right
      else if (name === "wobble") "connection error".left
      else User(name).just.right
  
    def getStars(user: User): String \/ Int =
      if (user.name.startsWith("w")) 10.right
      else "stars have been replaced by hearts".left
  }

Our unit tests for .stars might cover these cases:

  scala> stars("wibble")
  \/-(10)
  
  scala> stars("wobble")
  -\/(connection error)
  
  scala> stars("i'm a fish")
  -\/(user 'i'm a fish' not found)
  
  scala> stars("fommil")
  -\/(stars have been replaced by hearts)

As we’ve now seen several times, we can focus on testing the pure business logic without distraction.

Finally, if we return to our JsonClient algebra from Chapter 4.3

  trait JsonClient[F[_]] {
    def get[A: JsDecoder](
      uri: String Refined Url,
      headers: IList[(String, String)]
    ): F[A]
    ...
  }

recall that we only coded the happy path into the API. If our interpreter for this algebra only works for an F having a MonadError we get to define the kinds of errors as a tangential concern. Indeed, we can have two layers of error if we define the interpreter for a EitherT[IO, JsonClient.Error, ?]

  object JsonClient {
    sealed abstract class Error
    final case class ServerError(status: Int)       extends Error
    final case class DecodingError(message: String) extends Error
  }

which cover I/O (network) problems, server status problems, and issues with our modelling of the server’s JSON payloads.

7.4.3.1 Choosing an error type

The community is undecided on the best strategy for the error type E in MonadError.

One school of thought says that we should pick something general, like a String. The other school says that an application should have an ADT of errors, allowing different errors to be reported or handled differently. An unprincipled gang prefers using Throwable for maximum JVM compatibility.

There are two problems with an ADT of errors on the application level:

• it is very awkward to create a new error. One file becomes a monolithic repository of errors, aggregating the ADTs of individual subsystems.
• no matter how granular the errors are, the resolution is often the same: log it and try it again, or give up. We don’t need an ADT for this.

An error ADT is of value if every entry allows a different kind of recovery to be performed.

A compromise between an error ADT and a String is an intermediary format. JSON is a good choice as it can be understood by most logging and monitoring frameworks.

A problem with not having a stacktrace is that it can be hard to localise which piece of code was the source of an error. With sourcecode by Li Haoyi, we can include contextual information as metadata in our errors:

  final case class Meta(fqn: String, file: String, line: Int)
  object Meta {
    implicit def gen(implicit fqn: sourcecode.FullName,
                              file: sourcecode.File,
                              line: sourcecode.Line): Meta =
      new Meta(fqn.value, file.value, line.value)
  }
  
  final case class Err(msg: String)(implicit val meta: Meta)

Although Err is referentially transparent, the implicit construction of a Meta does not appear to be referentially transparent from a natural reading: two calls to Meta.gen (invoked implicitly when creating an Err) will produce different values because the location in the source code impacts the returned value:

  scala> println(Err("hello world").meta)
  Meta(com.acme,<console>,10)
  
  scala> println(Err("hello world").meta)
  Meta(com.acme,<console>,11)

To understand this, we have to appreciate that sourcecode.* methods are macros that are generating source code for us. If we were to write the above explicitly it is clear what is happening:

  scala> println(Err("hello world")(Meta("com.acme", "<console>", 10)).meta)
  Meta(com.acme,<console>,10)
  
  scala> println(Err("hello world")(Meta("com.acme", "<console>", 11)).meta)
  Meta(com.acme,<console>,11)

Yes, we’ve made a deal with the macro devil, but we could also write the Meta manually and have it go out of date quicker than our documentation.

7.4.3.2 IO and Throwable

IO does not have a MonadError but instead implements something similar to throw, catch and finally for Throwable errors:

  final class IO[A](val tramp: Trampoline[A]) {
    ...
    // catch
    def except(f: Throwable => IO[A]): IO[A] = ...
    // finally
    def ensuring[B](f: IO[B]): IO[A] = ...
    def onException[B](f: IO[B]): IO[A] = ...
  }
  object IO {
    // throw
    def throwIO[A](e: Throwable): IO[A] = IO(throw e)
    ...
  }

It is good to avoid using keywords where possible, as it means we have to remember less caveats of the language. If we need to interact with a legacy API with a predictable exception, like a string parser, we can use Maybe.attempt or \/.attempt and convert the non referentially transparent Throwable into a descriptive String.

7.4.4 ReaderT

The reader monad wraps A => F[B] allowing a program F[B] to depend on a runtime value A. For those familiar with dependency injection, the reader monad is the FP equivalent of Spring or Guice’s @Inject, without the XML and reflection.

ReaderT is just an alias to another more generally useful data type named after the mathematician Heinrich Kleisli.

  type ReaderT[F[_], A, B] = Kleisli[F, A, B]
  
  final case class Kleisli[F[_], A, B](run: A => F[B]) {
    def dimap[C, D](f: C => A, g: B => D)(implicit F: Functor[F]): Kleisli[F, C, D] =
      Kleisli(c => run(f(c)).map(g))
  
    def >=>[C](k: Kleisli[F, B, C])(implicit F: Bind[F]): Kleisli[F, A, C] = ...
    def >==>[C](k: B => F[C])(implicit F: Bind[F]): Kleisli[F, A, C] = this >=> Kleisli(k)
    ...
  }
  object Kleisli {
    implicit def kleisliFn[F[_], A, B](k: Kleisli[F, A, B]): A => F[B] = k.run
    ...
  }

An implicit conversion on the companion allows us to use a Kleisli in place of a function, so we can provide it as the parameter to a monad’s .bind, or >>=.

The most common use for ReaderT is to provide environment information to a program. In drone-dynamic-agents we need access to the user’s Oauth 2.0 Refresh Token to be able to contact Google. The obvious thing is to load the RefreshTokens from disk on startup, and make every method take an implicit tokens: RefreshToken. In fact, this is such a common requirement that Martin Odersky has proposed implicit functions.

A better solution is for our program to have an algebra that provides the configuration when needed, e.g.

  trait ConfigReader[F[_]] {
    def token: F[RefreshToken]
  }

We have reinvented MonadReader, the typeclass associated to ReaderT, where .ask is the same as our .token, and S is RefreshToken:

  @typeclass trait MonadReader[F[_], S] extends Monad[F] {
    def ask: F[S]
  
    def local[A](f: S => S)(fa: F[A]): F[A]
  }

with the implementation

  implicit def monad[F[_]: Monad, R] = new MonadReader[Kleisli[F, R, ?], R] {
    def point[A](a: =>A): Kleisli[F, R, A] = Kleisli(_ => F.point(a))
    def bind[A, B](fa: Kleisli[F, R, A])(f: A => Kleisli[F, R, B]) =
      Kleisli(a => Monad[F].bind(fa.run(a))(f))
  
    def ask: Kleisli[F, R, R] = Kleisli(_.pure[F])
    def local[A](f: R => R)(fa: Kleisli[F, R, A]): Kleisli[F, R, A] =
      Kleisli(f andThen fa.run)
  }

A law of MonadReader is that the S cannot change between invocations, i.e. ask >> ask === ask. For our usecase, this is to say that the configuration is read once. If we decide later that we want to reload configuration every time we need it, e.g. allowing us to change the token without restarting the application, we can reintroduce ConfigReader which has no such law.

In our OAuth 2.0 implementation we could first move the Monad evidence onto the methods:

  def bearer(refresh: RefreshToken)(implicit F: Monad[F]): F[BearerToken] =
    for { ...

and then refactor the refresh parameter to be part of the Monad

  def bearer(implicit F: MonadReader[F, RefreshToken]): F[BearerToken] =
    for {
      refresh <- F.ask

Fundamentally, any parameter can be moved into the MonadReader. This is of most value to your immediate caller when they simply want to thread through this information from above. With ReaderT, we can reserve implicit parameter blocks entirely for the use of typeclasses, reducing the mental burden of using Scala.

The other method in MonadReader is .local

  def local[A](f: S => S)(fa: F[A]): F[A]

We can change S and run a program fa within that local context, returning to the original S. A use case for .local is to generate a “stack trace” that makes sense to our domain. giving us nested logging! Leaning on the Meta data structure from the previous section, we define a function to checkpoint:

  def traced[A](fa: F[A])(implicit F: MonadReader[F, IList[Meta]]): F[A] =
    F.local(Meta.gen :: _)(fa)

and we can use it to wrap functions that operate in this context.

  def foo: F[Foo] = traced(getBar) >>= barToFoo

automatically passing through anything that is not explicitly traced. A compiler plugin or macro could do the opposite, opting everything in by default.

If we access .ask we can see the breadcrumb trail of exactly how we were called, without the distraction of bytecode implementation details. A referentially transparent stacktrace!

A defensive programmer may wish to truncate the IList[Meta] at a certain length to avoid the equivalent of a stack overflow. Indeed, a more appropriate data structure is Dequeue.

.local can also be used to keep track of contextual information that is directly relevant to the task at hand, like the number of spaces that must indent a line when pretty printing a human readable file format, bumping it by two spaces when we enter a nested structure.

Finally, if we cannot request a MonadReader because our application does not provide one, we can always return a ReaderT

  def bearer(implicit F: Monad[F]): ReaderT[F, RefreshToken, BearerToken] =
    ReaderT( token => for {
    ...

If a caller receives a ReaderT, and they have the token parameter to hand, they can call access.run(token) and get back an F[BearerToken].

Admittedly, since we don’t have many callers, we should just revert to a regular function parameter. MonadReader is of most use when:

1. we may wish to refactor the code later to reload config
2. the value is not needed by intermediate callers
3. or, we want to locally scope some variable

In a nutshell, dotty can keep its implicit functions… we already have ReaderT and MonadReader.

One last example. Monad transformers typically provide specialised Monad instances if their underlying type has one. So, for example, ReaderT has a MonadError, MonadPlus, etc if the underlying has one. Decoder typeclasses tend to have a signature that looks like A => F[B], recall

  @typeclass trait XDecoder[A] {
    def fromXml(x: Xml): String \/ A
  }

which has a single method of signature XNode => String \/ A, isomorphic to ReaderT[String \/ ?, Xml, A]. We can formalise this relationship with an Isomorphism. It’s easier to read by introducing type aliases

  type Out[a] = String \/ a
  type RT[a] = ReaderT[Out, Xml, a]
  val isoReaderT: XDecoder <~> RT =
    new IsoFunctorTemplate[XDecoder, RT] {
      def from[A](fa: RT[A]): XDecoder[A] = fa.run(_)
      def to[A](fa: XDecoder[A]): RT[A] = ReaderT[Out, Xml, A](fa.fromXml)
    }

Now our XDecoder has access to all the typeclasses that ReaderT has. The typeclass we need is MonadError[Decoder, String]

  implicit val monad: MonadError[XDecoder, String] = MonadError.fromIso(isoReaderT)

which we know to be useful for defining new decoders in terms of existing ones.

7.4.5 WriterT

The opposite to reading is writing. The WriterT monad transformer is typically for writing to a journal.

  final case class WriterT[F[_], W, A](run: F[(W, A)])
  object WriterT {
    def put[F[_]: Functor, W, A](value: F[A])(w: W): WriterT[F, W, A] = ...
    def putWith[F[_]: Functor, W, A](value: F[A])(w: A => W): WriterT[F, W, A] = ...
    ...
  }

The wrapped type is F[(W, A)] with the journal accumulated in W.

There is not just one associated monad, but two! MonadTell and MonadListen

  @typeclass trait MonadTell[F[_], W] extends Monad[F] {
    def writer[A](w: W, v: A): F[A]
    def tell(w: W): F[Unit] = ...
  
    def :++>[A](fa: F[A])(w: =>W): F[A] = ...
    def :++>>[A](fa: F[A])(f: A => W): F[A] = ...
  }
  
  @typeclass trait MonadListen[F[_], W] extends MonadTell[F, W] {
    def listen[A](fa: F[A]): F[(A, W)]
  
    def written[A](fa: F[A]): F[W] = ...
  }

MonadTell is for writing to the journal and MonadListen is to recover it. The WriterT implementation is

  implicit def monad[F[_]: Monad, W: Monoid] = new MonadListen[WriterT[F, W, ?], W] {
    def point[A](a: =>A) = WriterT((Monoid[W].zero, a).point)
    def bind[A, B](fa: WriterT[F, W, A])(f: A => WriterT[F, W, B]) = WriterT(
      fa.run >>= { case (wa, a) => f(a).run.map { case (wb, b) => (wa |+| wb, b) } })
  
    def writer[A](w: W, v: A) = WriterT((w -> v).point)
    def listen[A](fa: WriterT[F, W, A]) = WriterT(
      fa.run.map { case (w, a) => (w, (a, w)) })
  }

The most obvious example is to use MonadTell for logging, or audit reporting. Reusing Meta from our error reporting we could imagine creating a log structure like

  sealed trait Log
  final case class Debug(msg: String)(implicit m: Meta)   extends Log
  final case class Info(msg: String)(implicit m: Meta)    extends Log
  final case class Warning(msg: String)(implicit m: Meta) extends Log

and use Dequeue[Log] as our journal type. We could change our OAuth2 authenticate method to

  def debug(msg: String)(implicit m: Meta): Dequeue[Log] = Dequeue(Debug(msg))
  
  def authenticate: F[CodeToken] =
    for {
      callback <- user.start :++> debug("started the webserver")
      params   = AuthRequest(callback, config.scope, config.clientId)
      url      = config.auth.withQuery(params.toUrlQuery)
      _        <- user.open(url) :++> debug(s"user visiting $url")
      code     <- user.stop :++> debug("stopped the webserver")
    } yield code

We could even combine this with the ReaderT traces and get structured logs.

The caller can recover the logs with .written and do something with them.

However, there is a strong argument that logging deserves its own algebra. The log level is often needed at the point of creation for performance reasons and writing out the logs is typically managed at the application level rather than something each component needs to be concerned about.

The W in WriterT has a Monoid, allowing us to journal any kind of monoidic calculation as a secondary value along with our primary program. For example, counting the number of times we do something, building up an explanation of a calculation, or building up a TradeTemplate for a new trade while we price it.

A popular specialisation of WriterT is when the monad is Id, meaning the underlying run value is just a simple tuple (W, A).

  type Writer[W, A] = WriterT[Id, W, A]
  object WriterT {
    def writer[W, A](v: (W, A)): Writer[W, A] = WriterT[Id, W, A](v)
    def tell[W](w: W): Writer[W, Unit] = WriterT((w, ()))
    ...
  }
  final implicit class WriterOps[A](self: A) {
    def set[W](w: W): Writer[W, A] = WriterT(w -> self)
    def tell: Writer[A, Unit] = WriterT.tell(self)
  }

which allows us to let any value carry around a secondary monoidal calculation, without needing a context F[_].

In a nutshell, WriterT / MonadTell is how to multi-task in FP.

7.4.6 StateT

StateT lets us .put, .get and .modify a value that is handled by the monadic context. It is the FP replacement of var.

If we were to write an impure method that has access to some mutable state, held in a var, it might have the signature () => F[A] and return a different value on every call, breaking referential transparency. With pure FP the function takes the state as input and returns the updated state as output, which is why the underlying type of StateT is S => F[(S, A)].

The associated monad is MonadState

  @typeclass trait MonadState[F[_], S] extends Monad[F] {
    def put(s: S): F[Unit]
    def get: F[S]
  
    def modify(f: S => S): F[Unit] = get >>= (s => put(f(s)))
    ...
  }

StateT is implemented slightly differently than the monad transformers we have studied so far. Instead of being a case class it is an ADT with two members:

  sealed abstract class StateT[F[_], S, A]
  object StateT {
    def apply[F[_], S, A](f: S => F[(S, A)]): StateT[F, S, A] = Point(f)
  
    private final case class Point[F[_], S, A](
      run: S => F[(S, A)]
    ) extends StateT[F, S, A]
    private final case class FlatMap[F[_], S, A, B](
      a: StateT[F, S, A],
      f: (S, A) => StateT[F, S, B]
    ) extends StateT[F, S, B]
    ...
  }

which are a specialised form of Trampoline, giving us stack safety when we want to recover the underlying data structure, .run:

  sealed abstract class StateT[F[_], S, A] {
    def run(initial: S)(implicit F: Monad[F]): F[(S, A)] = this match {
      case Point(f) => f(initial)
      case FlatMap(Point(f), g) =>
        f(initial) >>= { case (s, x) => g(s, x).run(s) }
      case FlatMap(FlatMap(f, g), h) =>
        FlatMap(f, (s, x) => FlatMap(g(s, x), h)).run(initial)
    }
    ...
  }

StateT can straightforwardly implement MonadState with its ADT:

  implicit def monad[F[_]: Applicative, S] = new MonadState[StateT[F, S, ?], S] {
    def point[A](a: =>A) = Point(s => (s, a).point[F])
    def bind[A, B](fa: StateT[F, S, A])(f: A => StateT[F, S, B]) =
      FlatMap(fa, (_, a: A) => f(a))
  
    def get       = Point(s => (s, s).point[F])
    def put(s: S) = Point(_ => (s, ()).point[F])
  }

With .pure mirrored on the companion as .stateT:

  object StateT {
    def stateT[F[_]: Applicative, S, A](a: A): StateT[F, S, A] = ...
    ...
  }

and MonadTrans.liftM providing the F[A] => StateT[F, S, A] constructor as usual.

A common variant of StateT is when F = Id, giving the underlying type signature S => (S, A). Scalaz provides a type alias and convenience functions for interacting with the State monad transformer directly, and mirroring MonadState:

  type State[a] = StateT[Id, a]
  object State {
    def apply[S, A](f: S => (S, A)): State[S, A] = StateT[Id, S, A](f)
    def state[S, A](a: A): State[S, A] = State((_, a))
  
    def get[S]: State[S, S] = State(s => (s, s))
    def put[S](s: S): State[S, Unit] = State(_ => (s, ()))
    def modify[S](f: S => S): State[S, Unit] = ...
    ...
  }

For an example we can return to the business logic tests of drone-dynamic-agents. Recall from Chapter 3 that we created Mutable as test interpreters for our application and we stored the number of started and stoped nodes in var.

  class Mutable(state: WorldView) {
    var started, stopped: Int = 0
  
    implicit val drone: Drone[Id] = new Drone[Id] { ... }
    implicit val machines: Machines[Id] = new Machines[Id] { ... }
    val program = new DynAgentsModule[Id]
  }

We now know that we can write a much better test simulator with State. We’ll take the opportunity to upgrade the accuracy of the simulation at the same time. Recall that a core domain object is our application’s view of the world:

  final case class WorldView(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    pending: Map[MachineNode, Epoch],
    time: Epoch
  )

Since we’re writing a simulation of the world for our tests, we can create a data type that captures the ground truth of everything

  final case class World(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    started: Set[MachineNode],
    stopped: Set[MachineNode],
    time: Epoch
  )

The key difference being that the started and stopped nodes can be separated out. Our interpreter can be implemented in terms of State[World, a] and we can write our tests to assert on what both the World and WorldView looks like after the business logic has run.

The interpreters, which are mocking out contacting external Drone and Google services, may be implemented like this:

  import State.{ get, modify }
  object StateImpl {
    type F[a] = State[World, a]
  
    private val D = new Drone[F] {
      def getBacklog: F[Int] = get.map(_.backlog)
      def getAgents: F[Int]  = get.map(_.agents)
    }
  
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]   = get.map(_.alive)
      def getManaged: F[NonEmptyList[MachineNode]] = get.map(_.managed)
      def getTime: F[Epoch]                      = get.map(_.time)
  
      def start(node: MachineNode): F[Unit] =
        modify(w => w.copy(started = w.started + node))
      def stop(node: MachineNode): F[Unit] =
        modify(w => w.copy(stopped = w.stopped + node))
    }
  
    val program = new DynAgentsModule[F](D, M)
  }

and we can rewrite our tests to follow a convention where:

• world1 is the state of the world before running the program
• view1 is the application’s belief about the world
• world2 is the state of the world after running the program
• view2 is the application’s belief after running the program

For example,

  it should "request agents when needed" in {
    val world1          = World(5, 0, managed, Map(), Set(), Set(), time1)
    val view1           = WorldView(5, 0, managed, Map(), Map(), time1)
  
    val (world2, view2) = StateImpl.program.act(view1).run(world1)
  
    view2.shouldBe(view1.copy(pending = Map(node1 -> time1)))
    world2.stopped.shouldBe(world1.stopped)
    world2.started.shouldBe(Set(node1))
  }

We would be forgiven for looking back to our business logic loop

  state = initial()
  while True:
    state = update(state)
    state = act(state)

and use StateT to manage the state. However, our DynAgents business logic requires only Applicative and we would be violating the Rule of Least Power to require the more powerful MonadState. It is therefore entirely reasonable to handle the state manually by passing it in to update and act, and let whoever calls us use a StateT if they wish.

7.4.7 IndexedStateT

The code that we have studied thus far is not how scalaz implements StateT. Instead, a type alias points to IndexedStateT

  type StateT[F[_], S, A] = IndexedStateT[F, S, S, A]

The implementation of IndexedStateT is much as we have studied, with an extra type parameter allowing the input state S1 and output state S2 to differ:

  sealed abstract class IndexedStateT[F[_], -S1, S2, A] {
    def run(initial: S1)(implicit F: Bind[F]): F[(S2, A)] = ...
    ...
  }
  object IndexedStateT {
    def apply[F[_], S1, S2, A](
      f: S1 => F[(S2, A)]
    ): IndexedStateT[F, S1, S2, A] = Wrap(f)
  
    private final case class Wrap[F[_], S1, S2, A](
      run: S1 => F[(S2, A)]
    ) extends IndexedStateT[F, S1, S2, A]
    private final case class FlatMap[F[_], S1, S2, S3, A, B](
      a: IndexedStateT[F, S1, S2, A],
      f: (S2, A) => IndexedStateT[F, S2, S3, B]
    ) extends IndexedStateT[F, S1, S3, B]
    ...
  }

IndexedStateT does not have a MonadState when S1 ! S2=, although it has a Monad.

The following example is adapted from Index your State by Vincent Marquez. Consider the scenario where we must design an algebraic interface to access a key: Int to value: String lookup. This may have a networked implementation and the order of calls is essential. Our first attempt at the API may look something like:

  trait Cache[F[_]] {
    def read(k: Int): F[Maybe[String]]
  
    def lock: F[Unit]
    def update(k: Int, v: String): F[Unit]
    def commit: F[Unit]
  }

with runtime errors if .update or .commit is called without a .lock. A more complex design may involve multiple traits and a custom DSL that nobody remembers how to use.

Instead, we can use IndexedStateT to require that the caller is in the correct state. First we define our possible states as an ADT

  sealed abstract class Status
  final case class Ready()                          extends Status
  final case class Locked(on: ISet[Int])            extends Status
  final case class Updated(values: Int ==>> String) extends Status

and then revisit our algebra

  trait Cache[M[_]] {
    type F[in, out, a] = IndexedStateT[M, in, out, a]
  
    def read(k: Int): F[Ready, Ready, Maybe[String]]
    def readLocked(k: Int): F[Locked, Locked, Maybe[String]]
    def readUncommitted(k: Int): F[Updated, Updated, Maybe[String]]
  
    def lock: F[Ready, Locked, Unit]
    def update(k: Int, v: String): F[Locked, Updated, Unit]
    def commit: F[Updated, Ready, Unit]
  }

which will give a compiletime error if we try to .update without a .lock

  for {
        a1 <- C.read(13)
        _  <- C.update(13, "wibble")
        _  <- C.commit
      } yield a1
  
  [error]  found   : IndexedStateT[M,Locked,Ready,Maybe[String]]
  [error]  required: IndexedStateT[M,Ready,?,?]
  [error]       _  <- C.update(13, "wibble")
  [error]          ^

but allowing us to construct functions that can be composed by explicitly including their state:

  def wibbleise[M[_]: Monad](C: Cache[M]): F[Ready, Ready, String] =
    for {
      _  <- C.lock
      a1 <- C.readLocked(13)
      a2 = a1.cata(_ + "'", "wibble")
      _  <- C.update(13, a2)
      _  <- C.commit
    } yield a2

7.4.8 IndexedReaderWriterStateT

Those wanting to have a combination of ReaderT, WriterT and IndexedStateT will not be disappointed. The transformer IndexedReaderWriterStateT wraps (R, S1) => F[(W, A, S2)] with R having Reader semantics, W for monoidic writes, and the S parameters for indexed state updates.

  sealed abstract class IndexedReaderWriterStateT[F[_], -R, W, -S1, S2, A] {
    def run(r: R, s: S1)(implicit F: Monad[F]): F[(W, A, S2)] = ...
    ...
  }
  object IndexedReaderWriterStateT {
    def apply[F[_], R, W, S1, S2, A](f: (R, S1) => F[(W, A, S2)]) = ...
  }
  
  type ReaderWriterStateT[F[_], -R, W, S, A] = IndexedReaderWriterStateT[F, R, W, S, S, A]
  object ReaderWriterStateT {
    def apply[F[_], R, W, S, A](f: (R, S) => F[(W, A, S)]) = ...
  }

Abbreviations are provided because otherwise, let’s be honest, these types are so long they look like they are part of a J2EE API:

  type IRWST[F[_], -R, W, -S1, S2, A] = IndexedReaderWriterStateT[F, R, W, S1, S2, A]
  val IRWST = IndexedReaderWriterStateT
  type RWST[F[_], -R, W, S, A] = ReaderWriterStateT[F, R, W, S, A]
  val RWST = ReaderWriterStateT

IRWST is a more efficient implementation than a manually created transformer stack of ReaderT[WriterT[IndexedStateT[F, ...], ...], ...].

7.4.9 TheseT

TheseT allows errors to either abort the calculation or to be accumulated if there is some partial success. Hence keep calm and carry on.

The underlying data type is F[A \&/ B] with A being the error type, requiring a Semigroup to enable the accumulation of errors.

  final case class TheseT[F[_], A, B](run: F[A \&/ B])
  object TheseT {
    def `this`[F[_]: Functor, A, B](a: F[A]): TheseT[F, A, B] = ...
    def that[F[_]: Functor, A, B](b: F[B]): TheseT[F, A, B] = ...
    def both[F[_]: Functor, A, B](ab: F[(A, B)]): TheseT[F, A, B] = ...
  
    implicit def monad[F[_]: Monad, A: Semigroup] = new Monad[TheseT[F, A, ?]] {
      def bind[B, C](fa: TheseT[F, A, B])(f: B => TheseT[F, A, C]) =
        TheseT(fa.run >>= {
          case This(a) => a.wrapThis[C].point[F]
          case That(b) => f(b).run
          case Both(a, b) =>
            f(b).run.map {
              case This(a_)     => (a |+| a_).wrapThis[C]
              case That(c_)     => Both(a, c_)
              case Both(a_, c_) => Both(a |+| a_, c_)
            }
        })
  
      def point[B](b: =>B) = TheseT(b.wrapThat.point[F])
    }
  }

There is no special monad associated with TheseT, it is just a regular Monad. If we wish to abort a calculation we can return a This value, but we accumulate errors when we return a Both which also contains a successful part of the calculation.

TheseT can also be thought of from a different angle: A does not need to be an error. Similarly to WriterT, the A may be a secondary calculation that we are computing along with the primary calculation B. TheseT allows early exit when something special about A demands it, like when Charlie Bucket found the last golden ticket (A) he threw away his chocolate bar (B).

7.4.10 ContT

Continuation Passing Style (CPS) is a style of programming where functions never return, instead continuing to the next computation. CPS is popular in Javascript and Lisp as they allow non-blocking I/O via callbacks when data is available. A direct translation of the pattern into impure Scala looks like

  def foo[I, A](input: I)(next: A => Unit): Unit = next(doSomeStuff(input))

We can make this pure by introducing an F[_] context

  def foo[F[_], I, A](input: I)(next: A => F[Unit]): F[Unit]

and refactor to return a function for the provided input

  def foo[F[_], I, A](input: I): (A => F[Unit]) => F[Unit]

ContT is just a container for this signature, with a Monad instance

  final case class ContT[F[_], B, A](_run: (A => F[B]) => F[B]) {
    def run(f: A => F[B]): F[B] = _run(f)
  }
  object IndexedContT {
    implicit def monad[F[_], B] = new Monad[ContT[F, B, ?]] {
      def point[A](a: =>A) = ContT(_(a))
      def bind[A, C](fa: ContT[F, B, A])(f: A => ContT[F, B, C]) =
        ContT(c_fb => fa.run(a => f(a).run(c_fb)))
    }
  }

and convenient syntax to create a ContT from a monadic value:

  implicit class ContTOps[F[_]: Monad, A](self: F[A]) {
    def cps[B]: ContT[F, B, A] = ContT(a_fb => self >>= a_fb)
  }

However, the simple callback use of continuations brings nothing to pure functional programming because we already know how to sequence non-blocking, potentially distributed, computations: that’s what Monad is for and we can do this with .bind or a Kleisli arrow. To see why continuations are useful we need to consider a more complex example under a rigid design constraint.

7.4.10.1 Control Flow

Say we have modularised our application into components that can perform I/O, with each component owned by a different development team:

  final case class A0()
  final case class A1()
  final case class A2()
  final case class A3()
  final case class A4()
  
  def bar0(a4: A4): IO[A0] = ...
  def bar2(a1: A1): IO[A2] = ...
  def bar3(a2: A2): IO[A3] = ...
  def bar4(a3: A3): IO[A4] = ...

Our goal is to produce an A0 given an A1. Whereas Javascript and Lisp would reach for continuations to solve this problem (because the I/O could block) we can just chain the functions

  def simple(a: A1): IO[A0] = bar2(a) >>= bar3 >>= bar4 >>= bar0

We can lift .simple into its continuation form by using the convenient .cps syntax and a little bit of extra boilerplate for each step:

  def foo1(a: A1): ContT[IO, A0, A2] = bar2(a).cps
  def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).cps
  def foo3(a: A3): ContT[IO, A0, A4] = bar4(a).cps
  
  def flow(a: A1): IO[A0]  = (foo1(a) >>= foo2 >>= foo3).run(bar0)

So what does this buy us? Firstly, it’s worth noting that the control flow of this application is left to right

What if we are the authors of foo2 and we want to post-process the a0 that we receive from the right (downstream), i.e. we want to split our foo2 into foo2a and foo2b

Let’s add the constraint that we cannot change the definition of flow or bar0, perhaps it is not our code and is defined by the framework we are using.

It is not possible to process the output of a0 by modifying any of the remaining barX methods. However, with ContT we can modify foo2 to process the result of the next continuation:

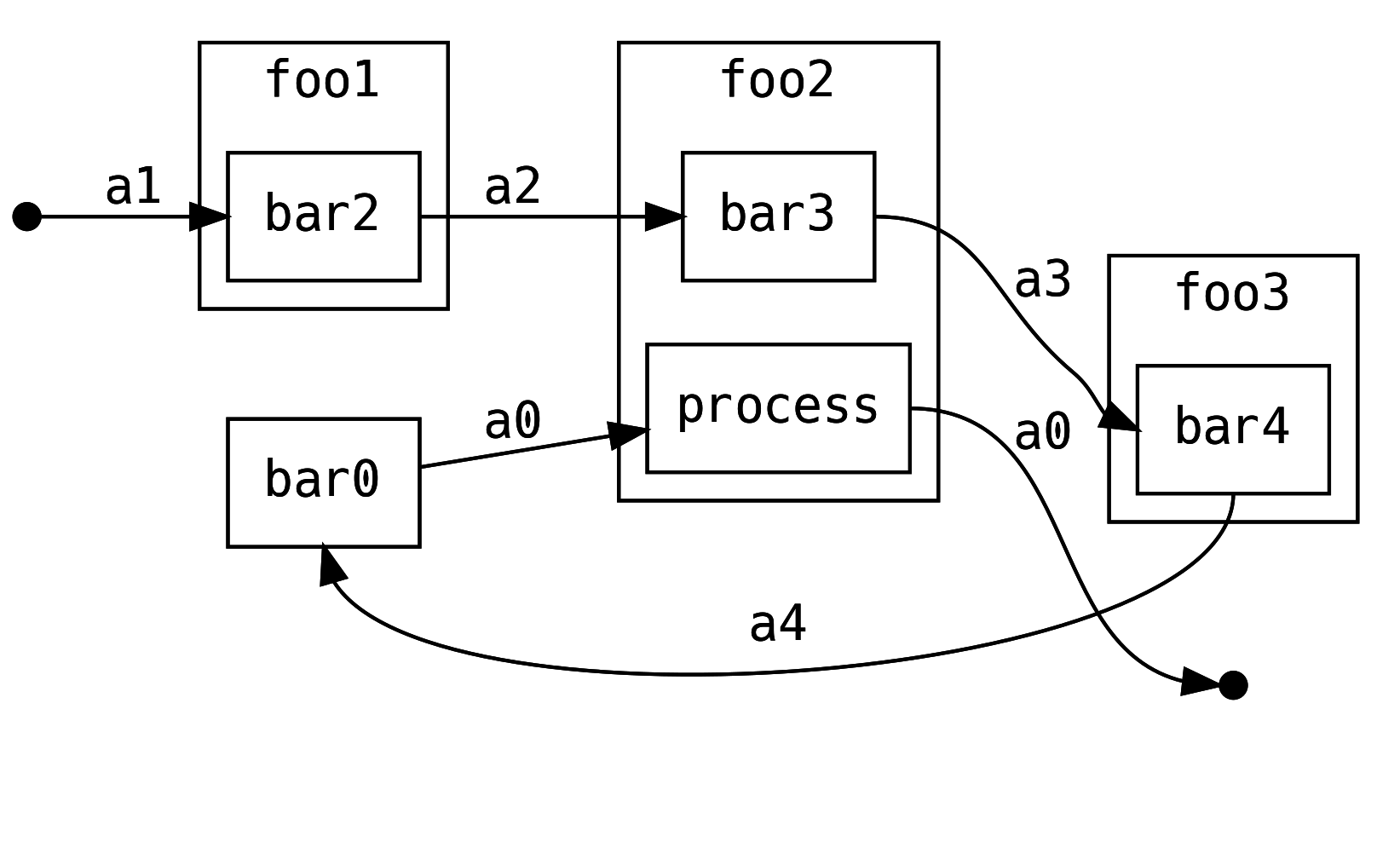
Which can be defined with

  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
    } yield process(a0)
  }

We are not limited to .map over the return value, we can .bind into another control flow turning the linear flow into a graph!

  def elsewhere: ContT[IO, A0, A4] = ???
  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
      a0_ <- if (check(a0)) a0.pure[IO]
             else elsewhere.run(bar0)
    } yield a0_
  }

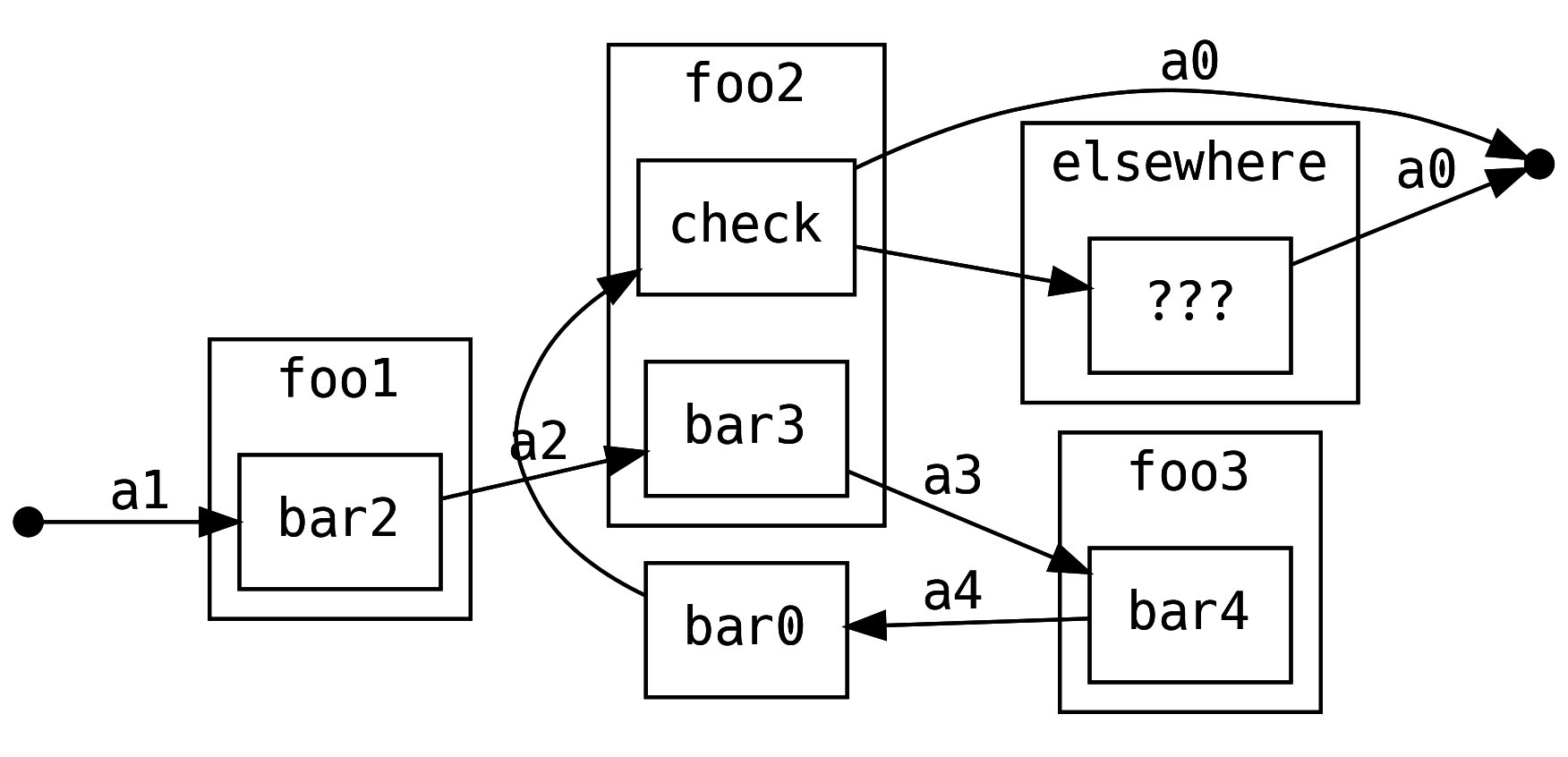
Or we can stay within the original flow and retry everything downstream

  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
      a0_ <- if (check(a0)) a0.pure[IO]
             else next(a3)
    } yield a0_
  }

This is just one retry, not an infinite loop. For example, we might want downstream to reconfirm a potentially dangerous action.

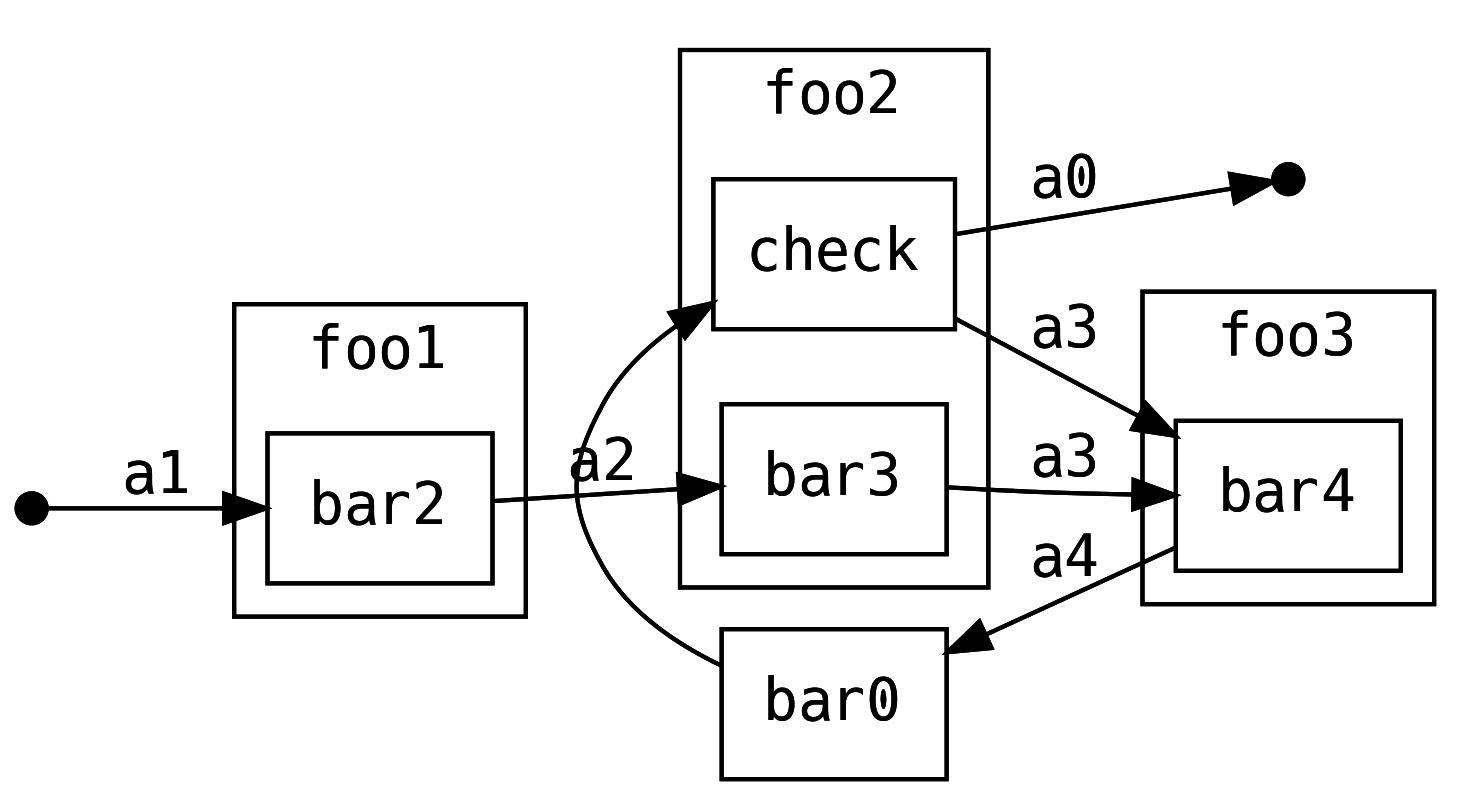
Finally, we can perform actions that are specific to the context of the ContT, in this case IO which lets us do error handling and resource cleanup:

  def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).ensuring(cleanup).cps

7.4.10.2 When to Order Spaghetti

It is not an accident that these diagrams look like spaghetti, that’s just what happens when we start messing with control flow. All the mechanisms we’ve discussed in this section are simple to implement directly if we can edit the definition of flow, therefore we do not typically need to use ContT.

However, if we are designing a framework, we should consider exposing the plugin system as ContT callbacks to allow our users more power over their control flow. Sometimes the customer just really wants the spaghetti.

For example, if the Scala compiler was written using CPS, it would allow for a principled approach to communication between compiler phases. A compiler plugin would be able to perform some action based on the inferred type of an expression, computed at a later stage in the compile. Similarly, continuations would be a good API for an extensible build tool or text editor.

A caveat with ContT is that it is not stack safe, so cannot be used for programs that run forever.

7.4.10.3 Great, kid. Don’t get ContT.

A more complex variant of ContT called IndexedContT wraps (A => F[B]) => F[C]. The new type parameter C allows the return type of the entire computation to be different to the return type between each component. But if B is not equal to C then there is no Monad.

Not missing an opportunity to generalise as much as possible, IndexedContT is actually implemented in terms of an even more general structure (note the extra s before the T)

  final case class IndexedContsT[W[_], F[_], C, B, A](_run: W[A => F[B]] => F[C])
  
  type IndexedContT[f[_], c, b, a] = IndexedContsT[Id, f, c, b, a]
  type ContT[f[_], b, a]           = IndexedContsT[Id, f, b, b, a]
  type ContsT[w[_], f[_], b, a]    = IndexedContsT[w, f, b, b, a]
  type Cont[b, a]                  = IndexedContsT[Id, Id, b, b, a]

where W[_] has a Comonad, and ContT is actually implemented as a type alias. Companion objects exist for these type aliases with convenient constructors.

Admittedly, five type parameters is perhaps a generalisation too far. But then again, over-generalisation is consistent with the sensibilities of continuations.

7.4.11 Transformer Stacks and Ambiguous Implicits

This concludes our tour of the monad transformers in scalaz.

When multiple transformers are combined, we call this a transformer stack and although it is verbose, it is possible to read off the features by reading the transformers. For example if we construct an F[_] context which is a set of composed transformers, such as

  type Ctx[A] = StateT[EitherT[IO, E, ?], S, A]

we know that we are adding error handling with error type E (there is a MonadError[Ctx, E]) and we are managing state A (there is a MonadState[Ctx, S]).

But there are unfortunately practical drawbacks to using monad transformers and their companion Monad typeclasses:

1. Multiple implicit Monad parameters mean that the compiler cannot find the correct syntax to use for the context.
2. Monads do not compose in the general case, which means that the order of nesting of the transformers is important.
3. All the interpreters must be lifted into the common context. For example, we might have an implementation of some algebra that uses for IO and now we need to wrap it with StateT and EitherT even though they are unused inside the interpreter.
4. There is a performance cost associated to each layer. And some monad transformers are worse than others. StateT is particularly bad but even EitherT can cause memory allocation problems for high throughput applications.

Let’s talk about workarounds.

7.4.11.1 No Syntax

Let’s say we have an algebra

  trait Lookup[F[_]] {
    def look: F[Int]
  }

and some data types

  final case class Problem(bad: Int)
  final case class Table(last: Int)

that we want to use in our business logic

  def foo[F[_]](L: Lookup[F])(
    implicit
      E: MonadError[F, Problem],
      S: MonadState[F, Table]
  ): F[Int] = for {
    old <- S.get
    i   <- L.look
    _   <- if (i === old.last) E.raiseError(Problem(i))
           else ().pure[F]
  } yield i

The first problem we encounter is that this fails to compile

  [error] value flatMap is not a member of type parameter F[Table]
  [error]     old <- S.get
  [error]              ^

There are some tactical solutions to this problem. The most obvious is to make all the parameters explicit

  def foo1[F[_]: Monad](
    L: Lookup[F],
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = ...

and require only Monad to be passed implicitly via context bounds. However, this means that we must manually wire up the MonadError and MonadState when calling foo1 and when calling out to another method that requires an implicit.

A second solution is to leave the parameters implicit and use name shadowing to make all but one of the parameters explicit. This allows upstream to use implicit resolution when calling us but we still need to pass parameters explicitly if we call out.

  @inline final def shadow[A, B, C](a: A, b: B)(f: (A, B) => C): C = f(a, b)
  
  def foo2a[F[_]: Monad](L: Lookup[F])(
    implicit
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = shadow(E, S) { (E, S) => ...

or we could shadow just one Monad, leaving the other one to provide our syntax and to be available for when we call out to other methods

  @inline final def shadow[A, B](a: A)(f: A => B): B = f(a)
  ...
  
  def foo2b[F[_]](L: Lookup[F])(
    implicit
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = shadow(E) { E => ...

A third option, with a higher up-front cost, is to create a custom Monad typeclass that holds implicit references to the two Monad classes that we care about

  trait MonadErrorState[F[_], E, S] {
    implicit def E: MonadError[F, E]
    implicit def S: MonadState[F, S]
  }

and a derivation of the typeclass given a MonadError and MonadState

  object MonadErrorState {
    implicit def create[F[_], E, S](
      implicit
        E0: MonadError[F, E],
        S0: MonadState[F, S]
    ) = new MonadErrorState[F, E, S] {
      def E: MonadError[F, E] = E0
      def S: MonadState[F, S] = S0
    }
  }

Now if we want access to S or E we get them via F.S or F.E

  def foo3a[F[_]: Monad](L: Lookup[F])(
    implicit F: MonadErrorState[F, Problem, Table]
  ): F[Int] =
    for {
      old <- F.S.get
      i   <- L.look
      _ <- if (i === old.last) F.E.raiseError(Problem(i))
      else ().pure[F]
    } yield i

Like the second solution, we can choose one of the Monad instances to be implicit within the block, achieved by importing it

  def foo3b[F[_]](L: Lookup[F])(
    implicit F: MonadErrorState[F, Problem, Table]
  ): F[Int] = {
    import F.E
    ...
  }

7.4.11.2 Composing Transformers

An EitherT[StateT[...], ...] has a MonadError but does not have a MonadState, whereas StateT[EitherT[...], ...] can provide both.

The workaround is to study the implicit derivations on the companion of the transformers and to make sure that the outer most transformer provides everything we need.

A rule of thumb is that more complex transformers go on the outside, with this chapter presenting transformers in increasing order of complex.

7.4.11.3 Lifting Interpreters

Continuing the same example, let’s say our Lookup algebra has an IO interpreter

  object LookupRandom extends Lookup[IO] {
    def look: IO[Int] = IO { util.Random.nextInt }
  }

but we want our context to be

  type Ctx[A] = StateT[EitherT[IO, Problem, ?], Table, A]

to give us a MonadError and a MonadState. This means we need to wrap LookupRandom to operate over Ctx.

Firstly, we want to make use of the .liftM syntax on Monad, which uses MonadTrans to lift from our starting F[A] into G[F, A]

  final class MonadOps[F[_]: Monad, A](fa: F[A]) {
    def liftM[G[_[_], _]: MonadTrans]: G[F, A] = ...
    ...
  }

It is important to realise that the type parameters to .liftM have two type holes, one of shape _[_] and another of shape _. If we create type aliases of this shape

  type Ctx0[F[_], A] = StateT[EitherT[F, Problem, ?], Table, A]
  type Ctx1[F[_], A] = EitherT[F, Problem, A]
  type Ctx2[F[_], A] = StateT[F, Table, A]

We can abstract over MonadTrans to lift a Lookup[F] to any Lookup[G[F, ?]] where G is a Monad Transformer:

  def liftM[F[_]: Monad, G[_[_], _]: MonadTrans](f: Lookup[F]) =
    new Lookup[G[F, ?]] {
      def look: G[F, Int] = f.look.liftM[G]
    }

Allowing us to wrap once for EitherT, and then again for StateT

  val wrap1 = Lookup.liftM[IO, Ctx1](LookupRandom)
  val wrap2: Lookup[Ctx] = Lookup.liftM[EitherT[IO, Problem, ?], Ctx2](wrap1)

Another way to achieve this, in a single step, is to use MonadIO which enables lifting an IO into a transformer stack:

  @typeclass trait MonadIO[F[_]] extends Monad[F] {
    def liftIO[A](ioa: IO[A]): F[A]
  }

with MonadIO instances for all the common combinations of transformers.

The boilerplate overhead to lift an IO interpreter to anything with a MonadIO instance is therefore two lines of code (for the interpreter definition), plus one line per element of the algebra, and a final line to call it:

  def liftIO[F[_]: MonadIO](io: Lookup[IO]) = new Lookup[F] {
    def look: F[Int] = io.look.liftIO[F]
  }
  
  val L: Lookup[Ctx] = Lookup.liftIO(LookupRandom)

7.4.11.4 Performance

The biggest problem with Monad Transformers is their performance overhead. EitherT has a reasonably low overhead, with every .flatMap call generating a handful of objects, but this can impact high throughput applications where every object allocation matters. Other transformers, such as StateT, effectively add a trampoline, and ContT keeps the entire call-chain retained in memory.

If performance becomes a problem, the solution is to not use Monad Transformers. At least not the transformer data structures. A big advantage of the Monad typeclasses, like MonadState is that we can create an optimised F[_] for our application that provides the typeclasses naturally. We will learn how to create an optimal F[_] over the next two chapters, when we deep dive into two structures which we have already seen: Free and IO.

7.5 A Free Lunch

Our industry craves safe high-level languages, trading developer efficiency and reliability for reduced runtime performance.

The Just In Time (JIT) compiler on the JVM performs so well that simple functions can have comparable performance to their C or C++ equivalents, ignoring the cost of garbage collection. However, the JIT only performs low level optimisations: branch prediction, inlining methods, unrolling loops, and so on.

The JIT does not perform optimisations of our business logic, for example batching network calls or parallelising independent tasks. The developer is responsible for writing the business logic and optimisations at the same time, reducing readability and making it harder to maintain. It would be good if optimisation was a tangential concern.

If instead, we have a data structure that describes our business logic in terms of high level concepts, not machine instructions, we can perform high level optimisation. Data structures of this nature are typically called Free structures and can be generated for free for the members of the algebraic interfaces of our program. For example, a Free Applicative can be generated that allows us to batch or de-duplicate expensive network I/O.

In this section we will learn how to create free structures, and how they can be used.

7.5.1 Free (Monad)

Fundamentally, a monad describes a sequential program where every step depends on the previous one. We are therefore limited to modifications that only know about things that we’ve already run and the next thing we are going to run.

As a refresher, Free is the data structure representation of a Monad and is defined by three members

  sealed abstract class Free[S[_], A] {
    def mapSuspension[T[_]](f: S ~> T): Free[T, A] = ...
    def foldMap[M[_]: Monad](f: S ~> M): M[A] = ...
    ...
  }
  object Free {
    implicit def monad[S[_], A]: Monad[Free[S, A]] = ...
  
    private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
    private final case class Return[S[_], A](a: A)     extends Free[S, A]
    private final case class Gosub[S[_], A0, B](
      a: Free[S, A0],
      f: A0 => Free[S, B]
    ) extends Free[S, B] { type A = A0 }
  
    def liftF[S[_], A](value: S[A]): Free[S, A] = Suspend(value)
    ...
  }

• Suspend represents a program that has not yet been interpreted
• Return is .pure
• Gosub is .bind

A Free[S, A] can be freely generated for any algebra S. To make this explicit, consider our application’s Machines algebra

  trait Machines[F[_]] {
    def getTime: F[Epoch]
    def getManaged: F[NonEmptyList[MachineNode]]
    def getAlive: F[Map[MachineNode, Epoch]]
    def start(node: MachineNode): F[Unit]
    def stop(node: MachineNode): F[Unit]
  }

We define a freely generated Free for Machines by creating a GADT with a data type for each element of the algebra. Each data type has the same input parameters as its corresponding element, is parameterised over the return type, and has the same name:

  object Machines {
    sealed abstract class Ast[A]
    final case class GetTime()                extends Ast[Epoch]
    final case class GetManaged()             extends Ast[NonEmptyList[MachineNode]]
    final case class GetAlive()               extends Ast[Map[MachineNode, Epoch]]
    final case class Start(node: MachineNode) extends Ast[Unit]
    final case class Stop(node: MachineNode)  extends Ast[Unit]
    ...

The GADT defines an Abstract Syntax Tree (AST) because each member is representing a computation in a program.

We then define .liftF, an implementation of Machines, with Free[Ast, ?] as the context. Every method simply delegates to Free.liftT to create a Suspend

  ...
    def liftF = new Machines[Free[Ast, ?]] {
      def getTime = Free.liftF(GetTime())
      def getManaged = Free.liftF(GetManaged())
      def getAlive = Free.liftF(GetAlive())
      def start(node: MachineNode) = Free.liftF(Start(node))
      def stop(node: MachineNode) = Free.liftF(Stop(node))
    }
  }

When we construct our program, parameterised over a Free, we run it by providing an interpreter (a natural transformation Ast ~> M) to the .foldMap method. For example, if we could provide an interpreter that maps to IO we can construct an IO[Unit] program via the free AST

  def program[F[_]: Monad](M: Machines[F]): F[Unit] = ...
  
  val interpreter: Machines.Ast ~> IO = ...
  
  val app: IO[Unit] = program[Free[Machines.Ast, ?]](Machines.liftF)
                        .foldMap(interpreter)

For completeness, an interpreter that delegates to a direct implementation is easy to write. This might be useful if the rest of the application is using Free as the context and we already have an IO implementation that we want to use:

  def interpreter[F[_]](f: Machines[F]): Ast ~> F = λ[Ast ~> F] {
    case GetTime()    => f.getTime
    case GetManaged() => f.getManaged
    case GetAlive()   => f.getAlive
    case Start(node)  => f.start(node)
    case Stop(node)   => f.stop(node)
  }

But our business logic needs more than just Machines, we also need access to the Drone algebra, recall defined as

  trait Drone[F[_]] {
    def getBacklog: F[Int]
    def getAgents: F[Int]
  }
  object Drone {
    sealed abstract class Ast[A]
    ...
    def liftF = ...
    def interpreter = ...
  }

What we want is for our AST to be a combination of the Machines and Drone ASTs. We studied Coproduct in Chapter 6, a higher kinded disjunction:

  final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A])

Now we can use the context Free[Coproduct[Machines.Ast, Drone.Ast, ?], ?].

We could manually create the coproduct but we would be swimming in boilerplate, and we’d have to do it all again if we wanted to add a third algebra.

The scalaz.Inject typeclass helps:

  type :<:[F[_], G[_]] = Inject[F, G]
  sealed abstract class Inject[F[_], G[_]] {
    def inj[A](fa: F[A]): G[A]
    def prj[A](ga: G[A]): Option[F[A]]
  }
  object Inject {
    implicit def left[F[_], G[_]]: F :<: Coproduct[F, G, ?]] = ...
    ...
  }

The implicit derivations generate Inject instances when we need them, letting us rewrite our liftF to work for any combination of ASTs:

  def liftF[F[_]](implicit I: Ast :<: F) = new Machines[Free[F, ?]] {
    def getTime                  = Free.liftF(I.inj(GetTime()))
    def getManaged               = Free.liftF(I.inj(GetManaged()))
    def getAlive                 = Free.liftF(I.inj(GetAlive()))
    def start(node: MachineNode) = Free.liftF(I.inj(Start(node)))
    def stop(node: MachineNode)  = Free.liftF(I.inj(Stop(node)))
  }

It is nice that F :<: G reads as if our Ast is a member of the complete F instruction set: this syntax is intentional.

Putting it all together, lets say we have a program that we wrote abstracting over Monad

  def program[F[_]: Monad](M: Machines[F], D: Drone[F]): F[Unit] = ...

and we have some existing implementations of Machines and Drone, we can create interpreters from them:

  val MachinesIO: Machines[IO] = ...
  val DroneIO: Drone[IO]       = ...
  
  val M: Machines.Ast ~> IO = Machines.interpreter(MachinesIO)
  val D: Drone.Ast ~> IO    = Drone.interpreter(DroneIO)

and combine them into the larger instruction set using a convenience method from the NaturalTransformation companion

  object NaturalTransformation {
    def or[F[_], G[_], H[_]](fg: F ~> G, hg: H ~> G): Coproduct[F, H, ?] ~> G = ...
    ...
  }
  
  type Ast[a] = Coproduct[Machines.Ast, Drone.Ast, a]
  
  val interpreter: Ast ~> IO = NaturalTransformation.or(M, D)

Then use it to produce an IO

  val app: IO[Unit] = program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
                        .foldMap(interpreter)

But we’ve gone in circles! We could have used IO as the context for our program in the first place and avoided Free. So why did we put ourselves through all this pain? Let’s see some reasons why Free might be useful.

7.5.1.1 Testing: Mocks and Stubs

It might sound hypocritical to propose that Free can be used to reduce boilerplate, given how much code we have written. However, there is a tipping point where the Ast pays for itself when we have many tests that require stub implementations.

If the .Ast and .liftF is defined for an algebra, we can create partial interpreters

  val M: Machines.Ast ~> Id = stub[Map[MachineNode, Epoch]] {
    case Machines.GetAlive() => Map.empty
  }
  val D: Drone.Ast ~> Id = stub[Int] {
    case Drone.GetBacklog() => 1
  }

which can be used to test our program

  program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
    .foldMap(or(M, D))
    .shouldBe(1)

By using partial functions, and not total functions, we are exposing ourselves to runtime errors. Many teams are happy to accept this risk in their unit tests since the test would fail if there is a programmer error.

Arguably we could also achieve the same thing with implementations of our algebras that implement every method with ???, overriding what we need on a case by case basis.

7.5.1.2 Monitoring

It is typical for server applications to be monitored by runtime agents that manipulate bytecode to insert profilers and extract various kinds of usage or performance information.

If our application’s context is Free, we do not need to resort to bytecode manipulation, we can instead implement a side-effecting monitor as an interpreter that we have complete control over.

For example, consider using this Ast ~> Ast “agent”

  val Monitor = λ[Demo.Ast ~> Demo.Ast](
    _.run match {
      case \/-(m @ Drone.GetBacklog()) =>
        JmxAbstractFactoryBeanSingletonProviderUtilImpl.count("backlog")
        Coproduct.rightc(m)
      case other =>
        Coproduct(other)
    }
  )

which records method invocations: we would use a vendor-specific routine in real code. We could also watch for specific messages of interest and log them as a debugging aid.

We can attach Monitor to our production Free application with

  .mapSuspension(Monitor).foldMap(interpreter)

or combine the natural transformations and run with a single

  .foldMap(Monitor.andThen(interpreter))

7.5.1.3 Monkey Patching: Part 1

As engineers, we know that our business users often ask for bizarre workarounds to be added to the core logic of the application. We might want to codify such corner cases as exceptions to the rule and handle them tangentially to our core logic.

For example, suppose we get a memo from accounting telling us

URGENT: Bob is using node #c0ffee to run the year end. DO NOT STOP THIS MACHINE!1!

There is no possibility to discuss why Bob shouldn’t be using our machines for his super-important accounts, so we have to hack our business logic and put out a release to production as soon as possible.

Our monkey patch can map into a Free structure, allowing us to return a pre-canned result (Free.pure) instead of scheduling the instruction. We special case the instruction in a custom natural transformation with its return value:

  val monkey = λ[Machines.Ast ~> Free[Machines.Ast, ?]] {
    case Machines.Stop(MachineNode("#c0ffee")) => Free.pure(())
    case other                                 => Free.liftF(other)
  }

eyeball that it works, push it to prod, and set an alarm for next week to remind us to remove it, and revoke Bob’s access to our servers.

Our unit test could use State as the target context, so we can keep track of all the nodes we stopped:

  type S = Set[MachineNode]
  val M: Machines.Ast ~> State[S, ?] = Mocker.stub[Unit] {
    case Machines.Stop(node) => State.modify[S](_ + node)
  }
  
  Machines
    .liftF[Machines.Ast]
    .stop(MachineNode("#c0ffee"))
    .foldMap(monkey)
    .foldMap(M)
    .exec(Set.empty)
    .shouldBe(Set.empty)

along with a test that “normal” nodes are not affected.

An advantage of using Free to avoid stopping the #c0ffee nodes is that we can be sure to catch all the usages instead of having to go through the business logic and look for all usages of .stop. If our application context is just an IO we could, of course, implement this logic in the Machines[IO] implementation but an advantage of using Free is that we don’t need to touch the existing code and can instead isolate and test this (temporary) behaviour, without being tied to the IO implementations.

7.5.1.4 Monkey Patching: Part 2

Infrastructure sends a memo:

To meet the CEO’s vision for this quarter, we are on a cost rationalisation and reorientation initiative.

Therefore, we paid Google a million dollars to develop a Batch API so we can start nodes more cost effectively.

PS: Your bonus depends on using the new API.

When we monkey patch, we are not limited to the original instruction set: we can introduce new ASTs. Rather than change our core business logic, we might decide to translate existing instructions into an extended set, introducing Batch:

  trait Batch[F[_]] {
    def start(nodes: NonEmptyList[MachineNode]): F[Unit]
  }
  object Batch {
    sealed abstract class Ast[A]
    ...
    def liftF = ...
  }

Let’s first set up a test for a simple program by defining the AST and target type:

  type Orig[a] = Coproduct[Machines.Ast, Drone.Ast, a]
  type T[a]    = State[S, a]

We track the started nodes in a data container so we can assert on them later

  final case class S(
    singles: IList[MachineNode],
    batches: IList[NonEmptyList[MachineNode]]
  ) {
    def addSingle(node: MachineNode) = S(node :: singles, batches)
    def addBatch(nodes: NonEmptyList[MachineNode]) = S(singles, nodes :: batches)
  }

and introduce some stub implementations

  val M: Machines.Ast ~> T = Mocker.stub[Unit] {
    case Machines.Start(node) => State.modify[S](_.addSingle(node))
  }
  val D: Drone.Ast ~> T = Mocker.stub[Int] {
    case Drone.GetBacklog() => 2.pure[T]
  }

We can expect that the following simple program will behave as expected and call Machines.Start twice:

  def program[F[_]: Monad](M: Machines[F], D: Drone[F]): F[Unit] =
    for {
      todo <- D.getBacklog
      _    <- (1 |-> todo).traverse(id => M.start(MachineNode(id.shows)))
    } yield ()
  
  program(Machines.liftF[Orig], Drone.liftF[Orig])
    .foldMap(or(M, D))
    .run(S(IList.empty, IList.empty))
    ._1
    .shouldBe(S(IList(MachineNode("2"), MachineNode("1")), IList.empty))

But we don’t want to use Machines.Start, we need Batch.Start to get our bonus. Expand the AST to keep track of the Waiting nodes that we are delaying, and add the Batch instructions:

  type Waiting      = IList[MachineNode]
  type Extension[a] = Coproduct[Batch.Ast, Orig, a]
  type Patched[a]   = StateT[Free[Extension, ?], Waiting, a]

along with a stub for the Batch algebra

  val B: Batch.Ast ~> T = Mocker.stub[Unit] {
    case Batch.Start(nodes) => State.modify[S](_.addBatch(nodes))
  }

We can convert from the Orig AST into Patched by providing a natural transformation that batches node starts:

  def monkey(max: Int) = new (Orig ~> Patched) {
    def apply[α](fa: Orig[α]): Patched[α] = fa.run match {
      case -\/(Machines.Start(node)) =>
        StateT { waiting =>
          if (waiting.length >= max) {
            val start = Batch.Start(NonEmptyList.nel(node, waiting))
            Free
              .liftF[Extension, Unit](leftc(start))
              .strengthL(IList.empty)
          } else
            Free
              .pure[Extension, Unit](())
              .strengthL(node :: waiting)
        }
  
      case _ =>
        Free
          .liftF[Extension, α](rightc(fa))
          .liftM[StateT[?[_], Waiting, ?]]
    }
  }

We’re using .strengthL to set the value of the Waiting state, with .pure again letting us avoid sending an instruction in this code branch.

We .foldMap twice because of the state, and combine the stubs again with .or:

  program(Machines.liftF[Orig], Drone.liftF[Orig])
    .foldMap(monkey(1))
    .run(IList.empty) // starting Waiting list
    .foldMap(or(B, or(M, D)))

Then we run the program and assert: that there are no nodes in the Waiting list, no node has been launched using the old API, and all nodes have been launched in one call to the batch API.

  .run(S(IList.empty, IList.empty))
  .shouldBe(
    (
      S(
        IList.empty, // no singles
        IList(NonEmptyList(MachineNode("2"), MachineNode("1"))) // bonus time!
      ),
      (
        IList.empty, // no Waiting
        () // the program output
      )
    )
  )

Congratulations, we’ve saved the company $50 every month, and it only cost a million dollars. But that was some other team’s budget, so it is OK.

We could have done the same monkey patch by hard coding the batching logic into our algebra implementations. In the defence of Free, we have decoupled the patch from the implementation, which means we can test it more thoroughly.

7.5.2 FreeAp (Applicative)

Despite this chapter being called Advanced Monads, the takeaway is: don’t use monads unless you really really have to. In this section, we will see why FreeAp (free applicative) is preferable to Free monads.

FreeAp is defined as the data structure representation of the ap and pure methods from the Applicative typeclass:

  sealed abstract class FreeAp[S[_], A] {
    def hoist[G[_]](f: S ~> G): FreeAp[G,A] = ...
    def foldMap[G[_]: Applicative](f: S ~> G): G[A] = ...
    def monadic: Free[S, A] = ...
    def analyze[M:Monoid](f: F ~> λ[α => M]): M = ...
    ...
  }
  object FreeAp {
    implicit def applicative[S[_], A]: Applicative[FreeAp[S, A]] = ...
  
    private final case class Pure[S[_], A](a: A) extends FreeAp[S, A]
    private final case class Ap[S[_], A, B](
      value: () => S[B],
      function: () => FreeAp[S, B => A]
    ) extends FreeAp[S, A]
  
    def pure[S[_], A](a: A): FreeAp[S, A] = Pure(a)
    def lift[S[_], A](x: =>S[A]): FreeAp[S, A] = ...
    ...
  }

The methods .hoist and .foldMap are like their Free analogues .mapSuspension and .foldMap.

As a convenience, we can generate a Free[S, A] from our FreeAp[S, A] with .monadic. This is especially useful to optimise smaller Applicative subsystems yet use them as part of a larger Free program.

Like Free, we must create a FreeAp for our ASTs, more boilerplate…

  def liftA[F[_]](implicit I: Ast :<: F) = new Machines[FreeAp[F, ?]] {
    def getTime = FreeAp.lift(I.inj(GetTime()))
    ...
  }

7.5.2.1 Batching Network Calls

We opened this chapter with grand claims about performance. Time to deliver.

Philip Stark’s Humanised version of Peter Norvig’s Latency Numbers serve as motivation for why we should focus on reducing network calls to optimise an application:

Although Free and FreeAp incur a memory allocation overhead, the equivalent of 100 seconds in the humanised chart, every time we can turn two sequential network calls into one batch call, we save nearly 5 years.

When we are in a Applicative context, we can safely optimise our application without breaking any of the expectations of the original program, and without cluttering the business logic.

Luckily, our main business logic only requires an Applicative, recall

  final class DynAgentsModule[F[_]: Applicative](D: Drone[F], M: Machines[F])
      extends DynAgents[F] {
    def act(world: WorldView): F[WorldView] = ...
    ...
  }

To begin, we create the lift boilerplate for the Batch algebra

  trait Batch[F[_]] {
    def start(nodes: NonEmptyList[MachineNode]): F[Unit]
  }
  object Batch {
    sealed abstract class Ast[A]
    final case class Start(nodes: NonEmptyList[MachineNode]) extends Ast[Unit]
  
    def liftA[F[_]](implicit I: Ast :<: F) = new Batch[FreeAp[F, ?]] {
      def start(nodes: NonEmptyList[MachineNode]) = FreeAp.lift(I.inj(Start(nodes)))
    }
  }

and then we’ll create an instance of DynAgentsModule with FreeAp as the context

  type Orig[a] = Coproduct[Machines.Ast, Drone.Ast, a]
  
  val world: WorldView = ...
  val program = new DynAgentsModule(Drone.liftA[Orig], Machines.liftA[Orig])
  val freeap  = program.act(world)

In Chapter 6, we studied the Const data type, which allows us to analyse a program. It should not be surprising that FreeAp.analyze is implemented in terms of Const:

  sealed abstract class FreeAp[S[_], A] {
    ...
    def analyze[M: Monoid](f: S ~> λ[α => M]): M =
      foldMap(λ[S ~> Const[M, ?]](x => Const(f(x)))).getConst
  }

We provide a natural transformation to record all node starts and .analyze our program to get all the nodes that need to be started:

  val gather = λ[Orig ~> λ[α => IList[MachineNode]]] {
    case Coproduct(-\/(Machines.Start(node))) => IList.single(node)
    case _                                    => IList.empty
  }
  val gathered: IList[MachineNode] = freeap.analyze(gather)

The next step is to extend the instruction set from Orig to Extended, which includes the Batch.Ast and write a FreeAp program that starts all our gathered nodes in a single network call

  type Extended[a] = Coproduct[Batch.Ast, Orig, a]
  def batch(nodes: IList[MachineNode]): FreeAp[Extended, Unit] =
    nodes.toNel match {
      case None        => FreeAp.pure(())
      case Some(nodes) => FreeAp.lift(Coproduct.leftc(Batch.Start(nodes)))
    }

We also need to remove all the calls to Machines.Start, which we can do with a natural transformation

  val nostart = λ[Orig ~> FreeAp[Extended, ?]] {
    case Coproduct(-\/(Machines.Start(_))) => FreeAp.pure(())
    case other                             => FreeAp.lift(Coproduct.rightc(other))
  }

Now we have two programs, and need to combine them. Recall the *> syntax for Functor

  val patched = batch(gathered) *> freeap.foldMap(nostart)

Putting it all together under a single method:

  def optimise[A](orig: FreeAp[Orig, A]): FreeAp[Extended, A] =
    (batch(orig.analyze(gather)) *> orig.foldMap(nostart))

That’s it! We .optimise every time we call act in our main loop, which is just a matter of plumbing.

7.5.3 Coyoneda (Functor)

Named after mathematician Nobuo Yoneda, we can freely generate a Functor data structure for any algebra S[_]

  sealed abstract class Coyoneda[S[_], A] {
    def run(implicit S: Functor[S]): S[A] = ...
    def trans[G[_]](f: F ~> G): Coyoneda[G, A] = ...
    ...
  }
  object Coyoneda {
    implicit def functor[S[_], A]: Functor[Coyoneda[S, A]] = ...
  
    private final case class Map[F[_], A, B](fa: F[A], f: A => B) extends Coyoneda[F, A]
    def apply[S[_], A, B](sa: S[A])(f: A => B) = Map[S, A, B](sa, f)
    def lift[S[_], A](sa: S[A]) = Map[S, A, A](sa, identity)
    ...
  }

and there is also a contravariant version

  sealed abstract class ContravariantCoyoneda[S[_], A] {
    def run(implicit S: Contravariant[S]): S[A] = ...
    def trans[G[_]](f: F ~> G): ContravariantCoyoneda[G, A] = ...
    ...
  }
  object ContravariantCoyoneda {
    implicit def contravariant[S[_], A]: Contravariant[ContravariantCoyoneda[S, A]] = ...
  
    private final case class Contramap[F[_], A, B](fa: F[A], f: B => A)
      extends ContravariantCoyoneda[F, A]
    def apply[S[_], A, B](sa: S[A])(f: B => A) = Contramap[S, A, B](sa, f)
    def lift[S[_], A](sa: S[A]) = Contramap[S, A, A](sa, identity)
    ...
  }

The API is somewhat simpler than Free and FreeAp, allowing a natural transformation with .trans and a .run (taking an actual Functor or Contravariant, respectively) to escape the free structure.

Coyo and cocoyo can be a useful utility if we want to .map or .contramap over a type, and we know that we can convert into a data type that has a Functor but we don’t want to commit to the final data structure too early. For example, we create a Coyoneda[ISet, ?] (recall ISet does not have a Functor) to use methods that require a Functor, then convert into IList later on.

If we want to optimise a program with coyo or cocoyo we have to provide the expected boilerplate for each algebra:

  def liftCoyo[F[_]](implicit I: Ast :<: F) = new Machines[Coyoneda[F, ?]] {
    def getTime = Coyoneda.lift(I.inj(GetTime()))
    ...
  }
  def liftCocoyo[F[_]](implicit I: Ast :<: F) = new Machines[ContravariantCoyoneda[F, ?]] {
    def getTime = ContravariantCoyoneda.lift(I.inj(GetTime()))
    ...
  }

An optimisation we get by using Coyoneda is map fusion (and contramap fusion), which allows us to rewrite

  xs.map(a).map(b).map(c)

into

  xs.map(x => c(b(a(x))))

avoiding intermediate representations. For example, if xs is a List of a thousand elements, we save two thousand object allocations because we only map over the data structure once.

However it is arguably a lot easier to just make this kind of change in the original function by hand, or to wait for the better-monadic-for project to automatically perform these optimisations across our codebase.

7.5.4 Extensible Effects

Programs are just data: free structures help to make this explicit and give us the ability to rearrange and optimise that data.

Free is more special than it appears: it can sequence arbitrary algebras and typeclasses.

For example, a free structure for MonadState is available. The Ast and .liftF are more complicated than usual because we have to account for the S type parameter on MonadState, and the inheritance from Monad:

  object MonadState {
    sealed abstract class Ast[S, A]
    final case class Get[S]()     extends Ast[S, S]
    final case class Put[S](s: S) extends Ast[S, Unit]
  
    def liftF[F[_], S](implicit I: Ast[S, ?] :<: F) =
      new MonadState[Free[F, ?], S] with BindRec[Free[F, ?]] {
        def get       = Free.liftF(I.inj(Get[S]()))
        def put(s: S) = Free.liftF(I.inj(Put[S](s)))
  
        val delegate         = Free.freeMonad[F]
        def point[A](a: =>A) = delegate.point(a)
        ...
      }
    ...
  }

This gives us the opportunity to use optimised interpreters. For example, we could store the S in an atomic field instead of building up a nested StateT trampoline.

We can create an Ast and .liftF for almost any algebra or typeclass! The only restriction is that the F[_] does not appear as a parameter to any of the instructions, i.e. it must be possible for the algebra to have an instance of Functor. This unfortunately rules out MonadError and Monoid.

As the AST of a free program grows, performance degrades because the interpreter must match over instruction sets with an O(n) cost. An alternative to scalaz.Coproduct is iotaz’s encoding, which uses an optimised data structure to perform O(1) dynamic dispatch (using integers that are assigned to each coproduct at compiletime).

For historical reasons a free AST for an algebra or typeclass is called Initial Encoding, and a direct implementation (e.g. with IO) is called Finally Tagless. Although we have explored interesting ideas with Free, it is generally accepted that finally tagless is superior. But to use finally tagless style, we need a high performance effect type that provides all the monad typeclasses we’ve covered in this chapter. We also still need to be able to run our Applicative code in parallel. This is exactly what we will cover next.

7.6 Parallel

There are two effectful operations that we almost always want to run in parallel:

1. .map over a collection of effects, returning a single effect. This is achieved by .traverse, which delegates to the effect’s .apply2.
2. running a fixed number of effects with the scream operator |@|, and combining their output, again delegating to .apply2.

However, in practice, neither of these operations execute in parallel by default. The reason is that if our F[_] is implemented by a Monad, then the derived combinator laws for .apply2 must be satisfied, which say

  @typeclass trait Bind[F[_]] extends Apply[F] {
    ...
    override def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] =
      bind(fa)(a => map(fb)(b => f(a, b)))
    ...
  }

In other words, Monad is explicitly forbidden from running effects in parallel.

However, if we have an F[_] that is not monadic, then it may implement .apply2 in parallel. We can use the @@ (tag) mechanism to create an instance of Applicative for F[_] @@ Parallel, which is conveniently assigned to the type alias Applicative.Par

  object Applicative {
    type Par[F[_]] = Applicative[λ[α => F[α] @@ Tags.Parallel]]
    ...
  }

Monadic programs can then request an implicit Par in addition to their Monad

  def foo[F[_]: Monad: Applicative.Par]: F[Unit] = ...

Scalaz’s Traverse syntax supports parallelism:

  implicit class TraverseSyntax[F[_], A](self: F[A]) {
    ...
    def parTraverse[G[_], B](f: A => G[B])(
      implicit F: Traverse[F], G: Applicative.Par[G]
    ): G[F[B]] = Tag.unwrap(F.traverse(self)(a => Tag(f(a))))
  }

If the implicit Applicative.Par[IO] is in scope, we can choose between sequential and parallel traversal:

  val input: IList[String] = ...
  def network(in: String): IO[Int] = ...
  
  input.traverse(network): IO[IList[Int]] // one at a time
  input.parTraverse(network): IO[IList[Int]] // all in parallel

Similarly, we can call .parApply or .parTupled after using scream operators

  val fa: IO[String] = ...
  val fb: IO[String] = ...
  val fc: IO[String] = ...
  
  (fa |@| fb).parTupled: IO[(String, String)]
  
  (fa |@| fb |@| fc).parApply { case (a, b, c) => a + b + c }: IO[String]

It is worth nothing that when we have Applicative programs, such as

  def foo[F[_]: Applicative]: F[Unit] = ...

we can use F[A] @@ Parallel as our program’s context and get parallelism as the default on .traverse and |@|. Converting between the raw and @@ Parallel versions of F[_] must be handled manually in the glue code, which can be painful. Therefore it is often easier to simply request both forms of Applicative

  def foo[F[_]: Applicative: Applicative.Par]: F[Unit] = ...

7.6.1 Breaking the Law

We can take a more daring approach to parallelism: opt-out of the law that .apply2 must be sequential for Monad. This is highly controversial, but works well for the majority of real world applications. we must first audit our codebase (including third party dependencies) to ensure that nothing is making use of the .apply2 implied law.

We wrap IO

  final class MyIO[A](val io: IO[A]) extends AnyVal

and provide our own implementation of Monad which runs .apply2 in parallel by delegating to a @@ Parallel instance

  object MyIO {
    implicit val monad: Monad[MyIO] = new Monad[MyIO] {
      override def apply2[A, B, C](fa: MyIO[A], fb: MyIO[B])(f: (A, B) => C): MyIO[C] =
        Applicative[IO.Par].apply2(fa.io, fb.io)(f)
      ...
    }
  }

We can now use MyIO as our application’s context instead of IO, and get parallelism by default.

For completeness: a naive and inefficient implementation of Applicative.Par for our toy IO could use Future:

  object IO {
    ...
    type Par[a] = IO[a] @@ Parallel
    implicit val ParApplicative = new Applicative[Par] {
      override def apply2[A, B, C](fa: =>Par[A], fb: =>Par[B])(f: (A, B) => C): Par[C] =
        Tag(
          IO {
            val forked = Future { Tag.unwrap(fa).interpret() }
            val b      = Tag.unwrap(fb).interpret()
            val a      = Await.result(forked, Duration.Inf)
            f(a, b)
          }
        )
  }

and due to a bug in the scala compiler that treats all @@ instances as orphans, we must explicitly import the implicit:

  import IO.ParApplicative

In the final section of this chapter we will see how scalaz’s IO is actually implemented.

7.7 IO

Scalaz’s IO is the fastest asynchronous programming construct in the Scala ecosystem: up to 50 times faster than Future and 20% faster than Monix.

IO is a free data structure specialised for use as a general effect monad.

  sealed abstract class IO[E, A] { ... }
  object IO {
    final class FlatMap         ... extends IO[E, A]
    final class Point           ... extends IO[E, A]
    final class Strict          ... extends IO[E, A]
    final class SyncEffect      ... extends IO[E, A]
    final class Fail            ... extends IO[E, A]
    final class AsyncEffect     ... extends IO[E, A]
    final class AsyncIOEffect   ... extends IO[E, A]
    final class Attempt         ... extends IO[E2, E1 \/ A]
    final class Fork            ... extends IO[E2, Fiber[E1, A]]
    final class Race            ... extends IO[E, A]
    final class Suspend         ... extends IO[E, A]
    final class Bracket         ... extends IO[E, B]
    final class Uninterruptible ... extends IO[E, A]
    final class Sleep           ... extends IO[E, Unit]
    final class Supervise       ... extends IO[E, A]
    final class Terminate       ... extends IO[E, A]
    final class Supervisor      ... extends IO[E, Throwable => IO[Void, Unit]]
    final class Run             ... extends IO[E2, ExitResult[E1, A]]
    ...
  }

IO has two type parameters: it has a Bifunctor allowing the error type to be an application specific ADT. But because we are on the JVM, and must interact with legacy libraries, a convenient type alias is provided that uses exceptions for the error type:

  type Task[A] = IO[Throwable, A]

7.7.1 Creating

There are multiple ways to create an IO that cover a variety of eager, lazy, safe and unsafe code blocks:

  object IO {
    // eager evaluation of an existing value
    def now[E, A](a: A): IO[E, A] = ...
    // lazy evaluation of a pure calculation
    def point[E, A](a: =>A): IO[E, A] = ...
    // lazy evaluation of a side-effecting, yet Total, code block
    def sync[E, A](effect: =>A): IO[E, A] = ...
    // lazy evaluation of a side-effecting code block that may fail
    def syncThrowable[A](effect: =>A): IO[Throwable, A] = ...
  
    // create a failed IO
    def fail[E, A](error: E): IO[E, A] = ...
    // asynchronously sleeps for a specific period of time
    def sleep[E](duration: Duration): IO[E, Unit] = ...
    ...
  }

with convenient Task constructors:

  object Task {
    def apply[A](effect: =>A): Task[A] = IO.syncThrowable(effect)
    def now[A](effect: A): Task[A] = IO.now(effect)
    def fail[A](error: Throwable): Task[A] = IO.fail(error)
    def fromFuture[E, A](io: Task[Future[A]])(ec: ExecutionContext): Task[A] = ...
  }

The most common constructors, by far, when dealing with legacy code are Task.apply and Task.fromFuture:

  val fa: Task[Future[String]] = Task { ... impure code here ... }
  
  Task.fromFuture(fa)(ExecutionContext.global): Task[String]

We can’t pass around raw Future, because it eagerly evaluates, so must always be constructed inside a safe block.

Note that the ExecutionContext is not implicit, contrary to the convention. Recall that in scalaz we reserve the implicit keyword for typeclass derivation, to simplify the language: ExecutionContext is configuration that must be provided explicitly.

7.7.2 Running

The IO interpreter is called RTS, for runtime system. Its implementation is beyond the scope of this book. We will instead focus on the features that IO provides.

IO is just a data structure, and is interpreted at the end of the world by extending SafeApp and implementing .run

  trait SafeApp extends RTS {
  
    sealed trait ExitStatus
    object ExitStatus {
      case class ExitNow(code: Int)                         extends ExitStatus
      case class ExitWhenDone(code: Int, timeout: Duration) extends ExitStatus
      case object DoNotExit                                 extends ExitStatus
    }
  
    def run(args: List[String]): IO[Void, ExitStatus]
  
    final def main(args0: Array[String]): Unit = ... calls run ...
  }

If we are integrating with a legacy system and are not in control of the entry point of our application, we can extend the RTS and gain access to unsafe methods to evaluate the IO at the entry point to our principled FP code.

For example, if we have an algebra that canonicalises values, and may hit disk or network to resolve filenames and URLs:

  trait Canon[F[_], A] {
    def canon(a: A): F[A]
  }

we can write a scalatest that extends RTS and call unsafePerformIO to interpret the IO

  import org.scalatest._
  import scalaz.ioeffect.{ RTS, Task }
  
  class CanonSpec extends FlatSpec with RTS {
    "Canon" should "canon File" in {
      unsafePerformIO((new File(".")).canon) shouldBe ...
    }
  }

7.7.3 Features

IO provides typeclass instances for Bifunctor, MonadError[E, ?], BindRec, Plus, MonadPlus (if E forms a Monoid), and an Applicative[IO.Par[E, ?]].

In addition to the functionality from the typeclasses, there are implementation specific methods:

  sealed abstract class IO[E, A] {
    // retries an action N times, until success
    def retryN(n: Int): IO[E, A] = ...
    // ... with exponential backoff
    def retryBackoff(n: Int, factor: Double, duration: Duration): IO[E, A] = ...
  
    // repeats an action with a pause between invocations, until it fails
    def repeat[B](interval: Duration): IO[E, B] = ...
  
    // cancel the action if it does not complete within the timeframe
    def timeout(duration: Duration): IO[E, Maybe[A]] = ...
  
    // runs `release` on success or failure.
    // Note that IO[Void, Unit] cannot fail.
    def bracket[B](release: A => IO[Void, Unit])(use: A => IO[E, B]): IO[E, B] = ...
    // alternative syntax for bracket
    def ensuring(finalizer: IO[Void, Unit]): IO[E, A] =
    // ignore failure and success, e.g. to ignore the result of a cleanup action
    def ignore: IO[Void, Unit] = ...
  
    // runs two effects in parallel
    def par[B](that: IO[E, B]): IO[E, (A, B)] = ...
    ...

It is possible for an IO to be in a terminated state, which represents work that is intended to be discarded (it is neither an error nor a success). The utilities related to termination are:

  ...
    // terminate whatever actions are running with the given throwable.
    // bracket / ensuring is honoured.
    def terminate[E, A](t: Throwable): IO[E, A] = ...
  
    // runs two effects in parallel, return the winner and terminate the loser
    def race(that: IO[E, A]): IO[E, A] = ...
  
    // ignores terminations
    def uninterruptibly: IO[E, A] = ...
  ...

7.7.4 Fiber

An IO may spawn fibers, a lightweight abstraction over a JVM Thread. We can .fork an IO, and .supervise any incomplete fibers to ensure that they are terminated when the IO action completes

  ...
    def fork[E2]: IO[E2, Fiber[E, A]] = ...
    def supervised(error: Throwable): IO[E, A] = ...
  ...

When we have a Fiber we can .join back into the IO, or interrupt the underlying work.

  trait Fiber[E, A] {
    def join: IO[E, A]
    def interrupt[E2](t: Throwable): IO[E2, Unit]
  }

We can use fibers to achieve a form of optimistic concurrency control. Consider the case where we have data that we need to analyse, but we also need to validate it. We can optimistically begin the analysis and cancel the work if the validation fails, which is performed in parallel.

  final class BadData(data: Data) extends Throwable with NoStackTrace
  
  for {
    fiber1   <- analysis(data).fork
    fiber2   <- validate(data).fork
    valid    <- fiber2.join
    _        <- if (!valid) fiber1.interrupt(BadData(data))
                else IO.unit
    result   <- fiber1.join
  } yield result

Another usecase for fibers is when we need to perform a fire and forget action. For example, low priority logging over a network.

7.7.5 Promise

A promise represents an asynchronous variable that can be set exactly once (with complete or error). An unbounded number of listeners can get the variable.

  final class Promise[E, A] private (ref: AtomicReference[State[E, A]]) {
    def complete[E2](a: A): IO[E2, Boolean] = ...
    def error[E2](e: E): IO[E2, Boolean] = ...
    def get: IO[E, A] = ...
  
    // interrupts all listeners
    def interrupt[E2](t: Throwable): IO[E2, Boolean] = ...
  }
  object Promise {
    def make[E, A]: IO[E, Promise[E, A]] = ...
  }

Promise is not something that we typically use in application code. It is a building block for high level concurrency frameworks.

7.7.6 IORef

IORef is the IO equivalent of an atomic mutable variable.

We can read the variable and we have a variety of ways to write or update it.

  final class IORef[A] private (ref: AtomicReference[A]) {
    def read[E]: IO[E, A] = ...
  
    // write with immediate consistency guarantees
    def write[E](a: A): IO[E, Unit] = ...
    // write with eventual consistency guarantees
    def writeLater[E](a: A): IO[E, Unit] = ...
    // return true if an immediate write succeeded, false if not (and abort)
    def tryWrite[E](a: A): IO[E, Boolean] = ...
  
    // atomic primitives for updating the value
    def compareAndSet[E](prev: A, next: A): IO[E, Boolean] = ...
    def modify[E](f: A => A): IO[E, A] = ...
    def modifyFold[E, B](f: A => (B, A)): IO[E, B] = ...
  }
  object IORef {
    def apply[E, A](a: A): IO[E, IORef[A]] = ...
  }

IORef is another building block and can be used to provide a high performance MonadState. For example, create a newtype specialised to Task

  final class StateTask[A](val io: Task[A]) extends AnyVal
  object StateTask {
    def create[S](initial: S): Task[MonadState[StateTask, S]] =
      for {
        ref <- IORef(initial)
      } yield
        new MonadState[StateTask, S] {
          override def get       = new StateTask(ref.read)
          override def put(s: S) = new StateTask(ref.write(s))
          ...
        }
  }

We can make use of this optimised StateMonad implementation in a SafeApp, where our .program depends on optimised MTL typeclasses:

  object FastState extends SafeApp {
    def program[F[_]](implicit F: MonadState[F, Int]): F[ExitStatus] = ...
  
    def run(@unused args: List[String]): IO[Void, ExitStatus] =
      for {
        stateMonad <- StateTask.create(10)
        output     <- program(stateMonad).io
      } yield output
  }

A more realistic application would take a variety of algebras and typeclasses as input.

7.7.6.1 MonadIO

The MonadIO that we previously studied was simplified to hide the E parameter. The actual typeclass is

  trait MonadIO[M[_], E] {
    def liftIO[A](io: IO[E, A])(implicit M: Monad[M]): M[A]
  }

with a minor change to the boilerplate on the companion of our algebra, accounting for the extra E:

  trait Lookup[F[_]] {
    def look: F[Int]
  }
  object Lookup {
    def liftIO[F[_]: Monad, E](io: Lookup[IO[E, ?]])(implicit M: MonadIO[F, E]) =
      new Lookup[F] {
        def look: F[Int] = M.liftIO(io.look)
      }
    ...
  }

7.8 Summary

1. The Future is broke, don’t go there.
2. Manage stack safety with a Trampoline.
3. The Monad Transformer Library (MTL) abstracts over common effects.
4. Monad Transformers provide default implementations of the MTL.
5. Free data structures let us analyse, optimise and easily test our programs.
6. IO gives us the ability to implement algebras as effects on the outside world and interact with legacy systems.
7. IO can perform effects in parallel and provides a high performance implementation of the MTL.