7. Zaawansowane Monady

Znajomość Zaawansowanych Monad to element obowiązkowy, aby móc nazwać się doświadczonym programistą funkcyjnym.

Jednocześnie jesteśmy deweloperami, którzy nieustannie pragną prostego życia, a więc i nasza definicja “zaawansowania” jest raczej skromna. Dla porównania: scala.concurrent.Future jest strukturą dużo bardziej skomplikowaną niż jakakolwiek z prezentowanych w tym rozdziale Monad.

7.1 Always in motion is the Future²²

Największym problemem z Future jest to, że rozpoczyna obliczenia w momencie stworzenia, tym samym łącząc definiowanie programu z jego interpretacją (czyli np. uruchomieniem).

Future jest też nie najlepszym wyborem ze względów wydajnościowych: za każdym razem, gdy wywołujemy .flatMap, domknięcie jest przekazywane do Executora, wywołując planowanie wątków i zmiany kontekstu. Nie jest niczym nadzwyczajnym, aby 50% mocy obliczeniowej CPU wykorzystywane było na te właśnie operacje zamiast rzeczywistej pracy. W efekcie program zrównoleglony za pomocą Future może okazać się wolniejszy od swojego sekwencyjnego odpowiednika.

Zachłanna ewaluacja w połączeniu z odwołaniami do executora sprawia, że niemożliwe jest określenie kiedy zadanie się rozpoczęło, kiedy się zakończyło ani jakie pod-zadania zostały rozpoczęte. Zatem nie powinno nas dziwić, że “rozwiązania” do monitorowania wydajności frameworków opartych o Future są solidnym źródłem utrzymania dla nowoczesnych odpowiedników sprzedawców “cudownych remediów”.

Co więcej, Future.flatMap wymaga niejawnego przekazania parametru typu ExecutionContext, zmuszając użytkownika do myślenia o logice biznesowej i semantyce uruchomienia w tym samym momencie.

7.2 Efekty i efekty uboczne

Jeśli nie możemy wywołać metod z efektami ubocznymi w naszej logice biznesowej ani w Future (ani w Id, Either, Const itd.), to kiedy możemy je wywołać? Odpowiedź brzmi: wewnątrz Monady, która opóźnia wykonanie do czasu interpretacji w punkcie wejścia do aplikacji. W takiej sytuacji możemy odnosić się do operacji I/O i mutacji jako efektów, które widoczne są wprost w systemie typów, odwrotnie niż ukryte i nieoczywiste efekty uboczne.

Najprostszą implementacją takiej Monady jest jest IO

  final class IO[A](val interpret: () => A)
  object IO {
    def apply[A](a: =>A): IO[A] = new IO(() => a)
  
    implicit val monad: Monad[IO] = new Monad[IO] {
      def point[A](a: =>A): IO[A] = IO(a)
      def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] = IO(f(fa.interpret()).interpret())
    }
  }

Metoda .interpret wywoływana jest tylko raz, na wejściu do naszej aplikacji:

  def main(args: Array[String]): Unit = program.interpret()

Niemniej, taka prosta implementacja niesie ze sobą dwa duże problemy:

1. może spowodować przepełnienie stosu
2. nie umożliwia równoległego wykonywania obliczeń

Oba te problemy zostaną przez nas przezwyciężone w tym rozdziale. Jednocześnie musimy pamiętać, że niezależnie jak skomplikowana jest wewnętrzna implementacja Monady, zasady tutaj opisane zachowują moc: modularyzujemy definicję programu i jego wykonanie, tak aby móc wyrazić efekty w sygnaturach typów, sprawiając tym samym, że rozumowanie o nich staje się możliwe, a reużycie kodu łatwiejsze.

7.3 Bezpieczeństwo stosu

Na JVMie każde wywołanie metody dodaje wpis do stosu wywołań aktualnego wątku (Thread), tak jakbyśmy dopisywali element na początek Listy. Kiedy metoda kończy działanie, wierzchni wpis jest usuwany. Maksymalna długość stosu wywołań determinowana jest przez flagę -Xss ustawianą przy uruchomieniu polecenia java. Wywołania ogonowo-rekursywne są wykrywane przez kompilator Scali i nie dodają wpisów do stosu. Kiedy przekroczymy dozwolony limit poprzez zawołanie zbyt wielu metod, napotkamy StackOverflowError.

Niestety, każde zagnieżdżone wywołanie na naszym IO, jak np. .flatMap, dodaje kolejne wywołania do stosu. Najprostszym sposobem, aby zaobserwować to zjawisko, jest powtórzenie akcji w nieskończoność i sprawdzenie, czy taki program przeżyje dłużej niż kilka sekund. Możemy użyć metody .forever pochodzącej z Apply (rodzica Monady):

  scala> val hello = IO { println("hello") }
  scala> Apply[IO].forever(hello).interpret()
  
  hello
  hello
  hello
  ...
  hello
  java.lang.StackOverflowError
      at java.io.FileOutputStream.write(FileOutputStream.java:326)
      at ...
      at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
      at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
      at ...

Scalaz definiuje typeklasę BindRec, którą mogą implementować Monady niezagrażające przeładowywaniem stosu (stack safe). Wymaga ona zachowywania stałego rozmiaru stosu przy rekurencyjnych wywołaniach bind:

  @typeclass trait BindRec[F[_]] extends Bind[F] {
    def tailrecM[A, B](f: A => F[A \/ B])(a: A): F[B]
  
    override def forever[A, B](fa: F[A]): F[B] = ...
  }

Nie dla wszystkich programów potrzebujemy jej instancji, ale jest ona istotna dla Monad ogólnego przeznaczenia.

Aby osiągnąć wspomniane bezpieczeństwo, należy zamienić wywołania metod na referencje do ADT, czyli monadę Free:

  sealed abstract class Free[S[_], A]
  object Free {
    private final case class Return[S[_], A](a: A)     extends Free[S, A]
    private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
    private final case class Gosub[S[_], A0, B](
      a: Free[S, A0],
      f: A0 => Free[S, B]
    ) extends Free[S, B] { type A = A0 }
    ...
  }

ADT Free to naturalna reprezentacja metod z interfejsu Monad:

1. Return reprezentuje .point
2. Gosub reprezentuje .bind / .flatMap

Kiedy ADT odwzorowuje argumenty powiązanej funkcji, nazywamy to kodowaniem Churcha (Church encodnig).

Typ Free to skrót od FreeMonad i nazywa się tak, ponieważ pozwala uzyskać za darmo monadę dla dowolnego S[_]. Moglibyśmy na przykład wskazać algebrę Drone lub Machines z rozdziału 3 i wygenerować struktury danych reprezentujące nasz program, które stałyby się naszym S[_]. Zastanowimy się jak może nam się to przydać pod koniec tego rozdziału.

7.3.1 Trampoline

Free jest typem bardziej ogólnym, niż tego w tym momencie potrzebujemy. Ustawiając algebrę S[_] na () => ?, czyli odroczone wykonanie znane jako thunk, otrzymamy typ Trampoline, który pozwoli nam zaimplementować bezpieczną instancję Monady

  object Free {
    type Trampoline[A] = Free[() => ?, A]
    implicit val trampoline: Monad[Trampoline] with BindRec[Trampoline] =
      new Monad[Trampoline] with BindRec[Trampoline] {
        def point[A](a: =>A): Trampoline[A] = Return(a)
        def bind[A, B](fa: Trampoline[A])(f: A => Trampoline[B]): Trampoline[B] =
          Gosub(fa, f)
  
        def tailrecM[A, B](f: A => Trampoline[A \/ B])(a: A): Trampoline[B] =
          bind(f(a)) {
            case -\/(a) => tailrecM(f)(a)
            case \/-(b) => point(b)
          }
      }
    ...
  }

.tailrecM pochodząca z BindRec uruchamia .bind tak długo, aż otrzymamy B. Mimo że technicznie rzecz biorąc, nie jest to implementacja, którą spełnia wymagania anotacji @tailrec, to zachowuje stałą wielkość stosu, ponieważ każde wywołanie zwraca obiekt ze sterty (heap), a rekurencja zostaje odroczona.

Dostępne są funkcje ułatwiające tworzenie Trampoline zarówno zachłannie (.done), jak i przez nazwę (.delay). Możemy też stworzyć instancję Trampoline, przekazując inną jej instancję poprzez nazwę (.suspend):

  object Trampoline {
    def done[A](a: A): Trampoline[A]                  = Return(a)
    def delay[A](a: =>A): Trampoline[A]               = suspend(done(a))
    def suspend[A](a: =>Trampoline[A]): Trampoline[A] = unit >> a
  
    private val unit: Trampoline[Unit] = Suspend(() => done(()))
  }

Kiedy widzimy w naszym kodzie Trampoline[A] możemy w głowie podstawić w jej miejsce A, ponieważ jej jedyną funkcją jest sprawienie, że nie przeładujemy stosu. Możemy uzyskać A, interpretując Free za pomocą .run.

7.3.2 Przykład: bezpieczna DLista

W poprzednim rozdziale przedstawiliśmy typ danych DList jako

  final case class DList[A](f: IList[A] => IList[A]) {
    def toIList: IList[A] = f(IList.empty)
    def ++(as: DList[A]): DList[A] = DList(xs => f(as.f(xs)))
    ...
  }

Jednak w rzeczywistości jego implementacja przypomina bardziej:

  final case class DList[A](f: IList[A] => Trampoline[IList[A]]) {
    def toIList: IList[A] = f(IList.empty).run
    def ++(as: =>DList[A]): DList[A] = DList(xs => suspend(as.f(xs) >>= f))
    ...
  }

Zamiast aplikować zagnieżdżone wywołanie f, używamy odraczającej Trampoline, którą interpretujemy za pomocą .run, kiedy zajdzie taka potrzeba, np. w toIList. Zmiany są minimalne, ale w efekcie otrzymaliśmy bezpieczną wersję DList, która nie przepełni stosu niezależnie od tego, jak duże będą przetwarzane listy.

7.3.3 Bezpieczne IO

Używając Trampoline, możemy w podobny sposób zabezpieczyć nasze IO:

  final class IO[A](val tramp: Trampoline[A]) {
    def unsafePerformIO(): A = tramp.run
  }
  object IO {
    def apply[A](a: =>A): IO[A] = new IO(Trampoline.delay(a))
  
    implicit val Monad: Monad[IO] with BindRec[IO] =
      new Monad[IO] with BindRec[IO] {
        def point[A](a: =>A): IO[A] = IO(a)
        def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] =
          new IO(fa.tramp >>= (a => f(a).tramp))
        def tailrecM[A, B](f: A => IO[A \/ B])(a: A): IO[B] = ...
      }
  }

Interpreter unsafePerformIO() specjalnie został nazwany w tak odstraszający sposób, aby zniechęcić do używania go poza punktem wejścia naszej aplikacji.

Tym razem nie zobaczymy StackOverflowError:

  scala> val hello = IO { println("hello") }
  scala> Apply[IO].forever(hello).unsafePerformIO()
  
  hello
  hello
  hello
  ...
  hello

Używanie Trampoline zazwyczaj wiąże się ze spadkiem wydajności w porównaniu do używania zwykłej referencji. Okazuje się, że Free nie jest tak do końca za darmo.

7.4 Biblioteka Transformatorów Monad

Transformatory monad to struktury danych, które opakowują pewną wartość i dostarczają monadyczny efekt.

W Rozdziale 2 używaliśmy OptionT, aby móc użyć wartości typu F[Option[A]] w konstrukcji for, tak jakby była to po prostu instancja F[A]. Uzyskaliśmy w ten sposób efekt opcjonalnej wartości. Aby osiągnąć ten sam rezultat, moglibyśmy też użyć MonadPlus.

Poniższy zbiór typów danych często nazywany jest Biblioteką Transformatorów Monad (Monad Transformer Library, MTL). W tym podrozdziale opiszemy każdy z nich, zwracając uwagę na, to do czego mogą być przydatne i jak są zbudowane.

7.4.1 MonadTrans

Każdy transformator ma ogólny kształt T[F[_], A], dostarczając instancje co najmniej Monady oraz Hoist(a więc i MonadTrans):

  @typeclass trait MonadTrans[T[_[_], _]] {
    def liftM[F[_]: Monad, A](a: F[A]): T[F, A]
  }
  
  @typeclass trait Hoist[F[_[_], _]] extends MonadTrans[F] {
    def hoist[M[_]: Monad, N[_]](f: M ~> N): F[M, ?] ~> F[N, ?]
  }

.liftM pozwala nam stworzyć instancję transformatora na podstawie F[A], na przykład, aby zbudować OptionT[IO, String], wystarczy wywołać .liftM[OptionT] na IO[String].

.hoist wyraża tę samą koncepcję, ale dla transformacji naturalnych.

W ogólności istnieją trzy sposoby na uzyskanie transformatora:

• z instancji typu wewnętrznego, używając konstruktora
• z pojedynczej instancji A, używają .pure z Monady
• z F[A], używając liftM z MonadTrans

Z racji tego, jak działa inferencja typów w Scali, często oznacza to, że dość skomplikowana sygnatura typu musi być zapisania explicite. Transformatory dostarczają nam trochę wygodniejsze konstruktory w swoich obiektach towarzyszących jako obejście tego problemu.

7.4.2 MaybeT

OptionT, MaybeT i LazyOptionT są zaimplementowane w podobny sposób, zapewniając opcjonalność poprzez odpowiednio Option, Maybe i LazyOption. Skupimy się na MaybeT, aby uniknąć powtarzania się.

  final case class MaybeT[F[_], A](run: F[Maybe[A]])
  object MaybeT {
    def just[F[_]: Applicative, A](v: =>A): MaybeT[F, A] =
      MaybeT(Maybe.just(v).pure[F])
    def empty[F[_]: Applicative, A]: MaybeT[F, A] =
      MaybeT(Maybe.empty.pure[F])
    ...
  }

dostarcza MonadPlus

  implicit def monad[F[_]: Monad] = new MonadPlus[MaybeT[F, ?]] {
    def point[A](a: =>A): MaybeT[F, A] = MaybeT.just(a)
    def bind[A, B](fa: MaybeT[F, A])(f: A => MaybeT[F, B]): MaybeT[F, B] =
      MaybeT(fa.run >>= (_.cata(f(_).run, Maybe.empty.pure[F])))
  
    def empty[A]: MaybeT[F, A] = MaybeT.empty
    def plus[A](a: MaybeT[F, A], b: =>MaybeT[F, A]): MaybeT[F, A] = a orElse b
  }

Powyższa implementacja może wydawać się skomplikowana, ale w rzeczywistości jedyne co tutaj się dzieje, to delegacja operacji do Monad[F] i opakowywanie wyniku w MaybeT. Sam klej i taśma.

Z tą monadą możemy pisać logikę obsługującą opcjonalność wewnątrz kontekstu F[_]. Alternatywnie musielibyśmy wszędzie umieszczać Option lub Maybe.

Wyobraźmy sobie, że odpytujemy portal społecznościowy, chcąc zliczyć liczbę gwiazdek danego użytkownika, zaczynając od Stringa, który może, lub nie, wskazywać na konkretnego użytkownika. Oto nasza algebra:

  trait Twitter[F[_]] {
    def getUser(name: String): F[Maybe[User]]
    def getStars(user: User): F[Int]
  }
  def T[F[_]](implicit t: Twitter[F]): Twitter[F] = t

Musimy wywołać getUser a wynik przekazać do getStars. Jeśli użyjemy typeklasy Monad, będzie to dość skomplikowane, gdyż musimy obsłużyć przypadek Empty:

  def stars[F[_]: Monad: Twitter](name: String): F[Maybe[Int]] = for {
    maybeUser  <- T.getUser(name)
    maybeStars <- maybeUser.traverse(T.getStars)
  } yield maybeStars

Jednak mając do dyspozycji MonadPlus, możemy wessać Maybe do F[_] za pomocą .orEmpty i skupić się na ważniejszych rzeczach:

  def stars[F[_]: MonadPlus: Twitter](name: String): F[Int] = for {
    user  <- T.getUser(name) >>= (_.orEmpty[F])
    stars <- T.getStars(user)
  } yield stars

Jednakże zwiększenie wymagań co do naszego kontekstu na typeklasę MonadPlus może spowodować problemy na późniejszym etapie, jeśli nie będzie ona dostępna. Rozwiązaniem jest zmiana kontekstu na MaybeT[F, ?] (co automatycznie daje nam instancję MonadPlus dla dowolnej Monady), albo użyć MaybeT wprost w zwracanym typie, za cenę nieco większej ilości kodu:

  def stars[F[_]: Monad: Twitter](name: String): MaybeT[F, Int] = for {
    user  <- MaybeT(T.getUser(name))
    stars <- T.getStars(user).liftM[MaybeT]
  } yield stars

Każdy zespół musi sam wybrać między tymi opcjami, na bazie tego jakich interpreterów planują używać dla swoich programów.

7.4.3 EitherT

Wartość opcjonalna to tak naprawdę szczególny przypadek wartości, która może być błędem, ale nic o tym błędzie nie wiemy. EitherT (i jego leniwy wariant LazyEitherT) pozwalają nam użyć wartości dowolnego typu do wyrażenia błędu, który powie nam, co poszło nie tak w naszych obliczeniach.

W praktyce EitherT to opakowana wartość typu F[A \/ B]

  final case class EitherT[F[_], A, B](run: F[A \/ B])
  object EitherT {
    def either[F[_]: Applicative, A, B](d: A \/ B): EitherT[F, A, B] = ...
    def leftT[F[_]: Functor, A, B](fa: F[A]): EitherT[F, A, B] = ...
    def rightT[F[_]: Functor, A, B](fb: F[B]): EitherT[F, A, B] = ...
    def pureLeft[F[_]: Applicative, A, B](a: A): EitherT[F, A, B] = ...
    def pure[F[_]: Applicative, A, B](b: B): EitherT[F, A, B] = ...
    ...
  }

z instancją MonadError

  @typeclass trait MonadError[F[_], E] extends Monad[F] {
    def raiseError[A](e: E): F[A]
    def handleError[A](fa: F[A])(f: E => F[A]): F[A]
  }

.raiseError i .handleError są samoopisującymi się odpowiednikami throw i catch, które znamy z pracy z wyjątkami.

MonadError dostarcza również dodatkową składnię do rozwiązywania popularnych problemów:

  implicit final class MonadErrorOps[F[_], E, A](self: F[A])(implicit val F: MonadError[F, E])\
 {
    def attempt: F[E \/ A] = ...
    def recover(f: E => A): F[A] = ...
    def emap[B](f: A => E \/ B): F[B] = ...
  }

.attempt przenosi błędy z kontekstu do wartości.

.recover służy do zamiany błędów na wartości dla wszystkich przypadków, w przeciwieństwie do .handleError, która pozwala nam zwrócić F[A], czyli tym samym częściowo obsłużyć błędy.

.emap, czyli either map, pozwala zaaplikować transformację, która sama w sobie może się nie udać.

MonadError dla EitherT wygląda następująco:

  implicit def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
    def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
    def bind[A, B](fa: EitherT[F, E, A])
                  (f: A => EitherT[F, E, B]): EitherT[F, E, B] =
      EitherT(fa.run >>= (_.fold(_.left[B].pure[F], b => f(b).run)))
    def point[A](a: =>A): EitherT[F, E, A] = EitherT.pure(a)
  
    def raiseError[A](e: E): EitherT[F, E, A] = EitherT.pureLeft(e)
    def handleError[A](fa: EitherT[F, E, A])
                      (f: E => EitherT[F, E, A]): EitherT[F, E, A] =
      EitherT(fa.run >>= {
        case -\/(e) => f(e).run
        case right => right.pure[F]
      })
  }

Nie powinno też dziwić, że możemy przepisać przykład z MonadPlus, używając MonadError i dostarczając informacje o błędzie:

  def stars[F[_]: Twitter](name: String)
                          (implicit F: MonadError[F, String]): F[Int] = for {
    user  <- T.getUser(name) >>= (_.orError(s"user '$name' not found")(F))
    stars <- T.getStars(user)
  } yield stars

gdzie .orError to funkcja pomocnicza zdefiniowana na Maybe.

  sealed abstract class Maybe[A] {
    ...
    def orError[F[_], E](e: E)(implicit F: MonadError[F, E]): F[A] =
      cata(F.point(_), F.raiseError(e))
  }

Wersja używająca EitherT bezpośrednio:

  def stars[F[_]: Monad: Twitter](name: String): EitherT[F, String, Int] = for {
    user <- EitherT(T.getUser(name).map(_ \/> s"user '$name' not found"))
    stars <- EitherT.rightT(T.getStars(user))
  } yield stars

Najprostszą instancją MonadError jest \/, idealny typ do testowania logiki biznesowej wymagającej tej typeklasy. Na przykład:

  final class MockTwitter extends Twitter[String \/ ?] {
    def getUser(name: String): String \/ Maybe[User] =
      if (name.contains(" ")) Maybe.empty.right
      else if (name === "wobble") "connection error".left
      else User(name).just.right
  
    def getStars(user: User): String \/ Int =
      if (user.name.startsWith("w")) 10.right
      else "stars have been replaced by hearts".left
  }

Nasz test dla .stars może pokryć takie warianty:

  scala> stars("wibble")
  \/-(10)
  
  scala> stars("wobble")
  -\/(connection error)
  
  scala> stars("i'm a fish")
  -\/(user 'i'm a fish' not found)
  
  scala> stars("fommil")
  -\/(stars have been replaced by hearts)

Po raz kolejny możemy skupić się na testowaniu logiki biznesowej bez zbędnych dystrakcji.

Możemy w końcu wrócić do naszego JsonClienta z Rozdziału 4.3

  trait JsonClient[F[_]] {
    def get[A: JsDecoder](
      uri: String Refined Url,
      headers: IList[(String, String)]
    ): F[A]
    ...
  }

gdzie w API zawarliśmy jedynie szczęśliwą ścieżkę wykonania. Jeśli nasz interpreter dla tej algebry działa jedynie dla F mających instancję MonadError musimy zdefiniować jakiego rodzaju błędy mogą się pojawić. I faktycznie, jeśli zdecydujemy się interpretować EitherT[IO, JsonClient.Error, ?], to możemy mieć dwie warstwy błędów

  object JsonClient {
    sealed abstract class Error
    final case class ServerError(status: Int)       extends Error
    final case class DecodingError(message: String) extends Error
  }

które pokrywają odpowiednio problemy ze statusem odpowiedzi serwera oraz z naszym modelem dekodowanych obiektów.

7.4.3.1 Wybieranie typu błędu

Społeczność jest podzielona co do najlepszej strategii wyrażania błędów za pomocą E w MonadError.

Jedna szkoła mówi, że powinniśmy wybrać jakiś ogólny typ, np. String. Druga twierdzi, że każda aplikacja powinna mieć ADT wyrażające błędy, aby każdy z nich mógł być raportowany i obsługiwany inaczej. Gang niepryncypialny woli używać Throwable dla maksymalnej kompatybilności z JVMem.

Wprowadzenie wspomnianego ADT niesie za sobą dwa problemy:

• dodawanie nowych błędów jest niewygodne, a jeden z plików musi stać się monolitycznym repozytorium błędów, agregując ADT z pojedynczych podsystemów.
• niezależnie jak drobnoziarniste będą błędy, ich obsługa jest zazwyczaj taka sama: zaloguj i spróbuj ponownie albo przerwij przetwarzanie. Nie potrzebujemy do tego ADT.

ADT niesie ze sobą wartość, jeśli każdy wariant pozwala na inną strategię obsługi.

Kompromisem między ADT i Stringiem jest format pośredni, jak np. JSON, który jest rozumiany przez większość bibliotek odpowiedzialnych za logowanie i monitoring.

Brak stacktrace’a może znacznie utrudnić zlokalizowanie fragmentu kodu odpowiedzialnego za zgłoszenie danego błędu. Możemy rozwiązać ten problem, używając biblioteki sourcecode autorstwa Li Haoyi:

  final case class Meta(fqn: String, file: String, line: Int)
  object Meta {
    implicit def gen(implicit fqn: sourcecode.FullName,
                              file: sourcecode.File,
                              line: sourcecode.Line): Meta =
      new Meta(fqn.value, file.value, line.value)
  }
  
  final case class Err(msg: String)(implicit val meta: Meta)

Mimo że Err jest referencyjnie transparentny, jego niejawna konstrukcja już nie. Dwa wywołania Meta.gen wyprodukują różne wartości, ponieważ ich umieszczenie w kodzie wpływa na zwracaną wartość:

  scala> println(Err("hello world").meta)
  Meta(com.acme,<console>,10)
  
  scala> println(Err("hello world").meta)
  Meta(com.acme,<console>,11)

Aby zrozumieć, czemu tak się dzieje, musimy zdać sobie sprawę, że metody sourcecode.* to tak naprawdę makra, które generują dla nas kod. Jeśli napiszemy tę samą logikę wprost, to wszystko stanie się jasne:

  scala> println(Err("hello world")(Meta("com.acme", "<console>", 10)).meta)
  Meta(com.acme,<console>,10)
  
  scala> println(Err("hello world")(Meta("com.acme", "<console>", 11)).meta)
  Meta(com.acme,<console>,11)

Zgadza się, zawarliśmy pakt z diabłem pod postacią makr, ale jeśli mielibyśmy tworzyć obiekty Meta ręcznie to nasz kod zdezaktualizowywałby się szybciej niż nasza dokumentacja.

7.4.4 ReaderT

Monada ReaderT opakowuje A => F[B] pozwalając programowi F[B] zależeć od wartości A znanej dopiero w czasie wykonania. Dla tych zaznajomionych ze wstrzykiwaniem zależności (dependency injection), jest to funkcyjny odpowiednik anotacji @Inject znanej ze Springa lub Guice’a, tyle że bez dodatku XMLa czy refleksji.

ReaderT jest w rzeczywistości jedynie aliasem do bardziej ogólnego typu danych nazwanego na cześć matematyka Henryka Kleisli.

  type ReaderT[F[_], A, B] = Kleisli[F, A, B]
  
  final case class Kleisli[F[_], A, B](run: A => F[B]) {
    def dimap[C, D](f: C => A, g: B => D)(implicit F: Functor[F]): Kleisli[F, C, D] =
      Kleisli(c => run(f(c)).map(g))
  
    def >=>[C](k: Kleisli[F, B, C])(implicit F: Bind[F]): Kleisli[F, A, C] = ...
    def >==>[C](k: B => F[C])(implicit F: Bind[F]): Kleisli[F, A, C] = this >=> Kleisli(k)
    ...
  }
  object Kleisli {
    implicit def kleisliFn[F[_], A, B](k: Kleisli[F, A, B]): A => F[B] = k.run
    ...
  }

Niejawna konwersja widoczna w obiekcie towarzyszącym pozwala nam używać Kleisli tam, gdzie spodziewamy się funkcji, w efekcie czego możemy przekazywać instancje tego typu jako parametr do .bind lub >>=.

Najpopularniejszym zastosowaniem ReaderT jest dostarczanie informacji ze środowiska do naszego programu. W drone-dynamic-agents potrzebujemy dostępu do tokenu odświeżającego OAuth 2.0 dla naszego użytkownika, aby móc połączyć się z serwerem Google’a. Oczywistym wydaje się odczytanie RefreshTokens z dysku przy starcie aplikacji i dodanie parametru RefreshToken do każdej metody. Okazuje się, że jest to problem na tyle częsty, że Martin Odersky zaproponował nowy mechanizm funkcji niejawnych, które mogłyby nam tutaj pomóc.

Lepszym rozwiązaniem jest zdefiniowanie algebry, która dostarczy potrzebnej nam konfiguracji, np:

  trait ConfigReader[F[_]] {
    def token: F[RefreshToken]
  }

Tym samym odkryliśmy typeklasę MonadReader, związaną z ReaderT, gdzie .ask jest tym samym co nasza metoda .token, a S to RefreshToken:

  @typeclass trait MonadReader[F[_], S] extends Monad[F] {
    def ask: F[S]
  
    def local[A](f: S => S)(fa: F[A]): F[A]
  }

wraz z implementacją

  implicit def monad[F[_]: Monad, R] = new MonadReader[Kleisli[F, R, ?], R] {
    def point[A](a: =>A): Kleisli[F, R, A] = Kleisli(_ => F.point(a))
    def bind[A, B](fa: Kleisli[F, R, A])(f: A => Kleisli[F, R, B]) =
      Kleisli(a => Monad[F].bind(fa.run(a))(f))
  
    def ask: Kleisli[F, R, R] = Kleisli(_.pure[F])
    def local[A](f: R => R)(fa: Kleisli[F, R, A]): Kleisli[F, R, A] =
      Kleisli(f andThen fa.run)
  }

Prawa obowiązujące MonadReader zastrzegają, że S nie może zmieniać się między wywołaniami, a więc ask >> ask === ask. W naszym przypadku oznacza to, że konfiguracja jest czytana raz. Jeśli później zdecydujemy, że chcielibyśmy przeładowywać konfigurację za każdym razem, gdy jest potrzebna, to możemy ponownie wprowadzić typ ConfigReader, który nie ma takich ograniczeń.

W naszej implementacji OAuth 2.0 możemy zacząć od przeniesienia parametru Monad do metod:

  def bearer(refresh: RefreshToken)(implicit F: Monad[F]): F[BearerToken] =
    for { ...

a następnie zamienić parametr refresh we fragment Monady

  def bearer(implicit F: MonadReader[F, RefreshToken]): F[BearerToken] =
    for {
      refresh <- F.ask

W ten sposób możemy przenieść dowolny parametr do MonadReader, co niesie największą wartość dla wywołań, które tylko przekazują tę wartość z zewnątrz.

Drugą metodą w MonadReaderze jest .local

  def local[A](f: S => S)(fa: F[A]): F[A]

Możemy zmodyfikować S i uruchomić fa wewnątrz takiego kontekstu. Przykładowym zastosowaniem .local może być generowanie “śladów stosu”, które mają sens dla naszej domeny, pozwalając nam tym samym na zagnieżdżone logowanie! Polegając na typie Meta z poprzedniego rozdziału, możemy zdefiniować poniższą funkcję:

  def traced[A](fa: F[A])(implicit F: MonadReader[F, IList[Meta]]): F[A] =
    F.local(Meta.gen :: _)(fa)

i używać jej do opakowywania funkcji, które wymagają takiego kontekstu

  def foo: F[Foo] = traced(getBar) >>= barToFoo

automatycznie przekazując dalej wszystko, co nie jest oznaczone wprost. Plugin do kompilatora albo makro mogłoby działać odwrotnie, śledząc wszystko automatycznie.

Jeśli wywołamy .ask, zobaczymy dokładne ślady prowadzące do naszego wywołania, bez detali implementacyjnych związanych z kodem bajtowym. Tym samym otrzymaliśmy referencyjnie transparenty ślad stosu!

Ostrożny programista mógłby chcieć w pewnym momencie przyciąć IList[Meta] aby uniknąć odpowiednika przepełnienia stosu. Tym samym bardziej odpowiednią strukturą danych byłaby Dequeue.

.local może być użyte również do śledzenie informacji kontekstowych, które są bezpośrednio związane z aktualnie wykonywanym zadaniem, jak na przykład liczba spacji potrzebnych do wcięcia linii, gdy wyświetlamy format przyjazny dla ludzi, zwiększając tę liczbę o dwa, gdy zwiększamy zagnieżdżenie.

W końcu, kiedy nie możemy zażądać instancji MonadReader, ponieważ nasza aplikacja nie umie takowej dostarczyć, możemy zawsze zwrócić ReaderT

  def bearer(implicit F: Monad[F]): ReaderT[F, RefreshToken, BearerToken] =
    ReaderT( token => for {
    ...

Jeśli wywołujący otrzyma ReaderT i ma pod ręką parametr token, to wystarczy, że wywoła access.run(token), aby otrzymać F[BearerToken].

Faktycznie, biorąc pod uwagę fakt, że nie mamy zbyt wiele wywołujących, powinniśmy wrócić do tradycyjnych parametrów funkcji. MonadReader ma na najwięcej zastosowań, gdy:

1. możemy chcieć w przyszłości przerefactorować kod, aby konfiguracja była przeładowywana
2. wartość nie jest używana przez metody pośredniczące (intermediate callers)
3. chcemy lokalnie zmienić jakąś zmienną

Dotty może zatrzymać funkcje niejawne dla siebie, my już mamy wszystko, czego nam trzeba: ReaderT i MonadReader.

7.4.5 WriterT

Odwrotnością czytania jest pisanie, a transformator monad WriterT służy właśnie do tego.

  final case class WriterT[F[_], W, A](run: F[(W, A)])
  object WriterT {
    def put[F[_]: Functor, W, A](value: F[A])(w: W): WriterT[F, W, A] = ...
    def putWith[F[_]: Functor, W, A](value: F[A])(w: A => W): WriterT[F, W, A] = ...
    ...
  }

Opakowywany typ to F[(W, A)], a nasz dziennik jest akumulowany wewnątrz W.

Mamy do dyspozycji nie jedną, a dwie powiązane monady: MonadTell i MonadListen!

  @typeclass trait MonadTell[F[_], W] extends Monad[F] {
    def writer[A](w: W, v: A): F[A]
    def tell(w: W): F[Unit] = ...
  
    def :++>[A](fa: F[A])(w: =>W): F[A] = ...
    def :++>>[A](fa: F[A])(f: A => W): F[A] = ...
  }
  
  @typeclass trait MonadListen[F[_], W] extends MonadTell[F, W] {
    def listen[A](fa: F[A]): F[(A, W)]
  
    def written[A](fa: F[A]): F[W] = ...
  }

MonadTell służy do spisywania dziennika a MonadListen do jego odtwarzania.

Ich implementacja dla WriterT wygląda następująco:

  implicit def monad[F[_]: Monad, W: Monoid] = new MonadListen[WriterT[F, W, ?], W] {
    def point[A](a: =>A) = WriterT((Monoid[W].zero, a).point)
    def bind[A, B](fa: WriterT[F, W, A])(f: A => WriterT[F, W, B]) = WriterT(
      fa.run >>= { case (wa, a) => f(a).run.map { case (wb, b) => (wa |+| wb, b) } })
  
    def writer[A](w: W, v: A) = WriterT((w -> v).point)
    def listen[A](fa: WriterT[F, W, A]) = WriterT(
      fa.run.map { case (w, a) => (w, (a, w)) })
  }

Oczywistym zastosowaniem MonadTell jest logowanie lub zbieranie danych audytowych. Raz jeszcze używając Meta możemy wyobrazić sobie taki log

  sealed trait Log
  final case class Debug(msg: String)(implicit m: Meta)   extends Log
  final case class Info(msg: String)(implicit m: Meta)    extends Log
  final case class Warning(msg: String)(implicit m: Meta) extends Log

i użyć Dequeue[Log] jako naszego dziennika. Tym razem zmodyfikujemy metodę authenticate z części kodu odpowiedzialnej za obsługę OAuth2.

  def debug(msg: String)(implicit m: Meta): Dequeue[Log] = Dequeue(Debug(msg))
  
  def authenticate: F[CodeToken] =
    for {
      callback <- user.start :++> debug("started the webserver")
      params   = AuthRequest(callback, config.scope, config.clientId)
      url      = config.auth.withQuery(params.toUrlQuery)
      _        <- user.open(url) :++> debug(s"user visiting $url")
      code     <- user.stop :++> debug("stopped the webserver")
    } yield code

Moglibyśmy nawet połączyć to podejście ze śledzeniem opartym o ReaderT, aby uzyskać ustrukturalizowany log zdarzeń.

Dziennik może zostać odzyskany za pomocą .written, a następnie dowolnie modyfikowany.

Jednak istnieje silny argument za tym, aby logowanie otrzymało swoją własną algebrę. Poziom logowania jest często potrzebny w momencie stworzenia wiadomości dla celów wydajnościowych, a ponadto logowanie często konfigurowane i zarządzane jest na poziomie całej aplikacji, a nie pojedynczych komponentów.

Parametr W w WriterT posiada Monoid, pozwalając nam tym samym na wszelkiego rodzaju monoidyczne operacje, które będą działy się równolegle do naszego głównego programu. Możemy na przykład zliczać, ile razy coś się wydarzyło, budować opis obliczeń lub tworzyć TradeTemplate dla nowej transakcji, gdy ją wyceniamy.

Popularną specjalizacją WriterT jest użycie go z monadą Id, sprawiając, że leżąca pod spodem wartość run to prosta tupla (W, A).

  type Writer[W, A] = WriterT[Id, W, A]
  object WriterT {
    def writer[W, A](v: (W, A)): Writer[W, A] = WriterT[Id, W, A](v)
    def tell[W](w: W): Writer[W, Unit] = WriterT((w, ()))
    ...
  }
  final implicit class WriterOps[A](self: A) {
    def set[W](w: W): Writer[W, A] = WriterT(w -> self)
    def tell: Writer[A, Unit] = WriterT.tell(self)
  }

W taki sposób możemy nieść dodatkową monoidyczną kalkulację obok dowolnej wartości bez kontekstu F[_].

W skrócie WriterT i MonadTell to sposoby na multizadaniowość w stylu FP.

7.4.6 StateT

StateT pozwala nam włożyć (.put), wyciągnąć (.get) i zmodyfikować (.modify) wartość zarządzaną przez monadyczny kontekst. Jest to czysto funkcyjny zamiennik dla var.

Jeśli mielibyśmy napisać nieczystą metodę korzystającą z mutowalnego stanu przechowywanego wewnątrz var, jej sygnatura mogłaby przyjąć postać () => F[A], a ona sama zwracałaby inną wartość przy każdym wywołaniu, zaburzając w ten sposób transparentność referencyjną. W czystym FP taka funkcja przyjmuje stan jako wejście i produkuje i zwraca zmodyfikowany stan jako wyjście. Dlatego też StateT opakowuje S => F[(S,A)].

Powiązana monada to MonadState:

  @typeclass trait MonadState[F[_], S] extends Monad[F] {
    def put(s: S): F[Unit]
    def get: F[S]
  
    def modify(f: S => S): F[Unit] = get >>= (s => put(f(s)))
    ...
  }

Struktura StateT jest zaimplementowana nieco inaczej niż transformatory, które widzieliśmy do tej pory, nie jest case klasą, lecz ADT z dwoma wariantami:

  sealed abstract class StateT[F[_], S, A]
  object StateT {
    def apply[F[_], S, A](f: S => F[(S, A)]): StateT[F, S, A] = Point(f)
  
    private final case class Point[F[_], S, A](
      run: S => F[(S, A)]
    ) extends StateT[F, S, A]
    private final case class FlatMap[F[_], S, A, B](
      a: StateT[F, S, A],
      f: (S, A) => StateT[F, S, B]
    ) extends StateT[F, S, B]
    ...
  }

które są wyspecjalizowaną formą Trampoline, dając nam bezpieczeństwo stosu, kiedy chcemy odwołać się do leżącej pod spodem struktury za pomocą .run:

  sealed abstract class StateT[F[_], S, A] {
    def run(initial: S)(implicit F: Monad[F]): F[(S, A)] = this match {
      case Point(f) => f(initial)
      case FlatMap(Point(f), g) =>
        f(initial) >>= { case (s, x) => g(s, x).run(s) }
      case FlatMap(FlatMap(f, g), h) =>
        FlatMap(f, (s, x) => FlatMap(g(s, x), h)).run(initial)
    }
    ...
  }

StateT ze swoim ADT w trywialny sposób implementuje MonadState

  implicit def monad[F[_]: Applicative, S] = new MonadState[StateT[F, S, ?], S] {
    def point[A](a: =>A) = Point(s => (s, a).point[F])
    def bind[A, B](fa: StateT[F, S, A])(f: A => StateT[F, S, B]) =
      FlatMap(fa, (_, a: A) => f(a))
  
    def get       = Point(s => (s, s).point[F])
    def put(s: S) = Point(_ => (s, ()).point[F])
  }

.pure otrzymał swoją kopię .stateT w obiekcie towarzyszącym:

  object StateT {
    def stateT[F[_]: Applicative, S, A](a: A): StateT[F, S, A] = ...
    ...
  }

a MonadTrans.liftM jak zawsze dostarcza nam konstruktor F[A] => StateT[F, S, A].

Popularną odmianą StateT jest F = Id. W takim wypadku opakowywany typ to S => (S, A). Scalaz definiuje alias typu State i wygodne funkcje to interakcji z nim, które udają MonadState:

  type State[a] = StateT[Id, a]
  object State {
    def apply[S, A](f: S => (S, A)): State[S, A] = StateT[Id, S, A](f)
    def state[S, A](a: A): State[S, A] = State((_, a))
  
    def get[S]: State[S, S] = State(s => (s, s))
    def put[S](s: S): State[S, Unit] = State(_ => (s, ()))
    def modify[S](f: S => S): State[S, Unit] = ...
    ...
  }

Wróćmy na chwilę do testów logiki biznesowej z drone-dynamic-agents. W Rozdziale 3 stworzyliśmy testowy interpreter Mutable, który przechowywał liczbę wystartowanych i zatrzymanych węzłów w var.

  class Mutable(state: WorldView) {
    var started, stopped: Int = 0
  
    implicit val drone: Drone[Id] = new Drone[Id] { ... }
    implicit val machines: Machines[Id] = new Machines[Id] { ... }
    val program = new DynAgentsModule[Id]
  }

Teraz wiemy już jak napisać dużo lepszy interpreter, używając State. Przy okazji skorzystamy z możliwości zwiększenia dokładności naszej symulacji. Przypomnijmy nasz kluczowy obiekt przechowujący obraz świata:

  final case class WorldView(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    pending: Map[MachineNode, Epoch],
    time: Epoch
  )

Skoro piszemy symulację świata na potrzeby naszych testów, to możemy zdefiniować typ danych przechwytujący pełen jego obraz

  final case class World(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    started: Set[MachineNode],
    stopped: Set[MachineNode],
    time: Epoch
  )

Główną różnicą jest to, że mamy do dyspozycji zmienne started i stopped. Nasz interpreter może być budowany na bazie State[World, a], pozwalając nam na weryfikacje tego, jak wygląda zarówno World, jak i WorldView po wykonaniu logiki biznesowej.

Interpretery udające zewnętrzne usługi Drone i Google będą wyglądać tak:

  import State.{ get, modify }
  object StateImpl {
    type F[a] = State[World, a]
  
    private val D = new Drone[F] {
      def getBacklog: F[Int] = get.map(_.backlog)
      def getAgents: F[Int]  = get.map(_.agents)
    }
  
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]   = get.map(_.alive)
      def getManaged: F[NonEmptyList[MachineNode]] = get.map(_.managed)
      def getTime: F[Epoch]                      = get.map(_.time)
  
      def start(node: MachineNode): F[Unit] =
        modify(w => w.copy(started = w.started + node))
      def stop(node: MachineNode): F[Unit] =
        modify(w => w.copy(stopped = w.stopped + node))
    }
  
    val program = new DynAgentsModule[F](D, M)
  }

a my możemy przepisać nasze testy tak, aby zachowywały konwencję:

• world1 to stan świata przed uruchomieniem programu
• view1 to widok świata z punktu widzenia aplikacji
• world2 to stan świata po uruchomieniu programu
• view2 to widok świata z punktu widzenia aplikacji po uruchomieniu programu

Przykład:

  it should "request agents when needed" in {
    val world1          = World(5, 0, managed, Map(), Set(), Set(), time1)
    val view1           = WorldView(5, 0, managed, Map(), Map(), time1)
  
    val (world2, view2) = StateImpl.program.act(view1).run(world1)
  
    view2.shouldBe(view1.copy(pending = Map(node1 -> time1)))
    world2.stopped.shouldBe(world1.stopped)
    world2.started.shouldBe(Set(node1))
  }

Moglibyśmy spojrzeć na naszą nieskończoną pętlę logiki biznesowej

  state = initial()
  while True:
    state = update(state)
    state = act(state)

i użyć w niej StateT do zarządzania stanem. Niestety, w ten sposób naruszylibyśmy Regułę Najmniejszej Mocy, wymagając MonadState zamiast aktualnie wymaganego Applicative. Tak więc całkowicie rozsądne jest zarządzanie ręczne i przekazywanie stanu do update i act.

7.4.7 IndexedStateT

Kod, który widzieliśmy do tej pory nie pochodzi ze Scalaz. Tak naprawdę StateT jest zaimplementowany tam jako alias typu wskazujący na kolejny typ: IndexedStateT.

  type StateT[F[_], S, A] = IndexedStateT[F, S, S, A]

Implementacja IndexedStateT jest bardzo podobna do tej, którą widzieliśmy do tej pory, z dodatkiem jednego parametru typu, który pozwala na to, by stan wejściowy S1 był inny niż stan wyjściowy S2:

  sealed abstract class IndexedStateT[F[_], -S1, S2, A] {
    def run(initial: S1)(implicit F: Bind[F]): F[(S2, A)] = ...
    ...
  }
  object IndexedStateT {
    def apply[F[_], S1, S2, A](
      f: S1 => F[(S2, A)]
    ): IndexedStateT[F, S1, S2, A] = Wrap(f)
  
    private final case class Wrap[F[_], S1, S2, A](
      run: S1 => F[(S2, A)]
    ) extends IndexedStateT[F, S1, S2, A]
    private final case class FlatMap[F[_], S1, S2, S3, A, B](
      a: IndexedStateT[F, S1, S2, A],
      f: (S2, A) => IndexedStateT[F, S2, S3, B]
    ) extends IndexedStateT[F, S1, S3, B]
    ...
  }

IndexedStateT nie posiada instancji MonadState kiedy S1 != S2, więc w takiej sytuacji musi nas zadowolić instancja samego Monad.

Poniższy przykład został zaadaptowany z prezentacji Vincentego Maqrqueza Index your State. Wyobraź sobie, że musimy zaprojektować algebraiczny interfejs dla dostępu do wartości typu String za pomocą klucza typu Int. Załóżmy, że jedna z implementacji będzie opierała się na komunikacji sieciowej, a kolejność wywołań jest kluczowa. Nasze pierwsze podejście mogłoby wyglądać tak:

  trait Cache[F[_]] {
    def read(k: Int): F[Maybe[String]]
  
    def lock: F[Unit]
    def update(k: Int, v: String): F[Unit]
    def commit: F[Unit]
  }

produkując błędy w czasie wykonania, jeśli .update lub .commit zostaną wywołane bez wcześniejszego użycia .lock. Alternatywą mógłby być skomplikowany DSL, którego nikt nie umiałby użyć bez zaglądania do dokumentacji.

Zamiast tego użyjemy IndexedStateT, aby wymusić odpowiedni stan na wywołującym. Zacznijmy od możliwych stanów wyrażonych jako ADT

  sealed abstract class Status
  final case class Ready()                          extends Status
  final case class Locked(on: ISet[Int])            extends Status
  final case class Updated(values: Int ==>> String) extends Status

i odświeżenia naszej algebry

  trait Cache[M[_]] {
    type F[in, out, a] = IndexedStateT[M, in, out, a]
  
    def read(k: Int): F[Ready, Ready, Maybe[String]]
    def readLocked(k: Int): F[Locked, Locked, Maybe[String]]
    def readUncommitted(k: Int): F[Updated, Updated, Maybe[String]]
  
    def lock: F[Ready, Locked, Unit]
    def update(k: Int, v: String): F[Locked, Updated, Unit]
    def commit: F[Updated, Ready, Unit]
  }

co spowoduje, że próba wywołania .update bez wcześniejszego .lock spowoduje błąd kompilacji

  for {
        a1 <- C.read(13)
        _  <- C.update(13, "wibble")
        _  <- C.commit
      } yield a1
  
  [error]  found   : IndexedStateT[M,Locked,Ready,Maybe[String]]
  [error]  required: IndexedStateT[M,Ready,?,?]
  [error]       _  <- C.update(13, "wibble")
  [error]          ^

pozwalając nam konstruować funkcje, które mogą być komponowane dzięki wyrażaniu swojego stanu explicite

  def wibbleise[M[_]: Monad](C: Cache[M]): F[Ready, Ready, String] =
    for {
      _  <- C.lock
      a1 <- C.readLocked(13)
      a2 = a1.cata(_ + "'", "wibble")
      _  <- C.update(13, a2)
      _  <- C.commit
    } yield a2

7.4.8 IndexedReaderWriterStateT

Ci, którzy chcieli kombinacji ReaderT, WriterT i InedexedStateT nie będą zawiedzeni. Transformator IndexedReaderWriterStateT opakowuje (R, S1) => F[(W, A, S2)] gdzie R to Reader, W służy do monoidycznych zapisów, a S do indeksowanych aktualizacji stanu.

  sealed abstract class IndexedReaderWriterStateT[F[_], -R, W, -S1, S2, A] {
    def run(r: R, s: S1)(implicit F: Monad[F]): F[(W, A, S2)] = ...
    ...
  }
  object IndexedReaderWriterStateT {
    def apply[F[_], R, W, S1, S2, A](f: (R, S1) => F[(W, A, S2)]) = ...
  }
  
  type ReaderWriterStateT[F[_], -R, W, S, A] = IndexedReaderWriterStateT[F, R, W, S, S, A]
  object ReaderWriterStateT {
    def apply[F[_], R, W, S, A](f: (R, S) => F[(W, A, S)]) = ...
  }

Do dyspozycji mamy skróty, bo trzeba przyznać, że te typy są tak długie, że wyglądają jak część API J2EE.

  type IRWST[F[_], -R, W, -S1, S2, A] = IndexedReaderWriterStateT[F, R, W, S1, S2, A]
  val IRWST = IndexedReaderWriterStateT
  type RWST[F[_], -R, W, S, A] = ReaderWriterStateT[F, R, W, S, A]
  val RWST = ReaderWriterStateT

IRWST to bardziej wydajny odpowiednik ręcznie skonstruowanego stosu transformatorów ReaderT[WriterT[IndexedStateT[F, ...], ...], ...].

7.4.9 TheseT

TheseT pozwala nam wybrać czy błędy mają zakończyć obliczenia, czy też mają być zakumulowane w przypadku częściowego sukcesu. Stąd zachowaj spokój i idź dalej (keep calm and carry on).

Opakowywany typ danych to F[A \&/ B], gdzie A to typ błędów, z wymaganą instancją Semigroup, jeśli chcemy je akumulować.

  final case class TheseT[F[_], A, B](run: F[A \&/ B])
  object TheseT {
    def `this`[F[_]: Functor, A, B](a: F[A]): TheseT[F, A, B] = ...
    def that[F[_]: Functor, A, B](b: F[B]): TheseT[F, A, B] = ...
    def both[F[_]: Functor, A, B](ab: F[(A, B)]): TheseT[F, A, B] = ...
  
    implicit def monad[F[_]: Monad, A: Semigroup] = new Monad[TheseT[F, A, ?]] {
      def bind[B, C](fa: TheseT[F, A, B])(f: B => TheseT[F, A, C]) =
        TheseT(fa.run >>= {
          case This(a) => a.wrapThis[C].point[F]
          case That(b) => f(b).run
          case Both(a, b) =>
            f(b).run.map {
              case This(a_)     => (a |+| a_).wrapThis[C]
              case That(c_)     => Both(a, c_)
              case Both(a_, c_) => Both(a |+| a_, c_)
            }
        })
  
      def point[B](b: =>B) = TheseT(b.wrapThat.point[F])
    }
  }

Nie istnieje żadna specjalna monada dla TheseT ponad Monad. Jeśli chcemy zakończyć obliczenia, zwracamy This, ale akumulujemy błędy, zwracając wartość Both, która zawiera także poprawnie obliczoną część wyniku.

Możemy spojrzeć na TheseT z innej strony: A nie musi być wcale błędem. Podobnie jak w przypadku WriterT, A może być nośnikiem dla innej wartości, którą obliczamy wraz z B. TheseT pozwala zatrzymać się, gdy coś specyficznego dla A tego od nas wymaga. Jak wtedy, gdy Charlie Bucket wyrzucił swoją czekoladę (B), jak tylko odnalazł Złoty Kupon (A).

7.4.10 ContT

Styl Przekazywania Kontynuacji (CPS, Continuation Passing Style) to styl programowania, w którym funkcje nigdy nie zwracają wartości, a zamiast tego kontynuują następne obliczenia. CPS jest popularny w JavaScripcie i Lispie, pozwalając na wykonywanie nieblokującego IO za pomocą callbacków, gdy dane stają się dostępne. Bezpośrednie przełożenie tego wzorca na nieczystą Scalę wygląda mniej więcej tak:

  def foo[I, A](input: I)(next: A => Unit): Unit = next(doSomeStuff(input))

Możemy sprawić, że ten kod stanie się czysty, wprowadzając kontekst F[_]

  def foo[F[_], I, A](input: I)(next: A => F[Unit]): F[Unit]

i zwracając funkcję dla danego wejścia

  def foo[F[_], I, A](input: I): (A => F[Unit]) => F[Unit]

ContT to opakowanie dla takiej właśnie sygnatury, z dodatkiem instancji typeklasy Monad

  final case class ContT[F[_], B, A](_run: (A => F[B]) => F[B]) {
    def run(f: A => F[B]): F[B] = _run(f)
  }
  object IndexedContT {
    implicit def monad[F[_], B] = new Monad[ContT[F, B, ?]] {
      def point[A](a: =>A) = ContT(_(a))
      def bind[A, C](fa: ContT[F, B, A])(f: A => ContT[F, B, C]) =
        ContT(c_fb => fa.run(a => f(a).run(c_fb)))
    }
  }

i wygodnej składni do tworzenia ContT z monadycznej wartości:

  implicit class ContTOps[F[_]: Monad, A](self: F[A]) {
    def cps[B]: ContT[F, B, A] = ContT(a_fb => self >>= a_fb)
  }

Jednak proste użycie callbacków nie wnosi nic do programowania czysto funkcyjnego, ponieważ poznaliśmy już sposób na sekwencyjne łączenie nieblokujących, potencjalnie rozproszonych obliczeń: Monadę. Aby zobaczyć dlaczego kontynuacje są użyteczne, musimy rozważyć bardziej złożony przykład ze sztywnymi ograniczeniami projektowymi.

7.4.10.1 Kontrola przepływu

Załóżmy, że podzieliliśmy naszą aplikację na moduły, które mogą wykonywać operacje I/O, a każdy z nich rozwijany jest przez osobny zespół:

  final case class A0()
  final case class A1()
  final case class A2()
  final case class A3()
  final case class A4()
  
  def bar0(a4: A4): IO[A0] = ...
  def bar2(a1: A1): IO[A2] = ...
  def bar3(a2: A2): IO[A3] = ...
  def bar4(a3: A3): IO[A4] = ...

Naszym celem jest wyprodukować A0 na podstawie otrzymanego A1. Tam, gdzie JavaScript lub Lisp sięgnęliby po kontynuacje (ponieważ IO może blokować), my możemy po prostu połączyć funkcje:

  def simple(a: A1): IO[A0] = bar2(a) >>= bar3 >>= bar4 >>= bar0

Możemy wynieść .simple do postaci kontynuacji, używając .cps i odrobiny boilerplate’u:

  def foo1(a: A1): ContT[IO, A0, A2] = bar2(a).cps
  def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).cps
  def foo3(a: A3): ContT[IO, A0, A4] = bar4(a).cps
  
  def flow(a: A1): IO[A0]  = (foo1(a) >>= foo2 >>= foo3).run(bar0)

Co zyskaliśmy? Po pierwsze, warto zauważyć, że przepływ kontroli w tej aplikacji biegnie od lewej do prawej strony.

Co, gdy jako autorzy foo2 chcielibyśmy zmodyfikować wartość a0, którą otrzymujemy z prawej strony? W praktyce oznacza to podzielenie foo2 na foo2a i foo2b

Dodajmy ograniczenie, że nie możemy zmodyfikować tego, jak zdefiniowane są metody flow i bar0. Może na przykład pochodzą one z frameworka lub biblioteki, których używamy.

Nie jesteśmy w stanie przeprocesować a0 poprzez modyfikację żadnej z pozostałych metod barX, jednak używając ContT, możemy zaimplementować metodę foo2 tak, aby mogła wykonać obliczenia na podstawie wyniku kontynuacji next:

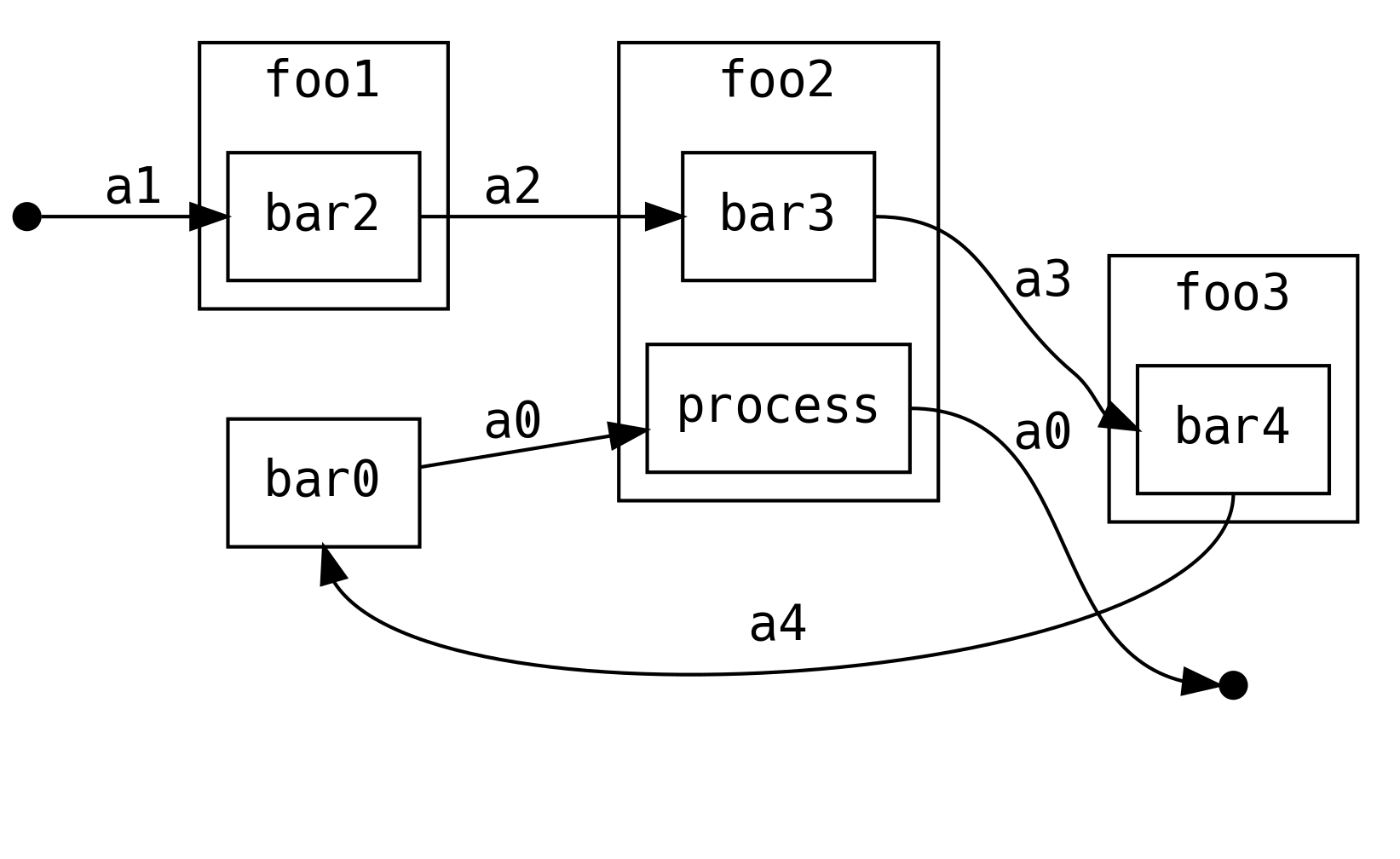
Na przykład w taki sposób:

  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
    } yield process(a0)
  }

Nie jesteśmy ograniczeni do .mapowania wartości. Możemy również wywołać .bind i zamienić liniowy przepływ w pełnoprawny graf!

  def elsewhere: ContT[IO, A0, A4] = ???
  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
      a0_ <- if (check(a0)) a0.pure[IO]
             else elsewhere.run(bar0)
    } yield a0_
  }

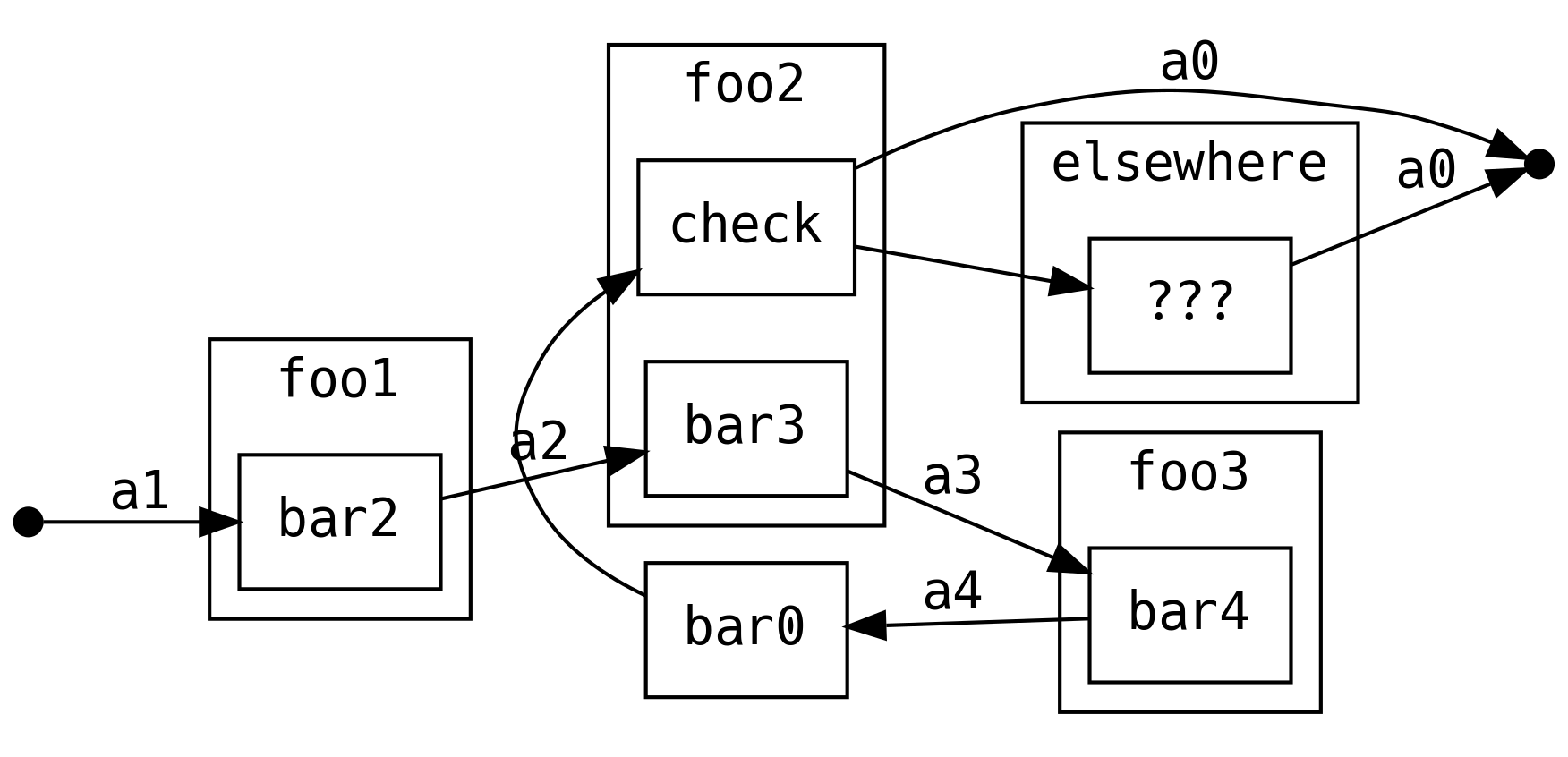
Możemy też zostać przy oryginalnym przepływie i ponowić wszystkie dalsze operacje.

  def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
    for {
      a3  <- bar3(a)
      a0  <- next(a3)
      a0_ <- if (check(a0)) a0.pure[IO]
             else next(a3)
    } yield a0_
  }

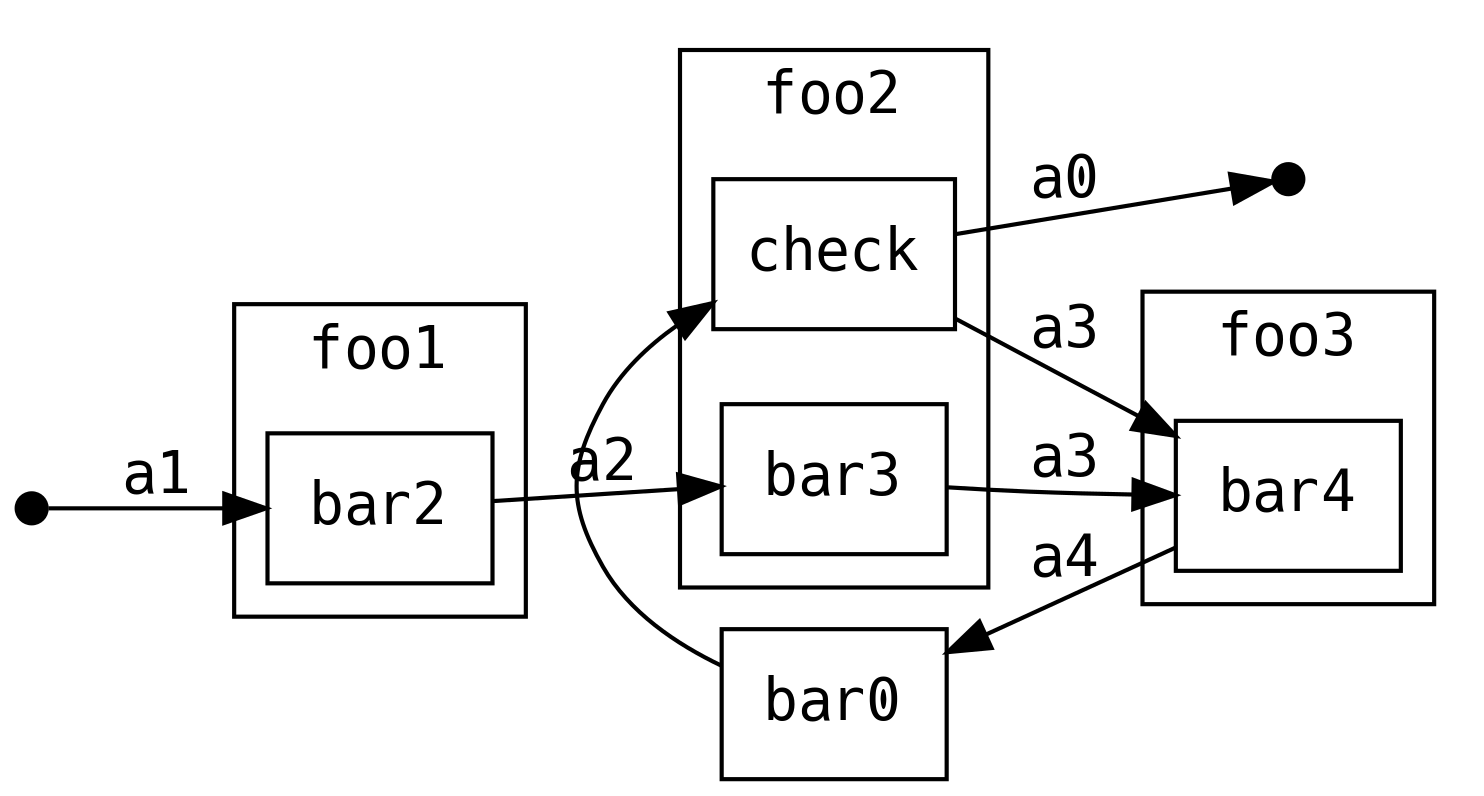
W tym wypadku ponawiamy operacje tylko raz, a nie w nieskończoność, np. upewniamy się, czy na pewno powinniśmy wykonać jakąś potencjalnie niebezpieczną operację.

W końcu możemy też wykonać akcje specyficzne dla kontekstu ContT, czyli w tym wypadku IO, który pozwala nam na obsługę błędów i uprzątnięcie zasobów:

  def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).ensuring(cleanup).cps

7.4.10.2 Kiedy zamówić spaghetti

Nie przez przypadek nasze diagramy wyglądają jak spaghetti. Tak właśnie dzieje się, kiedy zaczynamy bawić się przepływem kontroli. Wszystkie mechanizmy, które omówiliśmy w tym podrozdziale, można w łatwy sposób zaimplementować bezpośrednio, gdy możemy zmodyfikować flow, a więc nie musimy używać ContT.

Jednak jeśli projektowalibyśmy framework, to system pluginów opartych na ConT i pozwalający użytkownikom kontrolować przepływ byłby czymś wartym rozważenia. Czasem użytkownik po prostu chce spaghetti.

Gdyby kompilator Scali był napisany z użyciem CPS, to kolejne fazy kompilacji mogłyby komunikować się ze sobą w prosty i regularny sposób. Plugin kompilatora mógłby wykonywać akcje, bazując na wyinferowanym typie wyrażenia pochodzącym z późniejszej fazy kompilacji. Podobnie kontynuacje byłyby dobrym API dla narzędzie do budowania projektów (build tool) albo edytora tekstu.

Pułapką ConT jest fakt, że nie jest to struktura bezpieczna od przepełnienia stosu, a więc nie nadaje się do tworzenia programów, które nigdy się nie kończą.

7.4.10.3 Great, kid. Don’t get ContT.

Bardziej złożony wariant ContT znany jako IndexedContT opakowuje (A => F[B] => F[C]). Nowy parametr typu C definiuje typ zwracany przez cały program, który może być inny, niż ten przekazywany między komponentami. Jednak jeśli B nie jest równe C to nie jesteśmy w stanie zdefiniować Monady.

Korzystając z okazji do zgeneralizowania kodu tak, jak to tylko możliwe, zarówno typ IndexedContT, jak i ConT są w praktyce zaimplementowane jako aliasy na jeszcze bardziej ogólną strukturę IndexedContsT (zwróć uwagę na dodatkowe s przed T)

  final case class IndexedContsT[W[_], F[_], C, B, A](_run: W[A => F[B]] => F[C])
  
  type IndexedContT[f[_], c, b, a] = IndexedContsT[Id, f, c, b, a]
  type ContT[f[_], b, a]           = IndexedContsT[Id, f, b, b, a]
  type ContsT[w[_], f[_], b, a]    = IndexedContsT[w, f, b, b, a]
  type Cont[b, a]                  = IndexedContsT[Id, Id, b, b, a]

w której W[_] posiada instancję Comonad. Dla wspomnianych aliasów istnieją obiekty towarzyszące z pomocnymi konstruktorami.

Wprawdzie pięć parametrów typów to raczej przesada, ale takie przegeneralizowanie pozostaje spójne ze specyfiką kontynuacji.

7.4.11 Stosy transformatorów i niejednoznaczne parametry niejawne

Czas podsumować naszą wycieczkę wśród transformatorów monad zdefiniowanych w Scalaz.

Kiedy wiele transformatorów jest składanych ze sobą, nazywamy to stosem transformatorów (transformer stack), i mimo że jest to dość rozwlekłe, to można odczytać dostarczane w ten sposób funkcjonalności. Jeśli skonstruujemy kontekst F[_] taki jak

  type Ctx[A] = StateT[EitherT[IO, E, ?], S, A]

wiemy, że dodajemy obsługę błędów typu E (istnieje MonadError[Ctx. E]) i stan S (istnieje MonadState[Ctx, S]).

Niestety istnieją pewne praktyczne przeciwności co do stosowania takich stosów i towarzyszących im instancji typeklas:

1. Wiele niejawnych instancji Monad oznacza, że kompilator nie może odnaleźć odpowiedniej składni dla kontekstu
2. Monady nie komponują się w sposób ogólny, co oznacza, że kolejność zagnieżdżania ma znaczenie
3. Wszystkie interpretery muszą obsługiwać ten wspólny kontekst. Dla przykładu: jeśli mamy implementację pewnej algebry, która używa IO, to i tak musimy opakować ją w StateT i EitherT, mimo że nie będą one używane w interpreterze.
4. Każda warstwa niesie ze sobą koszt wydajnościowy. Niektóre transformatory są gorsze niż inne, np. StateT jest szczególnie kosztowny, ale nawet EitherT może sprawiać problemy z alokacją pamięci dla aplikacji o dużej przepustowości.

Porozmawiajmy o obejściach tych problemów.

7.4.11.1 Brak składni

Powiedzmy, że mamy algebrę

  trait Lookup[F[_]] {
    def look: F[Int]
  }

i typy danych

  final case class Problem(bad: Int)
  final case class Table(last: Int)

które chcielibyśmy użyć w naszej logice biznesowej:

  def foo[F[_]](L: Lookup[F])(
    implicit
      E: MonadError[F, Problem],
      S: MonadState[F, Table]
  ): F[Int] = for {
    old <- S.get
    i   <- L.look
    _   <- if (i === old.last) E.raiseError(Problem(i))
           else ().pure[F]
  } yield i

Pierwszy problem: nasz kod się nie kompiluje.

  [error] value flatMap is not a member of type parameter F[Table]
  [error]     old <- S.get
  [error]              ^

Istnieją pewne taktyczne rozwiązania tego problemu. Najbardziej oczywistym jest przyjęcie parametrów wprost

  def foo1[F[_]: Monad](
    L: Lookup[F],
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = ...

i wymaganie jedynie Monady niejawnie poprzez ograniczenie kontekstu. Jednak oznacza to, że musimy ręcznie przekazać MonadError i MonadState, kiedy wywołujemy foo1 oraz gdy wołamy inne metody, które wymagają parametrów niejawnych.

Drugim rozwiązaniem jest pozostawienie parametrów jako implicit i użycie przesłaniania nazw tak by wszystkie stały się jawne. Pozwala to innym wywoływać nas, używając niejawnego rozstrzygania, ale my nadal musimy przekazywać parametry wprost, gdy są potrzebne.

  @inline final def shadow[A, B, C](a: A, b: B)(f: (A, B) => C): C = f(a, b)
  
  def foo2a[F[_]: Monad](L: Lookup[F])(
    implicit
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = shadow(E, S) { (E, S) => ...

Moglibyśmy też przesłonić tylko jedną z Monad, pozostawiając drugą tak, by mogła być użyta do dostarczenia nam potrzebnej składni i gdy wywołujemy inne metody.

  @inline final def shadow[A, B](a: A)(f: A => B): B = f(a)
  ...
  
  def foo2b[F[_]](L: Lookup[F])(
    implicit
    E: MonadError[F, Problem],
    S: MonadState[F, Table]
  ): F[Int] = shadow(E) { E => ...

Trzecia opcja, która niesie ze sobą wyższy koszt początkowy, to stworzenie własnej typeklasy, która będzie przechowywać referencje do dwóch pozostałych, których potrzebujemy

  trait MonadErrorState[F[_], E, S] {
    implicit def E: MonadError[F, E]
    implicit def S: MonadState[F, S]
  }

i którą automatycznie wyderywujemy z dostępnych instancji MonadError i MonadState.

  object MonadErrorState {
    implicit def create[F[_], E, S](
      implicit
        E0: MonadError[F, E],
        S0: MonadState[F, S]
    ) = new MonadErrorState[F, E, S] {
      def E: MonadError[F, E] = E0
      def S: MonadState[F, S] = S0
    }
  }

Teraz, gdy potrzebujemy S lub E mamy do nich dostęp poprzez F.S i F.E

  def foo3a[F[_]: Monad](L: Lookup[F])(
    implicit F: MonadErrorState[F, Problem, Table]
  ): F[Int] =
    for {
      old <- F.S.get
      i   <- L.look
      _ <- if (i === old.last) F.E.raiseError(Problem(i))
      else ().pure[F]
    } yield i

I tak jak w drugim podejściu, możemy wybrać jedną z Monad jako niejawną w naszym bloku, importując ją

  def foo3b[F[_]](L: Lookup[F])(
    implicit F: MonadErrorState[F, Problem, Table]
  ): F[Int] = {
    import F.E
    ...
  }

7.4.11.2 Komponowanie transformatorów

EitherT[StateT[...], ...] posiada instancję MonadError, ale nie MonadState, natomiast StateT[EitherT[...], ...] daje nam obie.

Rozwiązaniem jest przestudiowanie reguł niejawnej derywacji transformatorów zawartych w obiektach towarzyszących, aby upewnić się, że najbardziej zewnętrzny z nich dostarcza wszystkie instancje, których potrzebujemy.

Zasada kciuka: im bardziej skomplikowany transformator, tym bliżej wierzchu stosu powinien być umieszczony. W tym rozdziale prezentowaliśmy je z rosnącym poziomem skomplikowania, co powinno ułatwić aplikację tej zasady.

7.4.11.3 Wynoszenie interpreterów

Kontynuując ten sam przykład, załóżmy, że nasza algebra Lookup ma interpreter oparty o IO

  object LookupRandom extends Lookup[IO] {
    def look: IO[Int] = IO { util.Random.nextInt }
  }

ale chcielibyśmy, aby nasz kontekst wyglądał tak

  type Ctx[A] = StateT[EitherT[IO, Problem, ?], Table, A]

aby móc używać MonadError i MonadState. Oznacza to, że musimy opakować LookupRandom tak, aby mógł operować na Ctx.

Najpierw użyjemy metody .liftM z MonadTrans, która wynosi F[A] do postaci G[F, A]

  final class MonadOps[F[_]: Monad, A](fa: F[A]) {
    def liftM[G[_[_], _]: MonadTrans]: G[F, A] = ...
    ...
  }

Ważne jest, aby pamiętać, że parametr typu przekazywany do .liftM sam ma dwa parametry, pierwszy o kształcie _[_] i drugi _. Jeśli stworzymy odpowiednie aliasy

  type Ctx0[F[_], A] = StateT[EitherT[F, Problem, ?], Table, A]
  type Ctx1[F[_], A] = EitherT[F, Problem, A]
  type Ctx2[F[_], A] = StateT[F, Table, A]

to możemy abstrahować ponad MonadTrans, aby wynieść Lookup[F] do dowolnego Lookup[G[F, ?]] tak długo jak G to transformator monad:

  def liftM[F[_]: Monad, G[_[_], _]: MonadTrans](f: Lookup[F]) =
    new Lookup[G[F, ?]] {
      def look: G[F, Int] = f.look.liftM[G]
    }

Możemy więc opakować algebrę kolejno dla EitherT i StateT

  val wrap1 = Lookup.liftM[IO, Ctx1](LookupRandom)
  val wrap2: Lookup[Ctx] = Lookup.liftM[EitherT[IO, Problem, ?], Ctx2](wrap1)

Innym sposobem osiągnięcia tego samego rezultatu w pojedynczym kroku jest użycie typeklasy MonadIO, która pozwala nam wynieść IO do stosu transformatorów:

  @typeclass trait MonadIO[F[_]] extends Monad[F] {
    def liftIO[A](ioa: IO[A]): F[A]
  }

i posiada instancje dla wszystkich popularnych kombinacji transformatorów.

Boilerplate potrzebny, by wynieść interpreter oparty o IO do dowolnego kontekstu posiadającego instancję MonadIO to dwie linie kodu (dla definicji interpretera), plus jedna linia dla każdego elementu algebry i jedna linia wywołująca konwersję:

  def liftIO[F[_]: MonadIO](io: Lookup[IO]) = new Lookup[F] {
    def look: F[Int] = io.look.liftIO[F]
  }
  
  val L: Lookup[Ctx] = Lookup.liftIO(LookupRandom)

7.4.11.4 Wydajność

Największym problemem Transformatorów Monad jest ich narzut wydajnościowy. EitherT ma dość mały narzut, gdzie każde wywołanie .flatMap generuje tylko garść obiektów, ale nawet to może wpłynąć na aplikacje wymagające wysokiej przepustowości, gdzie każda alokacja ma znaczenie. Inne transformatory, takie jak StateT, dodają trampolinę do każdego wywołania, a ContT przechowuje cały łańcuch wywołań w pamięci.

Jeśli wydajność staje się problemem, jedynym rozwiązaniem jest zrezygnować z Transformatorów Monad, a przynajmniej ich struktur danych. Dużą zaletą typeklas opartych o Monad, takich jak np. MonadState, jest fakt, że możemy stworzyć zoptymalizowany kontekst F[_], który będzie dostarczał wspomniane typeklasy. Zobaczymy jak stworzyć optymalne F[_] w następnych dwóch rozdziałach, kiedy bliżej przyjrzymy się poznanym już strukturom Free i IO.

7.5 Darmowy lunch

Nasza branża pragnie bezpiecznych, wysokopoziomowych języków, które pozwalają na zwiększenie wydajności deweloperów kosztem zmniejszonej wydajności kodu.

Kompilator Just In Time (JIT) na JVMie działa tak dobrze, że proste funkcje mogą działać porównywalnie szybko co ich odpowiedniki w C lub C++, ignorując koszt garbage collectora. Jednak JIT wykonuje jedynie optymalizacje niskopoziomowe: predykcję gałęzi (branch prediction), inlinowanie metod, rozwijanie pętli itd.

JIT nie zastosuje optymalizacji do naszej logiki biznesowej, jak na przykład łączenie wywołań sieciowych lub uruchamianie niezależnych zadań równolegle. Deweloper jest odpowiedzialny za tworzenie logiki biznesowej i jej optymalizacje, co efektywnie obniża czytelność i zwiększa koszt utrzymania kodu. Dobrze by było, gdyby wydajność i optymalizacja były problememami zupełnie niezależnymi.

Jeśli mielibyśmy do dyspozycji struktury danych, które opisują naszą logikę biznesową w kontekście wysokopoziomowych konceptów, a nie instrukcji maszynowych, moglibyśmy łatwo wykonać wysokopoziomowe optymalizacje. Takie struktury danych są zazwyczaj nazywane Darmowymi strukturami (Free structures) i mogą być generowane dla elementów naszych algebraicznych interfejsów dostarczając na za darmo instancje pewnych typeklas. Przykładowo, instancje Free Applicative mogą być wygenerowane i użyte do połączenia lub deduplikacji kosztownych operacji sieciowych.

W tym rozdziale zobaczymy jak tworzyć takie darmowe struktury i jak ich używać.

7.5.1 Free (Monad)

Zasadniczo, monada opisuje sekwencyjny program, gdzie każdy krok zależy od poprzedniego. Ograniczeni więc jesteśmy do modyfikacji, które wiedzą jedynie to, co już uruchomiliśmy i jaki krok uruchomimy jako następny.

Przypomnijmy, Free to struktura danych reprezentująca Monadę zdefiniowana jako trzy warianty:

  sealed abstract class Free[S[_], A] {
    def mapSuspension[T[_]](f: S ~> T): Free[T, A] = ...
    def foldMap[M[_]: Monad](f: S ~> M): M[A] = ...
    ...
  }
  object Free {
    implicit def monad[S[_], A]: Monad[Free[S, A]] = ...
  
    private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
    private final case class Return[S[_], A](a: A)     extends Free[S, A]
    private final case class Gosub[S[_], A0, B](
      a: Free[S, A0],
      f: A0 => Free[S, B]
    ) extends Free[S, B] { type A = A0 }
  
    def liftF[S[_], A](value: S[A]): Free[S, A] = Suspend(value)
    ...
  }

• Suspend reprezentuje program, który nie został jeszcze zinterpretowany
• Return to .pure
• Gosub to .bind

Instancja Free[S, A] może być wygenerowana za darmo dla dowolnej algebry S. Aby zobaczyć to wprost, rozważmy naszą algebrę Machines

  trait Machines[F[_]] {
    def getTime: F[Epoch]
    def getManaged: F[NonEmptyList[MachineNode]]
    def getAlive: F[Map[MachineNode, Epoch]]
    def start(node: MachineNode): F[Unit]
    def stop(node: MachineNode): F[Unit]
  }

Zdefiniujmy Free dla algebry Machines poprzez stworzenie ADT odpowiadającego jej elementom. Każdy typ danych ma te same parametry wejściowe, jest sparametryzowany typem zwracanym i ma taką samą nazwę:

  object Machines {
    sealed abstract class Ast[A]
    final case class GetTime()                extends Ast[Epoch]
    final case class GetManaged()             extends Ast[NonEmptyList[MachineNode]]
    final case class GetAlive()               extends Ast[Map[MachineNode, Epoch]]
    final case class Start(node: MachineNode) extends Ast[Unit]
    final case class Stop(node: MachineNode)  extends Ast[Unit]
    ...

Takie ADT jest Abstrakcyjnym drzewem składniowym (AST, Abstract Syntax Tree), ponieważ każdy element reprezentuje obliczenia w naszym programie.

Następnie zdefiniujmy .liftF, implementację Machines dla kontekstu Free[Ast, ?]. Każda metoda deleguje implementację do Free.liftF tworząc Suspend:

  ...
    def liftF = new Machines[Free[Ast, ?]] {
      def getTime = Free.liftF(GetTime())
      def getManaged = Free.liftF(GetManaged())
      def getAlive = Free.liftF(GetAlive())
      def start(node: MachineNode) = Free.liftF(Start(node))
      def stop(node: MachineNode) = Free.liftF(Stop(node))
    }
  }

Kiedy skonstruowaliśmy program sparametryzowany z użyciem Free, to aby go uruchomić, musimy przekazać interpreter (transformację naturalną Ast ~> M) do metody .foldMap. Jeśli mielibyśmy interpreter, który mapuje operacje do IO, moglibyśmy stworzyć program IO[Unit] z dostępnego AST

  def program[F[_]: Monad](M: Machines[F]): F[Unit] = ...
  
  val interpreter: Machines.Ast ~> IO = ...
  
  val app: IO[Unit] = program[Free[Machines.Ast, ?]](Machines.liftF)
                        .foldMap(interpreter)

Dla kompletności zaimplementujmy interpreter, który deleguje operacje do ich bezpośredniej implementacji. Taki interpreter może być użyteczny, jeśli reszta aplikacji również używa Free jako kontekstu, a my akurat mamy implementację algebry bazującą na IO pod ręką.

  def interpreter[F[_]](f: Machines[F]): Ast ~> F = λ[Ast ~> F] {
    case GetTime()    => f.getTime
    case GetManaged() => f.getManaged
    case GetAlive()   => f.getAlive
    case Start(node)  => f.start(node)
    case Stop(node)   => f.stop(node)
  }

Ale nasza logika biznesowa potrzebuje więcej niż tylko algebry Machines. Oprócz niej potrzebna jest też algebra Drones, zdefiniowana jako:

  trait Drone[F[_]] {
    def getBacklog: F[Int]
    def getAgents: F[Int]
  }
  object Drone {
    sealed abstract class Ast[A]
    ...
    def liftF = ...
    def interpreter = ...
  }

Chcielibyśmy, aby nasze AST było kombinacją AST pochodzących z obu tych algebr. W Rozdziale 6 poznaliśmy Coproduct, dysjunkcję wyższego rodzaju:

  final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A])

Możemy więc użyć kontekstu Free[Coproduct[Machines.Ast, Drone.Ast, ?], ?].

Moglibyśmy tworzyć instancję koproduktu ręcznie, ale utonęlibyśmy w morzu boilerplate’u, a później musielibyśmy robić to raz jeszcze, jeśli chcielibyśmy dodać trzecią algebrę.

Z pomocą przychodzi typeklasa scalaz.Inject.

  type :<:[F[_], G[_]] = Inject[F, G]
  sealed abstract class Inject[F[_], G[_]] {
    def inj[A](fa: F[A]): G[A]
    def prj[A](ga: G[A]): Option[F[A]]
  }
  object Inject {
    implicit def left[F[_], G[_]]: F :<: Coproduct[F, G, ?]] = ...
    ...
  }

Niejawna derywacja wygeneruje instancję Inject, kiedy będziemy ich potrzebować, pozwalając nam przepisać metodę liftF tak, aby działała dla dowolnej kombinacji AST:

  def liftF[F[_]](implicit I: Ast :<: F) = new Machines[Free[F, ?]] {
    def getTime                  = Free.liftF(I.inj(GetTime()))
    def getManaged               = Free.liftF(I.inj(GetManaged()))
    def getAlive                 = Free.liftF(I.inj(GetAlive()))
    def start(node: MachineNode) = Free.liftF(I.inj(Start(node)))
    def stop(node: MachineNode)  = Free.liftF(I.inj(Stop(node)))
  }

W tym wypadku Ast :<: F mówi nam, że Ast jest częścią pełnego zbioru instrukcji F.

Łącząc ze sobą wszystkie elementy, załóżmy, że mamy program, który abstrahuje ponad konkretną Monadą

  def program[F[_]: Monad](M: Machines[F], D: Drone[F]): F[Unit] = ...

oraz gotowe implementacja algebr Machines i Drone, z użyciem których możemy stworzyć interpretery:

  val MachinesIO: Machines[IO] = ...
  val DroneIO: Drone[IO]       = ...
  
  val M: Machines.Ast ~> IO = Machines.interpreter(MachinesIO)
  val D: Drone.Ast ~> IO    = Drone.interpreter(DroneIO)

i połączyć je w większy zbiór instrukcji używając pomocniczych metod z obiektu towarzyszącego NaturalTransformation

  object NaturalTransformation {
    def or[F[_], G[_], H[_]](fg: F ~> G, hg: H ~> G): Coproduct[F, H, ?] ~> G = ...
    ...
  }
  
  type Ast[a] = Coproduct[Machines.Ast, Drone.Ast, a]
  
  val interpreter: Ast ~> IO = NaturalTransformation.or(M, D)

aby następnie użyć ich do wyprodukowania IO

  val app: IO[Unit] = program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
                        .foldMap(interpreter)

Tym samym zatoczyliśmy koło! Mogliśmy przecież od razu użyć IO jako naszego kontekstu i uniknąć Free. Po co więc zadaliśmy sobie cały ten trud? Poniżej znajdziemy kilka przykładów, gdy Free staje się użyteczne.

7.5.1.1 Testowanie: mocki i stuby

Może to zabrzmieć obłudnie, jeśli po napisaniu całego tego boilerplate’u powiemy, że Free może służyć do zmniejszenia jego ilości. Istnieje jednak pewna granica, za którą Ast zaczyna mieć sens: gdy mamy dużo testów, które wymagają stubowania implementacji.

Jeśli .Ast i .liftF zostały zdefiniowane dla danej algebry, możemy tworzyć interpretery częściowe:

  val M: Machines.Ast ~> Id = stub[Map[MachineNode, Epoch]] {
    case Machines.GetAlive() => Map.empty
  }
  val D: Drone.Ast ~> Id = stub[Int] {
    case Drone.GetBacklog() => 1
  }

które posłużą nam do testowania naszego programu.

  program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
    .foldMap(or(M, D))
    .shouldBe(1)

Używając częściowych funkcji zamiast totalnych, narażamy się na błędy w czasie wykonania. Wiele zespołów godzi się na ten kompromis w swoich testach jednostkowych, bo popełniony błąd i tak zostanie wykryty, gdy testy te nie zakończą się sukcesem.

Moglibyśmy osiągnąć to samo zachowanie, implementując wszystkie metody z użyciem ??? i nadpisując te, których aktualnie potrzebujemy.

7.5.1.2 Monitoring

Aplikacje serwerowe są często monitorowane przez agenty, które manipulują bajtkodem aplikacji, wstrzykując profilery i wydobywając różnego rodzaju informacje o działaniu naszego kodu i jego wydajności.

Gdy naszym kontekstem jest Free, nie musimy uciekać się do manipulacji bajtkodem. Zamiast tego możemy zaimplementować interpreter, który będzie monitorować wykonywane operacje i raportować je z użyciem efektów ubocznych.

Rozważmy użycie takiego “agenta” o typie Ast ~> Ast, który zapisuje inwokacje metod:

  val Monitor = λ[Demo.Ast ~> Demo.Ast](
    _.run match {
      case \/-(m @ Drone.GetBacklog()) =>
        JmxAbstractFactoryBeanSingletonProviderUtilImpl.count("backlog")
        Coproduct.rightc(m)
      case other =>
        Coproduct(other)
    }
  )

Moglibyśmy też wychwytywać wiadomości, które nas szczególnie interesują i logować, gdy się pojawią.

Możemy dołączyć Monitor do naszej produkcyjnej aplikacji opartej na Free za pomocą

  .mapSuspension(Monitor).foldMap(interpreter)

lub połączyć transformacje naturalne wywołując pojedyncze

  .foldMap(Monitor.andThen(interpreter))

7.5.1.3 Monkey patching

Jako inżynierowie przywykliśmy już do próśb o dodanie dziwacznych zmian do kluczowej logiki aplikacji. Moglibyśmy chcieć wyrazić takie przypadki brzegowe jako wyjątki od reguły i obsługiwać je niezależnie od reszty aplikacji.

Wyobraźmy sobie, że otrzymaliśmy poniższą notatkę od działu księgowości

PILNE: Bob używa węzła #c0ffee przy sprawozdaniu rocznym. NIE ZATRZYMUJCIE TEJ MASZYNY!1!

Nie ma możliwości, aby wytłumaczyć Bobowi, że nie powinien używać naszych maszyn dla jego super ważnych zadań, tak więc musimy zhakować naszą logikę biznesową i wypuścić zmianę na środowisko produkcyjne tak szybko, jak to możliwe.

Nasza łatka (monkey patch) może być przetłumaczona na strukturę Free, pozwalając nam zwrócić wcześniej przygotowany wynik (Free.pure) zamiast wykonywania standardowych operacji. Implementacja to specjalna transformacja naturalna:

  val monkey = λ[Machines.Ast ~> Free[Machines.Ast, ?]] {
    case Machines.Stop(MachineNode("#c0ffee")) => Free.pure(())
    case other                                 => Free.liftF(other)
  }

I gotowe. Zerknąć czy działa, wypchnąć na produkcję i ustawić alarm na przyszły tydzień, żeby usunąć ten fragment i odebrać Bobowi dostęp do naszych serwerów.

W testach możemy użyć State, aby zapisywać wszystkie węzły, które zatrzymaliśmy:

  type S = Set[MachineNode]
  val M: Machines.Ast ~> State[S, ?] = Mocker.stub[Unit] {
    case Machines.Stop(node) => State.modify[S](_ + node)
  }
  
  Machines
    .liftF[Machines.Ast]
    .stop(MachineNode("#c0ffee"))
    .foldMap(monkey)
    .foldMap(M)
    .exec(Set.empty)
    .shouldBe(Set.empty)

Zaletą Free w tej sytuacji jest pewność, że obsłużyliśmy wszystkie użycia, nie musząc szukać ich w logice biznesowej. Jeśli kontekstem naszej aplikacji jest IO, to moglibyśmy oczywiście zaimplementować tę samą funkcjonalność w Machines[IO], ale używając Free, możemy taką zamianę wyizolować i przetestować bez dotykania istniejącego kodu i bez wiązania się z IO.

7.5.2 FreeAp (Applicative)

Mimo tego, że ten rozdział nazywa się Zaawansowane Monady, to kluczowe jest, że nie powinniśmy używać monad, dopóki naprawdę naprawdę nie musimy. W tym podrozdziale zobaczymy, czemu FreeAp (free applicative) jest lepszy od monady Free.

FreeAp zdefiniowany jest jako struktura danych reprezentujące metody ap i pure z typeklasy Applicative:

  sealed abstract class FreeAp[S[_], A] {
    def hoist[G[_]](f: S ~> G): FreeAp[G,A] = ...
    def foldMap[G[_]: Applicative](f: S ~> G): G[A] = ...
    def monadic: Free[S, A] = ...
    def analyze[M:Monoid](f: F ~> λ[α => M]): M = ...
    ...
  }
  object FreeAp {
    implicit def applicative[S[_], A]: Applicative[FreeAp[S, A]] = ...
  
    private final case class Pure[S[_], A](a: A) extends FreeAp[S, A]
    private final case class Ap[S[_], A, B](
      value: () => S[B],
      function: () => FreeAp[S, B => A]
    ) extends FreeAp[S, A]
  
    def pure[S[_], A](a: A): FreeAp[S, A] = Pure(a)
    def lift[S[_], A](x: =>S[A]): FreeAp[S, A] = ...
    ...
  }

Metody .hoist i .foldMap odpowiadają metodom .mapSuspension i .foldMap z Free.

Możemy też wygenerować Free[S, A] bezpośrednio z naszego FreeAp[S, A] używając .monadic, co jest szczególnie przydatne, gdy chcemy włączyć małe programy oparte o FreeAp do całego systemu opartego o Free.

Podobnie jak z Free, musimy stworzyć FreeAp dla naszego AST. Więcej boilerplate’u…

  def liftA[F[_]](implicit I: Ast :<: F) = new Machines[FreeAp[F, ?]] {
    def getTime = FreeAp.lift(I.inj(GetTime()))
    ...
  }

7.5.2.1 Grupowanie wywołań sieciowych

Rozpoczęliśmy ten rozdział wzniosłymi obietnicami dotyczącymi wydajności. Czas ich dotrzymać.

Aby zrozumieć, dlaczego powinniśmy zredukować ilość wywołań sieciowych, spójrzmy na ludzką wersję liczb latencji autorstwa Philipa Starka, bazującą na danych oryginalnie przygotowanych przez Petera Norviga.

Mimo że zarówno Free, jak i FreeAp niosą ze sobą narzut spowodowany alokacją pamięci (100 sekund na ludzkiej skali), to za każdym razem, gdy uda nam się połączyć dwa żądania sieciowe w jedno zyskujemy prawie 5 lat.

Kiedy jesteśmy w kontekście Applicative, możemy bezpiecznie optymalizować naszą aplikację bez zaburzania oczekiwań co do oryginalnego programu i bez komplikowania logiki biznesowej.

Przypomnijmy, że nasza główna logika biznesowa wymaga, na szczęście, jedynie instancji Applicative

  final class DynAgentsModule[F[_]: Applicative](D: Drone[F], M: Machines[F])
      extends DynAgents[F] {
    def act(world: WorldView): F[WorldView] = ...
    ...
  }

Zacznijmy od stworzenia boilerplate’u lift dla nowej algebry Batch

  trait Batch[F[_]] {
    def start(nodes: NonEmptyList[MachineNode]): F[Unit]
  }
  object Batch {
    sealed abstract class Ast[A]
    final case class Start(nodes: NonEmptyList[MachineNode]) extends Ast[Unit]
  
    def liftA[F[_]](implicit I: Ast :<: F) = new Batch[FreeAp[F, ?]] {
      def start(nodes: NonEmptyList[MachineNode]) = FreeAp.lift(I.inj(Start(nodes)))
    }
  }

oraz instancji DynAgentsModule używając FreeAp jako kontekstu

  type Orig[a] = Coproduct[Machines.Ast, Drone.Ast, a]
  
  val world: WorldView = ...
  val program = new DynAgentsModule(Drone.liftA[Orig], Machines.liftA[Orig])
  val freeap  = program.act(world)

W Rozdziale 6 poznaliśmy typ danych Const, który pozwala nam analizować wykonanie programu. Nie powinno więc dziwić, że FreeAp.analyze jest zaimplementowane z jego właśnie użyciem:

  sealed abstract class FreeAp[S[_], A] {
    ...
    def analyze[M: Monoid](f: S ~> λ[α => M]): M =
      foldMap(λ[S ~> Const[M, ?]](x => Const(f(x)))).getConst
  }

Używamy transformacji naturalnej i .analyze, aby zebrać wszystkie węzły, które powinny zostać wystartowane

  val gather = λ[Orig ~> λ[α => IList[MachineNode]]] {
    case Coproduct(-\/(Machines.Start(node))) => IList.single(node)
    case _                                    => IList.empty
  }
  val gathered: IList[MachineNode] = freeap.analyze(gather)

Następnym krokiem jest rozszerzenie zbioru instrukcji z Orig do Extended, tak by zawierał Batch.Ast, oraz napisanie programu z użyciem FreeAp, który wystartuje wszystkie zebrane wcześniej węzły pojedynczym żądaniem.

  type Extended[a] = Coproduct[Batch.Ast, Orig, a]
  def batch(nodes: IList[MachineNode]): FreeAp[Extended, Unit] =
    nodes.toNel match {
      case None        => FreeAp.pure(())
      case Some(nodes) => FreeAp.lift(Coproduct.leftc(Batch.Start(nodes)))
    }

Musimy również pozbyć się wszystkich wywołań Machines.Start, co możemy osiągnąć używając jeszcze jednej transformacji naturalnej

  val nostart = λ[Orig ~> FreeAp[Extended, ?]] {
    case Coproduct(-\/(Machines.Start(_))) => FreeAp.pure(())
    case other                             => FreeAp.lift(Coproduct.rightc(other))
  }

Mamy teraz dwa programy, które musimy połączyć. Przypomnijmy sobie operator *> z Apply

  val patched = batch(gathered) *> freeap.foldMap(nostart)

i złóżmy to wszystko razem jako jedną metodę

  def optimise[A](orig: FreeAp[Orig, A]): FreeAp[Extended, A] =
    (batch(orig.analyze(gather)) *> orig.foldMap(nostart))

I tyle! Teraz wystarczy użyć .optimise razem z act w głównej pętli naszego programu.

7.5.3 Coyoneda (Functor)

To “darmowa” (free) struktura danych zawdzięczająca swoją nazwę matematykowi Nobuo Yoneda. Pozwala nam ona wygenerować “za darmo” instancję typeklasy Functor dla dowolnej algebry S[_], tak długo, jak mamy w planie przetransformować ją do algebry, która taką instancję posiada.

  sealed abstract class Coyoneda[F[_], A] {
    def run(implicit F: Functor[F]): F[A] = ...
    def trans[G[_]](f: F ~> G): Coyoneda[G, A] = ...
    ...
  }
  object Coyoneda {
    implicit def functor[F[_], A]: Functor[Coyoneda[F, A]] = ...
  
    private final case class Map[F[_], A, B](fa: F[A], f: A => B) extends Coyoneda[F, A]
    def apply[F[_], A, B](sa: F[A])(f: A => B) = Map[F, A, B](sa, f)
    def lift[F[_], A](sa: F[A]) = Map[F, A, A](sa, identity)
    ...
  }

Również w wersji kontrawariantnej:

  sealed abstract class ContravariantCoyoneda[F[_], A] {
    def run(implicit F: Contravariant[F]): F[A] = ...
    def trans[G[_]](f: F ~> G): ContravariantCoyoneda[G, A] = ...
    ...
  }
  object ContravariantCoyoneda {
    implicit def contravariant[F[_], A]: Contravariant[ContravariantCoyoneda[F, A]] = ...
  
    private final case class Contramap[F[_], A, B](fa: F[A], f: B => A)
      extends ContravariantCoyoneda[F, A]
    def apply[F[_], A, B](sa: F[A])(f: B => A) = Contramap[F, A, B](sa, f)
    def lift[F[_], A](sa: F[A]) = Contramap[F, A, A](sa, identity)
    ...
  }

API jest nieco prostsze niż Free i FreeAp, udostępniając transformację poprzez .trans i możliwość pozbycia się struktury poprzez metodę .run (która przyjmuje faktyczną implementację Functora lub ContravariantFunctora).

Coyo i cocoyo są przydatne, gdy chcemy wywołać .map lub .contramap na typie, który takich metod nie posiada, ale wiemy, że w końcu i tak przekonwertujemy go do innego typu, pozbawionego tych ograniczeń, a na razie nie chcemy się z nim wiązać. Przykładowo możemy stworzyć Coyoneda[ISet, ?], pamiętając, że ISet nie posiada instancji typeklasy Functor, aby wywołać metody jej wymagające, a później przekonwertować taki obiekt do typu IList.

Aby użyć coyo lub cocoyo do optymalizacji naszego programu, musimy dostarczyć oczekiwany boilerplate dla każdej algebry, której będziemy używać:

  def liftCoyo[F[_]](implicit I: Ast :<: F) = new Machines[Coyoneda[F, ?]] {
    def getTime = Coyoneda.lift(I.inj(GetTime()))
    ...
  }
  def liftCocoyo[F[_]](implicit I: Ast :<: F) = new Machines[ContravariantCoyoneda[F, ?]] {
    def getTime = ContravariantCoyoneda.lift(I.inj(GetTime()))
    ...
  }

Optymalizacją, którą możemy zastosować to fuzja wywołań .map (map fusion), co pozwala nam przepisać

  xs.map(a).map(b).map(c)

na

  xs.map(x => c(b(a(x))))

unikając pośrednich reprezentacji. Jeśli, na przykład, xs to Lista z tysiącem elementów, to oszczędzamy dwa tysiące alokacji, wywołując .map tylko raz.

Jednak dużo prościej jest po prostu ręcznie zmienić oryginalną funkcję albo poczekać na scalaz-plugin, który automatycznie wykona tego typu optymalizacje.

7.5.4 Efekty rozszerzalne

Programy to tylko dane, a struktury typu free wyrażają to wprost, pozwalając nam na ich rearanżację i optymalizację.

Free jest bardziej niezwykła, niż nam się wydaje: pozwala sekwencyjnie łączyć arbitralne algebry i typeklasy.

Na przykład, istnieje Free dla MonadState. Ast i .liftF są nieco bardziej skomplikowane niż zwykle, bo muszą uwzględniać parametr typu S oraz dziedziczenie po typie Monad:

  object MonadState {
    sealed abstract class Ast[S, A]
    final case class Get[S]()     extends Ast[S, S]
    final case class Put[S](s: S) extends Ast[S, Unit]
  
    def liftF[F[_], S](implicit I: Ast[S, ?] :<: F) =
      new MonadState[Free[F, ?], S] with BindRec[Free[F, ?]] {
        def get       = Free.liftF(I.inj(Get[S]()))
        def put(s: S) = Free.liftF(I.inj(Put[S](s)))
  
        val delegate         = Free.freeMonad[F]
        def point[A](a: =>A) = delegate.point(a)
        ...
      }
    ...
  }

Daje nam to okazje do użycia zoptymalizowanego interpretera, który może na przykład przechowywać stan w atomowym polu, zamiast budować zagnieżdżone trampoliny StateT.

Możemy stworzyć Ast i .liftF dla niemal dowolnej algebry albo typeklasy. Jedyne ograniczenie jest takie, że F[_] nie może pojawiać się jako parametr w żadnej instrukcji, a więc algebra musi móc mieć instancję typeklasy Functor. Ograniczenie to wyklucza z użycia m.in. MonadError i Monoid.

Wraz z rozrostem AST programu obniża się wydajność interpretera, ponieważ instrukcja dopasowania (match) ma złożoność liniową względem obsługiwanych wariantów. Alternatywą do scalaz.Coproduct jest biblioteka iotaz, która używa zoptymalizowanej struktury danych, aby wykonać tę operację ze złożonością O(1) (używając liczb całkowitych przydzielanych wariantom na etapie kompilacji).

Z przyczyn historycznych free AST dla algebry lub typeklasy jest nazywane Initial Encoding, a bezpośrednia implementacja (np. z użyciem IO) to Finally Tagless. Mimo że omówiliśmy interesujące koncepty używając Free, to ogólnie przyjęta jest opinia, że finally tagless jest podejściem lepszym. Jednak aby użyć tego podejścia, musimy mieć do dyspozycji wydajny typ efektu, który dostarczy nam wszystkie typeklasy, które omówiliśmy. Ponadto nadal potrzebujemy sposobu na uruchomienie naszego kodu opartego o Applicative w sposób równoległy.

I dokładnie tym się teraz zajmiemy.

7.6 Parallel

Są dwie operacje wywołujące efekty, które prawie zawsze chcemy wykonywać równolegle:

1. .map na kolekcji efektów, zwracając pojedynczy efekt. Można to osiągnąć za pomocą metody .traverse, która deleguje do .apply2 danego efektu.
2. uruchomienie danej liczby efektów z użyciem operatora krzyku |@| i połączenie ich wyników, również delegując do .apply2.

W praktyce jednak żadna z tych operacji nie jest domyślnie wykonywana równolegle. Przyczyna jest prosta: jeśli nasze F[_] implementuje typeklasę Monad, wtedy muszą być zachowane jej prawa co do apply2, tj.

  @typeclass trait Bind[F[_]] extends Apply[F] {
    ...
    override def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] =
      bind(fa)(a => map(fb)(b => f(a, b)))
    ...
  }

Innymi słowy, Monadom wprost zabrania się wykonywania efektów równolegle.

Jednak, gdy mamy F[_], które nie jest monadyczne, wtedy może ono implementować .apply2 w sposób równoległy. Możemy użyć mechanizmu @@ (tagów), aby stworzyć instancję typeklasy Applicative dla F[_] @@ Parallel, która dorobiła się własnego aliasu Applicative.Par

  object Applicative {
    type Par[F[_]] = Applicative[λ[α => F[α] @@ Tags.Parallel]]
    ...
  }

Programy monadyczne mogą więc żądać niejawnego Par jako dodatku do ich Monad

  def foo[F[_]: Monad: Applicative.Par]: F[Unit] = ...

Metody Traverse ze Scalaz wspierają równoległe wykonanie:

  implicit class TraverseSyntax[F[_], A](self: F[A]) {
    ...
    def parTraverse[G[_], B](f: A => G[B])(
      implicit F: Traverse[F], G: Applicative.Par[G]
    ): G[F[B]] = Tag.unwrap(F.traverse(self)(a => Tag(f(a))))
  }

Jeśli w zakresie dostępna jest niejawna instancja Applictive.Par[IO], to możemy wybrać między sekwencyjną i równoległa trawersacją:

  val input: IList[String] = ...
  def network(in: String): IO[Int] = ...
  
  input.traverse(network): IO[IList[Int]] // one at a time
  input.parTraverse(network): IO[IList[Int]] // all in parallel

Podobnie możemy wywołać .parApply lub .parTupled po tym, jak użyliśmy operatorów krzyku

  val fa: IO[String] = ...
  val fb: IO[String] = ...
  val fc: IO[String] = ...
  
  (fa |@| fb).parTupled: IO[(String, String)]
  
  (fa |@| fb |@| fc).parApply { case (a, b, c) => a + b + c }: IO[String]

Warto zaznaczyć, że kiedy mamy do czynienia z programami opartymi o Applicative, takimi jak

  def foo[F[_]: Applicative]: F[Unit] = ...

możemy używać F[A] @@ Parallel jako kontekstu, sprawiając, że .traverse i |@| wykonywane będą równolegle. Konwersja między zwykłą i równoległą wersją F[_] musi być obsłużona ręcznie, co może być uciążliwe, więc często łatwiej jest po prostu wymagać obu form Applicative.

  def foo[F[_]: Applicative: Applicative.Par]: F[Unit] = ...

7.6.1 Łamiąc Prawo

Możemy przyjąć bardziej śmiałe podejście do zrównoleglania: zrezygnować z prawa, które każe .apply2 wykonywać operacje sekwencyjnie dla Monad. Jest to podejście mocno kontrowersyjne, ale działa zadziwiająco dobrze dla większości rzeczywistych aplikacji. Musimy zacząć od prześledzenia kodu w poszukiwaniu fragmentów, które mogłyby bazować na tym prawie, aby nie wprowadzić błędów. Później jest już tylko łatwiej.

Opakowujemy IO

  final class MyIO[A](val io: IO[A]) extends AnyVal

i dostarczamy naszą własną implementację Monady, która uruchamia .apply2 równolegle, poprzez oddelegowanie do instancji dla typu @@ Parallel

  object MyIO {
    implicit val monad: Monad[MyIO] = new Monad[MyIO] {
      override def apply2[A, B, C](fa: MyIO[A], fb: MyIO[B])(f: (A, B) => C): MyIO[C] =
        Applicative[IO.Par].apply2(fa.io, fb.io)(f)
      ...
    }
  }

Od teraz możemy używać MyIO zamiast IO jako kontekstu naszej aplikacji i korzystać z automatycznego zrównoleglania.

Dla kompletności: naiwna i niewydajna implementacja Applicative.Par dla naszego IO mogłaby używać Future:

  object IO {
    ...
    type Par[a] = IO[a] @@ Parallel
    implicit val ParApplicative = new Applicative[Par] {
      override def apply2[A, B, C](fa: =>Par[A], fb: =>Par[B])(f: (A, B) => C): Par[C] =
        Tag(
          IO {
            val forked = Future { Tag.unwrap(fa).interpret() }
            val b      = Tag.unwrap(fb).interpret()
            val a      = Await.result(forked, Duration.Inf)
            f(a, b)
          }
        )
  }

a z powodu błędu w kompilatorze Scali, który powoduje, że wszystkie instancje dla typów @@ traktowane są jako instancje osierocone, musimy explicite zaimportować tę niejawną wartość:

  import IO.ParApplicative

W ostatniej sekcji tego rozdziału zobaczymy, jak naprawdę zaimplementowany jest typ IO w Scalaz.

7.7 IO

IO ze Scalaz jest najszybszą strukturą danych pozwalającą na programowanie asynchroniczne, jaką możemy znaleźć w ekosystemie Scali, nawet do 50 razy szybsza niż Future.²³ Zaprojektowana została jako monada do obsługi efektów ogólnego przeznaczenia.

  sealed abstract class IO[E, A] { ... }
  object IO {
    private final class FlatMap         ... extends IO[E, A]
    private final class Point           ... extends IO[E, A]
    private final class Strict          ... extends IO[E, A]
    private final class SyncEffect      ... extends IO[E, A]
    private final class Fail            ... extends IO[E, A]
    private final class AsyncEffect     ... extends IO[E, A]
    ...
  }

IO ma dwa parametry typu, a tym samym posiada instancję typeklasy Bifunctor, która pozwala na zdefiniowanie błędów jako ADT specyficznego dla danej aplikacji. Niestety jesteśmy na JVMie oraz musimy współpracować z istniejącymi bibliotekami, dlatego też zdefiniowany został pomocny alias, który używa wyjątków jako typu błędów:

  type Task[A] = IO[Throwable, A]

7.7.1 Tworzenie

Istnieje wiele sposobów na stworzenie IO z zarówno zachłannych i leniwych, jak i bezpiecznych i niebezpiecznych bloków kodu:

  object IO {
    // eager evaluation of an existing value
    def now[E, A](a: A): IO[E, A] = ...
    // lazy evaluation of a pure calculation
    def point[E, A](a: =>A): IO[E, A] = ...
    // lazy evaluation of a side-effecting, yet Total, code block
    def sync[E, A](effect: =>A): IO[E, A] = ...
    // lazy evaluation of a side-effecting code block that may fail
    def syncThrowable[A](effect: =>A): IO[Throwable, A] = ...
  
    // create a failed IO
    def fail[E, A](error: E): IO[E, A] = ...
    // asynchronously sleeps for a specific period of time
    def sleep[E](duration: Duration): IO[E, Unit] = ...
    ...
  }

wraz z wygodnymi konstruktorami dla Taska:

  object Task {
    def apply[A](effect: =>A): Task[A] = IO.syncThrowable(effect)
    def now[A](effect: A): Task[A] = IO.now(effect)
    def fail[A](error: Throwable): Task[A] = IO.fail(error)
    def fromFuture[E, A](io: Task[Future[A]])(ec: ExecutionContext): Task[A] = ...
  }

Najczęściej używanym wariantem, szczególnie przy pracy z istniejącym kodem, jest Task.apply oraz Task.fromFuture:

  val fa: Task[Future[String]] = Task { ... impure code here ... }
  
  Task.fromFuture(fa)(ExecutionContext.global): Task[String]

Nie możemy przekazywać instancji Future bezpośrednio, ponieważ obliczenia wewnątrz niej rozpoczynają się zachłannie w momencie stworzenia, dlatego też tworzenie to musi odbyć się wewnątrz bezpiecznego bloku.

Zauważmy, że ExecutionContext nie jest przekazywany niejawnie, odwrotnie niż przyjęta konwencja. W Scalaz parametry niejawne zarezerwowane są dla typeklas, a ExecutionContext to parametr konfiguracyjny, a więc powinien być przekazany wprost.

7.7.2 Uruchamianie

Interpreter IO nazywa się RTS, od runtime system, ale jego implementacja wybiega poza zakres tej książki. W zamian omówimy funkcjonalności, które nam udostępnia.

IO to po prostu struktura danych, którą interpretujemy na końcu świata poprzez rozszerzenie SafeApp i zaimplementowanie metody .run

  trait SafeApp extends RTS {
  
    sealed trait ExitStatus
    object ExitStatus {
      case class ExitNow(code: Int)                         extends ExitStatus
      case class ExitWhenDone(code: Int, timeout: Duration) extends ExitStatus
      case object DoNotExit                                 extends ExitStatus
    }
  
    def run(args: List[String]): IO[Void, ExitStatus]
  
    final def main(args0: Array[String]): Unit = ... calls run ...
  }

Jeśli integrujemy się z istniejącym systemem i nie mamy kontroli nad punktem wejścia do naszej aplikacji, możemy rozszerzyć RTS, zyskując dostęp do niebezpiecznych metod, których możemy użyć, aby wyewaluować IO na wejściu do czysto funkcyjnej części kodu.

7.7.3 Funkcjonalności

IO dostarcza instancje dla Bifunctor, MonadError[E, ?], BindRec, Plus, MonadPlus (jeśli E formuje Monoid) oraz Applicative[IO.Par[E, ?]].

W dodatku do funkcjonalności pochodzących z typeklas dostajemy implementację kilku specyficznych metod:

  sealed abstract class IO[E, A] {
    // retries an action N times, until success
    def retryN(n: Int): IO[E, A] = ...
    // ... with exponential backoff
    def retryBackoff(n: Int, factor: Double, duration: Duration): IO[E, A] = ...
  
    // repeats an action with a pause between invocations, until it fails
    def repeat[B](interval: Duration): IO[E, B] = ...
  
    // cancel the action if it does not complete within the timeframe
    def timeout(duration: Duration): IO[E, Maybe[A]] = ...
  
    // runs `release` on success or failure.
    // Note that IO[Void, Unit] cannot fail.
    def bracket[B](release: A => IO[Void, Unit])(use: A => IO[E, B]): IO[E, B] = ...
    // alternative syntax for bracket
    def ensuring(finalizer: IO[Void, Unit]): IO[E, A] =
    // ignore failure and success, e.g. to ignore the result of a cleanup action
    def ignore: IO[Void, Unit] = ...
  
    // runs two effects in parallel
    def par[B](that: IO[E, B]): IO[E, (A, B)] = ...
    ...

Instancja IO może być zakończona (terminated), co oznacza, że praca, która była zaplanowana, zostanie odrzucona (nie jest to ani sukces, ani błąd). Narzędzia do pracy z tym stanem to:

  ...
    // terminate whatever actions are running with the given throwable.
    // bracket / ensuring is honoured.
    def terminate[E, A](t: Throwable): IO[E, A] = ...
  
    // runs two effects in parallel, return the winner and terminate the loser
    def race(that: IO[E, A]): IO[E, A] = ...
  
    // ignores terminations
    def uninterruptibly: IO[E, A] = ...
  ...

7.7.4 Fiber

IO może przywołać włókna (fibers), czyli lekką abstrakcję ponad wątkami udostępnianymi przez JVM. Możemy rozgałęziać (.fork) IO i nadzorować (.supervise) niezakończone włókna, aby upewnić się, że zostaną zakończone, kiedy IO się wykona:

  ...
    def fork[E2]: IO[E2, Fiber[E, A]] = ...
    def supervised(error: Throwable): IO[E, A] = ...
  ...

Kiedy mamy do dyspozycji włókno możemy je włączyć z powrotem do IO (.join) lub przerwać wykonywaną pracę (.interrupt).

  trait Fiber[E, A] {
    def join: IO[E, A]
    def interrupt[E2](t: Throwable): IO[E2, Unit]
  }

Możemy używać włókien do osiągnięcia optymistycznej kontroli współbieżności. Wyobraźmy sobie, że mamy dane (data), które chcemy przeanalizować oraz zwalidować. Możemy optymistycznie rozpocząć analizę i przerwać ją, gdy walidacja, która uruchomiona jest równolegle, zakończy się niepowodzeniem.

  final class BadData(data: Data) extends Throwable with NoStackTrace
  
  for {
    fiber1   <- analysis(data).fork
    fiber2   <- validate(data).fork
    valid    <- fiber2.join
    _        <- if (!valid) fiber1.interrupt(BadData(data))
                else IO.unit
    result   <- fiber1.join
  } yield result

Innym zastosowaniem włókien jest sytuacja, gdy chcemy rozpocząć akcję i o niej zapomnieć, jak na przykład niskopriorytetowe logowanie zdarzeń przez sieć.

7.7.5 Promise

Obietnica (Promise) reprezentuje asynchroniczną zmienną, która może być ustawiona dokładnie raz (poprzez .complete lub .error). Następnie dowolna liczba odbiorców może odczytać taką zmienną, używając .get.

  final class Promise[E, A] private (ref: AtomicReference[State[E, A]]) {
    def complete[E2](a: A): IO[E2, Boolean] = ...
    def error[E2](e: E): IO[E2, Boolean] = ...
    def get: IO[E, A] = ...
  
    // interrupts all listeners
    def interrupt[E2](t: Throwable): IO[E2, Boolean] = ...
  }
  object Promise {
    def make[E, A]: IO[E, Promise[E, A]] = ...
  }

Promise nie jest zazwyczaj używany w kodzie aplikacyjnym. Jest to raczej element zaprojektowany do budowania wyżejpoziomowych frameworków do obsługi współbieżności.

7.7.6 IORef

IORef to odpowiednik mutowalnej zmiennej w świecie IO.

Możemy odczytać jej wartość oraz dostajemy do dyspozycji szereg operacji do manipulacji nią.

  final class IORef[A] private (ref: AtomicReference[A]) {
    def read[E]: IO[E, A] = ...
  
    // write with immediate consistency guarantees
    def write[E](a: A): IO[E, Unit] = ...
    // write with eventual consistency guarantees
    def writeLater[E](a: A): IO[E, Unit] = ...
    // return true if an immediate write succeeded, false if not (and abort)
    def tryWrite[E](a: A): IO[E, Boolean] = ...
  
    // atomic primitives for updating the value
    def compareAndSet[E](prev: A, next: A): IO[E, Boolean] = ...
    def modify[E](f: A => A): IO[E, A] = ...
    def modifyFold[E, B](f: A => (B, A)): IO[E, B] = ...
  }
  object IORef {
    def apply[E, A](a: A): IO[E, IORef[A]] = ...
  }

IORef to kolejny typ danych, który może nam dostarczyć wysokowydajną instancję MonadState. Spróbujmy stworzyć nowy typ wyspecjalizowany do obsługi Tasków

  final class StateTask[A](val io: Task[A]) extends AnyVal
  object StateTask {
    def create[S](initial: S): Task[MonadState[StateTask, S]] =
      for {
        ref <- IORef(initial)
      } yield
        new MonadState[StateTask, S] {
          override def get       = new StateTask(ref.read)
          override def put(s: S) = new StateTask(ref.write(s))
          ...
        }
  }

Możemy wykorzystać tak zoptymalizowaną implementację MonadState w SafeApp, gdy nasz .program wymaga instancji tej typeklasy:

  object FastState extends SafeApp {
    def program[F[_]](implicit F: MonadState[F, Int]): F[ExitStatus] = ...
  
    def run(@unused args: List[String]): IO[Void, ExitStatus] =
      for {
        stateMonad <- StateTask.create(10)
        output     <- program(stateMonad).io
      } yield output
  }

Bardziej realistyczna aplikacja wymagałaby zdecydowanie większej liczby różnych typeklas i algebr jako wejścia.

7.7.6.1 MonadIO

Typ MonadIO, który wcześniej widzieliśmy, został uproszczony poprzez ukrycie parametru E. Prawdziwa jego forma wygląda tak:

  trait MonadIO[M[_], E] {
    def liftIO[A](io: IO[E, A])(implicit M: Monad[M]): M[A]
  }

wraz z drobną różnicą w boilerplacie kompaniującym naszej algebrze, uwzględniają dodatkowe E:

  trait Lookup[F[_]] {
    def look: F[Int]
  }
  object Lookup {
    def liftIO[F[_]: Monad, E](io: Lookup[IO[E, ?]])(implicit M: MonadIO[F, E]) =
      new Lookup[F] {
        def look: F[Int] = M.liftIO(io.look)
      }
    ...
  }

7.8 Podsumowanie

1. Typ Future jest zepsuty, nie idź tą drogą.
2. Możemy zapanować nad bezpieczeństwem stosu za pomocą Trampoline.
3. Biblioteka Transformatorów Monad (MTL) abstrahuje nad popularnymi efektami za pomocą typeklas.
4. Transformatory Monad dostarczają domyślnych implementacji dla typeklas z MTL.
5. Struktura Free pozwala nam analizować, optymalizować i łatwo testować nasze programy.
6. IO umożliwia implementowanie algebr jako efektów wykonywanych na świecie zewnętrznym.
7. IO może wykonywać efekty równolegle i jest wysoce wydajnym fundamentem dla dowolnej aplikacji.