6. Typy danych ze Scalaz

Kto nie kocha porządnej struktury danych? Odpowiedź brzmi nikt, a struktury danych są super!

W tym rozdziale poznamy typy danych przypominające kolekcje oraz takie, które wzbogacają Scalę o dodatkowe możliwości i zwiększają bezpieczeństwo typów.

Podstawowym powodem, dla którego używamy wielu różnych typów kolekcji, jest wydajność. Wektor i lista mogą zrobić to samo, ale ich charakterystyki wydajnościowe są inne: wektor oferuje dostęp do losowego elementu w czasie stałym, podczas gdy lista musi zostać w czasie tej operacji przetrawersowana.

Wszystkie kolekcje, które tutaj zaprezentujemy, są trwałe (persistent): jeśli dodamy lub usuniemy element, nadal możemy używać poprzedniej, niezmienionej wersji. Współdzielenie strukturalne (structural sharing) jest kluczowe dla wydajności trwałych struktur danych, gdyż bez tego musiałyby one być tworzone od nowa przy każdej operacji.

W przeciwieństwie do kolekcji z bibliotek standardowych Javy i Scali, w Scalaz typy danych nie tworzą hierarchii, a przez to są dużo prostsze do zrozumienia. Polimorfizm jest zapewniany przez zoptymalizowane instancje typeklas, które poznaliśmy w poprzednim rozdziale. Sprawia to, że zmiana implementacji podyktowana zwiększeniem wydajności, lub dostarczenie własnej, jest dużo prostsze.

6.1 Wariancja typów

Wiele z typów danych zdefiniowanych w Scalaz jest inwariantna. Dla przykładu IList[A] nie jest podtypem IList[B] nawet jeśli A <: B.

6.1.1 Kowariancja

Problem z kowariantnymi parametrami typu, takimi jak A w class List[+A], jest taki, że List[A] jest podtypem (a więc dziedziczy po) List[Any] i bardzo łatwo jest przez przypadek zgubić informacje o typach.

  scala> List("hello") ++ List(' ') ++ List("world!")
  res: List[Any] = List(hello,  , world!)

Zauważ, że druga lista jest typu List[Char] i kompilator niezbyt pomocnie wyinferował Any jako Najmniejszą Górną Granicę (Least Upper Bound, LUB). Porównajmy to z IList, która wymaga bezpośredniego wywołania .widen[Any], aby pozwolić na ten haniebny uczynek:

  scala> IList("hello") ++ IList(' ') ++ IList("world!")
  <console>:35: error: type mismatch;
   found   : Char(' ')
   required: String
  
  scala> IList("hello").widen[Any]
           ++ IList(' ').widen[Any]
           ++ IList("world!").widen[Any]
  res: IList[Any] = [hello, ,world!]

Podobnie, gdy kompilator inferuje typ z dopiskiem with Product with Serializable to najprawdopodobniej miało miejsce przypadkowe rozszerzenie typu spowodowane kowariancją.

Niestety, musimy uważać, nawet gdy konstruujemy typy inwariantne, ponieważ obliczenie LUB wykonywane jest również dla parametrów typu:

  scala> IList("hello", ' ', "world")
  res: IList[Any] = [hello, ,world]

Podobny problem powodowany jest przez typ Nothing, który jest podtypem wszystkich innych typów, wliczając w to ADT, klasy finalne, typy prymitywne oraz null.

Nie istnieją jednak wartości typu Nothing. Funkcje, które przyjmują Nothing jako parametr, nie mogą zostać uruchomione, a funkcje, które zwracają ten typ, nigdy nie zwrócą rezultatu. Typ Nothing został wprowadzony, aby umożliwić używanie kowariantnych parametrów typu, ale w konsekwencji umożliwił pisanie kodu, który nie może być uruchomiony, często przez przypadek. W Scalaz uważamy, że kowariantne parametry typu wcale nie są potrzebne, ograniczając się tym samym do praktycznego kodu, który może zostać uruchomiony.

6.1.2 Sprzeciwwariancja

Z drugiej strony, parametry kontrawariantne takie jak A w trait Thing[-A] mogą ujawnić niszczycielskie błędy w kompilatorze. Spójrzmy na to, co Paul Phillips (były członek zespołu pracującego nad scalac) nazywa contrarivariance:

  scala> :paste
         trait Thing[-A]
         def f(x: Thing[ Seq[Int]]): Byte   = 1
         def f(x: Thing[List[Int]]): Short  = 2
  
  scala> f(new Thing[ Seq[Int]] { })
         f(new Thing[List[Int]] { })
  
  res = 1
  res = 2

Tak jak byśmy oczekiwali, kompilator odnalazł najdokładniejsze dopasowanie metod do argumentów. Sprawa komplikuje się jednak gdy użyjemy wartości niejawnych

  scala> :paste
         implicit val t1: Thing[ Seq[Int]] =
           new Thing[ Seq[Int]] { override def toString = "1" }
         implicit val t2: Thing[List[Int]] =
           new Thing[List[Int]] { override def toString = "2" }
  
  scala> implicitly[Thing[ Seq[Int]]]
         implicitly[Thing[List[Int]]]
  
  res = 1
  res = 1

Niejawne rozstrzyganie odwraca definicje “najbardziej dokładnego dopasowania” dla typów kontrawariantnych, czyniąc je tym samym kompletnie bezużytecznymi do reprezentacji typeklas i czegokolwiek co wymaga polimorficznych funkcjonalności. Zachowanie to zostało poprawione w Dottym.

6.1.3 Ograniczenia podtypów

scala.Option ma metodę .flatten, która konwertuje Option[Option[B]] na Option[B]. Niestety kompilator Scali nie pozwala nam na poprawne zapisanie sygnatury tej metody. Rozważmy poniższą implementację, która pozornie wydaje się poprawna:

  sealed abstract class Option[+A] {
    def flatten[B, A <: Option[B]]: Option[B] = ...
  }

A wprowadzone w definicji .flatten przysłania A wprowadzone w definicji klasy. Tak więc jest to równoznaczne z

  sealed abstract class Option[+A] {
    def flatten[B, C <: Option[B]]: Option[B] = ...
  }

czyli nie do końca jest tym, czego chcieliśmy.

Jako obejście tego problemu wprowadzono klasy <:< i =:= wraz z niejawnymi metodami, które zawsze tworzą instancje dla poprawnych typów.

  sealed abstract class <:<[-From, +To] extends (From => To)
  implicit def conforms[A]: A <:< A = new <:<[A, A] { def apply(x: A): A = x }
  
  sealed abstract class =:=[ From,  To] extends (From => To)
  implicit def tpEquals[A]: A =:= A = new =:=[A, A] { def apply(x: A): A = x }

=:= może być użyty do wymuszenia, aby dwa parametry typu były dokładnie takie same. <:< służy do wyrażenia relacji podtypowania, pozwalając tym samym na implementację .flatten jako

  sealed abstract class Option[+A] {
    def flatten[B](implicit ev: A <:< Option[B]): Option[B] = this match {
      case None        => None
      case Some(value) => ev(value)
    }
  }
  final case class Some[+A](value: A) extends Option[A]
  case object None                    extends Option[Nothing]

Scalaz definiuje ulepszone wersje <:< i =:=: Liskov (z aliasem <=<) oraz Leibniz (===).

  sealed abstract class Liskov[-A, +B] {
    def apply(a: A): B = ...
    def subst[F[-_]](p: F[B]): F[A]
  
    def andThen[C](that: Liskov[B, C]): Liskov[A, C] = ...
    def onF[X](fa: X => A): X => B = ...
    ...
  }
  object Liskov {
    type <~<[-A, +B] = Liskov[A, B]
    type >~>[+B, -A] = Liskov[A, B]
  
    implicit def refl[A]: (A <~< A) = ...
    implicit def isa[A, B >: A]: A <~< B = ...
  
    implicit def witness[A, B](lt: A <~< B): A => B = ...
    ...
  }
  
  // type signatures have been simplified
  sealed abstract class Leibniz[A, B] {
    def apply(a: A): B = ...
    def subst[F[_]](p: F[A]): F[B]
  
    def flip: Leibniz[B, A] = ...
    def andThen[C](that: Leibniz[B, C]): Leibniz[A, C] = ...
    def onF[X](fa: X => A): X => B = ...
    ...
  }
  object Leibniz {
    type ===[A, B] = Leibniz[A, B]
  
    implicit def refl[A]: Leibniz[A, A] = ...
  
    implicit def subst[A, B](a: A)(implicit f: A === B): B = ...
    implicit def witness[A, B](f: A === B): A => B = ...
    ...
  }

Poza dostarczeniem przydatnych metod i niejawnych konwersji, <=< i === są bardziej pryncypialne niż ich odpowiedniki z biblioteki standardowej.

6.2 Ewaluacja

Java to język o ścisłej (strict) ewaluacji: wszystkie parametry przekazane do metody muszą zostać wyewaluowane do wartości, zanim metoda zostanie uruchomiona. Scala wprowadza pojęcie parametrów przekazywanych przez nazwę (by-name) za pomocą składni a: =>A. Takie parametry opakowywane są w zero-argumentową funkcję, która jest wywoływana za każdym razem, gdy odnosimy się do a. Widzieliśmy tego typu parametry wielokrotnie, gdy omawialiśmy typeklasy.

Scala pozwala również na ewaluacje wartości na żądanie za pomocą słowa kluczowego lazy: obliczenia są wykonywane najwyżej raz produkując wartość przy pierwszym użyciu. Niestety Scala nie wspiera ewaluacji na żądanie dla parametrów metod.

Scalaz formalizuje te trzy strategie ewaluacji za pomocą ADT

  sealed abstract class Name[A] {
    def value: A
  }
  object Name {
    def apply[A](a: =>A) = new Name[A] { def value = a }
    ...
  }
  
  sealed abstract class Need[A] extends Name[A]
  object Need {
    def apply[A](a: =>A): Need[A] = new Need[A] {
      private lazy val value0: A = a
      def value = value0
    }
    ...
  }
  
  final case class Value[A](value: A) extends Need[A]

Najsłabszą formą ewaluacji jest Name, która nie daje żadnych gwarancji obliczeniowych. Następna jest Need gwarantująca ewaluację najwyżej raz (at most once). Value jest obliczana przed utworzeniem, gwarantując tym samym ewaluację dokładnie raz (exactly once).

Gdybyśmy chcieli być pedantyczni, moglibyśmy wrócić do wszystkich typeklas, które poznaliśmy do tej pory i zamienić przyjmowane parametry w ich metodach na Name, Need i Value. Zamiast tego możemy też po prostu założyć, że normalne parametry mogą być zawsze opakowane w Value, a te przekazywane przez nazwę w Name.

Gdy piszemy czyste programy, możemy śmiało zamienić dowolne Name na Need lub Value, i vice versa, bez zmieniania poprawności programu. To jest właśnie esencja transparencji referencyjnej: zdolność do zamiany obliczeń na wartość wynikową lub wartości na obliczenia potrzebne do jej uzyskania.

W programowaniu funkcyjnym prawie zawsze potrzebujemy Value lub Need (znane też jako parametry ścisłe i leniwe), ale nie mamy zbyt wiele pożytku z Name. Ponieważ na poziomie języka nie mamy bezpośredniego wsparcia dla leniwych parametrów, metody często przyjmują wartości przez nazwę, a następnie konwertują je do Need, zwiększając tym samym wydajność.

Name dostarcza instancje poniższych typeklas:

• Monad
• Comonad
• Traverse1
• Align
• Zip / Unzip / Cozip

6.3 Memoizacja

Scalaz potrafi memoizować funkcje za pomocą typu Memo, który nie daje żadnych gwarancji co do ewaluacji z powodu dużej gamy różniących się implementacji:

  sealed abstract class Memo[K, V] {
    def apply(z: K => V): K => V
  }
  object Memo {
    def memo[K, V](f: (K => V) => K => V): Memo[K, V]
  
    def nilMemo[K, V]: Memo[K, V] = memo[K, V](identity)
  
    def arrayMemo[V >: Null : ClassTag](n: Int): Memo[Int, V] = ...
    def doubleArrayMemo(n: Int, sentinel: Double = 0.0): Memo[Int, Double] = ...
  
    def immutableHashMapMemo[K, V]: Memo[K, V] = ...
    def immutableTreeMapMemo[K: scala.Ordering, V]: Memo[K, V] = ...
  }

Metoda memo pozwala nam na tworzenie własnych implementacji Memo. nilMemo nie memoizuje w ogóle, a więc funkcja wykonywana jest za każdym wywołaniem. Pozostałe implementacje przechwytują wywołania funkcji i cache’ują wynik przy użyciu kolekcji z biblioteki standardowej.

Aby wykorzystać Memo, wystarczy, że opakujemy naszą funkcję z użyciem wybranej implementacji, a następnie używać będziemy zwróconej nam funkcji zamiast tej oryginalnej:

  scala> def foo(n: Int): String = {
           println("running")
           if (n > 10) "wibble" else "wobble"
         }
  
  scala> val mem = Memo.arrayMemo[String](100)
         val mfoo = mem(foo)
  
  scala> mfoo(1)
  running // evaluated
  res: String = wobble
  
  scala> mfoo(1)
  res: String = wobble // memoised

Jeśli funkcja przyjmuje więcej niż jeden argument, musimy wywołać na niej tupled, konwertując ją tym samym do jednoargumentowej funkcji przyjmującej tuple.

  scala> def bar(n: Int, m: Int): String = "hello"
         val mem = Memo.immutableHashMapMemo[(Int, Int), String]
         val mbar = mem((bar _).tupled)
  
  scala> mbar((1, 2))
  res: String = "hello"

Memo jest traktowany w specjalny sposób i typowe reguły czystości są nieco osłabione przy jego implementacji. Aby nosić miano czystego wystarczy, aby wykonanie K => V było referencyjnie transparentne. Przy implementacji możemy używać mutowalnych struktur danych lub wykonywać operacje I/O, np., aby uzyskać LRU lub rozproszony cache bez deklarowania efektów w sygnaturze typu. Inne funkcyjne języki programowania udostępniają automatyczną memoizację zarządzaną przez środowisko uruchomieniowe, Memo to nasz sposób na dodanie podobnej funkcjonalności do JVMa, niestety jedynie jako “opt-in”.

6.4 Tagowanie

W podrozdziale wprowadzającym Monoid stworzyliśmy Monoid[TradeTemplate] jednocześnie uświadamiając sobie, że domyślna instancja Monoid[Option[A]] ze Scalaz nie robi tego, czego byśmy od niej oczekiwali. Nie jest to jednak przeoczenie ze strony Scalaz: często będziemy napotykali sytuację, w której dany typ danych może mieć wiele poprawnych implementacji danej typeklasy, a ta domyślna nie robi tego, czego byśmy chcieli lub w ogóle nie jest zdefiniowana.

Najprostszym przykładem jest Monoid[Boolean] (koniunkcja && vs alternatywa ||) lub Monoid[Int] (mnożenie vs dodawanie).

Aby zaimplementować Monoid[TradeTemplate] musieliśmy albo zaburzyć spójność typeklas, albo użyć innej typeklasy niż Monoid.

scalaz.Tag został zaprojektowany jako rozwiązanie tego problemu, ale bez sprowadzania ograniczeń, które napotkaliśmy.

Definicja jest dość pokrzywiona, ale składnia dostarczana użytkownikowi jest bardzo przejrzysta. Oto w jaki sposób możemy oszukać kompilator i zdefiniować typ A @@ T, który zostanie uproszczony do A w czasie wykonania programu:

  type @@[A, T] = Tag.k.@@[A, T]
  
  object Tag {
    @inline val k: TagKind = IdTagKind
    @inline def apply[A, T](a: A): A @@ T = k(a)
    ...
  
    final class TagOf[T] private[Tag]() { ... }
    def of[T]: TagOf[T] = new TagOf[T]
  }
  sealed abstract class TagKind {
    type @@[A, T]
    def apply[A, T](a: A): A @@ T
    ...
  }
  private[scalaz] object IdTagKind extends TagKind {
    type @@[A, T] = A
    @inline override def apply[A, T](a: A): A = a
    ...
  }

Kilka użytecznych tagów znajdziemy w obiekcie Tags:

  object Tags {
    sealed trait First
    val First = Tag.of[First]
  
    sealed trait Last
    val Last = Tag.of[Last]
  
    sealed trait Multiplication
    val Multiplication = Tag.of[Multiplication]
  
    sealed trait Disjunction
    val Disjunction = Tag.of[Disjunction]
  
    sealed trait Conjunction
    val Conjunction = Tag.of[Conjunction]
  
    ...
  }

First i Last służą do wyboru między instancjami Monoidu, które wybierają odpowiednio pierwszy lub ostatni operand. Za pomocą Multiplication możemy zmienić zachowanie Monoidu dla typów liczbowych z dodawania na mnożenie. Disjunction i Conjunction pozwalają wybrać między && i || dla typu Boolean.

W naszym przykładzie definiującym TradeTemplate, zamiast Option[Currency] mogliśmy użyć Option[Currency] @@ Tags.Last. W rzeczywistości jest to przypadek tak częsty, że mogliśmy użyć wbudowanego aliasu LastOption

  type LastOption[A] = Option[A] @@ Tags.Last

i tym samym sprawić, że implementacja Monoid[TradeTemplate] będzie znacznie czystsza.

  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: LastOption[Currency],
    otc: LastOption[Boolean]
  )
  object TradeTemplate {
    implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
      (a, b) =>
        TradeTemplate(a.payments |+| b.payments,
                      a.ccy |+| b.ccy,
                      a.otc |+| b.otc),
        TradeTemplate(Nil, Tag(None), Tag(None))
    )
  }

Tworzymy wartości typu LastOption poprzez zaaplikowanie Tag na instancji Option. W tym wypadku wołamy Tag(None).

W rozdziale o derywacji typeklas pójdziemy o jeden krok dalej i stworzymy monoid automatycznie.

Kuszącym może wydać się pomysł użycia Tagów do oznaczania danych na potrzeby walidacji (np. String @@ PersonName), ale należy oprzeć się tym pokusom, gdyż za takim oznaczeniem nie stoją żadne weryfikacje wartości używanych w czasie wykonania. Tag powinien być używany tylko do selekcji typeklas, a do ograniczania możliwych wartości dużo lepiej jest użyć biblioteki Refined, którą poznaliśmy w Rozdziale 4.

6.5 Transformacje naturalne

Funkcja z jednego typu w drugi zapisywana jest w Scali jako A => B, ale jest to tylko syntax sugar dla typu Function1[A, B]. Scalaz dostarcza podobny mechanizm w formie F ~> G dla funkcji z konstruktora typu F[_] do G[_].

Intancje typu F ~> G nazywamy transformacjami naturalnymi (natural transformation) i mówimy, że są one uniwersalnie kwantyfikowane, ponieważ nie ma dla nich znaczenia zawartość F[_].

  type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]
  trait NaturalTransformation[-F[_], +G[_]] {
    def apply[A](fa: F[A]): G[A]
  
    def compose[E[_]](f: E ~> F): E ~> G = ...
    def andThen[H[_]](f: G ~> H): F ~> H = ...
  }

Przykładem transformacji naturalnej jest funkcja, która konwertuje IList na List

  scala> val convert = new (IList ~> List) {
           def apply[A](fa: IList[A]): List[A] = fa.toList
         }
  
  scala> convert(IList(1, 2, 3))
  res: List[Int] = List(1, 2, 3)

Lub, bardziej zwięźle, korzystając ze składni udostępnianej przez kind-projector:

  scala> val convert = λ[IList ~> List](_.toList)
  
  scala> val convert = Lambda[IList ~> List](_.toList)

Jednak w codziennej pracy zdecydowanie częściej będziemy używać transformacji naturalnych do konwersji między algebrami. Możemy, na przykład, chcieć zaimplementować naszą algebrę Machines, służącą do komunikacji z Google Container Engine, za pomocą gotowej, zewnętrznej algebry BigMachines. Zamiast zmieniać naszą logikę biznesową i wszystkie testy, tak aby używały nowej algebry, możemy spróbować napisać transformację naturalną BigMachines ~> Machines. Powrócimy do tego pomysłu w rozdziale o Zaawansowanych Monadach.

6.6 Isomorphism

Czasami mamy do czynienia z dwoma typami, które tak naprawdę są dokładnie tym samym. Powoduje to problemy z kompatybilnością, ponieważ kompilator tego nie wie. Najczęściej takie sytuacje mają miejsce, gdy chcemy użyć zewnętrznych bibliotek, które definiują coś, co już mamy w naszym kodzie.

W takich właśnie okolicznościach z pomocą przychodzi Isomorphism, który definiuje relację równoznaczności między dwoma typami. Ma on 3 warianty dla typów o różnym kształcie:

  object Isomorphism {
    trait Iso[Arr[_, _], A, B] {
      def to: Arr[A, B]
      def from: Arr[B, A]
    }
    type IsoSet[A, B] = Iso[Function1, A, B]
    type <=>[A, B] = IsoSet[A, B]
    object IsoSet {
      def apply[A, B](to: A => B, from: B => A): A <=> B = ...
    }
  
    trait Iso2[Arr[_[_], _[_]], F[_], G[_]] {
      def to: Arr[F, G]
      def from: Arr[G, F]
    }
    type IsoFunctor[F[_], G[_]] = Iso2[NaturalTransformation, F, G]
    type <~>[F[_], G[_]] = IsoFunctor[F, G]
    object IsoFunctor {
      def apply[F[_], G[_]](to: F ~> G, from: G ~> F): F <~> G = ...
    }
  
    trait Iso3[Arr[_[_, _], _[_, _]], F[_, _], G[_, _]] {
      def to: Arr[F, G]
      def from: Arr[G, F]
    }
    type IsoBifunctor[F[_, _], G[_, _]] = Iso3[~~>, F, G]
    type <~~>[F[_, _], G[_, _]] = IsoBifunctor[F, G]
  
    ...
  }

Aliasy typów IsoSet, IsoFunctor i IsoBiFunctor pokrywają najczęstsze przypadki: zwykłe funkcje, transformacje naturalne i binaturalne. Funkcje pomocnicze pozwalają nam generować instancje Iso z gotowych funkcji lub transformacji, ale często łatwiej jest użyć do tego klas Template. Na przykład:

  val listIListIso: List <~> IList =
    new IsoFunctorTemplate[List, IList] {
      def to[A](fa: List[A]) = fromList(fa)
      def from[A](fa: IList[A]) = fa.toList
    }

Jeśli wprowadzimy izomorfizm, możemy wygenerować wiele standardowych typeklas. Dla przykładu

  trait IsomorphismSemigroup[F, G] extends Semigroup[F] {
    implicit def G: Semigroup[G]
    def iso: F <=> G
    def append(f1: F, f2: =>F): F = iso.from(G.append(iso.to(f1), iso.to(f2)))
  }

pozwala nam wyderywować Semigroup[F] dla typu F, jeśli mamy F <=> G oraz Semigroup[G]. Niemal wszystkie typeklasy w hierarchii mają wariant dla typów izomorficznych. Jeśli złapiemy się na kopiowaniu implementacji danej typeklasy, warto rozważyć zdefiniowanie Isomorphismu.

6.7 Kontenery

6.7.1 Maybe

Widzieliśmy już Maybe, Scalazowe ulepszenie scala.Option. Jest to ulepszenie dzięki swojej inwariancji oraz braku jakichkolwiek nieczystych metod, taki jak Option.get, które mogą rzucać wyjątki.

Zazwyczaj typ ten używany jest do reprezentacji rzeczy, które mogą być nieobecne, bez podawania żadnej przyczyny ani wyjaśnienia dla tej nieobecności.

  sealed abstract class Maybe[A] { ... }
  object Maybe {
    final case class Empty[A]()    extends Maybe[A]
    final case class Just[A](a: A) extends Maybe[A]
  
    def empty[A]: Maybe[A] = Empty()
    def just[A](a: A): Maybe[A] = Just(a)
  
    def fromOption[A](oa: Option[A]): Maybe[A] = ...
    def fromNullable[A](a: A): Maybe[A] = if (null == a) empty else just(a)
    ...
  }

.empty i .just są lepsze niż tworzenie Just i Maybe bezpośrednio, ponieważ zwracają Maybe, pomagając tym samym w inferencji typów. Takie podejście często nazywane jest zwracaniem typu sumy (sum type), a więc mimo posiadania wielu implementacji zapieczętowanego traita (sealed trait) nigdy nie używamy konkretnych podtypów w sygnaturach metod.

Pomocnicza klasa niejawna pozwala nam zawołać .just na dowolnej wartości i uzyskać Maybe.

  implicit class MaybeOps[A](self: A) {
    def just: Maybe[A] = Maybe.just(self)
  }

Maybe posiada instancje wszystkich poniższych typeklas

• Align
• Traverse
• MonadPlus / IsEmpty
• Cobind
• Cozip / Zip / Unzip
• Optional

oraz deleguje implementację poniższych do instancji dla typu A

• Monoid / Band
• Equal / Order / Show

Dodatkowo, Maybe oferuje funkcjonalności niedostępne w żadnej typeklasie

  sealed abstract class Maybe[A] {
    def cata[B](f: A => B, b: =>B): B = this match {
      case Just(a) => f(a)
      case Empty() => b
    }
  
    def |(a: =>A): A = cata(identity, a)
    def toLeft[B](b: =>B): A \/ B = cata(\/.left, \/-(b))
    def toRight[B](b: =>B): B \/ A = cata(\/.right, -\/(b))
    def <\/[B](b: =>B): A \/ B = toLeft(b)
    def \/>[B](b: =>B): B \/ A = toRight(b)
  
    def orZero(implicit A: Monoid[A]): A = getOrElse(A.zero)
    def orEmpty[F[_]: Applicative: PlusEmpty]: F[A] =
      cata(Applicative[F].point(_), PlusEmpty[F].empty)
    ...
  }

.cata to zwięźlejsza alternatywa dla .map(f).getOrElse(b) dostępna również pod postacią | jeśli f to identity (co jest równoznaczne z .getOrElse).

.toLeft i .toRight oraz ich aliasy symbolicznie tworzą dysjunkcje (opisane w następnym podrozdziale), przyjmując jako parametr wartość używaną w przypadku napotkania Empty.

.orZero używa instancji typeklasy Monoid do zdobycia wartości domyślnej.

.orEmpty używa ApplicativePlus, aby stworzyć jednoelementowy lub pusty kontener. Pamiętajmy, że podobną funkcjonalność dla kolekcji udostępnia nam .to pochodzące z Foldable.

  scala> 1.just.orZero
  res: Int = 1
  
  scala> Maybe.empty[Int].orZero
  res: Int = 0
  
  scala> Maybe.empty[Int].orEmpty[IList]
  res: IList[Int] = []
  
  scala> 1.just.orEmpty[IList]
  res: IList[Int] = [1]
  
  scala> 1.just.to[List] // from Foldable
  res: List[Int] = List(1)

6.7.2 Either

Typ ulepszający scala.Either w Scalaz jest symbolem, ale przyjęło się nazywać go either lub Disjunction.

  sealed abstract class \/[+A, +B] { ... }
  final case class -\/[+A](a: A) extends (A \/ Nothing)
  final case class \/-[+B](b: B) extends (Nothing \/ B)
  
  type Disjunction[+A, +B] = \/[A, B]
  
  object \/ {
    def left [A, B]: A => A \/ B = -\/(_)
    def right[A, B]: B => A \/ B = \/-(_)
  
    def fromEither[A, B](e: Either[A, B]): A \/ B = ...
    ...
  }

z odpowiednią składnią

  implicit class EitherOps[A](val self: A) {
    final def left [B]: (A \/ B) = -\/(self)
    final def right[B]: (B \/ A) = \/-(self)
  }

pozwalającą na łatwe tworzenie wartości. Zauważ, że te metody przyjmują typ drugiej strony jako parametr. A więc jeśli chcesz stworzyć String \/ Int mając Int, wołając .right, musisz przekazać String.

  scala> 1.right[String]
  res: String \/ Int = \/-(1)
  
  scala> "hello".left[Int]
  res: String \/ Int = -\/(hello)

Symboliczna natura \/ sprawia, że dobrze się go czyta, gdy użyty jest jako infiks. Pamiętaj, że typy symboliczne w Scali wiążą argumenty od lewej, a więc zagnieżdżone \/ muszą być ujęte w nawiasy.

\/ posiada prawostronne (co oznacza, że flatMap wykonywany jest na \/-) instancje typeklas:

• Monad / MonadError
• Traverse / Bitraverse
• Plus
• Optional
• Cozip

oraz zależne od zawartości

• Equal / Order
• Semigroup / Monoid / Band

Dodatkowo dostajemy kilka niestandardowych metod

  sealed abstract class \/[+A, +B] { self =>
    def fold[X](l: A => X, r: B => X): X = self match {
      case -\/(a) => l(a)
      case \/-(b) => r(b)
    }
  
    def swap: (B \/ A) = self match {
      case -\/(a) => \/-(a)
      case \/-(b) => -\/(b)
    }
  
    def |[BB >: B](x: =>BB): BB = getOrElse(x) // Optional[_]
    def |||[C, BB >: B](x: =>C \/ BB): C \/ BB = orElse(x) // Optional[_]
  
    def +++[AA >: A: Semigroup, BB >: B: Semigroup](x: =>AA \/ BB): AA \/ BB = ...
  
    def toEither: Either[A, B] = ...
  
    final class SwitchingDisjunction[X](right: =>X) {
      def <<?:(left: =>X): X = ...
    }
    def :?>>[X](right: =>X) = new SwitchingDisjunction[X](right)
    ...
  }

.fold przypomina Maybe.cata i wymaga, aby obie strony zostały przemapowane do tego samego typu.

.swap zamienia strony miejscami, lewa na prawo, prawa na lewo.

Alias | na getOrElse jest podobny do tego w Maybe. Dostajemy też ||| jako alias na orElse.

+++ pozwala na łączenie dysjunkcji, priorytetyzując te, które wypełnione są po lewej stronie.

• right(v1) +++ right(v2) gives right(v1 |+| v2)
• right(v1) +++ left (v2) gives left (v2)
• left (v1) +++ right(v2) gives left (v1)
• left (v1) +++ left (v2) gives left (v1 |+| v2)

.toEither zapewnia kompatybilność z biblioteką standardową.

Połączenie :?>> i <<?: pozwala w wygodny sposób zignorować zawartość \/ wybierając jednocześnie nową wartość zależnie od jego typu.

  scala> 1 <<?: foo :?>> 2
  res: Int = 2 // foo is a \/-
  
  scala> 1 <<?: foo.swap :?>> 2
  res: Int = 1

6.7.3 Validation

Na pierwszy rzut oka typ Validation (zaliasowany jako \?/ czyli szczęśliwy Elvis) wydaje się być klonem Disjunction:

  sealed abstract class Validation[+E, +A] { ... }
  final case class Success[A](a: A) extends Validation[Nothing, A]
  final case class Failure[E](e: E) extends Validation[E, Nothing]
  
  type ValidationNel[E, +X] = Validation[NonEmptyList[E], X]
  
  object Validation {
    type \?/[+E, +A] = Validation[E, A]
  
    def success[E, A]: A => Validation[E, A] = Success(_)
    def failure[E, A]: E => Validation[E, A] = Failure(_)
    def failureNel[E, A](e: E): ValidationNel[E, A] = Failure(NonEmptyList(e))
  
    def lift[E, A](a: A)(f: A => Boolean, fail: E): Validation[E, A] = ...
    def liftNel[E, A](a: A)(f: A => Boolean, fail: E): ValidationNel[E, A] = ...
    def fromEither[E, A](e: Either[E, A]): Validation[E, A] = ...
    ...
  }

Z pomocną składnią

  implicit class ValidationOps[A](self: A) {
    def success[X]: Validation[X, A] = Validation.success[X, A](self)
    def successNel[X]: ValidationNel[X, A] = success
    def failure[X]: Validation[A, X] = Validation.failure[A, X](self)
    def failureNel[X]: ValidationNel[A, X] = Validation.failureNel[A, X](self)
  }

Jednak sama struktura danych to nie wszystko. Validation celowo nie posiada instancji Monad, ograniczając się do:

• Applicative
• Traverse / Bitraverse
• Cozip
• Plus
• Optional

oraz zależnych od zawartości:

• Equal / Order
• Show
• Semigroup / Monoid

Dużą zaletą ograniczenia się do Applicative jest to, że Validation używany jest wyraźnie w sytuacjach, w których chcemy zebrać wszystkie napotkane problemy, natomiast Disjunction zatrzymuje się przy pierwszym i ignoruje pozostałe. Aby wesprzeć akumulacje błędów, mamy do dyspozycji ValidationNel, czyli Validation z NonEmptyList[E] po stronie błędów.

Rozważmy wykonanie walidacji danych pochodzących od użytkownika za pomocą Disjunction i flatMap:

  scala> :paste
         final case class Credentials(user: Username, name: Fullname)
         final case class Username(value: String) extends AnyVal
         final case class Fullname(value: String) extends AnyVal
  
         def username(in: String): String \/ Username =
           if (in.isEmpty) "empty username".left
           else if (in.contains(" ")) "username contains spaces".left
           else Username(in).right
  
         def realname(in: String): String \/ Fullname =
           if (in.isEmpty) "empty real name".left
           else Fullname(in).right
  
  scala> for {
           u <- username("sam halliday")
           r <- realname("")
         } yield Credentials(u, r)
  res = -\/(username contains spaces)

Jeśli użyjemy |@|

  scala> (username("sam halliday") |@| realname("")) (Credentials.apply)
  res = -\/(username contains spaces)

nadal dostaniemy tylko pierwszy błąd. Wynika to z faktu, że Disjunction jest Monadą, a jego metody .applyX muszą być spójne z .flatMap i nie mogą zakładać, że operacje mogą być wykonywane poza kolejnością. Porównajmy to z:

  scala> :paste
         def username(in: String): ValidationNel[String, Username] =
           if (in.isEmpty) "empty username".failureNel
           else if (in.contains(" ")) "username contains spaces".failureNel
           else Username(in).success
  
         def realname(in: String): ValidationNel[String, Fullname] =
           if (in.isEmpty) "empty real name".failureNel
           else Fullname(in).success
  
  scala> (username("sam halliday") |@| realname("")) (Credentials.apply)
  res = Failure(NonEmpty[username contains spaces,empty real name])

Tym razem dostaliśmy z powrotem wszystkie napotkane błędy!

Validation ma wiele metod analogicznych do tych w Disjunction, takich jak .fold, .swap i +++, plus kilka ekstra:

  sealed abstract class Validation[+E, +A] {
    def append[F >: E: Semigroup, B >: A: Semigroup](x: F \?/ B]): F \?/ B = ...
  
    def disjunction: (E \/ A) = ...
    ...
  }

.append (z aliasem +|+) ma taką samą sygnaturę jak +++, ale preferuje wariant success

• failure(v1) +|+ failure(v2) zwraca failure(v1 |+| v2)
• failure(v1) +|+ success(v2) zwraca success(v2)
• success(v1) +|+ failure(v2) zwraca success(v1)
• success(v1) +|+ success(v2) zwraca success(v1 |+| v2)

.disjunction konwertuje Validated[A, B] do A \/ B. Dysjunkcja ma lustrzane metody .validation i .validationNel, pozwalając tym samym na łatwe przełączanie się między sekwencyjnym i równoległym zbieraniem błędów.

\/ i Validation są bardziej wydajnymi alternatywami dla wyjątków typu checked do walidacji wejścia, unikającymi zbierania śladu stosu (stacktrace). Wymagają one też od użytkownika obsłużenia potencjalnych błędów, sprawiając tym samym, że tworzone systemy są bardziej niezawodne.

6.7.4 These

Napotkaliśmy These, strukturę danych wyrażającą logiczne LUB, kiedy poznawaliśmy Align.

  sealed abstract class \&/[+A, +B] { ... }
  object \&/ {
    type These[A, B] = A \&/ B
  
    final case class This[A](aa: A) extends (A \&/ Nothing)
    final case class That[B](bb: B) extends (Nothing \&/ B)
    final case class Both[A, B](aa: A, bb: B) extends (A \&/ B)
  
    def apply[A, B](a: A, b: B): These[A, B] = Both(a, b)
  }

z metodami upraszczającymi konstrukcję

  implicit class TheseOps[A](self: A) {
    final def wrapThis[B]: A \&/ B = \&/.This(self)
    final def wrapThat[B]: B \&/ A = \&/.That(self)
  }
  implicit class ThesePairOps[A, B](self: (A, B)) {
    final def both: A \&/ B = \&/.Both(self._1, self._2)
  }

These ma instancje typeklas

• Monad
• Bitraverse
• Traverse
• Cobind

oraz zależnie od zawartości

• Semigroup / Monoid / Band
• Equal / Order
• Show

These (\&/) ma też wiele metod, których oczekiwalibyśmy od Disjunction (\/) i Validation (\?/)

  sealed abstract class \&/[+A, +B] {
    def fold[X](s: A => X, t: B => X, q: (A, B) => X): X = ...
    def swap: (B \&/ A) = ...
  
    def append[X >: A: Semigroup, Y >: B: Semigroup](o: =>(X \&/ Y)): X \&/ Y = ...
  
    def &&&[X >: A: Semigroup, C](t: X \&/ C): X \&/ (B, C) = ...
    ...
  }

.append ma 9 możliwych ułożeń i dane nigdy nie są tracone, ponieważ This i That mogą być zawsze zamienione w Both.

.flatMap jest prawostronna (Both i That), przyjmując Semigroupy dla strony lewej (This), tak aby móc połączyć zawartości, zamiast je porzucać. Metoda &&& jest pomocna, gdy chcemy połączyć dwie instancje \&/, tworząc tuple z prawej strony i porzucając tę stronę zupełnie, jeśli nie jest wypełniona w obu instancjach.

Mimo że zwracanie typu \&/ z naszych funkcji jest kuszące, to jego nadużywanie to antywzorzec. Głównym powodem dla używania \&/ jest łączenie i dzielenie potencjalnie nieskończonych strumieni danych w skończonej pamięci. Dlatego też dostajemy do dyspozycji kilka przydatnych funkcji do operowania na EphemeralStream (zaliasowanym tutaj, aby zmieścić się w jednej linii) lub czymkolwiek z instancją MonadPlus

  type EStream[A] = EphemeralStream[A]
  
  object \&/ {
    def concatThisStream[A, B](x: EStream[A \&/ B]): EStream[A] = ...
    def concatThis[F[_]: MonadPlus, A, B](x: F[A \&/ B]): F[A] = ...
  
    def concatThatStream[A, B](x: EStream[A \&/ B]): EStream[B] = ...
    def concatThat[F[_]: MonadPlus, A, B](x: F[A \&/ B]): F[B] = ...
  
    def unalignStream[A, B](x: EStream[A \&/ B]): (EStream[A], EStream[B]) = ...
    def unalign[F[_]: MonadPlus, A, B](x: F[A \&/ B]): (F[A], F[B]) = ...
  
    def merge[A: Semigroup](t: A \&/ A): A = ...
    ...
  }

6.7.5 Either wyższego rodzaju

Typ danych Coproduct (nie mylić z bardziej ogólnym pojęciem koproduktu w ADT) opakowuje Disjunction dla konstruktorów typu:

  final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A]) { ... }
  object Coproduct {
    def leftc[F[_], G[_], A](x: F[A]): Coproduct[F, G, A] = Coproduct(-\/(x))
    def rightc[F[_], G[_], A](x: G[A]): Coproduct[F, G, A] = Coproduct(\/-(x))
    ...
  }

Instancje typeklas po prostu delegują do instancji zdefiniowanych dla F[_] i G[_].

Najpopularniejszym przypadkiem, w którym zastosowanie znajduje Coproduct, to sytuacja, gdy chcemy stworzyć anonimowy koprodukt wielu ADT.

6.7.6 Nie tak szybko

Wbudowane w Scalę tuple oraz podstawowe typy danych takie jak Maybe lub Disjunction są ewaluowane zachłannie (eagerly-evaluated).

Dla wygody zdefiniowane zostały warianty leniwe, mające instancje oczekiwanych typeklas:

  sealed abstract class LazyTuple2[A, B] {
    def _1: A
    def _2: B
  }
  ...
  sealed abstract class LazyTuple4[A, B, C, D] {
    def _1: A
    def _2: B
    def _3: C
    def _4: D
  }
  
  sealed abstract class LazyOption[+A] { ... }
  private final case class LazySome[A](a: () => A) extends LazyOption[A]
  private case object LazyNone extends LazyOption[Nothing]
  
  sealed abstract class LazyEither[+A, +B] { ... }
  private case class LazyLeft[A, B](a: () => A) extends LazyEither[A, B]
  private case class LazyRight[A, B](b: () => B) extends LazyEither[A, B]

Wnikliwy czytelnik zauważy, że przedrostek Lazy jest nie do końca poprawny, a nazwy tych typów danych prawdopodobnie powinny brzmieć: ByNameTupleX, ByNameOption i ByNameEither.

6.7.7 Const

Const, zawdzięczający nazwę angielskiemu constant, jest opakowaniem na wartość typu A, razem z nieużywanym parametrem typu B.

  final case class Const[A, B](getConst: A)

Const dostarcza instancję Applicative[Const[A, ?]] jeśli tylko dostępny jest Monoid[A]:

  implicit def applicative[A: Monoid]: Applicative[Const[A, ?]] =
    new Applicative[Const[A, ?]] {
      def point[B](b: =>B): Const[A, B] =
        Const(Monoid[A].zero)
      def ap[B, C](fa: =>Const[A, B])(fbc: =>Const[A, B => C]): Const[A, C] =
        Const(fbc.getConst |+| fa.getConst)
    }

Najważniejszą własnością tej instancji jest to, że ignoruje parametr B, łącząc wartości typu A, które napotka.

Wracając do naszej aplikacji drone-dynamic-agents, powinniśmy najpierw zrefaktorować plik logic.scala, tak aby używał Applicative zamiast Monad. Poprzednią implementację stworzyliśmy, zanim jeszcze dowiedzieliśmy się, czym jest Applicative. Teraz wiemy jak zrobić to lepiej:

  final class DynAgentsModule[F[_]: Applicative](D: Drone[F], M: Machines[F])
    extends DynAgents[F] {
    ...
    def act(world: WorldView): F[WorldView] = world match {
      case NeedsAgent(node) =>
        M.start(node) >| world.copy(pending = Map(node -> world.time))
  
      case Stale(nodes) =>
        nodes.traverse { node =>
          M.stop(node) >| node
        }.map { stopped =>
          val updates = stopped.strengthR(world.time).toList.toMap
          world.copy(pending = world.pending ++ updates)
        }
  
      case _ => world.pure[F]
    }
    ...
  }

Skoro nasza logika biznesowa wymaga teraz jedynie Applicative, możemy zaimplementować nasz mock F[a] jako Const[String, a]. W każdym z przypadków zwracamy nazwę funkcji, która została wywołana:

  object ConstImpl {
    type F[a] = Const[String, a]
  
    private val D = new Drone[F] {
      def getBacklog: F[Int] = Const("backlog")
      def getAgents: F[Int]  = Const("agents")
    }
  
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]     = Const("alive")
      def getManaged: F[NonEmptyList[MachineNode]] = Const("managed")
      def getTime: F[Epoch]                        = Const("time")
      def start(node: MachineNode): F[Unit]        = Const("start")
      def stop(node: MachineNode): F[Unit]         = Const("stop")
    }
  
    val program = new DynAgentsModule[F](D, M)
  }

Z taką interpretacją naszego programu możemy zweryfikować metody, które są używane:

  it should "call the expected methods" in {
    import ConstImpl._
  
    val alive    = Map(node1 -> time1, node2 -> time1)
    val world    = WorldView(1, 1, managed, alive, Map.empty, time4)
  
    program.act(world).getConst shouldBe "stopstop"
  }

Alternatywnie, moglibyśmy zliczyć ilość wywołań za pomocą Const[Int, ?] lub IMap[String, Int].

W tym teście zrobiliśmy krok dalej poza tradycyjne testowanie z użyciem Mocków. Const pozwolił nam sprawdzić, co zostało wywołane bez dostarczania faktycznej implementacji. Podejście takie jest użyteczne, kiedy specyfikacja wymaga od nas, abyśmy wykonali konkretne wywołania w odpowiedzi na dane wejście. Dodatkowo, osiągnęliśmy to, zachowując pełną zgodność typów.

Idąc dalej tym tokiem myślenia, powiedzmy, że chcielibyśmy monitorować (w środowisku produkcyjnym) węzły, które zatrzymywane są w metodzie act. Możemy stworzyć implementacje Drone i Machines używając Const i zawołać je z naszej opakowanej wersji act

  final class Monitored[U[_]: Functor](program: DynAgents[U]) {
    type F[a] = Const[Set[MachineNode], a]
    private val D = new Drone[F] {
      def getBacklog: F[Int] = Const(Set.empty)
      def getAgents: F[Int]  = Const(Set.empty)
    }
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]     = Const(Set.empty)
      def getManaged: F[NonEmptyList[MachineNode]] = Const(Set.empty)
      def getTime: F[Epoch]                        = Const(Set.empty)
      def start(node: MachineNode): F[Unit]        = Const(Set.empty)
      def stop(node: MachineNode): F[Unit]         = Const(Set(node))
    }
    val monitor = new DynAgentsModule[F](D, M)
  
    def act(world: WorldView): U[(WorldView, Set[MachineNode])] = {
      val stopped = monitor.act(world).getConst
      program.act(world).strengthR(stopped)
    }
  }

Możemy to zrobić, ponieważ monitor jest czysty i uruchomienie go nie produkuje żadnych efektów ubocznych.

Poniższy fragment uruchamia program z ConstImpl, ekstrahując wszystkie wywołania do Machines.stop i zwracając wszystkie zatrzymane węzły razem WoldView.

  it should "monitor stopped nodes" in {
    val underlying = new Mutable(needsAgents).program
  
    val alive = Map(node1 -> time1, node2 -> time1)
    val world = WorldView(1, 1, managed, alive, Map.empty, time4)
    val expected = world.copy(pending = Map(node1 -> time4, node2 -> time4))
  
    val monitored = new Monitored(underlying)
    monitored.act(world) shouldBe (expected -> Set(node1, node2))
  }

Użyliśmy Const, aby zrobić coś, co przypomina niegdyś popularne w Javie Programowanie Aspektowe. Na bazie naszej logiki biznesowej zaimplementowaliśmy monitoring, nie komplikując tej logiki w żaden sposób.

A będzie jeszcze lepiej. Moglibyśmy uruchomić ConstImpl w środowisku produkcyjnym, aby zebrać informacje o tym, co ma zostać zatrzymane, a następnie dostarczyć zoptymalizowaną implementację korzystającą ze specyficznych dla implementacji wywołań batchowych.

Cichym bohaterem tej opowieści jest Applicative, a Const pozwala nam pokazać, co jest dzięki niemu możliwe. Jeśli musielibyśmy zmienić nasz program tak, aby wymagał Monady, nie moglibyśmy wtedy użyć Const, a zamiast tego zmuszeni bylibyśmy do napisania pełnoprawnych mocków, aby zweryfikować jakie funkcje zostały wywołane dla danych argumentów. Reguła Najmniejszej Mocy (Rule of Least Power) wymaga od nas, abyśmy używali Applicative zamiast Monad, kiedy tylko możemy.

6.8 Kolekcje

W przeciwieństwie do Collections API z biblioteki standardowej, Scalaz opisuje zachowanie kolekcji za pomocą hierarchii typeklas, np. Foldable, Traverse, Monoid. Co pozostaje do przeanalizowania, to konkretne struktury danych, ich charakterystyki wydajnościowe i wyspecjalizowane metody.

Ten podrozdział wnika w szczegóły implementacyjne każdego typu danych. Nie musimy zapamiętać wszystkiego, celem jest zrozumieć, jak działa każda ze struktur jedynie w ogólności.

Ponieważ wszystkie kolekcje dostarczają instancje mniej więcej tych samych typeklas, nie będziemy ich powtarzać. W większości przypadków jest to pewna wariacja poniższej listy.

• Monoid
• Traverse / Foldable
• MonadPlus / IsEmpty
• Cobind / Comonad
• Zip / Unzip
• Align
• Equal / Order
• Show

Struktury danych, które nigdy nie są puste dostarczają również

• Traverse1 / Foldable1

oraz Semigroup zamiast Monoid i Plus zamiast IsEmpty.

6.8.1 Listy

Używaliśmy IList[A] i NonEmptyList[A] tyle razy, że powinny już być nam znajome. Reprezentują on ideę klasycznej, jedno-połączeniowej listy:

  sealed abstract class IList[A] {
    def ::(a: A): IList[A] = ...
    def :::(as: IList[A]): IList[A] = ...
    def toList: List[A] = ...
    def toNel: Option[NonEmptyList[A]] = ...
    ...
  }
  final case class INil[A]() extends IList[A]
  final case class ICons[A](head: A, tail: IList[A]) extends IList[A]
  
  final case class NonEmptyList[A](head: A, tail: IList[A]) {
    def <::(b: A): NonEmptyList[A] = nel(b, head :: tail)
    def <:::(bs: IList[A]): NonEmptyList[A] = ...
    ...
  }

Główną zaletą IList nad List jest brak niebezpiecznych metod, takich jak .head (jest ona niebezpieczna, gdyż wyrzuca wyjątek w przypadku pustej kolekcji).

Dodatkowo, IList jest dużo prostsza, gdyż nie jest częścią hierarchii, oraz zużywa zdecydowanie mniej pamięci. Ponadto, List z biblioteki standardowej ma przerażająca implementację, używającą var, aby obejść problemy wydajnościowe:

  package scala.collection.immutable
  
  sealed abstract class List[+A]
    extends AbstractSeq[A]
    with LinearSeq[A]
    with GenericTraversableTemplate[A, List]
    with LinearSeqOptimized[A, List[A]] { ... }
  case object Nil extends List[Nothing] { ... }
  final case class ::[B](
    override val head: B,
    private[scala] var tl: List[B]
  ) extends List[B] { ... }

Tworzenie instancji List wymaga ostrożnej i powolnej, synchronizacji wątków, aby zapewnić bezpieczne publikowanie. IList nie ma żadnych tego typu wymagań, a więc może przegonić List pod względem wydajności.

6.8.2 EphemeralStream

Stream z biblioteki standardowej jest leniwą wersją Listy, ale obarczoną wyciekami pamięci i niebezpiecznymi metodami. EphemeralStream nie przetrzymuje referencji do wyliczonych wartości, łagodząc problemy z przetrzymywaniem pamięci. Jednocześnie pozbawiony jest niebezpiecznych metod, tak, jak Ilist.

  sealed abstract class EphemeralStream[A] {
    def headOption: Option[A]
    def tailOption: Option[EphemeralStream[A]]
    ...
  }
  // private implementations
  object EphemeralStream extends EphemeralStreamInstances {
    type EStream[A] = EphemeralStream[A]
  
    def emptyEphemeralStream[A]: EStream[A] = ...
    def cons[A](a: =>A, as: =>EStream[A]): EStream[A] = ...
    def unfold[A, B](start: =>B)(f: B => Option[(A, B)]): EStream[A] = ...
    def iterate[A](start: A)(f: A => A): EStream[A] = ...
  
    implicit class ConsWrap[A](e: =>EStream[A]) {
      def ##::(h: A): EStream[A] = cons(h, e)
    }
    object ##:: {
      def unapply[A](xs: EStream[A]): Option[(A, EStream[A])] =
        if (xs.isEmpty) None
        else Some((xs.head(), xs.tail()))
    }
    ...
  }

.cons, .unfold i .iterate to mechanizmy do tworzenia strumieni. ##:: (a więc i cons) umieszcza nowy element na początku EStreamu przekazanego przez nazwę. .unfold służy do tworzenia skończonych (lecz potencjalnie nieskończonych) strumieni poprzez ciągłe wywoływanie funkcji f zwracającej następną wartość oraz wejście do swojego kolejnego wywołania. .iterate tworzy nieskończony strumień za pomocą funkcji f wywoływanej na poprzednim jego elemencie.

EStream może pojawiać się w wyrażeniach pattern matchingu z użyciem symbolu ##::.

Mimo że EStream rozwiązuje problem przetrzymywania pamięci, nadal możemy ucierpieć z powodu powolnych wycieków pamięci, jeśli żywa referencja wskazuje na czoło nieskończonego strumienia. Problemy tej natury oraz potrzeba komponowania strumieni wywołujących efekty uboczne są powodem, dla którego istnieje biblioteka fs2.

6.8.3 CorecursiveList

Korekursja (corecursion) ma miejsce, gdy zaczynamy ze stanu bazowego i deterministycznie produkujemy kolejne stany przejściowe, tak jak miało to miejsce w metodzie EphemeralStream.unfold, którą niedawno omawialiśmy:

  def unfold[A, B](b: =>B)(f: B => Option[(A, B)]): EStream[A] = ...

Jest to działanie odwrotne do rekursji, która rozbija dane do stanu bazowego i kończy działanie.

CorecursiveList to struktura danych wyrażająca EphemeralStream.unfold i będąca alternatywą dla EStream, która może być wydajniejsza w niektórych przypadkach:

  sealed abstract class CorecursiveList[A] {
    type S
    def init: S
    def step: S => Maybe[(S, A)]
  }
  
  object CorecursiveList {
    private final case class CorecursiveListImpl[S0, A](
      init: S0,
      step: S0 => Maybe[(S0, A)]
    ) extends CorecursiveList[A] { type S = S0 }
  
    def apply[S, A](init: S)(step: S => Maybe[(S, A)]): CorecursiveList[A] =
      CorecursiveListImpl(init, step)
  
    ...
  }

Korekursja jest przydatna, gdy implementujemy Comonad.cojoin, jak w naszym przykładzie z Hood. CorecursiveList to dobry sposób na wyrażenie nieliniowych równań rekurencyjnych, jak te używane w biologicznych modelach populacji, systemach kontroli, makroekonomii i modelach bankowości inwestycyjnej.

6.8.4 ImmutableArray

Czyli proste opakowanie na mutowalną tablicę (Array) z biblioteki standardowej, ze specjalizacją dla typów prymitywnych:

  sealed abstract class ImmutableArray[+A] {
    def ++[B >: A: ClassTag](o: ImmutableArray[B]): ImmutableArray[B]
    ...
  }
  object ImmutableArray {
    final class StringArray(s: String) extends ImmutableArray[Char] { ... }
    sealed class ImmutableArray1[+A](as: Array[A]) extends ImmutableArray[A] { ... }
    final class ofRef[A <: AnyRef](as: Array[A]) extends ImmutableArray1[A](as)
    ...
    final class ofLong(as: Array[Long]) extends ImmutableArray1[Long](as)
  
    def fromArray[A](x: Array[A]): ImmutableArray[A] = ...
    def fromString(str: String): ImmutableArray[Char] = ...
    ...
  }

Typ Array jest bezkonkurencyjny, jeśli chodzi prędkość odczytu oraz wielkość stosu. Jednak nie występuje tutaj w ogóle współdzielenie strukturalne, więc niemutowalne tablice używane są zwykle tylko, gdy ich zawartość nie ulega zmianie lub jako sposób na bezpieczne owinięcie danych pochodzących z zastanych części systemu.

6.8.5 Dequeue

Dequeue (wymawiana jak talia kart - “deck”) to połączona lista, która pozwala na dodawanie i odczytywanie elementów z przodu (cons) lub tyłu (snoc) w stałym czasie. Usuwania elementów z obu końców jest stałe statystycznie.

  sealed abstract class Dequeue[A] {
    def frontMaybe: Maybe[A]
    def backMaybe: Maybe[A]
  
    def ++(o: Dequeue[A]): Dequeue[A] = ...
    def +:(a: A): Dequeue[A] = cons(a)
    def :+(a: A): Dequeue[A] = snoc(a)
    def cons(a: A): Dequeue[A] = ...
    def snoc(a: A): Dequeue[A] = ...
    def uncons: Maybe[(A, Dequeue[A])] = ...
    def unsnoc: Maybe[(A, Dequeue[A])] = ...
    ...
  }
  private final case class SingletonDequeue[A](single: A) extends Dequeue[A] { ... }
  private final case class FullDequeue[A](
    front: NonEmptyList[A],
    fsize: Int,
    back: NonEmptyList[A],
    backSize: Int) extends Dequeue[A] { ... }
  private final case object EmptyDequeue extends Dequeue[Nothing] { ... }
  
  object Dequeue {
    def empty[A]: Dequeue[A] = EmptyDequeue()
    def apply[A](as: A*): Dequeue[A] = ...
    def fromFoldable[F[_]: Foldable, A](fa: F[A]): Dequeue[A] = ...
    ...
  }

Implementacja bazuje na dwóch listach, jednej dla danych początkowych, drugiej dla końcowych. Rozważmy instancję przechowującą symbole a0, a1, a2, a3, a4, a5, a6

  FullDequeue(
    NonEmptyList('a0, IList('a1, 'a2, 'a3)), 4,
    NonEmptyList('a6, IList('a5, 'a4)), 3)

która może być zobrazowana jako

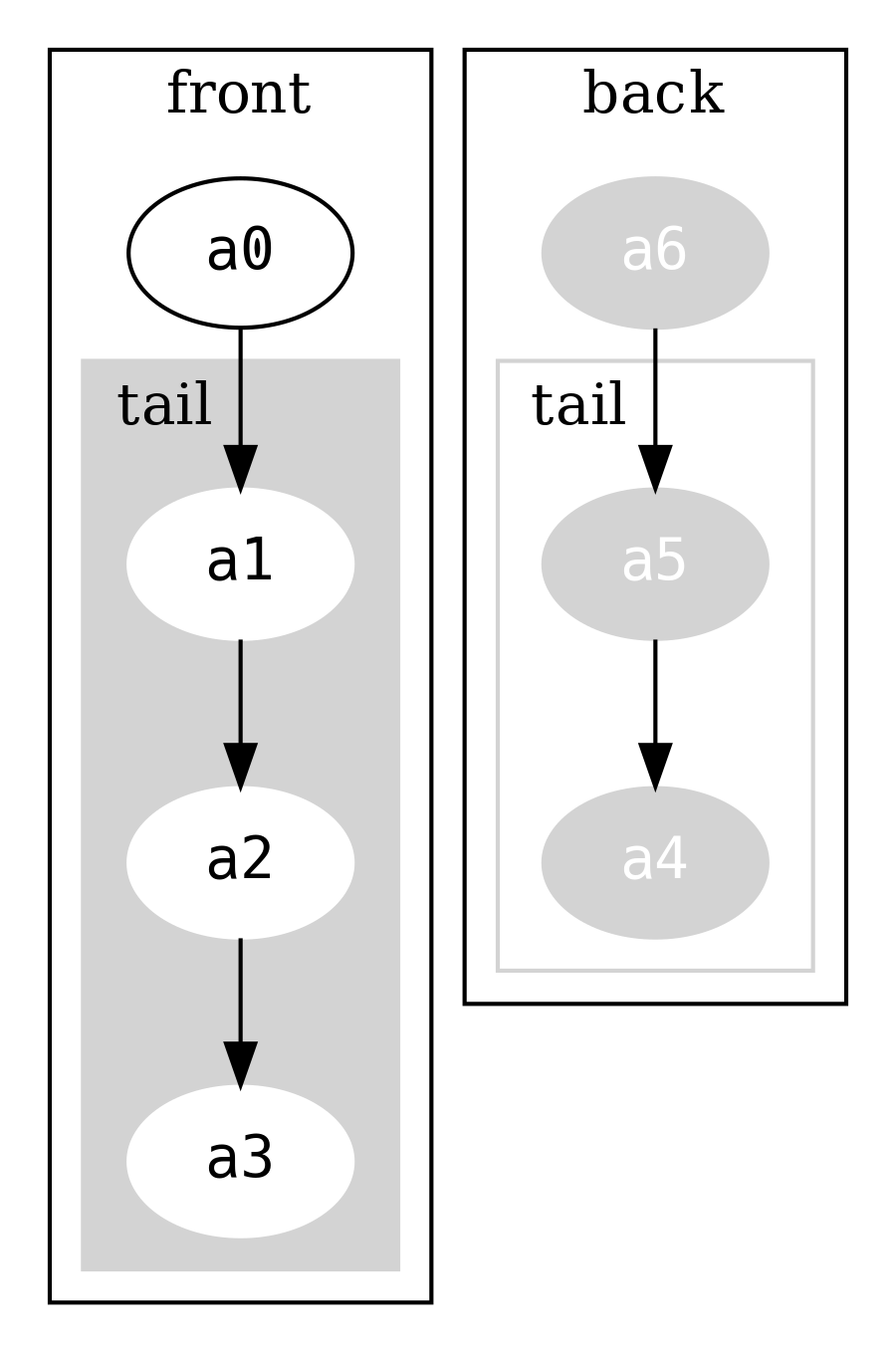
Zauważ, że lista przechowująca back jest w odwróconej kolejności.

Odczyt snoc (element końcowy) to proste spojrzenie na back.head. Dodanie elementu na koniec Dequeue oznacza dodanie go na początek back i stworzenie nowego FullDequeue (co zwiększy backSize o jeden). Prawie cała oryginalna struktura jest współdzielona. Porównaj to z dodaniem nowego elementu na koniec IList, co wymaga stworzenia na nowo całej struktury.

frontSize i backSize są używane do zbalansowywania front i back, tak, aby zawsze były podobnych rozmiarów. Balansowanie oznacza, że niektóre operacje mogą być wolniejsze od innych (np. gdy cała struktura musi być przebudowana), ale ponieważ dzieje się to okazjonalnie możemy ten koszt uśrednić i powiedzieć, że jest stały.

6.8.6 DList

Zwykłe listy mają kiepską wydajność, gdy duże listy są ze sobą łączone. Rozważmy koszt wykonania poniższej operacji:

  ((as ::: bs) ::: (cs ::: ds)) ::: (es ::: (fs ::: gs))

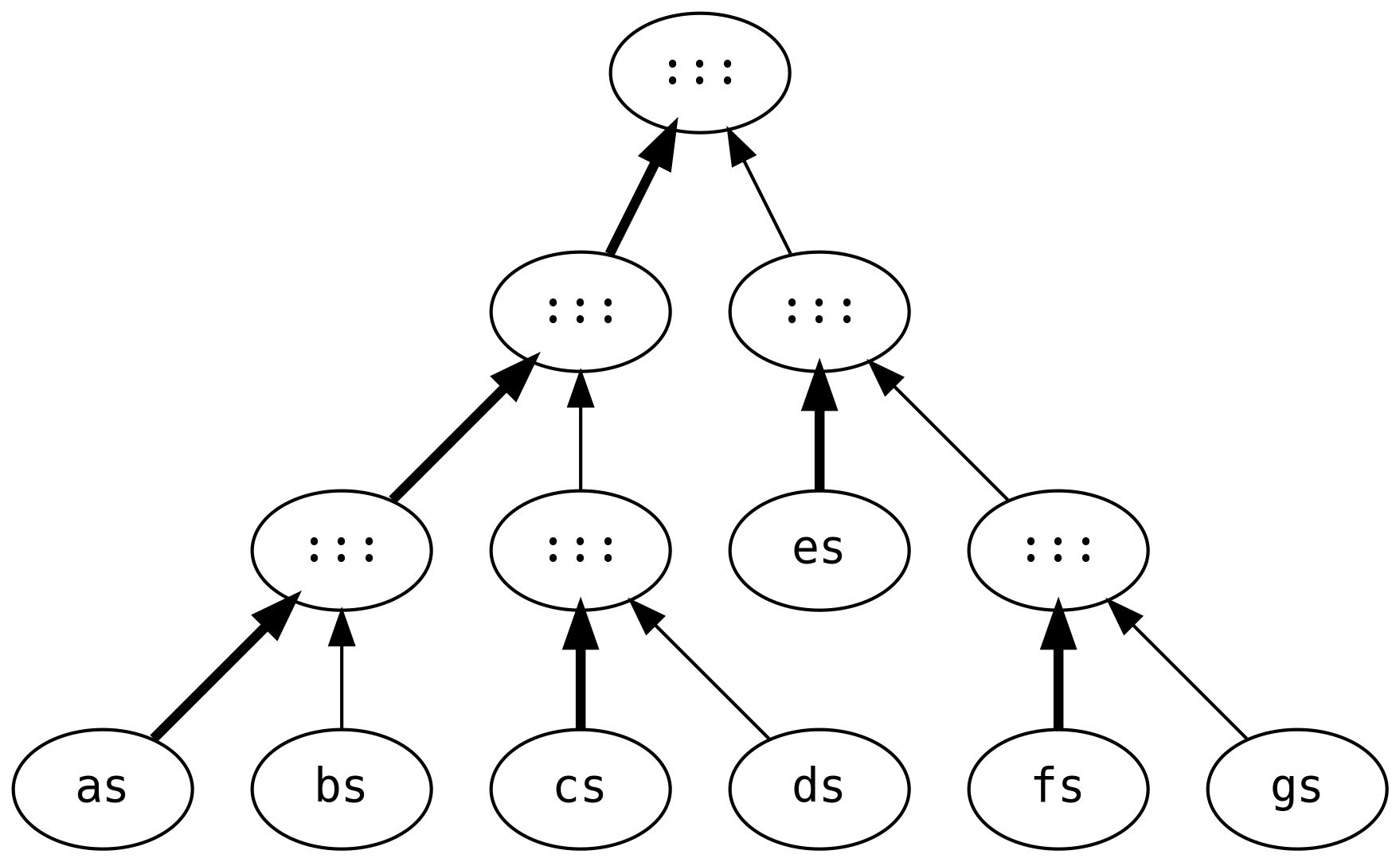
Tworzonych jest 6 list pośrednich, przechodząc i przebudowując każdą z list trzy krotnie (oprócz gs, która jest współdzielona na wszystkich etapach).

DList (od difference list, listy różnic) jest bardziej wydajnym rozwiązaniem dla tego scenariusza. Zamiast wykonywać obliczenia na każdym z etapów, wynik reprezentowany jest jako IList[A] => IList[A].

  final case class DList[A](f: IList[A] => IList[A]) {
    def toIList: IList[A] = f(IList.empty)
    def ++(as: DList[A]): DList[A] = DList(xs => f(as.f(xs)))
    ...
  }
  object DList {
    def fromIList[A](as: IList[A]): DList[A] = DList(xs => as ::: xs)
  }

Odpowiednikiem naszych obliczeń jest (symbole muszą zostać stworzone za pomocą DList.fromIList)

  (((a ++ b) ++ (c ++ d)) ++ (e ++ (f ++ g))).toIList

gdzie praca podzielona jest na prawostronne (czyli szybkie) złączenia

  (as ::: (bs ::: (cs ::: (ds ::: (es ::: (fs ::: gs))))))

wykorzystując szybki konstruktor na IList.

Jak zawsze, nie ma nic za darmo. Występuje tu narzut związany z alokacją pamięci, który może spowolnić nasz kod, jeśli ten i tak zakładał prawostronne złączenia. Największe przyspieszenie uzyskamy, gdy operacje są lewostronne, np.:

  ((((((as ::: bs) ::: cs) ::: ds) ::: es) ::: fs) ::: gs)

Lista różnic cierpi z powodu kiepskiego marketingu. Najprawdopodobniej znalazłaby się w bibliotece standardowej, gdyby tylko nazywała się ListBuilderFactory.

6.8.7 ISet

Struktury drzewiaste są doskonałe do przechowywania uporządkowanych danych, tak aby każdy węzeł binarny przechowywał elementy od niego mniejsze w jednej gałęzi, a większe w drugiej. Jednak naiwna implementacja takiej struktury może w łatwy sposób stać się niesymetryczna, gdyż symetria zależeć będzie od kolejności dodawanie elementów. Utrzymywanie perfekcyjnie zbalansowanego drzewa jest możliwe, ale jednocześnie niewiarygodnie nieefektywne, ponieważ każde wstawienie elementu do drzewa powodowałoby jego pełne przebudowanie.

ISet to implementacja drzewa z ograniczoną równowagą (bounded balance), co oznacza, że jest ono zrównoważone w przybliżeniu, używając size każdej gałęzi do równoważenia węzła.

  sealed abstract class ISet[A] {
    val size: Int = this match {
      case Tip()        => 0
      case Bin(_, l, r) => 1 + l.size + r.size
    }
    ...
  }
  object ISet {
    private final case class Tip[A]() extends ISet[A]
    private final case class Bin[A](a: A, l: ISet[A], r: ISet[A]) extends ISet[A]
  
    def empty[A]: ISet[A] = Tip()
    def singleton[A](x: A): ISet[A] = Bin(x, Tip(), Tip())
    def fromFoldable[F[_]: Foldable, A: Order](xs: F[A]): ISet[A] =
      xs.foldLeft(empty[A])((a, b) => a insert b)
    ...
  }

ISet wymaga, aby A miało instancję typeklasy Order oraz musi ona pozostawać taka sama pomiędzy wywołaniami, gdyż inaczej zaburzone zostaną wewnętrzne założenia, prowadząc tym samym do uszkodzenia danych. Innymi słowy, zakładamy spójność typeklas, a więc dla dowolnego A istnieje tylko jedna instancja Order[A].

ADT ISetu niestety pozwala na wyrażenie niepoprawnych drzew. Staramy się pisać ADT tak, aby w pełni opisywały to, co jest i nie jest możliwe poprzez restrykcję typów, ale nie zawsze jest to możliwe. Zamiast tego Tip i Bin są prywatne, powstrzymując użytkowników przed przypadkowym niepoprawnych drzew. .insert jest jedynym sposobem na konstrukcję drzew, definiując tym samym to, jak wygląda poprawna jego forma.

  sealed abstract class ISet[A] {
    ...
    def contains(x: A)(implicit o: Order[A]): Boolean = ...
    def union(other: ISet[A])(implicit o: Order[A]): ISet[A] = ...
    def delete(x: A)(implicit o: Order[A]): ISet[A] = ...
  
    def insert(x: A)(implicit o: Order[A]): ISet[A] = this match {
      case Tip() => ISet.singleton(x)
      case self @ Bin(y, l, r) => o.order(x, y) match {
        case LT => balanceL(y, l.insert(x), r)
        case GT => balanceR(y, l, r.insert(x))
        case EQ => self
      }
    }
    ...
  }

Wewnętrzne metody .balanceL i .balanceR są swoimi lustrzanymi odbiciami, a więc przestudiujemy jedynie .balanceL, która jest wywoływana, gdy dodawana wartość jest mniejsza niż aktualny węzeł. Jest ona również wołana przez metodę .delete.

  def balanceL[A](y: A, left: ISet[A], right: ISet[A]): ISet[A] = (left, right) match {
  ...

Równoważenie wymaga, abyśmy sklasyfikowali scenariusze, które mogą się zdarzyć. Przejdziemy przez nie kolejno, wizualizując (y, left, right) po lewej stronie i wersją zbalansowaną (znaną tez jako drzewo obrócone, rotated tree) po prawej.

• wypełnione koła obrazują Tip
• trzy kolumny to left | value | right pochodzące z Bin
• diamenty wizualizują dowolny ISet

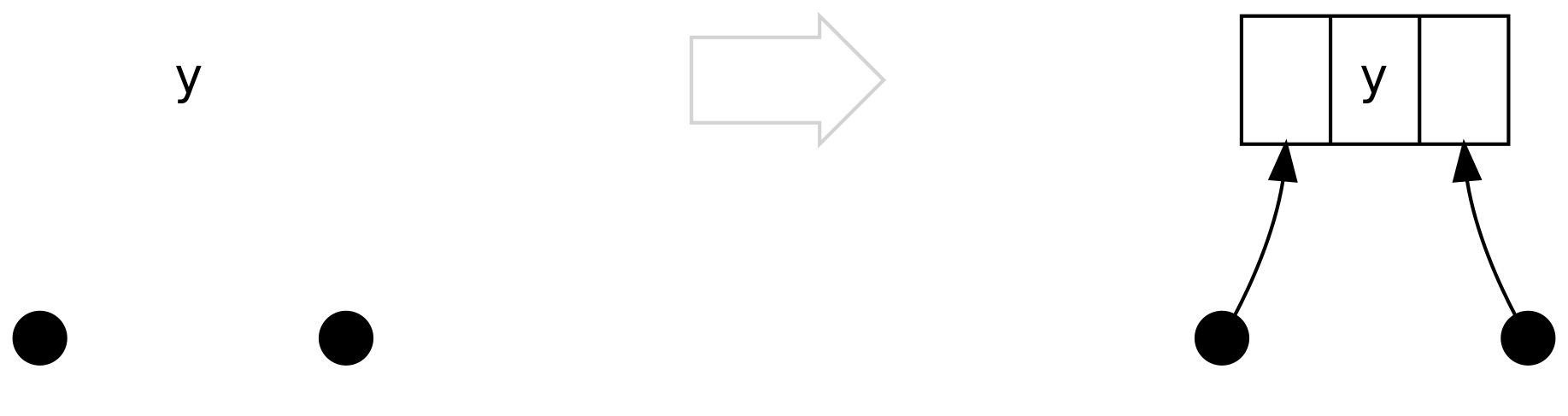
Pierwszy scenariusz jest trywialny i zachodzi, gdy obie strony to Tipy. Nigdy nie napotkamy tego scenariusza, wykonując .insert, ale może on wystąpić przy .delete

  case (Tip(), Tip()) => singleton(y)

Drugi przypadek ma miejsce, kiedy lewa strona to Bin zawierający jedynie Tip. Nie musimy nic równoważyć, dodajemy jedynie oczywiste połączenie:

  case (Bin(lx, Tip(), Tip()), Tip()) => Bin(y, left, Tip())

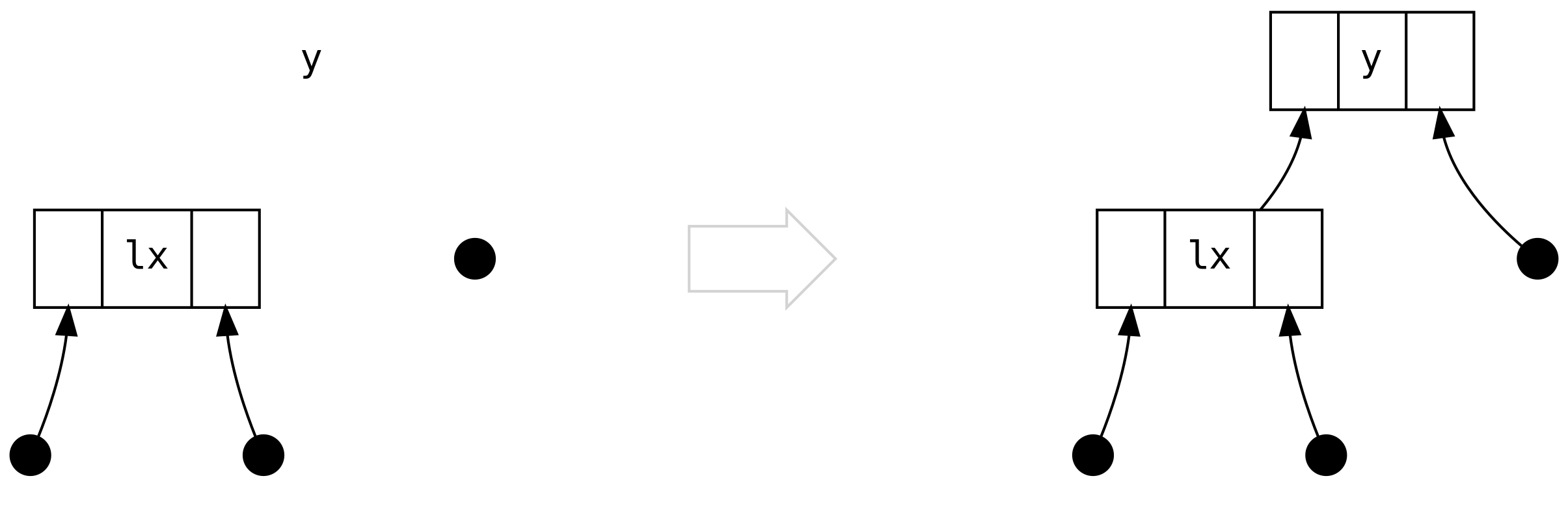
Przy trzecim scenariuszu zaczyna robić się interesująco: lewa strona to Bin zawierający Bin po swojej prawej stronie.

  case (Bin(lx, Tip(), Bin(lrx, _, _)), Tip()) =>
    Bin(lrx, singleton(lx), singleton(y))

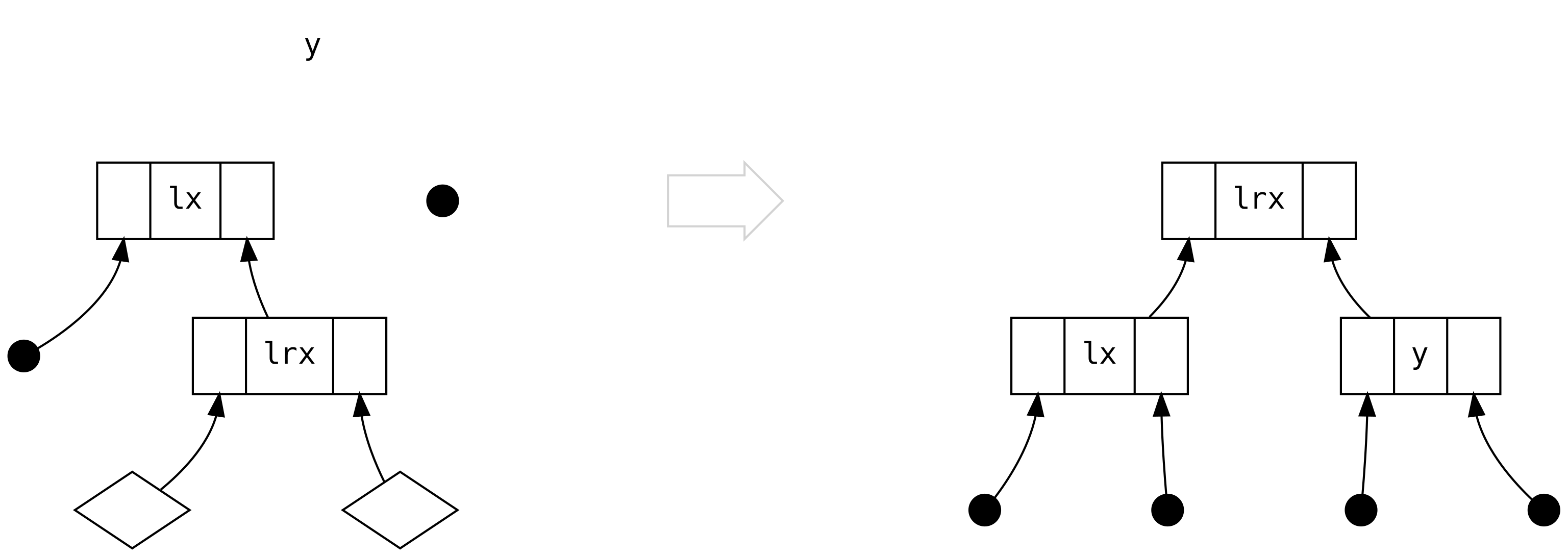
Ale co z dwoma diamentami poniżej lrx? Czy nie utraciliśmy właśnie informacji? Nie, nie utraciliśmy, ponieważ możemy wnioskować (na podstawie równoważenia wielkości), że są one zawsze puste (Tip). Nie istnieje żadna reguła w naszych scenariuszach, która pozwala na wyprodukowanie drzewa, w którym którykolwiek z tych węzłów to Bin.

Czwarty przypadek jest przeciwieństwem trzeciego.

  case (Bin(lx, ll, Tip()), Tip()) => Bin(lx, ll, singleton(y))

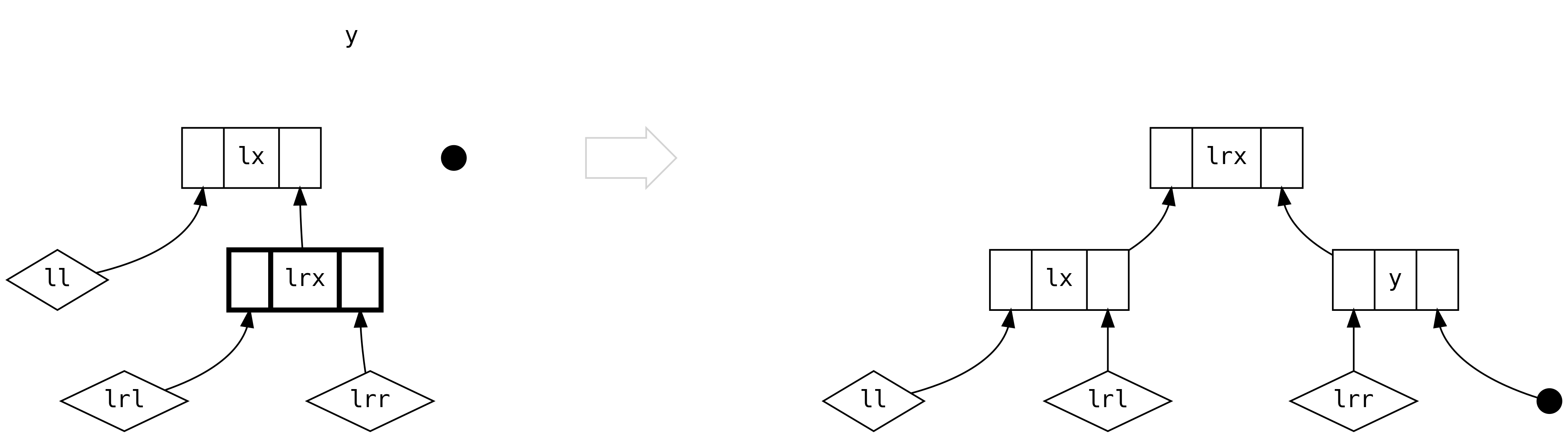
W scenariuszu piątym mamy do czynienia z pełnymi drzewami po obu stronach left i musimy oprzeć decyzję o dalszych krokach na ich wielkości.

  case (Bin(lx, ll, lr), Tip()) if (2*ll.size > lr.size) =>
    Bin(lx, ll, Bin(y, lr, Tip()))
  case (Bin(lx, ll, Bin(lrx, lrl, lrr)), Tip()) =>
    Bin(lrx, Bin(lx, ll, lrl), Bin(y, lrr, Tip()))

Dla pierwszej gałęzi, 2*ll.size > lr.size

a dla drugiej, 2*ll.size <= lr.size

Szósty przypadek wprowadza drzewo po prawej stronie. Gdy left jest puste, tworzymy oczywiste połączenie. Taka sytuacja nigdy nie pojawia się w wyniku .insert, ponieważ left jest zawsze pełne:

  case (Tip(), r) => Bin(y, Tip(), r)

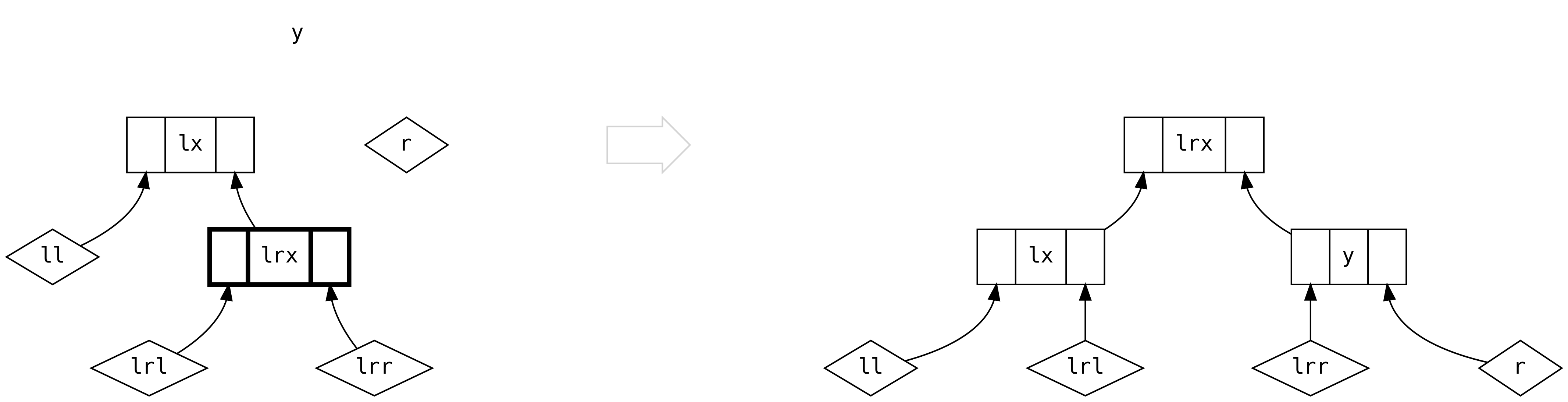
Ostatni scenariusz zachodzi, gdy mamy pełne drzewa po obu stronach. Jeśli left jest mniejszy niż trzykrotność right, możemy po prostu stworzyć nowy Bin.

  case _ if l.size <= 3 * r.size => Bin(y, l, r)

Jednak gdy ten warunek nie jest spełniony i left jest większy od right więcej niż trzykrotnie, musimy zrównoważyć drzewa jak w przypadku piątym.

  case (Bin(lx, ll, lr), r) if (2*ll.size > lr.size) =>
    Bin(lx, ll, Bin(y, lr, r))
  case (Bin(lx, ll, Bin(lrx, lrl, lrr)), r) =>
    Bin(lrx, Bin(lx, ll, lrl), Bin(y, lrr, r))

Tym samym doszliśmy do końca analizy metody .insert i tego, jak tworzony jest ISet. Nie powinno dziwić, że Foldable jest zaimplementowany w oparciu o przeszukiwanie w-głąb. Metody takie jak .minimum i .maximum są optymalne, gdyż struktura danych bazuje na uporządkowaniu elementów.

Warto zaznaczyć, że niektóre metody nie mogą być zaimplementowane tak wydajnie, jak byśmy chcieli. Rozważmy sygnaturę Foldable.element

  @typeclass trait Foldable[F[_]] {
    ...
    def element[A: Equal](fa: F[A], a: A): Boolean
    ...
  }

Oczywistą implementacją .element jest użyć przeszukiwania (prawie) binarnego ISet.contains. Jednak nie jest to możliwe, gdyż .element dostarcza Equal, a .contains wymaga instancji Order.

Z tego samego powodu ISet nie jest w stanie dostarczyć instancji typeklasy Functor, co w praktyce okazuje się sensownym ograniczeniem: wykonanie .map powodowałoby przebudowanie całej struktury. Rozsądnie jest przekonwertować nasz zbiór do innego typu danych, na przykład IList, wykonać .map i przekonwertować wynik z powrotem. W konsekwencji nie jesteśmy w stanie uzyskać Traverse[ISet] ani Applicative[ISet].

6.8.8 IMap

  sealed abstract class ==>>[A, B] {
    val size: Int = this match {
      case Tip()           => 0
      case Bin(_, _, l, r) => 1 + l.size + r.size
    }
  }
  object ==>> {
    type IMap[A, B] = A ==>> B
  
    private final case class Tip[A, B]() extends (A ==>> B)
    private final case class Bin[A, B](
      key: A,
      value: B,
      left: A ==>> B,
      right: A ==>> B
    ) extends ==>>[A, B]
  
    def apply[A: Order, B](x: (A, B)*): A ==>> B = ...
  
    def empty[A, B]: A ==>> B = Tip[A, B]()
    def singleton[A, B](k: A, x: B): A ==>> B = Bin(k, x, Tip(), Tip())
    def fromFoldable[F[_]: Foldable, A: Order, B](fa: F[(A, B)]): A ==>> B = ...
    ...
  }

Wygląda znajomo? W rzeczy samej, IMap (alias na operator prędkości światła ==>>) to kolejne równoważone drzewo, z tą różnicą, że każdy węzeł zawiera dodatkowe pole value: B, pozwalając na przechowywanie par klucz/wartość. Instancja Order wymagana jest jedynie dla typu klucza A, a dodatkowo dostajemy zestaw przydatnych metod do aktualizowania wpisów

  sealed abstract class ==>>[A, B] {
    ...
    def adjust(k: A, f: B => B)(implicit o: Order[A]): A ==>> B = ...
    def adjustWithKey(k: A, f: (A, B) => B)(implicit o: Order[A]): A ==>> B = ...
    ...
  }

6.8.9 StrictTree i Tree

Zarówno StrictTree, jak i Tree to implementacje Rose Tree, drzewiastej struktury danych z nieograniczoną ilością gałęzi w każdym węźle. Niestety, z powodów historycznych, zbudowane na bazie kolekcji z biblioteki standardowej…

  case class StrictTree[A](
    rootLabel: A,
    subForest: Vector[StrictTree[A]]
  )

Tree to leniwa (by-need) wersja StrictTree z wygodnymi konstruktorami

  class Tree[A](
    rootc: Need[A],
    forestc: Need[Stream[Tree[A]]]
  ) {
    def rootLabel = rootc.value
    def subForest = forestc.value
  }
  object Tree {
    object Node {
      def apply[A](root: =>A, forest: =>Stream[Tree[A]]): Tree[A] = ...
    }
    object Leaf {
      def apply[A](root: =>A): Tree[A] = ...
    }
  }

Użytkownik Rose Tree powinien sam zadbać o balansowanie drzewa, co jest odpowiednie, gdy chcemy wyrazić hierarchiczną wiedzę domenową jako strukturę danych. Dla przykładu, w sztucznej inteligencji Rose Tree może być użyte w algorytmach klastrowania do organizacji danych w hierarchie coraz bardziej podobnych rzeczy. Możliwe jest również wyrażenie dokumentów XML jako Rose Tree.

Pracując z danymi hierarchicznymi, dobrze jest rozważyć tę strukturę danych, zanim stworzymy swoją własną.

6.8.10 FingerTree

Finger tree (drzewo palczaste) to uogólniona sekwencja z zamortyzowanym stałym czasem dostępu do elementów i logarytmicznym złączaniem. A to typ elementów, a V na razie zignorujemy:

  sealed abstract class FingerTree[V, A] {
    def +:(a: A): FingerTree[V, A] = ...
    def :+(a: =>A): FingerTree[V, A] = ...
    def <++>(right: =>FingerTree[V, A]): FingerTree[V, A] = ...
    ...
  }
  object FingerTree {
    private class Empty[V, A]() extends FingerTree[V, A]
    private class Single[V, A](v: V, a: =>A) extends FingerTree[V, A]
    private class Deep[V, A](
      v: V,
      left: Finger[V, A],
      spine: =>FingerTree[V, Node[V, A]],
      right: Finger[V, A]
    ) extends FingerTree[V, A]
  
    sealed abstract class Finger[V, A]
    final case class One[V, A](v: V, a1: A) extends Finger[V, A]
    final case class Two[V, A](v: V, a1: A, a2: A) extends Finger[V, A]
    final case class Three[V, A](v: V, a1: A, a2: A, a3: A) extends Finger[V, A]
    final case class Four[V, A](v: V, a1: A, a2: A, a3: A, a4: A) extends Finger[V, A]
  
    sealed abstract class Node[V, A]
    private class Node2[V, A](v: V, a1: =>A, a2: =>A) extends Node[V, A]
    private class Node3[V, A](v: V, a1: =>A, a2: =>A, a3: =>A) extends Node[V, A]
    ...
  }

Przedstawmy FingerTree jako kropki, Finger jako prostokąty, a Node jako prostokąty wewnątrz prostokątów:

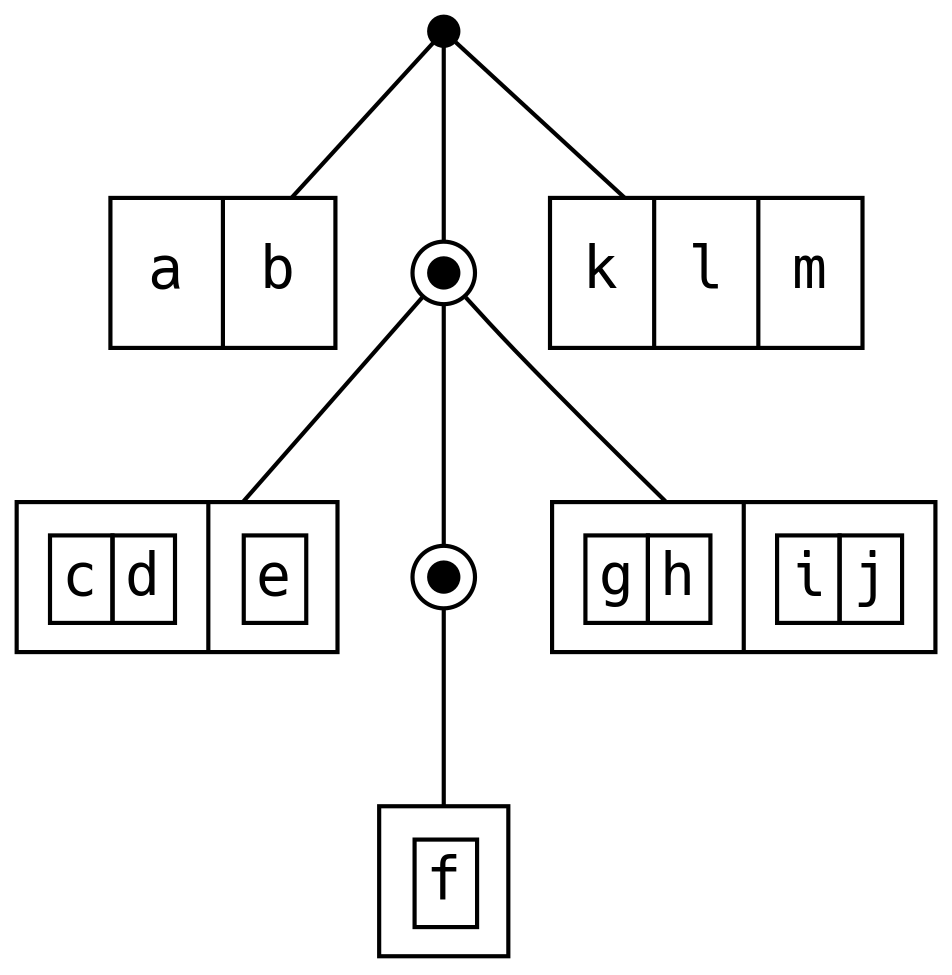
Dodanie elementy na początek FingerTree za pomocą +: jest wydajne, ponieważ Deep po prostu dodaje nowy element do swojego lewego (left) palca. Jeśli palec to Four, to przebudowujemy spine, tak, aby przyjął 3 z tych elementów jako Node3. Dodawanie na koniec (:+) odbywa się tak samo, ale w odwrotnej kolejności.

Złączanie za pomocą |+| lub <++> jest bardziej wydajne niż dodawanie po jednym elemencie, ponieważ instancje Deep mogą zachować swoje zewnętrzne gałęzie, przebudowując jedynie spine.

Do tej pory ignorowaliśmy V. Ukryliśmy też niejawny parametr obecny we wszystkich wariantach tego ADT: implicit measurer: Reducer[A, V].

Reducer to rozszerzenie typeklasy Monoid pozwalające na dodanie pojedynczych elementów do M

  class Reducer[C, M: Monoid] {
    def unit(c: C): M
  
    def snoc(m: M, c: C): M = append(m, unit(c))
    def cons(c: C, m: M): M = append(unit(c), m)
  }

Na przykład Reducer[A, IList[A]] może zapewnić wydajną implementację .cons

  implicit def reducer[A]: Reducer[A, IList[A]] = new Reducer[A, IList[A]] {
    override def unit(a: A): IList[A] = IList.single(a)
    override def cons(a: A, as: IList[A]): IList[A] = a :: as
  }

6.8.10.1 IndSeq

Jeśli jako V użyjemy Int, dostaniemy sekwencje zindeksowaną, gdzie miarą jest wielkość, pozwalając nam na wyszukiwanie elementu po indeksie poprzez porównywanie indeksu z rozmiarem każdej gałezi w drzewie:

  final class IndSeq[A](val self: FingerTree[Int, A])
  object IndSeq {
    private implicit def sizer[A]: Reducer[A, Int] = _ => 1
    def apply[A](as: A*): IndSeq[A] = ...
  }

6.8.10.2 OrdSeq

Inną odmianą FingerTree jest sekwencja uporządkowana, gdzie miarą jest największa wartość w danej gałęzi:

  final class OrdSeq[A: Order](val self: FingerTree[LastOption[A], A]) {
    def partition(a: A): (OrdSeq[A], OrdSeq[A]) = ...
    def insert(a: A): OrdSeq[A] = ...
    def ++(xs: OrdSeq[A]): OrdSeq[A] = ...
  }
  object OrdSeq {
    private implicit def keyer[A]: Reducer[A, LastOption[A]] = a => Tag(Some(a))
    def apply[A: Order](as: A*): OrdSeq[A] = ...
  }

OrdSeq nie posiada instancji żadnych typeklas, co sprawia, że przydatna jest tylko do stopniowego budowania uporządkowanej sekwencji (zawierającej duplikaty). Jeśli zajdzie taka potrzeba, możemy zawsze skorzystać z bazowego FingerTree.

6.8.10.3 Cord

Najpopularniejszym użyciem FingerTree jest przechowanie tymczasowej reprezentacji Stringów w instancjach Show. Budowanie pojedynczego Stringa może być tysiąckrotnie szybsze niż domyślna implementacja .toString dla case class, która tworzy nowy ciąg znaków dla każdej warstwy w ADT.

  final case class Cord(self: FingerTree[Int, String]) {
    override def toString: String = {
      val sb = new java.lang.StringBuilder(self.measure)
      self.foreach(sb.append) // locally scoped side effect
      sb.toString
    }
    ...
  }

Dla przykładu, instancja Cord[String] zwraca Three ze stringiem pośrodku i cudzysłowami po obu stronach

  implicit val show: Show[String] = s => Cord(FingerTree.Three("\"", s, "\""))

Sprawiając, że String wygląda tak jak w kodzie źródłowym

  scala> val s = "foo"
         s.toString
  res: String = foo
  
  scala> s.show
  res: Cord = "foo"

6.8.11 Kolejka Priorytetowa Heap

Kolejka priorytetowa to struktura danych, która pozwala na szybkie wstawianie uporządkowanych elementów (zezwalając na duplikaty) oraz szybki dostęp do najmniejszego elementu (czyli takiego z najwyższym priorytetem). Nie jest wymagane, aby elementy inne niż minimalny były przechowywane wg porządku. Naiwna implementacja mogłaby wyglądać tak:

  final case class Vip[A] private (val peek: Maybe[A], xs: IList[A]) {
    def push(a: A)(implicit O: Order[A]): Vip[A] = peek match {
      case Maybe.Just(min) if a < min => Vip(a.just, min :: xs)
      case _                          => Vip(peek, a :: xs)
    }
  
    def pop(implicit O: Order[A]): Maybe[(A, Vip[A])] = peek strengthR reorder
    private def reorder(implicit O: Order[A]): Vip[A] = xs.sorted match {
      case INil()           => Vip(Maybe.empty, IList.empty)
      case ICons(min, rest) => Vip(min.just, rest)
    }
  }
  object Vip {
    def fromList[A: Order](xs: IList[A]): Vip[A] = Vip(Maybe.empty, xs).reorder
  }

Taki push jest bardzo szybki (O(1)), ale reorder, a zatem i pop bazują na metodzie IList.sorted, której złożoność to O(n log n).

Scalaz implementuje kolejkę priorytetową za pomocą struktury drzewiastej, gdzie każdy węzeł ma wartość mniejszą niż jego dzieci. Heap pozwala na szybkie wstawianie (insert), złączanie (union), sprawdzanie wielkości (size), zdejmowanie (pop) i podglądanie (minimum0) najmniejszego elementu.

  sealed abstract class Heap[A] {
    def insert(a: A)(implicit O: Order[A]): Heap[A] = ...
    def +(a: A)(implicit O: Order[A]): Heap[A] = insert(a)
  
    def union(as: Heap[A])(implicit O: Order[A]): Heap[A] = ...
  
    def uncons(implicit O: Order[A]): Option[(A, Heap[A])] = minimumO strengthR deleteMin
    def minimumO: Option[A] = ...
    def deleteMin(implicit O: Order[A]): Heap[A] = ...
  
    ...
  }
  object Heap {
    def fromData[F[_]: Foldable, A: Order](as: F[A]): Heap[A] = ...
  
    private final case class Ranked[A](rank: Int, value: A)
  
    private final case class Empty[A]() extends Heap[A]
    private final case class NonEmpty[A](
      size: Int,
      tree: Tree[Ranked[A]]
    ) extends Heap[A]
  
    ...
  }

Heap zaimplementowany jest za pomocą Rose Tree z wartościami typu Ranked, gdzie rank to głębokość subdrzewa, pozwalająca na balansowanie całej struktury. Samodzielnie zarządzamy drzewem, tak aby minimum było zawsze na jego szczycie. Zaletą takiej reprezentacji jest to, że minimum0 jest darmowe:

  def minimumO: Option[A] = this match {
    case Empty()                        => None
    case NonEmpty(_, Tree.Node(min, _)) => Some(min.value)
  }

Dodając nowy element, porównujemy go z aktualnym minimum i podmieniamy je jeśli nowa wartość jest mniejsza:

  def insert(a: A)(implicit O: Order[A]): Heap[A] = this match {
    case Empty() =>
      NonEmpty(1, Tree.Leaf(Ranked(0, a)))
    case NonEmpty(size, tree @ Tree.Node(min, _)) if a <= min.value =>
      NonEmpty(size + 1, Tree.Node(Ranked(0, a), Stream(tree)))
  ...

Dodawanie wartości, które nie są minimum, skutkuje nieuporządkowanymi gałęziami drzewa. Kiedy napotkamy dwa, lub więcej, poddrzewa tej samej rangi, optymistycznie dodajemy minimum na początek:

  ...
    case NonEmpty(size, Tree.Node(min,
           (t1 @ Tree.Node(Ranked(r1, x1), xs1)) #::
           (t2 @ Tree.Node(Ranked(r2, x2), xs2)) #:: ts)) if r1 == r2 =>
      lazy val t0 = Tree.Leaf(Ranked(0, a))
      val sub =
        if (x1 <= a && x1 <= x2)
          Tree.Node(Ranked(r1 + 1, x1), t0 #:: t2 #:: xs1)
        else if (x2 <= a && x2 <= x1)
          Tree.Node(Ranked(r2 + 1, x2), t0 #:: t1 #:: xs2)
        else
          Tree.Node(Ranked(r1 + 1, a), t1 #:: t2 #:: Stream())
  
      NonEmpty(size + 1, Tree.Node(Ranked(0, min.value), sub #:: ts))
  
    case NonEmpty(size,  Tree.Node(min, rest)) =>
      val t0 = Tree.Leaf(Ranked(0, a))
      NonEmpty(size + 1, Tree.Node(Ranked(0, min.value), t0 #:: rest))
  }

Uniknięcie pełnego uporządkowania drzewa sprawia, że insert jest bardzo szybki (O(1)), a więc producenci wartości nie są karani. Jednak konsumenci muszą ponieść koszt tej decyzji, gdyż złożoność uncons to O(log n), z racji tego, że musimy odszukać nowe minimum i przebudować drzewo. Nadal jednak jest to implementacja szybsza od naiwnej.

union również odracza porządkowanie, pozwalając na wykonanie ze złożonością O(1).

Jeśli domyślna instancja Order[Foo] nie wyraża w poprawny sposób priorytetów, których potrzebujemy, możemy użyć Tagu i dostarczyć własną instancję Order[Foo @@ Custom] dla Heap[Foo @@ Custom].

6.8.12 Diev - interwały dyskretne

Możemy wydajnie wyrazić zbiór liczb całkowitych 6, 9, 2, 13, 8, 14, 10, 7, 5 jako serię domkniętych przedziałów: [2, 2], [5, 10], [13, 14]. Diev to wydajna implementacja tej metody dla dowolnego A, dla którego istnieje Enum[A]. Tym wydajniejsza im gęstsza jego zawartość.

  sealed abstract class Diev[A] {
    def +(interval: (A, A)): Diev[A]
    def +(value: A): Diev[A]
    def ++(other: Diev[A]): Diev[A]
  
    def -(interval: (A, A)): Diev[A]
    def -(value: A): Diev[A]
    def --(other: Diev[A]): Diev[A]
  
    def intervals: Vector[(A, A)]
    def contains(value: A): Boolean
    def contains(interval: (A, A)): Boolean
    ...
  }
  object Diev {
    private final case class DieVector[A: Enum](
      intervals: Vector[(A, A)]
    ) extends Diev[A]
  
    def empty[A: Enum]: Diev[A] = ...
    def fromValuesSeq[A: Enum](values: Seq[A]): Diev[A] = ...
    def fromIntervalsSeq[A: Enum](intervals: Seq[(A, A)]): Diev[A] = ...
  }

Kiedy aktualizujemy Diev, sąsiednie przedziały są łączone i porządkowane, tak, że dla każdego zbioru wartości istnieje unikalna reprezentacja.

  scala> Diev.fromValuesSeq(List(6, 9, 2, 13, 8, 14, 10, 7, 5))
  res: Diev[Int] = ((2,2)(5,10)(13,14))
  
  scala> Diev.fromValuesSeq(List(6, 9, 2, 13, 8, 14, 10, 7, 5).reverse)
  res: Diev[Int] = ((2,2)(5,10)(13,14))

Świetnym zastosowaniem dla tej struktury są przedziały czasu. Na przykład w TradeTemplate z wcześniejszego rozdziału.

  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: Option[Currency],
    otc: Option[Boolean]
  )

Jeśli okaże się, że lista payments jest bardzo gęsta, możemy zamienić ją na Diev dla zwiększenia wydajności, nie wpływając jednocześnie na logikę biznesową, gdyż polega ona na typeklasie Monoid, a nie metodach specyficznych dla Listy. Musimy tylko dostarczyć instancję Enum[LocalDate].

6.8.13 OneAnd

Przypomnij sobie Foldable, czyli odpowiednik API kolekcji ze Scalaz, oraz Foldable1, czyli jego wersję dla niepustych kolekcji. Do tej pory widzieliśmy instancję Foldable1 jedynie dla NonEmptyList. Okazuje się, że OneAnd to prosta struktura danych, która potrafi opakować dowolną kolekcję i zamienić ją w Foldable1:

  final case class OneAnd[F[_], A](head: A, tail: F[A])

Typ NonEmptyList[A] mógłby być aliasem na OneAnd[IList, A]. W podobny sposób możemy stworzyć niepuste wersje Stream, DList i Tree. Jednak może to zaburzyć gwarancje co do uporządkowania i unikalności elementów: OneAnd[ISet, A] to nie tyle niepusty ISet, a raczej ISet z zagwarantowanym pierwszym elementem, który może również znajdować się w tym zbiorze.

6.9 Podsumowanie

W tym rozdziale przejrzeliśmy typy danych, jakie Scalaz ma do zaoferowania.

Nie musimy zapamiętać wszystkiego. Niech każda z sekcji zasadzi ziarno pewnej koncepcji, które może o sobie przypomnieć, gdy będziemy szukać rozwiązania dla konkretnego problemu.

Świat funkcyjnych struktur danych jest aktywnie badany i rozwijany. Publikacje naukowe na ten temat ukazują się regularnie, pokazując nowe podejścia do znanych problemów. Implementacja nowych struktur bazujących na literaturze to dobry sposób na swój własny wkład do ekosystemu Scalaz.