5. Typeklasy ze Scalaz

W tym rozdziale przejdziemy przez niemal wszystkie typeklasy zdefiniowane w scalaz-core. Nie wszystkie z nich znajdują zastosowanie w drone-dynamic-agents, więc czasami będziemy używać samodzielnych przykładów.

Napotkać można krytykę w stosunku do konwencji nazewniczych stosowanych w Scalaz i programowaniu funkcyjnym w ogólności. Większość nazw podąża za konwencjami wprowadzonymi w Haskellu, który bazował z kolei na dziale matematyki zwanym Teorią kategorii. Możesz śmiało użyć aliasów typów, jeśli uważasz, że rzeczowniki pochodzące od głównej funkcjonalności są łatwiejsze do zapamiętania (np. Mappable, Pureable, FlatMappable).

Zanim wprowadzimy hierarchię typeklas, popatrzmy na cztery metody, które są najistotniejsze z punktu widzenia kontroli przepływu. Metod tych używać będziemy w większości typowych aplikacji funkcyjnych:

Wiemy, że operacje zwracające F[_] mogą być wykonywane sekwencyjnie wewnątrz konstrukcji for przy użyciu metody .flatMap, która zdefiniowana jest wewnątrz Monad[F]. Możemy myśleć o F[A] jak o kontenerze na pewien efekt, którego rezultatem jest wartość typu A. .flatMap pozwala nam wygenerować nowe efekty F[B] na podstawie rezultatów wykonania wcześniejszych efektów.

Oczywiście nie wszystkie konstruktory typu F[_] wiążą się z efektami ubocznymi, nawet jeśli mają instancję Monad[F], często są to po prostu struktury danych. Używając najmniej konkretnej (czyli najbardziej ogólnej) abstrakcji możemy w łatwy sposób współdzielić kod operujący na typach List, Either, Future i wielu innych.

Jeśli jedyne czego potrzebujemy to przetransformować wynik F[_], wystarczy, że użyjemy metody map, definiowanej w typeklasie Functor. W rozdziale 3 uruchamialiśmy efekty równolegle, tworząc produkt i mapując go. W Programowaniu Funkcyjnym obliczenia wykonywane równolegle są uznawane za słabsze niż te wykonywane sekwencyjnie.

Pomiędzy Monadą i Functorem leży Applicative, która definiuje metodę pure pozwalającą nam wynosić (lift) wartości do postaci efektów lub tworzyć struktury danych z pojedynczych wartości.

.sequence jest użyteczna, gdy chcemy poprzestawiać konstruktory typów. Gdy mamy F[G[_]] a potrzebujemy G[F[_]], np. zamiast List[Future[Int]] potrzebujemy Future[List[Int]], wtedy właśnie użyjemy .sequence.

5.1 Plan

Ten rozdział jest dłuższy niż zazwyczaj i wypełniony po brzegi informacjami. Przejście przez niego w wielu podejściach jest czymś zupełnie normalnym, a zapamiętanie wszystkiego wymagałoby supermocy. Potraktuj go raczej jako miejsce, do którego możesz wracać, gdy będziesz potrzebował więcej informacji.

Pominięte zostały typeklasy, które rozszerzają typ Monad, gdyż zasłużyły na swój własny rozdział.

Scalaz używa generacji kodu, ale nie za pomocą simulacrum. Niemniej, dla zwięzłości prezentujemy przykłady bazujące na anotacji @typeclass. Równoznaczna składanie dostępna jest, gdy zaimportujemy scalaz._ i Scalaz._, a jej implementacja znajduje się w pakiecie scalaz.syntax w kodzie źródłowym scalaz.

5.2 Rzeczy złączalne²⁰

  @typeclass trait Semigroup[A] {
    @op("|+|") def append(x: A, y: =>A): A
  
    def multiply1(value: F, n: Int): F = ...
  }
  
  @typeclass trait Monoid[A] extends Semigroup[A] {
    def zero: A
  
    def multiply(value: F, n: Int): F =
      if (n <= 0) zero else multiply1(value, n - 1)
  }
  
  @typeclass trait Band[A] extends Semigroup[A]

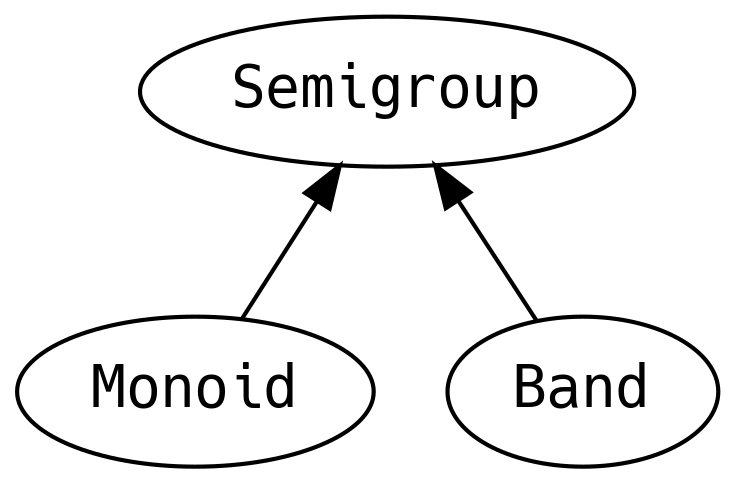
Semigroup (półgrupa) może być zdefiniowana dla danego typu, jeśli możemy połączyć ze sobą dwie jego wartości. Operacja ta musi być łączna (associative), co oznacza, że kolejność zagnieżdżonych operacji nie powinna mieć znaczenia, np:

  (a |+| b) |+| c == a |+| (b |+| c)
  
  (1 |+| 2) |+| 3 == 1 |+| (2 |+| 3)

Monoid jest półgrupą z elementem zerowym (zero, zwanym również elementem pustym (empty), tożsamym (identity) lub neutralnym). Połączenie zero z dowolną inną wartością a powinno zwracać to samo niezmienione a.

  a |+| zero == a
  
  a |+| 0 == a

Prawdopodobnie przywołaliśmy tym samym wspomnienie typu Numeric z Rozdziału 4. Istnieją implementacje typeklasy Monoid dla wszystkich prymitywnych typów liczbowych, ale koncepcja rzeczy złączalnych jest użyteczna również dla typów innych niż te liczbowe.

  scala> "hello" |+| " " |+| "world!"
  res: String = "hello world!"
  
  scala> List(1, 2) |+| List(3, 4)
  res: List[Int] = List(1, 2, 3, 4)

Band (pas) dodaje prawo, gwarantujące, że append wywołane na dwóch takich samych elementach jest idempotentne, tzn. zwraca tę samą wartość. Przykładem są typy, które mają tylko jedną wartość, takie jak Unit, kresy górne (least upper bound), lub zbiory (Set). Band nie wnosi żadnych dodatkowych metod, ale użytkownicy mogą wykorzystać dodatkowe gwarancje do optymalizacji wydajności.

Jako realistyczny przykład dla Monoidu, rozważmy system transakcyjny, który posiada ogromną bazę reużywalnych wzorów transakcji. Wypełnianie wartości domyślnych dla nowej transakcji wymaga wybrania i połączenia wielu wzorów, z zasadą “ostatni wygrywa”, jeśli dwa wzory posiadają wartości dla tego samego pola. “Wybieranie” jest wykonywane dla nas przez osobny system, a naszym zadaniem jest jedynie połączyć wzory według kolejności.

Stworzymy prosty schemat, aby zobrazować zasadę działania, pamiętając przy tym, że prawdziwy system oparty byłby na dużo bardziej skomplikowanym ADT.

  sealed abstract class Currency
  case object EUR extends Currency
  case object USD extends Currency
  
  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: Option[Currency],
    otc: Option[Boolean]
  )

Jeśli chcemy napisać metodę, która przyjmuje parametr templates: List[TradeTemplate], wystarczy, że zawołamy

  val zero = Monoid[TradeTemplate].zero
  templates.foldLeft(zero)(_ |+| _)

i gotowe!

Jednak aby móc zawołać zero lub |+| musimy mieć dostęp do instancji Monoid[TradeTemplate]. Chociaż w ostatnim rozdziale zobaczymy jak wyderywować taką instancję w sposób generyczny, na razie stworzymy ją ręcznie:

  object TradeTemplate {
    implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
      (a, b) => TradeTemplate(a.payments |+| b.payments,
                              a.ccy |+| b.ccy,
                              a.otc |+| b.otc),
      TradeTemplate(Nil, None, None)
    )
  }

Jednak nie jest to do końca to, czego byśmy chcieli, gdyż Monoid[Option[A]] łączy ze sobą wartości wewnętrzne, np.

  scala> Option(2) |+| None
  res: Option[Int] = Some(2)
  scala> Option(2) |+| Option(1)
  res: Option[Int] = Some(3)

podczas gdy my chcielibyśmy zachowania “ostatni wygrywa”. Możemy więc nadpisać domyślną instancję Monoid[Option[A]] naszą własną:

  implicit def lastWins[A]: Monoid[Option[A]] = Monoid.instance(
    {
      case (None, None)   => None
      case (only, None)   => only
      case (None, only)   => only
      case (_   , winner) => winner
    },
    None
  )

Wszystko kompiluje się poprawnie, więc wypróbujmy nasze dzieło…

  scala> import java.time.{LocalDate => LD}
  scala> val templates = List(
           TradeTemplate(Nil,                     None,      None),
           TradeTemplate(Nil,                     Some(EUR), None),
           TradeTemplate(List(LD.of(2017, 8, 5)), Some(USD), None),
           TradeTemplate(List(LD.of(2017, 9, 5)), None,      Some(true)),
           TradeTemplate(Nil,                     None,      Some(false))
         )
  
  scala> templates.foldLeft(zero)(_ |+| _)
  res: TradeTemplate = TradeTemplate(
                         List(2017-08-05,2017-09-05),
                         Some(USD),
                         Some(false))

Jedyne co musieliśmy zrobić to zdefiniować jeden mały kawałek logiki biznesowej, a całą resztę zrobił za nas Monoid!

Zauważ, że listy płatności są ze sobą łączone. Dzieje się tak, ponieważ domyślny Monoid[List] zachowuje się ten właśnie sposób. Gdyby wymagania biznesowe były inne, wystarczyłoby dostarczyć inną instancję Monoid[List[LocalDate]]. Przypomnij sobie z Rozdziału 4, że dzięki polimorfizmowi czasu kompilacji możemy zmieniać zachowanie append dla List[E] w zależności od E, a nie tylko od implementacji List.

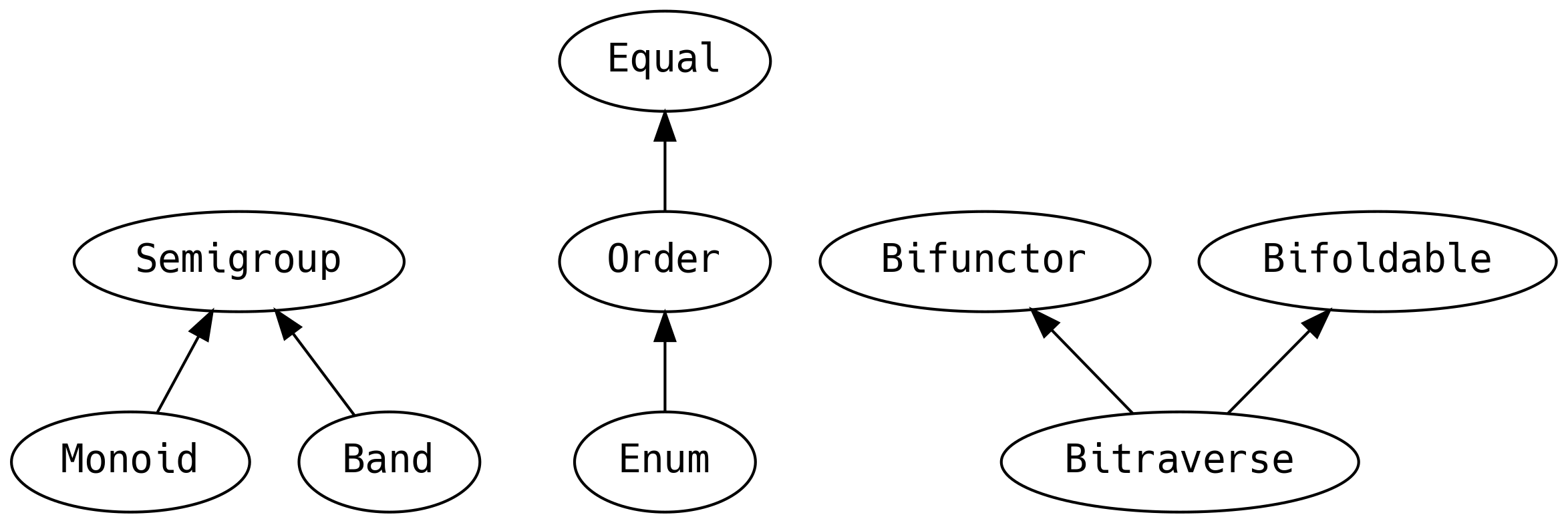
5.3 Rzeczy obiektowe

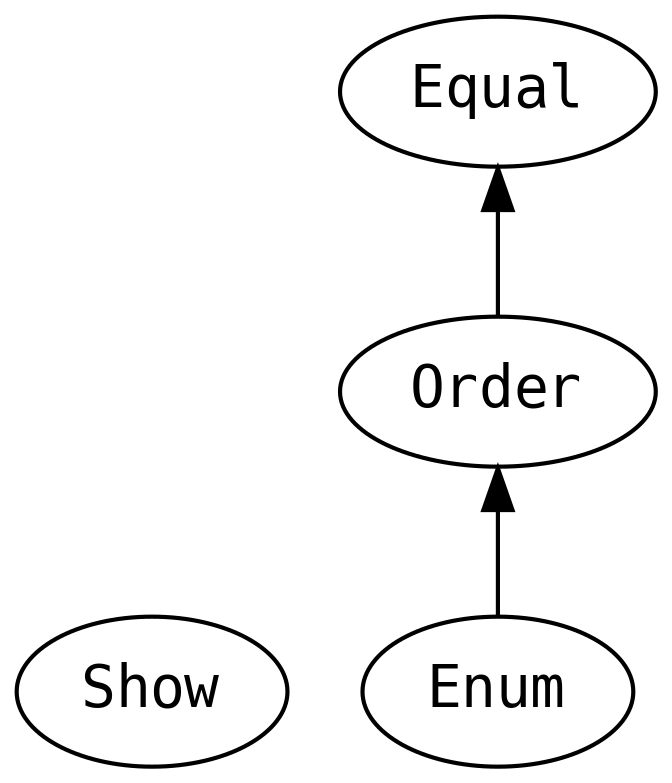
W rozdziale o Danych i funkcjonalnościach powiedzieliśmy, że sposób, w jaki JVM rozumie równość nie działa dla wielu typów, które możemy umieścić wewnątrz ADT. Problem ten wynika z faktu, że JVM był projektowany dla języka Java, a equals zdefiniowane jest w klasie java.lang.Object, nie ma więc możliwości, aby equals usunąć ani zagwarantować, że jest explicite zaimplementowany.

Niemniej, w FP wolimy używać typeklas do wyrażania polimorficznych zachowań i pojęcie równości również może zostać w ten sposób wyrażone.

  @typeclass trait Equal[F]  {
    @op("===") def equal(a1: F, a2: F): Boolean
    @op("/==") def notEqual(a1: F, a2: F): Boolean = !equal(a1, a2)
  }

=== (potrójne równa się, triple equals) jest bezpieczniejszy względem typów (typesafe) niż == (podwójne równa się, double equals), ponieważ użycie go wymaga, aby po obu stronach porównania znajdowały się instancje dokładnie tego samego typu. W ten sposób możemy zapobiec wielu częstym błędom.

equal ma te same wymagania jak Object.equals

• przemienność (commutative): f1 === f2 implikuje f2 === f1
• zwrotność (reflexive): f === f
• przechodniość (transitive): f1 === f2 && f2 === f3 implikuje f1 === f3

Poprzez odrzucenie uniwersalnego Object.equals, gdy konstruujemy ADT, nie bierzemy za pewnik, że wiemy jak porównywać instancje danego typu. Jeśli instancja Equal nie będzie dostępna, nasz kod się nie skompiluje.

Kontynuując praktykę odrzucania zaszłości z Javy, zamiast mówić, że dane są instancją java.lang.Comparable, powiemy, że mają instancję typeklasy Order:

  @typeclass trait Order[F] extends Equal[F] {
    @op("?|?") def order(x: F, y: F): Ordering
  
    override  def equal(x: F, y: F): Boolean = order(x, y) == Ordering.EQ
    @op("<" ) def lt(x: F, y: F): Boolean = ...
    @op("<=") def lte(x: F, y: F): Boolean = ...
    @op(">" ) def gt(x: F, y: F): Boolean = ...
    @op(">=") def gte(x: F, y: F): Boolean = ...
  
    def max(x: F, y: F): F = ...
    def min(x: F, y: F): F = ...
    def sort(x: F, y: F): (F, F) = ...
  }
  
  sealed abstract class Ordering
  object Ordering {
    case object LT extends Ordering
    case object EQ extends Ordering
    case object GT extends Ordering
  }

Order implementuje .equal, wykorzystując nową metodę prostą .order. Kiedy typeklasa implementuje kombinator prymitywny rodzica za pomocą kombinatora pochodnego, musimy dodać domniemane prawo podstawiania (implied law of substitution). Jeśli instancja Order ma nadpisać .equal z powodów wydajnościowych, musi ona zachowywać się dokładnie tak samo jak oryginał.

Rzeczy, które definiują porządek, mogą również być dyskretne, pozwalając nam na przechodzenie do poprzedników i następników:

  @typeclass trait Enum[F] extends Order[F] {
    def succ(a: F): F
    def pred(a: F): F
    def min: Option[F]
    def max: Option[F]
  
    @op("-+-") def succn(n: Int, a: F): F = ...
    @op("---") def predn(n: Int, a: F): F = ...
  
    @op("|->" ) def fromToL(from: F, to: F): List[F] = ...
    @op("|-->") def fromStepToL(from: F, step: Int, to: F): List[F] = ...
    @op("|=>" ) def fromTo(from: F, to: F): EphemeralStream[F] = ...
    @op("|==>") def fromStepTo(from: F, step: Int, to: F): EphemeralStream[F] = ...
  }

  scala> 10 |--> (2, 20)
  res: List[Int] = List(10, 12, 14, 16, 18, 20)
  
  scala> 'm' |-> 'u'
  res: List[Char] = List(m, n, o, p, q, r, s, t, u)

EphemeralStream omówimy w następnym rozdziale, na razie wystarczy nam wiedzieć, że jest to potencjalnie nieskończona struktura danych, która unika problemów z przetrzymywaniem pamięci obecnych w klasie Stream z biblioteki standardowej.

Podobnie do Object.equals, koncepcja metody .toString dostępnej w każdej klasie ma sens jedynie w Javie. Chcielibyśmy wymusić możliwość konwersji do ciągu znaków w czasie kompilacji i dokładnie to robi typeklasa Show:

  trait Show[F] {
    def show(f: F): Cord = ...
    def shows(f: F): String = ...
  }

Lepiej poznamy klasę Cord w rozdziale poświęconym typom danych, teraz jedyne co musimy wiedzieć, to to że Cord jest wydajną strukturą danych służącą do przechowywania i manipulowania instancjami typu String.

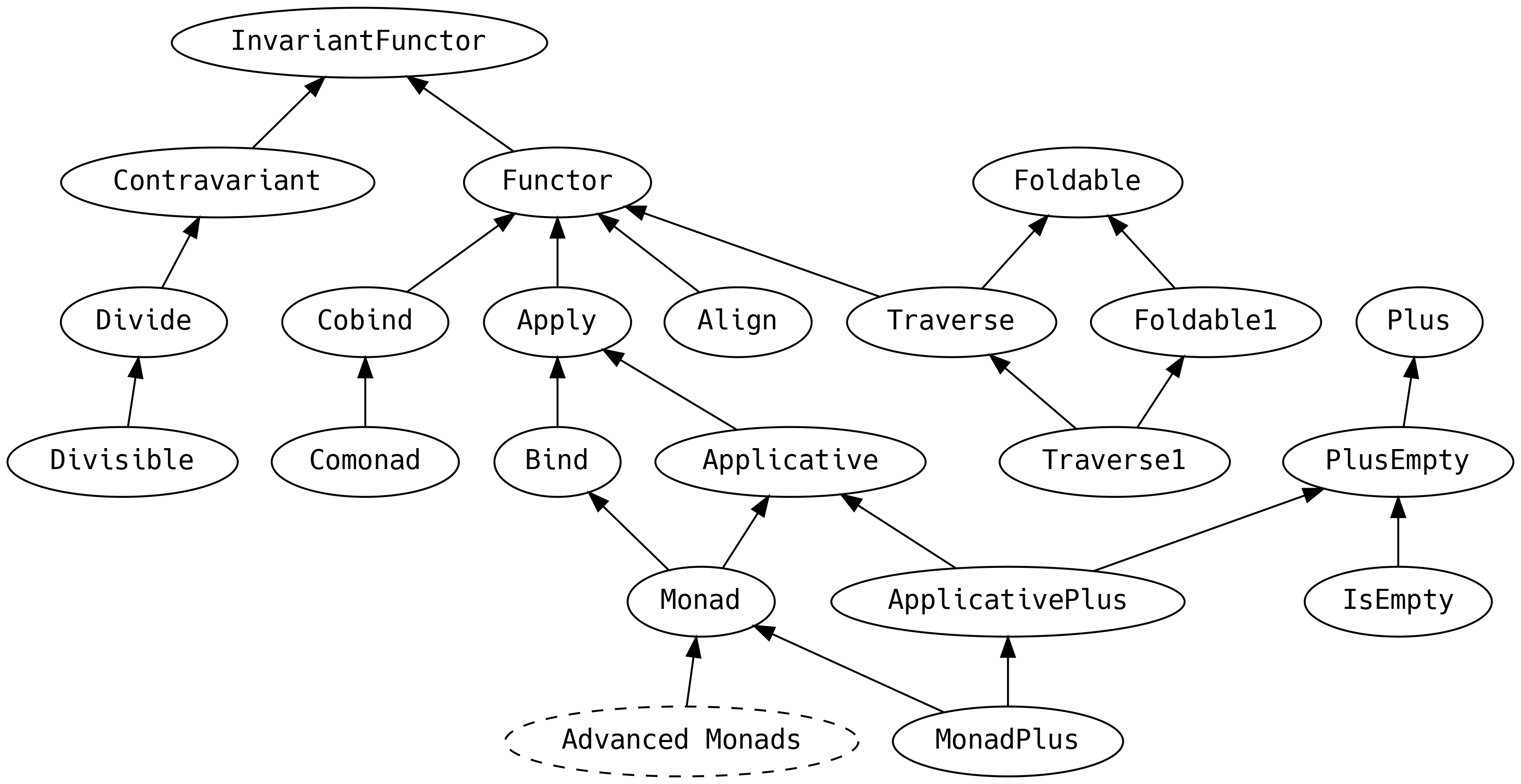
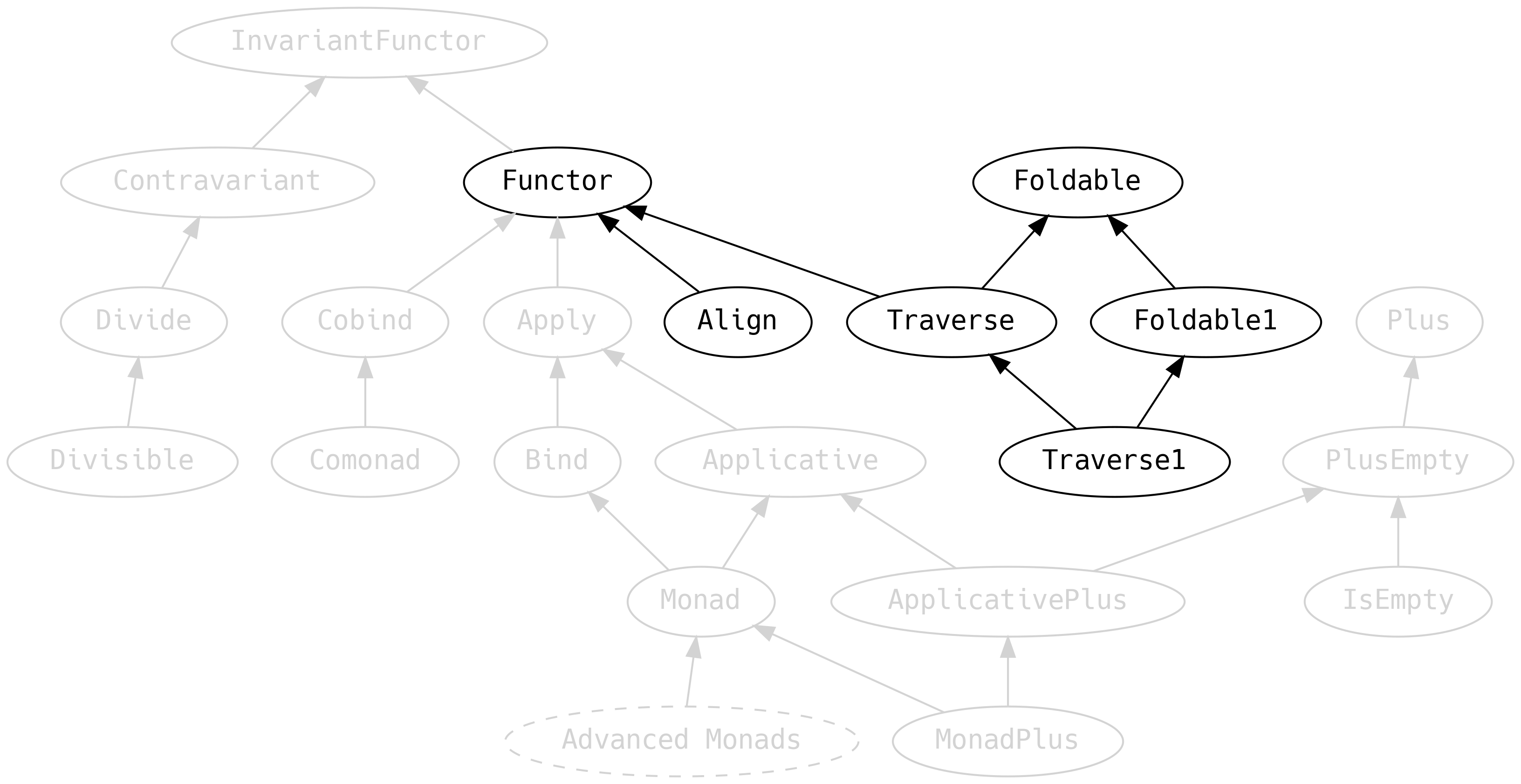
5.4 Rzeczy mapowalne

Skupmy się teraz na rzeczach, które możemy w jakiś sposób przemapowywać (map over) lub trawersować (traverse):

5.4.1 Funktor

  @typeclass trait Functor[F[_]] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
  
    def void[A](fa: F[A]): F[Unit] = map(fa)(_ => ())
    def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)] = map(fa)(a => (a, f(a)))
  
    def fpair[A](fa: F[A]): F[(A, A)] = map(fa)(a => (a, a))
    def strengthL[A, B](a: A, f: F[B]): F[(A, B)] = map(f)(b => (a, b))
    def strengthR[A, B](f: F[A], b: B): F[(A, B)] = map(f)(a => (a, b))
  
    def lift[A, B](f: A => B): F[A] => F[B] = map(_)(f)
    def mapply[A, B](a: A)(f: F[A => B]): F[B] = map(f)((ff: A => B) => ff(a))
  }

Jedyną metodą abstrakcyjną jest map i musi się ona komponować (składać, compose), tzn. mapowanie za pomocą f, a następnie g musi dawać ten sam wyniki jak mapowanie z użyciem złożenia tych funkcji (f ∘ g).

  fa.map(f).map(g) == fa.map(f.andThen(g))

Metoda map nie może też wykonywać żadnych zmian, jeśli przekazana do niej funkcja to identity (czyli x => x)

  fa.map(identity) == fa
  
  fa.map(x => x) == fa

Functor definiuje kilka pomocniczych metod wokół map, które mogą być zoptymalizowane przez konkretne instancje. Dokumentacja została celowo pominięta, aby zachęcić do samodzielnego odgadnięcia co te metody robią, zanim spojrzymy na ich implementację. Poświęć chwilę na przestudiowanie samych sygnatur, zanim ruszysz dalej:

  def void[A](fa: F[A]): F[Unit]
  def fproduct[A, B](fa: F[A])(f: A => B): F[(A, B)]
  
  def fpair[A](fa: F[A]): F[(A, A)]
  def strengthL[A, B](a: A, f: F[B]): F[(A, B)]
  def strengthR[A, B](f: F[A], b: B): F[(A, B)]
  
  // harder
  def lift[A, B](f: A => B): F[A] => F[B]
  def mapply[A, B](a: A)(f: F[A => B]): F[B]

1. void przyjmuje instancję F[A] i zawsze zwraca F[Unit], a więc gubi wszelkie przechowywane wartości, ale zachowuje strukturę.
2. fproduct przyjmuje takie same argumenty jak map, ale zwraca F[(A, B)], a więc łączy wynik operacji z wcześniejszą zawartością. Operacja ta przydaje się, gdy chcemy zachować argumenty przekazane do funkcji.
3. fpair powiela element A do postaci F[(A, A)]
4. strengthL łączy zawartość F[B] ze stałą typu A po lewej stronie.
5. strengthR łączy zawartość F[A] ze stałą typu B po prawej stronie.
6. lift przyjmuje funkcję A => Bi zwraca F[A] => F[B]. Innymi słowy, przyjmuje funkcję, która operuje na zawartości F[A] i zwraca funkcję, która operuje na F[A] bezpośrednio.
7. mapply to łamigłówka. Powiedzmy, że mamy F[_] z funkcją A => B w środku oraz wartość A, w rezultacie możemy otrzymać F[B]. Sygnatura wygląda podobnie do pure, ale wymaga od wołającego dostarczenia F[A => B].

fpair, strengthL i strengthR wyglądają całkiem bezużytecznie, ale przydają się, gdy chcemy zachować pewne informacje, które w innym wypadku zostałyby utracone.

Functor ma też specjalną składnię:

  implicit class FunctorOps[F[_]: Functor, A](self: F[A]) {
    def as[B](b: =>B): F[B] = Functor[F].map(self)(_ => b)
    def >|[B](b: =>B): F[B] = as(b)
  }

.as i >| to metody pozwalające na zastąpienie wyniku przez przekazaną stałą.

W naszej przykładowej aplikacji wprowadziliśmy jeden brzydki hak, definiując metody start i stop tak, aby zwracały swoje własne wejście:

  def start(node: MachineNode): F[MachineNode]
  def stop (node: MachineNode): F[MachineNode]

Pozwala nam to opisywać logikę biznesową w bardzo zwięzły sposób, np.

  for {
    _      <- m.start(node)
    update = world.copy(pending = Map(node -> world.time))
  } yield update

albo

  for {
    stopped <- nodes.traverse(m.stop)
    updates = stopped.map(_ -> world.time).toList.toMap
    update  = world.copy(pending = world.pending ++ updates)
  } yield update

Ale hak ten wprowadza zbędną komplikację do implementacji. Lepiej będzie, gdy pozwolimy naszej algebrze zwracać F[Unit] a następnie użyjemy as:

  m.start(node) as world.copy(pending = Map(node -> world.time))

oraz

  for {
    stopped <- nodes.traverse(a => m.stop(a) as a)
    updates = stopped.map(_ -> world.time).toList.toMap
    update  = world.copy(pending = world.pending ++ updates)
  } yield update

5.4.2 Foldable

Technicznie rzecz biorąc, Foldable przydaje się dla struktur danych, przez które możemy przejść a na koniec wyprodukować wartość podsumowującą. Jednak stwierdzenie to nie oddaje pełnej natury tej “jednotypeklasowej armii”, która jest w stanie dostarczyć większość tego, co spodziewalibyśmy się znaleźć w Collections API.

Do omówienia mamy tyle metod, że musimy je sobie podzielić. Zacznijmy od metod abstrakcyjnych:

  @typeclass trait Foldable[F[_]] {
    def foldMap[A, B: Monoid](fa: F[A])(f: A => B): B
    def foldRight[A, B](fa: F[A], z: =>B)(f: (A, =>B) => B): B
    def foldLeft[A, B](fa: F[A], z: B)(f: (B, A) => B): B = ...

Instancja Foldable musi zaimplementować jedynie foldMap i foldRight, aby uzyskać pełną funkcjonalność tej typeklasy, aczkolwiek poszczególne metody są często optymalizowane dla konkretnych struktur danych.

.foldMap ma alternatywną nazwę do celów marketingowych: MapReduce. Mając do dyspozycji F[A], funkcję z A na B i sposób na łączenie B (dostarczony przez Monoid wraz z elementem zerowym), możemy wyprodukować “podsumowującą” wartość typu B. Kolejność operacji nie jest narzucana, co pozwala na wykonywanie ich równolegle.

.foldRight nie wymaga, aby jej parametry miały instancję Monoidu, co oznacza, że musimy podać wartość zerową z oraz sposób łączenia elementów z wartością podsumowująca. Kierunek przechodzenia jest zdefiniowany jako od prawej do lewej, co sprawia, że operacje nie mogą być zrównoleglone.

foldLeft trawersuje elementy od lewej do prawej. Metoda ta może być zaimplementowana za pomocą foldMap, ale większość instancji woli dostarczyć osobną implementację dla tak podstawowej operacji. Ponieważ z reguły implementacje tej metody są ogonowo rekursywne (tail recursive), nie ma tutaj parametrów przekazywanych przez nazwę.

Jedyny prawem obowiązującym Foldable jest to, że foldLeft i foldRight powinny być spójne z foldMap dla operacji monoidalnych, np. dodawanie na koniec listy dla foldLeft i dodawanie na początek dla foldRight. Niemniej foldLeft i foldRight nie muszą być zgodne ze sobą nawzajem: w rzeczywistości często produkują odwrotne rezultaty.

Najprostszą rzeczą, którą możemy zrobić z foldMap to użyć funkcji identity i uzyskać tym samym fold (naturalną sumę elementów monoidalnych), z dodatkowymi wariantami pozwalającymi dobrać odpowiednią metodę zależnie od kryteriów wydajnościowych:

  def fold[A: Monoid](t: F[A]): A = ...
  def sumr[A: Monoid](fa: F[A]): A = ...
  def suml[A: Monoid](fa: F[A]): A = ...

Gdy uczyliśmy się o Monoidzie, napisaliśmy:

  scala> templates.foldLeft(Monoid[TradeTemplate].zero)(_ |+| _)

Teraz wiemy już, że było to niemądre i powinniśmy zrobić tak:

  scala> templates.toIList.fold
  res: TradeTemplate = TradeTemplate(
                         List(2017-08-05,2017-09-05),
                         Some(USD),
                         Some(false))

.fold nie zadziała na klasie List z biblioteki standardowej, ponieważ ta definiuje już metodę o nazwie fold, która robi coś podobnego na swój własny sposób.

Osobliwie nazywająca się metoda intercalate wstawia konkretną instancję typu A pomiędzy każde dwa elementy przed wykonaniem fold.

  def intercalate[A: Monoid](fa: F[A], a: A): A = ...

i jest tym samym uogólnioną wersją mkString:

  scala> List("foo", "bar").intercalate(",")
  res: String = "foo,bar"

foldLeft pozwala na dostęp do konkretnego elementu poprzez jego indeks oraz daje nam kilka innych, blisko związanych metod:

  def index[A](fa: F[A], i: Int): Option[A] = ...
  def indexOr[A](fa: F[A], default: =>A, i: Int): A = ...
  def length[A](fa: F[A]): Int = ...
  def count[A](fa: F[A]): Int = length(fa)
  def empty[A](fa: F[A]): Boolean = ...
  def element[A: Equal](fa: F[A], a: A): Boolean = ...

Scalaz jest biblioteką czystą, składającą się wyłącznie z funkcji totalnych. Tam, gdzie List.apply wyrzuca wyjątek, Foldable.index zwraca Option[A] oraz pozwala użyć wygodnego indexOr, który zwraca A, bazując na wartości domyślnej. .element podobny jest do .contains z biblioteki standardowej, ale używa Equal zamiast niejasno zdefiniowanego pojęcia równości pochodzącego z JVMa.

Metody te naprawdę wyglądają jak API kolekcji. No i oczywiście każdy obiekt mający instancje Foldable może być przekonwertowany na listę:

  def toList[A](fa: F[A]): List[A] = ...

Istnieją również konwersje do innych typów danych zarówno z biblioteki standardowej, jak i Scalaz, takie jak: .toSet, .toVector, .toStream, .to[T <: TraversableLike], .toIList itd.

Dostępne są również przydatne metody do weryfikacji predykatów

  def filterLength[A](fa: F[A])(f: A => Boolean): Int = ...
  def all[A](fa: F[A])(p: A => Boolean): Boolean = ...
  def any[A](fa: F[A])(p: A => Boolean): Boolean = ...

filterLength zlicza elementy, które spełniają predykat, all i any zwracają true, jeśli wszystkie (lub jakikolwiek) elementy spełniają predykat i mogą zakończyć działanie bez sprawdzania wszystkich elementów.

Możemy też podzielić F[A] na części bazując na kluczu B za pomocą metody splitBy

  def splitBy[A, B: Equal](fa: F[A])(f: A => B): IList[(B, Nel[A])] = ...
  def splitByRelation[A](fa: F[A])(r: (A, A) => Boolean): IList[Nel[A]] = ...
  def splitWith[A](fa: F[A])(p: A => Boolean): List[Nel[A]] = ...
  def selectSplit[A](fa: F[A])(p: A => Boolean): List[Nel[A]] = ...
  
  def findLeft[A](fa: F[A])(f: A => Boolean): Option[A] = ...
  def findRight[A](fa: F[A])(f: A => Boolean): Option[A] = ...

na przykład

  scala> IList("foo", "bar", "bar", "faz", "gaz", "baz").splitBy(_.charAt(0))
  res = [(f, [foo]), (b, [bar, bar]), (f, [faz]), (g, [gaz]), (b, [baz])]

Zwróć uwagę, że otrzymaliśmy dwa elementy zaindeksowane za pomocą 'b'.

splitByRelation pozwala uniknąć dostarczania instancji Equal, ale za to wymaga podania operatora porównującego.

splitWith dzieli elementy na grupy, które spełniają i nie spełniają predykatu. selectSplit wybiera grupy elementów, które spełniają predykat, a pozostałe odrzuca. To jedna z tych rzadkich sytuacji gdzie dwie metody mają tę samą sygnaturę, ale działają inaczej.

findLeft i findRight pozwalając znaleźć pierwszy element (od lewej lub prawej), który spełnia predykat.

Dalej korzystając z Equal i Order dostajemy metody distinct, które zwracają elementy unikalne.

  def distinct[A: Order](fa: F[A]): IList[A] = ...
  def distinctE[A: Equal](fa: F[A]): IList[A] = ...
  def distinctBy[A, B: Equal](fa: F[A])(f: A => B): IList[A] =

distinct jest zaimplementowany w sposób bardziej wydajny niż distinctE, ponieważ może bazować na kolejności, a dzięki niej odszukiwać elementy unikalne w sposób podobny do tego, w jaki działa algorytm quicksort. Dzięki temu jest zdecydowanie szybszy niż List.distinct. Struktury danych (takie jak zbiory) mogą implementować distinct w swoich Foldable bez dodatkowego wysiłku.

distinctBy pozwala na grupowanie, bazując na rezultacie wywołania podanej funkcji na każdym z oryginalnych elementów. Przykładowe użycie: grupowanie imion ze względu na pierwszą literę słowa.

Możemy wykorzystać Order również do odszukiwania elementów minimalnych i maksymalnych (lub obu ekstremów), wliczając w to warianty używające Of, lub By aby najpierw przemapować elementy do innego typu lub użyć innego typu do samego porównania.

  def maximum[A: Order](fa: F[A]): Option[A] = ...
  def maximumOf[A, B: Order](fa: F[A])(f: A => B): Option[B] = ...
  def maximumBy[A, B: Order](fa: F[A])(f: A => B): Option[A] = ...
  
  def minimum[A: Order](fa: F[A]): Option[A] = ...
  def minimumOf[A, B: Order](fa: F[A])(f: A => B): Option[B] = ...
  def minimumBy[A, B: Order](fa: F[A])(f: A => B): Option[A] = ...
  
  def extrema[A: Order](fa: F[A]): Option[(A, A)] = ...
  def extremaOf[A, B: Order](fa: F[A])(f: A => B): Option[(B, B)] = ...
  def extremaBy[A, B: Order](fa: F[A])(f: A => B): Option[(A, A)] =

Możemy na przykład zapytać o to, który element typu String jest maksimum ze względu (By) na swoją długość lub jaka jest maksymalna długość elementów (Of).

  scala> List("foo", "fazz").maximumBy(_.length)
  res: Option[String] = Some(fazz)
  
  scala> List("foo", "fazz").maximumOf(_.length)
  res: Option[Int] = Some(4)

Podsumowuje to kluczowe funkcjonalności Foldable. Cokolwiek spodziewalibyśmy się zobaczyć w API kolekcji, jest już prawdopodobnie dostępna dzięki Foldable, a jeśli nie jest, to prawdopodobnie być powinno.

Na koniec spojrzymy na kilka wariacji metod, które widzieliśmy już wcześniej. Zacznijmy od tych, które przyjmują instancję typu Semigroup zamiast Monoid:

  def fold1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  def foldMap1Opt[A, B: Semigroup](fa: F[A])(f: A => B): Option[B] = ...
  def sumr1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  def suml1Opt[A: Semigroup](fa: F[A]): Option[A] = ...
  ...

zwracając tym samym Option, aby móc obsłużyć puste struktury danych (Semigroup nie definiuje elementu zerowego).

Typeklasa Foldable1 zawiera dużo więcej wariantów bazujących na Semigroupie (wszystkie z sufiksem 1) i używanie jej ma sens dla struktur, które nigdy nie są puste, nie wymagając definiowania pełnego Monoidu dla elementów.

Co ważne, istnieją również warianty pracujące w oparciu o typy monadyczne. Używaliśmy już foldLeftM, kiedy po raz pierwszy pisaliśmy logikę biznesową naszej aplikacji. Teraz wiemy, że pochodzi ona z Foldable:

  def foldLeftM[G[_]: Monad, A, B](fa: F[A], z: B)(f: (B, A) => G[B]): G[B] = ...
  def foldRightM[G[_]: Monad, A, B](fa: F[A], z: =>B)(f: (A, =>B) => G[B]): G[B] = ...
  def foldMapM[G[_]: Monad, A, B: Monoid](fa: F[A])(f: A => G[B]): G[B] = ...
  def findMapM[M[_]: Monad, A, B](fa: F[A])(f: A => M[Option[B]]): M[Option[B]] = ...
  def allM[G[_]: Monad, A](fa: F[A])(p: A => G[Boolean]): G[Boolean] = ...
  def anyM[G[_]: Monad, A](fa: F[A])(p: A => G[Boolean]): G[Boolean] = ...
  ...

5.4.3 Traverse

Traverse to skrzyżowanie Functora z Foldable.

  trait Traverse[F[_]] extends Functor[F] with Foldable[F] {
    def traverse[G[_]: Applicative, A, B](fa: F[A])(f: A => G[B]): G[F[B]]
    def sequence[G[_]: Applicative, A](fga: F[G[A]]): G[F[A]] = ...
  
    def reverse[A](fa: F[A]): F[A] = ...
  
    def zipL[A, B](fa: F[A], fb: F[B]): F[(A, Option[B])] = ...
    def zipR[A, B](fa: F[A], fb: F[B]): F[(Option[A], B)] = ...
    def indexed[A](fa: F[A]): F[(Int, A)] = ...
    def zipWithL[A, B, C](fa: F[A], fb: F[B])(f: (A, Option[B]) => C): F[C] = ...
    def zipWithR[A, B, C](fa: F[A], fb: F[B])(f: (Option[A], B) => C): F[C] = ...
  
    def mapAccumL[S, A, B](fa: F[A], z: S)(f: (S, A) => (S, B)): (S, F[B]) = ...
    def mapAccumR[S, A, B](fa: F[A], z: S)(f: (S, A) => (S, B)): (S, F[B]) = ...
  }

Na początku rozdziału pokazaliśmy, jak ważne są metody traverse i sequence, gdy chcemy odwrócić kolejność konstruktorów typu (np. z List[Future[_]] na Future[List[_]]).

W Foldable nie mogliśmy założyć, że reverse jest pojęciem uniwersalnym, ale sprawa wygląda zupełnie inaczej, gdy mamy do dyspozycji Traverse.

Możemy też zipować ze sobą dwie rzeczy, które mają instancję Traverse, dostając None, gdy jedna ze stron nie ma już więcej elementów. Specjalnym wariantem tej operacji jest dodanie indeksów do każdego elementu za pomocą indexed.

zipWithL i zipWithR pozwalają połączyć elementy w nowy typ i od razu stworzyć F[C].

mapAccumL i mapAccumR to standardowe map połączone z akumulatorem. Jeśli nawyki z Javy każą nam sięgnąć po zmienna typu var i używać jej wewnątrz map, to najprawdopodobniej powinniśmy użyć mapAccumL.

Powiedzmy, że mamy listę słów i chcielibyśmy ukryć te, które już wcześniej widzieliśmy. Chcemy, aby algorytm działał również dla nieskończonych strumieni danych, a więc kolekcja może być przetworzona jedynie raz.

  scala> val freedom =
  """We campaign for these freedoms because everyone deserves them.
     With these freedoms, the users (both individually and collectively)
     control the program and what it does for them."""
     .split("\\s+")
     .toList
  
  scala> def clean(s: String): String = s.toLowerCase.replaceAll("[,.()]+", "")
  
  scala> freedom
         .mapAccumL(Set.empty[String]) { (seen, word) =>
           val cleaned = clean(word)
           (seen + cleaned, if (seen(cleaned)) "_" else word)
         }
         ._2
         .intercalate(" ")
  
  res: String =
  """We campaign for these freedoms because everyone deserves them.
     With _ _ the users (both individually and collectively)
     control _ program _ what it does _ _"""

Na koniec Traverse1, podobnie jak Foldable1, dostarcza warianty wspomnianych metod dla struktur danych, które nigdy nie są puste, przyjmując słabszą Semigroupę zamiast Monoidu i Apply zamiast Applicative. Przypomnijmy, że Semigroup nie musi dostarczać .empty, a Apply nie wymaga .point.

5.4.4 Align

Align służy do łączenia i wyrównywania wszystkiego, co ma instancję typu Functor. Zanim spojrzymy na Align, poznajmy typ danych \&/ (wymawiany jako te, these lub hurray!),

  sealed abstract class \&/[+A, +B]
  final case class This[A](aa: A) extends (A \&/ Nothing)
  final case class That[B](bb: B) extends (Nothing \&/ B)
  final case class Both[A, B](aa: A, bb: B) extends (A \&/ B)

A więc jest to wyrażenie alternatywy łącznej OR: A lub B, lub A i B jednocześnie.

  @typeclass trait Align[F[_]] extends Functor[F] {
    def alignWith[A, B, C](f: A \&/ B => C): (F[A], F[B]) => F[C]
    def align[A, B](a: F[A], b: F[B]): F[A \&/ B] = ...
  
    def merge[A: Semigroup](a1: F[A], a2: F[A]): F[A] = ...
  
    def pad[A, B]: (F[A], F[B]) => F[(Option[A], Option[B])] = ...
    def padWith[A, B, C](f: (Option[A], Option[B]) => C): (F[A], F[B]) => F[C] = ...

alignWith przyjmuje funkcję z albo A, albo B (albo obu) na C i zwraca wyniesioną funkcję z tupli F[A] i F[B] na F[C]. align konstruuje \&/ z dwóch F[_].

merge pozwala nam połączyć dwie instancje F[A] tak długo, jak jesteśmy w stanie dostarczyć instancję Semigroup[A]. Dla przykładu, Semigroup[Map[K,V]]] deleguje logikę do Semigroup[V], łącząc wartości dla tych samych kluczy, a w konsekwencji sprawiając, że Map[K, List[A]] zachowuje się jak multimapa:

  scala> Map("foo" -> List(1)) merge Map("foo" -> List(1), "bar" -> List(2))
  res = Map(foo -> List(1, 1), bar -> List(2))

a Map[K, Int] po prostu sumuje wartości.

  scala> Map("foo" -> 1) merge Map("foo" -> 1, "bar" -> 2)
  res = Map(foo -> 2, bar -> 2)

.pad i .padWith służą do częściowego łącznie struktur danych, które mogą nie mieć wymaganych wartości po jednej ze stron. Dla przykładu, jeśli chcielibyśmy zagregować niezależne głosy i zachować informację skąd one pochodziły:

  scala> Map("foo" -> 1) pad Map("foo" -> 1, "bar" -> 2)
  res = Map(foo -> (Some(1),Some(1)), bar -> (None,Some(2)))
  
  scala> Map("foo" -> 1, "bar" -> 2) pad Map("foo" -> 1)
  res = Map(foo -> (Some(1),Some(1)), bar -> (Some(2),None))

Istnieją też wygodne warianty align, które używają struktury \&/

  ...
    def alignSwap[A, B](a: F[A], b: F[B]): F[B \&/ A] = ...
    def alignA[A, B](a: F[A], b: F[B]): F[Option[A]] = ...
    def alignB[A, B](a: F[A], b: F[B]): F[Option[B]] = ...
    def alignThis[A, B](a: F[A], b: F[B]): F[Option[A]] = ...
    def alignThat[A, B](a: F[A], b: F[B]): F[Option[B]] = ...
    def alignBoth[A, B](a: F[A], b: F[B]): F[Option[(A, B)]] = ...
  }

i które powinny być jasne po przeczytaniu sygnatur. Przykłady:

  scala> List(1,2,3) alignSwap List(4,5)
  res = List(Both(4,1), Both(5,2), That(3))
  
  scala> List(1,2,3) alignA List(4,5)
  res = List(Some(1), Some(2), Some(3))
  
  scala> List(1,2,3) alignB List(4,5)
  res = List(Some(4), Some(5), None)
  
  scala> List(1,2,3) alignThis List(4,5)
  res = List(None, None, Some(3))
  
  scala> List(1,2,3) alignThat List(4,5)
  res = List(None, None, None)
  
  scala> List(1,2,3) alignBoth List(4,5)
  res = List(Some((1,4)), Some((2,5)), None)

Zauważ, że warianty A i B używają alternatywy łącznej, a This i That są wykluczające, zwracając None, gdy wartość istnieje po obu stronach lub nie istnieje po wskazanej stronie.

5.5 Wariancja

Musimy wrócić na moment do Functora i omówić jego przodka, którego wcześniej zignorowaliśmy

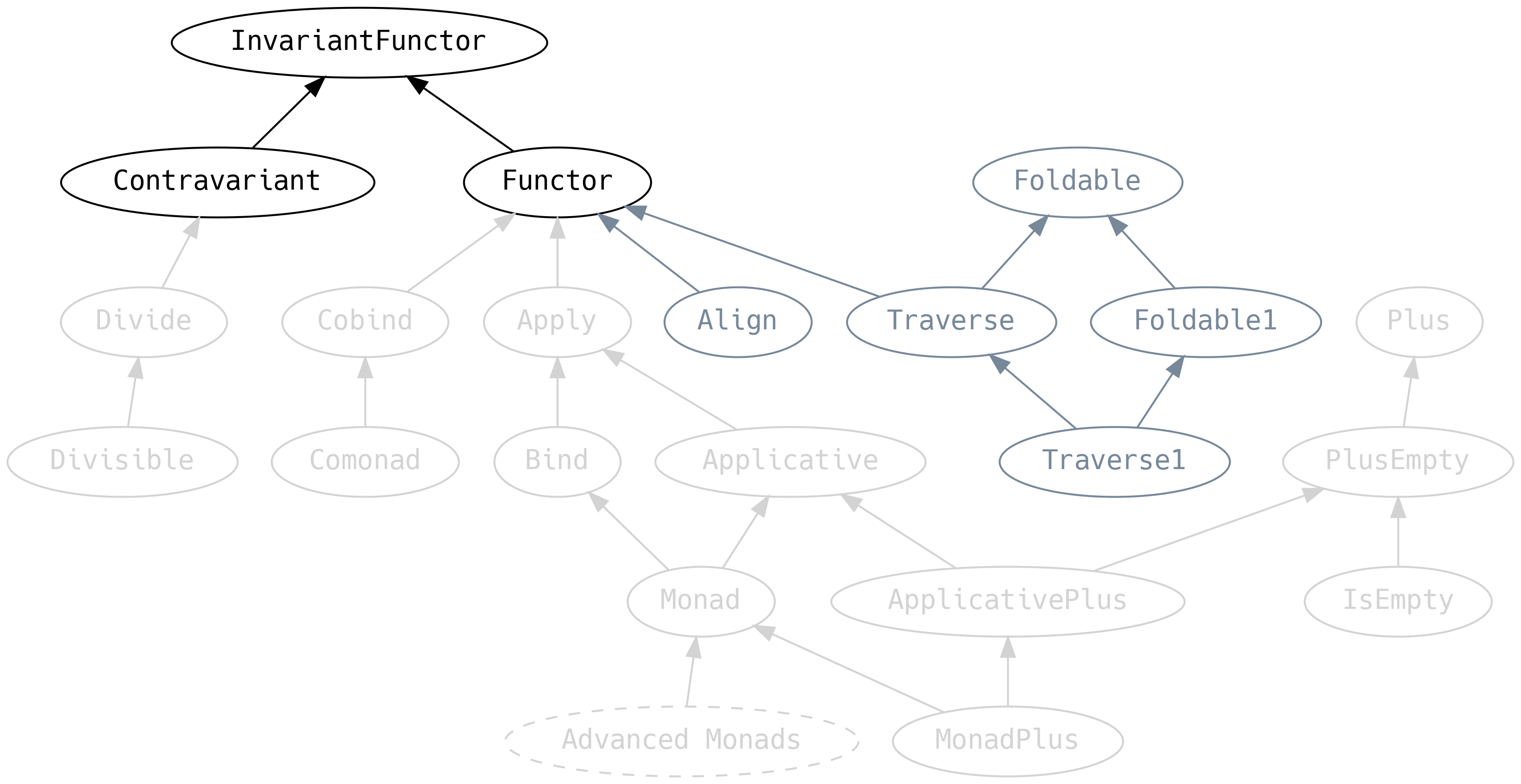
InvariantFunctor, znany również jako funktor wykładniczy, definiuje metodę xmap, która pozwala zamienić F[A] w F[B] jeśli przekażemy do niej funkcje z A na B i z B na A.

Functor to skrócona nazwa na to, co powinno nazywać się funktorem kowariantnym. Podobnie Contravariant to tak naprawdę funktor kontrawariantny.

Functor implementuje metodę xmap za pomocą map i ignoruje funkcję z B na A. Contravariant z kolei implementuje ją z użyciem contramap i ignoruje funkcję z A na B:

  @typeclass trait InvariantFunctor[F[_]] {
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B]
    ...
  }
  
  @typeclass trait Functor[F[_]] extends InvariantFunctor[F] {
    def map[A, B](fa: F[A])(f: A => B): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = map(fa)(f)
    ...
  }
  
  @typeclass trait Contravariant[F[_]] extends InvariantFunctor[F] {
    def contramap[A, B](fa: F[A])(f: B => A): F[B]
    def xmap[A, B](fa: F[A], f: A => B, g: B => A): F[B] = contramap(fa)(g)
    ...
  }

Co istotne, określenia kowariantny, kontrawariantny i inwariantny, mimo że związane na poziomie teoretycznym, nie przekładają się bezpośrednio na znaną ze Scali wariancję typów (czyli modyfikatory + i - umieszczane przy parametrach typów). Inwariancja oznacza tutaj, że możliwym jest przetłumaczenie zawartości F[A] do F[B]. Używając identity, możemy zobaczyć, że A może być w bezpieczny sposób zrzutowane (w górę lub w dół) do B, zależnie od wariancji funktora.

.map może być rozumiana poprzez swój kontrakt: “jeśli dasz mi F dla A i sposób na zamianę A w B, wtedy dam ci F dla B”.

Podobnie, .contramap mówi, że: “jeśli dasz mi F dla A i sposób na zamianę B w A, wtedy dam ci F dla B”.

Rozważymy następujący przykład: w naszej aplikacji wprowadzamy typy domenowe Alpha, Beta i Gamma, aby zabezpieczyć się przed pomieszaniem liczb w kalkulacjach finansowych:

  final case class Alpha(value: Double)

ale sprawia to, że nie mamy żadnych instancji typeklas dla tych nowych typów. Jeśli chcielibyśmy użyć takich wartości w JSONie, musielibyśmy dostarczyć JsEncoder i JsDecoder.

Jednakże, JsEncoder ma instancję typeklasy Contravariant a JsDecoder typeklasy Functor, a więc możemy wyderywować potrzebne nam instancje, spełniając kontrakt:

• “jeśli dasz mi JsDecoder dla Double i sposób na zamianę Double w Alpha, wtedy dam ci JsDecoder dla Alpha”.
• “jeśli dasz mi JsEncoder dla Double i sposób na zamianę Alpha w Double, wtedy dam ci JsEncoder dla Alpha”.

  object Alpha {
    implicit val decoder: JsDecoder[Alpha] = JsDecoder[Double].map(Alpha(_))
    implicit val encoder: JsEncoder[Alpha] = JsEncoder[Double].contramap(_.value)
  }

Metody w klasie mogą ustawić swoje parametry typu w pozycji kontrawariantnej (parametry metody) lub w pozycji kowariantnej (typ zwracany). Jeśli typeklasa łączy pozycje kowariantne i kontrawariantne może oznaczać to, że ma instancję typeklasy InvariantFunctor, ale nie Functor ani Contrawariant.

5.6 Apply i Bind

Potraktuj tę część jako rozgrzewkę przed typami Applicative i Monad

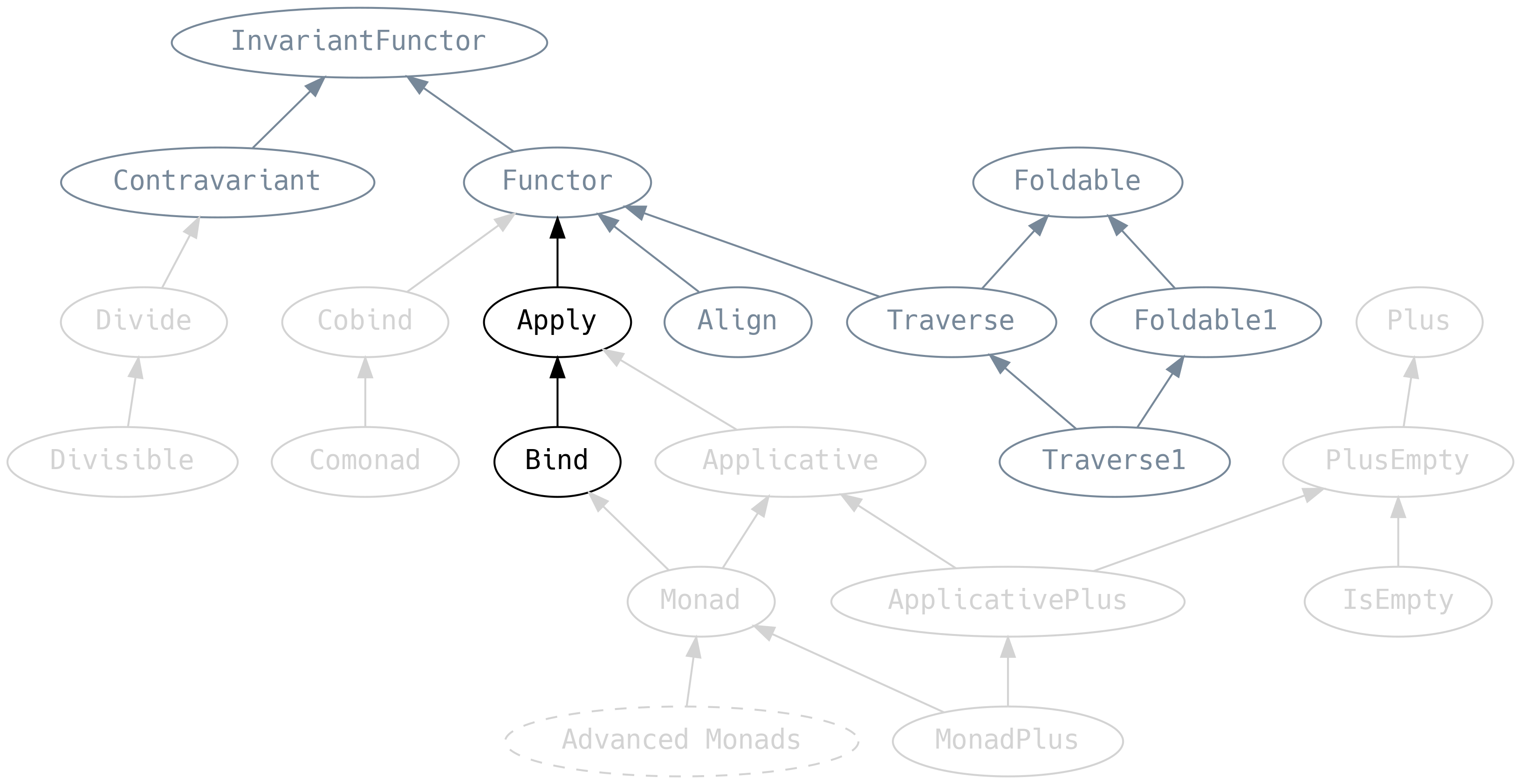
5.6.1 Apply

Apply rozszerza typeklasę Functor poprzez dodanie metody ap, która jest podobna do map w tym, że aplikuje otrzymaną funkcje na wartościach. Jednak w przypadku ap funkcja jest opakowana w ten sam kontekst co wartości, które są do niej przekazywane.

  @typeclass trait Apply[F[_]] extends Functor[F] {
    @op("<*>") def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B]
    ...

Warto poświęcić chwilę na zastanowienie się co to znaczy, że prosta struktura danych, taka jak Option[A], posiada następującą implementację .ap

  implicit def option[A]: Apply[Option[A]] = new Apply[Option[A]] {
    override def ap[A, B](fa: =>Option[A])(f: =>Option[A => B]) = f match {
      case Some(ff) => fa.map(ff)
      case None    => None
    }
    ...
  }

Aby zaimplementować .ap, musimy najpierw wydostać funkcję ff: A => B z f: Option[A => B], a następnie możemy przemapować fa z jej użyciem. Ekstrakcja funkcji z kontekstu to ważna funkcjonalność, którą przynosi Apply. Pozwala tym samym na łączenie wielu funkcji wewnątrz jednego kontekstu.

Wracając do Apply, znajdziemy tam rodzinę funkcji applyX, która pozwala nam łączyć równoległe obliczenia, a następnie mapować ich połączone wyniki:

  @typeclass trait Apply[F[_]] extends Functor[F] {
    ...
    def apply2[A,B,C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] = ...
    def apply3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
    ...
    def apply12[...]

Potraktuj .apply2 jako obietnicę: “jeśli dasz mi F z A i F z B oraz sposób na połączenie A i B w C, wtedy mogę dać ci F z C”. Istnieje wiele zastosowań dla tej obietnicy, a 2 najważniejsze to:

• tworzenie typeklas dla produktu C z jego składników A i B
• wykonywanie efektów równolegle, jak w przypadku algebr dla drone i google, które stworzyliśmy w Rozdziale 3, a następnie łączenie ich wyników.

W rzeczy samej, Apply jest na tyle użyteczne, że ma swoją własną składnię:

  implicit class ApplyOps[F[_]: Apply, A](self: F[A]) {
    def *>[B](fb: F[B]): F[B] = Apply[F].apply2(self,fb)((_,b) => b)
    def <*[B](fb: F[B]): F[A] = Apply[F].apply2(self,fb)((a,_) => a)
    def |@|[B](fb: F[B]): ApplicativeBuilder[F, A, B] = ...
  }
  
  class ApplicativeBuilder[F[_]: Apply, A, B](a: F[A], b: F[B]) {
    def tupled: F[(A, B)] = Apply[F].apply2(a, b)(Tuple2(_))
    def |@|[C](cc: F[C]): ApplicativeBuilder3[C] = ...
  
    sealed abstract class ApplicativeBuilder3[C](c: F[C]) {
      ..ApplicativeBuilder4
        ...
          ..ApplicativeBuilder12
  }

której użyliśmy w Rozdziale 3:

  (d.getBacklog |@| d.getAgents |@| m.getManaged |@| m.getAlive |@| m.getTime)

Operatory <* i *> (prawy i lewy ptak) oferują wygodny sposób na zignorowanie wyniku jednego z dwóch równoległych efektów.

Niestety, mimo wygody, którą daje operator |@\, jest z nim jeden problem: dla każdego kolejnego efektu alokowany jest nowy obiekt typu ApplicativeBuilder. Gdy prędkość obliczeń ograniczona jest przez operacje I/O nie ma to znaczenia. Jednak gdy wykonujesz obliczenia w całości na CPU, lepiej jest użyć krotnego wynoszenia (lifting with arity), które nie produkuje żadnych obiektów pośrednich:

  def ^[F[_]: Apply,A,B,C](fa: =>F[A],fb: =>F[B])(f: (A,B) =>C): F[C] = ...
  def ^^[F[_]: Apply,A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: (A,B,C) =>D): F[D] = ...
  ...
  def ^^^^^^[F[_]: Apply, ...]

na przykład:

  ^^^^(d.getBacklog, d.getAgents, m.getManaged, m.getAlive, m.getTime)

Możemy też zawołać applyX bezpośrednio:

  Apply[F].apply5(d.getBacklog, d.getAgents, m.getManaged, m.getAlive, m.getTime)

Mimo tego, że Apply używany jest najczęściej z efektami, działa równie dobrze ze strukturami danych. Rozważ przepisanie

  for {
    foo <- data.foo: Option[String]
    bar <- data.bar: Option[Int]
  } yield foo + bar.shows

jako

  (data.foo |@| data.bar)(_ + _.shows)

Gdy chcemy jedynie połączyć wyniki w tuple, istnieją metody, które służą dokładnie do tego:

  @op("tuple") def tuple2[A,B](fa: =>F[A],fb: =>F[B]): F[(A,B)] = ...
  def tuple3[A,B,C](fa: =>F[A],fb: =>F[B],fc: =>F[C]): F[(A,B,C)] = ...
  ...
  def tuple12[...]

  (data.foo tuple data.bar) : Option[(String, Int)]

Dostępne są też uogólnione wersje ap dla więcej niż dwóch parametrów:

  def ap2[A,B,C](fa: =>F[A],fb: =>F[B])(f: F[(A,B) => C]): F[C] = ...
  def ap3[A,B,C,D](fa: =>F[A],fb: =>F[B],fc: =>F[C])(f: F[(A,B,C) => D]): F[D] = ...
  ...
  def ap12[...]

razem z wariantami .lift, które przyjmują zwykłe funkcje i wynoszą je do kontekstu F[_], uogólniając Functor.lift

  def lift2[A,B,C](f: (A,B) => C): (F[A],F[B]) => F[C] = ...
  def lift3[A,B,C,D](f: (A,B,C) => D): (F[A],F[B],F[C]) => F[D] = ...
  ...
  def lift12[...]

oraz .apF, częściowo zaaplikowana wersja ap

  def apF[A,B](f: =>F[A => B]): F[A] => F[B] = ...

A na koniec .forever

  def forever[A, B](fa: F[A]): F[B] = ...

który powtarza efekt w nieskończoność bez zatrzymywania się. Przy jej użyciu instancja Apply musi być zabezpieczona prze przepełnieniem stosu (stack-safe), w przeciwnym wypadku wywołanie spowoduje StackOverflowError.

5.6.2 Bind

Bind wprowadza metodę .bind, która jest synonimiczna do .flatMap i pozwala na mapowanie efektów/struktur danych z użyciem funkcji zwracających nowy efekt/strukturę danych bez wprowadzania dodatkowych zagnieżdżeń.

  @typeclass trait Bind[F[_]] extends Apply[F] {
  
    @op(">>=") def bind[A, B](fa: F[A])(f: A => F[B]): F[B]
    def flatMap[A, B](fa: F[A])(f: A => F[B]): F[B] = bind(fa)(f)
  
    override def ap[A, B](fa: =>F[A])(f: =>F[A => B]): F[B] =
      bind(f)(x => map(fa)(x))
    override def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] =
      bind(fa)(a => map(fb)(b => f(a, b)))
  
    def join[A](ffa: F[F[A]]): F[A] = bind(ffa)(identity)
  
    def mproduct[A, B](fa: F[A])(f: A => F[B]): F[(A, B)] = ...
    def ifM[B](value: F[Boolean], t: =>F[B], f: =>F[B]): F[B] = ...
  
  }

Metoda .join może wydawać się znajoma tym, którzy używali .flatten z biblioteki standardowej. Przyjmuje ona zagnieżdżone konteksty i łączy je w jeden.

Wprowadzone zostały kombinatory pochodne dla .ap i .apply2, aby zapewnić spójność z .bind. Zobaczymy później, że to wymaganie niesie ze sobą konsekwencje dla potencjalnego zrównoleglania obliczeń.

mproduct przypomina Functor.fproduct i paruje wejście i wyjście funkcji wewnątrz F.

ifM to sposób na tworzenie warunkowych struktur danych lub efektów:

  scala> List(true, false, true).ifM(List(0), List(1, 1))
  res: List[Int] = List(0, 1, 1, 0)

ifM i ap są zoptymalizowane do cachowania i reużywania gałezi kodu. Porównajmy je z dłuższą wersją

  scala> List(true, false, true).flatMap { b => if (b) List(0) else List(1, 1) }

która produkuje nowe List(0) i List(1, 1) za każdym razem, gdy dana gałąź jest wywoływana.

Bind wprowadza też specjalne operatory:

  implicit class BindOps[F[_]: Bind, A] (self: F[A]) {
    def >>[B](b: =>F[B]): F[B] = Bind[F].bind(self)(_ => b)
    def >>![B](f: A => F[B]): F[A] = Bind[F].bind(self)(a => f(a).map(_ => a))
  }

Używając >> odrzucamy wejście do bind, a używając >>! odrzucamy wyjście`

5.7 Aplikatywy i monady

Z punkty widzenia oferowanych funkcjonalności, Applicative to Apply z dodaną metodą pure, a Monad rozszerza Applicative, dodając Bind.

  @typeclass trait Applicative[F[_]] extends Apply[F] {
    def point[A](a: =>A): F[A]
    def pure[A](a: =>A): F[A] = point(a)
  }
  
  @typeclass trait Monad[F[_]] extends Applicative[F] with Bind[F]

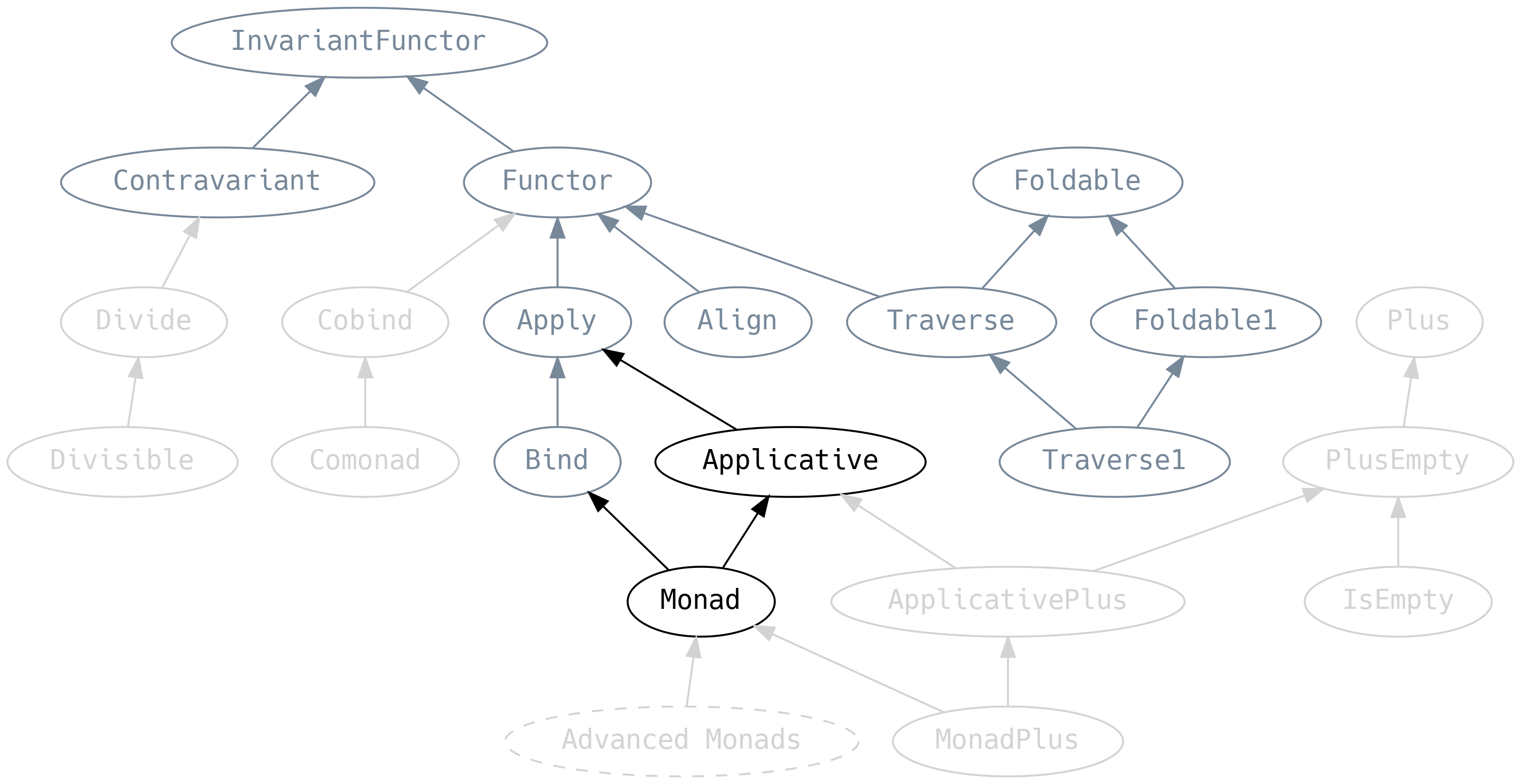
Pod wieloma względami Applicative i Monad są zwieńczeniem wszystkiego, co do tej pory widzieliśmy w tym rozdziale. .pure (lub .point - alias powszechnie używany przy strukturach danych) pozwala nam na tworzenie efektów lub struktur danych z pojedynczych wartości.

Instancje Applicative muszę spełniać prawa gwarantujące spójność metod:

• Tożsamość (Identity): fa <*> pure(identity) == fa (gdzie fa to F[A]) - zaaplikowanie pure(identity) nic nie zmienia
• Homomorfizm (Homomorphism): pure(a) <*> pure(ab) === pure(ab(a)), (gdzie ab to funkcja A => B) - zaaplikowanie funkcji osadzonej w kontekście F za pomocą pure na wartości potraktowanej w ten sam sposób jest równoznaczne z wywołaniem tej funkcji na wspomnianej wartości i wywołaniem pure na rezultacie.
• Zamiana (Interchange): pure(a) <*> fab === fab <*> pure(f => f(a)), (gdzie fab to F[A => B]) - pure jest tożsama lewo- i prawostronnie
• Mappy: map(fa)(f) === fa <*> pure(f)

Monad dodaje następujące prawa

• Tożsamość lewostronna (Left Identity): pure(a).bind(f) === f(a)
• Tożsamość prawostronna (Right Identity): a.bind(pure(_)) === a
• Łączność (Associativity): fa.bind(f).bind(g) === fa.bind(a => f(a).bind(g)) gdzie fa to F[A], f to A => F[B], a g to B => F[C].

Łączność mówi nam, że połączone wywołania bind muszą być zgodne z wywołaniami zagnieżdżonymi. Jednakże, nie oznacza to, że możemy zamieniać kolejność wywołań - to gwarantowałaby przemienność (commutativity). Dla przykładu, pamiętając, że flatMap to alias na bind, nie możemy zamienić

  for {
    _ <- machine.start(node1)
    _ <- machine.stop(node1)
  } yield true

na

  for {
    _ <- machine.stop(node1)
    _ <- machine.start(node1)
  } yield true

start i stop są nieprzemienne, ponieważ uruchomienie, a następnie zatrzymanie węzła jest czymś innym niż zatrzymanie i uruchomienie.

Nie mniej, zarówno start, jak i stop są przemienne same ze sobą samym, a więc możemy zamienić

  for {
    _ <- machine.start(node1)
    _ <- machine.start(node2)
  } yield true

na

  for {
    _ <- machine.start(node2)
    _ <- machine.start(node1)
  } yield true

Obie formy są równoznaczne w tym konkretnym przypadku, ale nie w ogólności. Robimy tutaj dużo założeń co do Google Container API, ale wydaje się to być rozsądnych wyjściem.

Okazuje się, że w konsekwencji powyższych praw Monada musi być przemienna, jeśli chcemy pozwolić na równoległe działanie metod applyX. W Rozdziale 3 oszukaliśmy uruchamiając efekty w ten sposób

  (d.getBacklog |@| d.getAgents |@| m.getManaged |@| m.getAlive |@| m.getTime)

ponieważ wiedzieliśmy, że są one ze sobą przemienne. Kiedy w dalszych rozdziałach zajmiemy się interpretacją naszej aplikacji, dostarczymy dowód na przemienność operacji lub pozwolimy na uruchomienie ich sekwencyjnie.

Subtelności sposobów radzenia sobie z porządkowaniem efektów, i tym, czym te efekty tak naprawdę są, zasługują na osobny rozdział. Porozmawiamy o nich przy Zaawansowanych monadach.

5.8 Dziel i rządź

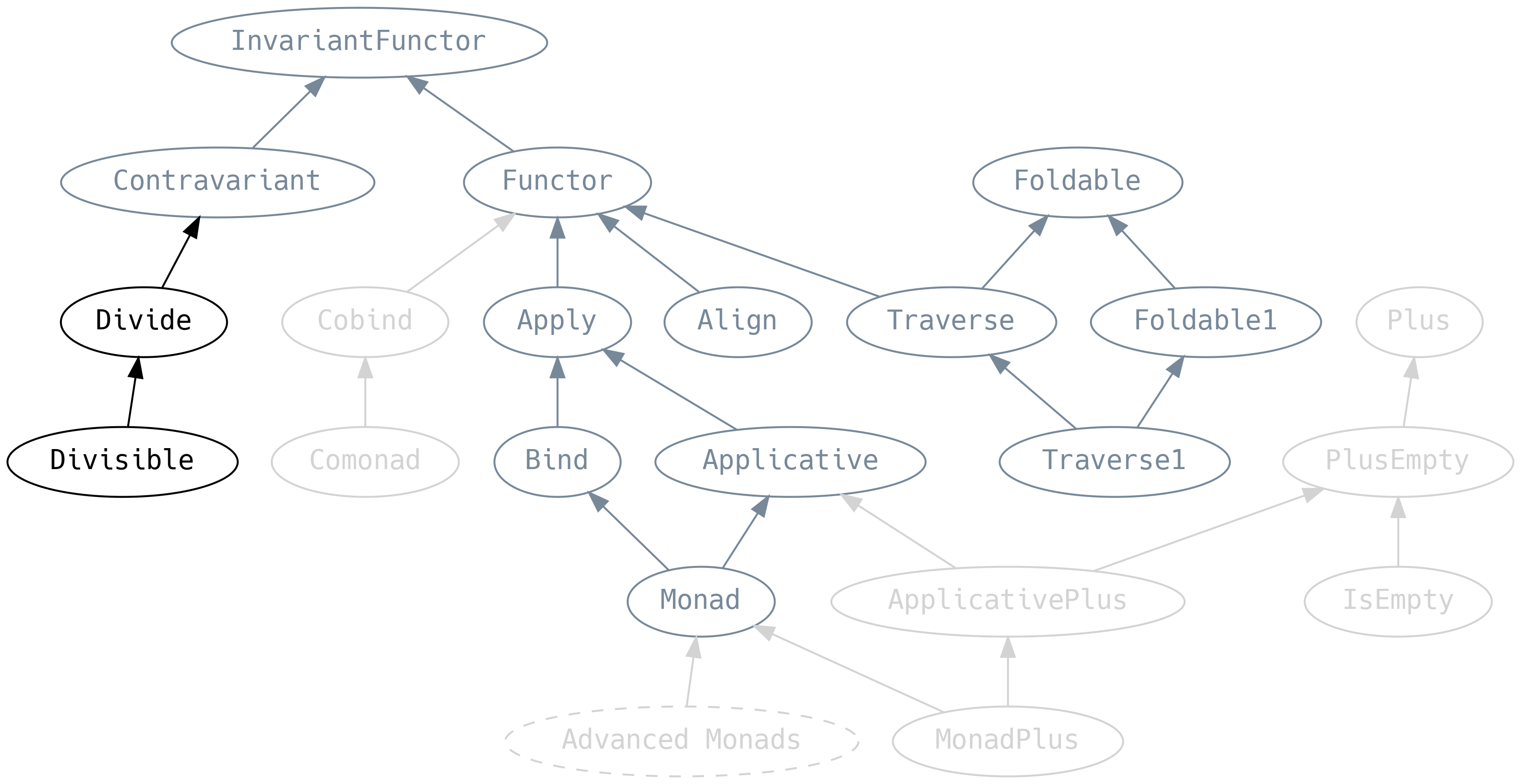
Divide to kontrawariantny odpowiednik Apply

  @typeclass trait Divide[F[_]] extends Contravariant[F] {
    def divide[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C] = divide2(fa, fb)(f)
  
    def divide1[A1, Z](a1: F[A1])(f: Z => A1): F[Z] = ...
    def divide2[A, B, C](fa: F[A], fb: F[B])(f: C => (A, B)): F[C] = ...
    ...
    def divide22[...] = ...

divide mówi nam, że jeśli potrafimy podzielić C na A i B oraz mamy do dyspozycji F[A] i F[B] to możemy stworzyć F[C]. Stąd też dziel i rządź.

Jest to świetny sposób na generowanie instancji kowariantnych typeklas dla typów będących produktami poprzez podzielenie tychże produktów na części. Scalaz oferuje instancje Divide[Equal], spróbujmy więc stworzyć Equal dla nowego typu Foo.

  scala> case class Foo(s: String, i: Int)
  scala> implicit val fooEqual: Equal[Foo] =
           Divide[Equal].divide2(Equal[String], Equal[Int]) {
             (foo: Foo) => (foo.s, foo.i)
           }
  scala> Foo("foo", 1) === Foo("bar", 1)
  res: Boolean = false

Podążając za Apply, Divide również dostarcza zwięzłą składnię dla tupli

  ...
    def tuple2[A1, A2](a1: F[A1], a2: F[A2]): F[(A1, A2)] = ...
    ...
    def tuple22[...] = ...
  }

Ogólnie rzecz biorąc, jeśli typeklasa, oprócz instancji Contravariant, jest w stanie dostarczyć również Divide, to znaczy, że jesteśmy w stanie wyderywować jej instancje dla dowolnej case klasy. Sprawa wygląda analogicznie dla typeklas kowariantnych z instancją Apply. Zgłębimy ten temat w rozdziale poświęconym Derywacji typeklas.

Divisible to odpowiednik Applicative dla rodziny Contravariant. Wprowadzana ona metodę .conquer, odpowiednik .pure:

  @typeclass trait Divisible[F[_]] extends Divide[F] {
    def conquer[A]: F[A]
  }

.conquer pozwala na tworzenie trywialnych implementacji, w których parametr typu jest ignorowany. Takie instancje nazywane są ogólnie kwantyfikowanymi (universally quantified). Na przykład, Divisible[Equal].conquer[INil[String]] tworzy instancję Equal, która zawsze zwraca true.

5.9 Plus

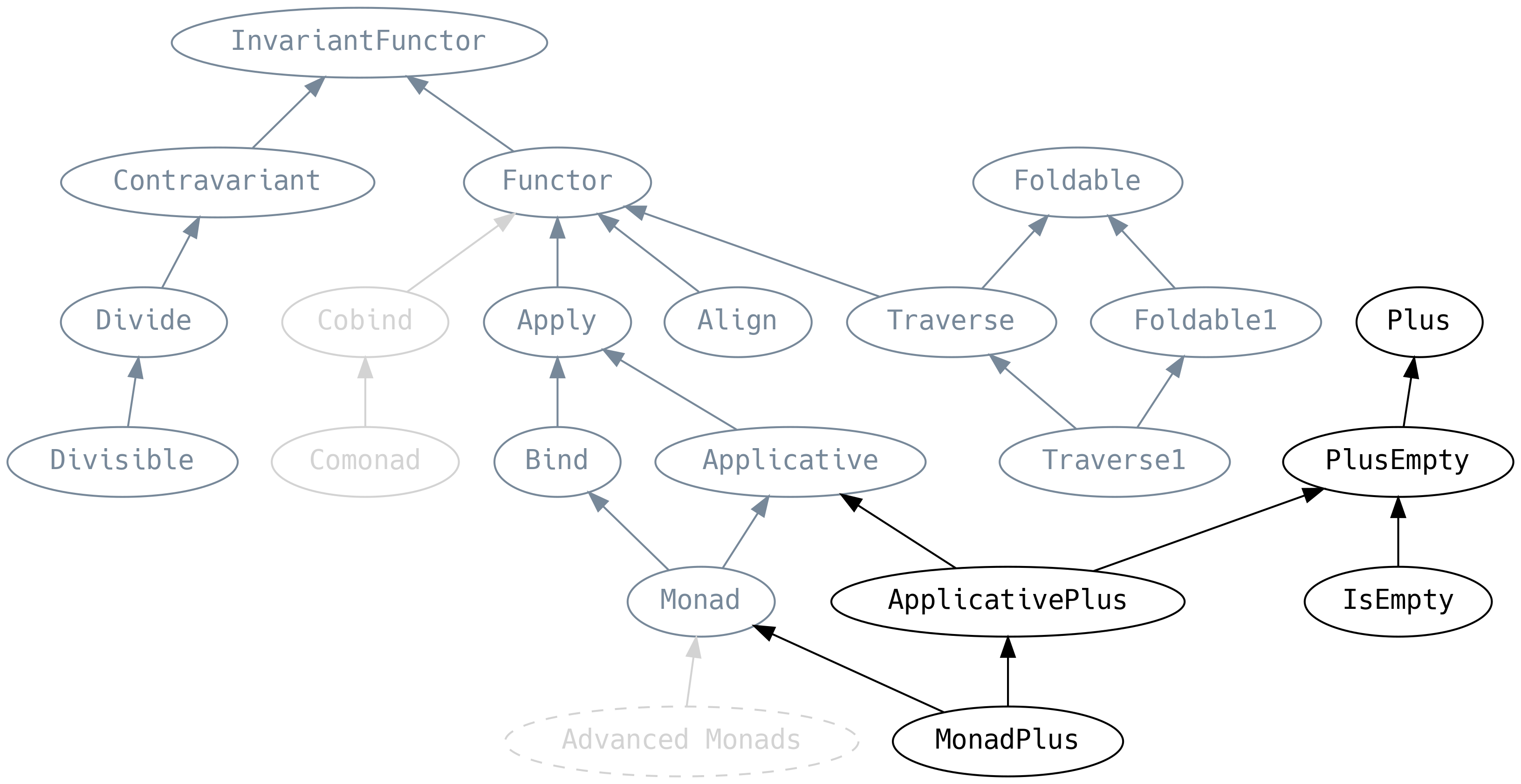
Plus to Semigroupa dla konstruktorów typu a PlusEmpty to odpowiednik Monoidu (obowiązują ich nawet te same prawa). Nowością jest typeklasa IsEmpty, która pozwala na sprawdzenie czy F[A] jest puste:

  @typeclass trait Plus[F[_]] {
    @op("<+>") def plus[A](a: F[A], b: =>F[A]): F[A]
  }
  @typeclass trait PlusEmpty[F[_]] extends Plus[F] {
    def empty[A]: F[A]
  }
  @typeclass trait IsEmpty[F[_]] extends PlusEmpty[F] {
    def isEmpty[A](fa: F[A]): Boolean
  }

Pozornie może się wydawać, że <+> zachowuje się tak samo, jak |+|:

  scala> List(2,3) |+| List(7)
  res = List(2, 3, 7)
  
  scala> List(2,3) <+> List(7)
  res = List(2, 3, 7)

Najlepiej jest przyjąć, że <+> operuje jedynie na F[_] nigdy nie patrząc na zawartość. Przyjęła się konwencja, że Plus ignoruje porażki i wybiera “pierwszego zwycięzcę”. Dzięki temu <+> może być używany jako mechanizm szybkiego wyjścia oraz obsługi porażek przez fallbacki.

  scala> Option(1) |+| Option(2)
  res = Some(3)
  
  scala> Option(1) <+> Option(2)
  res = Some(1)
  
  scala> Option.empty[Int] <+> Option(1)
  res = Some(1)

Na przykład, jeśli chcielibyśmy pominąć obiekty None wewnątrz NonEmptyList[Option[Int]] i wybrać pierwszego zwycięzcę (Some), możemy użyć <+> w połączeniu z Foldable1.foldRight1:

  scala> NonEmptyList(None, None, Some(1), Some(2), None)
         .foldRight1(_ <+> _)
  res: Option[Int] = Some(1)

Teraz, gdy znamy już Plus, okazuje się, że wcale nie musieliśmy zaburzać koherencji typeklas w sekcji o Rzeczach złączalnych (definiując lokalną instancję Monoid[Option[A]]). Naszym celem było “wybranie ostatniego zwycięzcy”, co jest tożsame z wybranie pierwszego po odwróceniu kolejności elementów. Zwróć uwagę na użycie Interceptora TIE z ccy i otc w odwróconej kolejności.

  implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
    (a, b) => TradeTemplate(a.payments |+| b.payments,
                            b.ccy <+> a.ccy,
                            b.otc <+> a.otc),
    TradeTemplate(Nil, None, None)
  )

Applicative i Monad mają wyspecjalizowaną wersję PlusEmpty

  @typeclass trait ApplicativePlus[F[_]] extends Applicative[F] with PlusEmpty[F]
  
  @typeclass trait MonadPlus[F[_]] extends Monad[F] with ApplicativePlus[F] {
    def unite[T[_]: Foldable, A](ts: F[T[A]]): F[A] = ...
  
    def withFilter[A](fa: F[A])(f: A => Boolean): F[A] = ...
  }

.unite pozwala nam zwinąć strukturę danych, używając PlusEmpty[F].monoid zamiast Monoidu zdefiniowanego dla typu wewnętrznego. Dla List[Either[String, Int]] oznacza to, że instancje Left[String] zamieniane są na .empty, a następnie wszytko jest złączane. Jest to wygodny sposób na pozbycie się błędów:

  scala> List(Right(1), Left("boo"), Right(2)).unite
  res: List[Int] = List(1, 2)
  
  scala> val boo: Either[String, Int] = Left("boo")
         boo.foldMap(a => a.pure[List])
  res: List[String] = List()
  
  scala> val n: Either[String, Int] = Right(1)
         n.foldMap(a => a.pure[List])
  res: List[Int] = List(1)

withFilter pozwala nam na użycie konstrukcji for, którą opisywaliśmy w Rozdziale 2. Można nawet powiedzieć, że Scala ma wbudowane wsparcie nie tylko dla Monad, ale i MonadPlus!

Wracając na moment do Foldable, możemy odkryć kilka metod, których wcześniej nie omawialiśmy:

  @typeclass trait Foldable[F[_]] {
    ...
    def msuml[G[_]: PlusEmpty, A](fa: F[G[A]]): G[A] = ...
    def collapse[X[_]: ApplicativePlus, A](x: F[A]): X[A] = ...
    ...
  }

msuml wykonuje fold, używając Monoidu z PlusEmpty[G], a collapse używa foldRight w kombinacji z instancją PlusEmpty typu docelowego:

  scala> IList(Option(1), Option.empty[Int], Option(2)).fold
  res: Option[Int] = Some(3) // uses Monoid[Option[Int]]
  
  scala> IList(Option(1), Option.empty[Int], Option(2)).msuml
  res: Option[Int] = Some(1) // uses PlusEmpty[Option].monoid
  
  scala> IList(1, 2).collapse[Option]
  res: Option[Int] = Some(1)

5.10 Samotne wilki

Niektóre z typeklas w Scalaz są w pełni samodzielne i nie należą do ogólnej hierarchii.

5.10.1 Zippy

  @typeclass trait Zip[F[_]]  {
    def zip[A, B](a: =>F[A], b: =>F[B]): F[(A, B)]
  
    def zipWith[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C)
                        (implicit F: Functor[F]): F[C] = ...
  
    def ap(implicit F: Functor[F]): Apply[F] = ...
  
    @op("<*|*>") def apzip[A, B](f: =>F[A] => F[B], a: =>F[A]): F[(A, B)] = ...
  
  }

Metoda kluczowa tutaj to zip. Jest to słabsza wersja Divide.tuple2. Jeśli dostępny jest Functor[F] to .zipWith może zachowywać się jak Apply.apply2. Używając ap, możemy nawet stworzyć pełnoprawne Apply[F] z instancji Zip[F] i Functor[F].

.apzip przyjmuje F[A] i wyniesioną funkcję F[A] => F[B] produkując F[(A, B)], podobnie do Functor.fproduct.

  @typeclass trait Unzip[F[_]]  {
    @op("unfzip") def unzip[A, B](a: F[(A, B)]): (F[A], F[B])
  
    def firsts[A, B](a: F[(A, B)]): F[A] = ...
    def seconds[A, B](a: F[(A, B)]): F[B] = ...
  
    def unzip3[A, B, C](x: F[(A, (B, C))]): (F[A], F[B], F[C]) = ...
    ...
    def unzip7[A ... H](x: F[(A, (B, ... H))]): ...
  }

Bazą jest unzip dzielący F[(A,B)] na F[A] i F[B], a firsts i seconds pozwalają na wybranie jednej z części. Co ważne, unzip jest odwrotnością zip.

Metody od unzip3 do unzip7 to aplikacje unzip pozwalające zmniejszyć ilość boilerplatu. Na przykład, jeśli dostaniemy garść zagnieżdżonych tupli to Unzip[Id] jest wygodnym sposobem na ich wypłaszczenie:

  scala> Unzip[Id].unzip7((1, (2, (3, (4, (5, (6, 7)))))))
  res = (1,2,3,4,5,6,7)

W skrócie, Zip i Unzip są słabszymi wersjami Divide i Apply dostarczającymi użyteczne funkcjonalności bez zobowiązywania F do składania zbyt wielu obietnic.

5.10.2 Optional

Optional to uogólnienie struktur danych, które mogą opcjonalnie zawierać jakąś wartość, np. Option lub Either.

Przypomnijmy, że \/ (dysjunkcja) ze Scalaz jest ulepszoną wersją scala.Either. Poznamy też Maybe - ulepszoną wersję scala.Option.

  sealed abstract class Maybe[A]
  final case class Empty[A]()    extends Maybe[A]
  final case class Just[A](a: A) extends Maybe[A]

  @typeclass trait Optional[F[_]] {
    def pextract[B, A](fa: F[A]): F[B] \/ A
  
    def getOrElse[A](fa: F[A])(default: =>A): A = ...
    def orElse[A](fa: F[A])(alt: =>F[A]): F[A] = ...
  
    def isDefined[A](fa: F[A]): Boolean = ...
    def nonEmpty[A](fa: F[A]): Boolean = ...
    def isEmpty[A](fa: F[A]): Boolean = ...
  
    def toOption[A](fa: F[A]): Option[A] = ...
    def toMaybe[A](fa: F[A]): Maybe[A] = ...
  }

Powyższe metody powinny wydawać się znajome, może z wyjątkiem pextract, która pozwala F[_] na zwrócenie przechowywanej wartości lub specyficznego dla implementacji F[B]. Na przykład Optional[Option].pextract zwróci nam Option[Nothing] \/ A, czyli None \/ A.

Scalaz daje nam operator trenarny dla wszystkich typów mających swoją instancję Optional.

  implicit class OptionalOps[F[_]: Optional, A](fa: F[A]) {
    def ?[X](some: =>X): Conditional[X] = new Conditional[X](some)
    final class Conditional[X](some: =>X) {
      def |(none: =>X): X = if (Optional[F].isDefined(fa)) some else none
    }
  }

Przykład:

  scala> val knock_knock: Option[String] = ...
         knock_knock ? "who's there?" | "<tumbleweed>"

5.11 Ko-rzeczy

Ko-rzecz zazwyczaj ma sygnaturę przeciwną do tego, co robi rzecz, ale nie musi koniecznie być jej odwrotnością. Aby podkreślić relacje między rzeczą i ko-rzeczą, wszędzie gdzie to możliwe zawrzemy obie sygnatury.

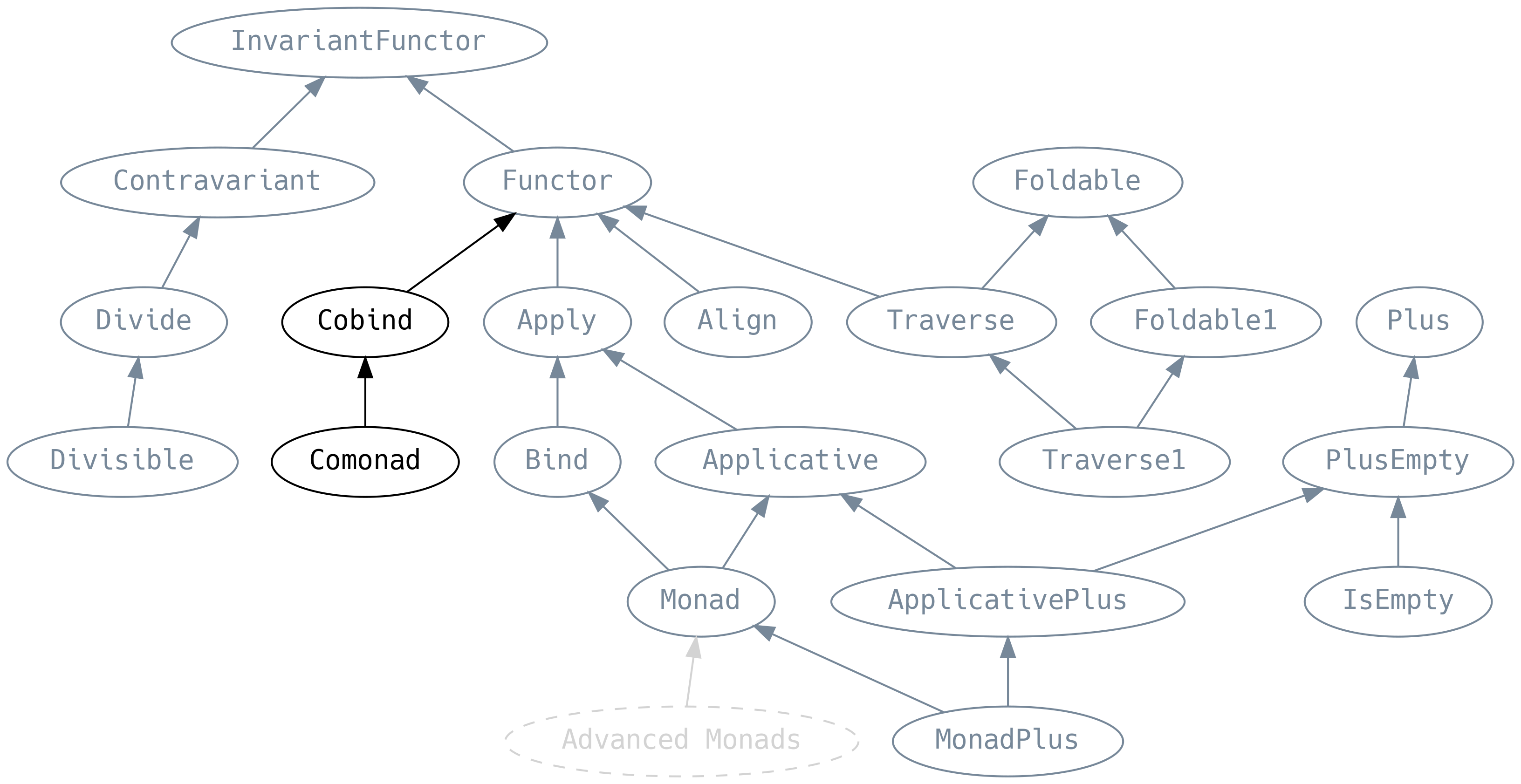
5.11.1 Cobind

  @typeclass trait Cobind[F[_]] extends Functor[F] {
    def cobind[A, B](fa: F[A])(f: F[A] => B): F[B]
  //def   bind[A, B](fa: F[A])(f: A => F[B]): F[B]
  
    def cojoin[A](fa: F[A]): F[F[A]] = ...
  //def   join[A](ffa: F[F[A]]): F[A] = ...
  }

cobind (znany również jako coflatmap) przyjmuje funkcję F[A] => B, która operuje na F[A], a nie jego elementach. Ale nie zawsze będzie to pełne fa, często jest to substruktura stworzona przez metodę cojoin (znaną również jako coflatten), która rozwija strukturę danych.

Przekonywające przykłady użycia Cobind są rzadkie, jednak kiedy spojrzymy na tabele permutacji metod typeklasy Functor, ciężko jest uzasadnić, czemu niektóre metody miałyby być ważniejsze od innych.

5.11.2 Comonad

  @typeclass trait Comonad[F[_]] extends Cobind[F] {
    def copoint[A](p: F[A]): A
  //def   point[A](a: =>A): F[A]
  }

.copoint (znany też jako .copure) wydostaje element z kontekstu. Efekty z reguły nie posiadają instancji tej typeklasy, gdyż na przykład interpretacja IO[A] do A zaburza transparentność referencyjną. Dla struktur danych jednakże może to być na przykład wygodny sposób na pokazanie wszystkich elementów wraz z ich sąsiadami.

Rozważmy strukturę sąsiedztwa (Hood), która zawiera pewien element (focus) oraz elementy na lewo i prawo od niego (lefts i rights).

  final case class Hood[A](lefts: IList[A], focus: A, rights: IList[A])

lefts i right powinny być uporządkowane od najbliższego do najdalszego elementu względem elementu środkowego focus, tak abyśmy mogli przekonwertować taką strukturę do IList za pomocą poniższej implementacji

  object Hood {
    implicit class Ops[A](hood: Hood[A]) {
      def toIList: IList[A] = hood.lefts.reverse ::: hood.focus :: hood.rights

Możemy zaimplementować metody do poruszania się w lewo (previous) i w prawo (next)

  ...
      def previous: Maybe[Hood[A]] = hood.lefts match {
        case INil() => Empty()
        case ICons(head, tail) =>
          Just(Hood(tail, head, hood.focus :: hood.rights))
      }
      def next: Maybe[Hood[A]] = hood.rights match {
        case INil() => Empty()
        case ICons(head, tail) =>
          Just(Hood(hood.focus :: hood.lefts, head, tail))
      }

Wprowadzając metodę more, jesteśmy w stanie obliczyć wszystkie możliwe do osiągnięcia pozycje (positions) w danym Hood.

  ...
      def more(f: Hood[A] => Maybe[Hood[A]]): IList[Hood[A]] =
        f(hood) match {
          case Empty() => INil()
          case Just(r) => ICons(r, r.more(f))
        }
      def positions: Hood[Hood[A]] = {
        val left  = hood.more(_.previous)
        val right = hood.more(_.next)
        Hood(left, hood, right)
      }
    }

Możemy teraz stworzyć Comonad[Hood]

  ...
    implicit val comonad: Comonad[Hood] = new Comonad[Hood] {
      def map[A, B](fa: Hood[A])(f: A => B): Hood[B] =
        Hood(fa.lefts.map(f), f(fa.focus), fa.rights.map(f))
      def cobind[A, B](fa: Hood[A])(f: Hood[A] => B): Hood[B] =
        fa.positions.map(f)
      def copoint[A](fa: Hood[A]): A = fa.focus
    }
  }

cojoin daje nam Hood[Hood[IList]] zawierające wszystkie możliwe sąsiedztwa w naszej początkowej liście

  scala> val middle = Hood(IList(4, 3, 2, 1), 5, IList(6, 7, 8, 9))
  scala> middle.cojoin
  res = Hood(
          [Hood([3,2,1],4,[5,6,7,8,9]),
           Hood([2,1],3,[4,5,6,7,8,9]),
           Hood([1],2,[3,4,5,6,7,8,9]),
           Hood([],1,[2,3,4,5,6,7,8,9])],
          Hood([4,3,2,1],5,[6,7,8,9]),
          [Hood([5,4,3,2,1],6,[7,8,9]),
           Hood([6,5,4,3,2,1],7,[8,9]),
           Hood([7,6,5,4,3,2,1],8,[9]),
           Hood([8,7,6,5,4,3,2,1],9,[])])

Okazuje się, że cojoin to tak naprawdę positions! A więc możemy nadpisać ją, używając bezpośredniej (a przez to wydajniejszej) implementacji

  override def cojoin[A](fa: Hood[A]): Hood[Hood[A]] = fa.positions

Comonad generalizuje koncepcję sąsiedztwa dla arbitralnych struktur danych. Hood jest przykładem zippera (brak związku z Zip). Scalaz definiuje typ danych Zipper dla strumieni (jednowymiarowych nieskończonych struktur danych), które omówimy w następnym rozdziale.

Jednym z zastosowanie zippera jest automat komórkowy (cellular automata), który wylicza wartość każdej komórki w następnej generacji na podstawie aktualnych wartości sąsiadów tej komórki.

5.11.3 Cozip

  @typeclass trait Cozip[F[_]] {
    def cozip[A, B](x: F[A \/ B]): F[A] \/ F[B]
  //def   zip[A, B](a: =>F[A], b: =>F[B]): F[(A, B)]
  //def unzip[A, B](a: F[(A, B)]): (F[A], F[B])
  
    def cozip3[A, B, C](x: F[A \/ (B \/ C)]): F[A] \/ (F[B] \/ F[C]) = ...
    ...
    def cozip7[A ... H](x: F[(A \/ (... H))]): F[A] \/ (... F[H]) = ...
  }

Mimo że nazwa tej typeklasy brzmi Cozip, lepiej jest spojrzeć na jej symetrię względem metody unzip. Tam, gdzie unzip zamienia F[_] zawierające produkt (tuple) na produkt zawierający F[_], tam cozip zamienia F[_] zawierające koprodukty (dysjunkcje) na koprodukt zawierający F[_].

5.12 Bi-rzeczy

Czasem mamy do czynienia z typami, które przyjmują dwa parametry typu i chcielibyśmy przemapować obie jego strony. Możemy na przykład śledzić błędy po lewej stronie Either i chcieć przetransformować wiadomości z tychże błędów.

Typeklasy Functor / Foldable / Traverse mają swoich krewnych, którzy pozwalają nam mapować obie strony wspieranych typów.

  @typeclass trait Bifunctor[F[_, _]] {
    def bimap[A, B, C, D](fab: F[A, B])(f: A => C, g: B => D): F[C, D]
  
    @op("<-:") def leftMap[A, B, C](fab: F[A, B])(f: A => C): F[C, B] = ...
    @op(":->") def rightMap[A, B, D](fab: F[A, B])(g: B => D): F[A, D] = ...
    @op("<:>") def umap[A, B](faa: F[A, A])(f: A => B): F[B, B] = ...
  }
  
  @typeclass trait Bifoldable[F[_, _]] {
    def bifoldMap[A, B, M: Monoid](fa: F[A, B])(f: A => M)(g: B => M): M
  
    def bifoldRight[A,B,C](fa: F[A, B], z: =>C)(f: (A, =>C) => C)(g: (B, =>C) => C): C
    def bifoldLeft[A,B,C](fa: F[A, B], z: C)(f: (C, A) => C)(g: (C, B) => C): C = ...
  
    def bifoldMap1[A, B, M: Semigroup](fa: F[A,B])(f: A => M)(g: B => M): Option[M] = ...
  }
  
  @typeclass trait Bitraverse[F[_, _]] extends Bifunctor[F] with Bifoldable[F] {
    def bitraverse[G[_]: Applicative, A, B, C, D](fab: F[A, B])
                                                 (f: A => G[C])
                                                 (g: B => G[D]): G[F[C, D]]
  
    def bisequence[G[_]: Applicative, A, B](x: F[G[A], G[B]]): G[F[A, B]] = ...
  }

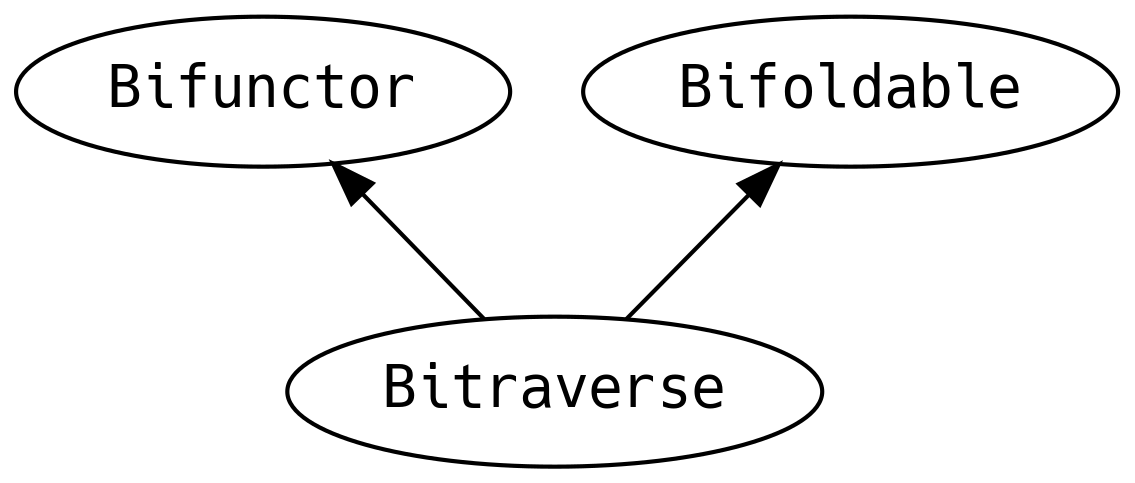
Mimo że sygnatury metod są dość rozwlekłe, to są to niemal dokładnie te same metody, które znamy z typeklas Functor, Foldable i Traverse, z tą różnicą, że przyjmują dwie funkcje zamiast jednej. Czasami funkcje te muszą zwracać ten sam typ, aby wyniki można było połączyć za pomocą Monoidu lub Semigroupy.

  scala> val a: Either[String, Int] = Left("fail")
         val b: Either[String, Int] = Right(13)
  
  scala> b.bimap(_.toUpperCase, _ * 2)
  res: Either[String, Int] = Right(26)
  
  scala> a.bimap(_.toUpperCase, _ * 2)
  res: Either[String, Int] = Left(FAIL)
  
  scala> b :-> (_ * 2)
  res: Either[String,Int] = Right(26)
  
  scala> a :-> (_ * 2)
  res: Either[String, Int] = Left(fail)
  
  scala> { s: String => s.length } <-: a
  res: Either[Int, Int] = Left(4)
  
  scala> a.bifoldMap(_.length)(identity)
  res: Int = 4
  
  scala> b.bitraverse(s => Future(s.length), i => Future(i))
  res: Future[Either[Int, Int]] = Future(<not completed>)

Dodatkowo możemy wrócić na chwile do MonadPlus (czyli Monady z metodami filterWith i unite), aby zobaczyć, że potrafi ona rozdzielać (separate) zawartość Monady, jeśli tylko jej typ ma instancję Bifoldable.

  @typeclass trait MonadPlus[F[_]] {
    ...
    def separate[G[_, _]: Bifoldable, A, B](value: F[G[A, B]]): (F[A], F[B]) = ...
    ...
  }

Jest to bardzo przydatny mechanizm, kiedy mamy do czynienia z kolekcją bi-rzeczy i chcemy podzielić ją na kolekcję A i kolekcję B.

  scala> val list: List[Either[Int, String]] =
           List(Right("hello"), Left(1), Left(2), Right("world"))
  
  scala> list.separate
  res: (List[Int], List[String]) = (List(1, 2), List(hello, world))

5.13 Podsumowanie

Dużo tego! Właśnie odkryliśmy standardową bibliotekę polimorficznych funkcjonalności. Ale patrząc na to z innej perspektywy: w Collections API z biblioteki standardowej Scali jest więcej traitów niż typeklas w Scalaz.

To całkiem normalne, jeśli twoja czysto funkcyjna aplikacja korzysta jedynie z małej części omówionych typeklas, a większość funkcjonalności czerpie z typeklas i algebr domenowych. Nawet jeśli twoje domenowe typeklasy są tylko wyspecjalizowanymi odpowiednikami tych zdefiniowanych w Scalaz, to jest zupełnie ok, aby zrefaktorować je później.

Aby ułatwić nieco sprawę, dołączyliśmy cheat-sheet wszystkich typeklas i ich głównych metod w załączniku. Jest on zainspirowany przez Scalaz Cheatsheet Adama Rosiena.

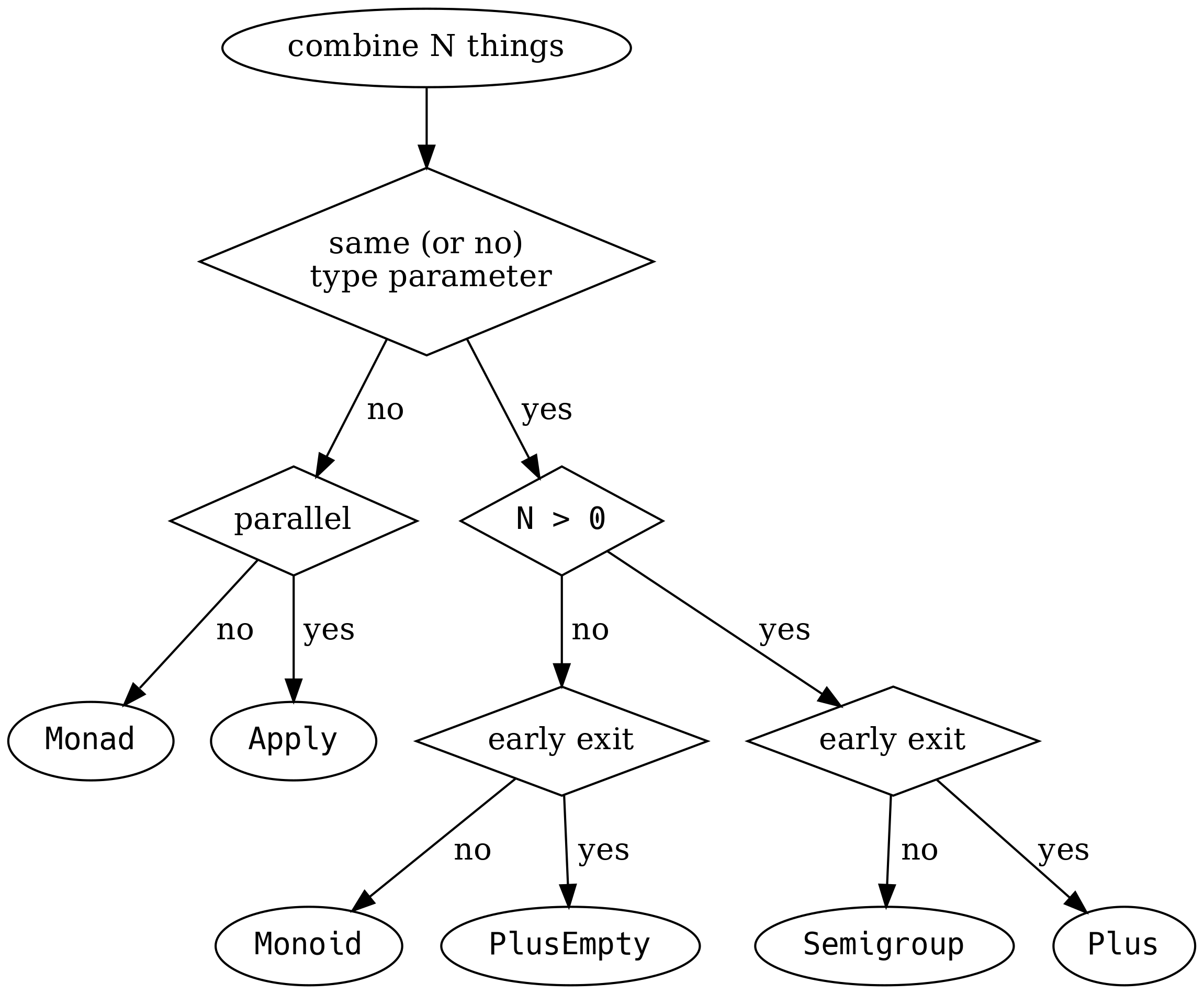
Aby pomóc jeszcze bardziej, Valentin Kasas pokazuję jak połączyć N rzeczy