6. Tipos de datos de Scalaz

¿Quién no ama una buena estructura de datos? La respuesta es nadie, porque las estructuras de datos son increíbles.

En este capítulo exploraremos los tipos de datos en Scalaz que son similares a colecciones, así como los tipos de datos que aumentan Scala, como lenguaje, con semántica y seguridad de tipos adicional.

La razón principal por la que nos preocupamos por tener muchas colecciones a nuestra disposición es por rendimiento. Un vector y una lista pueden hacer lo mismo, pero sus características son diferentes: un vector tiene un costo de búsqueda constante mientras que una lista debe ser recorrida.

Todas las colecciones presentadas aquí son persistentes: si agregamos o removemos un elemento todavía podemos usar la versión anterior. Compartir estructuralmente es esencial para el rendimiento de las estructuras de datos persistentes, de otra manera la colección entera se reconstruye con cada operación.

A diferencia de las colecciones de Java y Scala, no hay jerarquía de datos en Scalaz: estas colecciones son mucho más simples de entender. La funcionalidad polimórfica se proporciona por instancias opmitizadas de typeclases que estudiamos en el capítulo anterior. Esto simplifica cambiar implementaciones por razones de rendimiento, y proporcionar la propia.

6.1 Variancia de tipo

Muchos de los tipos de datos de Scalaz son invariantes en sus parámetros de tipo. Por ejemplo, IList[A] no es un subtipo de IList[B] cuando A <: B.

6.1.1 Covariancia

El problema con los tipos de parámetro covariantes, tales como class List[+A], es que List[A] es un subtipo de List[Any] y es fácil perder accidentalmente información de tipo.

  scala> List("hello") ++ List(' ') ++ List("world!")
  res: List[Any] = List(hello,  , world!)

Note que la segunda lista es una List[Char] y que el compilador ha inferido incorrectamente el LUB (Least Upper Bound, o límite mínimo inferior) es Any. Compare con IList, que requiere una aplicación explícita de .widen[Any] para ejecutar el crimen atroz:

  scala> IList("hello") ++ IList(' ') ++ IList("world!")
  <console>:35: error: type mismatch;
   found   : Char(' ')
   required: String
  
  scala> IList("hello").widen[Any]
           ++ IList(' ').widen[Any]
           ++ IList("world!").widen[Any]
  res: IList[Any] = [hello, ,world!]

De manera similar, cuando el compilador infiere el tipo como with Product with Serializable es un indicador fuerte de que un ensanchamiento accidental ha ocurrido debido a la covariancia.

Desafortunadamente debemos ser cuidadosos cuando construimos tipos de datos invariantes debido a que los cálculos LUB se realizan sobre los parámetros:

  scala> IList("hello", ' ', "world")
  res: IList[Any] = [hello, ,world]

Otro problema similar surge a partir del tipo Nothing, el cuál es un subtipo del resto de tipos, incluyendo ADTs selladas (sealed), clases finales (final), primitivas y null.

No hay valores de tipo Nothing: las funciones que toman un Nothing como un parámetro no pueden ejecutarse y las funciones que devuelven Nothing nunca devuelven un valor (o terminan). Nothing fue introducido como un mecanismo para habilitar los tipos de parámetros covariantes, pero una consecuencia es que podemos escribir código que no puede ejecutarse, por accidente. Scalaz dice que no necesitamos parámetros de tipo covariantes lo que significa que nos estamos limitando a nosotros mismos a escribir código práctico que puede ser ejecutado.

6.1.2 Contrarivarianza

Por otro lado, los tipos de parámetro contravariantes, tales como trait Thing[-A] pueden poner de manifiesto errores devastadores en el compilador. Considere la demostración de Paul Phillips’ (ex miembro del equipo del compilador scalac) de lo que él llama contrarivarianza:

  scala> :paste
         trait Thing[-A]
         def f(x: Thing[ Seq[Int]]): Byte   = 1
         def f(x: Thing[List[Int]]): Short  = 2
  
  scala> f(new Thing[ Seq[Int]] { })
         f(new Thing[List[Int]] { })
  
  res = 1
  res = 2

Como era de esperarse, el compilador está encontrando el argumento más específico en cada invocación de f. Sin embargo, la resolución implícita da resultados inesperados:

  scala> :paste
         implicit val t1: Thing[ Seq[Int]] =
           new Thing[ Seq[Int]] { override def toString = "1" }
         implicit val t2: Thing[List[Int]] =
           new Thing[List[Int]] { override def toString = "2" }
  
  scala> implicitly[Thing[ Seq[Int]]]
         implicitly[Thing[List[Int]]]
  
  res = 1
  res = 1

La resolución implícita hace un intercambio de su definición de “más específico” para los tipos contravariantes, logrando que sean inútiles para los typeclases o para cualquier cosa que requiera funcionalidad polimórfica. Este comportamiento es fijo en Dotty.

6.1.3 Las limitaciones del mecanismo de subclases

scala.Option tiene un método .flatten que los dejará convertir Option[Option[B]] en un Option[B]. Sin embargo, el sistema de tipos de Scala es incapaz de dejarnos escribir la signatura de tipos requerida. Considere lo siguiente que parece correcto, pero que tiene un error sutil:

  sealed abstract class Option[+A] {
    def flatten[B, A <: Option[B]]: Option[B] = ...
  }

The A introducida en .flatten está ocultando la A introducida por la clase. Es equivalente a escribir

  sealed abstract class Option[+A] {
    def flatten[B, C <: Option[B]]: Option[B] = ...
  }

que no es la restricción deseada.

Para resolver esta limitación, Scala define clases infijas <:< y =:= junto con la evidencia implícita que siempre crea un testigo (witness).

  sealed abstract class <:<[-From, +To] extends (From => To)
  implicit def conforms[A]: A <:< A = new <:<[A, A] { def apply(x: A): A = x }
  
  sealed abstract class =:=[ From,  To] extends (From => To)
  implicit def tpEquals[A]: A =:= A = new =:=[A, A] { def apply(x: A): A = x }

=:= puede usarse para requerir que dos parámetros de tipo sean exactamente iguales y <:< se usa para describir relaciones de subtipo, dejandonos implementar .flatten como

  sealed abstract class Option[+A] {
    def flatten[B](implicit ev: A <:< Option[B]): Option[B] = this match {
      case None        => None
      case Some(value) => ev(value)
    }
  }
  final case class Some[+A](value: A) extends Option[A]
  case object None                    extends Option[Nothing]

Scalaz mejora sobre <:< y =:= con Liskov (que tiene el alias <~<) y Leibniz (====).

  sealed abstract class Liskov[-A, +B] {
    def apply(a: A): B = ...
    def subst[F[-_]](p: F[B]): F[A]
  
    def andThen[C](that: Liskov[B, C]): Liskov[A, C] = ...
    def onF[X](fa: X => A): X => B = ...
    ...
  }
  object Liskov {
    type <~<[-A, +B] = Liskov[A, B]
    type >~>[+B, -A] = Liskov[A, B]
  
    implicit def refl[A]: (A <~< A) = ...
    implicit def isa[A, B >: A]: A <~< B = ...
  
    implicit def witness[A, B](lt: A <~< B): A => B = ...
    ...
  }
  
  // type signatures have been simplified
  sealed abstract class Leibniz[A, B] {
    def apply(a: A): B = ...
    def subst[F[_]](p: F[A]): F[B]
  
    def flip: Leibniz[B, A] = ...
    def andThen[C](that: Leibniz[B, C]): Leibniz[A, C] = ...
    def onF[X](fa: X => A): X => B = ...
    ...
  }
  object Leibniz {
    type ===[A, B] = Leibniz[A, B]
  
    implicit def refl[A]: Leibniz[A, A] = ...
  
    implicit def subst[A, B](a: A)(implicit f: A === B): B = ...
    implicit def witness[A, B](f: A === B): A => B = ...
    ...
  }

Además de los métodos generalmente útiles y las conversiones implícitas, la evidencia de Scalaz <~< y === usa mejores principios que en la librería estándar.

6.2 Evaluación

Java es un lenguaje con evaluación estricta: todos los parámetros para un método deben evaluarse a un valor antes de llamar el método. Scala introduce la noción de parámetros por nombre (by-name) en los métodos con la sintaxis a: => A. Estos parámetros se envuelven en una finción de cero argumentos que se invoca cada vez que se referencia la a. Hemos visto por nombre muchas veces en las typeclases.

Scala también tiene por necesidad (by-need), con la palabra lazy: el cómputo se evalúa a lo sumo una vez para producir el valor. Desgraciadamente, Scala no soporta la evaluación por necesidad de los parámetros del método.

Scalaz formaliza los tres estrategias de evaluación con un ADT

  sealed abstract class Name[A] {
    def value: A
  }
  object Name {
    def apply[A](a: =>A) = new Name[A] { def value = a }
    ...
  }
  
  sealed abstract class Need[A] extends Name[A]
  object Need {
    def apply[A](a: =>A): Need[A] = new Need[A] {
      private lazy val value0: A = a
      def value = value0
    }
    ...
  }
  
  final case class Value[A](value: A) extends Need[A]

La forma de evaluación más débil es Name, que no proporciona garantías computacionales. A continuación está Need, que garantiza la evaluación como máximo una vez.

Si deseamos ser super escrupulosos podríamos revisar todas las typeclases y hacer sus métodos tomar parámetros por Name, Need o Value. En vez de esto, podemos asumir que los parámetros normales siempre pueden envolverse en un Value, y que los parámetros (by-name) por nombre pueden envolverse con Name.

Cuando escribimos programas puros, somos libres de reemplazar cualquier Name con Need o Value, y viceversa, sin necesidad de cambiar lo correcto del programa. Esta es la esencia de la transparencia referencial: la habilidad de cambiar un cómputo por su valor, o un valor por su respectivo cómputo.

En la programación funcional casi siempre deseamos Value o Need (también conocido como estricto y perezoso): hay poco valor en Name. Debido a que no hay soporte a nivel de lenguaje para parámetros de método perezosos, los métodos típicamente solicitan un parámetro por nombre y entonces lo convierten a Need de manera interna, proporcionando un aumento en el rendimiento.

Name proporciona instancias de las siguientes typeclases

• Monad
• Comonad
• Traverse1
• Align
• Zip / Unzip / Cozip

6.3 Memoisation

Scalaz tiene la capacidad de memoizar funciones, formalizada por Memo, que no hace ninguna garantía sobre la evaluación debido a la diversidad de implementaciones:

  sealed abstract class Memo[K, V] {
    def apply(z: K => V): K => V
  }
  object Memo {
    def memo[K, V](f: (K => V) => K => V): Memo[K, V]
  
    def nilMemo[K, V]: Memo[K, V] = memo[K, V](identity)
  
    def arrayMemo[V >: Null : ClassTag](n: Int): Memo[Int, V] = ...
    def doubleArrayMemo(n: Int, sentinel: Double = 0.0): Memo[Int, Double] = ...
  
    def immutableHashMapMemo[K, V]: Memo[K, V] = ...
    def immutableTreeMapMemo[K: scala.Ordering, V]: Memo[K, V] = ...
  }

memo nos permite crear implementaciones de Memo, nilMemo no memoiza, evaluando la función normalmente. Las implementaciones resultantes interceptan llamadas a la función y guardan en cache los resultados obtenidos en una implementación que usa colecciones de la librería estándar.

Para usar Memo simplemente envolvemos una función con una implementación de Memo y entonces invocamos a la función memoizada:

  scala> def foo(n: Int): String = {
           println("running")
           if (n > 10) "wibble" else "wobble"
         }
  
  scala> val mem = Memo.arrayMemo[String](100)
         val mfoo = mem(foo)
  
  scala> mfoo(1)
  running // evaluated
  res: String = wobble
  
  scala> mfoo(1)
  res: String = wobble // memoised

Si la función toma más de un parámetro, entonces debemos invocar .tupled sobre el método, con la versión memoisada tomando una tupla.

  scala> def bar(n: Int, m: Int): String = "hello"
         val mem = Memo.immutableHashMapMemo[(Int, Int), String]
         val mbar = mem((bar _).tupled)
  
  scala> mbar((1, 2))
  res: String = "hello"

Memo típicamente se trata como un artificio especial y la regla usual sobre la pureza se relaja para las implementaciones. La pureza únicamente requiere que nuestras implementaciones de Memo sean referencialmente transparentes en la evaluación de K => V. Podríamos usar datos mutables y realizar I/O en la implementación de Memo, por ejemplo usando un LRU o un caché distribuido, sin tener que declarar un efecto en las signaturas de tipo. Otros lenguajes de programación funcional tienen memoización manejada por el ambiente de runtime y Memo es nuestra manera de extender la JVM para tener un soporte similar, aunque desgraciadamente únicamente de una manera que requiere opt-in.

6.4 Tagging (etiquetar)

En la sección que se introdujo Monoid construimos un Monoid[TradeTeamplate] y nos dimos cuenta de que Scalaz no hace lo que desearíamos con Monoid[Option[A]]. Este no es una omisión de Scalaz, con frecuencia podemos notar que un tipo de datos puede implementar una tipeclass fundamental en múltiples formas válidas y que la implementación por default no hace lo que deseariamos, o simplemente no está definida.

Los ejemplos básicos son Monoid[Boolean] (la conjunción && vs la disjunción ||) y Monoid[Int] (multiplicación vs adición).

Para implementar Monoid[TradeTemplate] tuvimos que romper la coherencia de typeclases, o usar una typeclass distinta.

scalaz.Tag está diseñada para lidiar con el problema de coherencia que surge con múltiples implementaciones de typeclases, sin romper la coherencia de las typeclases.

La definición es algo compleja, pero la sintáxis al usar scalaz.Tag es bastante limpia. Así es como logramos convencer al compilador para que nos permita definir el tipo infijo A @@ T que es borrado en A en tiempo de ejecución:

  type @@[A, T] = Tag.k.@@[A, T]
  
  object Tag {
    @inline val k: TagKind = IdTagKind
    @inline def apply[A, T](a: A): A @@ T = k(a)
    ...
  
    final class TagOf[T] private[Tag]() { ... }
    def of[T]: TagOf[T] = new TagOf[T]
  }
  sealed abstract class TagKind {
    type @@[A, T]
    def apply[A, T](a: A): A @@ T
    ...
  }
  private[scalaz] object IdTagKind extends TagKind {
    type @@[A, T] = A
    @inline override def apply[A, T](a: A): A = a
    ...
  }

Algunas etiquetas/tags útiles se proporcionan en el objeto Tags

  object Tags {
    sealed trait First
    val First = Tag.of[First]
  
    sealed trait Last
    val Last = Tag.of[Last]
  
    sealed trait Multiplication
    val Multiplication = Tag.of[Multiplication]
  
    sealed trait Disjunction
    val Disjunction = Tag.of[Disjunction]
  
    sealed trait Conjunction
    val Conjunction = Tag.of[Conjunction]
  
    ...
  }

First/Last se usan para seleccionar instancias d Monoid que escogen el primero o el último (diferente de cero) operando. Multiplication es para multiplicación numérica en vez de adición. Disjunction/Conjuntion son para seleccionar && o ||, respectivamente.

En nuestro TradeTemplate, en lugar de usar Option[Currency] podríamos usar Option[Currency] @@ Tags.Last. En verdad, este uso es tan común que podemos usar el alias previamente definido, LastOption.

  type LastOption[A] = Option[A] @@ Tags.Last

y esto nos permite escribir una implementación mucho más limpia de Monoid[TradeTemplate]

  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: LastOption[Currency],
    otc: LastOption[Boolean]
  )
  object TradeTemplate {
    implicit val monoid: Monoid[TradeTemplate] = Monoid.instance(
      (a, b) =>
        TradeTemplate(a.payments |+| b.payments,
                      a.ccy |+| b.ccy,
                      a.otc |+| b.otc),
        TradeTemplate(Nil, Tag(None), Tag(None))
    )
  }

Para crear un valor de tipo LastOption, aplicamos Tag a un Option. Aquí estamos invocando Tag(None).

En el capítulo sobre derivación de typeclases, iremos un paso más allá y derivaremos automáticamente el monoid.

Es tentador usar Tag para marcar tipos de datos para alguna forma de validación (por ejemplo, String @@ PersonName), pero deberíamos evitar esto porque no existe un chequeo del contenido en tiempo de ejecución. Tag únicamente debería ser usado para propósitos de selección de typeclases. Prefiera el uso de la librería Refined, que se introdujo en el Capítulo 4, para restringir valores.

6.5 Transformaciones naturales

Una función de un tipo a otro se escribe en Scala como A => B, y se trata de una conveniencia sintáctica para Function1[A, B]. Scalaz proporciona una conveniencia sintáctica F ~> G para funciones sobre los constructores de tipo F[_] a G[_].

Esta notación, F ~ G, se conoce como transformación natural y son universalmente cuantificables debido a que no nos importa el contenido de F[_].

  type ~>[-F[_], +G[_]] = NaturalTransformation[F, G]
  trait NaturalTransformation[-F[_], +G[_]] {
    def apply[A](fa: F[A]): G[A]
  
    def compose[E[_]](f: E ~> F): E ~> G = ...
    def andThen[H[_]](f: G ~> H): F ~> H = ...
  }

Un ejemplo de una transformación natural es la función que convierte una IList en una List.

  scala> val convert = new (IList ~> List) {
           def apply[A](fa: IList[A]): List[A] = fa.toList
         }
  
  scala> convert(IList(1, 2, 3))
  res: List[Int] = List(1, 2, 3)

O, de manera más concisa, usando las conveniencias sintácticas proporcionadas por el plugin kind-projector:

  scala> val convert = λ[IList ~> List](_.toList)
  
  scala> val convert = Lambda[IList ~> List](_.toList)

Sin embargo, en el desarrollo del día a día, es mucho más probable que usemos una transformación natural para mapear entre álgebras. Por ejemplo, en drone-dynamic-agents tal vez deseemos implementar nuestra álgebra de Machines que usa Google Container Engine con una álgebra ad-hoc, BigMachines. En lugar de cambiar toda nuestra lógica de negocio y probar usando esta nueva interfaz BigMachines, podríamos escribir una transformación natural de Machines ~> BigMachines. Volveremos a esta idea en el capítulo de Mónadas Avanzadas.

6.6 Isomorphism (isomorfismos)

Algunas veces tenemos dos tipos que en realidad son equivalentes (la misma cosa), lo que ocasiona problemas de compatibiliad debido a que el compilador no sabe lo que nosotros sí sabemos. Esto pasa típicamente cuando usamos código de terceros que tiene algo que ya tenemos.

Ahí es cuando Isomorphism nos puede ayudar. Un isomorfismo define una relación formal “es equivalente a” entre dos tipos. Existen tres variantes, para

  object Isomorphism {
    trait Iso[Arr[_, _], A, B] {
      def to: Arr[A, B]
      def from: Arr[B, A]
    }
    type IsoSet[A, B] = Iso[Function1, A, B]
    type <=>[A, B] = IsoSet[A, B]
    object IsoSet {
      def apply[A, B](to: A => B, from: B => A): A <=> B = ...
    }
  
    trait Iso2[Arr[_[_], _[_]], F[_], G[_]] {
      def to: Arr[F, G]
      def from: Arr[G, F]
    }
    type IsoFunctor[F[_], G[_]] = Iso2[NaturalTransformation, F, G]
    type <~>[F[_], G[_]] = IsoFunctor[F, G]
    object IsoFunctor {
      def apply[F[_], G[_]](to: F ~> G, from: G ~> F): F <~> G = ...
    }
  
    trait Iso3[Arr[_[_, _], _[_, _]], F[_, _], G[_, _]] {
      def to: Arr[F, G]
      def from: Arr[G, F]
    }
    type IsoBifunctor[F[_, _], G[_, _]] = Iso3[~~>, F, G]
    type <~~>[F[_, _], G[_, _]] = IsoBifunctor[F, G]
  
    ...
  }

Los aliases de tipos IsoSet, IsoFunctor e IsoBifunctor cubren los casos comunes: una función regular, una transformación natural y binatural. Las funciones de conveniencia nos permiten generar instancias de funciones existentes o transformaciones naturales. Sin embargo, con frecuencia es más fácil usar una de las clases abstractas Template para definir un isomorfismo. Por ejemplo:

  val listIListIso: List <~> IList =
    new IsoFunctorTemplate[List, IList] {
      def to[A](fa: List[A]) = fromList(fa)
      def from[A](fa: IList[A]) = fa.toList
    }

Si introducimos un isomorfismo, con frecuencia podemos generar muchas de las typeclases estándar. Por ejemplo,

  trait IsomorphismSemigroup[F, G] extends Semigroup[F] {
    implicit def G: Semigroup[G]
    def iso: F <=> G
    def append(f1: F, f2: =>F): F = iso.from(G.append(iso.to(f1), iso.to(f2)))
  }

lo que nos permite derivar un Semigroup[F] para un tipo F si ya tenemos un isomorfismo F <=> G y un semigrupo Semigroup[G]. Casi todas las typeclases en la jerarquía proporcionan una invariante isomórfica. Si nos encontramos en la situación en la que copiamos y pegamos una implementación de una typeclass, es útil considerar si Isomorphism es una mejor solución.

6.7 Contenedores

6.7.1 Maybe

Ya nos hemos encontrado con la mejora de Scalaz sobre scala.Option, que se llama Maybe. Es una mejora porque es invariante y no tiene ningún método inseguro como Option.get, el cual puede lanzar una excepción.

Con frecuencia se usa para representar una cosa que puede o no estar presente sin proporcionar ninguna información adicional de porqué falta información.

  sealed abstract class Maybe[A] { ... }
  object Maybe {
    final case class Empty[A]()    extends Maybe[A]
    final case class Just[A](a: A) extends Maybe[A]
  
    def empty[A]: Maybe[A] = Empty()
    def just[A](a: A): Maybe[A] = Just(a)
  
    def fromOption[A](oa: Option[A]): Maybe[A] = ...
    def fromNullable[A](a: A): Maybe[A] = if (null == a) empty else just(a)
    ...
  }

Los métodos .empty y .just en el objeto compañero son preferidas en lugar de usar Empty o Just debido a que regresan Maybe, ayudándonos con la inferencia de tipos. Este patrón con frecuencia es preferido a regresar un tipo suma, que es cuando tenemos múltiples implementaciones de un sealed trait pero nunca usamos us subtipo específico en una signatura de método.

UNa clase implícita conveniente nos permite invocar.just sobre cualquier valor y recibir un Maybe.

  implicit class MaybeOps[A](self: A) {
    def just: Maybe[A] = Maybe.just(self)
  }

Maybe tiene una instancia de typeclass para todas las cosas

• Align
• Traverse
• MonadPlus / IsEmpty
• Cobind
• Cozip / Zip / Unzip
• Optional

e instancias delegadas que dependen de A

• Monoid / Band
• Equal / Order / Show

Además de las instancias arriba mencionadas, Maybe tiene funcionalidad que no es soportada por una typeclass polimórfica.

  sealed abstract class Maybe[A] {
    def cata[B](f: A => B, b: =>B): B = this match {
      case Just(a) => f(a)
      case Empty() => b
    }
  
    def |(a: =>A): A = cata(identity, a)
    def toLeft[B](b: =>B): A \/ B = cata(\/.left, \/-(b))
    def toRight[B](b: =>B): B \/ A = cata(\/.right, -\/(b))
    def <\/[B](b: =>B): A \/ B = toLeft(b)
    def \/>[B](b: =>B): B \/ A = toRight(b)
  
    def orZero(implicit A: Monoid[A]): A = getOrElse(A.zero)
    def orEmpty[F[_]: Applicative: PlusEmpty]: F[A] =
      cata(Applicative[F].point(_), PlusEmpty[F].empty)
    ...
  }

.cata proporciona una alternativa más simple para .map(f).gerOrElse(b) y tiene la forma más simple | si el mapeo es identity (es decir, simplemente .getOrElse).

.toLeft y .toRight, y sus aliases simbólicos, crean una disjunción (explicada en la sección siguiente) al tomar un valor por default para el caso Empty.

.orZero toma un Monoid para definir el valor por default.

.orEmpty usa un ApplicativePlus para crear un elemento único o un contenedor vacío, sin olvidar que ya tenemos soporte para las colecciones de la librería estándar con el método .to que viene de la instancia Foldable.

  scala> 1.just.orZero
  res: Int = 1
  
  scala> Maybe.empty[Int].orZero
  res: Int = 0
  
  scala> Maybe.empty[Int].orEmpty[IList]
  res: IList[Int] = []
  
  scala> 1.just.orEmpty[IList]
  res: IList[Int] = [1]
  
  scala> 1.just.to[List] // from Foldable
  res: List[Int] = List(1)

6.7.2 Either

La mejora de Scalaz sobre scalaz.Either es simbólica, pero es común hablar de este caso como either o una Disjunction.

  sealed abstract class \/[+A, +B] { ... }
  final case class -\/[+A](a: A) extends (A \/ Nothing)
  final case class \/-[+B](b: B) extends (Nothing \/ B)
  
  type Disjunction[+A, +B] = \/[A, B]
  
  object \/ {
    def left [A, B]: A => A \/ B = -\/(_)
    def right[A, B]: B => A \/ B = \/-(_)
  
    def fromEither[A, B](e: Either[A, B]): A \/ B = ...
    ...
  }

con la sintaxis correspondiente

  implicit class EitherOps[A](val self: A) {
    final def left [B]: (A \/ B) = -\/(self)
    final def right[B]: (B \/ A) = \/-(self)
  }

y permite una construcción sencilla de los valores. Note que los métodos de extensión toman el tipo del otro lado. De modo que si deseamos crear un valor de tipo String \/ Int y tenemos un Int, debemos pasar String cuando llamamos .right.

  scala> 1.right[String]
  res: String \/ Int = \/-(1)
  
  scala> "hello".left[Int]
  res: String \/ Int = -\/(hello)

La naturaleza simbólica de \/ hace que sea de fácil lectura cuando se muestra con notación infija. Note que los tipos simbólicos en Scala se asocian desde el lado izquierdo y que \/ deben tener paréntesis, por ejemplo (A \/ (B \/ (C \/ D)).

\/ tiene instancias sesgadas a la derecha (es decir, flatMap aplica a \/-) para:

• Monad / MonadError
• Traverse / Bitraverse
• Plus
• Optional
• Cozip

y dependiendo del contenido

• Equal / Order
• Semigroup / Monoid / Band

Además, hay métodos especiales

  sealed abstract class \/[+A, +B] { self =>
    def fold[X](l: A => X, r: B => X): X = self match {
      case -\/(a) => l(a)
      case \/-(b) => r(b)
    }
  
    def swap: (B \/ A) = self match {
      case -\/(a) => \/-(a)
      case \/-(b) => -\/(b)
    }
  
    def |[BB >: B](x: =>BB): BB = getOrElse(x) // Optional[_]
    def |||[C, BB >: B](x: =>C \/ BB): C \/ BB = orElse(x) // Optional[_]
  
    def +++[AA >: A: Semigroup, BB >: B: Semigroup](x: =>AA \/ BB): AA \/ BB = ...
  
    def toEither: Either[A, B] = ...
  
    final class SwitchingDisjunction[X](right: =>X) {
      def <<?:(left: =>X): X = ...
    }
    def :?>>[X](right: =>X) = new SwitchingDisjunction[X](right)
    ...
  }

.fold es similar a Maybe.cata y requiere que tanto el lado derecho como el lado izquierdo se mapeen al mismo tipo.

.swap intercambia los lados izquierdo y derecho.

El alias | para getOrElse parece similar a Maybe.

The | alias to getOrElse appears similarly to Maybe. We also get ||| as an alias to orElse.

+++ es para combinar disjunciones con los lados izquierdos tomando precedencia sobre los lados derechos:

• right(v1) +++ right(v2) da right(v1 |+| v2)
• right(v1) +++ left (v2) da left (v2)
• left (v1) +++ right(v2) da left (v1)
• left (v1) +++ left (v2) da left (v1 |+| v2)

.toEither está para proporcionar compatibilidad hacia atrás con la librería estándar de Scala.

La combinación de :?>> y <<? son una sintáxis conveniente para ignorar el contenido de una \/, pero escoger un valor por default basándose en su tipo.

  scala> 1 <<?: foo :?>> 2
  res: Int = 2 // foo is a \/-
  
  scala> 1 <<?: foo.swap :?>> 2
  res: Int = 1

6.7.3 Validation

A primera vista, Validation (con alias simbólico \?/, Elvis feliz) aparece ser un clon de Disjunction:

  sealed abstract class Validation[+E, +A] { ... }
  final case class Success[A](a: A) extends Validation[Nothing, A]
  final case class Failure[E](e: E) extends Validation[E, Nothing]
  
  type ValidationNel[E, +X] = Validation[NonEmptyList[E], X]
  
  object Validation {
    type \?/[+E, +A] = Validation[E, A]
  
    def success[E, A]: A => Validation[E, A] = Success(_)
    def failure[E, A]: E => Validation[E, A] = Failure(_)
    def failureNel[E, A](e: E): ValidationNel[E, A] = Failure(NonEmptyList(e))
  
    def lift[E, A](a: A)(f: A => Boolean, fail: E): Validation[E, A] = ...
    def liftNel[E, A](a: A)(f: A => Boolean, fail: E): ValidationNel[E, A] = ...
    def fromEither[E, A](e: Either[E, A]): Validation[E, A] = ...
    ...
  }

Con sintáxis conveniente

  implicit class ValidationOps[A](self: A) {
    def success[X]: Validation[X, A] = Validation.success[X, A](self)
    def successNel[X]: ValidationNel[X, A] = success
    def failure[X]: Validation[A, X] = Validation.failure[A, X](self)
    def failureNel[X]: ValidationNel[A, X] = Validation.failureNel[A, X](self)
  }

Sin embargo, la estructura de datos no es la historia completa. En Scalaz, Validation no tiene una instancia de ninguna Monad, y esto es intencional, restringiéndose a versiones sesgadas a la derecha de:

• Applicative
• Traverse / Bitraverse
• Cozip
• Plus
• Optional

y dependiendo del contenido

• Equal / Order
• Show
• Semigroup / Monoid

La gran ventaja de restringirnos a Applicative es que Validation es explícitamente para situaciones donde deseamos reportar todas las fallas, mientras que Disjunction se usa para detenernos en el primer fallo. Para

The big advantage of restricting to Applicative is that Validation is explicitly for situations where we wish to report all failures, whereas Disjunction is used to stop at the first failure. To accommodate failure accumulation, a popular form of Validation is ValidationNel, having a NonEmptyList[E] in the failure position.

Consider performing input validation of data provided by a user using Disjunction and flatMap:

  scala> :paste
         final case class Credentials(user: Username, name: Fullname)
         final case class Username(value: String) extends AnyVal
         final case class Fullname(value: String) extends AnyVal
  
         def username(in: String): String \/ Username =
           if (in.isEmpty) "empty username".left
           else if (in.contains(" ")) "username contains spaces".left
           else Username(in).right
  
         def realname(in: String): String \/ Fullname =
           if (in.isEmpty) "empty real name".left
           else Fullname(in).right
  
  scala> for {
           u <- username("sam halliday")
           r <- realname("")
         } yield Credentials(u, r)
  res = -\/(username contains spaces)

Si usamos la sintáxis |@|

  scala> (username("sam halliday") |@| realname("")) (Credentials.apply)
  res = -\/(username contains spaces)

Todavía obetenemos el primer error. Esto es porque Disjuntion es una Monad, y sus métodos .applyX deben ser consistentes con .flatMap y no asumir que ninguna operación pueden realizarse fuera de orden. Compare con:

  scala> :paste
         def username(in: String): ValidationNel[String, Username] =
           if (in.isEmpty) "empty username".failureNel
           else if (in.contains(" ")) "username contains spaces".failureNel
           else Username(in).success
  
         def realname(in: String): ValidationNel[String, Fullname] =
           if (in.isEmpty) "empty real name".failureNel
           else Fullname(in).success
  
  scala> (username("sam halliday") |@| realname("")) (Credentials.apply)
  res = Failure(NonEmpty[username contains spaces,empty real name])

Esta vez, tenemos todas las fallas!

Validation tiene muchos de los métodos en Disjunction, tales como .fold, .swap y +++, además de algunas extra:

  sealed abstract class Validation[+E, +A] {
    def append[F >: E: Semigroup, B >: A: Semigroup](x: F \?/ B]): F \?/ B = ...
  
    def disjunction: (E \/ A) = ...
    ...
  }

.append (con el alias simbólico +|+) tiene la misma signatura de tipo que +++ pero da preferencia al caso de éxito

• failure(v1) +|+ failure(v2) da failure(v1 |+| v2)
• failure(v1) +|+ success(v2) da success(v2)
• success(v1) +|+ failure(v2) da success(v1)
• success(v1) +|+ success(v2) da success(v1 |+| v2)

.disjunction convierte un valor Validated[A, B] en un A \/ B. Disjunction tiene los métodos .validation y .validationNel para convertir en una Validation, permitiendo la fácil conversión entre acumulación sequencial y paralela de errores.

\/ y Validation son las versiones de PF con mayor rendimiento, equivalentes a una excepción de validación de entrada, evitando tanto un stacktrace y requiriendo que el que realiza la invocación lidie con las fallas resultando en sistemas más robustos.

6.7.4 These

Encontramos These, un codificación en forma de datos de un OR lógicamente inclusivo, cuando aprendimos sobre Align

  sealed abstract class \&/[+A, +B] { ... }
  object \&/ {
    type These[A, B] = A \&/ B
  
    final case class This[A](aa: A) extends (A \&/ Nothing)
    final case class That[B](bb: B) extends (Nothing \&/ B)
    final case class Both[A, B](aa: A, bb: B) extends (A \&/ B)
  
    def apply[A, B](a: A, b: B): These[A, B] = Both(a, b)
  }

y con una sintáxis para una construcción conveniente

  implicit class TheseOps[A](self: A) {
    final def wrapThis[B]: A \&/ B = \&/.This(self)
    final def wrapThat[B]: B \&/ A = \&/.That(self)
  }
  implicit class ThesePairOps[A, B](self: (A, B)) {
    final def both: A \&/ B = \&/.Both(self._1, self._2)
  }

These tiene instancias de una typeclass para

• Monad
• Bitraverse
• Traverse
• Cobind

y dependiendo del contenido

• Semigroup / Monoid / Band
• Equal / Order
• Show

These (\&/) tiene muchos de los métodos que que esperamos de ``Disjunction (\/) y Validation (?/`)

  sealed abstract class \&/[+A, +B] {
    def fold[X](s: A => X, t: B => X, q: (A, B) => X): X = ...
    def swap: (B \&/ A) = ...
  
    def append[X >: A: Semigroup, Y >: B: Semigroup](o: =>(X \&/ Y)): X \&/ Y = ...
  
    def &&&[X >: A: Semigroup, C](t: X \&/ C): X \&/ (B, C) = ...
    ...
  }

.append tiene 9 posibles arreglos y los datos nunca se tiran porque los casos de This y That siempre pueden convertirse en Both.

.flatMap está sesgado hacia la derecha (Both y That), tomando un Semigroup del contenido de la izquierda (This) para combinar en lugar de fallar temprano. &&& es una manera conveniente de hacer un binding sobre dos valores de tipo These, creando una tupla a la derecha y perdiendo datos si no está presente en cada uno de estos (these).

Aunque es tentador usar \&/ en los tipos de retorno, el uso excesivo es un antipatrón. La razón principal para usar \&/ es para combinar o dividir streams de datos potencialmente infinitos en memoria finita. En el objeto compañero existen funciones convenientes para lidiar con EphemeralStream (con un alias para que quepan en una sola línea) o cualquier cosa con un MonadPlus.

  type EStream[A] = EphemeralStream[A]
  
  object \&/ {
    def concatThisStream[A, B](x: EStream[A \&/ B]): EStream[A] = ...
    def concatThis[F[_]: MonadPlus, A, B](x: F[A \&/ B]): F[A] = ...
  
    def concatThatStream[A, B](x: EStream[A \&/ B]): EStream[B] = ...
    def concatThat[F[_]: MonadPlus, A, B](x: F[A \&/ B]): F[B] = ...
  
    def unalignStream[A, B](x: EStream[A \&/ B]): (EStream[A], EStream[B]) = ...
    def unalign[F[_]: MonadPlus, A, B](x: F[A \&/ B]): (F[A], F[B]) = ...
  
    def merge[A: Semigroup](t: A \&/ A): A = ...
    ...
  }

6.7.5 Higher Kinded Either

El tipo de datos Coproduct (no confunda con el concepto más general de un coproducto en un ADT) envuelve una Disjunction para los constructores de tipo:

  final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A]) { ... }
  object Coproduct {
    def leftc[F[_], G[_], A](x: F[A]): Coproduct[F, G, A] = Coproduct(-\/(x))
    def rightc[F[_], G[_], A](x: G[A]): Coproduct[F, G, A] = Coproduct(\/-(x))
    ...
  }

Las instancias de un typeclass simplemente delegan a aquellos de F[_] y G[_].

El caso de uso más popular para un Coproduct es cuando deseamos crear un coproducto anónimo de múltiples ADTs.

6.7.6 No tan estricta

Las tuplas de Scala integradas, y los tipos de datos básicos como Maybe y la Disjunction son tipos de valores evaluados de manera estricta.

Por conveniencia, las alternativas por nombre para Name se proporcionan, teniendo las instancias de typeclass esperadas:

  sealed abstract class LazyTuple2[A, B] {
    def _1: A
    def _2: B
  }
  ...
  sealed abstract class LazyTuple4[A, B, C, D] {
    def _1: A
    def _2: B
    def _3: C
    def _4: D
  }
  
  sealed abstract class LazyOption[+A] { ... }
  private final case class LazySome[A](a: () => A) extends LazyOption[A]
  private case object LazyNone extends LazyOption[Nothing]
  
  sealed abstract class LazyEither[+A, +B] { ... }
  private case class LazyLeft[A, B](a: () => A) extends LazyEither[A, B]
  private case class LazyRight[A, B](b: () => B) extends LazyEither[A, B]

El lector astuto notará que Lazy no está bien nombrado, y estos tipos de datos quizá deberían ser: ByNameTupleX, ByNameOption y ByNameEither.

6.7.7 Const

Const, para constante, es un envoltorio para un valor de tipo A, junto con un parámetro de tipo B.

  final case class Const[A, B](getConst: A)

Const proporciona una instancia de Applicative[Const[A, ?]] si hay un Monoid[A] disponible:

  implicit def applicative[A: Monoid]: Applicative[Const[A, ?]] =
    new Applicative[Const[A, ?]] {
      def point[B](b: =>B): Const[A, B] =
        Const(Monoid[A].zero)
      def ap[B, C](fa: =>Const[A, B])(fbc: =>Const[A, B => C]): Const[A, C] =
        Const(fbc.getConst |+| fa.getConst)
    }

La cosa más importante sobre este Applicative es que ignora los parámetros B, continuando sin fallar y únicamente combinando los valores constantes que encuentra.

Volviendo atrás a nuestra aplicación de ejemplo drone-dynamic-agents, deberíamos refactorizar nuestro archivo logic.scala para usar Applicative en lugar de Monad. Escribimos logic.scala antes de que supieramos sobre Applicative y ahora lo sabemos mejor:

  final class DynAgentsModule[F[_]: Applicative](D: Drone[F], M: Machines[F])
    extends DynAgents[F] {
    ...
    def act(world: WorldView): F[WorldView] = world match {
      case NeedsAgent(node) =>
        M.start(node) >| world.copy(pending = Map(node -> world.time))
  
      case Stale(nodes) =>
        nodes.traverse { node =>
          M.stop(node) >| node
        }.map { stopped =>
          val updates = stopped.strengthR(world.time).toList.toMap
          world.copy(pending = world.pending ++ updates)
        }
  
      case _ => world.pure[F]
    }
    ...
  }

Dado que nuestra lógica de negocio únicamente requiere de un Applicative, podemos escribir implementaciones simuladas con F[a] como Const[String, a]. En tal caso, devolvemos los nombres de la función que se invoca:

  object ConstImpl {
    type F[a] = Const[String, a]
  
    private val D = new Drone[F] {
      def getBacklog: F[Int] = Const("backlog")
      def getAgents: F[Int]  = Const("agents")
    }
  
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]     = Const("alive")
      def getManaged: F[NonEmptyList[MachineNode]] = Const("managed")
      def getTime: F[Epoch]                        = Const("time")
      def start(node: MachineNode): F[Unit]        = Const("start")
      def stop(node: MachineNode): F[Unit]         = Const("stop")
    }
  
    val program = new DynAgentsModule[F](D, M)
  }

Con nuestra interpretación de nuestro programa, podemos realizar aserciones sobre los métodos que son invocados:

  it should "call the expected methods" in {
    import ConstImpl._
  
    val alive    = Map(node1 -> time1, node2 -> time1)
    val world    = WorldView(1, 1, managed, alive, Map.empty, time4)
  
    program.act(world).getConst shouldBe "stopstop"
  }

De manera alternativa, podríamos haber contado el total de métodos al usar Const[Int, ?] o en un IMap[String, Int].

Con esta prueba, hemos ido más allá de realizar pruebas con implementaciones simuladas con una prueba Const que hace aserciones sobre lo que se invoca sin tener que proporcionar implementaciones. Esto es útil si nuestra especificación demanda que hagamos ciertas llamadas para ciertas entradas, por ejemplo, para propósitos de contabilidad. Además, hemos conseguido esto con seguridad en tiempo de compilación.

Tomando esta línea de pensamiento un poco más allá, digamos que deseamos monitorear (en tiempo de producción) los nodos que estamos deteniendo en act. Podemos crear implementaciones de Drone y Machines con Const, invocándolos desde nuestra versión envuelta de act

  final class Monitored[U[_]: Functor](program: DynAgents[U]) {
    type F[a] = Const[Set[MachineNode], a]
    private val D = new Drone[F] {
      def getBacklog: F[Int] = Const(Set.empty)
      def getAgents: F[Int]  = Const(Set.empty)
    }
    private val M = new Machines[F] {
      def getAlive: F[Map[MachineNode, Epoch]]     = Const(Set.empty)
      def getManaged: F[NonEmptyList[MachineNode]] = Const(Set.empty)
      def getTime: F[Epoch]                        = Const(Set.empty)
      def start(node: MachineNode): F[Unit]        = Const(Set.empty)
      def stop(node: MachineNode): F[Unit]         = Const(Set(node))
    }
    val monitor = new DynAgentsModule[F](D, M)
  
    def act(world: WorldView): U[(WorldView, Set[MachineNode])] = {
      val stopped = monitor.act(world).getConst
      program.act(world).strengthR(stopped)
    }
  }

Podemos hacer esto porque monitor es puro y ejecutarlo no produce efectos laterales.

Esto ejecuta el programa con ConstImpl, extrayendo todas las llamadas a Machines.stop, entonces devolviéndolos junto con la WorldView. Podemos hacer pruebas unitarias así:

  it should "monitor stopped nodes" in {
    val underlying = new Mutable(needsAgents).program
  
    val alive = Map(node1 -> time1, node2 -> time1)
    val world = WorldView(1, 1, managed, alive, Map.empty, time4)
    val expected = world.copy(pending = Map(node1 -> time4, node2 -> time4))
  
    val monitored = new Monitored(underlying)
    monitored.act(world) shouldBe (expected -> Set(node1, node2))
  }

Hemos usado Const para hacer algo que es como la Programación Orientada a Aspectos (Aspect Oriented Programming), que alguna vez fue popular en Java. Construimos encima de nuestra lógica de negocios para soportar una preocupación de monitoreo, sin tener que complicar la lógica de negocios.

Se pone incluso mejor. Podemos ejecutar ConstImpl en producción para reunir lo que deseamos para detenernos (stop), y entonces proporcionar una implementación optimizada de act que puede usar llamadas por batches/lotes que puede ser de implementación específica.

El héroe siliencioso de esta historia es Applicative. Const nos deja ver lo que es posible. Si necesitamos cambiar nuestro programa para que requiera una Monad, no podemos seguir usando Const y es necesario escribir mocks completos para poder hacer aserciones sobre lo que se llama sobre ciertas entradas. La Regla del Poder Mínimo demanda que usemos Applicative en lugar de Monad siempre que podamos.

6.8 Colecciones

A diferencia de la API de colecciones de la librería estándar, Scalaz describe comportamientos en las colecciones en la jerarquía de typeclases, por ejemplo, Foldable, Traverse, Monoid. Lo que resta por estudiar son las implementaciones en términos de estructuras de datos, que tienen características de rendimiento distintas y métodos muy específicos.

Esta sección estudia detalles de implementación para cada tipo de datos. No es esencial recordar todo lo que se presenta aquí: la meta es ganar entendimiento a un nivel de abstracción alto de cómo funciona cada estructura de datos.

Debido a que los tipos de datos de todas las colecciones nos proporcionan más o menos la misma lista de instancias de typeclases, debemos evitar repetir la lista, que siempre es una variación de la lista:

• Monoid
• Traverse / Foldable
• MonadPlus / IsEmpty
• Cobind / Comonad
• Zip / Unzip
• Align
• Equal / Order
• Show

Las estructuras de datos que es posible probar que no son vacías pueden proporcionar:

• Traverse1 / Foldable1

y proporcionar Semigroup en lugar de Monoid, Plus en lugar de IsEmpty.

6.8.1 Listas

Ya hemos usado IList[A] y NonEmptyList[A] tantas veces al momento que a estas alturas deberían ser familiares. Codifican una estructura de datos clásica, la lista ligada:

  sealed abstract class IList[A] {
    def ::(a: A): IList[A] = ...
    def :::(as: IList[A]): IList[A] = ...
    def toList: List[A] = ...
    def toNel: Option[NonEmptyList[A]] = ...
    ...
  }
  final case class INil[A]() extends IList[A]
  final case class ICons[A](head: A, tail: IList[A]) extends IList[A]
  
  final case class NonEmptyList[A](head: A, tail: IList[A]) {
    def <::(b: A): NonEmptyList[A] = nel(b, head :: tail)
    def <:::(bs: IList[A]): NonEmptyList[A] = ...
    ...
  }

La ventaja principal de IList sobre List de la librería estándar es que no hay métodos inseguros, como .head que lanza una excepción sobre listas vacías.

Adicionalmente, IList es mucho más simple, sin tener una jerarquía de clases y un tamaño del bytecode mucho más pequeño. Además, List de la librería estándar tiene una implementación terrible que usa var para parchar problemas de rendimiento en el diseño de las colecciones de la librería estándar:

  package scala.collection.immutable
  
  sealed abstract class List[+A]
    extends AbstractSeq[A]
    with LinearSeq[A]
    with GenericTraversableTemplate[A, List]
    with LinearSeqOptimized[A, List[A]] { ... }
  case object Nil extends List[Nothing] { ... }
  final case class ::[B](
    override val head: B,
    private[scala] var tl: List[B]
  ) extends List[B] { ... }

La creación de una instancia de List requiere de la creación cuidadosa, y lenta, de sincronización de Threads para asegurar una publicación segura. IList no requiere de tales hacks y por lo tanto puede superar a List.

6.8.2 EphemeralStream

Stream de la librería estándar es una versión perezosa de List, pero está plagada con fugas de memoria y métodos inseguros. EphemeralStream no mantiene referencias a valores calculados, ayudando a mitigar los problemas de retención de memoria, removiendo los métodos inseguros en el mismo espíritu que IList.

  sealed abstract class EphemeralStream[A] {
    def headOption: Option[A]
    def tailOption: Option[EphemeralStream[A]]
    ...
  }
  // private implementations
  object EphemeralStream extends EphemeralStreamInstances {
    type EStream[A] = EphemeralStream[A]
  
    def emptyEphemeralStream[A]: EStream[A] = ...
    def cons[A](a: =>A, as: =>EStream[A]): EStream[A] = ...
    def unfold[A, B](start: =>B)(f: B => Option[(A, B)]): EStream[A] = ...
    def iterate[A](start: A)(f: A => A): EStream[A] = ...
  
    implicit class ConsWrap[A](e: =>EStream[A]) {
      def ##::(h: A): EStream[A] = cons(h, e)
    }
    object ##:: {
      def unapply[A](xs: EStream[A]): Option[(A, EStream[A])] =
        if (xs.isEmpty) None
        else Some((xs.head(), xs.tail()))
    }
    ...
  }

.cons, .unfold e .iterate son mecanismos para la creación de streams, y la sintaxis conveniente ##:: pone un nuevo elemento en la cabeza de una referencia por nombre EStream. .unfold es para la creación de un stream finito (pero posiblemente infinito) al aplicar repetidamente una función f para obtener el siguiente valor y la entrada para la siguiente f. .iterate crea un stream infinito al aplicar repetidamente una función f en el elemento previo.

EStream puede aparecer en patrones de emparejamiento con el símbolo ##::, haciendo un match para la sintaxis para .cons.

Aunque EStream lidia con el problema de retención de valores de memoria, todavía es posible sufrir de fugas de memoria lentas si una referencia viva apunta a la cabeza de un stream infinito. Los problemas de esta naturaleza, así como la necesidad de realizar composición de streams con efectos, es la razón de que fs2 exista.

6.8.3 CorecursiveList

La correcursión es cuando empezamos de un estado base y producimos pasos subsecuentes de manera determinística, como el método EphemeralStream.unfold que acabamos de estudiar:

  def unfold[A, B](b: =>B)(f: B => Option[(A, B)]): EStream[A] = ...

Contraste con una recursion, que pone datos en un estado base y entonces termina.

Una CorecursiveList es una codificación de datos de un EphemeralStream.unfold, ofreciendo una alternativa a EStream que puede lograr un rendimiento mejor en algunas circunstancias:

  sealed abstract class CorecursiveList[A] {
    type S
    def init: S
    def step: S => Maybe[(S, A)]
  }
  
  object CorecursiveList {
    private final case class CorecursiveListImpl[S0, A](
      init: S0,
      step: S0 => Maybe[(S0, A)]
    ) extends CorecursiveList[A] { type S = S0 }
  
    def apply[S, A](init: S)(step: S => Maybe[(S, A)]): CorecursiveList[A] =
      CorecursiveListImpl(init, step)
  
    ...
  }

La correcursión es útil cuando estamos implementando Comonad.cojoin, como en nuestro ejemplo de Hood. CorecursiveList es una buena manera de codificar ecuaciones con recurrencia no lineales como las que se usan en el modelado de poblaciones de biología, sistemas de control, macro economía, y los modelos de inversión de bancos.

6.8.4 ImmutableArray

Un simple wrapper alrededor del Array mutable de la librería estándar, con especializaciones primitivas:

  sealed abstract class ImmutableArray[+A] {
    def ++[B >: A: ClassTag](o: ImmutableArray[B]): ImmutableArray[B]
    ...
  }
  object ImmutableArray {
    final class StringArray(s: String) extends ImmutableArray[Char] { ... }
    sealed class ImmutableArray1[+A](as: Array[A]) extends ImmutableArray[A] { ... }
    final class ofRef[A <: AnyRef](as: Array[A]) extends ImmutableArray1[A](as)
    ...
    final class ofLong(as: Array[Long]) extends ImmutableArray1[Long](as)
  
    def fromArray[A](x: Array[A]): ImmutableArray[A] = ...
    def fromString(str: String): ImmutableArray[Char] = ...
    ...
  }

Array no tiene rival en términos de rendimiento al hacer lectura y el tamaño del heap. Sin embargo, no se está comportiendo memoria estructuralmente cuando se crean nuevos arreglos, y por lo tanto los arreglos se usan típicamente cuando no se espera que los contenidos cambien, o como una manera segura de envolver de manera segura datos crudos de un sistema antiguo/legacy.

6.8.5 Dequeue

Un Dequeue (pronunciado como en “deck of cards”) es una lista ligada que permite que los elementos se coloquen o se devuelvan del frente (cons) o en la parte trasera (snoc) en tiempo constante. Remover un elemento de cualquiera de los extremos es una operación de tiempo constante, en promedio.

  sealed abstract class Dequeue[A] {
    def frontMaybe: Maybe[A]
    def backMaybe: Maybe[A]
  
    def ++(o: Dequeue[A]): Dequeue[A] = ...
    def +:(a: A): Dequeue[A] = cons(a)
    def :+(a: A): Dequeue[A] = snoc(a)
    def cons(a: A): Dequeue[A] = ...
    def snoc(a: A): Dequeue[A] = ...
    def uncons: Maybe[(A, Dequeue[A])] = ...
    def unsnoc: Maybe[(A, Dequeue[A])] = ...
    ...
  }
  private final case class SingletonDequeue[A](single: A) extends Dequeue[A] { ... }
  private final case class FullDequeue[A](
    front: NonEmptyList[A],
    fsize: Int,
    back: NonEmptyList[A],
    backSize: Int) extends Dequeue[A] { ... }
  private final case object EmptyDequeue extends Dequeue[Nothing] { ... }
  
  object Dequeue {
    def empty[A]: Dequeue[A] = EmptyDequeue()
    def apply[A](as: A*): Dequeue[A] = ...
    def fromFoldable[F[_]: Foldable, A](fa: F[A]): Dequeue[A] = ...
    ...
  }

La forma en la que funciona es que existen dos listas, una para los datos al frente y otra para los datos en la parte trasera. Considere una instancia para mantener los símbolos a0, a1, a2, a3, a4, a5, a6

  FullDequeue(
    NonEmptyList('a0, IList('a1, 'a2, 'a3)), 4,
    NonEmptyList('a6, IList('a5, 'a4)), 3)

que puede visualizarse como

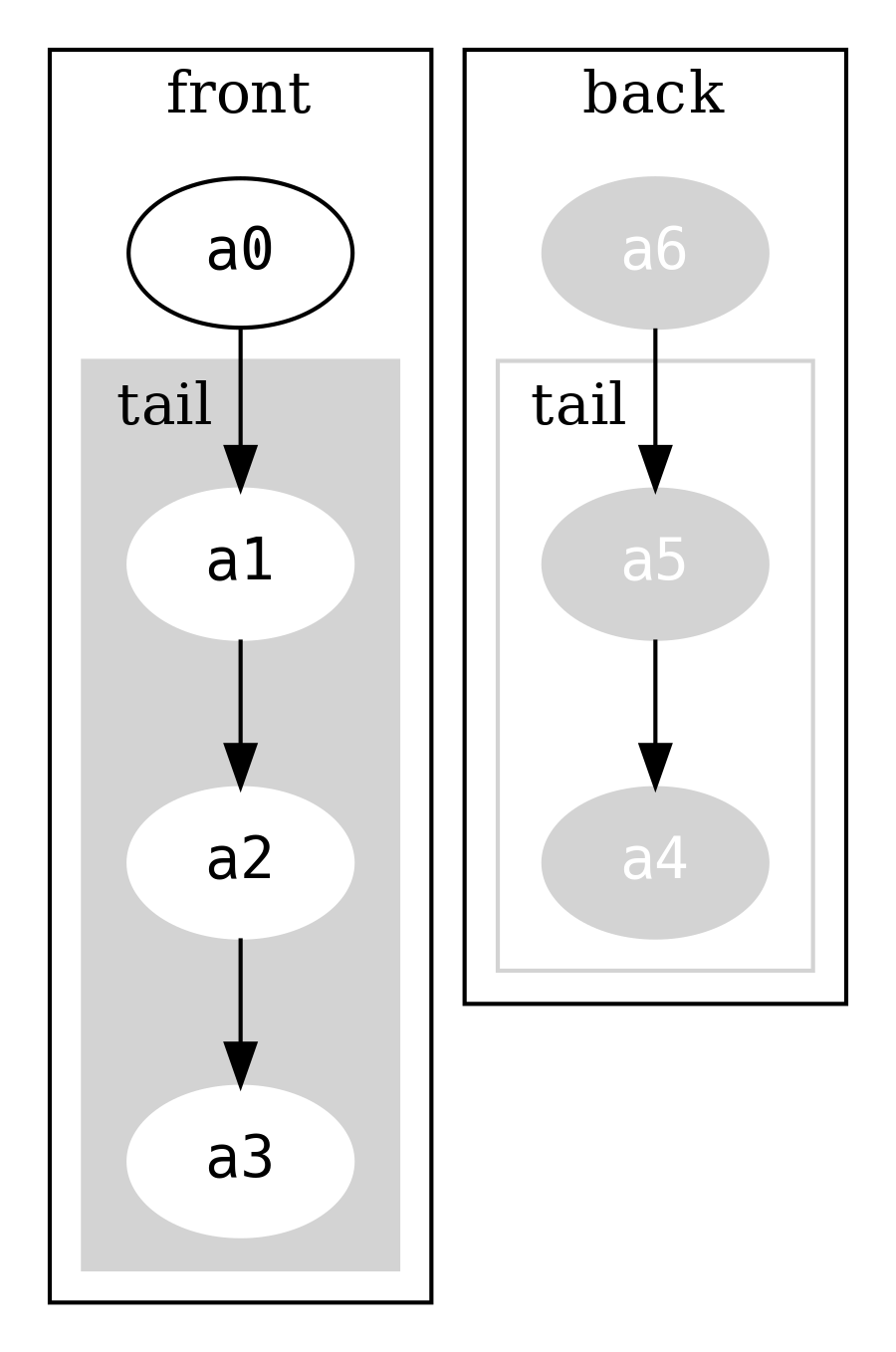
Note que la lista que mantiene back está en orden inverso.

Leer el elemento final, snoc, es una simple lectura en back.head. Añadir un elemento al final del Dequeue significa añadir un nuevo elemento al frente de la lista back, y recrear el envoltorio FullDequeue (que incrementará el tamaño de backSize en uno). Casi toda la estructura original es compartida. Compare a agregar un nuevo elemento al final de una IList, que envolvería recrear la estructura completa.

El frontSize y el backSize se usan para rebalancear el front y el back de modo que casi siempre son del mismo tamaño. Rebalancear significa que algunas operaciones sean más lentas que otras (por ejemplo, cuando la estructura de datos debe ser reconstruida) pero debido a que únicamente ocurre ocasionalmente, podríamos tomar el promedio del costo y decir que es constante.

6.8.6 DList

Las listas ligadas tienen características de rendimiento muy pobres cuando se añaden grandes listas. Considere el trabajo que está envuelto en evaluar lo siguiente:

  ((as ::: bs) ::: (cs ::: ds)) ::: (es ::: (fs ::: gs))

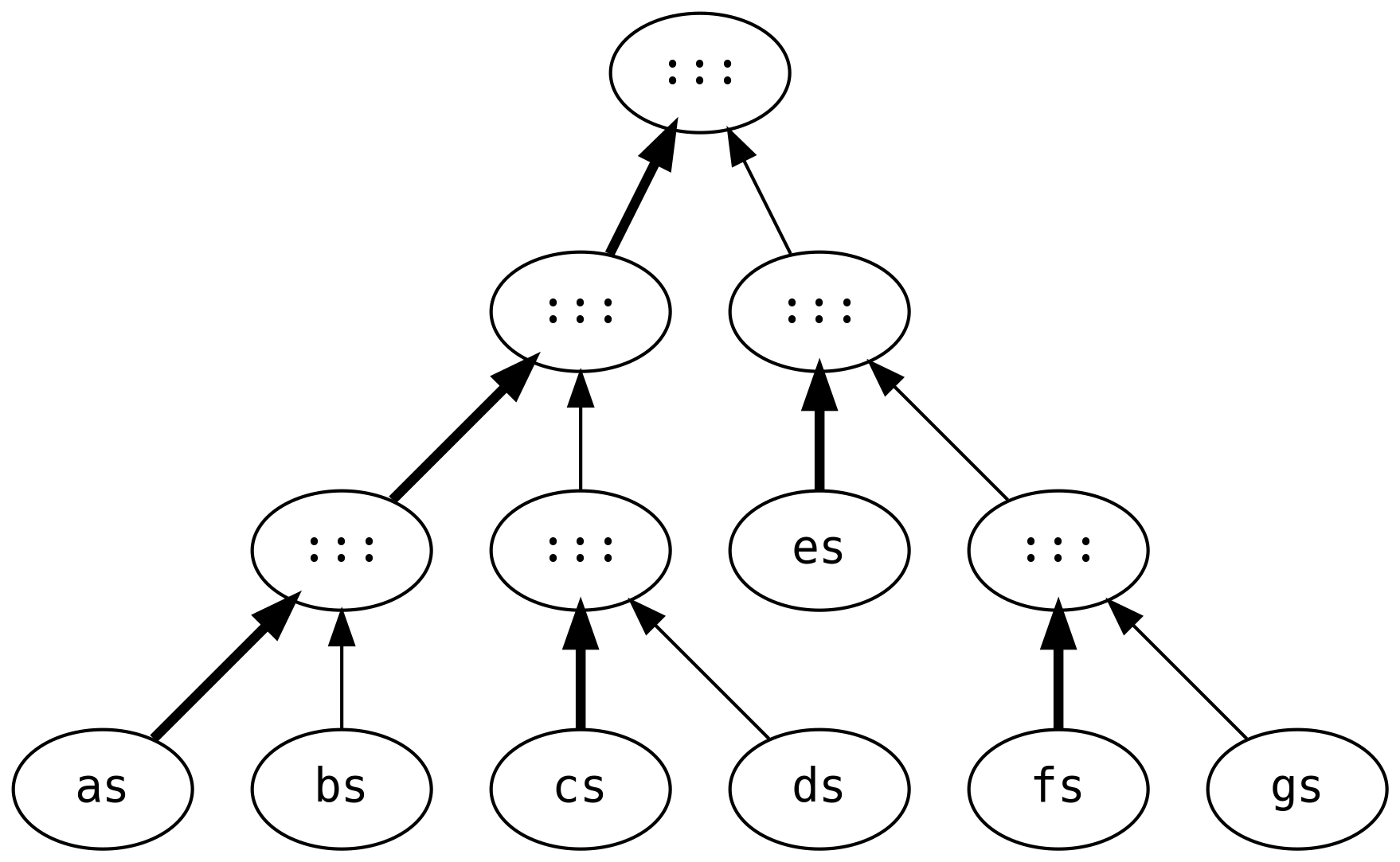
Esto crea seis listas intermedias, recorriendo y reconstruyendo cada lista tres veces (con la excepción de gs que se comparte durante todas las etapas).

La DList (de lista por diferencias) es la solución más eficiente para este escenario. En lugar de realizar cálculos en cada etapa, es representada como la función IList[A] => IList[A]

  final case class DList[A](f: IList[A] => IList[A]) {
    def toIList: IList[A] = f(IList.empty)
    def ++(as: DList[A]): DList[A] = DList(xs => f(as.f(xs)))
    ...
  }
  object DList {
    def fromIList[A](as: IList[A]): DList[A] = DList(xs => as ::: xs)
  }

El cálculo equivalente es (los símbolos son creados a partir de DList.fromIList)

  (((a ++ b) ++ (c ++ d)) ++ (e ++ (f ++ g))).toIList

que reparte el trabajo en appends asociativos a la derecha (es decir, rápidos)

  (as ::: (bs ::: (cs ::: (ds ::: (es ::: (fs ::: gs))))))

utilizando el constructor rápido sobre IList.

Como siempre, no hay nada gratis. Existe un costo extra de asignación (alocación) dinámica de memoria que puede reducir la velocidad del código que resulta naturalmente en appends asociativos a la derecha. El incremento de velocidad más grande ocurre cuando operaciones IList son asociativas hacia la izquierda, por ejemplo

  ((((((as ::: bs) ::: cs) ::: ds) ::: es) ::: fs) ::: gs)

Las listas de diferencia sufren de un marketing malo. Tal vez si su nombre fuera ListBuilderFactory estarían en la librería estándar.

6.8.7 ISet

Las estructuras de árboles son excelentes para almacenar datos ordenados, con cada nodo binario manteniendo elementos que son menores en una rama, y mayores en la otra. Sin embargo, implementaciones ingenuas de la estructura de datos árbol pueden desbalancearse dependiendo del orden de inserción. Es posible mantener un árbol perfectamente balanceado, pero es increíblemente ineficiente dado que cada inserción efectivamente reconstruye el árbol completo.

ISet es una implementación de un árbol con balanceo acotado, significando que está aproximadamente balanceado, usando el tamaño (size) de cada rama para balancear el nodo.

  sealed abstract class ISet[A] {
    val size: Int = this match {
      case Tip()        => 0
      case Bin(_, l, r) => 1 + l.size + r.size
    }
    ...
  }
  object ISet {
    private final case class Tip[A]() extends ISet[A]
    private final case class Bin[A](a: A, l: ISet[A], r: ISet[A]) extends ISet[A]
  
    def empty[A]: ISet[A] = Tip()
    def singleton[A](x: A): ISet[A] = Bin(x, Tip(), Tip())
    def fromFoldable[F[_]: Foldable, A: Order](xs: F[A]): ISet[A] =
      xs.foldLeft(empty[A])((a, b) => a insert b)
    ...
  }

ISet requiere que A tenga un Order. La instancia Order[A] debe permanecer igual entre llamadas o las invariantes internas serán inválidas, llevándonos a tener datos corrompidos: es decir, estamos asumiendo la coherencia de typeclases tales que Order[A] es única para cualquier A.

La ADT ISet desgraciadamente permite árboles inválidos. Nos esforzamos por escribir ADTs que describan completamente lo que es y no es válido usando restricciones de tipo, pero algunas veces tenemos situaciones donde únicamente es posible lograrlo con el toque inspirado de un inmortal. En lugar de esto, Tip / Bin son private, para evitar que los usuarios construyan, accidentalmente, árboles inválidos. .insert es la única manera de construir un ISet, y por lo tanto definir lo que es un árbol válido.

  sealed abstract class ISet[A] {
    ...
    def contains(x: A)(implicit o: Order[A]): Boolean = ...
    def union(other: ISet[A])(implicit o: Order[A]): ISet[A] = ...
    def delete(x: A)(implicit o: Order[A]): ISet[A] = ...
  
    def insert(x: A)(implicit o: Order[A]): ISet[A] = this match {
      case Tip() => ISet.singleton(x)
      case self @ Bin(y, l, r) => o.order(x, y) match {
        case LT => balanceL(y, l.insert(x), r)
        case GT => balanceR(y, l, r.insert(x))
        case EQ => self
      }
    }
    ...
  }

Los métodos internos .balanceL y .balanceR son espejos uno del otro, de modo que únicamente estudiamos .balanceL, que también se llama cuando el valor que estamos insertando es menor que el nodo actual. También se invoca por el método .delete.

  def balanceL[A](y: A, left: ISet[A], right: ISet[A]): ISet[A] = (left, right) match {
  ...

El balanceo requiere que clasifiquemos los escenarios que pueden ocurrir. Estudiaremos cada posible escenario, visualizando (y, left, right) al lado izquierdo de la página, con la estructura balanceada a la derecha, también conocido como el árbol rotado.

• círculos llenos visualizan un Tip
• tres columbas visualizan los campos left | value | right de Bin
• los diamantes visualizan cualquier ISet

El primer escenario es el caso trivial, que es cuando, tanto el lado left y el right son Tip. De hecho, nunca encontraremos este escenario a partir de .insert, pero lo encontramos en .delete.

  case (Tip(), Tip()) => singleton(y)

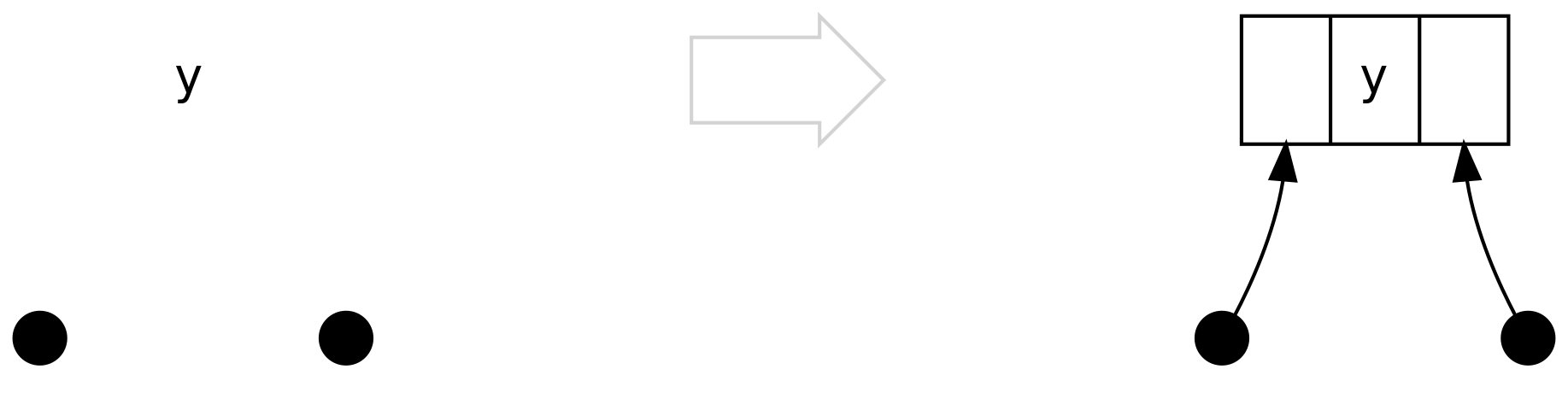
El segundo caso es cuando left es un Bin que contiene únicamente a Tip, y no necesitamos balancear nada, simplemente creamos la conexión obvia:

  case (Bin(lx, Tip(), Tip()), Tip()) => Bin(y, left, Tip())

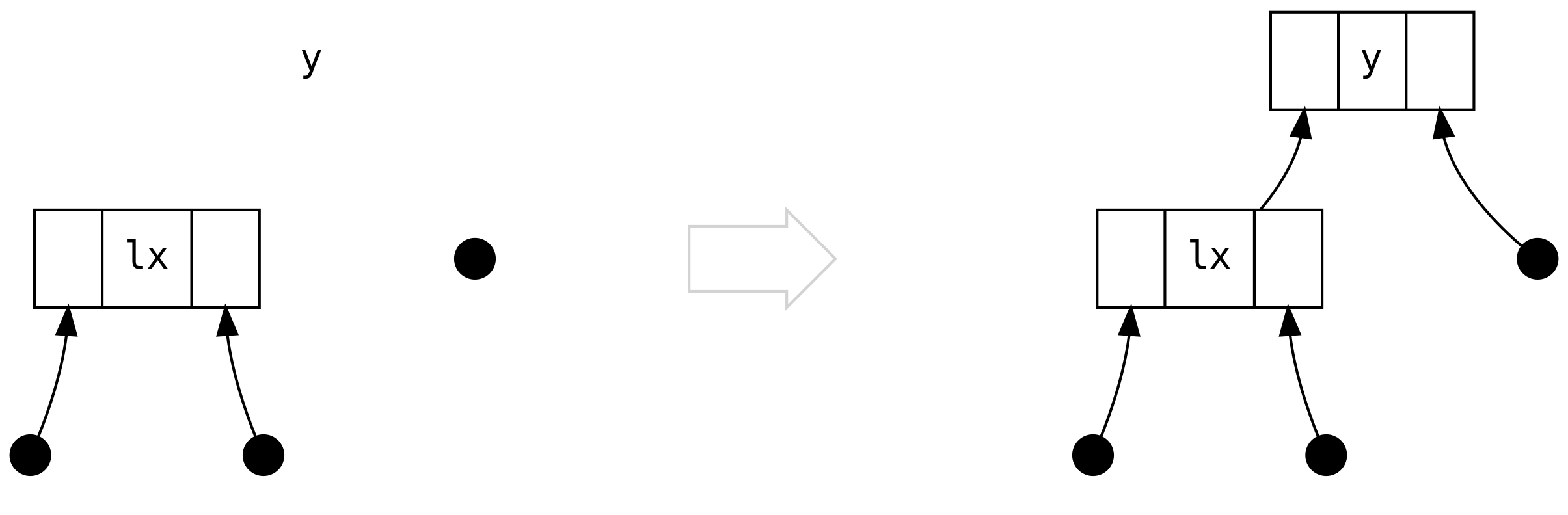
El tercer caso es cuando esto empieza a ponerse interesante: left es un Bin conteniendo únicamente un Bin a su right.

  case (Bin(lx, Tip(), Bin(lrx, _, _)), Tip()) =>
    Bin(lrx, singleton(lx), singleton(y))

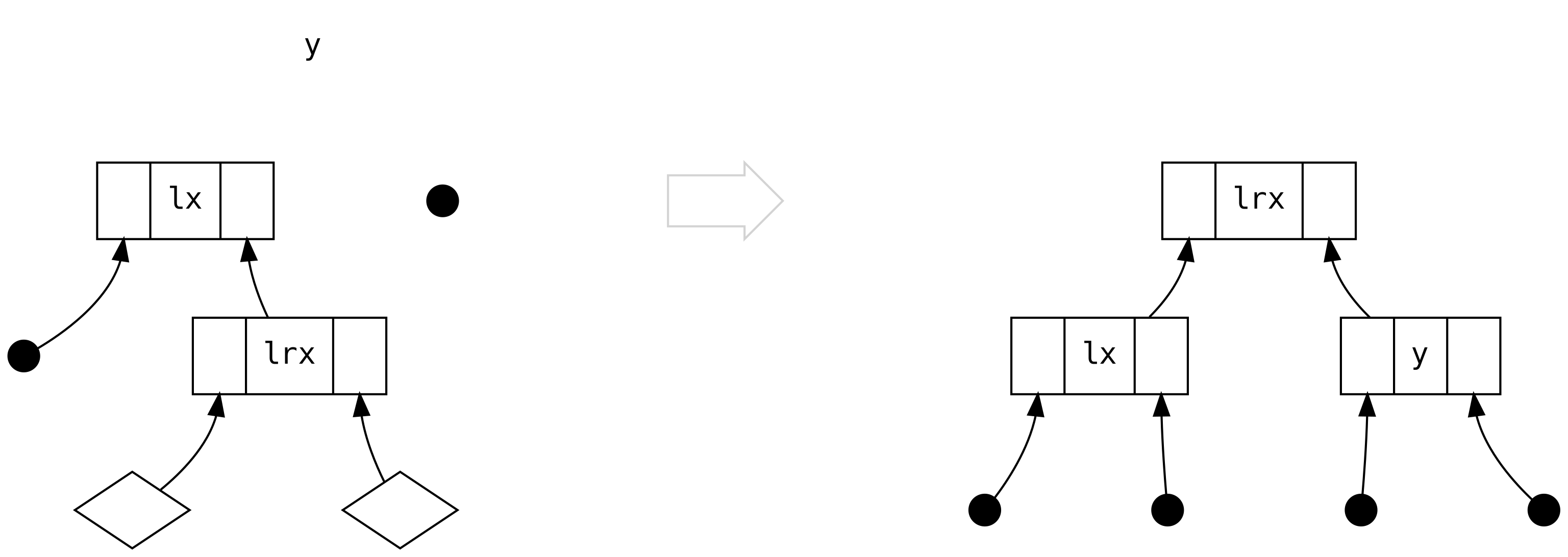
Pero qué ocurrió a los dos diamantes que están debajo de lrx? No acabamos de perder información? No, no perdimos información, porque podemos razonar (basándonos en el balanceo del tamaño) que siempre son Tip! No hay regla en cuanto a cualquiera de los siguientes escenarios (o en .balanceR) que pueden producir un árbol donde los diamantes son Bin.

El cuarto caso es el opuesto del tercer caso.

  case (Bin(lx, ll, Tip()), Tip()) => Bin(lx, ll, singleton(y))

El quinto caso es cuando tenemos árboles completos en ambos lados del lado left y de todos modos debemos usar sus tamañaos relativos para decidir cómo rebalancear.

  case (Bin(lx, ll, lr), Tip()) if (2*ll.size > lr.size) =>
    Bin(lx, ll, Bin(y, lr, Tip()))
  case (Bin(lx, ll, Bin(lrx, lrl, lrr)), Tip()) =>
    Bin(lrx, Bin(lx, ll, lrl), Bin(y, lrr, Tip()))

Para la primera rama, 2*ll.size > lr.size

y para la segunda rama 2*ll.size <= lr.size

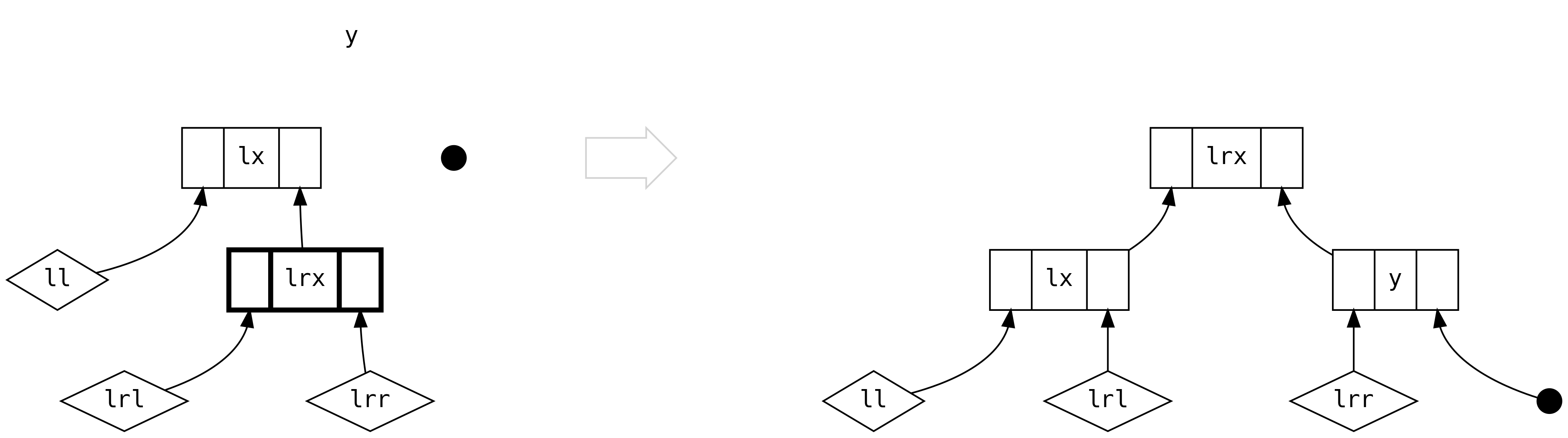
El sexto escenario introduce un árbol en lado (derecho) right. Cuando el lado left está vacío creamos la conexión obvia. Ese escenario nunca surge a partir de .insert porque el lado .left siempre está no vacío:

  case (Tip(), r) => Bin(y, Tip(), r)

El escenario final ocurre cuando tenemos árboles no vacíos en ambos lados. A menos que el lado left sea tres veces o más el tamaño del lado right, podemos hacer lo más sencillo y crear un nuevo Bin.

  case _ if l.size <= 3 * r.size => Bin(y, l, r)

Sin embargo, si el lado left debiera tener más de tres veces el tamaño del lado right, debemos balancear basándonos en los tamaños relativos de ll y lr, como en el escenario cinco.

  case (Bin(lx, ll, lr), r) if (2*ll.size > lr.size) =>
    Bin(lx, ll, Bin(y, lr, r))
  case (Bin(lx, ll, Bin(lrx, lrl, lrr)), r) =>
    Bin(lrx, Bin(lx, ll, lrl), Bin(y, lrr, r))

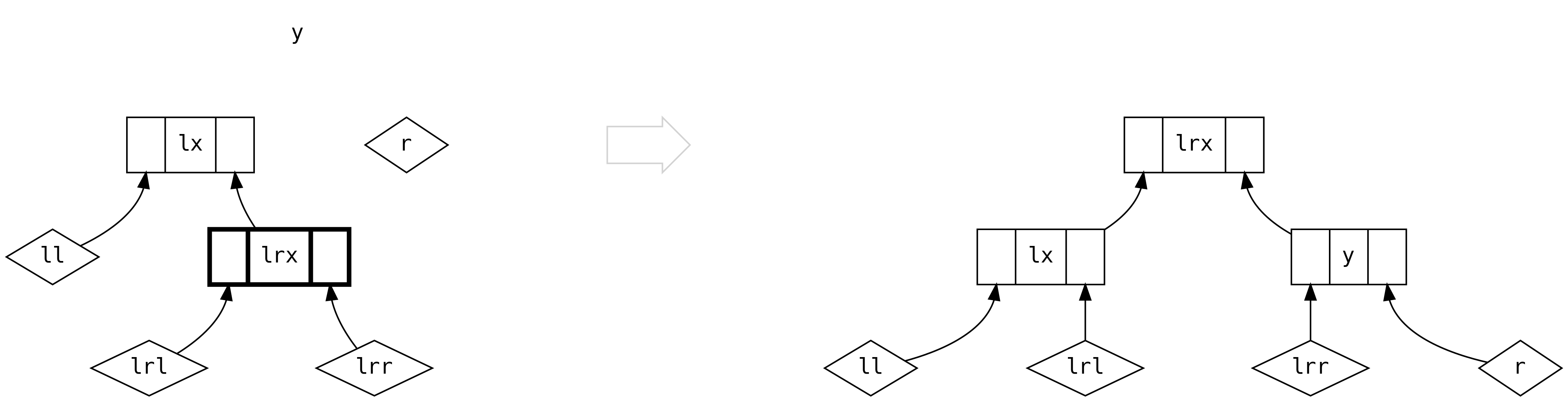
Esto concluye nuestro estudio del método .insert y cómo se construye un ISet. No debería ser sorpresivo que Foldable esté implementado en términos de una búsqueda en lo profundo, junto con left y right, como es apropiado. Métodos tales como .minimum y .maximum son óptimos porque la estructura de datos ya codifica el orden.

Es valioso hacer ntar quealgunos métodos de typeclass no pueden ser implementados de manera tan eficiente como quisieramos. Considere la signatura de Foldable.element

  @typeclass trait Foldable[F[_]] {
    ...
    def element[A: Equal](fa: F[A], a: A): Boolean
    ...
  }

Una implememntación obiva para .element es (de manera práctica) delegar a la búsqueda binaria ISet.contains. Sin embargo, no es posible debido a que .element proporciona Equal mientras que .contains requiere de Order.

ISet es incapaz de proporcionar un Functor por la misma razón. En la práctica esto es una restricción sensible: realizar un .map significaría reconstruir toda la estructura de datos completa. Tiene sentido convertir a un tipo de datos distinto, tales como IList, realizando el .map, y convirtiendo de vuelta. Una consecuencia es que ya no es posible tener un Traverse[ISet] o Applicative[Set].

6.8.8 IMap

  sealed abstract class ==>>[A, B] {
    val size: Int = this match {
      case Tip()           => 0
      case Bin(_, _, l, r) => 1 + l.size + r.size
    }
  }
  object ==>> {
    type IMap[A, B] = A ==>> B
  
    private final case class Tip[A, B]() extends (A ==>> B)
    private final case class Bin[A, B](
      key: A,
      value: B,
      left: A ==>> B,
      right: A ==>> B
    ) extends ==>>[A, B]
  
    def apply[A: Order, B](x: (A, B)*): A ==>> B = ...
  
    def empty[A, B]: A ==>> B = Tip[A, B]()
    def singleton[A, B](k: A, x: B): A ==>> B = Bin(k, x, Tip(), Tip())
    def fromFoldable[F[_]: Foldable, A: Order, B](fa: F[(A, B)]): A ==>> B = ...
    ...
  }

¡Esto es muy familiar! En realidad, IMap (un alias para el operador de la velocidad de la luz) es otro árbol balanceado en tamaño, pero con un campo extra value: B en cada rama del árbol binario, permitiendo almacenar pares de llave/valor. Únicamente el tipo clave A necesita un Order y una clase conveniente de métodos son proporcionados para permitir una actualización fácil de entradas.

  sealed abstract class ==>>[A, B] {
    ...
    def adjust(k: A, f: B => B)(implicit o: Order[A]): A ==>> B = ...
    def adjustWithKey(k: A, f: (A, B) => B)(implicit o: Order[A]): A ==>> B = ...
    ...
  }

Tree es una versión by need (por necesidad) de StrictTree con constructores convenientes

  class Tree[A](
    rootc: Need[A],
    forestc: Need[Stream[Tree[A]]]
  ) {
    def rootLabel = rootc.value
    def subForest = forestc.value
  }
  object Tree {
    object Node {
      def apply[A](root: =>A, forest: =>Stream[Tree[A]]): Tree[A] = ...
    }
    object Leaf {
      def apply[A](root: =>A): Tree[A] = ...
    }
  }

Se espera que el usuario de un Rose Tree lo balancee manualmente, lo que lo hace adecuado para casos donde es útil codificar conocimiento especializado de cierta jerarquía del dominio en la estructura de datos. Por ejemplo, en el campo de la inteligencia artificial, un árbol de Rose puede ser usado en algoritmos de agrupamiento para organizar datos en una jerarquía de cosas cada vez más similares. Es posible representar documentos XML con un árbol Rose.

Cuando trabajamos con datos jerárquicos, considere usar un árbol Rose en lugar de hacer una estructura de datos a la medida.

6.8.9 FingerTree

Los árboles de dedo son secuencias generalizadas con un costo de búsqueda amortizado y concatenación logarítmica. A es el tipo de datos, ignore V por ahora:

  sealed abstract class FingerTree[V, A] {
    def +:(a: A): FingerTree[V, A] = ...
    def :+(a: =>A): FingerTree[V, A] = ...
    def <++>(right: =>FingerTree[V, A]): FingerTree[V, A] = ...
    ...
  }
  object FingerTree {
    private class Empty[V, A]() extends FingerTree[V, A]
    private class Single[V, A](v: V, a: =>A) extends FingerTree[V, A]
    private class Deep[V, A](
      v: V,
      left: Finger[V, A],
      spine: =>FingerTree[V, Node[V, A]],
      right: Finger[V, A]
    ) extends FingerTree[V, A]
  
    sealed abstract class Finger[V, A]
    final case class One[V, A](v: V, a1: A) extends Finger[V, A]
    final case class Two[V, A](v: V, a1: A, a2: A) extends Finger[V, A]
    final case class Three[V, A](v: V, a1: A, a2: A, a3: A) extends Finger[V, A]
    final case class Four[V, A](v: V, a1: A, a2: A, a3: A, a4: A) extends Finger[V, A]
  
    sealed abstract class Node[V, A]
    private class Node2[V, A](v: V, a1: =>A, a2: =>A) extends Node[V, A]
    private class Node3[V, A](v: V, a1: =>A, a2: =>A, a3: =>A) extends Node[V, A]
    ...
  }

Visualizando FingerTree como puntos, Finger como cajas y Node como cajas dentro de cajas:

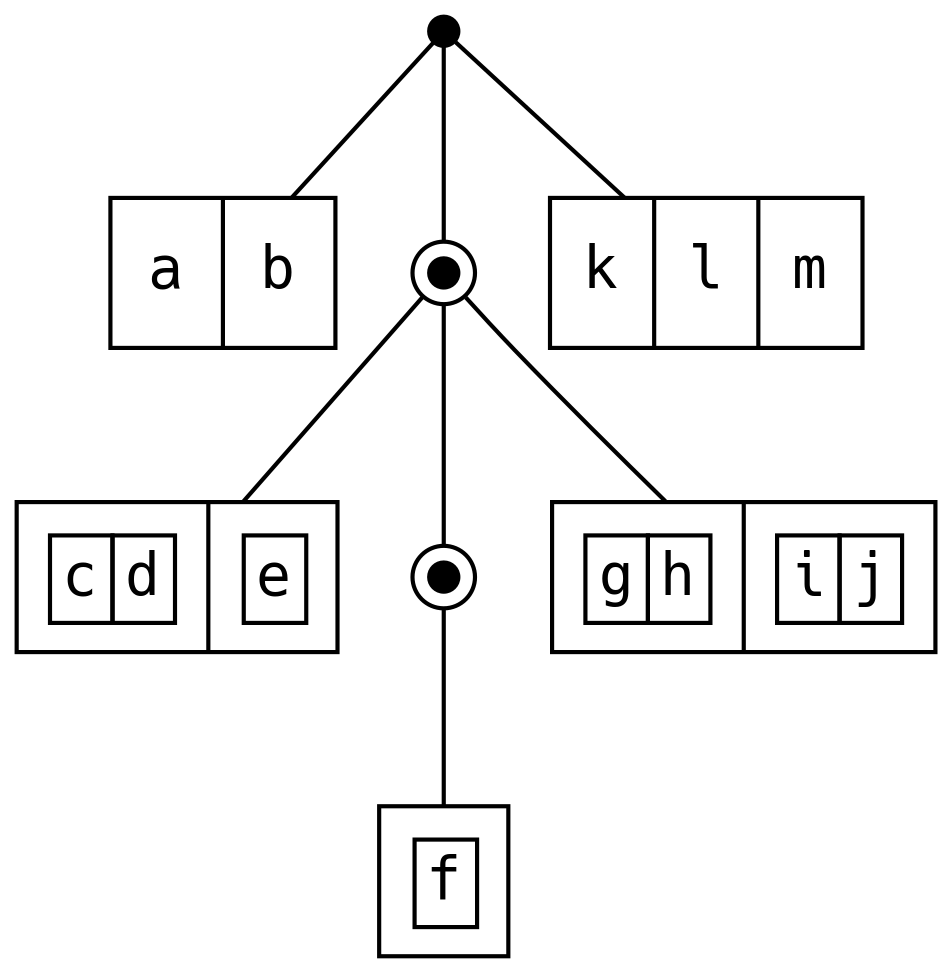
Agregar elementos al frente de un FingerTree con +: es eficiente porque Deep simplemente añade un nuevo elemento al dedo del lado left. Si el dedo es un Four, reconstruimos la espina (spine) para tomar 3 de los elementos como un Node3. Agregando al final, :+, es lo mismo pero en reversa.

Agregar cosas |+| (también <++>) es más eficiente que agregar un elemento a la vez debido a que el caso de dos árboles Deep pueden retener las ramas externas, reconstruyendo la espina basándose en las 16 posibles combinaciones de los dos valores Finger en la mitad.

En la discusión anterior nos saltamos V. En la descripción de la ADT no se muestra una implicit measurer: Reducer[A, V] en cada elemento de la ADT.

Reducer es una extensión de Monoid que permite que un solo elemento se agregue a una M.

  class Reducer[C, M: Monoid] {
    def unit(c: C): M
  
    def snoc(m: M, c: C): M = append(m, unit(c))
    def cons(c: C, m: M): M = append(unit(c), m)
  }

Por ejemplo, Reducer[A, IList[A]] puede proporcionar un .cons eficiente

  implicit def reducer[A]: Reducer[A, IList[A]] = new Reducer[A, IList[A]] {
    override def unit(a: A): IList[A] = IList.single(a)
    override def cons(a: A, as: IList[A]): IList[A] = a :: as
  }

6.8.9.1 IndSeq

Si usamos Int como V, podemos obtener una secuencia indexada, donde la medida es el tamaño, permitiéndonos realizar una búsqueda basada en el índice al comparar el índice deseado con el tamaño de cada rama en la estructura:

  final class IndSeq[A](val self: FingerTree[Int, A])
  object IndSeq {
    private implicit def sizer[A]: Reducer[A, Int] = _ => 1
    def apply[A](as: A*): IndSeq[A] = ...
  }

Otro uso de FingerTree es una secuencia ordenada, donde la medida almacena el valor más largo contenido en cada rama:

6.8.9.2 OrdSeq

  final class OrdSeq[A: Order](val self: FingerTree[LastOption[A], A]) {
    def partition(a: A): (OrdSeq[A], OrdSeq[A]) = ...
    def insert(a: A): OrdSeq[A] = ...
    def ++(xs: OrdSeq[A]): OrdSeq[A] = ...
  }
  object OrdSeq {
    private implicit def keyer[A]: Reducer[A, LastOption[A]] = a => Tag(Some(a))
    def apply[A: Order](as: A*): OrdSeq[A] = ...
  }

OrdSeq no tiene instancias de typeclases de modo que únicamente es útil para construir incrementalmente una secuencia ordenada, con duplicados. Podemos acceder al FingerTree subyacente cuando sea necesario.

6.8.9.3 Cord

El caso más común de FingerTree es un almacén intermedio para representaciones de String en Show. Construir una sola String puede ser miles de veces más rápido que la implementación default de case class de .toString anidadas, que construye una String para cada capa en la ADT.

  final case class Cord(self: FingerTree[Int, String]) {
    override def toString: String = {
      val sb = new java.lang.StringBuilder(self.measure)
      self.foreach(sb.append) // locally scoped side effect
      sb.toString
    }
    ...
  }

Por ejemplo, la instancia Cord[String] devuelve una Three con la cadena a la mitad y comillas en ambos lados

  implicit val show: Show[String] = s => Cord(FingerTree.Three("\"", s, "\""))

Por lo tanto una String se muestra tal y como se escribe en el código fuente

  scala> val s = "foo"
         s.toString
  res: String = foo
  
  scala> s.show
  res: Cord = "foo"

6.8.10 Cola de prioridad Heap

Una cola de prioridad es una estructura de datos que permite una rápida inserción de elementos ordenados, permitiendo duplicados, con un rápido acceso al valor mínimo (la prioridad más alta). La estructura no es necesaria para almacenar los elementos no mínimos en orden. Una implementación ingenua de una cola de prioridad podría ser

  final case class Vip[A] private (val peek: Maybe[A], xs: IList[A]) {
    def push(a: A)(implicit O: Order[A]): Vip[A] = peek match {
      case Maybe.Just(min) if a < min => Vip(a.just, min :: xs)
      case _                          => Vip(peek, a :: xs)
    }
  
    def pop(implicit O: Order[A]): Maybe[(A, Vip[A])] = peek strengthR reorder
    private def reorder(implicit O: Order[A]): Vip[A] = xs.sorted match {
      case INil()           => Vip(Maybe.empty, IList.empty)
      case ICons(min, rest) => Vip(min.just, rest)
    }
  }
  object Vip {
    def fromList[A: Order](xs: IList[A]): Vip[A] = Vip(Maybe.empty, xs).reorder
  }

Este push es muy rápido O(1), pero el reorder (y por lo tanto pop) depende de IList.sorted con un costo de O(n log n).

Scalaz codifica una cola de prioridad con una estructura de árbol donde cada nodo tiene un valor menor que sus hijos. Heap tiene un operaciones rápidas push (insert), union, size, pop (uncons) y peek (minimumO):

  sealed abstract class Heap[A] {
    def insert(a: A)(implicit O: Order[A]): Heap[A] = ...
    def +(a: A)(implicit O: Order[A]): Heap[A] = insert(a)
  
    def union(as: Heap[A])(implicit O: Order[A]): Heap[A] = ...
  
    def uncons(implicit O: Order[A]): Option[(A, Heap[A])] = minimumO strengthR deleteMin
    def minimumO: Option[A] = ...
    def deleteMin(implicit O: Order[A]): Heap[A] = ...
  
    ...
  }
  object Heap {
    def fromData[F[_]: Foldable, A: Order](as: F[A]): Heap[A] = ...
  
    private final case class Ranked[A](rank: Int, value: A)
  
    private final case class Empty[A]() extends Heap[A]
    private final case class NonEmpty[A](
      size: Int,
      tree: Tree[Ranked[A]]
    ) extends Heap[A]
  
    ...
  }

Heap está implementado con un Rose Tree de valores Ranked, donde rank es la profundidad del sub-árbol, permitiéndonos balancear la profundidad del árbol. Manualmente mantenemos el árbol de modo que el valor mínimo está en la raíz. Una ventaja de que se codifique el valor mínimo en la estructura de datos es que minimum0 (conocido también como peek) es una búsqueda inmediata y sin costo alguno:

  def minimumO: Option[A] = this match {
    case Empty()                        => None
    case NonEmpty(_, Tree.Node(min, _)) => Some(min.value)
  }

Cuando insertamos una nueva entrada, comparamos el valor mínimo actual y lo reemplazamos si la nueva entrada es más pequeña:

  def insert(a: A)(implicit O: Order[A]): Heap[A] = this match {
    case Empty() =>
      NonEmpty(1, Tree.Leaf(Ranked(0, a)))
    case NonEmpty(size, tree @ Tree.Node(min, _)) if a <= min.value =>
      NonEmpty(size + 1, Tree.Node(Ranked(0, a), Stream(tree)))
  ...

Las inserciones de valores que no son mínimos resulta en una estructura de datos desordenada en las ramas del nodo mínimo. Cuando encontramos dos o más subárboles de rango idéntico, colocamos el valor mínimo de manera optimista al frente:

  ...
    case NonEmpty(size, Tree.Node(min,
           (t1 @ Tree.Node(Ranked(r1, x1), xs1)) #::
           (t2 @ Tree.Node(Ranked(r2, x2), xs2)) #:: ts)) if r1 == r2 =>
      lazy val t0 = Tree.Leaf(Ranked(0, a))
      val sub =
        if (x1 <= a && x1 <= x2)
          Tree.Node(Ranked(r1 + 1, x1), t0 #:: t2 #:: xs1)
        else if (x2 <= a && x2 <= x1)
          Tree.Node(Ranked(r2 + 1, x2), t0 #:: t1 #:: xs2)
        else
          Tree.Node(Ranked(r1 + 1, a), t1 #:: t2 #:: Stream())
  
      NonEmpty(size + 1, Tree.Node(Ranked(0, min.value), sub #:: ts))
  
    case NonEmpty(size,  Tree.Node(min, rest)) =>
      val t0 = Tree.Leaf(Ranked(0, a))
      NonEmpty(size + 1, Tree.Node(Ranked(0, min.value), t0 #:: rest))
  }

Al evitar un ordenamiento completo del árbol hacemos que insert sea muy rápido, O(1), de modo que los productores que agregan elementos a la cola no son penalizados. Sin embargo, el consumidor paga el costo cuando invoca uncons, con deleteMin teniendo un costo O(log n) debido a que debe buscar el valor mínimo, y removerlo del árbol al reconstruirlo. Esto es rápido cuando se compara con una implementación ingenua.

La operación union también retrasa el ordenamiento permitiéndo que se realice en O(1).

Si Order[Foo] no captura correctamente la prioridad que deseamos para el Heap[Foo], podemos usar Tag y proporcionar un Order[Foo @@ Custom] ad-hoc para un Heap[Foo @@ Custom].

6.8.11 Diev (Discrete Intervals)

Podemos codificar eficientemente los valores enteros (desordenados) 6, 9, 2, 13, 8, 14, 10, 7, 5 como intervalos inclusivos [2, 2], [5, 10], [13, 14]. Diev tiene una codificación eficiente de intervalos para elementos A que tienen un Enum[A], haciéndose más eficientes a medida que el contenido se hace más denso.

  sealed abstract class Diev[A] {
    def +(interval: (A, A)): Diev[A]
    def +(value: A): Diev[A]
    def ++(other: Diev[A]): Diev[A]
  
    def -(interval: (A, A)): Diev[A]
    def -(value: A): Diev[A]
    def --(other: Diev[A]): Diev[A]
  
    def intervals: Vector[(A, A)]
    def contains(value: A): Boolean
    def contains(interval: (A, A)): Boolean
    ...
  }
  object Diev {
    private final case class DieVector[A: Enum](
      intervals: Vector[(A, A)]
    ) extends Diev[A]
  
    def empty[A: Enum]: Diev[A] = ...
    def fromValuesSeq[A: Enum](values: Seq[A]): Diev[A] = ...
    def fromIntervalsSeq[A: Enum](intervals: Seq[(A, A)]): Diev[A] = ...
  }

Cuando actualizamos el Diev, los intervalos adyacentes se fusionan (y entonces ordenados) tales que hay una representación única para un conjunto dado de valores.

  scala> Diev.fromValuesSeq(List(6, 9, 2, 13, 8, 14, 10, 7, 5))
  res: Diev[Int] = ((2,2)(5,10)(13,14))
  
  scala> Diev.fromValuesSeq(List(6, 9, 2, 13, 8, 14, 10, 7, 5).reverse)
  res: Diev[Int] = ((2,2)(5,10)(13,14))

Un gran caso de uso para Diev es para almacenar periodos de tiempo. Por ejemplo, en nuestro TradeTemplate del capítulo anterior

  final case class TradeTemplate(
    payments: List[java.time.LocalDate],
    ccy: Option[Currency],
    otc: Option[Boolean]
  )

si encontramos que los payments son muy densos, tal vez deseemos intercambiar a una representación Diev por razones de rendimiento, sin ningún cambio en nuestra lógica de negocios porque usamos un Monoid, no ningún método específico de List. Sin embargo, tendríamos que proporcionar un Enum[LocalDate], que de otra manera sería algo útil y bueno que tener.

6.8.12 OneAnd

Recuerde que Foldable es el equivalente de Scalaz de una API de colecciones y que Foldable1 es para colecciones no vacías. Hasta el momento hemos revisado únicamente NonEmptyList para proporcionar un Foldable1. La estructura de datos simple OneAnd envuelve cualquier otra colección y la convierte en un Foldable1.

  final case class OneAnd[F[_], A](head: A, tail: F[A])

NonEmptyList[A] podría ser un alias a OneAnd[IList, A]. De manera similar, podemos crear Stream no vacío, y estructuras DList y Tree. Sin embargo, podría terminar con las características de ordenamiento y unicidad de la estructura de datos subyacente: un OneAnd[ISet, A] no es un ISet no vacío, se trata de un ISet con la garantía de que se tiene un primer elemento que también puede estar en el ISet.

6.9 Sumario

En este capítulo hemos revisado rápidamente los tipos de datos que Scalaz tiene que ofrecer.

No es necesario recordad todo lo estudiado en este capítulo: piense que cada sección es la semilla o corazón de una idea.

El mundo de las estructuras de datos funcionales es una área activa de investigación. Publicaciones académicas aparecen regularmente con nuevos enfoques a viejos problemas. La implementación de una estructura de datos funcionales a partir de la literatura sería una buena contribución al ecosistema de Scalaz.