7. Mónadas avanzadas
Usted tiene que conocer cosas como las mónadas avanzadas para ser un programador funcional avanzado.
Sin embargo, somos desarrolladores buscando una vida simple, y nuestra
idea de “avanzado” es modesta. Para ponernos en contexto:
scala.concurrent.Future es más complicada y con más matices que
cualquier Monad en este capítulo.
En este capítulo estudiaremos algunas de las implementaciones más
importantes de Monad.
7.1 Future siempre está en movimiento
El problema más grande con Future es que programa trabajo rápidamente
durante su construcción. Como descubrimos en la introducción, Future
mezcla la definición del programa con su interpretación (es decir, con
su ejecución).
Future también es malo desde una perspectiva de rendimiento: cada vez
que .flatMap es llamado, una cerradura se manda al Ejecutor, resultando
en una programación de hilos y en cambios de contexto innecesarios. No es
inusual ver 50% del poder de nuestro CPU lidiando con planeación de hilos.
Tanto es así que la paralelización de trabajo con Futuro puede volverlo
más lento.
En combinación, la evaluación estricta y el despacho de ejecutores significa que
es imposible de saber cuándo inició un trabajo, cuando terminó, o las subtareas
que se despacharon para calcular el resultado final. No debería sorprendernos
que las “soluciones” para el monitoreo de rendimiento para frameworks basados en
Future sean buenas opciones para las ventas.
Además, Future.flatMap requiere de un ExecutionContext en el ámbito
implícito: los usuarios están forzados a pensar sobre la lógica de negocios
y la semántica de ejecución a la vez.
7.2 Efectos y efectos laterales
Si no podemos llamar métodos que realicen efectos laterales en nuestra lógica
de negocios, o en Future (or Id, or Either, o Const, etc), entonces,
¿cuándo podemos escribirlos? La respuesta es: en una Monad que retrasa la
ejecución hasta que es interpretada por el punto de entrada de la aplicación.
En este punto, podemos referirnos a I/O y a la mutación como un efecto en
el mundo, capturado por el sistema de tipos, en oposición a tener efectos
laterales ocultos.
La implementación simple de tal Monad es IO, formalizando la versión que
escribimos en la introducción:
final class IO[A](val interpret: () => A)
object IO {
def apply[A](a: =>A): IO[A] = new IO(() => a)
implicit val monad: Monad[IO] = new Monad[IO] {
def point[A](a: =>A): IO[A] = IO(a)
def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] = IO(f(fa.interpret()).interpret())
}
}
El método .interpret se llama únicamente una vez, en el punto de entrada de una
aplicación.
def main(args: Array[String]): Unit = program.interpret()
Sin embargo, hay dos grandes problemas con este simple IO:
- Puede ocasionar un sobreflujo de la pila
- No soporta cómputos paralelos
Ambos problemas serán abordados en este capítulo. Sin embargo, sin importar lo
complicado de una implementación interna de una Monad, los principios aquí
descritos seguirán siendo ciertos: estamos modularizando la definición de un
programa y su ejecución, tales que podemos capturar los efectos en la signatura
de los tipos, permitiéndonos razonar sobre ellos, y reusar más código.
7.3 Seguridad de la pila
En la JVM, toda invocación a un método, agrega una entrada a la pila de llamadas
del hilo (Thread), como agregar al frente de una List. Cuando el método
completa, el método en la cabeza (head) es descartado/eliminado. La longitud
máxima de la pila de llamadas es determinada por la bandera -Xss cuando se
llama a java. Los métodos que realizan una recursión de cola, son detectados
por el compilador de Scala y no agregan una entrada. Si alcanzamos el límite,
al invocar demasiados métodos encadenados, obtenemos una excepción de
StackOverflowError.
Desgraciadamente, toda invocación anidada de .flatMap (sobre una instancia de
IO) agrega otro método de invocación a la pila. La forma más sencilla de ver
esto es repetir esta acción por siempre, y ver si logra sobrevivir más de unos
cuántos segundos. Podemos usar .forever, que viene de Apply (un “padre” de
Monad):
scala> val hello = IO { println("hello") }
scala> Apply[IO].forever(hello).interpret()
hello
hello
hello
...
hello
java.lang.StackOverflowError
at java.io.FileOutputStream.write(FileOutputStream.java:326)
at ...
at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
at monadio.IO$$anon$1.$anonfun$bind$1(monadio.scala:18)
at ...
Scalaz tiene una typeclass que las instancias de Monad pueden implementar si
son seguras: BindRec requiere de un espacio de pila constante para bind
recursivo:
@typeclass trait BindRec[F[_]] extends Bind[F] {
def tailrecM[A, B](f: A => F[A \/ B])(a: A): F[B]
override def forever[A, B](fa: F[A]): F[B] = ...
}
No necesitamos BindRec para todos los programas, pero es esencial para una
implementación de propósito general de Monad.
La manera de conseguir seguridad en la pila es la conversión de invocaciones de
métodos en referencias a una ADT, la mónada Free:
sealed abstract class Free[S[_], A]
object Free {
private final case class Return[S[_], A](a: A) extends Free[S, A]
private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
private final case class Gosub[S[_], A0, B](
a: Free[S, A0],
f: A0 => Free[S, B]
) extends Free[S, B] { type A = A0 }
...
}
La ADT Free es una es una representación del tipo de datos natural de la
interfaz Monad:
-
Returnrepresenta.point -
Gosubrepresenta.bind/.flatMap
Cuando una ADT es un reflejo de los argumentos de las funciones relacionadas, recibe el nombre de una codificación Church.
Free recibe este nombre debido a que puede ser generada de manera gratuita
para cualquier S[_]. Por ejemplo, podríamos hacer que S sea una de las
álgebras Drone o Machines del Capítulo 3 y generar una representación de la
estructura de datos de nuestro programa. Regresaremos más tarde a este punto
para explicar por qué razón esto es de utilidad.
7.3.1 Trampoline
Free es más general de lo necesario. Haciendo que el álgebra S[_] sea () => ?,
un cálculo diferido o un thunk, obtenemos Trampoline que puede implementar una
Monad de manera que se conserva el uso seguro de la pila.
object Free {
type Trampoline[A] = Free[() => ?, A]
implicit val trampoline: Monad[Trampoline] with BindRec[Trampoline] =
new Monad[Trampoline] with BindRec[Trampoline] {
def point[A](a: =>A): Trampoline[A] = Return(a)
def bind[A, B](fa: Trampoline[A])(f: A => Trampoline[B]): Trampoline[B] =
Gosub(fa, f)
def tailrecM[A, B](f: A => Trampoline[A \/ B])(a: A): Trampoline[B] =
bind(f(a)) {
case -\/(a) => tailrecM(f)(a)
case \/-(b) => point(b)
}
}
...
}
La implementación de BindRec, .tailrecM, ejecuta .bind hasta que obtenemos
una B. Aunque no se trata, técnicamente, de una implementación @tailrec, usa
un espacio de pila constante debido a que cada llamada devuelve un objeto en el
heap, con recursión postergada.
Se proporcionan funciones convenientes para la creación estricta de un
Trampoline (.done) o por nombre (.delay). También podemos crear un
Trampoline a partir de un Trampoline por nombre (.suspend):
object Trampoline {
def done[A](a: A): Trampoline[A] = Return(a)
def delay[A](a: =>A): Trampoline[A] = suspend(done(a))
def suspend[A](a: =>Trampoline[A]): Trampoline[A] = unit >> a
private val unit: Trampoline[Unit] = Suspend(() => done(()))
}
Cuando vemos un Trampoline[A] en el código, siempre es posible sustituirlo
mentalmente con una A, debido a que únicamente está añadiendo seguridad al uso
de la pila a un cómputo puro. Obtenemos la A al interpretar Free, provisto
por .run.
7.3.2 Ejemplo: DList con seguridad en el manejo de la pila
En el capítulo anterior hemos descrito el tipo de datos DList como
final case class DList[A](f: IList[A] => IList[A]) {
def toIList: IList[A] = f(IList.empty)
def ++(as: DList[A]): DList[A] = DList(xs => f(as.f(xs)))
...
}
Sin embargo, la implementación actual se ve más parecida a:
final case class DList[A](f: IList[A] => Trampoline[IList[A]]) {
def toIList: IList[A] = f(IList.empty).run
def ++(as: =>DList[A]): DList[A] = DList(xs => suspend(as.f(xs) >>= f))
...
}
En lugar de aplicar llamadas anidadas a f, usamos un Trampoline suspendido.
Interpretamos el trampolín con .run únicamente cuando es necesario, por
ejemplo, en toIList. Los cambios son mínimo, pero ahora tenemos una DList
con uso seguro de la pila que puede reordenar la concatenación de un número
largo de listas sin ocasionar un sobreflujo de la pila.
7.3.3 IO con uso seguro de la pila
De manera similar, nuestra IO puede hacerse segura (respecto al uso de la
pila), gracias a Trampoline:
final class IO[A](val tramp: Trampoline[A]) {
def unsafePerformIO(): A = tramp.run
}
object IO {
def apply[A](a: =>A): IO[A] = new IO(Trampoline.delay(a))
implicit val Monad: Monad[IO] with BindRec[IO] =
new Monad[IO] with BindRec[IO] {
def point[A](a: =>A): IO[A] = IO(a)
def bind[A, B](fa: IO[A])(f: A => IO[B]): IO[B] =
new IO(fa.tramp >>= (a => f(a).tramp))
def tailrecM[A, B](f: A => IO[A \/ B])(a: A): IO[B] = ...
}
}
El intérprete, .unsafePerformIO(), ahora tiene un nombre intencionalmente
terrorífico para desalentar su uso, con la excepción del punto de entrada de una
aplicación.
Esta vez, no obtendremos un error por sobreflujo de la pila:
scala> val hello = IO { println("hello") }
scala> Apply[IO].forever(hello).unsafePerformIO()
hello
hello
hello
...
hello
El uso de un Trampoline típicamente introduce una regresión en el desempeño
comparado a la implementación normal de referencia. Es Free en el sentido de
que se genera de manera automática, no en el sentido literal.
7.4 Librería de transformadores de mónadas
Las transformadores de mónadas son estructuras de datos que envuelven un valor subyacente y proporcionan un efecto monádico.
Por ejemplo, en el capítulo 2 usamos OptionT para que pudiéramos usar
F[Option[A]] en una comprehensión for como si se tratase de F[A]. Esto le
dio a nuestro programa el efecto de un valor opcional. De manera alternativa,
podemos conseguir el efcto de opcionalidad si tenemos una MonadPlus.
A este subconjunto de tipos de datos y extensiones a Monad con frecuencia se
le conoce como una Librería de Transformadores de Mónadas (MTL, por sus
siglas en inglés), como se resume enseguida. En esta sección, explicaremos cada
uno de los transformadores, por qué razón son útiles, y cómo funcionan.
| Efecto | Equivalencia | Transformador | Typeclass |
|---|---|---|---|
| opcionalidad | F[Maybe[A]] |
MaybeT |
MonadPlus |
| errores | F[E \/ A] |
EitherT |
MonadError |
| un valor en tiempo de ejecución | A => F[B] |
ReaderT |
MonadReader |
| journal / multi tarea | F[(W, A)] |
WriterT |
MonadTell |
| estado en cambio | S => F[(S, A)] |
StateT |
MonadState |
| mantén la calma y continúa | F[E \&/ A] |
TheseT |
|
| control de flujo | (A => F[B]) => F[B] |
ContT |
7.4.1 MonadTrans
Cada transformador tiene la forma general T[F[_], A], proporcionando al menos una instancia de
Monad y Hoist (y por lo tanto de MonadTrans):
@typeclass trait MonadTrans[T[_[_], _]] {
def liftM[F[_]: Monad, A](a: F[A]): T[F, A]
}
@typeclass trait Hoist[F[_[_], _]] extends MonadTrans[F] {
def hoist[M[_]: Monad, N[_]](f: M ~> N): F[M, ?] ~> F[N, ?]
}
.liftM nos permite crear un transformador de mónadas si tenemos un F[A]. Por ejemplo,
podemos crear un OptionT[IO, String] al invocar ` .liftM[OptionT] en una IO[String]`.
.hoist es la misma idea, pero para transformaciones naturales.
Generalmente, hay tres maneras de crear un transformador de mónadas:
- A partir de la estructura equivalente, usando el constructor del transformador
- A partir de un único valor
A, usando.pureusando la sintaxis deMonad - A partir de
F[A], usando.liftMusando la sintaxis deMonadTrans
Debido a la forma en la que funciona la inferencia de tipos en Scala, esto con frecuencia significa que un parámetro de tipo complejo debe escribirse de manera explícita. Como una forma de lidiar con el problema, los transformadores proporcionan constructores convenientes en su objeto compañero que los hacen más fáciles de usar.
7.4.2 MaybeT
OptionT, MaybeT y LazyOption tienen implementaciones similares, proporcionando
opcionalidad a través de Option, Maybe y LazyOption, respectivamente. Nos
enfocaremos en MaybeT para evitar la repetición.
final case class MaybeT[F[_], A](run: F[Maybe[A]])
object MaybeT {
def just[F[_]: Applicative, A](v: =>A): MaybeT[F, A] =
MaybeT(Maybe.just(v).pure[F])
def empty[F[_]: Applicative, A]: MaybeT[F, A] =
MaybeT(Maybe.empty.pure[F])
...
}
proporcionando una MonadPlus
implicit def monad[F[_]: Monad] = new MonadPlus[MaybeT[F, ?]] {
def point[A](a: =>A): MaybeT[F, A] = MaybeT.just(a)
def bind[A, B](fa: MaybeT[F, A])(f: A => MaybeT[F, B]): MaybeT[F, B] =
MaybeT(fa.run >>= (_.cata(f(_).run, Maybe.empty.pure[F])))
def empty[A]: MaybeT[F, A] = MaybeT.empty
def plus[A](a: MaybeT[F, A], b: =>MaybeT[F, A]): MaybeT[F, A] = a orElse b
}
Esta mónada se ve un poco complicada, pero simplemente está delegando todo a la
Monad[F] y entonces envolviendo todo dentro de un MaybeT. Simplemente es
código para cumplir con el trabajo.
Con esta mónada podemos escribir lógica que maneja la opcionalidad en el
contexto de F[_], más bien que estar lidiando con Option o Maybe.
Por ejemplo, digamos que estamos interactuando con un sitio social para contar
el número de estrellas que tiene el usuario, y empezamos con una cadena (String)
que podría o no corresponder al usuario. Tenemos esta álgebra:
trait Twitter[F[_]] {
def getUser(name: String): F[Maybe[User]]
def getStars(user: User): F[Int]
}
def T[F[_]](implicit t: Twitter[F]): Twitter[F] = t
Necesitamos invocar getUser seguido de getStars. Si usamos Monad como nuestro
contexto, nuestra función es difícil porque tendremos que lidiar con el caso Empty:
def stars[F[_]: Monad: Twitter](name: String): F[Maybe[Int]] = for {
maybeUser <- T.getUser(name)
maybeStars <- maybeUser.traverse(T.getStars)
} yield maybeStars
Sin embargo, si tenemos una MonadPlus como nuestro contexto, podemos poner
Maybe dentro de F[_] usando .orEmpty, y olvidarnos del asunto:
def stars[F[_]: MonadPlus: Twitter](name: String): F[Int] = for {
user <- T.getUser(name) >>= (_.orEmpty[F])
stars <- T.getStars(user)
} yield stars
Sin embargo, agregar un requerimiento de MonadPlus puede ocasionar problemas más
adelante en el proceso, si el contexto no tiene una. La solución es, o cambiar el
contexto del programa a MaybeT[F, ?] (elevando el contexto de Monad[F] a una
MonadPlus), o para usar explícitamente MaybeT en el tipo de retorno, a costa de
un poco de código adicional:
def stars[F[_]: Monad: Twitter](name: String): MaybeT[F, Int] = for {
user <- MaybeT(T.getUser(name))
stars <- T.getStars(user).liftM[MaybeT]
} yield stars
La decisión de requerir una Monad más poderosa vs devolver un transformador es
algo que cada equipo puede decidir por sí mismo basándose en los intérpretes que
planee usar en sus programas.
7.4.3 EitherT
Un valor opcional es el caso especial de un valor que puede ser un error, pero no
sabemos nada sobre el error. EitherT (y la variante perezosa LazyEitherT) nos
permite usar cualquier tipo que deseemos como el valor del error, porporcionando
información contextual sobre lo que pasó mal.
EitherT es un envoltorio sobre F[A \/ B]
final case class EitherT[F[_], A, B](run: F[A \/ B])
object EitherT {
def either[F[_]: Applicative, A, B](d: A \/ B): EitherT[F, A, B] = ...
def leftT[F[_]: Functor, A, B](fa: F[A]): EitherT[F, A, B] = ...
def rightT[F[_]: Functor, A, B](fb: F[B]): EitherT[F, A, B] = ...
def pureLeft[F[_]: Applicative, A, B](a: A): EitherT[F, A, B] = ...
def pure[F[_]: Applicative, A, B](b: B): EitherT[F, A, B] = ...
...
}
Monad es una MonadError
@typeclass trait MonadError[F[_], E] extends Monad[F] {
def raiseError[A](e: E): F[A]
def handleError[A](fa: F[A])(f: E => F[A]): F[A]
}
.raiseError y .handleError son descriptivos en sí mismos: el equivalente
de lanzar (throw) y atrapar (catch) una excepción, respectivamente.
MonadError tiene sintaxis adicional para lidiar con problemas comunes:
implicit final class MonadErrorOps[F[_], E, A](self: F[A])(implicit val F: MonadError[F, E])\
{
def attempt: F[E \/ A] = ...
def recover(f: E => A): F[A] = ...
def emap[B](f: A => E \/ B): F[B] = ...
}
.attempt trae los errores dentro del valor, lo cual es útil para exponer
los errores en los subsistemas como valores de primera clase.
.recover es para convertir un error en un valor en todos los casos, en
oposición a .handleError que toma una F[A] y por lo tanto permite una
recuperación parcial.
.emap, es para aplicar transformaciones que pueden fallar.
El MonadError para EitherT es:
implicit def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
def monad[F[_]: Monad, E] = new MonadError[EitherT[F, E, ?], E] {
def bind[A, B](fa: EitherT[F, E, A])
(f: A => EitherT[F, E, B]): EitherT[F, E, B] =
EitherT(fa.run >>= (_.fold(_.left[B].pure[F], b => f(b).run)))
def point[A](a: =>A): EitherT[F, E, A] = EitherT.pure(a)
def raiseError[A](e: E): EitherT[F, E, A] = EitherT.pureLeft(e)
def handleError[A](fa: EitherT[F, E, A])
(f: E => EitherT[F, E, A]): EitherT[F, E, A] =
EitherT(fa.run >>= {
case -\/(e) => f(e).run
case right => right.pure[F]
})
}
No debería sorprender que podamos reescribir el ejemplo con MonadPlus con
MonadError, insertando mensajes informativos de error:
def stars[F[_]: Twitter](name: String)
(implicit F: MonadError[F, String]): F[Int] = for {
user <- T.getUser(name) >>= (_.orError(s"user '$name' not found")(F))
stars <- T.getStars(user)
} yield stars
donde .orError es un método conveniente sobre Maybe
sealed abstract class Maybe[A] {
...
def orError[F[_], E](e: E)(implicit F: MonadError[F, E]): F[A] =
cata(F.point(_), F.raiseError(e))
}
La versión que usa EitherT directamente es:
def stars[F[_]: Monad: Twitter](name: String): EitherT[F, String, Int] = for {
user <- EitherT(T.getUser(name).map(_ \/> s"user '$name' not found"))
stars <- EitherT.rightT(T.getStars(user))
} yield stars
La instancia más simple de MonadError es la de \/, perfecta para probar
lógica de negocios que es requerida por una MonadError. Por ejemplo,
final class MockTwitter extends Twitter[String \/ ?] {
def getUser(name: String): String \/ Maybe[User] =
if (name.contains(" ")) Maybe.empty.right
else if (name === "wobble") "connection error".left
else User(name).just.right
def getStars(user: User): String \/ Int =
if (user.name.startsWith("w")) 10.right
else "stars have been replaced by hearts".left
}
Nuestras pruebas unitarias para .stars pueden cubrir estos casos:
scala> stars("wibble")
\/-(10)
scala> stars("wobble")
-\/(connection error)
scala> stars("i'm a fish")
-\/(user 'i'm a fish' not found)
scala> stars("fommil")
-\/(stars have been replaced by hearts)
Así como hemos visto varias veces, podemos enfocarnos en probar la lógica de negocios sin distracciones.
Finalmente, si devolvemos nuestra álgebra JsonClient del capítulo 4.3
trait JsonClient[F[_]] {
def get[A: JsDecoder](
uri: String Refined Url,
headers: IList[(String, String)]
): F[A]
...
}
recuerde que únicamente hemos codificado el camino feliz en la API. Si nuestro
intérprete para esta álgebra únicamente funciona para una F que tiene una
MonadError, podemos definir los tipos de errores como una preocupación
tangencial. En verdad, podemos tener dos capas de errores si definimos el
intérprete para una EitherT[IO, JsonClient.Error, ?]
object JsonClient {
sealed abstract class Error
final case class ServerError(status: Int) extends Error
final case class DecodingError(message: String) extends Error
}
que cubre los problemas de I/O (red), problemas de estado del servidor, y asuntos con el modelado de los payloads JSON de nuestro servidor.
7.4.3.1 Escogiendo un tipo de errores
La comunidad no se ha decidido sobre la mejor estrategia para el tipo de
errores E en MonadError.
Una escuela de pensamiento dice que deberíamos escoger algo general, como una
cadena (String). La otra escuela de pensamiento dice que una aplicación
debería tener una ADT de errores, permitiendo que errores distintos sean
reportados o manejados de manera diferente. Una “pandilla” de gente prefiere
usar Throwable para tener máxima compatibilidad con la JVM.
Hay dos problemas con una ADT de errores a nivel de la aplicación:
- Es muy torpe crear un nuevo error. Una archivo se vuelve un repositorio monolítico de errores, agregando las ADTs de subsistemas individuales.
- Sin importar qué tan granular sea el reporte de errores, la solución es con frecuencia la misma, realice un log de los datos e intente de nuevo, o ríndase. No necesitamos una ADT para esto.
Una ADT de errores es útil si cada valor permite la ejecución de una estrategia distinta de recuperación.
El compromiso entre una ADT de errores y una cadena String está en un formato
intermedio. JSON es una buena elección si puede entenderse por la mayoría de los
frameworks de loggeo y monitoreo.
Un problema con la ausencia de stacktraces es que puede ser complicado ubicar
cúal porción de código fue la causa del error. Con sourcecode de Li
Haoyi, podemos incluir información
contextual como metadatos sobre nuestros errores:
final case class Meta(fqn: String, file: String, line: Int)
object Meta {
implicit def gen(implicit fqn: sourcecode.FullName,
file: sourcecode.File,
line: sourcecode.Line): Meta =
new Meta(fqn.value, file.value, line.value)
}
final case class Err(msg: String)(implicit val meta: Meta)
Aunque Err es referencialmente transparente, la construcción implícita de
Meta no parece ser referencialmente transparente desde una lectura natural:
dos invocaciones a Meta.gen (que se invoca implícitamente cuando se crea un
Err) producirán diferentes valores porque la ubicación en el código fuente
impacta el valor retornado:
scala> println(Err("hello world").meta)
Meta(com.acme,<console>,10)
scala> println(Err("hello world").meta)
Meta(com.acme,<console>,11)
Para entender esto, tenemos que apreciar que los métodos sourcecode.* son
macros que están generando código fuente para nosotros. Si tuvieramos que
escribir el código arriba de manera explícita sería claro lo que está
sucediendo:
scala> println(Err("hello world")(Meta("com.acme", "<console>", 10)).meta)
Meta(com.acme,<console>,10)
scala> println(Err("hello world")(Meta("com.acme", "<console>", 11)).meta)
Meta(com.acme,<console>,11)
Sí, hemos usado macros, pero también pudimos escribir Meta manualmente
y hubiera sido necesario hacerla obsoleta antes que nuestra documentación.
7.4.4 ReaderT
La mónada reader envuelve A => F[B] permitiendo que un programa F[B] dependa
del valor de tiempo de ejecución A. Para aquellos que etán familiarizados con
la inyección de dependencias, la mónada reader es el equivalente funcional de la
inyección @Inject de Spring o de Guice, sin el uso de XML o reflexión.
ReaderT es simplemente un alias de otro tipo de datos que con frecuencia es más
general, y que recibe su nombre en honor al matemático Heinrich Kleisli.
type ReaderT[F[_], A, B] = Kleisli[F, A, B]
final case class Kleisli[F[_], A, B](run: A => F[B]) {
def dimap[C, D](f: C => A, g: B => D)(implicit F: Functor[F]): Kleisli[F, C, D] =
Kleisli(c => run(f(c)).map(g))
def >=>[C](k: Kleisli[F, B, C])(implicit F: Bind[F]): Kleisli[F, A, C] = ...
def >==>[C](k: B => F[C])(implicit F: Bind[F]): Kleisli[F, A, C] = this >=> Kleisli(k)
...
}
object Kleisli {
implicit def kleisliFn[F[_], A, B](k: Kleisli[F, A, B]): A => F[B] = k.run
...
}
Una conversión implícita en el objeto companion nos permite usar Kleisli en
lugar de una función, de modo que puede proporcionarse como el parámetro de
.bind, o >>=.
El uso más común para ReaderT es proporcionar información del contexto a un
programa. En drone-dynamic-agents necesitamos acceso al token Oauth 2.0 del
usuario para ser capaz de contactar a Google. El proceder obvio es cargar
RefreshTokens del disco al momento de arranque, y hacer que cada método tome
un parámetro RefreshToken. De hecho, se trata de un requerimiento tan común
que Martin Odersky propuso las funciones
implícitas.
Una mejor solución para nuestro programa es tener un álgebra de configuración que proporcione la configuración cuando sea necesario, es decir
trait ConfigReader[F[_]] {
def token: F[RefreshToken]
}
Hemos reinventado MonadReader, la typeclass que está asociada a ReaderT, donde
.ask es la misma que nuestra .token y S es RefreshToken:
@typeclass trait MonadReader[F[_], S] extends Monad[F] {
def ask: F[S]
def local[A](f: S => S)(fa: F[A]): F[A]
}
con la implementación
implicit def monad[F[_]: Monad, R] = new MonadReader[Kleisli[F, R, ?], R] {
def point[A](a: =>A): Kleisli[F, R, A] = Kleisli(_ => F.point(a))
def bind[A, B](fa: Kleisli[F, R, A])(f: A => Kleisli[F, R, B]) =
Kleisli(a => Monad[F].bind(fa.run(a))(f))
def ask: Kleisli[F, R, R] = Kleisli(_.pure[F])
def local[A](f: R => R)(fa: Kleisli[F, R, A]): Kleisli[F, R, A] =
Kleisli(f andThen fa.run)
}
Una ley de MonadReader es que S no puede cambiar entre invocaciones, es
decir ask >> ask === ask. Para nuestro caso de uso, esto significa que la
configuración se lee una única vez. Si decidimos después que deseamos recargar
nuestra configuración cada vez que sea necesario, por ejemplo, al permitir el
cambio de token sin reiniciar la aplicación, podemos reintroducir ConfigReader
que no tiene tal ley.
En nuestra implementación OAuth 2.0 podemos primero mover la evidencia de
Monad a los métodos:
def bearer(refresh: RefreshToken)(implicit F: Monad[F]): F[BearerToken] =
for { ...
y entonces refactorizar el parámetro refresh para que sea parte de Monad
def bearer(implicit F: MonadReader[F, RefreshToken]): F[BearerToken] =
for {
refresh <- F.ask
Cualquier parámetro puede moverse dentro de MonadReader. Esto es del mayor
valor posible para los usuarios que simplemente desean pasar esta información.
Con ReaderT, podemos reservar bloques de parámetros implícitos, para un uso
exclusivo de typeclases, reduciendo la carga mental que viene con el uso de
Scala.
El otro método en MonadReader es .local
def local[A](f: S => S)(fa: F[A]): F[A]
Podemos cambiar S y ejecutar un programa fa cdentro del contexto local,
devolviendo la S original. Un caso de uso para .local es la generación de un
stacktrace que tenga sentido para nuestro dominio, ¡proporcionándonos un logging
anidado! A partir de lo que aprendimos en nuestra estructura de datos Meta de
la sección anterior, definimos una función para realizar un chequeo:
def traced[A](fa: F[A])(implicit F: MonadReader[F, IList[Meta]]): F[A] =
F.local(Meta.gen :: _)(fa)
y la podemos usar para envolver funciones que operan en este contexto
def foo: F[Foo] = traced(getBar) >>= barToFoo
automáticamente pasando cualquier información que no se esté rastreando de manera explícita. Un plugin para el compilador o una macro podría realizar lo opuesto, haciendo que todo se realice por default.
Si accedemos a .ask podemos ver el rastro completo de cómo se realizaron las
llamadas, sin la distracci[on de los detalles en la implementación del bytecode.
¡Un stacktrace referencialmente transparente!
Un programador a la defensiva podría truncar la IList[Meta] a cierta longitud
para evitar el equivalente de un sobreflujo de pila. En realidad, una estructura
de datos más apropiada es Dequeue.
.local puede también usarse para registrar la información contextual que es
directamente relavante a la tarea que se está realizando, como el número de
espacios que debemos indentar una línea cuando se está imprimiendo un archivo
con formato legible por humanos, haciendo que esta indentación aumente en dos
espacios cuando introducimos una estructura anidada.
Finalmente, si no podemos pedir una MonadReader porque nuestra aplicación no
proporciona una, siempre podemos devolver un ReaderT.
def bearer(implicit F: Monad[F]): ReaderT[F, RefreshToken, BearerToken] =
ReaderT( token => for {
...
Si alguien que recibe un ReaderT, y tienen el parámetro token a la mano,
entonces pueden invocar access.run(token) y tener de vuelta un
F[BearerToken].
Dado que no tenemos muchos callers, deberíamos simplemente revertir a un
parámetro de función regular. MonadReader es de mayor utilidad cuando:
- Deseamos refactorizar el código más tarde para recargar la configuración
- El valor no es necesario por usuarios (llamadas) intermedias
- o, cuando deseamos restringir el ámbito/alcance para que sea local
Dotty puede quedarse con sus funciones implícitas… nosotros ya tenemos
ReaderT y MonadReader.
7.4.5 WriterT
Lo opuesto a la lectura es la escritura. El transformador de mónadas WriterT
es usado típicamente para escribir a un journal.
final case class WriterT[F[_], W, A](run: F[(W, A)])
object WriterT {
def put[F[_]: Functor, W, A](value: F[A])(w: W): WriterT[F, W, A] = ...
def putWith[F[_]: Functor, W, A](value: F[A])(w: A => W): WriterT[F, W, A] = ...
...
}
El tipo envuelto es F[(W, A)] y el journal se acumula en W.
¡No hay únicamente una mónada asociada, sino dos! MonadTell y MonadListen
@typeclass trait MonadTell[F[_], W] extends Monad[F] {
def writer[A](w: W, v: A): F[A]
def tell(w: W): F[Unit] = ...
def :++>[A](fa: F[A])(w: =>W): F[A] = ...
def :++>>[A](fa: F[A])(f: A => W): F[A] = ...
}
@typeclass trait MonadListen[F[_], W] extends MonadTell[F, W] {
def listen[A](fa: F[A]): F[(A, W)]
def written[A](fa: F[A]): F[W] = ...
}
MonadTell es para escribir al journal y MonadListen es para recuperarlo. La
implementación de WriterT es
implicit def monad[F[_]: Monad, W: Monoid] = new MonadListen[WriterT[F, W, ?], W] {
def point[A](a: =>A) = WriterT((Monoid[W].zero, a).point)
def bind[A, B](fa: WriterT[F, W, A])(f: A => WriterT[F, W, B]) = WriterT(
fa.run >>= { case (wa, a) => f(a).run.map { case (wb, b) => (wa |+| wb, b) } })
def writer[A](w: W, v: A) = WriterT((w -> v).point)
def listen[A](fa: WriterT[F, W, A]) = WriterT(
fa.run.map { case (w, a) => (w, (a, w)) })
}
El ejemplo más obvio es usar MonadTell para loggear información, o para
reportar la auditoría. Reusar Meta para reportar errores podría servir para
crear una estructura de log como
sealed trait Log
final case class Debug(msg: String)(implicit m: Meta) extends Log
final case class Info(msg: String)(implicit m: Meta) extends Log
final case class Warning(msg: String)(implicit m: Meta) extends Log
y usar Dequeue[Log] como nuestro tipo de journal. Podríamos cambiar nuestro
método OAuth2 authenticate a
def debug(msg: String)(implicit m: Meta): Dequeue[Log] = Dequeue(Debug(msg))
def authenticate: F[CodeToken] =
for {
callback <- user.start :++> debug("started the webserver")
params = AuthRequest(callback, config.scope, config.clientId)
url = config.auth.withQuery(params.toUrlQuery)
_ <- user.open(url) :++> debug(s"user visiting $url")
code <- user.stop :++> debug("stopped the webserver")
} yield code
Incluso podríamos conbinar esto con las trazas de ReaderT y tener logs
estructurados.
El que realiza la llamada puede recuperar los logs con .written y hacer algo
con ellos.
Sin embargo, existe el argumento fuerte de que el logging merece su propia álgebra. El nivel de log es con frecuencia necesario en el momento de creación por razones de rendimiento y la escritura de logs es típicamente manejado a nivel de la aplicación más bien que algo sobre lo que cada componente necesite estar preocupado.
La W en WriterT tiene un Monoid, permitiéndonos escribir al journal
cualquier clase de cálculoo monoidal como un valor secundario junto con nuestro
programa principal. Por ejemplo, el conteo del número de veces que hacemos algo,
construyendo una explicación del cálculo, o la construcción de una
TradeTemplate para una nueva transacción mientras que asignamos un precio.
Una especialización popular de WriterT ocurre cuando la mónada es Id,
indicando que el valor subyacente run es simplemente la tupla simple (W, A).
type Writer[W, A] = WriterT[Id, W, A]
object WriterT {
def writer[W, A](v: (W, A)): Writer[W, A] = WriterT[Id, W, A](v)
def tell[W](w: W): Writer[W, Unit] = WriterT((w, ()))
...
}
final implicit class WriterOps[A](self: A) {
def set[W](w: W): Writer[W, A] = WriterT(w -> self)
def tell: Writer[A, Unit] = WriterT.tell(self)
}
que nos permite dejar que cualquier valor lleve consigo un cálculo monoidal
secundario, sin la necesidad de un contexto F[_].
En resumen, WriterT / MonadTell es la manera de conseguir multi tareas en la
programación funcional.
7.4.6 StateT
StateT nos permite ejecutar .put, .get y .modify sobre un valor que es
manejado por el contexto monádico. Es el reemplazo funcional de var.
Si fueramos a escribir un método impuro que tiene acceso a algún estado mutable,
y contenido en un var, pudiera haber tenido la firma () => F[A] y devolver
un valor diferente en cada invocación, rompiendo con la transparencia
referencial. Con la programación funcional pura, la función toma el estado como
la entrada y devuelve el estado actualizado como la salida, que es la razón por
la que el tipo subyacente de StateT es S => F[(S, A)].
La mónada asociada es MonadState
@typeclass trait MonadState[F[_], S] extends Monad[F] {
def put(s: S): F[Unit]
def get: F[S]
def modify(f: S => S): F[Unit] = get >>= (s => put(f(s)))
...
}
StateT se implementa de manera ligeramente diferente que los transformadores
de mónada que hemos estudiado hasta el momento. En lugar de usar un case class
es una ADT con dos miembros:
sealed abstract class StateT[F[_], S, A]
object StateT {
def apply[F[_], S, A](f: S => F[(S, A)]): StateT[F, S, A] = Point(f)
private final case class Point[F[_], S, A](
run: S => F[(S, A)]
) extends StateT[F, S, A]
private final case class FlatMap[F[_], S, A, B](
a: StateT[F, S, A],
f: (S, A) => StateT[F, S, B]
) extends StateT[F, S, B]
...
}
que es una forma especializada de Trampoline, proporcionandonos seguridad en
el uso de la pila cuando deseamos recuperar la estructura de datos subyacente,
.run:
sealed abstract class StateT[F[_], S, A] {
def run(initial: S)(implicit F: Monad[F]): F[(S, A)] = this match {
case Point(f) => f(initial)
case FlatMap(Point(f), g) =>
f(initial) >>= { case (s, x) => g(s, x).run(s) }
case FlatMap(FlatMap(f, g), h) =>
FlatMap(f, (s, x) => FlatMap(g(s, x), h)).run(initial)
}
...
}
StateT puede implemnentar de manera directa MonadState con su ADT:
implicit def monad[F[_]: Applicative, S] = new MonadState[StateT[F, S, ?], S] {
def point[A](a: =>A) = Point(s => (s, a).point[F])
def bind[A, B](fa: StateT[F, S, A])(f: A => StateT[F, S, B]) =
FlatMap(fa, (_, a: A) => f(a))
def get = Point(s => (s, s).point[F])
def put(s: S) = Point(_ => (s, ()).point[F])
}
con .pure reflejado en el objeto compañero como .stateT:
object StateT {
def stateT[F[_]: Applicative, S, A](a: A): StateT[F, S, A] = ...
...
}
y MonadTrans.liftM proporcionando el constructor F[A] => StateT[F, S, A]
como es usual.
Una variante común de StateT es cuando F = Id, proporcionando la signatura
de tipo subyacente S => (S, A). Scalaz proporciona un alias de tipo y
funciones convenientes para interactuar con el transformador de mónadas State
de manera directa, y reflejando MonadState:
type State[a] = StateT[Id, a]
object State {
def apply[S, A](f: S => (S, A)): State[S, A] = StateT[Id, S, A](f)
def state[S, A](a: A): State[S, A] = State((_, a))
def get[S]: State[S, S] = State(s => (s, s))
def put[S](s: S): State[S, Unit] = State(_ => (s, ()))
def modify[S](f: S => S): State[S, Unit] = ...
...
}
Para un ejemplo podemos regresar a las pruebas de lógica de negocios de
drone-dynamic-agents. Recuerde del Capítulo 3 que creamos Mutablep como
intérpretes de prueba para nuestra aplicación y que almacenamos el número de
started y los nodos stopped en una var`.
class Mutable(state: WorldView) {
var started, stopped: Int = 0
implicit val drone: Drone[Id] = new Drone[Id] { ... }
implicit val machines: Machines[Id] = new Machines[Id] { ... }
val program = new DynAgentsModule[Id]
}
Ahora sabemos que podemos escribir un mucho mejor simulador de pruebas con
State. Tomaremos la oportunidad de hacer un ajuste a la precisión de nuestra
simulación al mismo tiempo. Recuerde que un objeto clave de nuestro dominio de
aplicación es la visión del mundo:
final case class WorldView(
backlog: Int,
agents: Int,
managed: NonEmptyList[MachineNode],
alive: Map[MachineNode, Epoch],
pending: Map[MachineNode, Epoch],
time: Epoch
)
Dado que estamos escribiendo una simulación del mundo para nuestras pruebas, podemos crear un tipo de datos que capture la realidad de todo
final case class World(
backlog: Int,
agents: Int,
managed: NonEmptyList[MachineNode],
alive: Map[MachineNode, Epoch],
started: Set[MachineNode],
stopped: Set[MachineNode],
time: Epoch
)
La diferencia principal es que los nodos que están en los estados started y
stopped pueden ser separados. Nuestr intérprete puede ser implementado en
términos de State[World, a] y popdemos escribir nuestras pruebas para realizar
aserciones sobre la forma en la que se ve el World y WorldView después de
haber ejecutado la lógica de negocios.
Los intérpretes, que están simulando el contacto externo con los servicios Drone y Google, pueden implementarse como:
import State.{ get, modify }
object StateImpl {
type F[a] = State[World, a]
private val D = new Drone[F] {
def getBacklog: F[Int] = get.map(_.backlog)
def getAgents: F[Int] = get.map(_.agents)
}
private val M = new Machines[F] {
def getAlive: F[Map[MachineNode, Epoch]] = get.map(_.alive)
def getManaged: F[NonEmptyList[MachineNode]] = get.map(_.managed)
def getTime: F[Epoch] = get.map(_.time)
def start(node: MachineNode): F[Unit] =
modify(w => w.copy(started = w.started + node))
def stop(node: MachineNode): F[Unit] =
modify(w => w.copy(stopped = w.stopped + node))
}
val program = new DynAgentsModule[F](D, M)
}
y podemos reescribir nuestras pruebas para seguir la convención donde:
-
world1es el estado del mundo antes de ejecutar el programa -
view1es la creencia/visión de la aplicación sobre el mundo -
world2es el estado del mundo después de ejecutar el programa -
view2es la creencia/visión sobre la aplicación después de ejecutar el programa
Por ejemplo,
it should "request agents when needed" in {
val world1 = World(5, 0, managed, Map(), Set(), Set(), time1)
val view1 = WorldView(5, 0, managed, Map(), Map(), time1)
val (world2, view2) = StateImpl.program.act(view1).run(world1)
view2.shouldBe(view1.copy(pending = Map(node1 -> time1)))
world2.stopped.shouldBe(world1.stopped)
world2.started.shouldBe(Set(node1))
}
Esperemos que el lector nos perdone al mirar atrás a nuestro bucle anterior con implementación de lógica de negocio
state = initial()
while True:
state = update(state)
state = act(state)
y usar StateT para manejar el estado (state). Sin embargo, nuestra lógica de
negocios DynAgents requiere únicamente de Applicative y estaríamos violando
la ley del poder mínimo al requerir MonadState que es estrictamente más
poderoso. Es, por lo tanto, enteramente razonable manejar el estado manualmente
al pasarlo en un update y act, y dejar que quien realiza una llamada use un
StateT si así lo desea.
7.4.7 IndexedStateT
El código que hemos estudiado hasta el momento no es como Scalaz implementa
StateT. En lugar de esto, un type alias apunta a IndexedStateT
type StateT[F[_], S, A] = IndexedStateT[F, S, S, A]
La implementación de IndexedStateT es básicamente la que ya hemos estudiado,
con un parámetro de tipo extra que permiten que los estados de entrada S1 y
S2 difieran:
sealed abstract class IndexedStateT[F[_], -S1, S2, A] {
def run(initial: S1)(implicit F: Bind[F]): F[(S2, A)] = ...
...
}
object IndexedStateT {
def apply[F[_], S1, S2, A](
f: S1 => F[(S2, A)]
): IndexedStateT[F, S1, S2, A] = Wrap(f)
private final case class Wrap[F[_], S1, S2, A](
run: S1 => F[(S2, A)]
) extends IndexedStateT[F, S1, S2, A]
private final case class FlatMap[F[_], S1, S2, S3, A, B](
a: IndexedStateT[F, S1, S2, A],
f: (S2, A) => IndexedStateT[F, S2, S3, B]
) extends IndexedStateT[F, S1, S3, B]
...
}
IndexedStateT no tiene una MonadState cuando S1 != s2, aunque sí tiene una
Monad.
El siguiente ejemplo está adaptado de Index your State de Vincent Marquez.
Considere el escenario en el que deseamos diseñar una interfaz algebraica para
una búsqueda de un mapeo de un Inta un String. Se puede tratar de una
implementación en red y el orden de las invocaciones es esencial. Nuestro primer
intento de realizar la API es algo como lo siguiente:
trait Cache[F[_]] {
def read(k: Int): F[Maybe[String]]
def lock: F[Unit]
def update(k: Int, v: String): F[Unit]
def commit: F[Unit]
}
con errores en tiempo de ejecución si .update o .commit es llamada sin un
.lock. Un diseño más complejo puede envolver múltiples traits y una DSL a la
medida que nadie recuerde cómo usar.
En vez de esto, podemos usar IndexedStateT para requerir que la invocación se
realice en el estado correcto. Primero definimos nuestros estados posibles como
una ADT.
sealed abstract class Status
final case class Ready() extends Status
final case class Locked(on: ISet[Int]) extends Status
final case class Updated(values: Int ==>> String) extends Status
y entonces revisitar nuestra álgebra
trait Cache[M[_]] {
type F[in, out, a] = IndexedStateT[M, in, out, a]
def read(k: Int): F[Ready, Ready, Maybe[String]]
def readLocked(k: Int): F[Locked, Locked, Maybe[String]]
def readUncommitted(k: Int): F[Updated, Updated, Maybe[String]]
def lock: F[Ready, Locked, Unit]
def update(k: Int, v: String): F[Locked, Updated, Unit]
def commit: F[Updated, Ready, Unit]
}
lo que nos ocasionará un error en tiempo de compilación si intentamos realizar
un .update sin un .lock
for {
a1 <- C.read(13)
_ <- C.update(13, "wibble")
_ <- C.commit
} yield a1
[error] found : IndexedStateT[M,Locked,Ready,Maybe[String]]
[error] required: IndexedStateT[M,Ready,?,?]
[error] _ <- C.update(13, "wibble")
[error] ^
pero nos permite construir funciones que pueden componerse al incluirlas explícitamente en su estado:
def wibbleise[M[_]: Monad](C: Cache[M]): F[Ready, Ready, String] =
for {
_ <- C.lock
a1 <- C.readLocked(13)
a2 = a1.cata(_ + "'", "wibble")
_ <- C.update(13, a2)
_ <- C.commit
} yield a2
7.4.8 IndexedReaderWriterStateT
Aquellos que deseen una combinación de ReaderT, WriterT e IndexedStateT
no serán decepcionados. El transformador IndexedReaderWriterStateT envuelve
(R, S1) => F[(W, A, S2)] con R teniendo una semántica de Reader, W es
para escrituras monoidales, y los parámetros S para actualizaciones de
estado indexadas.
sealed abstract class IndexedReaderWriterStateT[F[_], -R, W, -S1, S2, A] {
def run(r: R, s: S1)(implicit F: Monad[F]): F[(W, A, S2)] = ...
...
}
object IndexedReaderWriterStateT {
def apply[F[_], R, W, S1, S2, A](f: (R, S1) => F[(W, A, S2)]) = ...
}
type ReaderWriterStateT[F[_], -R, W, S, A] = IndexedReaderWriterStateT[F, R, W, S, S, A]
object ReaderWriterStateT {
def apply[F[_], R, W, S, A](f: (R, S) => F[(W, A, S)]) = ...
}
Las abreviaturas se proporcionan porque de otra manera, con toda honestidad, estos tipos son tan largos que parecen que son parte de una API de J2EE:
type IRWST[F[_], -R, W, -S1, S2, A] = IndexedReaderWriterStateT[F, R, W, S1, S2, A]
val IRWST = IndexedReaderWriterStateT
type RWST[F[_], -R, W, S, A] = ReaderWriterStateT[F, R, W, S, A]
val RWST = ReaderWriterStateT
IRWST es una implementación más eficiente que una pila de transformadores
creadas como ReaderT[WriterT[IndexedStateT[F, ...], ...], ...].
7.4.9 TheseT
TheseT permite que los errores aborten los cálculos o que se acumulen si
existe un éxito parcial. Por esta razón recibe el nombre de mantén la calma y
continúa.
El tipo de datos subyacente es F[A \&/ B] con una A siendo el tipo del
error, requiriendo que exista un Semigroup para permitir la acumulación de
errores
final case class TheseT[F[_], A, B](run: F[A \&/ B])
object TheseT {
def `this`[F[_]: Functor, A, B](a: F[A]): TheseT[F, A, B] = ...
def that[F[_]: Functor, A, B](b: F[B]): TheseT[F, A, B] = ...
def both[F[_]: Functor, A, B](ab: F[(A, B)]): TheseT[F, A, B] = ...
implicit def monad[F[_]: Monad, A: Semigroup] = new Monad[TheseT[F, A, ?]] {
def bind[B, C](fa: TheseT[F, A, B])(f: B => TheseT[F, A, C]) =
TheseT(fa.run >>= {
case This(a) => a.wrapThis[C].point[F]
case That(b) => f(b).run
case Both(a, b) =>
f(b).run.map {
case This(a_) => (a |+| a_).wrapThis[C]
case That(c_) => Both(a, c_)
case Both(a_, c_) => Both(a |+| a_, c_)
}
})
def point[B](b: =>B) = TheseT(b.wrapThat.point[F])
}
}
No hay mónada especial asociada con TheseT, que simplemente es una Monad
regular. Si desearamos abortar el cálculo podríamos devolver un valor This,
pero estamos acumulando errores cuando devolvemos una Both que también
contiene la parte exitosa del cálculo.
TheseT también puede analizarse desde una perspectiva distinta: A no
necesita ser un error. De manera similar a WriterT, la A puede ser un
cálculo secundario que estamos realizando junto con un cálculo primario B.
TheseT permite la salida temprana cuando algo especial sobre A lo demanda.
7.4.10 ContT
El estilo de programación conocido como CPS (por sus siglas en inglés Continuation Passing Style) consiste en el uso de funciones que nunca regresan, y en lugar de esto, continúan al siguiente cómputo. CPS es popular en JavaScript y en Lisp dado que permiten el uso de callbacks cuando los datos están disponibles. Una implementación equivalente del patrón en Scala impuro se vería como
def foo[I, A](input: I)(next: A => Unit): Unit = next(doSomeStuff(input))
y podríamos hacer que el cómputo fuera puro al introducir el contexto F[_]
def foo[F[_], I, A](input: I)(next: A => F[Unit]): F[Unit]
y refactorizar para devolver una función para la entrada provista
def foo[F[_], I, A](input: I): (A => F[Unit]) => F[Unit]
ContT es simplemente un contenedor con esta signatura, con una instancia de
Monad
final case class ContT[F[_], B, A](_run: (A => F[B]) => F[B]) {
def run(f: A => F[B]): F[B] = _run(f)
}
object IndexedContT {
implicit def monad[F[_], B] = new Monad[ContT[F, B, ?]] {
def point[A](a: =>A) = ContT(_(a))
def bind[A, C](fa: ContT[F, B, A])(f: A => ContT[F, B, C]) =
ContT(c_fb => fa.run(a => f(a).run(c_fb)))
}
}
y sintaxis conveniente para crear una ContT a partir de un valor monádico:
implicit class ContTOps[F[_]: Monad, A](self: F[A]) {
def cps[B]: ContT[F, B, A] = ContT(a_fb => self >>= a_fb)
}
Sin embargo, el uso simple de callbacks en las continuaciones no trae nada a la
programación funcional pura debido a que ya conocemos cómo secuenciar cómputos
que no bloqueen, potencialmente distribuidos: es para esto que sirve Monad y
podemos hacer esto con un .bind o con una flecha Kleisli. Para observar por
qué razón las continuaciones son útiles necesitamos considerar un ejemplo más
complejo bajo una restricción de diseño más rígida.
7.4.10.1 Control de Flujo
Digamos que hemos modularizado nuestra aplicación usando componentes que pueden realizar I/O, y que cada componente es desarrollado por equipo distintos:
final case class A0()
final case class A1()
final case class A2()
final case class A3()
final case class A4()
def bar0(a4: A4): IO[A0] = ...
def bar2(a1: A1): IO[A2] = ...
def bar3(a2: A2): IO[A3] = ...
def bar4(a3: A3): IO[A4] = ...
Nuestra meta es producir una A0 dada una A1. Mientras que JavaScript y Lisp
usarían continuaciones para resolver este problema (debido a que la I/O es
bloqueante), podríamos simplemente encadenar las funciones
def simple(a: A1): IO[A0] = bar2(a) >>= bar3 >>= bar4 >>= bar0
Podríamos elevar .simple a su forma escrita con continuaciones al usar sintaxis
conveniente .cps y un poco de código extra (boilerplate) para cada paso:
def foo1(a: A1): ContT[IO, A0, A2] = bar2(a).cps
def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).cps
def foo3(a: A3): ContT[IO, A0, A4] = bar4(a).cps
def flow(a: A1): IO[A0] = (foo1(a) >>= foo2 >>= foo3).run(bar0)
De modo que, ¿qué nos brinda esto? Primeramente, es digno de mención que el flujo de control de la aplicación es de izquierda a derecha

¿Que tal si fuéramos los autores de foo2 y desearamos post-procesar la a0
que recivimos de la derecha (de más adelante en el proceso de cómputo), es
decir, deseamos dividir nuestro foo2 en foo2a y foo2b

Agregue la restricción de que no es posible cambiar la definición de flow o
bar0. Tal vez no es nuestro código y está definido por el framework que
estemos usando.
No es posible procesar la salida de a0 al modificar cualquiera de los métodos
restantes barX. Sin embargo, con ContT podemos modificar foo2 para
procesar el resultado de la continuación next:
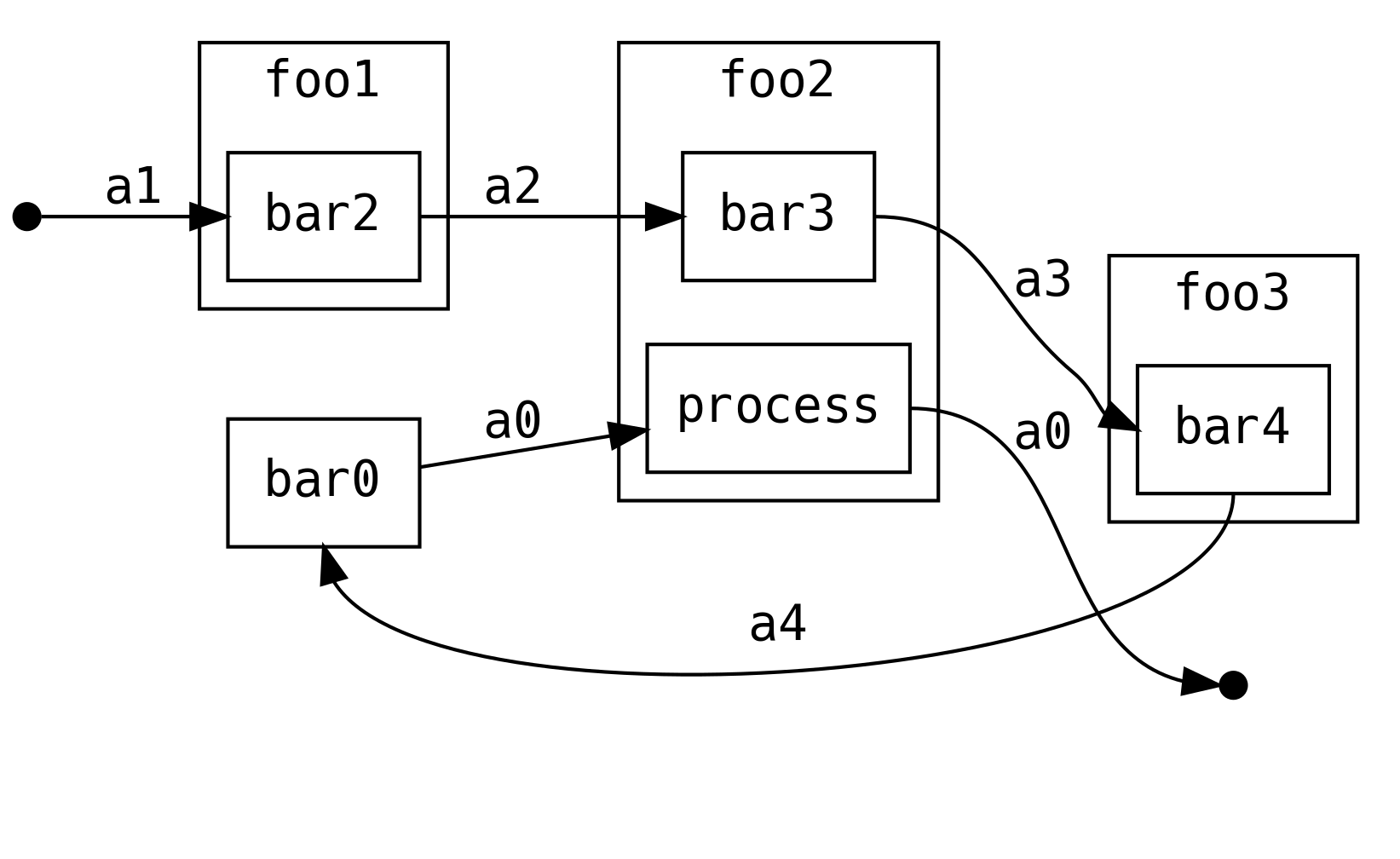
que puede definirse con
def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
for {
a3 <- bar3(a)
a0 <- next(a3)
} yield process(a0)
}
No estamos limitados a mapear sobre el valor devuelto, ¡también podemos realizar
un .bind en otro control de flujo devolviendo el flujo lineal en un grafo!
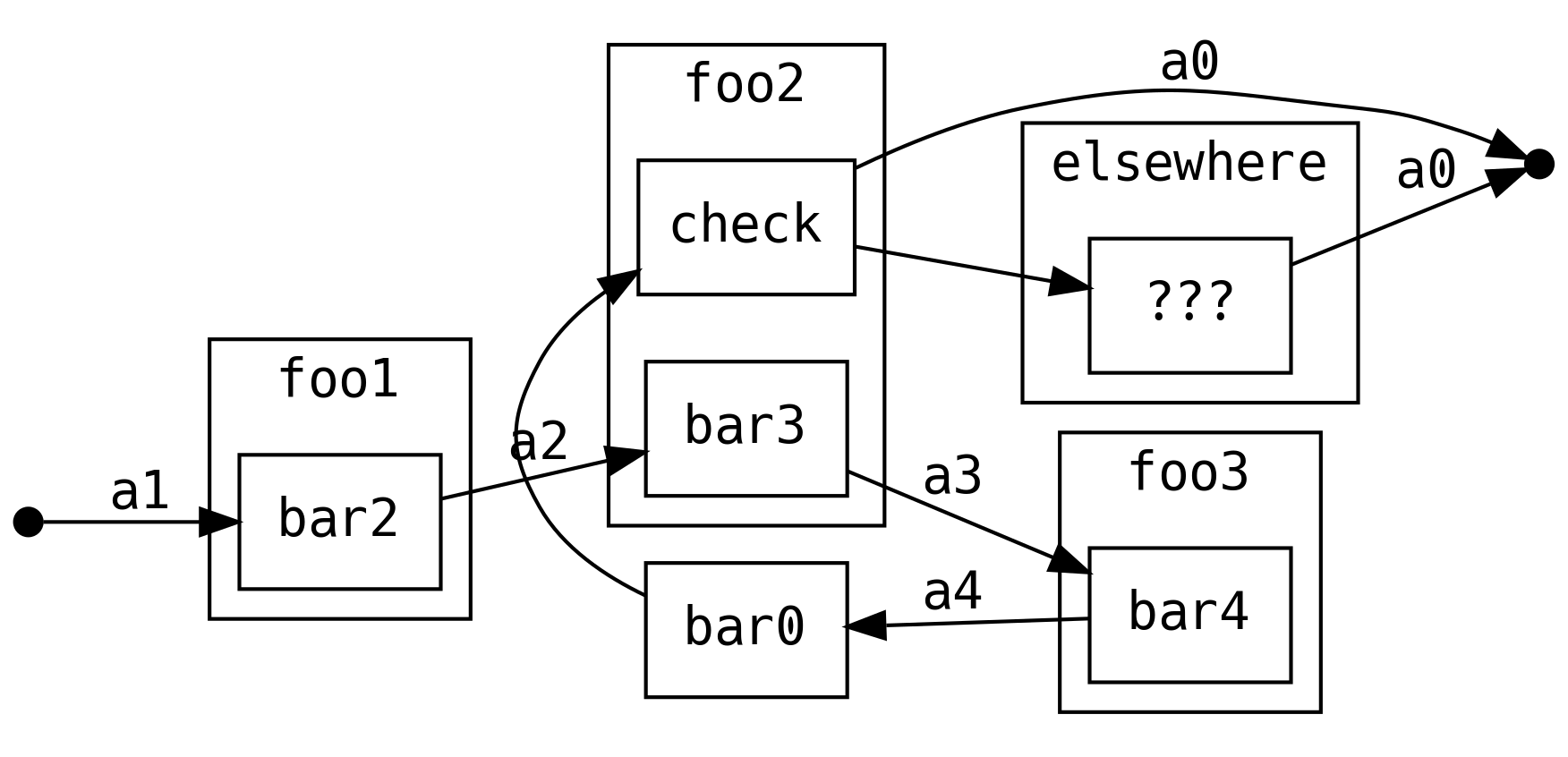
def elsewhere: ContT[IO, A0, A4] = ???
def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
for {
a3 <- bar3(a)
a0 <- next(a3)
a0_ <- if (check(a0)) a0.pure[IO]
else elsewhere.run(bar0)
} yield a0_
}
O podemos mantenernos dentro del flujo original y reintentar todo lo que sigue
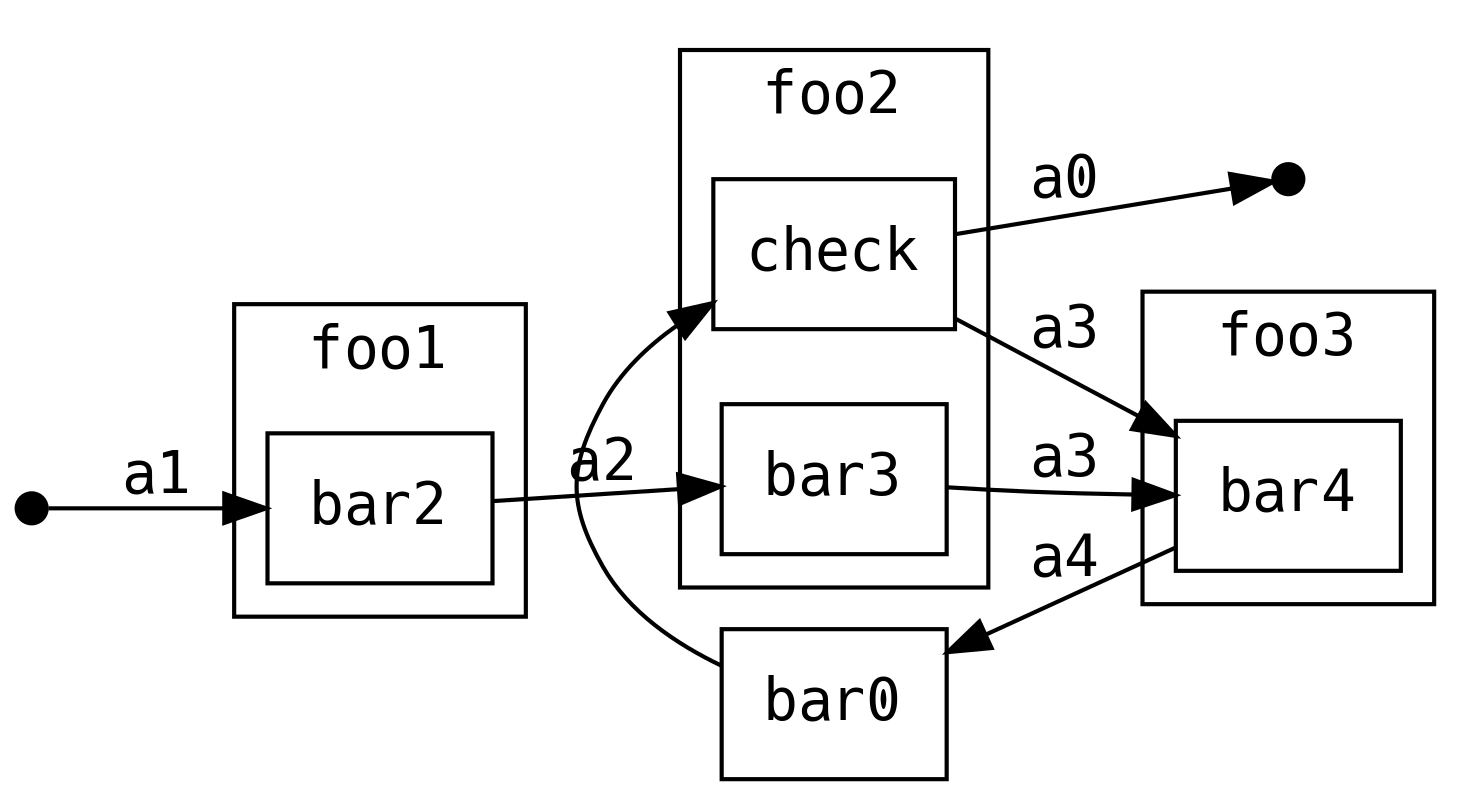
def foo2(a: A2): ContT[IO, A0, A3] = ContT { next =>
for {
a3 <- bar3(a)
a0 <- next(a3)
a0_ <- if (check(a0)) a0.pure[IO]
else next(a3)
} yield a0_
}
Se trata de únicamente un reintento, no de un ciclo infinito. Por ejemplo, podríamos solicitar que cómputos subsiguientes reconfirmaran una acción potencialmente peligrosa.
Finalmente, podemos realizar acciones que son específicas dentro del contexto de
ContT, en este caso IO que nos deja hacer un manejo de errores y limpieza de
recursos.
def foo2(a: A2): ContT[IO, A0, A3] = bar3(a).ensuring(cleanup).cps
7.4.10.2 Cuándo ordenar espagueti
No es un accidente que estos diagramas se vean como espagueti, y eso es
exactamente lo que ocurre cuando empezamos a manipular el control de flujo.
Todos los mecanismos que hemos discutido en esta sección son simples de
implementar directamente si podemos editar la definición de flow, y por lo
tanto no requerimos usar ContT.
Sin embargo, si estamos diseñando un framework, deberíamos podemos considerar el
sistema de plugins como callbacks de ContT para permitir a nuestros usuarios
más poder sobre el control de flujo. Algunas veces el cliente simplemente quiere
el espagueti.
Por ejemplo, si el compilador de Scala estuviera escrito usando CPS, permitiría un enfoque basado en principios para comunicar las fases del compilador. Un plugin para el compilador sería capaz de realizar algunas acciones basándose en el tipo inferido de una expresión, calculado en una etapa posterior del proceso de compilación. De manera similar, las continuaciones serían una buena API para una herramienta extensible para los builds, o para un editor de texto.
Algo que debería considerarse con ContT es que no tiene un uso seguro de la pila,
de modo que no es posible usarla para programas que se ejecutan por siempre.
7.4.10.3 No use ContT
Una variante más compleja de ContT llamada IndexedContT envuelve
(A => F[B]) => F[C]. El nuevo parámetro de tipo C permite al tipo de retorno del
cómputo completo sea diferente del tipo de retorno entre cada componente. Pero si
B no es igual a C entonces no hay una Monad.
Sin perder la oportunidad de generalizar tanto como sea posible, IndexedContT es
realmente implementada en términos de una estructura aún más general (note la
s estra antes de la T)
final case class IndexedContsT[W[_], F[_], C, B, A](_run: W[A => F[B]] => F[C])
type IndexedContT[f[_], c, b, a] = IndexedContsT[Id, f, c, b, a]
type ContT[f[_], b, a] = IndexedContsT[Id, f, b, b, a]
type ContsT[w[_], f[_], b, a] = IndexedContsT[w, f, b, b, a]
type Cont[b, a] = IndexedContsT[Id, Id, b, b, a]
donde W[_] tiene una Comonad, y ContT está implementada como un alias de tipo.
Los objetos compañeros existen para contener los aliases de tipo con constructores
de tipo convenientes.
La verdad es que, cinco parámetros de tipo es tal vez una generalización bastante amplia (tal vez demasiado). Pero de nuevo, la sobre-generalización es consistente con las sensibilidades de las continuaciones.
7.4.11 Las pilas de transformadores y los implícitos ambiguos
Esto concluye nuestro tour de los transformadores de mónadas en Scalaz.
Cuando se combinan múltiples transformadores, llamamos a esto una
pila de transformadores y aunque es muy verboso, es posible leer las
características al leer los transformadores. Por ejemplo, si construimos un
contexto F[_] que sea un conjunto de transformadores compuestos, tales como
type Ctx[A] = StateT[EitherT[IO, E, ?], S, A]
sabemos que estamos agregando manejadores de errores con un tipo de error E
(existe un MonadError[Ctx, E]) y estamos manejando el estado A (existe una
MonadState[Ctx, S]).
Lamentablemente, existen desventajas prácticas al uso de transformadores de
mónadas y sus compañeras de typeclases Monad:
- Múltiples parámetros implícitos de
Monadsignifican que el compilador no puede encontrar la sintaxis correcta que debe usarse para el contexto. - Las mónadas no se pueden componer en el caso general, lo que significa que el orden de anidación de los transformadores es importante.
- Todos los intérpretes deben elevarse al contexto común. Por ejemplo,
podríamos tener una implementación de alguna álgebra que use
IOy ahora es necesario envolverla dentro deStateTyEitherTincluso cuando son usados dentro del intérprete. - Existen costos de desempeño asociados a cada capa. Y algunos transformadores
de mónadas son peores que otros.
StateTes particularmente malo pero inclusoEitherTpuede ocasionar problemas de asignación de memoria para aplicaciones de alto desempeño.
Por eso es necesario considerar soluciones.
7.4.12 Sin sintaxis
Digamos que tenemos un álgebra
trait Lookup[F[_]] {
def look: F[Int]
}
y algunos tipos de datos
final case class Problem(bad: Int)
final case class Table(last: Int)
que deseemos usar en nuestra lógica de negocios
def foo[F[_]](L: Lookup[F])(
implicit
E: MonadError[F, Problem],
S: MonadState[F, Table]
): F[Int] = for {
old <- S.get
i <- L.look
_ <- if (i === old.last) E.raiseError(Problem(i))
else ().pure[F]
} yield i
El primer problema que encontramos es que esto no compila
[error] value flatMap is not a member of type parameter F[Table]
[error] old <- S.get
[error] ^
Existen algunas soluciones tácticas a este problema. La más obvia es hacer que todos los parámetros sean explícitos
def foo1[F[_]: Monad](
L: Lookup[F],
E: MonadError[F, Problem],
S: MonadState[F, Table]
): F[Int] = ...
y requerir únicamente que Monad sea pasado de manera implícita por medio de
límites de contexto. Sin embargo, esto significa que debemos alambrar
manualmente la MonadError y MonadState cuando invocamos foo1 y cuando
llamamos otro método que requiere un implícito.
Una segunda solución es dejar los parámetros como implícitos y usar el shadowing de nombres para hacer todos excepto uno de los parámetros explícitos. Esto permite que computos previos usen la resolución implícita cuando nos llaman pero todavía necesitamos pasar los parámetros de manera explícita si las llamamos.
@inline final def shadow[A, B, C](a: A, b: B)(f: (A, B) => C): C = f(a, b)
def foo2a[F[_]: Monad](L: Lookup[F])(
implicit
E: MonadError[F, Problem],
S: MonadState[F, Table]
): F[Int] = shadow(E, S) { (E, S) => ...
o podríamos hacer shadow de una sola Monad, dejando que la otra proporcione
nuestra sintaxis y que esté disponible para cuando llamamos a otros métodos.
@inline final def shadow[A, B](a: A)(f: A => B): B = f(a)
...
def foo2b[F[_]](L: Lookup[F])(
implicit
E: MonadError[F, Problem],
S: MonadState[F, Table]
): F[Int] = shadow(E) { E => ...
Una tercera opción, con un costo un poco más elevado, es la creación de una
typeclass de Monad a la medida, que contenga referencias implícitas a las dos
clases de Monad que nos interesan
trait MonadErrorState[F[_], E, S] {
implicit def E: MonadError[F, E]
implicit def S: MonadState[F, S]
}
y una derivación de la typeclass dada por una MonadError y MonadState
object MonadErrorState {
implicit def create[F[_], E, S](
implicit
E0: MonadError[F, E],
S0: MonadState[F, S]
) = new MonadErrorState[F, E, S] {
def E: MonadError[F, E] = E0
def S: MonadState[F, S] = S0
}
}
Ahora, si deseamos acceder a S o E podemos obtenerlas por medio de F.S o
F.E
def foo3a[F[_]: Monad](L: Lookup[F])(
implicit F: MonadErrorState[F, Problem, Table]
): F[Int] =
for {
old <- F.S.get
i <- L.look
_ <- if (i === old.last) F.E.raiseError(Problem(i))
else ().pure[F]
} yield i
Como segunda solución, podemos escoger una de las instancias de Monad para que
sea implícita dentro del bloque, y esto se puede conseguir al importarla
def foo3b[F[_]](L: Lookup[F])(
implicit F: MonadErrorState[F, Problem, Table]
): F[Int] = {
import F.E
...
}
7.4.12.1 Composición de transformadores
Un EitherT[StateT[...], ...] tiene un MonadError pero no tiene un
MonadState, mientras que StateT[EitherT[...], ...] puede proporcionar ambos.
La solución es estudiar las derivaciones implícitas en el objeto compañero de los transformadores y podemos asegurarnos de que los transformadores más externos proporcionan todo lo que necesitamos.
Una regla de oro es que hay que usar los transformadores más complejos en el exterior, y este capítulo presentó los transformadores en orden creciente de complejidad.
7.4.12.2 Elevando transformadores
Continuando con el mismo ejemplo, digamos que nuestra álgebra Lookup tiene un
intérprete IO
object LookupRandom extends Lookup[IO] {
def look: IO[Int] = IO { util.Random.nextInt }
}
pero deseamos que nuestro contexto sea
type Ctx[A] = StateT[EitherT[IO, Problem, ?], Table, A]
para proporcionarnos un MonadError y un MonadState. Esto significa que
necesitamos envolver LookupRandom para que opere sobre nuestro Ctx.
Las probabilidades de tener los tipos correctos en el primer intento son de aproximadamente 3,720 a uno.
Primero, deseamos usar la sintaxis .liftM disponible en Monad, que usa
MonadTrans para elevar desde nuestro F[A] hacia G[F, A]
final class MonadOps[F[_]: Monad, A](fa: F[A]) {
def liftM[G[_[_], _]: MonadTrans]: G[F, A] = ...
...
}
Es importante darse cuenta de que los parámetros de tipo de .liftM tienen dos
hoyos, uno de la forma _[_] y el otro de forma _. Si creamos aliases de tipo
para estas formas
type Ctx0[F[_], A] = StateT[EitherT[F, Problem, ?], Table, A]
type Ctx1[F[_], A] = EitherT[F, Problem, A]
type Ctx2[F[_], A] = StateT[F, Table, A]
podemos abstraer sobre MonadTrans para elevar un Lookup[F] a cualquier
Lookup[G[F, ?]] donde G es un transformador de mónadas.
def liftM[F[_]: Monad, G[_[_], _]: MonadTrans](f: Lookup[F]) =
new Lookup[G[F, ?]] {
def look: G[F, Int] = f.look.liftM[G]
}
Permitiéndonos envolver una vez para EitherT, y de nuevo para StateT
val wrap1 = Lookup.liftM[IO, Ctx1](LookupRandom)
val wrap2: Lookup[Ctx] = Lookup.liftM[EitherT[IO, Problem, ?], Ctx2](wrap1)
Otra forma de lograr esto, en un único paso, es usar MonadIO que permite
elevar una IO en una pila de transformadores:
@typeclass trait MonadIO[F[_]] extends Monad[F] {
def liftIO[A](ioa: IO[A]): F[A]
}
con instancias de MonadIO para todas las combinaciones comunes de transformadores.
El costo extra del código repetitivo para elevar un intérprete IO a cualquier
instancia de MonadIO es por lo tanto de dos líneas de código (para la
definición del intérprete), más una linea por elemento del álgebra, y una línea
final para invocarla:
def liftIO[F[_]: MonadIO](io: Lookup[IO]) = new Lookup[F] {
def look: F[Int] = io.look.liftIO[F]
}
val L: Lookup[Ctx] = Lookup.liftIO(LookupRandom)
Un plugin del compilador que produce automáticamente .liftM, .liftIO, y
código repetitivo adicional que surja en este capítulo, ¡sería una excelente
contribución al ecosistema!
7.4.12.3 Desempeño
El problema más grande con los transformadores de mónadas es el costo adicional
en términos de rendimiento. EitherT tenía un costo extra relativamente bajo,
donde cada invocación de .flatMap generaba un grupo de objetos, pero esto
puede afectar aplicaciones de alto rendimiento donde cada asignación de memoria
adicional importa. Otros transformadores, tales como StateT, efectivamente
agregan un trampolín, y ContT mantiene la cadena de invocaciones entera
retenida en memoria.
Para algunas aplicaciones no es importante la asignación de memoria si su límite está impuesto por redes o por I/O. Siempre mida.
Si el rendimiento se vuelve un problema, la solución es no usar transformadores
de mónadas. Al menos no las estructuras de datos de los transformadores. Una
gran ventaja de las typeclases de Monad es que podemos crear una versión
optimizada F[_] para nuestra aplicación que proporcione las typeclasses
naturalmente. Aprenderemos cómo crear una F[_] en los próximos dos capítulos,
cuando estudiemos seriamente dos estructuras que ya hemos visto: Free y IO.
7.5 Una comida gratis
Nuestra industria ruega el uso de lenguajes de alto nivel que sean seguros, intercambiando la eficiencia de los desarrolladores y la confiabilidad por un tiempo reducido durante la ejecución.
El compilador JIT (por sus siglas en inglés: Just In Time) en la JVM tiene un desempeño tan alto que funciones simples tienen un desempeño comparable a sus equivalentes en C o C++, ignorando el costo del recolector de basura. Sin embargo, el JIT realiza únicamente optimizaciones de bajo nivel: predicción de bifurcaciones, el inlining (sustitución) de métodos, despliegue de ciclos, y así sucesivamente.
El JIT no realiza optimizaciones de nuestra lógica de negocios, por ejemplo realizar un agrupamiento de las llamadas de red, o la paralelización de tareas independientes. El desarrollador es responsable de escribir la lógica de negocio y las optimizaciones a la vez, reduciendo la legibilidad y haciendo el código más difícil de mantener. Sería muy bueno si las optimizaciones fueran asuntos de importancia secundaria.
Si, en vez de esto, tenemos una estructura de datos que describe nuestra lógica de negocios en términos de conceptos de alto nivel, no de instrucciones de máquina, podemos realizar optimizaciones de alto nivel. Las estructuras de datos de esta naturaleza se llaman, típicamente, estructuras Free (libres) y pueden generarse automáticamente para los miembros de interfaces algebraicas de nuestro programa. Por ejemplo, un Free Applicative puede ser generado para permitirnos ejecutar agrupamiento por lotes o la simplificación de I/O costosa a través de la red.
En esta sección aprenderemos cómo crear estructuras libres, y cómo pueden ser usadas.
7.5.1 Free (Monad)
Fundamentalmente, las mónadas describen un programa secuencial donde cada paso depende del previo. Por lo tanto estamos limitados a modificaciones que sólo saben sobre cosas que ya hemos ejecutado y la próxima que vamos a ejecutar.
Estuvo muy de moda, cerca de 2105, escribir programas en términos de Free
de modo que esto consiste tanto en un ejercicio como en la comprensión de
este tipo de código, así como de la capacidad de escribirlo y usarlo.
Es necesario escribir mucho código repetitivo en la creación de una estructura
libre. Podemos usar este estudio de Free para aprender cómo generar
el código repetitivo.
Como un recordatorio, Free es la representación de la estructura de datos de
una Monad y está definido por tres miembros
sealed abstract class Free[S[_], A] {
def mapSuspension[T[_]](f: S ~> T): Free[T, A] = ...
def foldMap[M[_]: Monad](f: S ~> M): M[A] = ...
...
}
object Free {
implicit def monad[S[_], A]: Monad[Free[S, A]] = ...
private final case class Suspend[S[_], A](a: S[A]) extends Free[S, A]
private final case class Return[S[_], A](a: A) extends Free[S, A]
private final case class Gosub[S[_], A0, B](
a: Free[S, A0],
f: A0 => Free[S, B]
) extends Free[S, B] { type A = A0 }
def liftF[S[_], A](value: S[A]): Free[S, A] = Suspend(value)
...
}
-
Suspendrepresenta un programa que todavía no ha sido interpretado -
Returnes.pure -
Gosubes.bind
Un valor Free[S, A] puede ser generada de manera automática para cualquier
álgebra S. Para hacer esto explícito, considere nuesra aplicación del álgebra
de Machines
trait Machines[F[_]] {
def getTime: F[Epoch]
def getManaged: F[NonEmptyList[MachineNode]]
def getAlive: F[Map[MachineNode, Epoch]]
def start(node: MachineNode): F[Unit]
def stop(node: MachineNode): F[Unit]
}
Podemos definir una estructura Free generada para Machines al crear una ADT
con un tipo de datos para cada elemento en el álgebra. Cada tipo de datos tiene
los mismos tipos de parámetros como su elemento correspondiente, está
parametrizado sobre el tipo de retorno, y tiene el mismo nombre:
object Machines {
sealed abstract class Ast[A]
final case class GetTime() extends Ast[Epoch]
final case class GetManaged() extends Ast[NonEmptyList[MachineNode]]
final case class GetAlive() extends Ast[Map[MachineNode, Epoch]]
final case class Start(node: MachineNode) extends Ast[Unit]
final case class Stop(node: MachineNode) extends Ast[Unit]
...
La ADT define un AST (por sus siglas en inglés Abstract Syntax Tree) debido a que cada miembro está representando un cómputo en un programa.
La estructura Free generada libremente para Machines es
Free[Machines.Ast, ?], es decir, para la AST, not Free[Machines, ?].
Es fácil cometer un error, dado que el último compilará, pero no tiene
significado.
Entonces definimos .liftF, una implementación de Machines, con Free[Ast, ?]
siendo el contexto. Todo método simplemente delega a Free.liftT para crear un
Suspend
...
def liftF = new Machines[Free[Ast, ?]] {
def getTime = Free.liftF(GetTime())
def getManaged = Free.liftF(GetManaged())
def getAlive = Free.liftF(GetAlive())
def start(node: MachineNode) = Free.liftF(Start(node))
def stop(node: MachineNode) = Free.liftF(Stop(node))
}
}
cuando construimos un programa, parametrizado sobre un valor Free, lo ejecutamos
al proporcionar un intérprete (una transformación natural Ast ~> M) al método
.foldMap. Por ejemplo, si pudieramos proporcionar un intérprete que mapee a
IO podemos construir un IO[Unit] por medio del AST libre
def program[F[_]: Monad](M: Machines[F]): F[Unit] = ...
val interpreter: Machines.Ast ~> IO = ...
val app: IO[Unit] = program[Free[Machines.Ast, ?]](Machines.liftF)
.foldMap(interpreter)
En aras de la exhaustividad, un intérprete que delega a una implementación
directa es fácil de escribir. Esto puede ser útil si el resto de la aplicación
está usando Free como el contexto y nosotros tenemos una implementación IO
que deseamos usar:
def interpreter[F[_]](f: Machines[F]): Ast ~> F = λ[Ast ~> F] {
case GetTime() => f.getTime
case GetManaged() => f.getManaged
case GetAlive() => f.getAlive
case Start(node) => f.start(node)
case Stop(node) => f.stop(node)
}
Pero nuestra lógica de negocios requiere de más que simplemente Machines,
también requerimos acceder a nuestra álgebra de Drone, y recuerde que está
definido como
trait Drone[F[_]] {
def getBacklog: F[Int]
def getAgents: F[Int]
}
object Drone {
sealed abstract class Ast[A]
...
def liftF = ...
def interpreter = ...
}
Lo que deseamos es que nuestra AST sea la combinación de ASTs para Machines y
Drone. Estudiamos Coproduct en el capítulo 6, que es una disjunción de alta
clase (una higher kinded disjunction):
final case class Coproduct[F[_], G[_], A](run: F[A] \/ G[A])
Podemos usar el contexto Free[Coproduct[Machines.Ast, Drone.Ast, ?], ?].
Podríamos crear manualmente el coproducto pero estaríamos nadando en código repetivo, y tendríamos que repetirlo todo de nuevo si desearamos agregar una tercer álgebra.
La typeclass con el nombre scalaz.Inject ayuda:
type :<:[F[_], G[_]] = Inject[F, G]
sealed abstract class Inject[F[_], G[_]] {
def inj[A](fa: F[A]): G[A]
def prj[A](ga: G[A]): Option[F[A]]
}
object Inject {
implicit def left[F[_], G[_]]: F :<: Coproduct[F, G, ?]] = ...
...
}
Las derivaciones implícitas generan instancias de Inject cuando las
requerimos, permitiéndonos reescribir nuestros liftF para que funcionen con
cualquier combinación de ASTs:
def liftF[F[_]](implicit I: Ast :<: F) = new Machines[Free[F, ?]] {
def getTime = Free.liftF(I.inj(GetTime()))
def getManaged = Free.liftF(I.inj(GetManaged()))
def getAlive = Free.liftF(I.inj(GetAlive()))
def start(node: MachineNode) = Free.liftF(I.inj(Start(node)))
def stop(node: MachineNode) = Free.liftF(I.inj(Stop(node)))
}
Sería bueno que F :<: G se leyera como si nuestro Ast fuera un miembro del
conjunto completo de instrucciones F: esta sintaxis es intencional.
Un plugin del compilador que automáticamente genera el código repetitivo de
scalaz.Free sería una contribución fantástica al ecosistema! No solamente
es doloroso escribir este código, sino que existe el potencial de que un error
de dedo arruine nuestro día: si dos miembros del álgebra tiene la misma signatura
de tipo, podríamos no notarlo.
Poniendo todo junto, digamos que tenemos un program que escribimos abstrayendo
sobre Monad
def program[F[_]: Monad](M: Machines[F], D: Drone[F]): F[Unit] = ...
y tenemos algunas implementaciones existentes de Machines y Drone, y podemos
crear interpretes a partir de ellos:
val MachinesIO: Machines[IO] = ...
val DroneIO: Drone[IO] = ...
val M: Machines.Ast ~> IO = Machines.interpreter(MachinesIO)
val D: Drone.Ast ~> IO = Drone.interpreter(DroneIO)
y combinarlos en un conjunto de instrucciones más grande usando un método
conveniente de nuestro objeto compañero en NaturalTransformation
object NaturalTransformation {
def or[F[_], G[_], H[_]](fg: F ~> G, hg: H ~> G): Coproduct[F, H, ?] ~> G = ...
...
}
type Ast[a] = Coproduct[Machines.Ast, Drone.Ast, a]
val interpreter: Ast ~> IO = NaturalTransformation.or(M, D)
Y entonces usarlo para produir un IO
val app: IO[Unit] = program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
.foldMap(interpreter)
¡Pero hemos viajado en círculos! Podríamos haber usado IO como el contexto de
nuestro programa en primer lugar y haber evitado Free. De modo que por qué
pasamos por todos estos problemas? A continuación tenemos algunos ejemplos de
cuando Free podría ser de utilidad.
7.5.1.1 Pruebas con Mocks y Stubs
Puede parecer hipócrita proponer que Free pueda usarse para reducir el
boilerplate, dada la gran cantidad de código que hemos escrito. Sin embargo,
existe un punto de inflexión cuando el Ast paga por sí mismo cuando tenemos
muchas pruebas que requieren implementaciones stub.
Si los métodos .Ast y .liftF están definidos para un álgebra, podemos crear
intérpretes parciales
val M: Machines.Ast ~> Id = stub[Map[MachineNode, Epoch]] {
case Machines.GetAlive() => Map.empty
}
val D: Drone.Ast ~> Id = stub[Int] {
case Drone.GetBacklog() => 1
}
que puede ser usado para probar nuestro program
program[Free[Ast, ?]](Machines.liftF, Drone.liftF)
.foldMap(or(M, D))
.shouldBe(1)
Al usar funciones parciales, y no funciones totales, estamos exponiéndonos a errores en tiempo de ejecución. Muchos equipos están felices de aceptar este costo en sus pruebas unitarias dado que el test fallaría si hay un error del programador.
También es posible lograr lo mismo con implementaciones de nuestras álgebras que
implementen cada método con ???, haciendo un override de cada cosa necesaria
según sea el caso.
La librería smock es más poderosa, pero
para los propósitos de este breve ejemplo podemos definir los stub por
nosotros mismos usando un truco de inferencia de tipos que puede encontrarse
por todas partes en el código fuente de Scalaz. La razón de que Stub sea
una clase separada es que únicamente tengamos que proporcionar el parámetro
de tipo A, a la vez que F y G se infieren del lado izquierdo de la
expresión:
7.5.1.2 Monitoreo
Es típico que las aplicaciones de servidor sean monitoreadas por agentes de ejecución que manipulan el bytecode para insertar profilers y extraer información de distintas clases de uso o rendimiento.
Si el contexto de nuestra aplicación es Free, no es necesario recurrir a la
manipulación de bytecode, y en vez de esto es posible implementar un monitor de
efectos laterales como un intérprete sobre el que tenemos completo control.
La introspección en tiempo de ejecución es uno de los pocos casos en los que
se justifica el uso de un efecto lateral. Si el monitoreo no es visible al
programa en sí mismo, todavía es válida la transparencia referencial. Este
también es el argumento usado por los equipos que usan efectos laterales al
hacer logging para depurar programas, y nuestro argumento para permitir
mutaciones en la implementación de Memo.
Por ejemplo, considere usar este agente Ast ~> Ast:
val Monitor = λ[Demo.Ast ~> Demo.Ast](
_.run match {
case \/-(m @ Drone.GetBacklog()) =>
JmxAbstractFactoryBeanSingletonProviderUtilImpl.count("backlog")
Coproduct.rightc(m)
case other =>
Coproduct(other)
}
)
que almacena invocaciones del método: podríamos usar una rutina específica del vendedor en código real. También podríamos monitorear mensajes de interés específicos y registrarlos como una ayuda de depuración.
Podemos adjuntar Monitor a nuestra aplicación de producción Free con
.mapSuspension(Monitor).foldMap(interpreter)
o combinar las transformaciones naturales y ejecutarlas con un único
.foldMap(Monitor.andThen(interpreter))
7.5.1.3 Parches al código
Como ingenieros, estamos acostumbrados a peticiones de soluciones bizarras que es necesario añadir a la lógica central de la aplicación. Tal vez deseemos programar tales casos especiales como excepciones a la regla y manejarlos de manera tangencial a la lógica central de nuestro programa.
Por ejemplo, suponga que obtenemos un memo de contabilidad indicándonos lo siguiente
URGENTE: Bob está usando el nodo
#c0feepara ejecutar el final del año. ¡NO DETENGA ESTA MÁQUINA!
No hay posibilidad de discutir porqué Bob no debería estar usando nuestras máquinas para sus cuentas super importantes, de modo que es necesario hackear nuestra lógica de negocio y poner un release a producción tan pronto como sea posible.
Nuestro parche al código puede mapear a una estructura Free, permitiéndonos
regresar un resultado predeterminado (Free.pure) en lugar de programar la
ejecución de la instrucción. Creamos un caso especial para la instrucción en una
transformación natural personalizada con su valor de retorno:
val monkey = λ[Machines.Ast ~> Free[Machines.Ast, ?]] {
case Machines.Stop(MachineNode("#c0ffee")) => Free.pure(())
case other => Free.liftF(other)
}
después de haber revisado que funcione, subimos el cambio a producción, y ponemos una alarma para la próxima semana para recordarnos de removerla, y quitar los permisos de accesso de Bob de nuestros servidores.
Nuestra prueba unitaria podría usar State como el contexto objetivo, de modo
que podamos darle seguimiento a todos los nodos que detuvimos:
type S = Set[MachineNode]
val M: Machines.Ast ~> State[S, ?] = Mocker.stub[Unit] {
case Machines.Stop(node) => State.modify[S](_ + node)
}
Machines
.liftF[Machines.Ast]
.stop(MachineNode("#c0ffee"))
.foldMap(monkey)
.foldMap(M)
.exec(Set.empty)
.shouldBe(Set.empty)
junto con una prueba de que los nodos “normales” no son afectados.
Una ventaja de usar Free para evitar detener los nodos #c0fee es que podemos
estar seguros de atrapar todos los usos en lugar de tener que revisar la lógica
del negocio y buscar todos los usos de .stop. Si nuestro contexto de la
aplicación es simplemente IO podríamos, por supuesto, implementar esta lógica
en la implementación de Machines[IO] pero una ventaja de usar Free es que no
necesitamos tocar el código existente y podemos aislar y probar este
comportamiento (temporal) sin seguir atado a las implementaciones de IO.
7.5.2 FreeApp (Applicative)
A pesar de que este capítulo se llama Mónadas avanzadas, el punto que
debemos recordar es: no deberíamos usar mónadas a menos que realmente
tengamos que usarlas. En esta sección, veremos porqué FreeAp (un aplicativo
free), es preferible a las mónadas Free.
FreeAp se define como la representación de la estructura de datos de los
métodos ap y pure de la typeclass Applicative:
sealed abstract class FreeAp[S[_], A] {
def hoist[G[_]](f: S ~> G): FreeAp[G,A] = ...
def foldMap[G[_]: Applicative](f: S ~> G): G[A] = ...
def monadic: Free[S, A] = ...
def analyze[M:Monoid](f: F ~> λ[α => M]): M = ...
...
}
object FreeAp {
implicit def applicative[S[_], A]: Applicative[FreeAp[S, A]] = ...
private final case class Pure[S[_], A](a: A) extends FreeAp[S, A]
private final case class Ap[S[_], A, B](
value: () => S[B],
function: () => FreeAp[S, B => A]
) extends FreeAp[S, A]
def pure[S[_], A](a: A): FreeAp[S, A] = Pure(a)
def lift[S[_], A](x: =>S[A]): FreeAp[S, A] = ...
...
}
Los métodos .hoist y .foldMap son como los análogos de Free
.mapSuspension y .foldMap.
Como una conveniencia, podemos generar una Free[S, A] a partir de nuestro
FreeAp[S, A] con .monadic. Esto es de especial utilidad para optimizar
subsistemas más pequeños y sin embargo usarlos como parte de un programa Free
más grande.
Como Free, donde debemos crear una FreeAp para nuestras ASTs, más
boilerplate…
def liftA[F[_]](implicit I: Ast :<: F) = new Machines[FreeAp[F, ?]] {
def getTime = FreeAp.lift(I.inj(GetTime()))
...
}
7.5.2.1 Haciendo llamadas agrupadas a la red
Iniciamos este capítulo con afirmaciones grandes sobre rendimiento. Es tiempo de cumplir.
La versión humanizada de Philip Stark de los Números de latencia de Peter Norvig sirven de motivación para enfocarnos en la reducción de las llamadas a la red para optimisar una aplicación:
| Computadora | Escala de tiempo humana | Analogía humana |
|---|---|---|
| Referencia a cache L1 | 0.5 segs | Un latido del corazón |
| Error en la predicción de bifurcación | 5 segs | Bostezo |
| Referencia a cache L2 | 7 segs | Bostezo largo |
| Mutex lock/unlock | 25 segs | Preparar una taza de té |
| Referencia a memoria principal | 100 segs | Cepillarse los dientes |
| Comprimir 1 KB con Zippy | 50 min | Pipeline de CI de scalac |
| Enviar 2 KB por una red de 1 Gbps | 5.5 hr | Tren de Londres a Edinburgo |
| Lectura aleatoria de SSD | 1.7 días | Fin de semana |
| Lectura sequencial de 1 MB de memoria | 2.9 días | Fin de semana largo |
| Viaje redondo dentro del mismo centro de datos | 5.8 días | Vacaciones largas de EE.UU. |
| Lectura sequencial de 1 MB de SSD | 11.6 días | Fiesta corta de la Union Europea |
| Búsqueda en disco | 16.5 semanas | Periodo de la universidad |
| Lectura sequencial de 1 MB de disco | 7.8 meses | Maternidad pagada completamente en Noruega |
| Envío de un paquete de CA->Holanda->CA | 4.8 años | Periodo de gobierno |
Aunque Free y ``FreeAp` incurren en un costo extra de asignación dinámica de
memoria, el equivalente a 100 segundos en la tabla humanizada, cada vez que
convertimos dos invocaciones de red en una invocación agrupada, ahorramos casi 5
años.
Cuando estamos en un contexto Applicative, podemos optimizar con seguridad
nuestra aplicación sin incumplir ninguna de las expectativas del programa
original, y sin llenar desordenadamente nuestra lógica de negocios.
Felizmente, nuestra lógica de negocio únicamente requiere de un Applicative,
recuerde
final class DynAgentsModule[F[_]: Applicative](D: Drone[F], M: Machines[F])
extends DynAgents[F] {
def act(world: WorldView): F[WorldView] = ...
...
}
Para empezar, crearemos el código repetitivo de lift para una álgebra nueva
Batch
trait Batch[F[_]] {
def start(nodes: NonEmptyList[MachineNode]): F[Unit]
}
object Batch {
sealed abstract class Ast[A]
final case class Start(nodes: NonEmptyList[MachineNode]) extends Ast[Unit]
def liftA[F[_]](implicit I: Ast :<: F) = new Batch[FreeAp[F, ?]] {
def start(nodes: NonEmptyList[MachineNode]) = FreeAp.lift(I.inj(Start(nodes)))
}
}
y entonces crearemos una instancia de DynAgentsModule con FreeAp como el
contexto
type Orig[a] = Coproduct[Machines.Ast, Drone.Ast, a]
val world: WorldView = ...
val program = new DynAgentsModule(Drone.liftA[Orig], Machines.liftA[Orig])
val freeap = program.act(world)
En el capítulo 6, estudiamos el tipo de datos Const, que nos permite analizar
un programa. No debería sorprendernos que FreeAp.analize esté implementado en
términos de Const:
sealed abstract class FreeAp[S[_], A] {
...
def analyze[M: Monoid](f: S ~> λ[α => M]): M =
foldMap(λ[S ~> Const[M, ?]](x => Const(f(x)))).getConst
}
Proporcionamos una transformación natural para registrar todos los inicios de
nodos y analizar (.analize) nuestro programa para obtener todos los nodos que
necesitan iniciarse:
val gather = λ[Orig ~> λ[α => IList[MachineNode]]] {
case Coproduct(-\/(Machines.Start(node))) => IList.single(node)
case _ => IList.empty
}
val gathered: IList[MachineNode] = freeap.analyze(gather)
El siguiente paso es extender el conjunto de instrucciones de Orig a
Extended, lo que incluye el Batch.Ast y escribir un programa FreeApp que
inicie todos nuestros nodos reunidos (gathered) en una única invocación a la
red.
type Extended[a] = Coproduct[Batch.Ast, Orig, a]
def batch(nodes: IList[MachineNode]): FreeAp[Extended, Unit] =
nodes.toNel match {
case None => FreeAp.pure(())
case Some(nodes) => FreeAp.lift(Coproduct.leftc(Batch.Start(nodes)))
}
También necesitamos remover todas las llamadas a Machines.Start, lo cual
podemos hacer con una transformación natural
val nostart = λ[Orig ~> FreeAp[Extended, ?]] {
case Coproduct(-\/(Machines.Start(_))) => FreeAp.pure(())
case other => FreeAp.lift(Coproduct.rightc(other))
}
Ahora tenemos dos programas, y necesitamos combinarlos. Recuerde la sintaxis
*> de Apply
val patched = batch(gathered) *> freeap.foldMap(nostart)
Poniéndolo todo junto en un mismo método:
def optimise[A](orig: FreeAp[Orig, A]): FreeAp[Extended, A] =
(batch(orig.analyze(gather)) *> orig.foldMap(nostart))
¡Eso es todo! Llamamos .optimise en cada invocación de act en nuestro ciclo
principal, lo cual es simplemente una cuestión mecánica.
7.5.3 Coyoneda (Functor)
Nombrada en honor al matemático Nobuo Yoneda, podemos generar de manera gratuita
una estructura de datos Functor para cualquier álgebra S[_]
sealed abstract class Coyoneda[S[_], A] {
def run(implicit S: Functor[S]): S[A] = ...
def trans[G[_]](f: F ~> G): Coyoneda[G, A] = ...
...
}
object Coyoneda {
implicit def functor[S[_], A]: Functor[Coyoneda[S, A]] = ...
private final case class Map[F[_], A, B](fa: F[A], f: A => B) extends Coyoneda[F, A]
def apply[S[_], A, B](sa: S[A])(f: A => B) = Map[S, A, B](sa, f)
def lift[S[_], A](sa: S[A]) = Map[S, A, A](sa, identity)
...
}
y también existe una versión contravariante
sealed abstract class ContravariantCoyoneda[S[_], A] {
def run(implicit S: Contravariant[S]): S[A] = ...
def trans[G[_]](f: F ~> G): ContravariantCoyoneda[G, A] = ...
...
}
object ContravariantCoyoneda {
implicit def contravariant[S[_], A]: Contravariant[ContravariantCoyoneda[S, A]] = ...
private final case class Contramap[F[_], A, B](fa: F[A], f: B => A)
extends ContravariantCoyoneda[F, A]
def apply[S[_], A, B](sa: S[A])(f: B => A) = Contramap[S, A, B](sa, f)
def lift[S[_], A](sa: S[A]) = Contramap[S, A, A](sa, identity)
...
}
El término coloquial para Coyoneda es coyo y para ContravariantCoyoneda
es cocoyo.
La API es algo más simple que Free y FreeAp, permitiendo una transformación
natural con .trans y un .run (tomando un Functor o Contravariant,
respectivamente) para escapar de la estructura libre.
Coyo y cocoyo pueden ser de utilidad si deseamos realizar un .map o
.contramap sobre un tipo, y sabemos que podemos convertir en un tipo de datos
que tiene un Functor pero no deseamos comprometernos demasiado temprano con la
estructura de datos final. Por ejemplo, podemos crear un Coyoneda[ISet, ?]
(recuerde que ISet no tiene un Functor) para usar métodos que requieren un
Functor, y después convertir en una IList.
Si deseamos optimizar un programa con coyo o cocoyo tenemos que proporcionar el boilerplate esperada para cada álgebra:
def liftCoyo[F[_]](implicit I: Ast :<: F) = new Machines[Coyoneda[F, ?]] {
def getTime = Coyoneda.lift(I.inj(GetTime()))
...
}
def liftCocoyo[F[_]](implicit I: Ast :<: F) = new Machines[ContravariantCoyoneda[F, ?]] {
def getTime = ContravariantCoyoneda.lift(I.inj(GetTime()))
...
}
Una optimización que obtenemos al usar Coyoneda es la fusión de mapeos (y
fusión de contramapeos), lo que nos permite reescribir
xs.map(a).map(b).map(c)
en
xs.map(x => c(b(a(x))))
evitando representaciones intermedias. Por ejemplo, si xs es una List de mil
elementos, evitamos la creación de dos mil objetos porque sólo realizamos un
mapeo sobre la estructura de datos una sola vez.
Sin embargo, es mucho más fácil realizar este cambio en la función de manera
manual, o esperar a que el proyecto
scalaz-plugin sea liberado y que
realice automáticamente este tipo de optimizaciones.
7.5.4 Efectos extensibles
Los programas son simplemente datos: las estructuras libres hacen esto explícito y nos dan la habilidad de reordenar y optimizar estos datos.
Free es más especial de lo que aparente: puede secuenciar álgebras y
typeclasses arbitrarias.
Por ejemplo, está disponible una estructura libre para MonadState. Ast y
.liftF son más complicadas de lo usual debido a que tenemos que tomar en
cuenta el parámetro de tipo en MonadState, y la herencia a partir de Monad:
object MonadState {
sealed abstract class Ast[S, A]
final case class Get[S]() extends Ast[S, S]
final case class Put[S](s: S) extends Ast[S, Unit]
def liftF[F[_], S](implicit I: Ast[S, ?] :<: F) =
new MonadState[Free[F, ?], S] with BindRec[Free[F, ?]] {
def get = Free.liftF(I.inj(Get[S]()))
def put(s: S) = Free.liftF(I.inj(Put[S](s)))
val delegate = Free.freeMonad[F]
def point[A](a: =>A) = delegate.point(a)
...
}
...
}
Esto nos brinda la oportunidad de usar intérpretes optimizados. Por ejemplo,
podríamos almacenar la S en un campo atómico en lugar de construir un
trampolin StateT anidado.
¡Podríamos crear una Ast y un .liftF para casi cualquier álgebra o
typeclass! La única restricción es que la F[_] no aparezca como un parámetro
de alguna de las instrucciones, es decir, debe ser posible que el álgebra tenga
una instancia de Functor. Tristemente, esto descarta a MonadError y
Monoid.
La razón por la que las codificaciones libres no funcionan para toda las álgebras y typeclasses es realmente sutil.
Considere lo que sucede si creamos un Ast para MonadError, con F[_] en
posición contravariante, es dicir como un parámetro.
Cuando surja la necesidad de interpretar un programa que use MonadError.Ast
debemos construir el coproducto de instrucciones. Digamos que extendemos un
programa Drone:
¡El código anterior no compila debido a que Ast se refiere a sí mismo!
Las álgebras que no están hechas por completo de firmas de functores
covariantes, es decir, F[_] en posición de retorno, son imposibles de
interpretar debido a que el tipo resultante de este programa hace referencia
a sí mismo. De hecho el nombre álgebrahemos estado usando tiene sus raíces
en álgebras-F, donde la F es
debido a la palabra Functor.
Agradezco a Edmund Noble por iniciar esta discusión.
A medida que el AST de un programa libre crece, el rendimiento se degrada debido
a que el intérprete debe realizar un match sobre el conjunto de instrucciones
con un costo O(n). Una alternativa a scalaz.Coproduct es la codificación de
iotaz, que usa una estructura de datos
optimizada para realizar un despacho dinámico de costo O(1) (usando enteros
que son asignados a cada coproducto en tiempo de compilación).
Por razones históricas una AST libre para un álgebra o typeclass se conoce como
Codificación Inicial, y una implementación directa (por ejemplo, con IO) se
conoce como Sin Etiqueta Final. Aunque hemos explorado ideas interesantes con
Free, generalmente se acepta que Sin Etiqueta Final es superior. Pero para
poder usar el estilo de Sin Etiqueta Final, requerimos de un tipo para efectos
de alto rendimiento que proporcione todas las typeclasses que hemos cubierto en
este capítulo. También necesitaríamos ser capaces de ejecutar nuestro código
Applicative en paralelo. Esto es exactamente lo que estudiaremos a
continuación.
7.6 Parallel
Existen dos operaciones con efectos que casi siempre querremos ejecutar en paralelo:
- Realizar un
.mapsobre una colección de efectos, devolviendo un único efecto. Esto se consigue por medio de.traverse, que delega al método.apply2del efecto. - Ejecutar un número fijo de efectos con el operador de grito
|@|, y combinar sus salidas, de nuevo delegando al método.apply2.
Sin embargo, en la práctica, ninguna de estas operaciones se ejecutan en
paralelo por default. La razón es que si nuestra F[_] se implementa por una
Monad, entonces las leyes derivadas para los combinadores .apply2 deben
satisfacerse, las cuales dicen:
@typeclass trait Bind[F[_]] extends Apply[F] {
...
override def apply2[A, B, C](fa: =>F[A], fb: =>F[B])(f: (A, B) => C): F[C] =
bind(fa)(a => map(fb)(b => f(a, b)))
...
}
En otras palabras, Monad está explícitamente prohibido para ejecutar efectos
en paralelo.
Sin embargo, si tenemos una F[_] que no sea monádica, entonces puede
implementar .apply2 en paralelo. Podemos usar el mecanismo de (etiqueta) @@
para crear una instancia de Applicative para F[_] @@ Parallel, que de manera
conveniente se le asigna el alias de tipo Applicative.Par
object Applicative {
type Par[F[_]] = Applicative[λ[α => F[α] @@ Tags.Parallel]]
...
}
Los programas monádicos pueden entonces demandar un Par implícito además de su
Monad
def foo[F[_]: Monad: Applicative.Par]: F[Unit] = ...
La sintaxis de Traverse de Scalaz soporta paralelismo:
implicit class TraverseSyntax[F[_], A](self: F[A]) {
...
def parTraverse[G[_], B](f: A => G[B])(
implicit F: Traverse[F], G: Applicative.Par[G]
): G[F[B]] = Tag.unwrap(F.traverse(self)(a => Tag(f(a))))
}
Si el implícito Applicative.Par[IO] está dentro del alcance, podemos escoger
entre recorrer de manera secuencial o paralela:
val input: IList[String] = ...
def network(in: String): IO[Int] = ...
input.traverse(network): IO[IList[Int]] // one at a time
input.parTraverse(network): IO[IList[Int]] // all in parallel
De manera similar, podemos invocar .parApply o .parTupled después de usar
los operadores de grito
val fa: IO[String] = ...
val fb: IO[String] = ...
val fc: IO[String] = ...
(fa |@| fb).parTupled: IO[(String, String)]
(fa |@| fb |@| fc).parApply { case (a, b, c) => a + b + c }: IO[String]
Es digno de mención que cuando tenemos programas Applicative, tales como
def foo[F[_]: Applicative]: F[Unit] = ...
podemos usar F[A] @@ Parallel como nuestro contexto del programa y obtener
paralelismo como el default en .traverse y |@|. La conversión entre las
versiones normal y @@ Parallel de F[_] debe hacerse manualmente en el
código, lo que puede resultar doloroso. Por lo tanto, con frecuencia es más
simple demandar ambas formas de Applicative
def foo[F[_]: Applicative: Applicative.Par]: F[Unit] = ...
7.6.1 Rompiendo la ley
Podríamos tomar un enfoque aún más audaz para el paralelismo: salirnos de la ley
que demanda que .apply2 sea secuencial para Monad. Esto es altamente
controversial, pero funciona bien para la mayoría de las aplicaciones del mundo
real. Es necesario auditar nuestro código (incluyendo las dependencias de
terceros) para asegurarnos de que nada está haciendo uso de la ley implicada de
.apply2.
Envolvemos IO
final class MyIO[A](val io: IO[A]) extends AnyVal
y proporcionamos nuestra propia implementación de Monad que ejecute .apply2
en paralelo al delegar a la instancia @@ Parallel
object MyIO {
implicit val monad: Monad[MyIO] = new Monad[MyIO] {
override def apply2[A, B, C](fa: MyIO[A], fb: MyIO[B])(f: (A, B) => C): MyIO[C] =
Applicative[IO.Par].apply2(fa.io, fb.io)(f)
...
}
}
Ahora es posible usar MyIO como nuestro contexto de la aplicación en lugar de
IO, y obtener paralelismo por default.