5. Scalaz Typeclasses
En este capítulo tendremos un tour de la mayoría de las typeclasses en scalaz-core. No usamos
todas en drone-dynamic-agents de modo que daremos ejemplos standalone cuando sea apropiado.
Ha habido críticas con respecto a los nombres usados en Scalaz, y en la programación funcional en
general. La mayoría de los nombres siguen las convenciones introducidas en el lenguaje de
programación funcional Haskell, basándose en la Teoría de las Categorías. Siéntase libre de crear
type aliases si los verbos basados en la funcionalidad primaria son más fáciles de recordar cuando
esté aprendiendo (por ejemplo, Mappable, Pureable, FlatMappable).
Antes de introducir la jerarquía de typeclasses, echaremos un vistazo a los cuatro métodos más importantes desde una perspectiva de control de flujo: los métodos que usaremos más en las aplicaciones típicas de PF:
| Typeclass | Method | Desde | Dado | Hacia |
|---|---|---|---|---|
Functor |
map |
F[A] |
A => B |
F[B] |
Applicative |
pure |
A |
F[A] |
|
Monad |
flatMap |
F[A] |
A => F[B] |
F[B] |
Traverse |
sequence |
F[G[A]] |
G[F[A]] |
Sabemos que las operaciones que regresan un F[_] pueden ejecutarse secuencialmente en una for
comprehension mediante .flatMap definida en su Monad[F]. El contexto F[_] puede considerarse
como un contenedor para un efecto intencional que tiene una A como la salida: flatMap nos
permite generar nuevos efectos F[B] en tiempo de ejecución basándose en los resultados de evaluar
efectos previos.
Por supuesto, no todos los constructores de tipo F[_] tienen efectos, incluso si tienen una
Monad[_]. Con frecuencia son estructuras de datos. Mediante el uso de la abstracción menos
específica, podemos reusar código para List, Either, Future y más.
Si únicamente necesitamos transformar la salida de un F[_], esto simplemente es un map,
introducido por Functor. En el capítulo 3, ejecutamos efectos en paralelo mediante la creación de
un producto y realizando un mapeo sobre ellos. En programación funcional, los cómputos
paralelizables son considerados menos poderosos que los secuenciales.
Entre Monad y Functor se encuentra Applicative, que define pure que nos permite alzar un
valor en un efecto, o la creación de una estructura de datos a partir de un único valor.
.sequence es útil para rearreglar constructores de tipo. Si tenemos un F[G[_]] pero requerimos
un G[F[_]], por ejemplo, List[Future[Int]] pero requerimos un Future[List[_]], entonces
ocupamos .sequence.
5.1 Agenda
Este capítulo es más largo de lo usual y está repleto de información: es perfectamente razonable abordarlo en varias sesiones de estudio. Recordar todo requeriría poderes sobrehumanos, de modo que trate este capítulo como una manera de buscar más información.
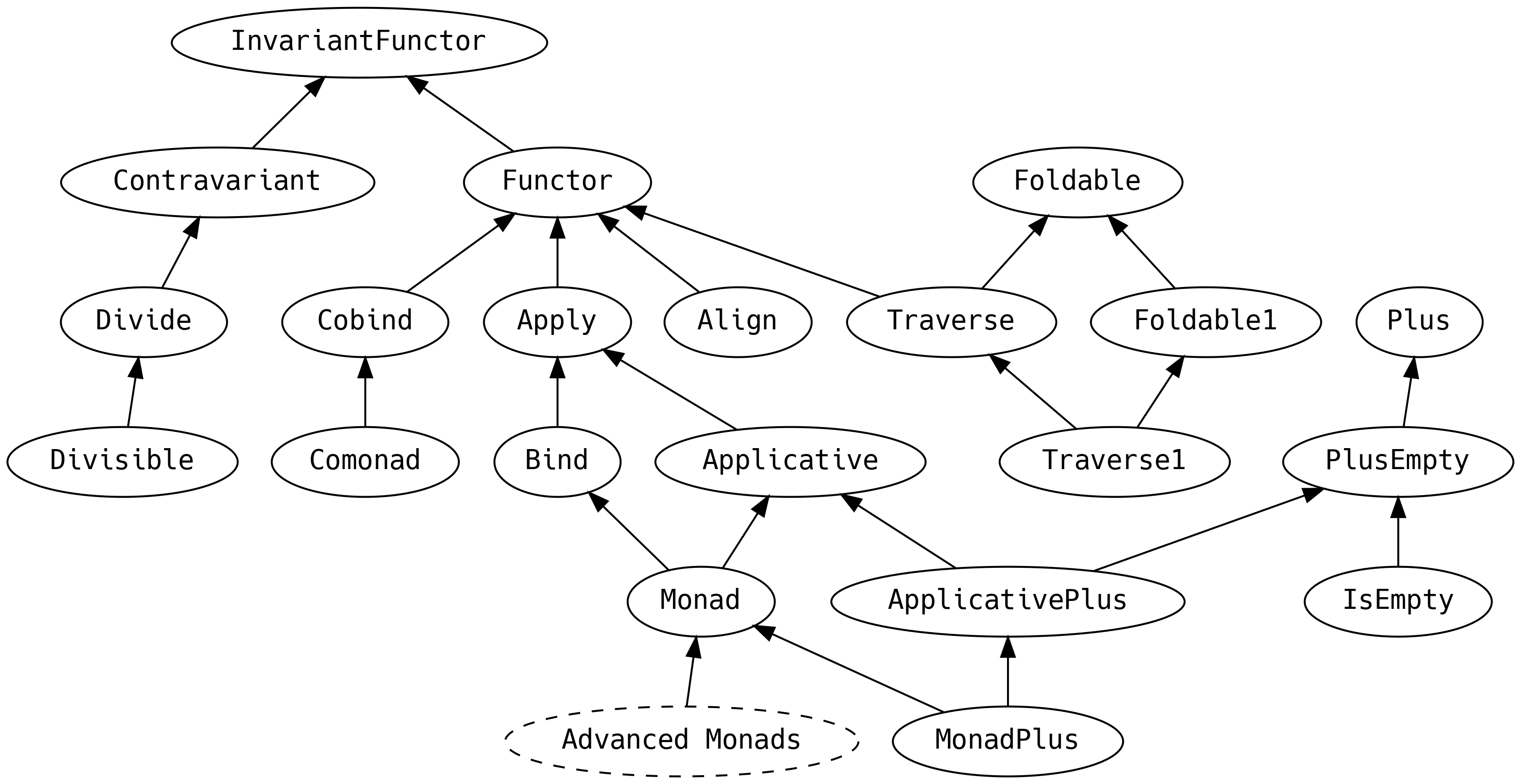
Es notable la ausencia de typeclasses que extienden Monad. Estas tendrán su propio capítulo más
adelante.
Scalaz usa generación de código, no simulacrum. Sin embargo, por brevedad, presentaremos los
fragmentos de código con @typeclass. La sintaxis equiovalente estará disponible cuando hagamos un
import scalaz._, Scalaz._ y estará disponible en el paquete scalaz.syntax en el código fuente de
scalaz.
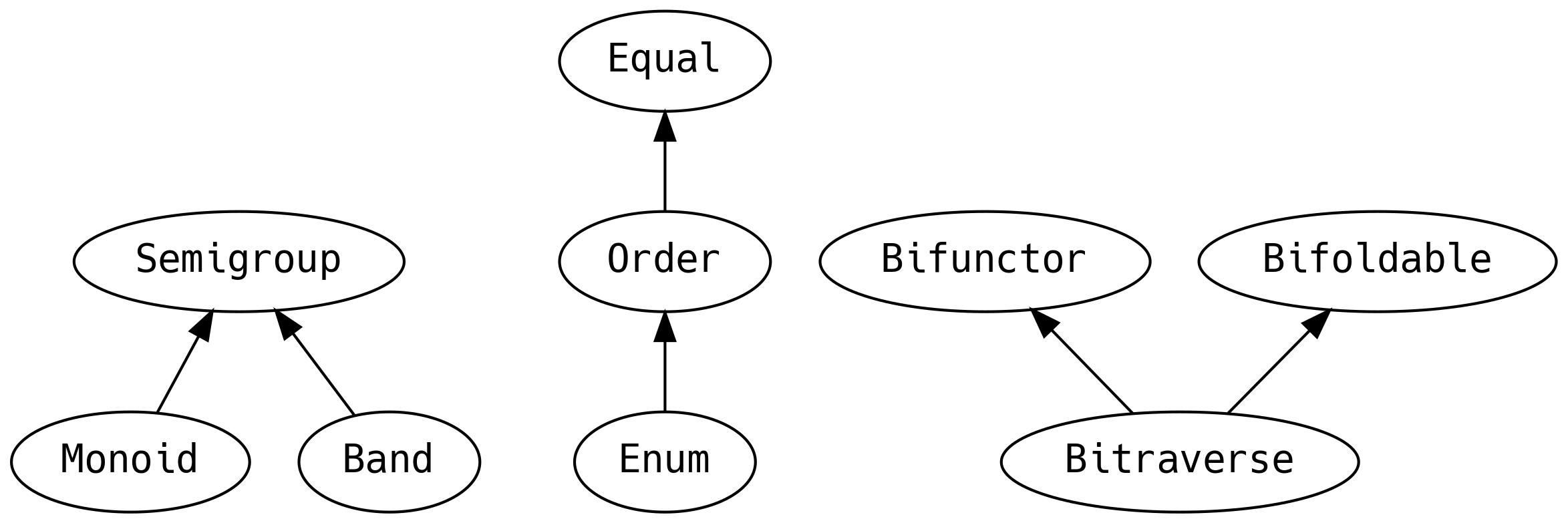

5.2 Cosas que pueden agregarse
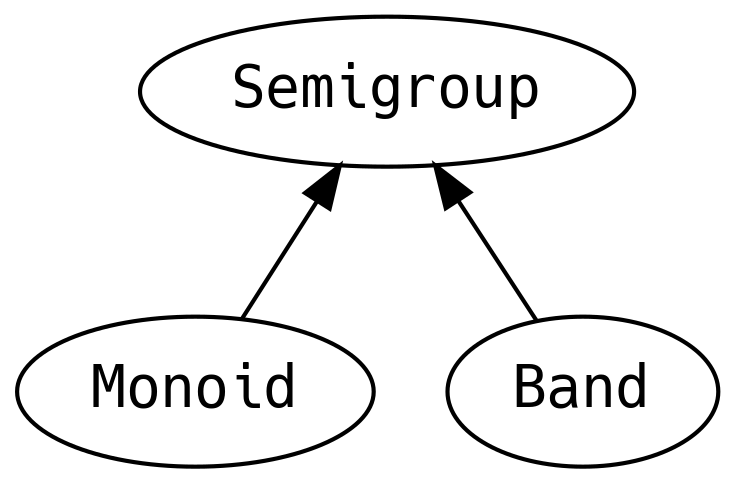
Un Semigroup puede definirse para un tipo si dos valores pueden combinarse. El operador debe ser
asociativo, es decir, que el orden de las operaciones anidadas no debería importar, es decir
Un Monoid es un Semigroup con un elemento zero (también llamado empty –vacío– o identity
–identidad–). Combinar zero con cualquier otra a debería dar otra a .
Esto probablemente le traiga memorias sobre Numeric del capítulo 4. Existen implementaciones de
Monoid para todos los tipos numéricos primitivos, pero el concepto de cosas que se pueden
agregar es útil más allá de los números.
Band tiene la ley de que la operación append de dos elementos iguales es idempotente, es decir
devuelve el mismo valor. Ejemplos de esto pueden ser cualesquier cosa que sólo pueda tener un valor,
tales como Unit, los límites superiores más pequeños, o un Set (conjunto). Band no proporciona
métodos adicionales y sin embargo los usuarios pueden aprovechar las garantías que brinda con fines
de optimización del rendimiento.
Como un ejemplo realista de Monoid, considere un sistema de comercio que tenga una base de datos
grande de plantillas de transacciones comerciales reusables. Llenar las plantillas por default para
una nueva transacción implica la selección y combinación de múltiples plantillas, con la regla del
“último gana” para realizar uniones si dos plantillas proporcionan un valor para el mismo campo. El
trabajo de “seleccionar” trabajo ya se realiza por nosotros mediante otro sistema, es nuestro
trabajo combinar las plantillas en orden.
Crearemos un esquema simple de plantillas para demostrar el principio, pero tenga en mente que un sistema realista tendría un ADT más complicado.
Si escribimos un método que tome templates: List[TradeTemplate], entonces necesitaremos llamar
únicamente
¡y nuestro trabajo está hecho!
Pero para poder usar zero o invocar |+| debemos tener una instancia de Monoid[TradeTemplate].
Aunque derivaremos genéricamente este en un capítulo posterior, por ahora crearemos la instancia en
el companion:
Sin embargo, esto no hace lo que queremos porque Monoid[Option[A]] realizará una agregación de su
contenido, por ejemplo,
mientras que deseamos implementar la regla del “último gana”. Podríamos hacer un override del valor
default Monoid[Option[A]] con el nuestro propio:
Ahora todo compila, de modo que si lo intentamos…
Todo lo que tuvimos que hacer fue implementar una pieza de lógica de negocios y, !el Monoid se
encargó de todo por nosotros!
Note que la lista de payments se concatenó. Esto es debido a que el Monoid[List] por default usa
concatenación de elementos y simplemente ocurre que este es el comportamiento deseado aquí. Si el
requerimiento de negocios fuera distinto, la solución sería proporcionar un
Monoid[List[LocalDate]] personalizado. Recuerde del capítulo 4 que con el polimorfismo de tiempo
de compilación tenemos una implementacion distinta de append dependiendo de la E en List[E],
no sólo de la clase de tiempo de ejecución List.
5.3 Cosas parecidas a objetos
En el capítulo sobre Datos y Funcionalidad dijimos que la noción de la JVM de igualdad se derrumba
para muchas cosas que podemos poner en una ADT. El problema es que la JVM fue diseñada para Java, y
equals está definido sobre java.lang.Object aunque esto tenga sentido o no. No existe manera de
remover equals y no hay forma de garantizar que esté implementado.
Sin embargo, en PF preferimos el uso de typeclasses para tener funcionalidad polimórfica e incluso el concepto de igualdad es capturado en tiempo de compilación.
En verdad === (triple igual) es más seguro desde la perspectiva de tipos que ==(doble igual)
porque únicamente puede compilarse cuando los tipos son los mismos en ambos lados de la comparación.
Esto atrapa muchos errores.
equal tiene los mismos requisitos de implementación que Object.equals
-
conmutativo
f1 === f2implicaf2 === f1 -
reflexivo
f === f -
transitivo
f1 === f2 && f2 === f3implica quef1 === f3
Al desechar el concepto universal de Object.equals no damos por sentado el concepto de igualdad
cuando construimos un ADT, y nos detiene en tiempo de compilación de esperar igualdad cuando en
realidad no existe tal.
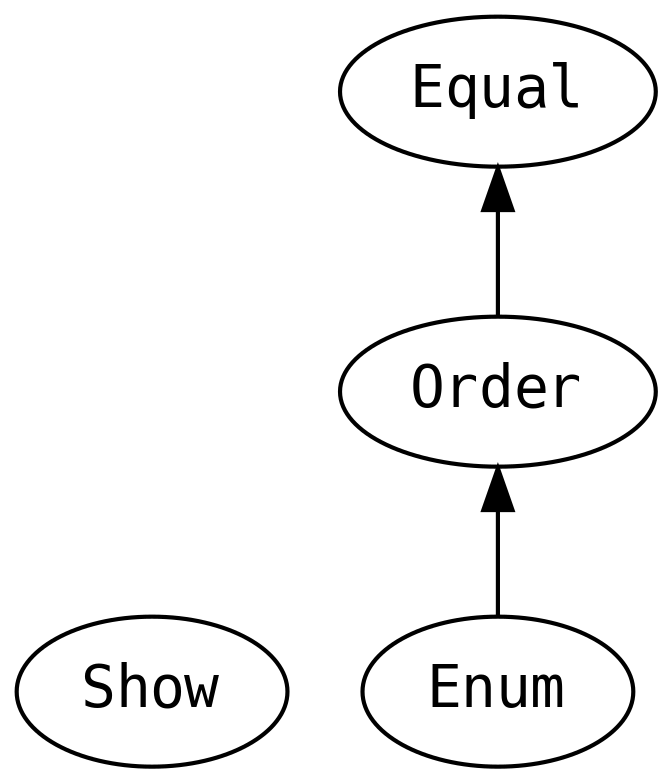
Continuando con la tendencia de reemplazar conceptos viejos de Java, más bien que considerar que los
datos son un java.lang.Comparable, ahora tienen un Order de acuerdo con
Order implementa .equal en términos de la primitiva nueva .order. Cuando una typeclass
implementa el combinador primitivo de su padre con un combinador derivado, se agrega una
ley implicación de sustitución para el typeclass. Si una instancia de Order fuera a hacer un
override de .equal por razones de desempeño, debería comportase de manera idéntica a la original.
Las cosas que tienen un orden también podrían ser discretas, permitiéndonos avanzar o retroceder hacia un sucesor o predecesor:
Discutiremos EphemeralStream en el siguiente capítulo, por ahora sólo necesitamos saber que se
trata de una estructura de datos potencialmente infinita que evita los problemas de retención de
memoria en el tipo Stream de la librería estándar.
De manera similar a Object.equals, el concepto de .toString en toda clases no tiene sentido en
Java. Nos gustaría hacer cumplir el concepto de “poder representar como cadena” en tiempo de
compilación y esto es exactamente lo que se consigue con Show:
Exploraremos Cord con más detalle en el capítulo que trate los tipos de datos, por ahora sólo
necesitamos saber que es una estructura de datos eficiente para el almacenamiento y manipulación de
String.
5.4 Cosas que se pueden mapear o transformar
Ahora nos enfocamos en las cosas que pueden mapearse, o recorrerse, en cierto sentido:
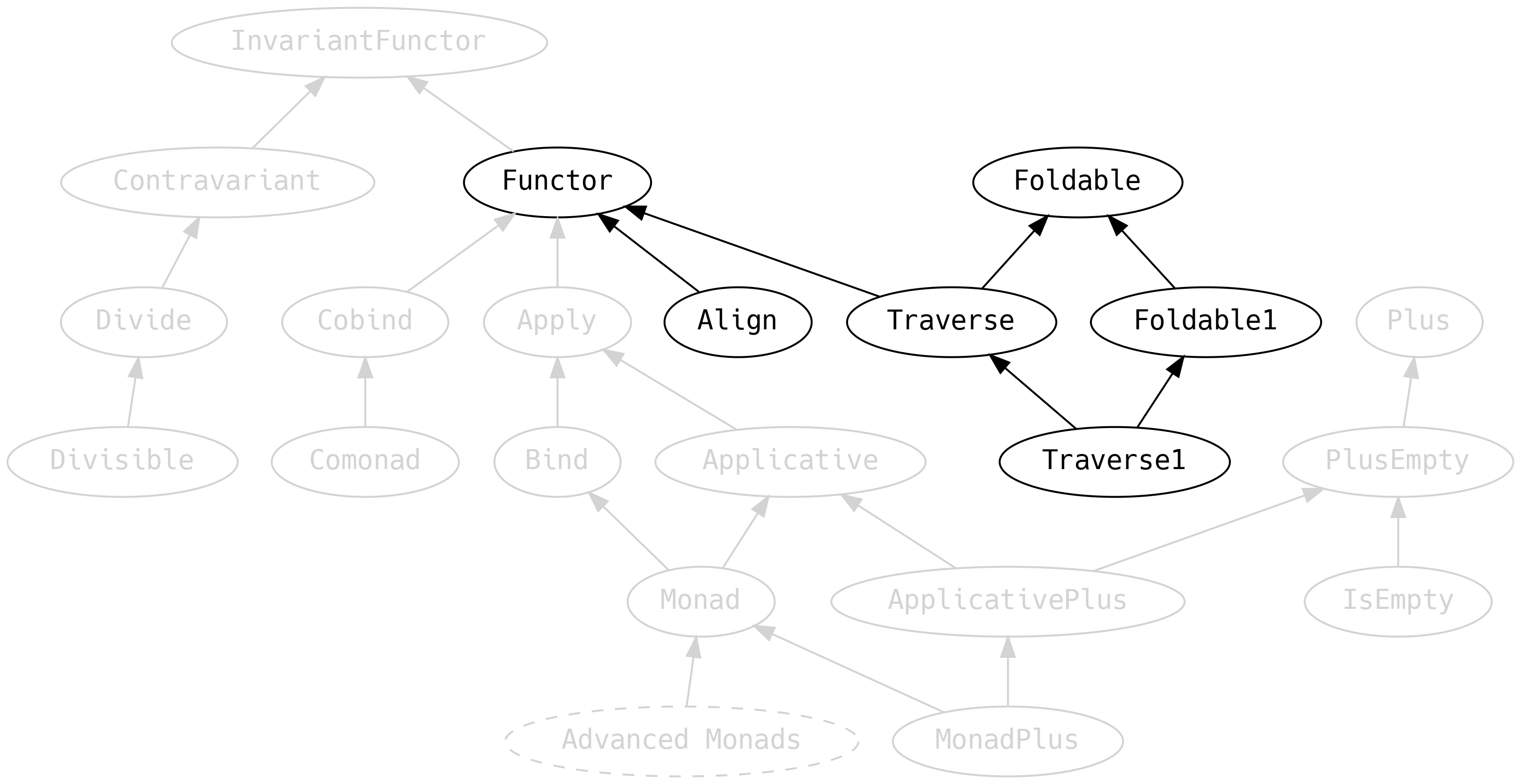
5.4.1 Functor
El único método abstracto es map, y debe ser posible hacer una composición, es decir, mapear con
una f y entonces nuevamente con una g es lo mismo que hacer un mapeo una única vez con la
composición de f y g:
El map también debe realizar una operación nula si la función provista es la identidad (es decir,
x => x)
Functor define algunos métodos convenientes alrededor de map que pueden optimizarse para algunas
instancias específicas. La documentación ha sido intencionalmente omitida en las definiciones arriba
para incentivar el análisis de lo que hace un método antes de que vea la implementación. Por favor,
deténgase unos momentos estudiando únicamente las signaturas de tipo de los siguientes métodos antes
de avanzar más:
-
voidtoma una instancia deF[A]y siempre devuelve unF[Unit], y se olvida de todos los valores a la vez que preserva la estructura. -
fproducttoma la misma entrada quemappero devuelveF[(A, B)], es decir, devuelve el contenido dentro de una tupla, con el resultado obtenido al aplicar la función. Esto es útil cuando deseamos retener la entrada. -
fpairrepite todos los elementos deAen una tuplaF[(A, A)] -
strengthLempareja el contenido de unaF[B]con una constanteAa la izquierda. -
strenghtRempareja el contenido de unaF[A]con una constanteBa la derecha. -
lifttoma una funciónA => By devuelve unaF[A] => F[B]. En otras palabras, toma una función del contenido de unaF[A]y devuelve una función que opera en elF[A]directamente. -
mapplynos obliga a pensar un poco. Digamos que tenemos unaF[_]de funcionesA => By el valorA, entonces podemos obtener unF[B]. Tiene una firma/signatura similar a la depurepero requiere que el que hace la llamada proporcioneF[A => B].
fpair, strenghL y strengthR tal vez parezcan inútiles, pero mostrarán su utilidad cuando
deseemos retener algo de información que de otra manera se perdería en el ámbito.
Functor tiene una sintaxis especial:
.as y >| es una forma de reemplazar la salida con una constante.
En nuestra aplicación de ejemplo, como un hack espantoso (que no admitimos hasta ahora), definimos
start y stop de modo que devolvieran su entrada:
Esto nos permitió escribir lógica breve de negocios como
y
pero este hack nos obliga a poner complejidad innecesaria en las implementaciones. Es mejor si
dejamos que nuestras álgebras regresen F[Unit] y usar as:
y
5.4.2 Foldable
Técnicamente, Foldable es para estructuras de datos que pueden recorrerse y producir un valor que
las resuma. Sin embargo, esto no dice lo suficiente sobre el hecho de que se trata de un arma
poderosa proporcionada por las typeclasses que nos puede proporcionar la mayoría de lo que esperamos
ver en una API de colecciones.
Hay tantos métodos que necesitaremos revisarlos en partes, empezando con los métodos abstractos:
Una instancia de Foldable necesita implementar únicamente foldMap y foldRight para obtener
toda la funcionalidad en esta typeclass, aunque los métodos están típicamente optimizqados para
estructuras de datos específicas.
.foldMap tiene un nombre usado en mercadotecnia: MapReduce. Dada una F[A], una función de
A a B, y una forma de combinar una B (proporcionada por el Monoid, junto con el zero B),
podemos producir el valor resumen de tipo B. No existe un orden impuesto en las operaciones,
permitiendonos realizar cómputos paralelos.
foldRight no requiere que sus parámetros tengan un Monoid, significando esto que necesita un
valor inicial z y una manera de combinar cada elemento de la estructura de datos con el valor
resumen. El orden en el que se recorren los elementos es de derecha a izquierda y es por esta razón
que no puede paralelizarse.
foldLeft recorre los elementos de izquierda a derecha. foldLeft puede implementarse en términos
de foldMap, pero la mayoría de las instancias escogen implementarlas porque se trata de una
operación básica. Dado que normalmente se implementa con recursión de cola, no existen parámetros
byname.
La única ley para Foldable es que foldLeft y foldRight deberían ser consistentes con foldMap
para operaciones monoidales, por ejemplo, agregando un elemento a una lista para foldLeft y
anteponiendo un elemento a la lista para foldRight. Sin embargo, foldLeft y foldRight no
necesitan ser consistentes la una con la otra: de hecho con frecuencia producen el inverso que
produce el otro.
La cosa más sencilla que se puede hacer con foldMap es usar la función identity (identidad),
proporcionando fold (la suma natural de los elementos monoidales), con variantes derecha/izquierda
para permitirnos escoger basándonos en criterios de rendimiento:
Recuerde que cuando aprendimos sobre Monoid, escribimos lo siguiente:
Sabemos que esto es tonto y que pudimos escribir:
.fold no funciona en la List estándar debido a que ya tiene un método llamado fold que hace
su propia cosa a su manera especial.
El método llamado de manera extraña intercalate inserta una A específica entre cada elemento
antes de realizar el fold
que es una versión generalizada del método de la librería estándar mkString:
El foldLeft proporciona el medio para obtener cualquier elemento mediante un índice para recorrer
la estructura, incluyendo un grupo grande de métodos relacionados:
Scalaz es una librería funcional pura que tiene únicamente funciones totales. Mientras que
List(0) puede lanzar excepciones, Foldable.index devuelve una Option[A] con el método
conveniente .indexOr regreseando una A cuando se proporciona un valor por default. .element es
similar al método de la librería estándar .contains pero usa Equal más bien que la mal definida
igualdad de la JVM.
Estos métods realmente suenan como una API de colecciones. Y, por supuesto, toda cosa con una
instancia de Foldable puede convertirse en una List
También existen conversiones a otros tipos de datos de la librería estándar de Scala y de Scalaz,
tales como .toSet, .toVector, .toStream, .to[T <: TraversableLike], toIList y la lista
continúa.
Existen verificadores de predicados útiles
filterLenght es una forma de contar cuántos elementos son true para el predicado, all y any\
devuelven true is todos (o algún) elemento cumple con el predicado, y pueden terminar de manera
temprana.
Ya hemos visto la NonEmptyList en capítulos anteriores. Con el propósito de ser breves usaremos
el type alias Nel en lugar de NonEmptyList.
También hemos visto IList en capítulos anteriores, recuerde que se trata de una alternativa a
la List de la librería estándar cuyos métodos impuros, como apply, han sido removidos.
Podemos dividir en partes una F[A] que resulten en la misma B con splitBy
por ejemplo
haciendo la observación de que sólamente existen dos valores indexados por 'b'.
splitByRelation evita la necesidad de tener una Equal pero debemos proporcionar el operador de
comparación.
splitWith divide los elementos en grupos que alternativamente satisfacen y no el predicado.
selectSplit selecciona grupos de elementos que satisfacen el predicado, descartando los otros.
Este es uno de esos casos raros en donde dos métodos comparten la misma firma/signatura, pero tienen
significados distintos.
findLeft y findRight sirven para extraer el primer elemento (de la izquierda o de la derecha)
que cumpla un predicado.
Haciendo uso adicional de Equal y Order, tenemos métodos distinct que devuelven agrupaciones.
distinct se implementa de manera más eficiente que distinctE debido a que puede usar el
ordenamiento y por lo tanto usar un algoritmo tipo quicksort que es mucho más rápido que la
implementación ingenua de List.distinct. Las estructuras de datos (tales como los conjuntos)
pueden implementar distinct y su Foldable sin realizar ningún trabajo.
distinctBy permite la agrupación mediante la aplicación de una función a sus elementos. Por
ejemplo, agrupar nombres por su letra inicial.
Podemos hacer uso adicional de Order al extraer el elemento mínimo o máximo (o ambos extremos)
incluyendo variaciones usando el patrón Of o By para mapear primero a otro tipo o usar un tipo
diferente para hacer la otra comparación.
Por ejemplo podríamos preguntar cuál String es máxima By (por) longitud, o cuál es la máxima
longitud Of (de) los elementos.
Esto concluye con las características clave de Foldable. El punto clave a recordar es que
cualquier cosa que esperaríamos encontrar en una librearía de colecciones está probablemente en
Foldable y si no está ahí, probablemente debería estarlo.
Concluiremos con algunas variantes de los métodos que ya hemos visto. Primero, existen métodos que
toman un Semigroup en lugar de un Monoid:
devolviendo Option para tomar encuenta las estructuras de datos vacías (recuerde que Semigroup
no tiene un zero).
Los métodos se leen como una-Opción, y no 10 pt com en la tipografía.
La typeclass Foldable1 contiene muchas más variantes usando Semigroup de los métodos que usan
Monoid mostrados aquí (todos ellos con el sufijo 1) y tienen sentido para estructuras de datos
que nunca están vacías, sin requerrir la existencia de un Monoid para los elementos.
De manera importante, existen variantes que toman valores de retorno monádicos. Ya hemos usado
foldLeft cuando escribimos por primera vez la lógica de negocios de nuestra aplicación, ahora
sabemos que proviene de Foldable:
5.4.3 Traverse
Traverse es lo que sucede cuando hacemos el cruce de un Functor con un Foldable
Al principio del capítulo mostramos la importancia de traverse y sequence para invertir los
constructores de tipo para que se ajusten a un requerimiento (por ejemplo, de List[Future[_]] a
Future[List[_]]).
En Foldable no fuimos capaces de asumir que reverse fuera un concepto universal, pero ahora
podemos invertir algo.
También podemos hacer un zip de dos cosas que tengan un Traverse, obteniendo un None cuando
uno de los dos lados se queda sin elementos, usando zipL o zipR para decidir cuál lado truncar
cuando las longitudes no empatan. Un caso especial de zip es agregar un índice a cada entrada con
indexed.
zipWithL y zipWithR permiten la combinación de dos lados de un zip en un nuevo tipo, y
entonces devuelven simplemente un F[C].
mapAccumL y mapAccumR son map regular combinado con un acumulador. Si nos topamos con la
situación de que nuestra costumbre vieja proveniente de Java nos quiere hacer usar una var, y
deseamos referirnos a ella en un map, deberíamos estar usando mapAccumL.
Por ejemplo, digamos que tenemos una lista de palabras y que deseamos borrar las palabras que ya hemos encontrado. El algoritmo de filtrado no permite procesar las palabras de la lista una segunda vez de modo que pueda escalarse a un stream infinito:
Finalmente Traversable1, como Foldable1, proporciona variantes de estos métodos para las
estructuras de datos que no pueden estar vacías, aceptando Semigroup (más débil) en lugar de un
Monoid, y un Apply en lugar de un Applicative. Recuerde que Semigroup no tiene que
proporcionar un .empty, y Apply no tiene que proporcionar un .point.
5.4.4 Align
Align es sobre unir y rellenar algo con un Functor. Antes de revisar Align, conozca al tipo de
datos \&/ (pronunciado como These, o ¡Viva!).
es decir, se trata de una codificación con datos de un OR lógico inclusivo. A o B o ambos A
y B.
alignWith toma una función de ya sea una A o una B (o ambos) a una C y devuelve una función
alzada de una tupla de F[A] y F[B] a una F[C]. align construye \&/ a partir de dos F[_].
merge nos permite combinar dos F[A] cuando A tiene un Semigroup. Por ejemplo, la
implementación de Semigroup[Map[K, V]] delega a un Semigroup[V], combinando dos entradas de
resultados en la combinación de sus valores, teniendo la consecuencia de que Map[K, List[A]] se
comporta como un multimapa:
y un Map[K, Int] simplemente totaliza sus contenidos cuando hace la unión
.pad y .padWith son para realizar una unión parcial de dos estructuras de datos que puedieran
tener valores faltantes en uno de los lados. Por ejemplo si desearamos agregar votos independientes
y retener el conocimiento de donde vinieron los votos
Existen variantes convenientes de align que se aprovechan de la estructura de \&/
las cuáles deberían tener sentido a partir de las firmas/signaturas de tipo. Ejemplos:
Note que las variantes A y B usan OR inclusivo, mientras que las variantes This y That son
exclusivas, devolviendo None si existe un valor en ambos lados, o ningún valor en algún lado.
5.5 Variancia
Debemos regresar a Functor por un momento y discutir un ancestro que previamente habíamos
ignorado:
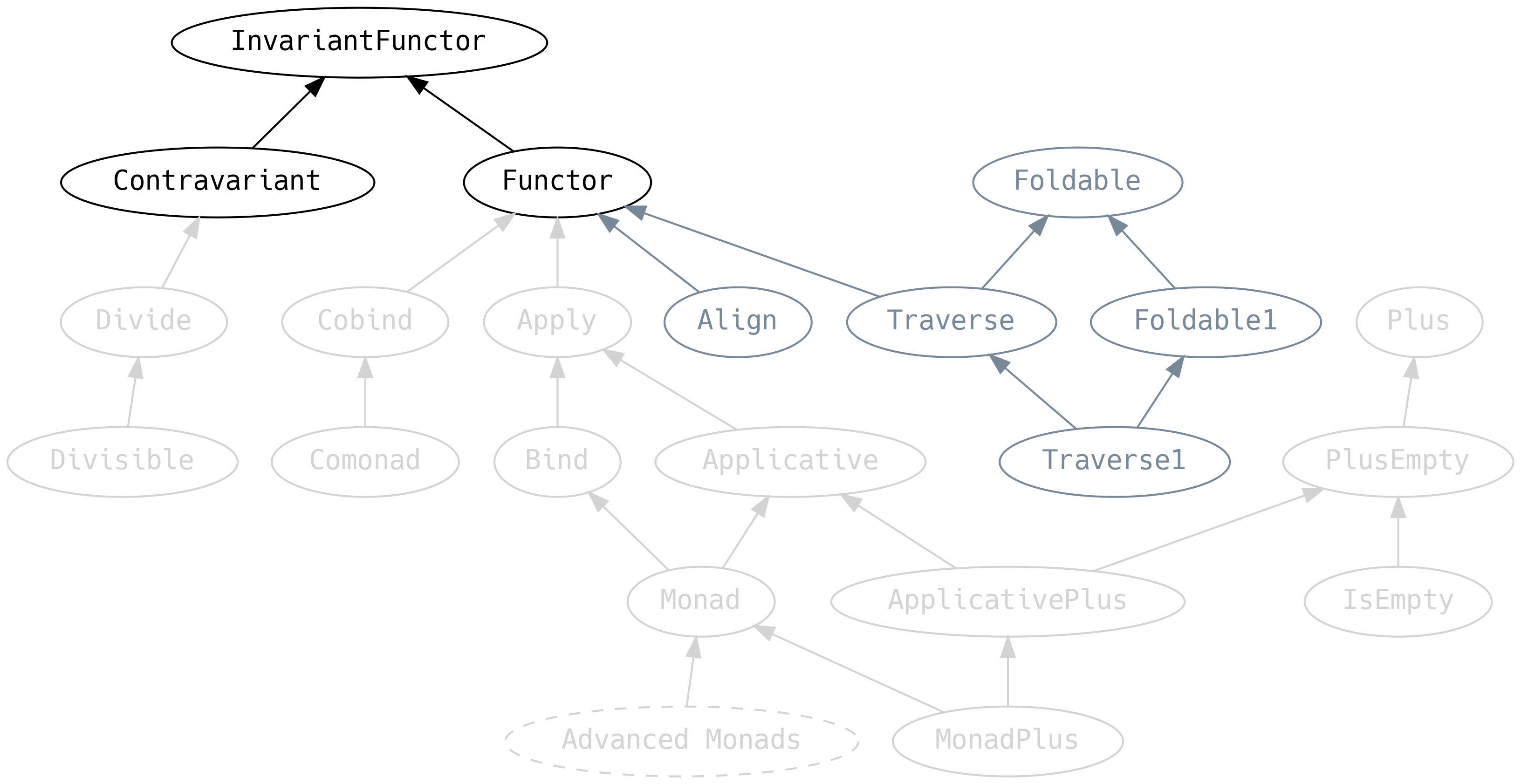
InvariantFunctor, también conocido como el functor exponencial, tiene un método xmap que dice
que dada una función de A a B, y una función de B a A, podemos entonces convertir F[A] a
F[B].
Functor es una abreviación de lo que deberíamos llamar functor covariante. Pero dado que
Functor es tan popular este conserva la abreviación. De manera similar, Contravariant debería
ser llamado functor contravariante.
Functor implementa xmap con map e ignora la función de B a A. Contravariant, por otra
parte, implementa xmap con contramap e ignora la función de A a B:
Es importante notar que, aunque están relacionados a nivel teórico, las palabras covariante,
contravariante e invariante no se refieren directamente a la variancia de tipos en Scala (es
decir, con los prefijos + y - que pudieran escribirse en las firmas/signaturas de los tipos).
Invariancia aquí significa que es posible mapear el contenido de la estructura F[A] en F[B].
Usando la función identidad (identity) podemos ver que A puede convertirse de manera segura en
una B dependiendo de la variancia del functor.
.map puede entenderse por medio del contrato “si me das una F de A y una forma de convertir
una B en una A, entonces puedo darte una F de B”.
Consideraremos un ejemplo: en nuestra aplicación introducimos tipos específicos del dominio Alpha,
Beta, Gamma, etc, para asegurar que no estemos mezclando números en un cálculo financiero:
pero ahora nos encontramos con el problema de que no tenemos ninguna typeclass para estos nuevos
tipos. Si usamos los valores en los documentos JSON, entonces tenemos que escribir instancias de
JsEncoder y JsDecoder.
Sin embargo, JsEncoder tiene un Contravariant y JsDecoder tiene un Functor, de modo que es
posible derivar instancias. Llenando el contrato:
- “si me das un
JsDecoderpara unDouble, y una manera de ir de unDoublea unAlpha, entonces yo puedo darte unJsDecoderpara unAlpha”. - “si me das un
JsEncoderpar unDouble, y una manera de ir de unAlphaa unDouble, entonces yo puedo darte unJsEncoderpara unAlpha”.
Los métodos en una typeclass pueden tener sus parámetros de tipo en posición contravariante
(parámetros de método) o en posición covariante (tipo de retorno). Si una typeclass tiene una
combinación de posiciones covariantes y contravariantes, tal vez también tenga un
functor invariante. Por ejemplo, Semigroup y Monoid tienen un InvariantFunctor, pero no un
Functor o un Contravariant.
5.6 Apply y Bind
Considere ésto un calentamiento para Applicative y Monad
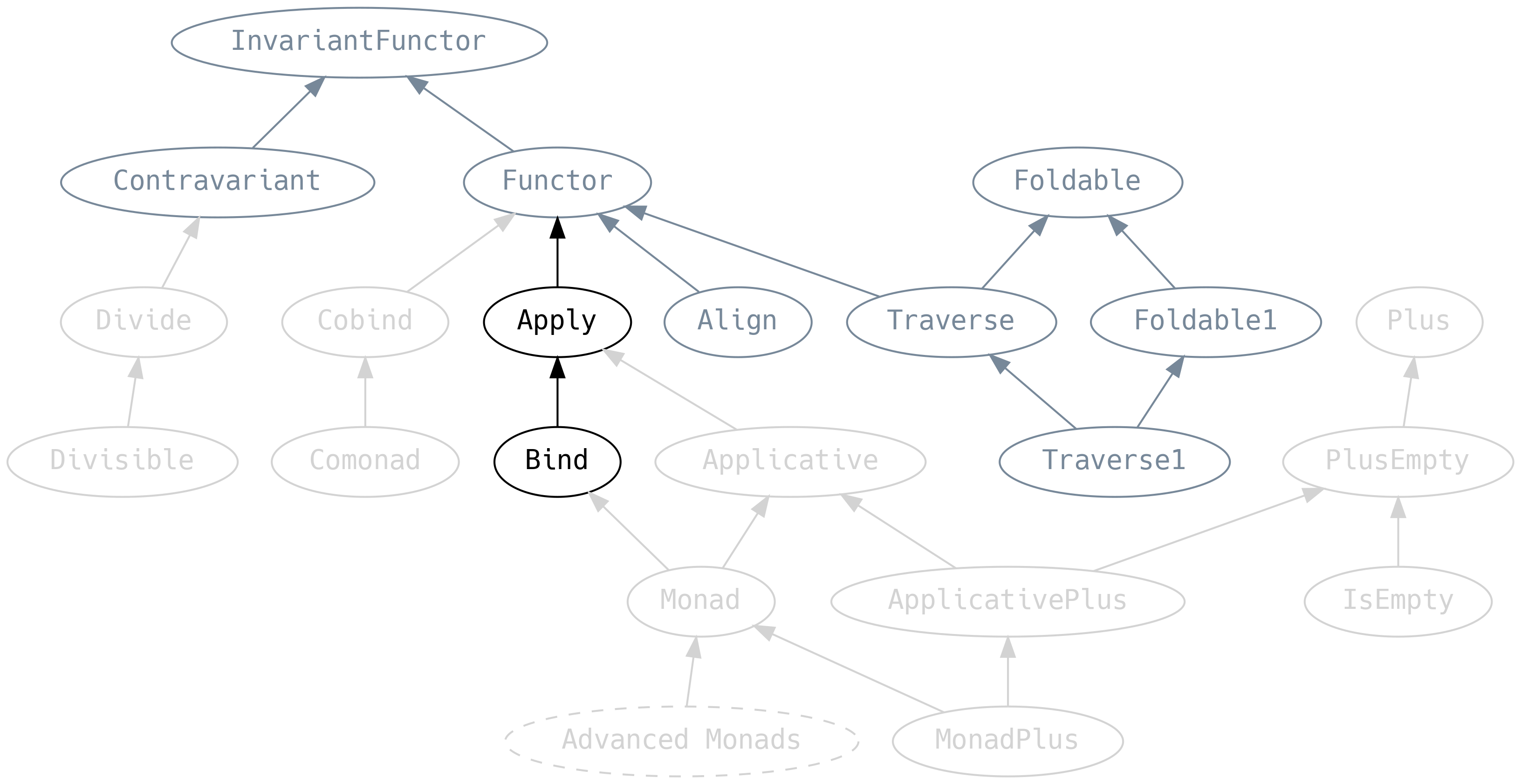
5.6.1 Apply
Apply extiende Functor al agregar un método llamado ap que es similar a map en el sentido de
que aplica una función a valores. Sin embargo, con ap, la función está en el mismo contexto que
los valores.
<*> es el operador Avanzado TIE Fighter, como lo usaría Darth Vader. Es apropiado dado que
parece como un padre enojado.
Vale la pena tomarse un momento y considerar lo que significa para una estructura de datos simple
como Option[A], el que tenga la siguiente implementación de .ap
Para implementar .ap primero debemos extraer la función ff: A => B de f: Option[A => B], y
entonces podemos mapear sobre fa. La extracción de la función a partir del contexto es el poder
importante que Apply tiene, permitiendo que múltiples funciones se combinen dentro del contexto.
Regresanto a Apply, encontramos la función auxiliar .applyX que nos permite combinar funciones
paralelas y entonces mapear sobre la salida combinada:
Lea .apply2 como un contrato con la promesa siguiente: “si usted me da una F de A y una F de
B, con una forma de combinar A y B en una C, entonces puedo devolverle una F de C”.
Existen muchos casos de uso para este contrato y los dos más importantes son:
- construir algunas typeclasses para el tipo producto
Ca partir de sus constituyentesAyB - ejecutar efectos en paralelo, como en las álgebras del drone y de google que creamos en el Capítulo 3, y entonces combinando sus resultados.
En verdad, Apply es tan útil que tiene una sintáxis especial:
que es exactamente lo que se usó en el Capítulo 3:
El operador |@| tiene muchos nombres. Algunos lo llaman la sintaxis de producto cartesiano,
otros lo llaman el panecillo de canela, el Almirante Ackbar o el Macaulay Culkin.
preferimos llamarlo operador El grito, en honor a la pintura de Munch, debido a que también
es el sonido que nuestro CPU hace cuando está paralelizando Todas las Cosas.
La sintaxis <*y *> (el ave hacia la izquierda y hacia la derecha) ofrece una manera conveniente
de ignorar la salida de uno de dos efectos paralelos.
Desgraciadamente, aunque la syntaxis con |@| es clara, hay un problema pues se crea un nuevo
objeto de tipo ApplicativeBuilder por cada efecto adicional. Si el trabajo es principalmente de
naturaleza I/O, el costo de la asignación de memoria es insignificante. Sin embargo, cuando el
trabajo es mayormente de naturaleza computacional, es preferible usar la sintaxis alternativa
de alzamiento con aridad, que no produce ningún objeto intermedio:
y se usa así:
o haga una invocación directa de `applyX
A pesar de ser más común su uso con efectos, Applyfunciona también con estructuras de datos.
Considere reescribir
como
Si nosotros deseamos únicamente la salida combinada como una tupla, existen métodos para hacer sólo eso:
Existen también versiones generalizadas de ap para más de dos parámetros:
junto con métodos .lift que toman funciones normales y las alzan al contexto F[_], la
generalización de Functor.lift
y .apF, una sintáxis parcialmente aplicada para ap
Finalmente .forever
que repite el efecto sin detenerse. La instancia de Apply debe tener un uso seguro del stack o
tendremos StackOverflowError.
5.6.2 Bind
Bind introduces .bind, que es un sinónimo de .flatMap, que permite funciones sobre el
resultado de un efecto regresar un nuevo efecto, o para funciones sobre los valores de una
estructura de datos devolver nuevas estructuras de datos que entonces son unidas.
El método .join debe ser familiar a los usuarios de .flatten en la librería estándar, y toma un
contexto anidado y lo convierte en uno sólo.
Combinadores derivados se introducen para .ap y .apply2 que requieren consistencia con .bind.
Veremos más adelante que esta ley tiene consecuencias para las estrategias de paralelización.
mproduct es como Functor.fproduct y empareja la entrada de una función con su salida, dentro de
F.
ifM es una forma de construir una estructura de datos o efecto condicional:
ifM y ap están optimizados para crear un cache y reusar las ramas de código, compare a la forma
más larga
que produce una nueva List(0) o List(1, 1) cada vez que se invoca una alternativa.
Todas estas clases de optimizaciones son posibles en PF, porque todos los métodos son deterministas, lo que se conoce como referencialmente transparentes.
Si un método devuelve un valor distinto cada vez que se invoca, es impuro y arruina el razonamiento y las optimizaciones que de otra manera podríamos hacer.
Si la F es un efecto, tal vez una de nuestras álgebras (drone o Google), no significa que el
resultado de llamar al álgebra se almacene en caché. Más bien una referencia a la operación es
la que se guarda en caché. La optimización de rendimiento con ifM es notable únicamente para
estructuras de datos, y es más pronunciada con la dificultad del trabajo en cada alternativa.
Exploraremos el concepto de determinismo y de almacenamiento en caché en más detalle en el próximo capítulo.
Bind también tiene sintaxis especial
>> se usa cuando deseamos descartar la entrada a bind y >>! cuando deseamos ejecutar un efecto
pero descartar su salida.
5.7 Applicative y Monad
Desde un punto de vista de funcionalidad, Applicative es Apply con un método pure, y Monad
extiende Applicative con Bind.
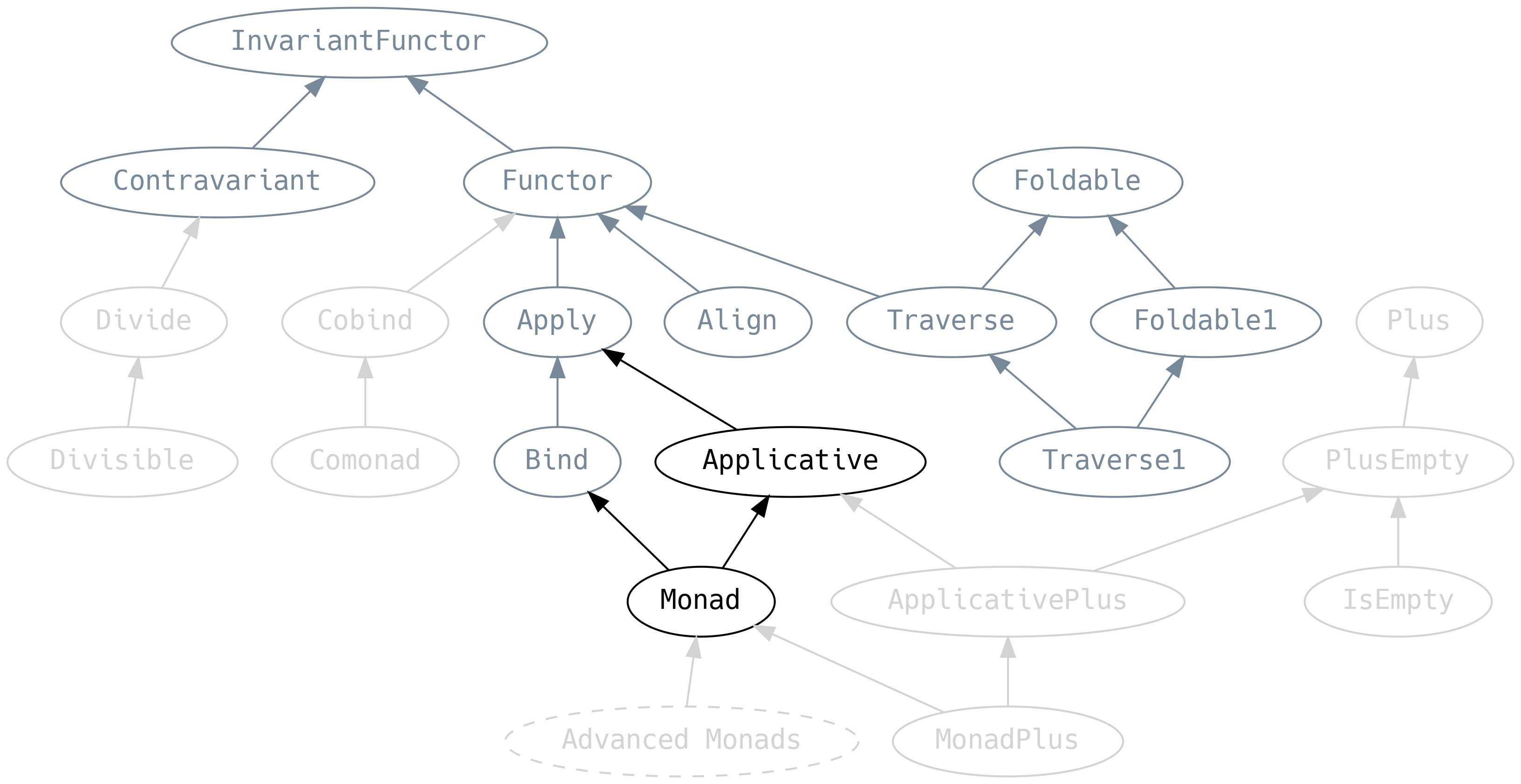
En muchos sentidos, Applicative y Monad son la culminación de todo lo que hemos visto en este
capítulo. .pure (o .point como se conoce más comúnmente para las estructuras de datos) nos
permite crear efectos o estructuras de datos a partir de valores.
Las instancias de Applicative deben satisfacer algunas leyes, asegurándose así de que todos los
métodos sean consistentes:
-
Identidad:
fa <*> pure(identity) === fa, (dondefaestá enF[A]) es decir, aplicarpure(identity)no realiza ninguna operación. -
Homomorfismo:
pure(a) <*> pure(ab) === pure(ab(a))(dondeabes unaA => B), es decir aplicar una funciónpurea un valorpurees lo mismo que aplicar la función al valor y entonces usarpuresobre el resultado. -
Intercambio:
pure(a) <*> fab === fab <*> pure (f => f(a)), (dondefabes unaF[A => B]), es decirpurees la identidad por la izquierda y por la derecha. -
Mapeo:
map(fa)(f) === fa <*> pure(f)
Monad agrega leyes adicionales:
-
Identidad por la izquierda:
pure(a).bind(f) === f(a) -
Identidad por la derecha:
a.bind(pure(_)) === a -
Asociatividad:
fa.bind(f).bind(g) === fa.bind(a => f(a).bind(g))dondefaes unaF[A],fes unaA => F[B]yges unaB => F[C].
La asociatividad dice que invocaciones repetidas de bind deben resultar en lo mismo que
invocaciones anidadas de bind. Sin embargo, esto no significa que podamos reordenar, lo que sería
conmutatividad. Por ejemplo, recordando que flatMap es un alias de bind, no podemos reordenar
como
start y stop no son conmutativas, porque ¡el efecto deseado de iniciar y luego detener un
nodo es diferente a detenerlo y luego iniciarlo!
Pero start es conmutativo consigo mismo, y stop es conmutativo consigo mismo, de modo que
podemos reescribir
como
que son equivalentes para nuestra álgebra, pero no en general. Aquí se están haciendo muchas suposiciones sobre la API de Google Container, pero es una elección razonable que podemos hacer.
Una consecuencia práctica es que una Monad debe ser conmutativa si sus métodos applyX pueden
ser ejecutados en paralelo. En el capítulo 3 hicimos trampa cuando ejecutamos estos efectos en
paralelo
porque sabemos que son conmutativos entre sí. Cuando tengamos que interpretar nuestra aplicación, más adelante en el libro, tendremos que proporcionar evidencia de que estos efectos son de hecho conmutativos, o una implementación asíncrona podría escoger efectuar las operaciones de manera secuencial por seguridad.
Las sutilezas de cómo lidiar con el reordenamiento de efectos, y cuáles son estos efectos, merece un capítulo dedicado sobre mónadas avanzadas.
5.8 Divide y conquistarás
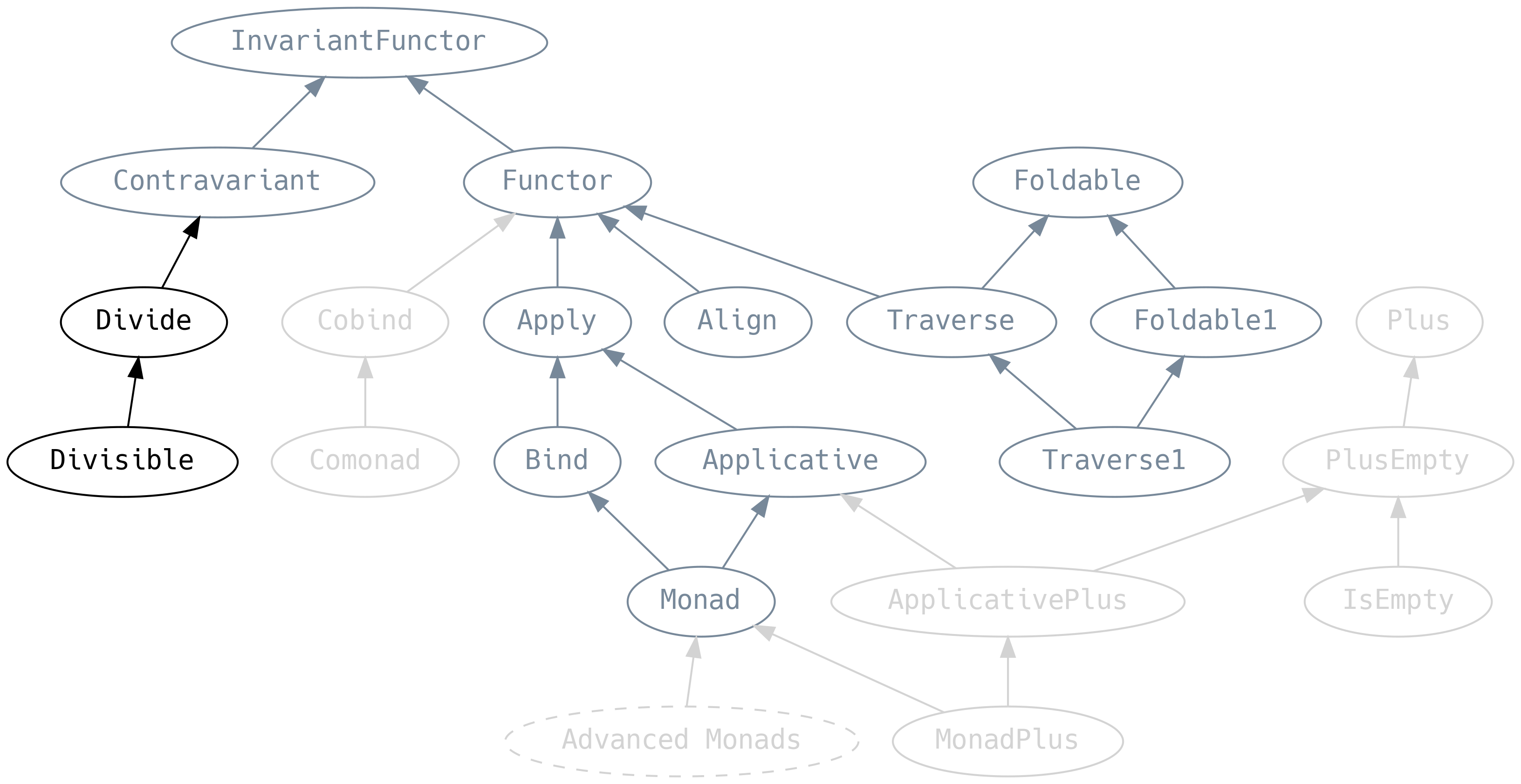
Divide es el análogo Contravariant de Apply
divide dice que si podemos partir una C en una A y una B, y se nos da una F[A] y una
F[B], entonces podemos tener una F[C]. De ahí la frase divide y conquistarás.
Esta es una gran manera de generar instancias contravariantes de una typeclass para tipos producto
mediante la separación de los productos en sus partes constituyentes. Scalaz tiene una instancia de
Divide[Equal], así que vamos a construir un Equal para un nuevo tipo producto Foo
Siguiendo los patrones en Apply, Divide también tiene una sintaxis clara para las tuplas. Es un
enfoque más suave que divide de modo que podamos reinar con el objetivo de dominar el mundo:
Generalmente, si las typeclasses de un codificador pueden proporcionar una instancia de Divide,
más bien que detenerse en Contravariant, entonces se hace posible la derivación de instancias para
cualquier case class. De manera similar, las typeclasses de decodificadores pueden proporcionar
una instancia de Apply. Exploraremos esto en un capítulo dedicado a la derivación de typeclasses.
Divisible es el análogo contravariante (Contravariant) de Applicative e introduce .conquer,
el equivalente a .pure
.conquer también permite la creación trivial de implementaciones donde el parámetro de tipo es
ignorado. Tales valores se llaman universalmente cuantificados. Por ejemplo,
Divisible[Equal].conquer[INil[String]] devuelve una implementación de Equal para una lista vacía
de String que siempre es true.
5.9 Plus
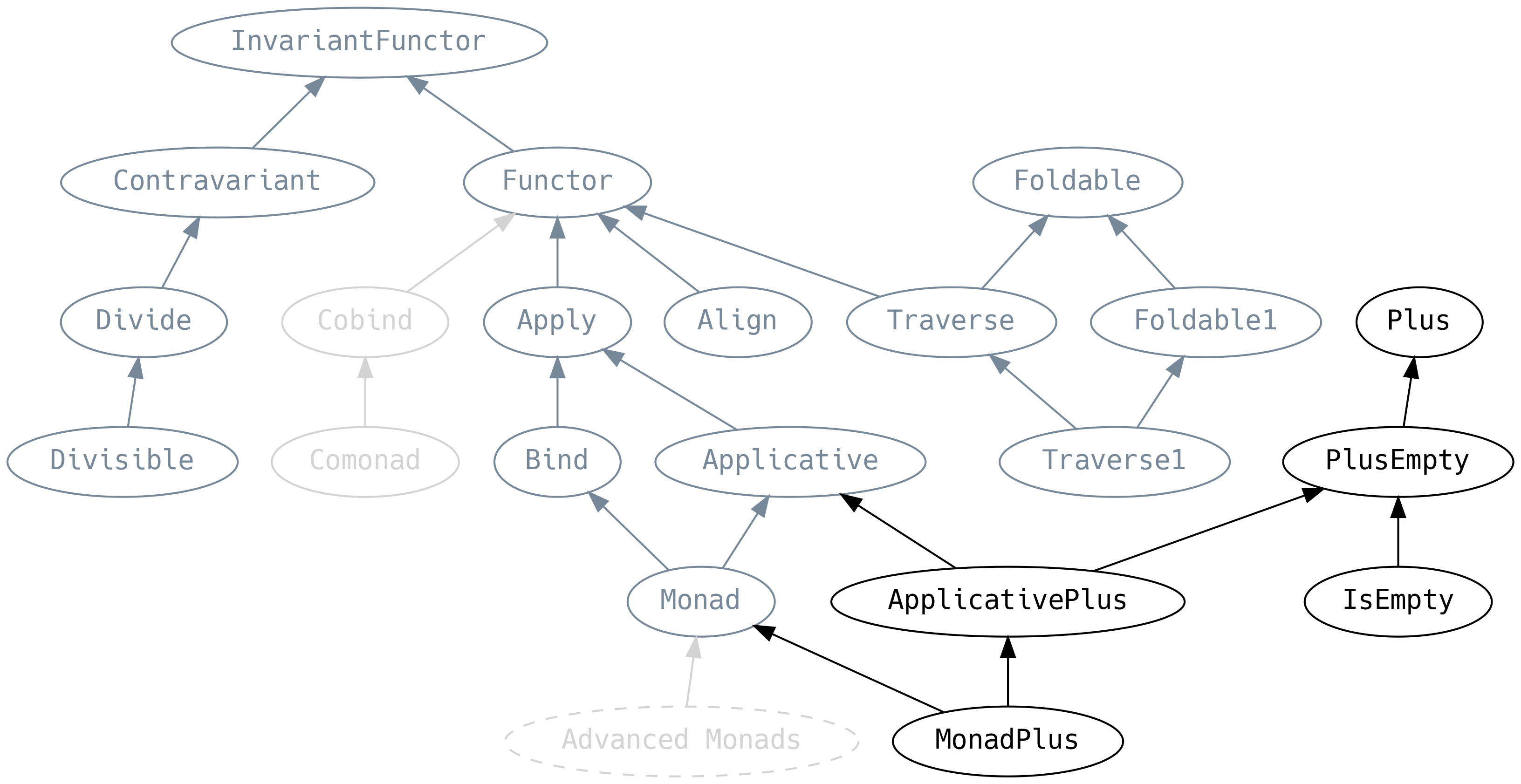
Plus es un Semigroup pero para constructores de tipo, y PlusEmpty es el equivalente de
Monoid (incluso tienen las mismas leyes) mientras que IsEmpty es novedoso y nos permite
consultar si un F[A] está vacío:
<+> es el interceptor TIE, y a estas alturas ya casi nos quedamos sin naves caza TIE…
Aunque superficialmente pueda parecer como si <+> se comportara como |+|
es mejor pensar que este operador funciona únicamente al nivel de F[_], nunca viendo al contenido.
Plus tiene la convención de que debería ignorar las fallas y “escoger al primer ganador”. <+>
puede por lo tanto ser usado como un mecanismo de salida temprana (con pérdida de información) y de
manejo de fallas mediante alternativas:
Por ejemplo, si tenemos una NonEmptyList[Option[Int]] y deseamos ignorar los valores None
(fallas) y escoger el primer ganador (Some), podemos invocar <+> de Foldable1.foldRight1:
De hecho, ahora que sabemos de Plus, nos damos cuenta de que no era necesaria violar la coherencia
de typeclases (cuando definimos un Monoid[Option[A]] con alcance local) en la sección sobre
Cosas que se pueden agregar. Nuestro objectivo era “escoger el último ganador”, que es lo mismo que
“escoge al ganador” si los argumentos se intercambian. Note el uso del interceptor TIE para ccy y
otc con los argumentos intercambiados.
Applicative y Monad tienen versiones especializadas de PlusEmpty
.unite nos permite hacer un fold de una estructura de datos usando el contenedor externo
PlusEmpy[F].monoid más bien que el contenido interno Monoid. Para List[Either[String, Int]]
esto significa que los valores se convierten en .empty, cuando todo se concatena. Una forma
conveniente de descartar los errores:
withFilternos permite hacer uso del soporte para for comprehension de Scala, como se discutió en
el capítulo 2. Es justo decir que el lenguaje Scala tiene soporte incluído para MonadPlus, no sólo
Monad!
Regreseando a Foldable por un momento, podemos revelar algunos métodos que no discutimos antes:
msuml realiza un fold utilizando el Monoidde PlusEmpty[G] y collapse realiza un
foldRight usando PlusEmpty del tipo target:
5.10 Lobos solitarios
Algunas typeclasses en Scalaz existen por sí mismas y no son parte de una jerarquía más grande.

5.10.1 Zippy
El método esencial zip que es una versión menos poderosa que Divide.tuple2, y si un Functor[F]
se proporciona entonces zipWithpuede comportarse como Apply.apply2. En verdad, un Apply[F]
puede crearse a partir de Zip[F] y un Functor[F] mediante invocar ap.
apzip toma un F[A] y una función elevada de F[A] => F[B], produciendo un F[(A, B)] similar
a Functor.fproduct.
<*|*> es el operador del aterrador Jawa.
El método central es unzip con firsts y seconds que permite elegir ya sea el primer o segundo
elemento de una tupla en la F. De manera importante, unzip es lo opuesto de zip.
Los métodos unzip3 a unzip7 son aplicaciones repetidas de unzip para evitar escribir código
repetitivo. Por ejemplo, si se le proporcionara un conjunto de tuplas anidadas, el Unzip[Id] es
una manera sencilla de deshacer la anidación:
En resumen, Zip y Unzip son versiones menos poderosas de Divide y Apply, y proporcionan
características poderosas sin requerir que F haga demasiadas promesas.
5.10.2 Optional
Optional es una generalización de estructuras de datos que opcionalmente pueden contener un valor,
como Option y Either.
Recuerde que una \/ (disjunción) es la versión mejorada de Scalaz de Scalaz.Either. También
veremos Maybe de Scalaz, que es la versión mejorada de scala.Option.
Estos métodos le deberían ser familiares, con la excepción, quizá, de pextract, que es una forma
de dejar que F[_] regrese una implementación específica F[B] o el valor. Por ejemplo,
Optional[Option].pextract devuelve Option[Nothing] \/ A, es decir, None \/ A.
Scalaz proporciona un operador ternario para las cosas que tienen un Optional
por ejemplo
5.11 Co-things
Una co-cosa típicamente tiene la firma/signatura de tipo opuesta a lo que sea que una cosa hace, pero no necesariamente a la inversa. Para enfatizar la relación entre una cosa y una co-cosa, incluiremos la firma/signatura de la cosa siempre que sea posible.
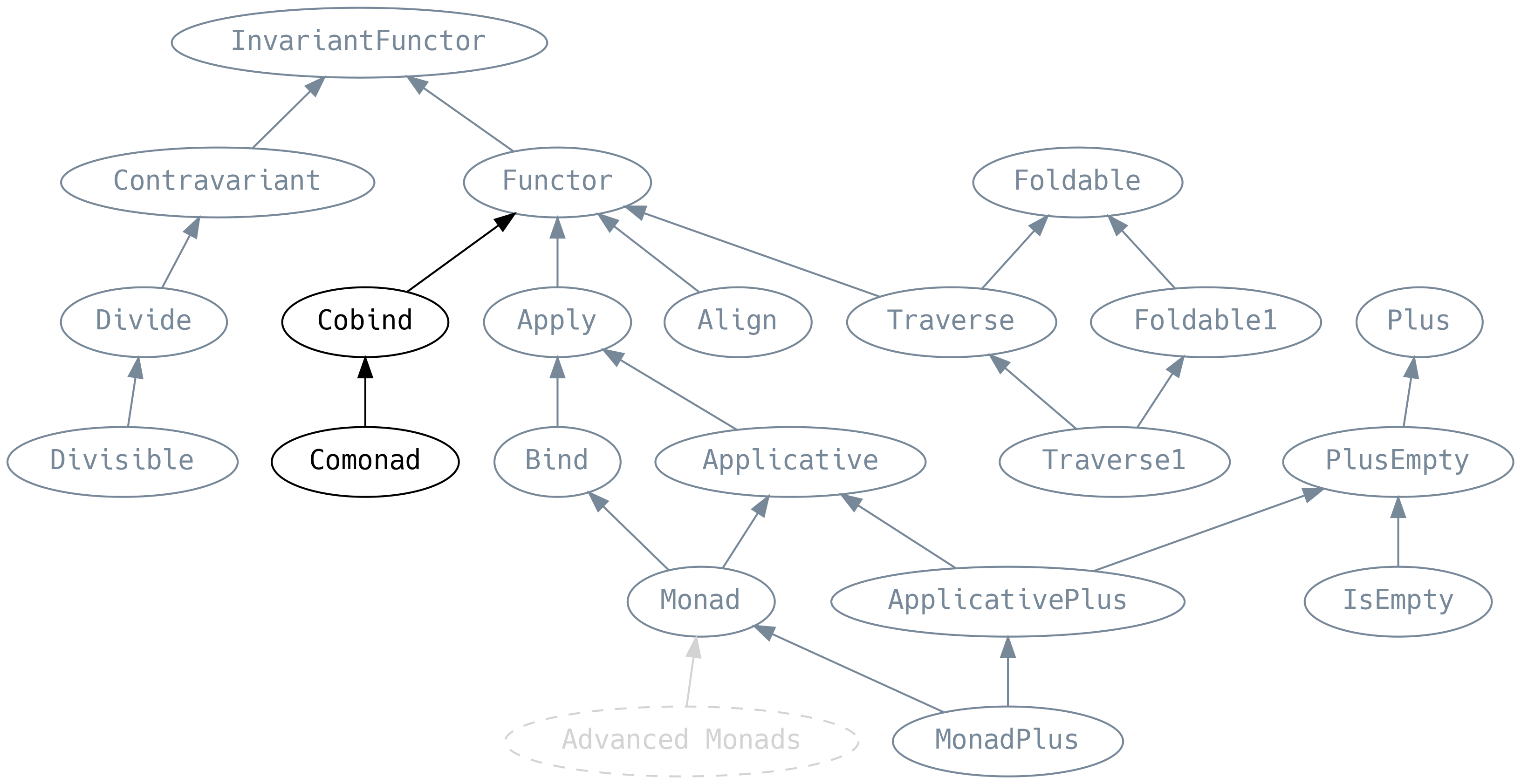

5.11.1 Cobind
cobind (también conocido como coflatmap) toma una F[A] => B que actúa en una F[A] más bien
que sobre sus elementos. Pero no se trata necesariamente de una fa completa, es con frecuencia
alguna subestructura como la define un cojoin (también conocida como coflatten) que expande una
estructura de datos.
Los casos de uso interesantes para Cobind son raros, aunque cuando son mostrados en la tabla de
permutación de la tabla Functor (para F[_], A, y B) es difícil discutir porqué cualquier
método debería ser menos importante que los otros:
| método | parámetro |
|---|---|
map |
A => B |
contramap |
B => A |
xmap |
(A => B, B => A) |
ap |
F[A => B] |
bind |
A => F[B] |
cobind |
F[A] => B |
5.11.2 Comonad
.copoint (también coonocido como .copure) desenvuelve un elemento de su contexto. Los efectos no
tienen típicamente una instancia de Comonad dado que se violaría la transparencia referencial al
interpretar una IO[A] en una A. Pero para estructuras de datos similares a colecciones, es una
forma de construir una vista de todos los elementos al mismo tiempo que de su vecindad.
Considere la vecindad de una lista que contiene todos los elementos a la izquierda de un elemento
(lefts), el elemento en sí mismo (el focus), y todos los elementos a su derecha (rights).
Los lefts y los rights deberían ordenarse con el elemento más cercano al focus en la cabeza,
de modo que sea posible recuperar la lista original IList por medio de .toList.
Podemos escribir métodos que nos dejen mover el foco una posición a la izquierda (previous), y una
posición a la derecha (next)
Mediante la introducción de more para aplicar repetidamente una función opcional a Hood podemos
calcular todas las positions (posiciones) que Hood puede tomar en la lista
Ahora podemos implementar una Comonad[Hood]
cojoin nos da proporciona una Hood[Hood[IList]] que contiene todas las posibles vecindades en
nuestra IList.
En verdad, ¡cojoin es simplemente positions! Podríamos hacer un override con una
implementación más directa y eficiente
Comonad generaliza el concepto de Hood a estructuras de datos arbitrarias. Hood es un ejemplo
de un zipper (que no está relacionado a Zip). Scalaz viene con un tipo de datos Zipper para
los streams (es decir , estructuras de datos infinitas unidimensionales), que discutiremos en el
siguiente capítulo.
Una aplicación de zipper es para automatas celulares, que calculan el valor de cada celda en la siguiente generación mediante realizar un cómputo basándose en la vecindad de dicha celda.
5.11.3 Cozip
Aunque se llame cozip, quizá es más apropiado enfocar nuestra atención en su simetría con unzip.
Mientras que unzip divide F[_] de tuplas (productos) en tuplas de F[_], cozip divide F[_]
de disjunciones (coproductos) en disjunciones de F[_].
5.12 Bi-cosas
Algunas veces podríamos encontrar una cosa que tiene dos hoyos de tipo y deseemos realizar un map
en ambos lados. Por ejemplo, podríamos estar rastreando las fallas a la izquierda de un Either y
tal vez querríamos hacer algo con los mensajes de error.
La typeclass Functor/Foldable/Traverse tienen parientes extraños que nos permiten hacer un
mapeo de ambas maneras.
relatives that allow us to map both ways.
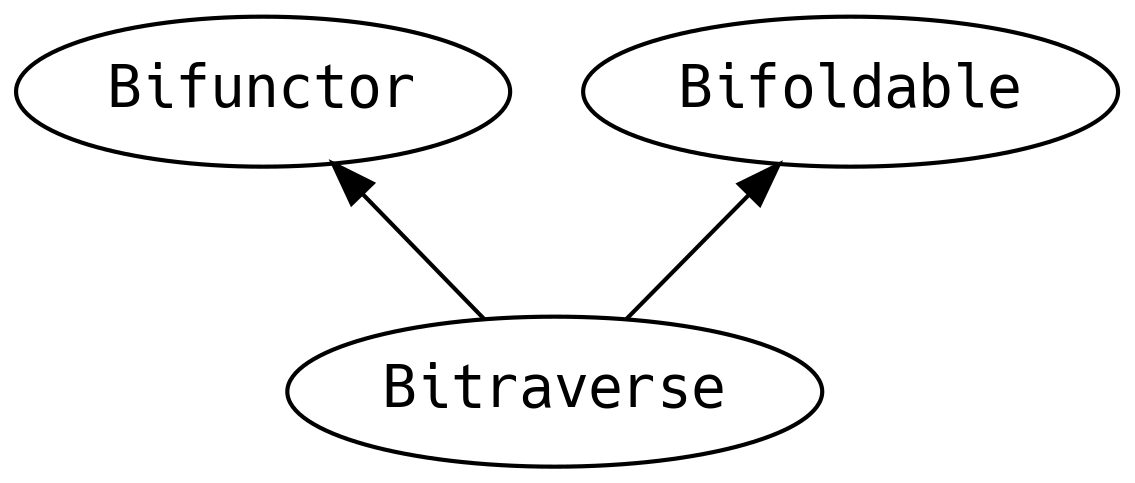
!<-: y :-> son los operadores felices!
Aunque las signaturas de tipo son verbosas, no son más que los métodos esenciales de Functor,
Foldable, y Bitraverse que toman dos funciones en vez de una sola, con frecuencia requiriendo
que ambas funciones devuelvan el mismo tipo de modo que sus resultados puedan ser combinados con un
Monoid o un Semigroup.
Adicionalmente, podemos revisitar MonadPlus (recuerde que se trata de un Monad con la habilidad
extra de realizar un filterWith y unite) y ver que puede separar el contenido Bifoldable de
un Monad.
Esto es muy útil se tenemos una colección de bi-cosas y desamos reorganizarlas en una colección de\
A y una colección de B.
5.13 Resumen
!Esto fue bastante material! Hemos apenas explorado la librería estándar de funcionalidad polimórfica. Pero para poner el asunto en perspectiva: hay más traits en la API de collecciones de la librería estándar de Scala que typeclasses en Scalaz.
Es normal que una aplicación de PF usar un porcentaje pequeño de la jerarquía de tipos, con la mayoría de su funcionalidad viniendo de álgebras particulares del dominio y de typeclasses. Inclusive si las typeclasses del dominio específico son simples clones especializados de algo que ya existe en Scalaz, está bien refactorizarlo después.
Para ayudar al lector, hemos incluído un sumario de las typeclasses y sus métodos primarios en el apéndice, tomando inspiración del sumario cuyo autor es Adam Rosien’s: Scalaz Cheatsheet.
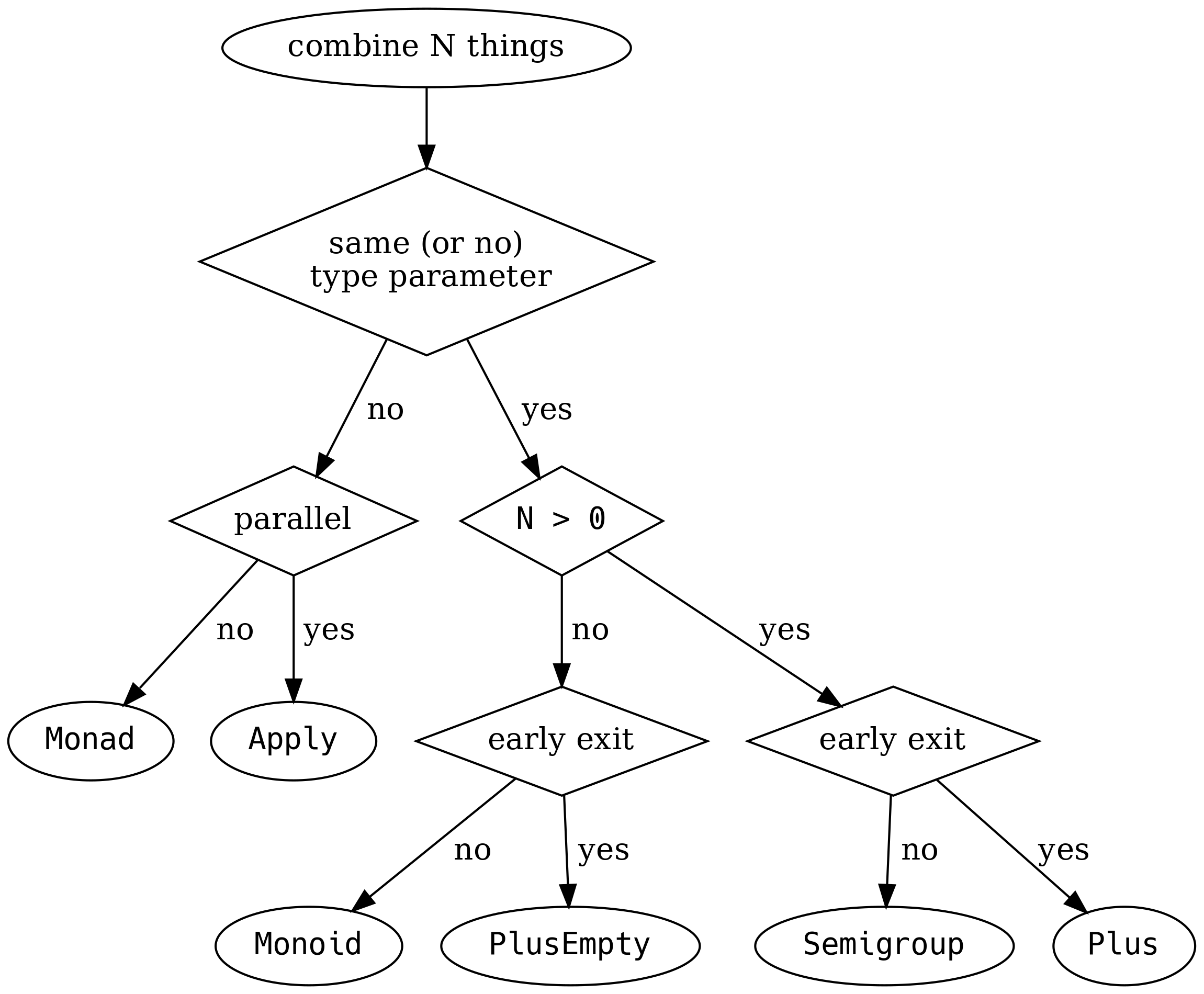
Para ayudarle, Valentin Kasas explica cómo combinar Ncosas: