3. Diseño de aplicaciones

En este capítulo escribiremos la lógica de negocio y las pruebas para una aplicación de servidor puramente funcional. El código fuente para esta aplicación se incluye bajo el directorio example junto con la fuente del libro, aunque se recomienda no leer el código fuente hasta el final del capítulo porque habrá refactorizaciones significativas a medida que aprendamos más sobre la programación funcional.

3.1 Especificación

Nuestra aplicación administrará una granja de compilación just-in-time (justo a tiempo) con un presupuesto limitado. Escuchará al servidor de integración continua Drone, y creará agentes trabajadores usando Google Container Engine (GKE) para lograr las demandas de la cola de trabajo.

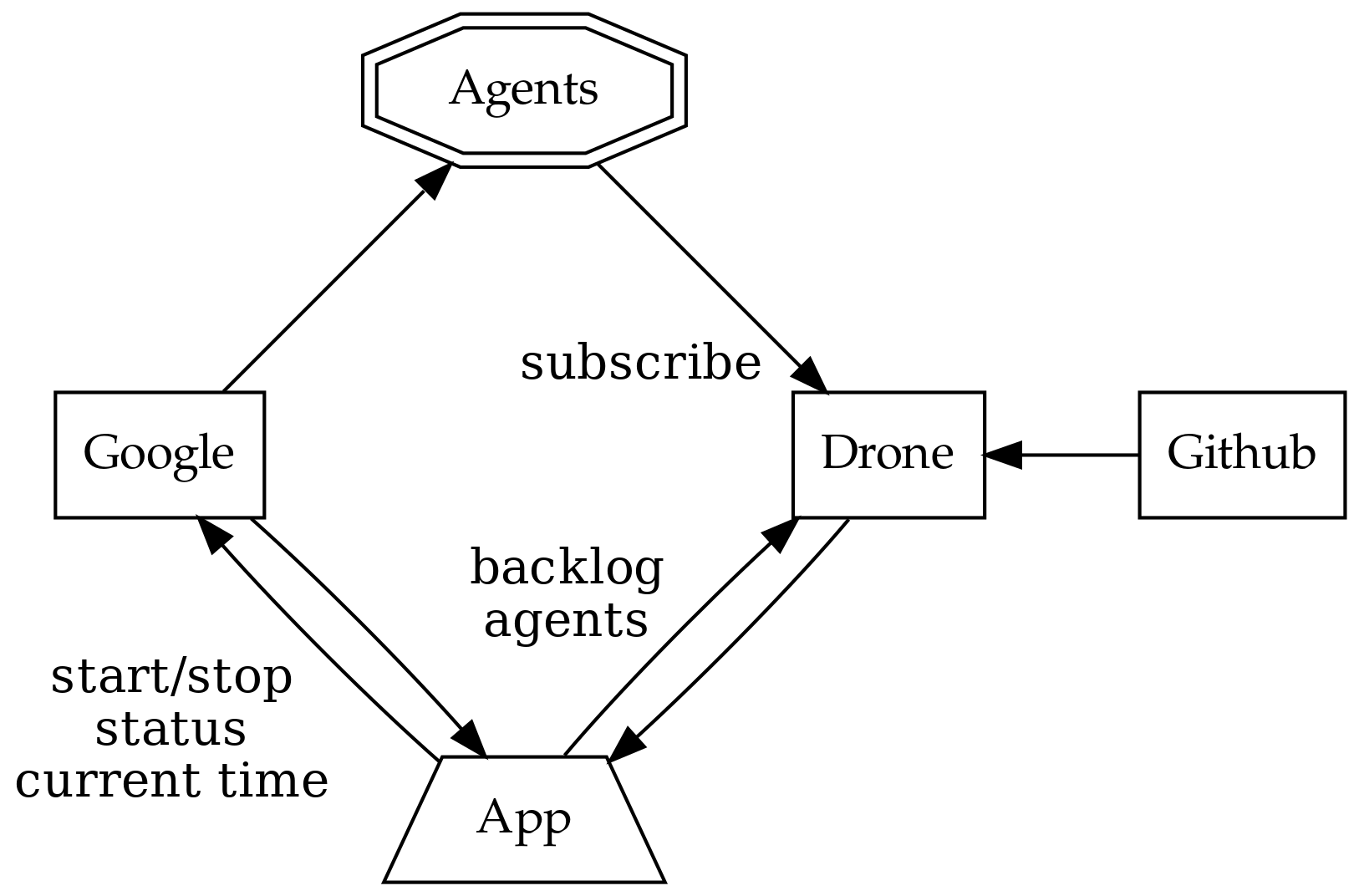
El drone recibe trabajo cuando un contribuidor manda un pull request de github a uno de los proyectos administrados. El dron asigna el trabajo a sus agentes, cada uno procesando una actividad a la vez.

La meta de nuestra aplicación es asegurar que hay suficientes agentes para completar el trabajo, con un límite de capacidad para el número de agentes, a la vez que se minimiza el costo total. Nuestra aplicación necesita conocer el número de artículos en el backlog y el número disponible de agentes.

Google puede crear nodos, y cada uno puede hospedar múltiples agentes de dron. Cuando un agente inicia, se registra a sí mismo con un dron y el dron se encarga del ciclo de vida (incluyendo las invocaciones de supervivencia para detectar los agentes removidos).

GKE cobra una cuota por minuto de tiempo de actividad, redondeado (hacia arriba) al la hora más cercana para cada nodo. No se trata de simplemente crear un nuevo nodo por cada trabajo en la cola de actividades, debemos reusar nodos y retenerlos haste su minuto # 58 para obtener el mayor valor por el dinero.

Nuestra aplicación necesita ser capaz de empezar y detener nodos, así como verificar su estatus (por ejemplo, los tiempos de actividad, y una lista de los nodos inactivos) y conocer qué tiempos GKE piensa que debe haber.

Además, no hay una API para hablar directamente con un agente de modo que no sabemos si alguno de los agentes individuales está realizando algún trabajo para el servidor de drones. Si accidentalmente detenemos un agente mientras está realizando trabajo, es inconveniente y requiere que un humano reinicie el trabajo.

Los contribuidores pueden añadir agentes manualmente a la granja, de modo que contar agentes y nodos no es equivalente. No es necesario proporcionar algún nodo si hay agentes disponibles.

El modo de falla siempre debería tomar al menos la opción menos costosa.

Tanto Drone como GKE tienen una interfaz JSON sobre una API REST con autenticación OAuth 2.0.

3.2 Interfaces / Algebras

Ahora codificaremos el diagrama de arquitectura de la sección previa. Primeramente, necesitamos definir un tipo de datos simple para almacenar un momento (tiempo) en milisegundos porque este concepto simple no existe ni en la librería estándar de Java ni en la de Scala:

  import scala.concurrent.duration._

  final case class Epoch(millis: Long) extends AnyVal {
    def +(d: FiniteDuration): Epoch = Epoch(millis + d.toMillis)
    def -(e: Epoch): FiniteDuration = (millis - e.millis).millis
  }

En PF, una álgebra toma el lugar de una interface en Java, o el conjunto de mensajes válidos para un Actor de Akka. Esta es la capa donde definimos todas las interacciones colaterales de nuestro sistema.

Existe una interacción estrecha entre la escritura de la lógica de negocio y su álgebra: es un buen nivel de abstracción para diseñar un sistema.

  trait Drone[F[_]] {
    def getBacklog: F[Int]
    def getAgents: F[Int]
  }

  final case class MachineNode(id: String)
  trait Machines[F[_]] {
    def getTime: F[Epoch]
    def getManaged: F[NonEmptyList[MachineNode]]
    def getAlive: F[Map[MachineNode, Epoch]]
    def start(node: MachineNode): F[MachineNode]
    def stop(node: MachineNode): F[MachineNode]
  }

Ya hemos usado NonEmptyList, creado fácilmente mediante la invocación de .toNel sobre un objecto List de la librería estándar (que devuelve un Option[NonEmptyList]), y el resto debería resultar familiar.

3.3 Lógica de negocios

Ahora escribiremos la lógica de negocios que define el comportamiento de la aplicación, considerando únicamente la situación más positiva.

Necesitamos una clase WorldView para mantener una instantánea de nuestro conocimiento del mundo. Si estuvieramos diseñando esta aplicación en Akka, WorldView probablemente sería un var en un Actor con estado.

WorldView acumula los valores de retorno de todos los métodos en las álgebras, y agrega un campo pendiente (pending) para darle seguimiento a peticiones que no han sido satisfechas.

  final case class WorldView(
    backlog: Int,
    agents: Int,
    managed: NonEmptyList[MachineNode],
    alive: Map[MachineNode, Epoch],
    pending: Map[MachineNode, Epoch],
    time: Epoch
  )

Ahora estamos listos para escribir nuestra lógica de negocio, pero necesitamos indicar que dependemos de Droney de Machines.

Podemos escribir la interfaz para nuestra lógica de negocio

  trait DynAgents[F[_]] {
    def initial: F[WorldView]
    def update(old: WorldView): F[WorldView]
    def act(world: WorldView): F[WorldView]
  }

e implementarla con un módulo. Un módulo depende únicamente de otros módulos, álgebras y funciones puras, y puede ser abstraída sobre F. Si una implementación de una interfaz algebraica está acoplada a cierto tipo específico, por ejemplo, IO, se llama un intérprete.

  final class DynAgentsModule[F[_]: Monad](D: Drone[F], M: Machines[F])
    extends DynAgents[F] {

El límite de contexto Monad significa que F es monádico, permitiéndonos usar map, pure y, por supuesto, flatMap por medio de for comprehensions.

Requerimos acceso al álgebra de Drone y Machines como D y M, respectivamente. El uso de una sola letra mayúscula para el nombre es una convención de nombre común para las implementaciones de mónadas y álgebras.

Nuestra lógica de negocio se ejecutará en un ciclo infinito (pseudocódigo)

  state = initial()
  while True:
    state = update(state)
    state = act(state)

3.3.1 initial

En initial llamamos a todos los servicios externos y acumulamos sus resultados en un WorldView. Por default se asigna el campo pending a un Map vacío.

  def initial: F[WorldView] = for {
    db <- D.getBacklog
    da <- D.getAgents
    mm <- M.getManaged
    ma <- M.getAlive
    mt <- M.getTime
  } yield WorldView(db, da, mm, ma, Map.empty, mt)

Recuerde del Capítulo 1 que flatMap (es decir, cuando usamos el generador <-) nos permite operar sobre un valor que se calcula en tiempo de ejecución. Cuando devolvemos un F[_] devolvemos otro programa que será interpretado en tiempo de ejecución, sobre el cual podemos a continuación invocar flatMap. Es de esta manera como encadenamos secuencialmente código con efectos colaterales, al mismo tiempo que somos capaces de proporcionar una implementación pura para las pruebas. PF podría ser descrita como Extreme Mocking.

3.3.2 update

update debería llamar a initial para refrescar nuestra visión del mundo, preservando acciones pending conocidas.

Si un nodo ha cambiado su estado, la quitamos de pending y si una acción pendiente está tomando más de 10 minutos para lograr algo, asumimos que ha fallado y olvidamos que se solicitó trabajo al mismo.

  def update(old: WorldView): F[WorldView] = for {
    snap <- initial
    changed = symdiff(old.alive.keySet, snap.alive.keySet)
    pending = (old.pending -- changed).filterNot {
      case (_, started) => (snap.time - started) >= 10.minutes
    }
    update = snap.copy(pending = pending)
  } yield update

  private def symdiff[T](a: Set[T], b: Set[T]): Set[T] =
    (a union b) -- (a intersect b)

Funciones concretas como .symdiff no requieren intérpretes de prueba, tienen entradas y salidas explícitas, de modo que podríamos mover todo el código puro a métodos autónomos en un object sin estado, que se puede probar en aislamiento. Estamos conformes con probar únicamente los métodos públicos, prefiriendo que nuestra lógica de negocios sea fácil de leer.

3.3.3 act

El método act es ligeramente más complejo, de modo que lo dividiremos en dos partes por claridad: la detección de cúando es necesario tomar una acción, seguida de la ejecución de la acción. Esta simplificación significa que únicamente podemos realizar una acción por invocación, pero esto es razonable porque podemos controlar las invocaciones y podemos escoger ejecutar nuevamente act hasta que no se tome acción alguna.

Escribiremos los detectores de los diferentes escenarios como extractores para WorldView, los cuáles no son más que formas expresivas de escribir condiciones if / else.

Necesitamos agregar agentes a la granja si existe una lista de trabajo pendiente (backlog), no tenemos agentes, no tenemos nodos vivos, y no hay acciones pendientes. Regresamos un nodo candidato que nos gustaría iniciar:

  private object NeedsAgent {
    def unapply(world: WorldView): Option[MachineNode] = world match {
      case WorldView(backlog, 0, managed, alive, pending, _)
           if backlog > 0 && alive.isEmpty && pending.isEmpty
             => Option(managed.head)
      case _ => None
    }
  }

Si no hay backlog, deberíamos detener todos los nodos que están detenidos (no están haciendo ningún trabajo). Sin embargo, dado que Google cobra por hora nosotros únicamente apagamos las máquinas en su minuto 58, para obtener el máximo de nuestro dinero. Devolvemos una lista no vacía de los nodos que hay que detener.

Como una red de seguridad financiera, todos los nodos deben tener un tiempo de vida máximo de 5 horas.

  private object Stale {
    def unapply(world: WorldView): Option[NonEmptyList[MachineNode]] = world match {
      case WorldView(backlog, _, _, alive, pending, time) if alive.nonEmpty =>
        (alive -- pending.keys).collect {
          case (n, started) if backlog == 0 && (time - started).toMinutes % 60 >= 58 => n
          case (n, started) if (time - started) >= 5.hours => n
        }.toList.toNel

      case _ => None
    }
  }

Ahora que hemos detectado los escenario que pueden ocurrir, podemos escribir el método act. Cuando se planea que un nodo se inicie o se detenga, lo agregamos a pending tomando nota del tiempo en el que se programó la acción.

  def act(world: WorldView): F[WorldView] = world match {
    case NeedsAgent(node) =>
      for {
        _ <- M.start(node)
        update = world.copy(pending = Map(node -> world.time))
      } yield update

    case Stale(nodes) =>
      nodes.foldLeftM(world) { (world, n) =>
        for {
          _ <- M.stop(n)
          update = world.copy(pending = world.pending + (n -> world.time))
        } yield update
      }

    case _ => world.pure[F]
  }

Dado que NeedsAgent y Stale no cubren todas las situaciones posibles, requerimos de un case _ que atrape todas las situaciones posibles restantes, y que no haga nada. Recuerde del Capítulo 2 que .pure crea el contexto monádico del for a partir de un valor.

foldLeftM es como foldLeft, pero cada iteración de un fold puede devolver un valor monádico. En nuestro caso, cada iteración del fold devuelve F[WorldView]. El M es por Monádico. Nos encontraremos con más de estos métodos lifted (alzados) que se comportan como uno esperaría, tomando valores monádicos en lugar de valores.

3.4 Unit Tests

El enfoque de FP de escribir aplicaciones es el sueño de un diseñador: delegar la escritura de las implementaciones algebraicas a otros miembros del equipo mientras que se enfoca en lograr que la lógica de negocios cumpla con los requerimientos.

Nuestra aplicación es altamente dependiente de la temporización y de los servicios web de terceros. Si esta fuera una aplicación POO tradicional, crearíamos mocks para todas las invocaciones de métodos, o probaríamos los buzones de salida de los actores. El mocking en PF es equivalente a proporcionar implementaciones alternativas de las álgebras dependientes. Las álgebras ya aislan las partes del sistema que necesitan tener un mock, por ejemplo, interpretándolas de manera distinta en las pruebas unitarias.

Empezaremos con algunos datos de prueba

  object Data {
    val node1   = MachineNode("1243d1af-828f-4ba3-9fc0-a19d86852b5a")
    val node2   = MachineNode("550c4943-229e-47b0-b6be-3d686c5f013f")
    val managed = NonEmptyList(node1, node2)

    val time1: Epoch = epoch"2017-03-03T18:07:00Z"
    val time2: Epoch = epoch"2017-03-03T18:59:00Z" // +52 mins
    val time3: Epoch = epoch"2017-03-03T19:06:00Z" // +59 mins
    val time4: Epoch = epoch"2017-03-03T23:07:00Z" // +5 hours

    val needsAgents = WorldView(5, 0, managed, Map.empty, Map.empty, time1)
  }
  import Data._

Implementamos algebras al extender Drone y Machines con un contexto monádico específico, siendo Id el más simple.

Nuestras implementaciones mock simplemente repiten un WorldView fijo. Ya hemos aislado el estado de nuestro sistema, de modo que podemos usar var para almacenar el estado:

  class Mutable(state: WorldView) {
    var started, stopped: Int = 0

    private val D: Drone[Id] = new Drone[Id] {
      def getBacklog: Int = state.backlog
      def getAgents: Int = state.agents
    }

    private val M: Machines[Id] = new Machines[Id] {
      def getAlive: Map[MachineNode, Epoch] = state.alive
      def getManaged: NonEmptyList[MachineNode] = state.managed
      def getTime: Epoch = state.time
      def start(node: MachineNode): MachineNode = { started += 1 ; node }
      def stop(node: MachineNode): MachineNode = { stopped += 1 ; node }
    }

    val program = new DynAgentsModule[Id](D, M)
  }

Cuando escribimos una prueba unitaria (aquí usando FlatSpec desde Scalatest), creamos una instancia de Mutable y entonces importamos todos sus miembros.

Tanto nuestro drone y machine implícitos usan el contexto de ejecución Id y por lo tanto interpretar este programa con ellos devuelve un Id[WorldView] sobre el cual podemos hacer aserciones.

En este caso trivial simplemente verificamos que el método initial devuelva el mismo valor que usamos en nuestras implementaciones estáticas:

  "Business Logic" should "generate an initial world view" in {
    val mutable = new Mutable(needsAgents)
    import mutable._

    program.initial shouldBe needsAgents
  }

Entonces podemos crear pruebas más avanzadas de los métodos update y act, ayudándonos a eliminar bugs y refinar los requerimientos:

  it should "remove changed nodes from pending" in {
    val world = WorldView(0, 0, managed, Map(node1 -> time3), Map.empty, time3)
    val mutable = new Mutable(world)
    import mutable._

    val old = world.copy(alive = Map.empty,
                         pending = Map(node1 -> time2),
                         time = time2)
    program.update(old) shouldBe world
  }

  it should "request agents when needed" in {
    val mutable = new Mutable(needsAgents)
    import mutable._

    val expected = needsAgents.copy(
      pending = Map(node1 -> time1)
    )

    program.act(needsAgents) shouldBe expected

    mutable.stopped shouldBe 0
    mutable.started shouldBe 1
  }

Sería aburrido ejecutar el conjunto de pruebas completo. Las siguientes pruebas serían fáciles de implementar usando el mismo enfoque:

• No solicitar agentes cuando haya pendientes
• No apagar los agentes si los nodos son muy jóvenes
• Apagar los agentes cuando no hay backlog y los nodos ocasionarán costos pronto
• No apague a los agentes si hay acciones pendientes
• Apague a los agentes cuando no hay backlog si son muy viejos
• Apague a los agentes, incluso si potencialmente están haciendo trabajo, si son muy viejos
• Ignore las acciones pendientes que no responden durante las actualizaciones

Todas estas pruebas son síncronas y aisladas al hilo de ejecutor de prueba (que podría estar ejecutando pruebas en paralelo). Si hubieramos diseñado nuestro conjunto de pruebas en Akka, nuestras pruebas estarían sujetas a tiempos de espera arbitrarias y las fallas estarían ocultas en los archivos de registro.

El disparo en la productividad de las pruebas simples para la lógica de negocios no puede ser exagerada. Considere que el 90% del tiempo ocupado por el desarrollador de aplicaciones usado en la interacción con el cliente está en la refinación, actualización y fijación de estas reglas de negocios. Todo lo demás es un detalle de implementación.

3.5 Paralelismo

La aplicación que hemos diseñado ejecuta cada uno de sus métodos algebraicos secuencialmente. Pero hay algunos lugares obvios donde el trabajo puede ejecutarse en paralelo.

3.5.1 initial

En nuestra definición de initial podríamos solicitar toda la información que requerimos a la vez en lugar de hacer una consulta a la vez.

En contraste con flatMap para operaciones secuenciales, Scalaz usa la sintaxis Apply para operaciones paralelas:

  ^^^^(D.getBacklog, D.getAgents, M.getManaged, M.getAlive, M.getTime)

y también puede usar notación infija:

  (D.getBacklog |@| D.getAgents |@| M.getManaged |@| M.getAlive |@| M.getTime)

Si cada una de las operaciones paralelas regresa un valor en el mismo contexto monádico, podemos aplicar una función a los resultados cuando todos ellos sean devueltos. Reescribiendo initial para tomar ventaja de esto:

  def initial: F[WorldView] =
    ^^^^(D.getBacklog, D.getAgents, M.getManaged, M.getAlive, M.getTime) {
      case (db, da, mm, ma, mt) => WorldView(db, da, mm, ma, Map.empty, mt)
    }

3.5.2 act

En la lógica actual para act, estamos deteniéndonos en cada nodo secuencialmente, esperando por el resultado, y entonces procediendo. Pero podríamos detener todos los nodos en paralelo y entonces actualizar nuestra vista del mundo.

Una desventaja de hacerlo de esta manera es que cualquier falla ocasionará que se paren los cómputos antes de actualizar el campo pending. Pero se trata de una concesión razonable dado que nuestra función update manejará el caso cuando un node se apague inesperadamente.

Necesitamos un método que funcione en NonEmptyList que nos permita hacer un map sobre cada elemento en un F[MachineNode], devolviendo un F[NonEmptyList[MachineNode]]. El método se llama traverse, y cuando invoquemos un flatMap sobre este tendremos un NonEmptyList[MachineNode] con el cuál lidiaremos de una manera sencilla:

  for {
    stopped <- nodes.traverse(M.stop)
    updates = stopped.map(_ -> world.time).toList.toMap
    update = world.copy(pending = world.pending ++ updates)
  } yield update

Podría argumentarse, que este código es más fácil de entender que la versión secuencial.

3.6 Summary

1. Las algebras definen las interfaces entre sistemas.
2. Los módulos son implementaciones de un álgebra en términos de otras álgebras.
3. Los intérpretes son implementaciones concretas de un álgebra para una F[_] fija.
4. Los intérpretes de prueba pueden reemplazar las partes con efectos colaterales de un sistema, proporcionando un grado elevado de cobertura de las pruebas.