29. Arithmetic operators
The five arithmetic operators (+, -, *, /, %) are familiar to most people from their early school days.
Additive Operators
| Operator | Name |
|---|---|
| + | Plus |
| - | Minus |
The additive operators provide for basic addition and subtraction.
assert 1 + 1 == 2
assert 10 - 9 == 1
Additive operators are left-associative - they are assessed from left to right:
assert 1 + 4 - 3 == 2
Multiplicative Operators
| Operator | Name |
|---|---|
| * | Multiply |
| / | Divide |
| % | Remainder |
The remainder operator (%) is also commonly referred to as the modulus operator and returns the remainder of a division:
assert 13 % 2 == 1
Multiplicative operators are left-associative:
assert 10 * 6 / 2 == 30
The Power operator
| Operator | Name |
|---|---|
| ** | Power |
The power operator (**) is used to raise a number to the power of the second number:
assert 5**3 == 125
Precedence
Multiplicative operators have precedence over additive operators.
assert 10 - 1 * 10 == 0
If the result above is surprising and the expected result was 90 then parentheses “()” should have been used:
assert (10 - 1) * 10 == 90
The elements within parentheses have precedence over the rest of the evaluation. This results in (10 - 1) being evaluated first and the result being multiplied by 10.
If we consider Pythagoras’ theorem: (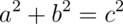 ) the operator precedence will yield the correct answer without requiring parentheses:
) the operator precedence will yield the correct answer without requiring parentheses:
assert 3 * 3 + 4 * 4 == 5 * 5
However, we could use parentheses purely for the sake of clarity:
assert (3 * 3) + (4 * 4) == (5 * 5)
Nested parentheses can be used to further delineate an expression. The innermost parentheses are evaluated first, then moving outwards:
assert ((10 - 1) * 10) / 2 == 45
In the equation above, (10 - 1) is evaluated first, the result (9) is then multiplied by 10 and that result (90) being divided by 2.
For significantly more complex calculations such as the quadratic equation (below) parentheses are required if the calculation is to be performed in a single expression:
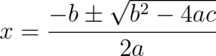
def a = 5
def b = 6
def c = 1
def x
x = ((-1 * b) + Math.sqrt((b**2) - (4 * a * c))) / (2 * a)
assert x == -0.2