2 Financial instruments and pricing engines
「金融商品(の価格計算)ライブラリは、金融商品の価格を計算する方法を提供するものである」と言ったら、“ラ・パリサードの真理”と同じく、当たり前の事を述べているにすぎないかもしれません。しかし、ライブラリの設計者にとって、価格計算の方法の提供というのは課題の一部でしかありません。金融商品ライブラリには、将来、新たな価格計算機能を追加する為に、必要な機能を持たせる必要があります。(訳注:ラ・パリサードの真理とは、中世のフランス軍人de La Palisse氏の墓標の文が“もし彼が死んでいなければ、彼は生きていただろう”と誤訳された事から、当たり前の真実の事を意味する。)
機能拡張の要請は、2つの方向で必要になると予想されます。ひとつは、新しい金融商品への対応、もうひとつは、同じ商品について別の価格計算方法を追加していくことです。いずれの方向であっても、拡張性を持たせるには、いくつかの必要条件がありますが、デザインパターン的な用語で言えば、「いずれの方向の要請にも合致するものでなければならない」。本チャプターでは、そのような拡張性の要請とそれに対する解決方法について説明します。
2.1 The Instrument class
われわれ(金融モデルのプログラマー)の世界では、Financial Instrumentsは、それ自体ですでに基本概念です。従って、自らをオブジェクト指向プログラマーと自認している人なら、まずこれをBase Classとして構成し、そこから様々な種類の金融商品の派生クラスを定義していくでしょう。
その考え方をもとにすれば、例えば(そのBase Classが持つべき機能として)次のようなプログラムコードを書きたくなるのではないでしょうか
for (i = portfolio.begin(); i != portfolio.end(); ++i)
totalNPV += i->NPV();
(訳注:ポートフォリオ配列の中に、どのような金融商品の派生クラスオブジェクトが含まれていても、ベースクラスで定義された共通のメソッドNPV( )で価格が返ってくるような仕組みにしておけば、様々な商品のポートフォリオの総額を計算する場合、上記のような簡単なコードで記述できるという事)
このように関数を定義すれば、具体的な商品のタイプを気にする必要ありません。しかし、このプログラムコードではNPV( )のメソッドにどのような引数を渡せばよいのか解らないし、さらにどのようなメソッドを呼び出すのかも解りません。上記の一見無害に見えるCodeについても、一旦引いて、(このBase Classが持つべき)インターフェースについてよく考えてみる必要があります。
2.1.1 インターフェースと要件
金融市場では、-非常に単純な商品から非常に複雑な商品に至る-広範な商品が取引されており、ある特定の商品(例えば株式オプション)のクラスに特有のメソッドが、他の商品(例えば金利スワップ)では意味をなさないという事は十分起こり得ます。従ってInstrumentsベースクラスで定義すべき、すべての金融商品に共通のメソッドの数は極めて限られました。我々は、その共通するメソッドを、現在価値を返すメソッド(場合によっては推定誤差の値も含めて)と、その金融商品が満期を過ぎているかどうかを返すメソッドだけにしました。商品によって、(そのメソッドが)どのような引数を取るべきかについて、(最近改変されたC++11のvariadic templatesのような技術を使っても)、ベースクラスでは特定できない為、そのメソッドは引数を取らない形で宣言しています。従って、メソッドに必要な入力項目は、金融商品ごとに、保存されなければなりません。その結果、Instrumentクラスのインターフェースは下記Listing2.1のようになっています。
Instrument class.class Instrument {
public:
virtual ~Instrument();
virtual Real NPV() const = 0;
virtual Real errorEstimate() const = 0;
virtual bool isExpired() const = 0;
};
プログラミングの慣行に従って、当初、各メソッドはすべて純粋仮想関数にしました。ただ、これは(ガーシュインのオペラPorgy and Bessに登場する麻薬密売人のSportin’ Lifeが指摘したように)必ずそうしなければならないというものではありません。ベースクラスで具体的に定義・実装した方が良いようなプログラムの動作があるかもしれません。本当にそうなのか調べるために、一般的な金融商品に期待される共通の動作が何であるのか、またそれを実行させる為のプログラムで共通するところはあるのか、よく分析してみる必要がありました。その結果、QuantLibの開発過程のなかで、2つの必要事項が見つかり、開発期間中に実装の方法を変更しました。ここでは、それらの現時点での実装内容を説明します。
ひとつは、特定の金融商品について、価格計算の方法が複数存在し(例えば、解析解で価格計算をする方法と、数値解でそれを行う方法)、その実装を継承の仕組みを使わずにできないだろうかということです。読者の方はこれを聞いて、Strategy Patternを使えばいいのではと思われるかもしれません。その通りです。本チャプターのSection2.2で、その実装方法を説明します。
もうひとつは、金融商品の価格は、市場データに依存しているという事実からくるものです。市場データは、本質的に時間の経過によって変化するものです。従って、その商品の価格も時間の経過によって変化していきます。また、金融商品の価格変化は、市場データを提供するソースが複数存在しうるという点からも発生します。我々は、ひとつの金融商品が複数のデータソースとリンクできるようにする必要があると考えました。その場合、価格計算のメソッドを呼び出した時は、その都度、最新データを使って金融商品の価格を再計算させるような仕組みが必要と考えました。また、複数のデータソースを任意に選択できるような仕組みも必要と考えました。そして、データソースを変更した場合は、その金融商品にとっては、市場データのアップデートと同じ取扱い(都度価格の再計算を行う)とすべきとも考えました。
効率性の低下も関心事でした。例えば、多くの金融商品をひとまとめにして、定期的に時価を確認して、ポートフォリオの全体の価値を適宜モニターするとします。その際、単純な仕組みでは、時価の変更が無かった商品についても、すべて価格の再計算を行ってしまう可能性がありました。従って、Instrumentクラスのメソッドの中に、時価を一時保管する仕組みを取り入れました。時価の再計算は、市場データの更新があった場合のみ行い、それ以外の場合は、一時保管されている値を使うような仕組みです。
2.1.2 実装
どの金融商品についても共通な、価格を一時保管したり、再計算したりする仕組みを司るプログラムコードは、2種類のデザインパターンを使って書かれています。(デザインパターンについては巻末(Gamma et al, 1995)の文献を参照)
入力データに変更があった場合、InstrumentクラスはObserverパターンを使って、その変更の通知を受ける仕組みにしています。Observerパターンについては、Appendix Aを参照下さい。(但し、Appendixを読んだからといって、巻末(Gamma et al, 1995)にある「Gang of Four(4人組)」の(有名な)本を読まない理由にしないでください。)とりあえず、ここではどのようにそれが使われているか解説します。
(金融商品と市場データとの関係から)明らかなように、InstrumentクラスはObserverの役割を持ち、市場データはObservableの役割をもっています。入力データ(訳注:市場データ)が更新された場合、それを(ObserverであるInstrumentに)通知されるような仕組みを構築する為には、Observerが、その入力データを保管しているオブジェクト(Observable)への‘参照’を保持しておく必要があります。このような仕組みにするには、何らかのSmart Pointer(訳注:メモリーリークを防ぐため、ポインターの指し示すメモリー領域の管理を自動的に行ってくれるポインター)が必要になると気づかれるでしょう。しかし、ポインターの仕組みだけでは、我々が必要としているメカニズムにとって十分ではありません。すでに説明した通り、入力データの変更は、市場価格が動く以外に、データソースの変更からも発生します。(訳注:例えば、同じ銘柄の株が複数の取引所で取引されている場合、データソースは一本だけではない)
(Smart)ポインターを1つしか持たない場合、それが参照するオブジェクトの直近のデータのみにしかアクセスできません。我々が必要とするのは、ポインターを保持するポインターです。この仕組みは、QuantLibの中では、Handleという名前のクラス・テンプレートを使って実装されています。これについても、詳細はAppendix Aを参照下さい。このセクションの論点との関連で言えば、ある特定のHandleの複数のコピーは、ひとつのオブジェクトに対するリンクを共有しているという点です。仮に、ポインターが別のオブジェクトを指すようになった場合、Handleのすべてのコピーにそれが通知され、それらのHandleを保持しているオブジェクト(訳注:Instruments)に対し、新しいポイント先(のデータ)を通知する仕組みになっています。さらに、Handleは、そこが指し示しているオブジェクト(訳注:市場データを保持するオブジェクト)から、それを監視するすべてのObserver(訳注:市場データをモニターしているInstruments)に対し、データ変更の通知を転送する仕組みを持っています。
そして、市場データの役割を持ち、Handleクラスの中で保持できる、様々な種類のObservableクラスを実装しました。その中で、最も基本的なクラスがQuoteクラスで、市場価格を一個だけ保持する機能を持っています。金融商品の価格計算に必要な市場データ(Observable)は、その他にも、もっと複雑な構造を持つイールドカーブやボラティリティのTermStructureクラスなどがあります。(それらのクラスも、最終的には一個しかデータを持たないQuoteクラスのインスタンスに行きつきます。イールドカーブオブジェクトはBootstrappingを行うため、預金金利やスワップレートを保持するQuoteクラスのインスタンスを必要とします)
Instrumentベースクラスが持つもう1つの課題は、具体的な価格計算のアルゴリズムは派生クラスで実装するとして、ベースクラスにおいて価格の再計算を行った後の値を一旦保持しておくメカニズムを、どのように抽象化するか、という事です。このメカニズムは、Template Methodパターンを使って導入しました(このパターンについても巻末 [1] の本を参照)。QuantLibの初期の頃のバージョンでは、この仕組みをInstrumentクラスそのものに、含めていました。その後のバージョンで設計を変更し、その仕組みを抜き出して別のクラスに持たせることとしまた。そのクラスはLazyObjectという名前で呼ばれており、ライブラリの中で、他の用途にも使われています。このクラスの概要は、下記Listing 2.2に示します。
LazyObject class.class LazyObject : public virtual Observer,
public virtual Observable {
protected:
mutable bool calculated_;
virtual void performCalculations() const = 0;
public:
void update() { calculated_ = false; }
virtual void calculate() const {
if (!calculated_) {
calculated_ = true;
try {
performCalculations();
} catch (...) {
calculated_ = false;
throw;
}
}
}
};
プログラムコードは極めて単純です。bool型のメンバー変数 calculated_は、価格の計算結果が“直近のものかどうか”のフラッグを保持します。ここにあるupdate()メソッドは、(ベースクラスである)Observerのメソッドを実装したものであり、Observableクラスから(入力データが更新されたという)通知が届いた場合に、メンバー変数calculated_をfalseにセットし、すでにある価格計算結果を、古いものとして扱います。
calculate()メソッドは、Template Methodパターンを使って実装されています。巻末(Gamma et al, 1995) の4人組の本にある通り、メソッドの内容のうち、すべての派生クラスに渡って共通な動作はベースクラスで実装され(このケースでは一時保存された計算結果のフラッグの取扱い)、派生クラス毎に実装すべき部分については、仮想関数(このケースではperformCalculations() )に任されます。その仮想関数は、ベースクラスのメソッドの中で呼び出されます。従って、派生クラスでは、具体的な計算方法を(performCalculations()の実装の中で)特定すればよいだけで、計算結果の一時保存について考える必要がありません。派生クラスの実装部分は、ベースクラスのメソッドの中に(コンパイルの際に)組み込まれます。
計算結果の一時保存のロジックは単純です。もし、現在保存されている計算結果データがすでに古くなってしまった場合は(calculated_ フラッグがfalseにセットされている)、派生クラスにおいて価格の再計算を行い、calculated_フラッグを再びtrueに戻します。もし現在保存されているデータが最新分であれば何もしません。
ロジックは簡単でも、実装はそれほど単純ではありません。まず、bool型であるcalculated_のフラッグ変更の手続きを、なぜtryブロックの手前で行う必要があったのでしょうか?また、catchブロックの中で、なぜcalculated_フラッグの設定を元に戻す操作を行ってからエラー処理へ飛ぶのでしょうか? もしかしたら、以下のようなプログラムコードであっても、同じ効果を持たせる事ができたのではないか、と考えられませんか?
if (!calculated_) {
performCalculations();
calculated_ = true;
}
こうしなかった理由は、performCalculations()メソッドが再帰的にcalculate()メソッドを呼び出す場合が想定されるからです(例えばLazyObjectがイールドTermStructureで、Bootstrappingを行うような場合)。もしcalculated_をtrueにセットしなかった場合、上記構文中のif条件は継続してチェックされ、performCalculations()が再び呼びだされ、無限ループに陥ってしまいます。(performCalculations()が実行される前に)このフラッグをtrueにセットする事により、そういった事が防げます。しかし、(仮にperformCalculations()の実行時に)エラーにより例外処理に飛ぶ場合は、その前に、このフラッグをfalseに戻しておく必要があります。その後、さらに再例外処理に飛び、インストールされているエラー処理Handlerにプロセスが移動します。
LazyObjectには、さらにいくつかのメソッドが用意されており、ユーザーに再計算を行わせないようにしたり、逆に強制したりできるようになっています。これについてはここでは説明しません。興味がある方は、かの有名なObi-Wan Kenobiのアドバイスに従って下さい―“Read the Source, Luke”。
InstrumentクラスはLazyObjectから派生しています。上で説明したLazyObjectのインターフェース(ここではcalculate()メソッド)を、Instrumentクラス用にデコレート(訳注:Decorator Patternを使って、ベースクラスの仮想関数calculate()に、派生クラスで機能を追加している)しています。その内容は、若干の追加のコードも含めて、下記Listing 2.3のとおりです。
Instrument class.class Instrument : public LazyObject {
protected:
mutable Real NPV_;
public:
Real NPV() const {
calculate();
return NPV_;
}
void calculate() const {
if (isExpired()) {
setupExpired();
calculated_ = true;
} else {
LazyObject::calculate();
}
}
virtual void setupExpired() const {
NPV_ = 0.0;
}
};
ここで追加されたコードも、Template Methodパターンに従って、派生クラスに、そのInstrumentに固有な計算アルゴリズムの実装を委任できるようにしています。(訳注:このクラスの段階でperformCalculations()を実装しておらず、さらに派生するクラスでの実装を前提にしている。)このクラスは、価格計算結果を一時保存するメンバー変数、NPV_を持っています。派生クラスではそこで必要なメンバー変数を追加で宣言する事ができます。(注:Instrumentクラスでは、ここでは書いていませんが、その他にerrorEstimate_変数が定義されており、NPV_に関する論点がそのまま適用できます)。
calculate()メソッドの本体は、仮想関数であるisExpired()を呼び出して、その商品の期限が到来しているかどうかをチェックしています。かりに期限が到来しているのであれば、さらに仮想関数setupExpired()を呼び出し、NPV_を適切な値にセットします。デフォールトの設定は NPV_を 0に設定しますが、派生クラスで別の適切な値とする事も可能です。その後calculated_フラッグをtrueに設定します。もし、その商品がまだ満期を迎えていないのであれば、ベースクラスであるLazyObjectのcalculate()メソッドが呼び出され、そのメソッドはさらにperformCalculations()を呼びだします。このような仕組みをとると、performCalculations()に一定の作業を必ずさせる必要があります。すなわちNPV_に計算結果を、(メンバー変数に)書き込む事です。(その他派生クラスに特有のメンバー変数への値の代入も必要になります。)最後に商品の価格(NPV)を返すNPV( )メソッドですが、NPV_の値を返す前に、calculate()メソッドを呼び出して、その値をまず計算するようにしています。
2.1.3 例:金利スワップ
このセクションの説明の最後に、これまで説明してきた(Instrumentクラスの)機能をもとに、個別の金融商品をどのように実装するか説明します。
例として‘金利スワップ’を使いたいと思います。当然ご存知の通り、この商品は、定期的にキャッシュフローを交換する契約です。この商品の価値(Net Present Value ‘NPV’)は、受取キャッシュフローと支払いキャッシュフローの現在価値を計算し、合算したものです。
当然ながら、金利スワップはInstrumentクラスの派生クラスとして実装されています。その概要をListing 2.4に示します。(この実装内容は、若干古いバージョンのものですが、簡単に説明できるので、例として使います)
Swap class.class Swap : public Instrument {
public:
Swap(const vector<shared_ptr<CashFlow> >& firstLeg,
const vector<shared_ptr<CashFlow> >& secondLeg,
const Handle<YieldTermStructure>& termStructure);
bool isExpired() const;
Real firstLegBPS() const;
Real secondLegBPS() const;
protected:
// methods
void setupExpired() const;
void performCalculations() const;
// data members
vector<shared_ptr<CashFlow> > firstLeg_, secondLeg_;
Handle<YieldTermStructure> termStructure_;
mutable Real firstLegBPS_, secondLegBPS_;
};
このクラスは、メンバー変数として、価格計算に必要な情報のオブジェクトを持っています。すなわち、2つのキャッシュフロー(Cashflow Legs)と、それを現在価値に割引くための金利期間構造(Yield Term Structure)です。それに加え、計算結果を格納するための2つの変数を持ちます。さらに、(ベースクラスである)Instrumentクラスのインターフェースを、具体的に実装する為のメソッドと、それ以外にも金利スワップに特有の値を返すメソッドを宣言しています。(訳注:isExpired()、setupExpired()、performCalculations()、はベースクラスで仮想関数として宣言されている。また firstLegBPS() 、secondLegBPS()、はSwapに特有の値を返すメソッド)
Swapクラスとそれに関連するクラスの関係図を、下記Figure 2.1に載せておきます。
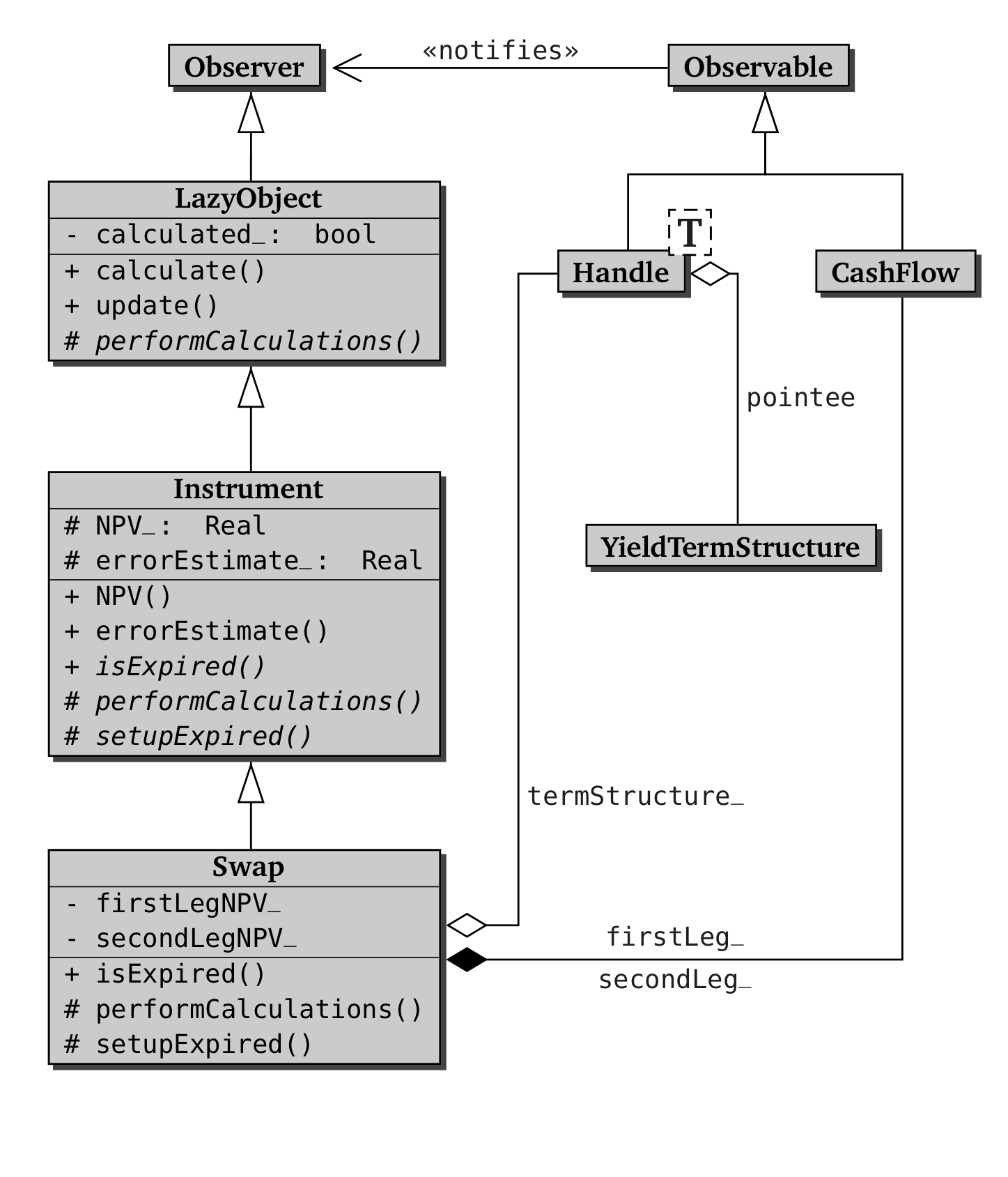
Swap class.このクラスをInstrumentベースクラスへ適合させる為、3つの手順を踏んでいますが、3番目の手順は派生クラスによっては任意です。それに関係するメソッドを下記Listingに示します。
Swap class. (続き)Swap::Swap(const vector<shared_ptr<CashFlow> >& firstLeg,
const vector<shared_ptr<CashFlow> >& secondLeg,
const Handle<YieldTermStructure>& termStructure)
: firstLeg_(firstLeg), secondLeg_(secondLeg),
termStructure_(termStructure) {
registerWith(termStructure_);
vector<shared_ptr<CashFlow> >::iterator i;
for (i = firstLeg_.begin(); i!= firstLeg_.end(); ++i)
registerWith(*i);
for (i = secondLeg_.begin(); i!= secondLeg_.end(); ++i)
registerWith(*i);
}
bool Swap::isExpired() const {
Date settlement = termStructure_->referenceDate();
vector<shared_ptr<CashFlow> >::const_iterator i;
for (i = firstLeg_.begin(); i!= firstLeg_.end(); ++i)
if (!(*i)->hasOccurred(settlement))
return false;
for (i = secondLeg_.begin(); i!= secondLeg_.end(); ++i)
if (!(*i)->hasOccurred(settlement))
return false;
return true;
}
void Swap::setupExpired() const {
Instrument::setupExpired();
firstLegBPS_= secondLegBPS_ = 0.0;
}
void Swap::performCalculations() const {
NPV_ = - Cashflows::npv(firstLeg_,**termStructure_)
+ Cashflows::npv(secondLeg_,**termStructure_);
errorEstimate_ = Null<Real>();
firstLegBPS_ = - Cashflows::bps(firstLeg_, **termStructure_);
secondLegBPS_ = Cashflows::bps(secondLeg_, **termStructure_);
}
Real Swap::firstLegBPS() const {
calculate();
return firstLegBPS_;
}
Real Swap::secondLegBPS() const {
calculate();
return secondLegBPS_;
}
最初のステップは、コンストラクターによって実行されており、2種類のCash Flowsオブジェクトと、それらを現在価値に割引く為に必要な、金利のTerm Structureオブジェクトを引数で取り、それぞれメンバー変数へ代入します。さらにコンストラクターによって生成されたSwapオブジェクト自身を、Cash FlowsオブジェクトとTerm Structureオブジェクトに対し、Observerとして登録する事も含まれています。前のセクションでも説明した通り、この登録により各Cash Flowオブジェクトは、その内容に変更があった場合は、(Observerである)Swapオブジェクトに通知し、価格の再計算を促します。
2番目のステップは、必要なインターフェース(各種メソッド)を実装する事です。isExpired()メソッドのロジックは極めて簡単で、メンバー変数に保持しているキャッシュフローについて、それぞれの支払日をチェックします。ひとつでも、支払日が到来していないキャッシュフローが存在していれば、not expiredとして情報を返します。もし未到来のキャッシュフローが全く無い場合は、その商品はexpiredとなります。その場合、setupExpired()メソッドが呼び出されます。このメソッドはベースクラスであるInstrumentクラスの持つインターフェースですが、ここでは、そのベースクラスのメソッドを呼び出すのに加え、各Cash Flows Legの現在価値を0に設定する動作をします。
最後のステップは、performCalculations()の実装です。この計算は、外部のCashflowsクラスが持つ2つの関数を呼び出して行われます。(読者の方がもし何か騙されていると感じたならば、ここでの具体例のポイントは、計算手順をどのように実装するかではなく、それをひとつのクラスの中にまとめる方法を解説するのが目的であるという点を考慮して下さい。おかしいと思われる点については、後の章で、Cashflowsクラスとそれに関連する複数の関数の説明を行いますので、そこで確認して下さい。) ひとつめの呼び出される関数は、npv( )で、上記で概略を説明したアルゴリズムを、そのまま実装したもので、将来キャッシュフローの現在価値を順番に足しあげています。変数NPV_には、2つのキャッシュフローの現在価値の差額(ネット金額)を代入します。ふたつ目の外部関数は、bps()で、両方のキャッシュフロー全体のbasis-point sensitivity(金利感応度)を計算しています。キャッシュフローLeg毎に関数が呼び出され、計算結果はそれぞれ別のメンバー変数に格納されます。計算結果についは(数値解析による価格計算を行っていないので)推定誤差がゼロであり、errorEstimate_変数は Null<Real>()-特別な浮動小数点の値で、無効な数字を表示するために使用される-に設定されます。(NaN (Not a Number)を使う方が良かったかもしれませんが、それを感知する方法を異なる環境へ移植するのが困難です。Boost::optionalを使う方法については調べてみる必要があるかも知れません)
最後のステップは、この派生クラスで追加された、計算結果を保持するメンバー変数の値を出力する手順です。ここでは、その変数に対応するメソッド(firstLegBPS()とsecondLegBPS())が実装されており、その保持された変数を出力する際、まずlazilyに(訳注:入力データの変動があった場合にのみ実行されるという意味)計算を実行するようにしています。
Swapクラスの実装は以上です。Instrumentクラスに被せてプログラムコードを書くことにより、Swapクラスでは親クラスのプログラムコードの恩恵を受けています。すなわち、入力データの変更通知があったかどうかによって、価格の再計算を行い、その値を一時保存するという動作を、Swapクラスでプログラムコードを書かなくても、行わせることができるようになっています。
2.1.4 今後の開発予定
読者の方は、上の具体例とInstrumentクラス全般について、私が定義した方法に欠点があることに気付かれたかもしれません。汎用化したにもかかわらず、我々が実装したSwapクラスは、2つのキャッシュフローが異なった通貨の場合、対応できません。Instrumentクラスについても、もしユーザーが通貨の異なる2種類のInstrumentの価値を合算しようとする場合にも同様の問題が発生します。その場合、ユーザーの方はマニュアルで、自分で一方の通貨の価格をもう一方の商品の通貨の価格に換算してから行う必要がありあす。
このような問題は、プログラムの実装におけるひとつの弱点から発生しています。すなわち、価格計算の結果をReal型(単純な浮動小数点の型)で返すようにしてしまった事です。その結果、計算結果について、実務の世界では当たり前の、通貨の情報が失われてしまいました。
この弱点については、計算結果を(Realではなく)Moneyクラスで返すようにすれば解消するかもしれません。このクラスのインスタンスは通貨の情報を持たせることができ、さらに、ユーザーのセッティング次第では、自動的に共通の通貨(例えば、会計で使う通貨)に換算する動作を加える事も可能です。
しかし、これは非常に大きな変更になり、プログラムコードの相当大きな部分に、複雑な形で影響を与えることになります。従って、この弱点への対応には、相当真剣に取り組まなければなりません。
もうひとつの(より微妙な)弱点は、Swapクラスは2種類の抽象化されたComponents(訳注:インスタンスの持つ基本情報のオブジェクト)を明確に分離できていない事です。即ち、スワップ契約を特定する情報(Cash Flows)と、それを時価評価するための市場データ(Term Structure)を明確に区分できていない事です。
その問題の解決方法は、Instrumentのインスタンスの中に、前者の情報(タームシートに書かれているスワップ契約の内容そのもの)のみを保持させ、市場データについては別の所で持たせるようにする事です。(概念的にその方がより明確である事に加え、外部の関数が、その金融商品の情報を別のフォーマットに変換するような場合-例えば、FpMLフォーマットに変換したり、あるいは戻したりするような場合-に、非常に有効になるでしょう。)(訳注:FpML:Financial Products Markup Language: XMLをベースにしたデリバティブズ取引などの情報交換の為の言語)
その方法については、次のセクションで説明します。
2.2 価格計算エンジン
このChapterの冒頭で申し上げた、Model Libraryに要求される2つの要請の内、2つ目について説明します。ある具体的な金融商品について、価格計算の方法は、1つとは限らない事、さらにユーザーは様々な理由で複数の計算方法を使う場合がある、という事です。ひとつ典型的な例として、株のヨーロピアンオプションで考えてみましょう。ある人は、Black-Scholesの公式を使って、オプションの市場価格からImplied Volatility(オプション価格に内包されているVolatility)を計算したいと考えます。あるいは、そこから、Stochastic Volatility Modelのカリブレーション(パラメータの調整)を行って、より複雑なオプションの価格計算に使ったりします。さらに、Black-Scholesの公式とFinite-difference scheme(有限差分法)を使ったアルゴリズムの計算結果を比べて、有限差分モデルの検証に使ったりします。さらには、モンテカルロシミュレーション法による複雑なオプション価格の計算において、ヨーロピアンオプションの解析解を、control variate(訳注:モンテカルロシミュレーションによる解の収束速度をアップさせる為の制御変量)として使ったりします。
従って、ひとつの金融商品について、複数の方法で価格計算ができるような仕組みにしたい訳です。その場合、当然ながらperformCalculations()メソッドを複数個実装するという方法は、望ましくありません。なぜなら、そうする為には、ひとつの金融商品について、複数のクラスを作らなければならなくなるからです。そうする為には例えば、EuropeanOptionクラスから、AnalyticEuropeanOptionクラスとMcEuropeanOptionクラスを派生させる事になりますが、この方法だと、2つの点で問題があります。まず概念的に考えて、ひとつの商品の為にふたつの箱を用意するようなものです。Gertrude Steinの言い回しを使えば、「ヨーロピアンオプションがヨーロピアンオプションであると言っているのは、ヨーロピアンオプションはヨーロピアンオプションであるという意味である。」という事です(訳注:Steinのオリジナルの表現は、“Rose is a Rose is a Rose is a Rose.”)また、使用上の問題として、run-time(プログラム実行時)に価格計算方法の変更ができないという点です。
この問題の解決方法は、Strategy Patternを使う事です。すなわち、その商品のオブジェクトに、価格計算方法をカプセル化した他のオブジェクトを持たせる事です。そのようなオブジェクトをPricing Engine(価格計算エンジン)と呼ぶことにします。ある特定の商品オブジェクトが、その商品に対応したPricing Engineを選択できるようにし、その選択したPricing Engineに、計算に必要な引数を渡し、そのEngineが価格計算を行い、そのEngineから計算結果を返させるような仕組みが想定されます。そうすると、InstrumentオブジェクトのインターフェースであるperformCalculations()の実装は、おおむね下記のようなプログラムコードになると推察されます。
void SomeInstrument::performCalculations() const {
NPV_ = engine_->calculate(arg1, arg2, ... , argN);
}
ここでは、(performCalculations()の中で呼び出される)Pricing Engineのcalculate()メソッドを、ベースクラスで仮想関数としてインターフェースを定義し、具体的な計算方法は、派生クラスとなるPricing Engineで実装する事が想定されます。
残念ながら、この方法によるアプローチは、想定通りに機能しません。問題は、calculate()を呼び出すプログラムコード(訳注:performCalculations()の実装部分)を、ベースクラスの中で1回の実装で済ませたいのに、それが出来ないという事です。なぜならベースクラスは、個別の商品毎に必要な、Pricing Engineの引数を知る余地がありません。それらはInstrumentの派生クラス毎に、数も型も千差万別です。同じ事は、Pricing Engineが返す計算結果についても言えます。例えば、金利スワップであれば、固定金利と変動金利スプレッドのFair Value(市場レートにフィットした固定金利の水準)を計算して返す事が想定されますが、一般的なヨーロピアンオプションでは、価格以外に様々なGreeks(訳注:ギリシャ文字、転じて様々なリスク感応度のこと。)を返す事も想定されます。
上記のサンプルコードように、Pricing Engineに渡す引数を明示して列挙するようなインターフェースは、望ましくない結果をもたらします。異なる金融商品に対応する、異なるPricing Engineは、当然ながら異なったインターフェースを持つはずであり、それを一本のベースクラスで表現する事はできません。そうすると、InstrumentからPricing Engineのcalculate()を呼び出すメソッドは、Instrumentの派生クラス毎に作り直さなければならなくなります。そこに大変な困難が存在します。
我々が選択した解決策は、Pricing Engineの引数や返値を、arguments とresultsという柔軟な構造体でやりとりする方法でした。この2つの構造体を派生させて、個別の金融商品(のPricing Engine)ごとに必要な“引数”と“返し値”の構造体を作り、Pricing Engineオブジェクトに保持させます。またInstrument(の派生クラスの)オブジェクトは、Pricing Engineの持つ引数と返し値の情報を、書き込んだり読み込んだりできるようにします。
Listing 2.5に、このような構造を組みこんだPricing Engineクラスの定義と、その内部クラスとして定義されたargumentsクラスと resultsクラス、さらに、補助的役割を持つGenericEngineクラス・テンプレートのコードを示します。この最後のクラスは、Pricing Engineのインターフェースの大半を実装しており、QuantLibを利用したい開発者は、個別のPricing Engineのcalculate()メソッドのみを実装すれば良いだけです。argumentsとresultsクラスには、使いやすいように(入力データの)ドロップBoxを使えるメソッドが備え付けられています。すなわちarguments::validate()メソッドは、入力データとして受け取った引数が、有効なデータ範囲の中に納まっているかどうかチェックする機能をもっています。また、results::reset()メソッドは、Pricing Engineが価格計算を開始する前に、前回計算した結果を消去します。
PricingEngine and of related classes.class PricingEngine : public Observable {
public:
class arguments;
class results;
virtual ~PricingEngine() {}
virtual arguments* getArguments() const = 0;
virtual const results* getResults() const = 0;
virtual void reset() const = 0;
virtual void calculate() const = 0;
};
class PricingEngine::arguments {
public:
virtual ~arguments() {}
virtual void validate() const = 0;
};
class PricingEngine::results {
public:
virtual ~results() {}
virtual void reset() = 0;
};
// ArgumentsType must inherit from arguments;
// ResultType from results.
template<class ArgumentsType, class ResultsType>
class GenericEngine : public PricingEngine {
public:
PricingEngine::arguments* getArguments() const {
return &arguments_;
}
const PricingEngine::results* getResults() const {
return &results_;
}
void reset() const { results_.reset(); }
protected:
mutable ArgumentsType arguments_;
mutable ResultsType results_;
};
この考え方をベースに作られた新しいクラスを使って、汎用的なperformCalculations()の実装例を示すことができます。すでに述べたStrategy パターンに加え、ここではTemplate Methodパターンも使って、Instrumentの派生クラスで足りない機能を書き加えられるようにしています。そのプログラムコードをListing 2.6に示します。インナークラスのInstrument::resultsクラスが定義されている所に注意して下さい。このクラスは、Pricing Engine::resultsクラスから派生しており、個別のInstrument用の計算結果を保持します。(Instrument;;resultsクラスは、std::mapオブジェクトをメンバー変数として保持しており、そこに追加の計算結果を保持できるようになっています。但し、それを記述したコードは下記では省略されています。)
Instrument class.class Instrument : public LazyObject {
public:
class results;
virtual void performCalculations() const {
QL_REQUIRE(engine_, "null pricing engine");
engine_->reset();
setupArguments(engine_->getArguments());
engine_->getArguments()->validate();
engine_->calculate();
fetchResults(engine_->getResults());
}
virtual void setupArguments(
PricingEngine::arguments*) const {
QL_FAIL("setupArguments() not implemented");
}
virtual void fetchResults(
const PricingEngine::results* r) const {
const Instrument::results* results =
dynamic_cast<const Value*>(r);
QL_ENSURE(results != 0, "no results returned");
NPV_ = results->value;
errorEstimate_ = results->errorEstimate;
}
template <class T> T result(const string& tag) const;
protected:
boost::shared_ptr<PricingEngine> engine_;
};
class Instrument::results
: public virtual PricingEngine::results {
public:
Value() { reset(); }
void reset() {
value = errorEstimate = Null<Real>();
}
Real value;
Real errorEstimate;
};
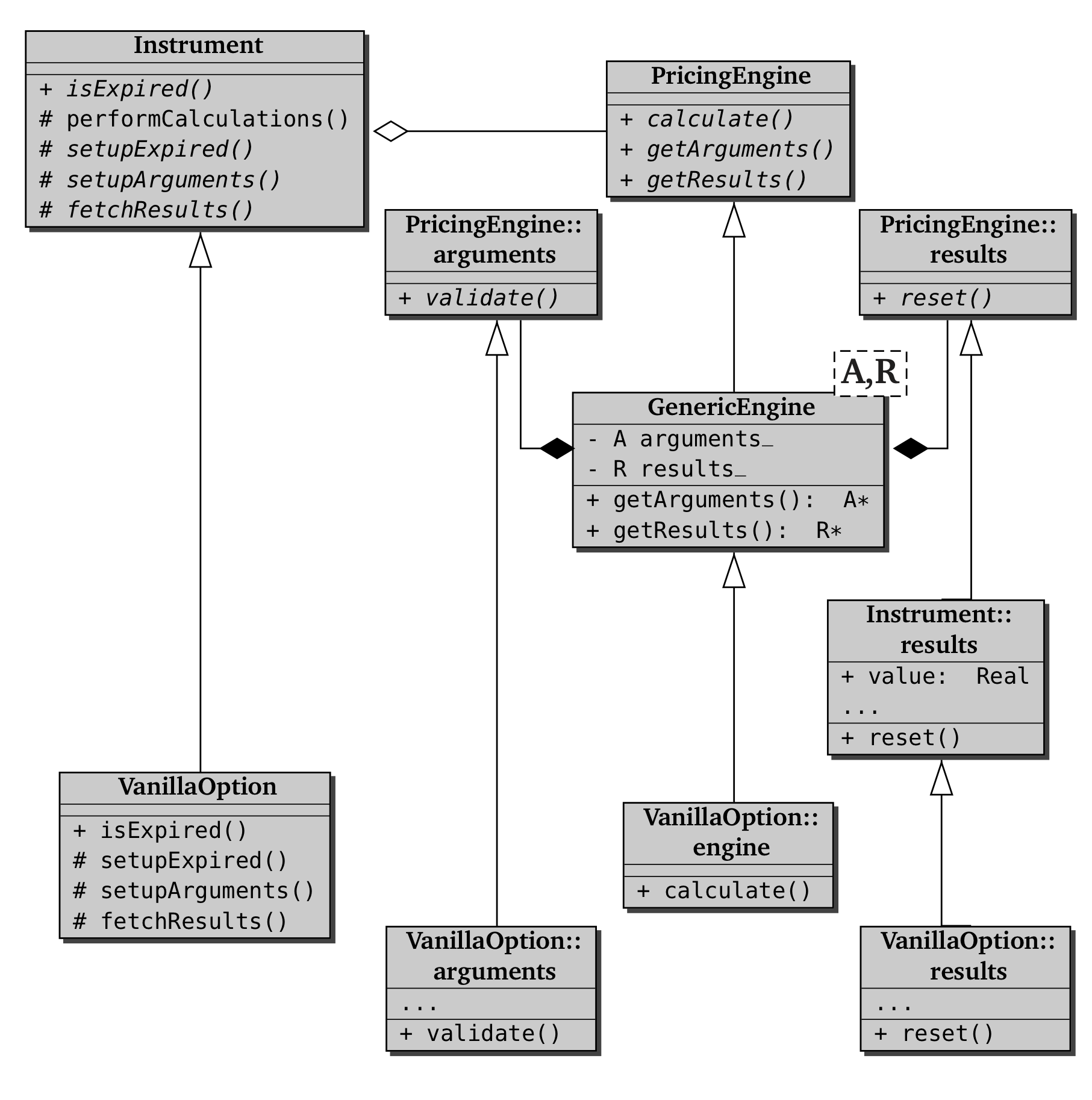
performCalculations()メソッドの実際の動作は、それを補助する複数のクラス(すなわち、Instrument, Pricing Engine、arguments およびresultsの各クラス)に作業分担されています。そのような補助の動作(次の段落で説明)を理解するには、下記のFigure 2.2:UMLシーケンス図(Unified Model Language Sequence)をよく見て下さい。さらに、各クラス間の静的な関係はFigure 2.3を参照下さい。
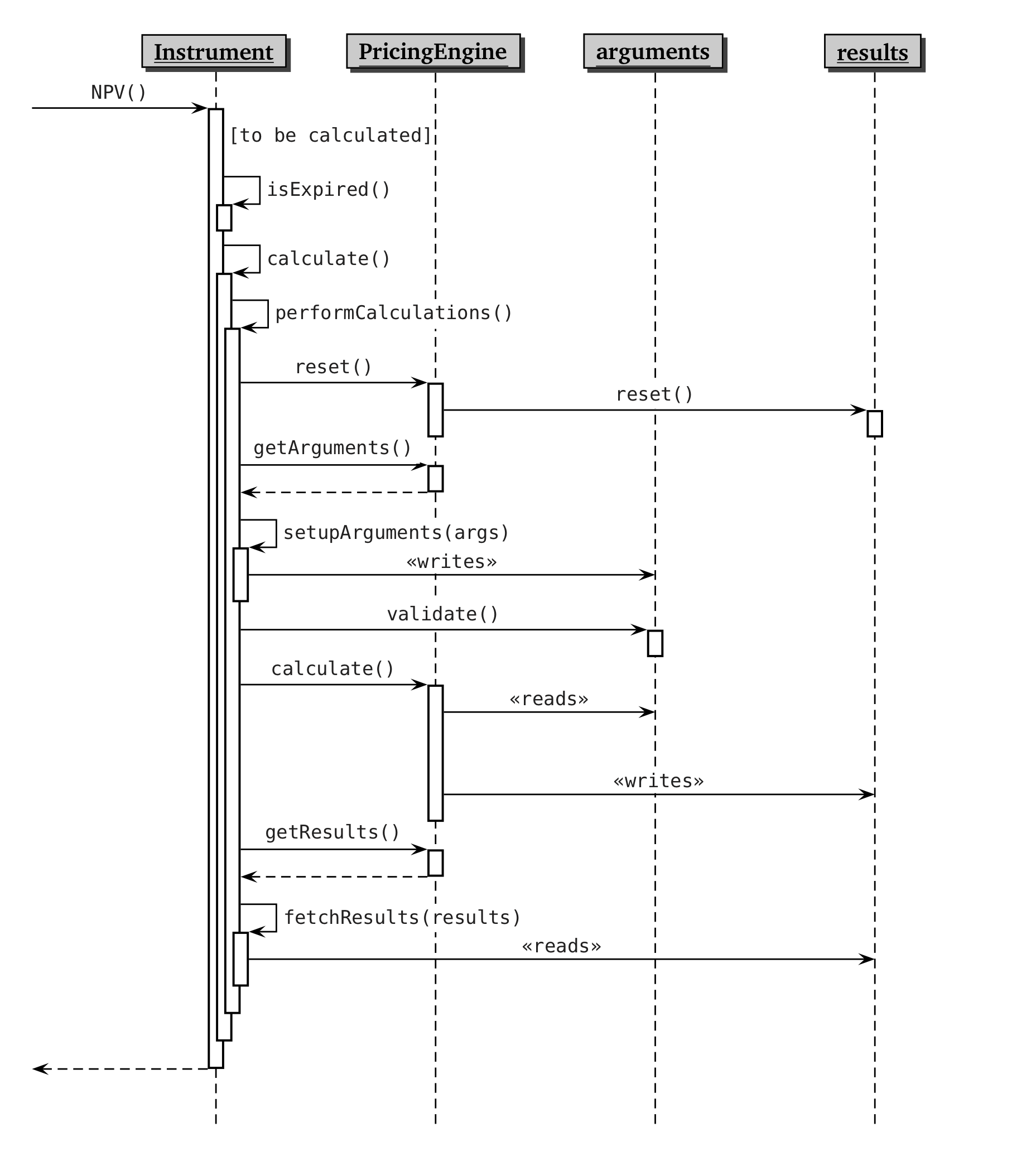
Instrument, PricingEngine, and related classes including a derived instrument class. InstrumentクラスのNPV( )メソッドを呼び出すと(もしその商品が満期を迎えていなくて、価格やリスク量を計算する必要がある状態にあるのなら)、そこからさらにperformCalculations()を呼び出します。そこからInstrumentオブジェクトとPricing Engineとの間の連携が始まります。まず最初に、Instrumentは、Pricing Engineそのものが存在しているかどうかチェックし、もしそうでないなら計算をそこでストップします。もしPricing Engineが見つかったなら、Instrumentは、Pricing Engineに対し、データのリセットを指令します。その指令は、reset( )メソッドを使って、そのInstrument固有のresults構造体に伝達され、その構造体の中の古いデータを消去し、新しい計算結果を保持できる状態にします。
ここで、Template Methodパターンが登場します。Instrumentオブジェクトは、Pricing Engineオブジェクトに対し、arguments構造体を渡すよう要求し、Pricing Engineは、その構造体のポインターを返します。そのポインターはInstrumentのsetupArguments()メソッドに渡されますが、このメソッドがTemplate Methodパターンにおける可変部分の役割を果たします。このメソッドは、まず渡された引数(arguments構造体)がその商品に適合するものかどうかチェックし、もしそうなら、そのarguments構造体に、自分のメンバー変数を代入していきます。最後に、arguments構造体は、入力されたデータが有効範囲内のものかどうかをvalidate()メソッドを使って行います。
この段階で、Strategy Patternの用意ができました。引数が準備できたので、Pricing Engineオブジェクトは、その商品の価格計算を、(そのPricing Engine独自のアルゴリズムを実装した)calculate()メソッドを使って実行するよう要求されます。Pricing Engineは、argumentsから受け取った入力データを使って計算を実行し、計算結果をresults構造体へ書き込みます。
Pricing Engineが以上の動作を完了した後、実行手順はInstrumentオブジェクトに戻り、Template Methodパターンが引き続き読み解かれます。すなわちfetchResults()メソッドが呼び出され、Pricing Engineに対しresults構造体を渡すよう要求し、そのオブジェクトがDowncastされ、そのメンバー変数へのアクセスを可能にし、その内容を自らのメンバー変数にコピーします。Instrumentベースクラスは、すべての商品に共通のresults構造体をデフォールトで定義しており、各派生クラスで、さらに追加の計算結果を保有するよう拡張できます。
2.2.1 例: シンプルなオプション
ここで、ひとつ例を示す必要があるでしょう。一言だけ注意をしておくと、QuantLibの中にプレインバニラ- すなわち単純な株のコール・プット オプションで、行使タイミングがヨーロピアンやアメリカンやバーミューダタイプ - のオプションクラスは、深いクラス階層の奥底に存在します。ベースクラスとしてInstrumentクラスがあり、そこからまずOptionクラスが派生し、さらに対象資産が一個のオプションを定義するOneAssetOptionクラスが派生し、さらに一つ二つのクラスを経由して最終的にVanillaOptionクラスに行きつきます。
この様に、多くの層を経由させた理由は当然あります。OneAssetOptionクラスの定義は他のオプション、例えばアジアンオプションでも使えますし、Optionクラスは、様々なタイプのバスケットオプションに使えます。残念ながら、そのせいで、単純なオプションの価格計算のプログラムコードが、多層な階層に分散されており、解りやすく説明する為の実例としては使いにくいものになっています。そこで、ここでの説明だけの為に、実装内容はQuantLibのLibraryと同じものですが、Instrumentクラスから直接派生させた仮想のVanillaOptionクラスを作り、中間にある派生クラスの実装内容もその中に取り込んでしまいました。
Listing 2.7にこの仮想VanillaOptionクラスの実装内容を示します。まずInstrumentベースクラスのインターフェースで実装が必要なメソッドを宣言し、次にこのクラスで追加された計算結果のデータ(名前にある通り、オプションのGreeks(感応度))を読みだせるメソッド群を宣言しています。前の章で指摘した通り、それらのデータはmutableで宣言されており、論理的にconst宣言されたcalculate()メソッドによっても、値を変更出来ます。
VanillaOption class.class VanillaOption : public Instrument {
public:
// accessory classes
class arguments;
class results;
class engine;
// constructor
VanillaOption(const boost::shared_ptr<Payoff>&,
const boost::shared_ptr<Exercise>&);
// implementation of instrument method
bool isExpired() const;
void setupArguments(Arguments*) const;
void fetchResults(const Results*) const;
// accessors for option-specific results
Real delta() const;
Real gamma() const;
Real theta() const;
// ...more greeks
protected:
void setupExpired() const;
// option data
boost::shared_ptr<Payoff> payoff_;
boost::shared_ptr<Exercise> exercise_;
// specific results
mutable Real delta_;
mutable Real gamma_;
mutable Real theta_;
// ...more
};
class VanillaOption::arguments
: public PricingEngine::arguments {
public:
// constructor
arguments();
void validate() const;
boost::shared_ptr<Payoff> payoff;
boost::shared_ptr<Exercise> exercise;
};
class Greeks : public virtual PricingEngine::results {
public:
Greeks();
Real delta, gamma;
Real theta;
Real vega;
Real rho, dividendRho;
};
class VanillaOption::results : public Instrument::results,
public Greeks {
public:
void reset();
};
class VanillaOption::engine
: public GenericEngine<VanillaOption::arguments,
VanillaOption::results> {};
VanillaOptionクラスは、自分自身に必要なメンバー変数やメソッドの他に、いくつかのアクセサリークラスを宣言しています。すなわち、このクラス特有の(内部クラスとなる)argumentsと results構造体、および基本となるPricingEngineクラスです。これらのクラスはすべて、Optionクラスとの関係性を明確にするために、VanillaOptionクラスの内部クラスとして定義されています。それらのインターフェースについても、上記Listingの中で示されています。
これらのアクセサリークラスについて、2点コメントします。一点目は、この例を紹介した際に私が述べたことに反し、(クラス内クラスとして、このクラス特有の計算結果を保持するために定義されたはずの)VanillaOption::resultsクラスの中で、メンバー変数を全く宣言していません。これは、実装内容の詳細な仕組みを際立たせる為に、わざとそうしました。プログラム開発者は、いくつかの商品に共通するような計算結果を保持する構造体を定義したいと考えるかもせれません。そのような構造体は、派生クラスを作ることにより再利用が可能になるからです。Greeks構造体の例がまさにそれです。(訳注:様々なオプションで共通のリスク感応度の値を、Greeksという名前の構造体で定義しておけば、オプション毎にresults構造体のメンバー変数を定義せず、Greeks構造体を再利用すれば簡単で済む。)従って、このクラス(VanillaOption::results)は、Greeks構造体とInstrument::resultsクラスから派生させて、最終的な構造が構築されています。その際に、かの悪名高い菱形継承を避ける為、(Greeks::resultsもInstruments::resultsも)PricingEngine::resultsクラスからの仮想継承にしなければなりません。(継承のダイアモンドについては、例えば巻末(Stroustrup, 2013)参照)(訳注:VanillaOption::resultsは、Instrument::resultsとGreeks::resultsの2つのベースクラスから派生しているが、この2つのベースクラスは、いずれもPricingEngine::resultsから派生している。この場合、仮想継承にしておかないと、派生クラスからベースクラスのメソッドを呼び出す時、2つのルートが発生して曖昧さが発生する。)
二点目は、このVanillaOptionクラス特有のPricing Engineクラスは、テンプレートクラスであるGenericEngineから直接継承し、適切なargumentsクラスとresultsクラスを使ってインスタンスを生成するだけで十分であったという事です。以下に説明するとおり、派生クラスは、ただ単にcalculate()メソッドを実装するだけで十分です。
さあ、いよいよVanillaOptionクラスの実装内容(Listing 2.8)の説明に移りたいと思います。
VanillaOption class.VanillaOption::VanillaOption(
const boost::shared_ptr<StrikedTypePayoff>& payoff,
const boost::shared_ptr<Exercise>& exercise)
: payoff_(payoff), exercise_(exercise) {}
bool VanillaOption::isExpired() const {
Date today = Settings::instance().evaluationDate();
return exercise_->lastDate() < today;
}
void VanillaOption::setupExpired() const {
Instrument::setupExpired();
delta_ = gamma_ = theta_ = ... = 0.0;
}
void VanillaOption::setupArguments(
PricingEngine::arguments* args) const {
VanillaOption::arguments* arguments =
dynamic_cast<VanillaOption::arguments*>(args);
QL_REQUIRE(arguments != 0, "wrong argument type");
arguments->exercise = exercise_;
arguments->payoff = payoff_;
}
void VanillaOption::fetchResults(
const PricingEngine::results* r) const {
Instrument::fetchResults(r);
const VanillaOption::results* results =
dynamic_cast<const VanillaOption::results*>(r);
QL_ENSURE(results != 0, "wrong result type");
delta_ = results->delta;
... // other Greeks
}
Real VanillaOption::delta() const {
calculate();
QL_ENSURE(delta_ != Null<Real>(), "delta not given");
return delta_;
}
コンストラクターは、具体的なオプションの条件を決める複数のオブジェクトを引数として取ります。これらについては後々の章またはAppendix Aで説明します。今の段階で簡単に説明しておくと、(引数のひとつ)payoffオブジェクトはストライク(行使価格)とオプションタイプ(コールかプットか)の情報を持ち、exerciseオブジェクトは行使日と行使タイプ(ヨーロピアン、アメリカン、バーミューダン)の情報を持ちます。引数で渡されたこれらオブジェクトのインスタンスは、メンバー変数に保持されます。ここでは、市場データの情報は渡されていない点に注意して下さい。市場データは別の所で渡されています。
オプション期日到来に関するメソッドは極めて単純です。isExpired()メソッドは、最終オプション行使日が過ぎていないかどうかチェックし、setupExpired()メソッドは、ベースクラスで実装されたメソッドを呼び出すと同時に、いくつかのメンバー変数(Greeks)を0にセットします。
setupArguments() とfetchResults()メソッドの実装内容はもう少し複雑です。setupArguments()メソッドは、まず引数として受け取った汎用arguments(ここではPricingEngine::arguments*)のポインターをVanillaOption::arguments型へダウンキャスト(型変換)します。もし、型が合っていない場合は、そこで例外処理に飛び、型が合っている場合は動作が継続します。次に。VanillaOptionオブジェクトのメンバー変数は、逐語的に(型変換後の)argumentsオブジェクトのメンバー変数にコピーされていきます。しかし、別々のPricing Engineで、同じような計算(例えば、日付を時間に換算する計算)が必要な場合があるかも知れません。そういった場合は、setupArguments()のメソッドの中で一回実装するだけで済みます。
fetchResults()メソッドは、setupArguments()メソッドと対を成すものです。このメソッドも、引数として受け取ったresultsオブジェクトのポインターをダウンキャスト(型変換)する事から始まります。型の適合性の確認を行った後、resultsオブジェクトの内容を自分のメンバー変数にコピーしていきます。
シンプルではありますが、上記のような実装で、実際に金融商品を稼働することができます。稼働するとは、Pricing Engineを備えれば、必要な価格計算ができるという事です。そのようなPricing Engineの例を、Black-Scholes-Mertonによるヨーロピアンオプションの解析解モデルで実装したプログラムコードをListing 2.9に示します。
VanillaOption class.class AnalyticEuropeanEngine
: public VanillaOption::engine {
public:
AnalyticEuropeanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&
process)
: process_(process) {
registerWith(process);
}
void calculate() const {
QL_REQUIRE(
arguments_.exercise->type() == Exercise::European,
"not an European option");
shared_ptr<PlainVanillaPayoff> payoff =
dynamic_pointer_cast<PlainVanillaPayoff>(
arguments_.payoff);
QL_REQUIRE(process, "Black-Scholes process needed");
... // other requirements
Real spot = process_->stateVariable()->value();
... // other needed quantities
BlackCalculator black(payoff, forwardPrice,
stdDev, discount);
results_.value = black.value();
results_.delta = black.delta(spot);
... // other greeks
}
private:
shared_ptr<GeneralizedBlackScholesProcess> process_;
};
コンストラクターは、Black Scholesモデルの確率過程を記述するオブジェクトを引数として取ります。このオブジェクトは、市場データ(対象資産とその現在価値、リスクフリー金利、配当利回り、ボラティリティ)の情報を保持しており、それらをメンバー変数にコピーします。ここでも又、実際の計算過程は、他のクラス(BlackCalculatorクラス)のインターフェースの奥に隠れてしまいましたが、プログラムコードを見れば、計算に必要なデータのやり取りの様子はわかると思います。
calculate()メソッドは、まずいくつかの事前データチェックからスタートします。これには少し驚かれるかもしれません。なぜなら、これらのデータはcalculate()がスタートする時点ですでにチェック済のはずだからです。しかし、どんなPricing Engineでも、計算をスタートする前に、さらなるデータチェックをする場面があるかもしれません。上記のプログラムでは、オプションがヨーロピアンか否か、payoffが単純なCallまたはPutなのか、というチェックを行い、後者の手続きはさらに、必要とするクラスに型変換するプロセスまでも含みます。(boost::dynamic_pointer_castは、shared pointerの為のdynamic_castと同じです。)
このメソッドのプログラムコードの真中あたりに、Pricing Engineが引数から必要な情報を取り出している部分があります。ここでは、対象資産の現在価格やその他の価格計算に必要な情報(対象資産のオプション期日での先渡し価格、満期時におけるDiscount Factor)などです。(QuantLibのソースコードにすべて記述されているので、確認して下さい)
最後に、計算アルゴリズムが実行され、計算結果がresults構造体の該当箇所にそれぞれコピーされます。これで、calculate()メソッドと事例の紹介を終わります。